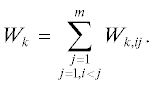Журнал физической химии, 2019, T. 93, № 4, стр. 627-631

Одним из открытых вопросов современной теории разделения многокомпонентных изотопных и молекулярных смесей является поиск универсального потенциала разделения, который бы стал полным аналогом соответствующего потенциала, широко используемого в случае разделения бинарных смесей. Основная идея использования потенциала разделения в бинарном случае заключается в том, что данная функция позволяет, опираясь, только на внешние параметры разделительной установки (концентрации на входе и выходах) охарактеризовать “разделительные усилия”, связанные с получением в ней требуемого продукта (например, смеси обогащенного урана). На практике это позволяет ввести единую шкалу эффективности разделения, не учитывая специфики конкретного метода, используемого для решения задачи получения продукта с заданными характеристиками, что оказалось крайне удобным для проведения практических, в том числе, экономических расчетов [1].

Разделительный потенциал для бинарной смеси имеет вид:

где x – концентрация “ключевого” компонента.

Данный вид потенциала получен в классической теории Пайерлса–Дирака на основе следующих аксиом:

• разделительный потенциал Ф(x) является только функцией концентрации смеси;

• разделительная способность отдельного элемента

(n – количество видов смеси, получаемых в результате процесса разделения исходной смеси компонентов, индексы 0 и j определяют соответственно параметры исходной и обогащенных смесей: q⁰ и q^j – количественные потоки исходной и обогащенных смесей в единицу времени) не зависит от концентрации смеси [2, 3].

Выражение (1) строго обосновывает теория “несмешивающего” (идеального) каскада, который при определенных условиях (малое или большое симметричное разделение на ступенях) соответствует оптимальным условиям разделения – минимуму числа разделительных элементов (минимуму суммарного потока) для выполнения заданной программы разделения [2–4]. Функцию (1) можно считать универсальной и общепринятой характеристикой процесса разделения бинарной смеси.

Однако в теории разделения многокомпонентных смесей единая и аналогичная бинарному случаю трактовка разделительного потенциала многокомпонентной смеси так и не появилась. Тем не менее, попытки введения подобной величины предпринимались в [5–16]. Большинство из предложенных вариантов введены либо из интуитивных соображений, либо с использованием аксиоматических предположений (в частности, новой трактовки аксиом Пайерлса–Дирака, или различной интерпретации процесса разделения смеси в виде поэтапного независимого бинарного разделения смесей, состоящих из пар компонентов или их совокупностей и т.п.) [16]. При таком подходе остаются открытыми следующие вопросы:

• физическое обоснование введенных потенциалов;

• практическая ценность введенных потенциалов;

• причина отсутствия единой согласованной теории потенциала разделения многокомпонентных смесей.

Попытка ответить на первый вопрос предпринята авторами работ [17, 18] на примере так называемого “обобщенного” потенциала

(придерживаясь авторских обозначений ${{x}_{j}}$ – концентрация j-го компонента, m – число компонентов смеси), предложенного П.Г. Кузнецовым и др. в 1963 году [5].

Вывод и интерпретация этого соотношения, согласно работам [17, 18], основаны на следующих предположениях:

• работа разделения, характеризующая “усилия”, совершаемые каскадом при разделении смеси, W_k может быть представлена как сумма

где W_k,ij – относится к каждой, по терминологии авторов, “выбранной” паре компонентов, составляющих многокомпонентную смесь;

• эффективность каскада определяется, “симметричностью” работы его ступеней, причем авторы предполагают возможность несмешивания на входе в каждую ступень по нескольким относительным концентрациям из выбранных пар компонентов.

Ввиду того, что сделанные авторами предположения и утверждения представляются, по нашему мнению, недостаточно корректными, приведем наши замечания и точку зрения по данному вопросу.

1. Формула $\sum {{{W}_{{k,ij}}}} $ подразумевает, очевидно, что разделение многокомпонентной смеси происходит в виде независимого бинарного разделения смеси состоящей из пар компонентов. Поскольку каждый компонент смеси “взаимодействует” с каждым из остальных (m – 1) компонентов, работу разделения четырехкомпонентной смеси (A,B,C,D – компоненты смеси) [17, 18] логично представлять в виде:

Однако, в работе [18] о $\sum {{{W}_{{k,ij}}}} $ говорят как о сумме “выбранных” пар компонентов смеси, не приводя принцип, согласно которому производится “выбор” этих пар. При этом работа разделения четырехкомпонентной смеси, представляется в виде:

т.е. “выбранными” оказываются две пары (AB,CD) из шести возможных. В результате остается не ясным критерий выбора таких пар и обоснованность данного предположения в принципе.

2. Логично предположить, что в [17, 18] авторы располагают компоненты четырехкомпонентной смеси в последовательный ряд: A(1)–B(2)–C(3)–D(4) согласно возрастанию (или убыванию) “активности” компонентов. В этом случае для относительных коэффициентов разделения будут справедливы следующие соотношения: ${{\alpha }_{{ij}}} > 1,$ ${{\alpha }_{{ij}}} = \alpha _{{ji}}^{{ - 1}}$ при $i < j$ и ${{\alpha }_{{ii}}} = 1$. Учитывая очевидное соотношение ${{\alpha }_{{ij}}} = {{\alpha }_{{il}}}{{\alpha }_{{lj}}}$ можно утверждать, что приведенные в [18] равенства ${{\alpha }_{{BD}}} = {{\alpha }_{{CA}}}$ $({{\alpha }_{{24}}} = {{\alpha }_{{31}}})$ и ${{\alpha }_{{AD}}} = {{\alpha }_{{CB}}}$ $({{\alpha }_{{14}}} = {{\alpha }_{{32}}})$ не могут быть выполнены.

В случае разделения многокомпонентных смесей математическая модель массопереноса компонентов в каскаде представляет собой систему дифференциальных уравнений (для “тонкого” разделения) [19], либо систему разностных уравнений (для случая немалых коэффициентов разделения ${{\alpha }_{{ij}}}$) [11, 20, 21] анализ которых приводит к выводу о невозможности построения трехпоточного каскада для разделения многокомпонентных смесей, который аналогично идеальному каскаду для бинарной смеси имел бы “несмешивание” по всем концентрациям на входах в разделительные ступени одновременно. Другими словами невозможность введения универсального разделительного потенциала для многокомпонентной смеси является следствием отсутствия в этом случае “эталонного” каскада, роль которого при разделении бинарных смесей играет идеальный каскад. Одновременно множественность возможных граничных условий в задаче оптимизации (минимум суммарного потока), решение которой в общем случае возможно только численными методами [22]) также свидетельствует об отсутствии универсальной характеристики для произвольного процесса разделения. Поэтому использование полученных из формальных соображений физически необоснованных соотношений для различного потенциала (включаю потенциал П.Г. Кузнецова и др.) в расчетах и интерпретации таких характеристик как термодинамическая работа разделения, суммарный поток “наилучшего” каскада, на наш взгляд, нецелесообразно.

В работе [18] представлена процедура расчета суммарного потока каскада с постоянными относительными коэффициентами разделения ${{\alpha }_{{ij}}}$ с последующим использованием полученного результата для обоснования соотношения, определяющего разделительные усилия, совершаемые при переработке многокомпонентной смеси. В процессе расчета использовано условие, что “симметричность” разделения на ступенях каскада возможна более, чем для одной пары компонентов в разделяемой смеси.

В этой связи следует отметить, что в случае постоянства коэффициентов разделения ${{\alpha }_{{ij}}}$ система уравнений переноса имеет аналитическое решение, связывающее “внешние” и “внутренние” параметры. Этому решению отвечает так называемый “квазиидеальный” каскад [11, 20, 21]. Другими словами, нет необходимости рассчитывать такой каскад постепенно, пользуясь соответствующими реккурентными соотношениями, как это сделано в работе [18]. В частном случае это решение допускает построение каскада с отсутствием смешивания по одной (и только одной) паре выбранных “ключевых” компонентов ${{R}_{{nk}}} = {{{{x}_{n}}} \mathord{\left/ {\vphantom {{{{x}_{n}}} {{{x}_{k}}}}} \right. \kern-0em} {{{x}_{k}}}}$ (n, k – номера ключевых компонентов) на входе в ступени. Подобный каскад получил название R-каскада или MARC (Matched Abundance Ratio Cascade) [11, 20, 21, 23, 24].

Невозможность осуществления одновременно несмешивания по нескольким относительным концентрациям (например, по ${{R}_{{{\text{AB}}}}}$ и ${{R}_{{{\text{CD}}}}}$ в [18]) следует как из строгого анализа системы уравнений переноса, так из очевидного соображения: при разделении m-компонентной смеси (число независимых уравнений, описывающих перенос компонентов (m–1)) единственным параметром, обеспечивающим “симметричность” разделения на ступени является функция распределения потока питания ступеней L(s) (s – номер ступени), которая для каждой пары “ключевых” компонентов будет иметь свой индивидуальный функциональный вид.

В работах [15, 16] проведено исследование применимости различных форм разделительного потенциала (включая потенциал П.Г. Кузнецова и др.) для оценки эффективности разделения многокомпонентных смесей в многоступенчатых установках (каскадах). Результаты численных экспериментов по оптимизации каскадов показали, что каждый из потенциалов соответствует какому-то частному случаю и не может быть использован в качестве универсальной характеристики для произвольного процесса разделения.

Таким образом, на наш взгляд потенциал

как и предложенные к настоящему моменту другие варианты разделительных потенциалов, не может быть использован как полноценный аналог соответствующей функции, широко применяемой в случае разделения бинарных смесей.

В заключение приведем случай, когда введение “локального” разделительного потенциала может быть строго обосновано [25]. Это возможно осуществить с использованием модели R-каскада, которая обладает следующими свойствами:

• если компоненты смеси пронумерованы от 1 до m, так что ${{\alpha }_{{ik}}} > 1$ при i < k, то при k = n + 1 на одном конце каскада (в потоке $q{\kern 1pt} '$) обогащаются все компоненты с номерами от 1 до n, а на другом (в потоке $q{\kern 1pt} ''$) – все компоненты с номерами от n + + 1 до m. Варьирование номера n-го компонента позволяет решить (в существующих пределах) проблему обогащения смеси промежуточным компонентом;

• относительная концентрация ${{R}_{{nk}}}$ зависит от номера ступени s следующим образом:

где f – номер ступени, в которую подают поток питания q, N – номер ступени, из которой отбирают поток $q{\kern 1pt} '$; $R_{{nk}}^{0}$ – относительная концентрация в потоке питания q; $R_{{nk}}^{'}$ – относительная концентрация в потоке $q{\kern 1pt} '$; $R_{{nk}}^{{''}}$ – относительная концентрация в потоке $q{\kern 1pt} ''$. Для всех остальных ${{R}_{{ik}}}$ ($i \ne n$) соотношение (6) не выполняется;

• теория R-каскада позволяет получить ответ на вопрос о соответствии его характеристик характеристикам так называемого “оптимального” каскада, определяемого, как правило, путем численной оптимизации параметров по критерию $\sum {L = \min } $ при заданных концентрациях целевого компонента в выходных потоках $(x_{n}^{*},x_{n}^{{''}})$ [22]. При соответствующем выборе опорного компонента $(k = {{k}_{{{\text{opt}}}}})$ суммарный поток R-каскада и суммарный поток “оптимального” каскада с точностью до долей процента совпадают [26, 27]. Другими словами, параметры наилучшего R-каскада для поставленной задачи можно считать оптимальными.

Формула для суммарного потока R-каскада выглядит следующим образом [21]:

где $x_{j}^{'},\;x_{j}^{{''}},\;x_{j}^{0}$ – концентрации j-го компонента в потоках $q{\kern 1pt} '$, $q{\kern 1pt} ''$ и q соответственно; ${{\beta }_{j}} = \frac{{{{\alpha }_{{jk}}}}}{{\alpha _{{nk}}^{{1/2}}}}$.

Используя (6), (7) находят распределение потока питания ступеней и концентрации компонентов по ступеням каскада, а также величину суммарного потока $J = \sum\nolimits_{s = 1}^N {L(s)} $ в каскаде [21]. Если соотношение (7) переписать в виде

то (8) целесообразно придать следующий смысл: его правая часть ${{W}_{k}}$ = $q{\kern 1pt} '\Phi (\vec {x}')$ + $q{\kern 1pt} ''\Phi (\vec {x}{\kern 1pt} '')$ – $q\Phi ({{\vec {x}}^{0}})$ представляет собой величину “полезной” разделительной работы в единицу времени, выполняемой каскадом при обогащении целевого компонента с номером n до заданных концентраций $x_{n}^{'}$ и $x_{n}^{{''}}$ в потоках $q{\kern 1pt} '$ и $q{\kern 1pt} ''$ соответственно. Левая часть (8) представляет собой сумму разделительных способностей (мощностей) ступеней каскада, каждая из которых “настроена” на преимущественное обогащение целевого компонента при его заданных концентрациях на концах каскада.

Для слабого обогащения (${{\varepsilon }_{{ij}}} = {{\alpha }_{{ij}}} - 1 \ll 1$ ) соотношение (9) и (10) преобразуются к виду

При m = 2 (случай бинарной смеси) (9) сводится к классической формуле $\Phi (x)$ = $(2x - 1)\ln \left( {\frac{x}{{1 - x}}} \right)$.

Разделительный потенциал (9), не являясь универсальной характеристикой, соответствует частной (но для практики важной задачей выделения целевого компонента при его заданных концентрациях на концах каскада (в потоках $q{\kern 1pt} '$ и $q{\kern 1pt} ''$)).

Вопрос о взаимосвязи разделительного потенциала (9) с термодинамическим потенциалом ${{\Phi }_{s}}(\vec {x})$ = $\sum\nolimits_{j = 1}^m {{{x}_{j}}\ln {{x}_{j}}} $ открыт. Возможно на него удастся ответить, применив подход, используемый в [2, 3, 28].

В завершение необходимо подчеркнуть, что ни один из предложенных на сегодняшний день потенциалов разделения для многокомпонентных смесей, в отличие от их аналога для бинарных смесей, не позволяет решить главную задачу, а именно, оценить полное число разделительных элементов в каскаде без расчета и оптимизации его параметров.

Таким образом, следует отметить, что “обобщенный” потенциал разделения $\Phi (\vec {x})$ = = $\Phi ({{x}_{1}},...,{{x}_{m}})$ = $\sum\nolimits_{j = 1}^m {{{x}_{j}}\ln \left( {\frac{{{{x}_{j}}}}{{1 - {{x}_{j}}}}} \right)} $, как и другие предложенные к настоящему моменту варианты разделительных потенциалов в случае многокомпонентных смесей, не может выступать в качестве полноценного аналога соответствующей функции, широко применяемой в случае разделения бинарных смесей.