1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 93, № 4, 2019

Журнал физической химии, 2019, T. 93, № 4, стр. 485-496

Учет межмолекулярных колебаний в термодинамических функциях жидкого инертного газа

Ю. К. Товбин a, b, *

a Российская академия наук, Институт общей и неорганической химии им. Н.С. Курнакова
Москва, Россия

b Государственный научный центр Российской Федерации “Научно-исследовательский физико-химический институт им. Л.Я Карпова”
Москва, Россия

* E-mail: tovbin@nifhi.ru

Поступила в редакцию 27.06.2018

Полный текст (PDF)

Аннотация

Рассмотрены способы расчета межатомных колебаний в жидкости на примере инертного газа. Использована дискретно-континуальная теория в рамках модели решеточного газа. Сформулирован подход для построения выражений для статистических сумм колебательных движений атомов жидкости, постоянно находящихся в связанном состоянии. Получены уравнения равновесного распределения молекул в объеме для концентраций и парных функций распределений в квазихимическом приближении, учитывающем эффекты прямых корреляций. Выделены два подхода к описанию локальных относительных смещений связанных молекул с различной величиной амплитуды при условии предварительного установления локального равновесия по импульсу по сравнению с локальным равновесием по массе. Полученные уравнения сопоставлены с ранее предложенными подходами.

Ключевые слова: связанные состояния молекул, межмолекулярные колебания, жидкость, инертный газ, термодинамические характеристики, модель решеточного газа

Одна из проблем расчета термодинамических функций жидкого состояния простых веществ и смесей – учет влияния межмолекулярных колебаний молекул и способы их интерпретации. В жидкой фазе все частицы находятся в связанном состоянии, и колебания – один из видов их теплового движения. Они необходимы для интерпретации инфракрасных спектров и комбинационного рассеяния, для анализа динамических задач об элементарных реакциях в жидкой фазе и процессов массо- и теплопереноса. Экспериментальные данные о колебательных спектрах могут служить независимым источником информации о межмолекулярных взаимодействиях, и, естественно, необходимы для расчета и интерпретации термодинамических функций.

Потенциальные функции межмолекулярного взаимодействия простых жидкостей имеют радиус потенциала взаимодействия, превышающий их собственный размер в несколько раз. Потенциальная энергия межчастичных взаимодействий Upot(r) определяет главный вклад в термодинамические функции плотных фаз по сравнению с их средней кинетической энергией 〈Еkin〉.

Для описания жидкого состояния привлекаются все методы статистической физики: теоретические построения уравнений для распределений молекул (континуальные интегральные уравнения и дискретная модель решеточного газа) и стохастические методы Монте-Карло и молекулярной динамики.

Процедура построения всех интегродифференциальных и интегральных уравнений (ИУ) жидкого состояния на основе цепочки Боголюбова–Бора–Грина–Киркуда–Ивона (ББГКИ) [1–6] показывает, что первым этапом перехода к функциям распределений (ФР) от статистической суммы системы QN с полной энергией (гамильтонианом) в виде

(1)
$H = \sum\limits_{1 \leqslant i \leqslant N} {\frac{{{{{\mathbf{p}}}_{i}}^{2}}}{{2{{m}_{i}}}}} + \sum\limits_{1 \leqslant i < j \leqslant N} {{{E}_{{ij}}}({\text{|}}{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}{\text{|}})} $
является интегрирование по импульсам всех частиц и отделение конфигурационного интеграла
(2)
$\begin{gathered} {{Q}_{N}}(conf) = \int\limits_V { \cdot \cdot \cdot \int\limits_V {d{{r}_{1}}} } \cdot \cdot \cdot d{{r}_{N}} \times \\ \times \;\exp \left( { - \beta \sum\limits_{1 \leqslant i < j \leqslant N} {{{E}_{{ij}}}({\text{|}}{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}{\text{|}})} } \right). \\ \end{gathered} $
Здесь pi и mi – импульс и масса i-й частицы, 1 ≤ i ≤ N, N – число частиц системы, Eij – энергия парного взаимодействия частиц с координатами ri и rj. В итоге статистическая сумма системы QN записывается как
(3)
$\begin{gathered} {{Q}_{N}} = \langle \exp [ - \beta H(\{ p,r\} )]\rangle = \\ = {{\left( {\frac{{2\pi mkT}}{{{{h}^{2}}}}} \right)}^{{3N/2}}}\frac{{{{Q}_{N}}(conf)}}{{N!}}, \\ \end{gathered} $
где h – постоянная Планка, β = (kBT)–1, kB – постоянная Больцмана; сомножитель ${{\left( {2\pi mkT} \right)}^{{3/2}}}$ в степени числа частиц N представляет собой результат интегрирования по импульсам одной поступательно движущейся частицы в объеме системы V при заданной температуре Т; фигурные скобки означают полный список всех импульсов и координат частиц.

После отделения импульса конфигурационный интеграл ${{Q}_{N}}(conf)$ не может содержать колебания – они описываются тем же исходным гамильтонианом (1) при разложении смещений в окрестности положений равновесия частиц и проведении интегрирования уравнений движения Ньютона в окрестности этих равновесий. Таким образом, в цепочке ББГКИ и ИУ отражаются межмолекулярные смещения, которые могут быть реализованы в широком диапазоне относительных смещений, а колебательные движения как самостоятельный тип движения специально не выделяются.

В модели решеточного газа (МРГ) традиционно считается [7–12], что внутренние колебательные движения отделяются от конфигурационных состояний частиц системы, и колебания разделяются на внутри- и межмолекулярные. Мотивацией для такого разделения служит различие указанных частот, как правило, на порядок и больше. Однако, при этом сами межмолекулярные колебания, как правило, исключаются из рассмотрения.

Метод Монте-Карло не учитывает колебания практически во всех своих вариантах, кроме специально ориентированных задач на колебания [13]. Аналогичная ситуация с методом молекулярной динамики, хотя он может использоваться для расчета колебательного спектра в твердых телах. Для твердого тела вводят специальные техники выделения функций распределений частот, чтобы можно было рассчитать термодинамические функции для бездефектного кристалла или кластера [14–16].

Суть различия между учетом потенциальной энергией за счет смещений в больцмановском факторе выражения (2) и за счет колебаний заключается в точности учета потенциального вклада. Формально расстояния r в Eij(r) меняются в широком диапазоне от радиуса твердой сферы (r = σ) до бесконечности, хотя реальный диапазон смещений частиц в функции Eij(r) ограничен величиной порядка 3σ. Однако, в эту область помещается достаточно большое количество частиц – до ~102 (или до шести координационных сфер). Поэтому с точки зрения дискретного рассмотрения соседей речь идет о колебаниях большого числа частиц. Для колебательного движения сначала решается динамическая задача на частоты – ищется их спектр. При этом из потенциальных функций (через вторые производные) ищутся силовые постоянные. Затем по спектру строится статсумма Qvib. В уравнениях колебательной динамики ближайшие соседи учитываются одновременно при фиксированном их расположении относительно центра, что позволяет получить локальные частоты. Такие расстояния относятся к относительно малым смещениям. Расстояния смещений в обычных гармонических колебаниях ~0.1λ, где λ – длина связи. С учетом ангармонических поправок общее относительное смещение соседей не превышает величины 0.3λ. Но в целом, колебательная динамика дает возможность описать не только локальные колебания, но и более общие коллективные движения в системе, по аналогии с твердым телом.

Хотя в расчетах термодинамических функций жидких систем используется одна и та же потенциальная функция, но остается вопрос: будут ли конечные результаты идентичны при использовании этих двух подходов и, если есть различие, то в чем оно проявляется. До настоящего времени неясно, как соотносятся потенциальные вклады в этих двух разных подходах. Такие различия могут влиять как через величину шага интегрирования ИУ, так и через точность описания взаимной корреляции всех окружающих соседей при одновременном их рассмотрении колебательной динамикой, которая не может быть отражена в ИУ.

Для неидеальных газов есть как работы [4, 17] без выделения колебательного вклада, так и более поздние работы с моделями ассоциативного типа, в которых специально стали вводить частоты колебаний и которые были стимулированы разработкой кинетических уравнений для неравновесных процессов [18].

Для твердого тела колебания – единственный вид теплового движения, однако, могут быть использованы оба подхода [19], хотя исходным будет предварительное определение спектра частот [20–22]. Но для твердого тела также вводят априорное интегрирование по импульсу и переходят к моделям с механическими модулями [19]: гармонические и ангармонические разного порядка (при этом микроскопическая интерпретация механических модулей требует возврата к импульсам).

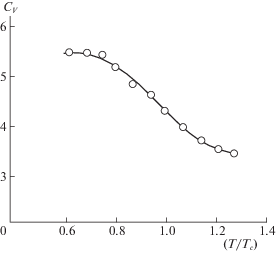
Экспериментальные измерения жидкого аргона были выполнены уже давно [23, 24]. На рис. 1 показаны измерения теплоемкости CV в широком диапазоне температур [23, 24]. При высоких температурах эта величина приближается сверху к 3 кал/(моль К), как для газа, при низких температурах – приближается снизу к 6 кал/(моль К), как для твердых тел, в критической температуре CV = = 4.5 кал/(моль К). Эти данные обычно однозначно трактуются как экспериментальное доказательство необходимости учета, помимо поступательного движения атомов, межмолекулярных колебаний в плотных газах и жидкостях. Отличие величины CV (при Т/Тс = 0.6), указанной на рис. 1, от ~6 кал/(моль К) при температуре кристаллизации Т/Тс ~ 0.54 должно быть связано с изменением теплоемкости при фазовом переходе первого рода и вкладом изменения парной ФР θAA, определяющей Upot = zεAAθAA, z – число ближайших соседей. Наличие парной ФР в Upot несколько уменьшает значения CV , область их изменения полностью согласуется с представлениями о смене поступательных движений на колебательные.

Рис. 1.

Зависимость теплоемкости аргона (кал/(моль К)) от приведенной температуры (фрагмент рисунка из [23, 24]).

Этот вывод основан на теореме вириала [25, 26], согласно которой, для гармонического осциллятора вклад потенциальной энергии в теплоемкость равен вкладу кинетической энергии. Он отвечает как изолированному осциллятору, так и твердому телу. В теореме вириала оперируют с той ограниченной областью потенциала, которая считается главной для данной задачи. Так, для притягивающей ветви потенциала Ми (n–m) имеем среднее значение потенциальной энергии равное m〈Upot〉/2 = 〈Еkin〉 для точки отсчета на больших расстояниях. В этом случае 〈Upot〉 = 2〈Еkin〉/m, что дает, например, для m = 6, вклад в CV намного меньше, чем вклад для гармонического осциллятора 〈Upot〉 = 〈Еkin〉 вблизи минимума потенциальной функции. То же самое можно считать и для обычного ангармонического вклада в Upot= bx2 – dx3, когда 〈Upot〉 = –2〈Еkin〉/3. Обе выделенные области потенциала Upot, как главные, не соответствуют эксперименту на рис. 1.

С формальной точки зрения, отличие между учетом смещений и колебаний заключается в том, что для учета смещений предварительно выполняется процедура усреднения по всем импульсам независимо от типа конфигурационного интеграла, тогда как для учета локальных колебаний сначала фиксируется локальная конфигурация, и для нее проводится усреднение по импульсам (т.е. импульсы не могут предварительно отделяться). Поэтому даже для твердого тела, для которого учет колебаний является стандартной процедурой учета кинетической энергии [19–22], чтобы получить колебательный спектр из цепочки ББГКИ необходим переход к равновесию из неравновесной цепочки ББГКИ [27], которая оперирует в полном фазовом пространстве {xi} = = {pi,ri} импульсов {pi} и координат {ri}.

Чтобы ответить на поставленные выше вопросы, необходимо сначала построить уравнения жидкого состояния, которые бы отражали в явном виде колебательные движения и возможность существования негармонических смещений молекул. Это – главная цель данной работы.

Другой важный мотив построения новых уравнений – тот факт, что сложность использования ИУ ограничивает их применение в практических задачах и вынуждает прибегать к методам Монте-Карло и молекулярной динамики, либо специально загрублять ИУ в методе функционала плотности. В этом отношении дискретно-континуальное описание на базе МРГ позволяет значительно дальше продвинуться при использовании теории в практических задачах описания жидких систем, особенно с неоднородным распределением компонентов: для адсорбционных процессов, процессов образования новых фаз, и в расчете их поверхностного натяжения.

Ниже построены уравнения равновесного распределения для концентраций и парных ФР с явным учетом колебательных движений на базе кластерного подхода. Основы этого подхода здесь излагаются на простейшем примере для однородного объема. В этом подходе любой объем системы разбивается на элементарные ячейки, содержащие не более одной молекулы. Это позволяет учесть собственный объем молекул и их межчастичные взаимодействия.

ДИСКРЕТНОЕ ОПИСАНИЕ ПРОСТРАНСТВА

Для учета влияния соседей на движения молекул в плотных фазах воспользуемся кластерным подходом к построению молекулярных распределений в трех агрегатных состояниях. Он с единой точки зрения позволяет учесть разные по природе агрегатные состояния веществ и границ раздела из фаз [28]. Техника построений уравнений в кластерном подходе была ориентирована на описание состояний занятости дискретных ячеек объемом ω0, на которые разбивается весь объем системы V, M = V/ω0 – число ячеек в системе [29]. Символ ωf использован для объема ячейки с номером f вместо ${{v}_{f}}$, чтобы отличить этот символ от скорости частицы, определяющей ее импульс. В кластерном подходе, как и в континуальном подходе, расчет статистической суммы исследуемой системы заменяется решением системы уравнений относительно кластерных ФР, которые характеризуют вероятности реализации различных локальных конфигураций молекул θ(1, …, M) с координатами r1, … rM .

Занятость узлов решетки. Состояние занятости каждого узла решетки определяется сортом частицы, которая в нем находится. В любом узле решетки может находиться частица любого сорта, и каждое конкретное состояние занятости узла f является случайной величиной, определяемой [29] как: $\gamma _{f}^{i} = {\text{1}}$, если в узле f находится частица сорта i, и $\gamma _{f}^{i} = 0$, если в узле f находится частица сорта j, j ≠ i. Данное определение отражает, что: 1) в любом узле обязательно находится частица какого-либо сорта:

(4)
$\sum\limits_{i = 1}^s {\gamma _{f}^{i} = 1;} \quad {\text{и }}\quad \gamma _{f}^{i}\gamma _{f}^{j} = \gamma _{f}^{i}{{\Delta }_{{ij}}}.$

2) любой узел занят частицей только одного сорта, где ${{\Delta }_{{ij}}}$ – символ Кронекера.

Задание номера ячейки f означает задание координаты частицы i, оно однозначно, если подразумевается положение частицы в ее центре, и требуется указание дополнительного приращения $r_{f}^{i}$, если частица может смещаться от центра ячейки. В этом случае случайная величина $\gamma _{f}^{i}(r_{f}^{i})$ определяет событие того, что центр массы частицы i находится в точке r внутри ячейки f, r ∈ ω(f), где ω(f) – объем ячейки f [28, 30]. Расстояние между двумя частицами i и j в ячейках f и g в объемной фазе обозначим как ${{r}_{{ij}}} = \left| {{\mathbf{r}}_{f}^{i} + {\mathbf{r}}_{{fg}}^{{ij}} - r_{g}^{j}} \right|$, где ${\mathbf{r}}_{{fg}}^{{ij}}$ – вектор между двумя средними положениями молекул i и j в ячейках f и g, находящихся на расстоянии ρ координационных сфер, ρ ≤ R. При использовании потенциала Ми или ЛД связанным состояниям отвечают расстояния R до 5–6 координационных сфер. В силу блокирования объема узла объемом частицы имеем следующие обобщенные соотношения:

(4а)
$\begin{gathered} \gamma _{f}^{i}(r_{f}^{i})\gamma _{f}^{j}(r_{f}^{j}) = \gamma _{f}^{i}(r_{f}^{i}){{\Delta }_{{ij}}} \\ {\text{и }}\quad \sum\limits_{i = 1}^s {\int\limits_{r_{f}^{i} \in {{\omega }_{f}}} {\gamma _{f}^{i}(r_{f}^{i})dr_{f}^{i}} } = 1. \\ \end{gathered} $
В нашей задаче описание состояния занятости узлов должно быть дополнено состоянием импульса (или скорости) частицы. Будем приписывать частице i в данном узле f скорость частицы $v_{f}^{i}$. Обозначим через ${{x}_{i}} = ({{r}_{i}},{{v}_{i}})$ координаты рассматриваемой молекулы i в фазовом пространстве координат и скоростей (или импульсов, pi – импульс молекулы i). Для них соответственно выполняются расширенные связи (4а) с учетом импульсных составляющих
(4б)
$\begin{gathered} \gamma _{f}^{i}(x_{f}^{i})\gamma _{f}^{j}(x_{f}^{j}) = \gamma _{f}^{i}(r_{f}^{i}){{\Delta }_{{ij}}} \\ {\text{и }}\quad \sum\limits_{i = 1}^s {\int\limits_{{\mathbf{r}}_{f}^{i} \in {{\omega }_{f}}} {\int\limits_{ - \infty }^\infty {\gamma _{f}^{i}(x_{f}^{i})d{\mathbf{v}}_{f}^{i}d{\mathbf{r}}_{f}^{i}} } } = 1. \\ \end{gathered} $
Используемые здесь локальные функции распределения в полном фазовом пространстве $P\left( {\left\{ {{\mathbf{r}}_{f}^{i},{\mathbf{v}}_{f}^{i}} \right\}} \right) \equiv P\left( {\left\{ {x_{f}^{i}} \right\}} \right)$ отличаются от континуальных функций распределений в кинетической теории [18, 30] своей нормировкой на объем ячейки, а не на объем системы. Они не определены вне рассматриваемых ячеек: $P{{\left( {\left\{ {x_{f}^{i}} \right\}} \right)}_{{{{{\mathbf{r}}}_{f}} \notin {{\omega }_{f}}}}} = 0$, где 1 ≤ ≤ f ≤ M, rf ∈ ωf. Граничные условия в пространстве скоростей совпадают с обычными условиями: эти функции обращаются в нуль при устремлении модуля скорости к бесконечности $P{{\left( {\left\{ {x_{f}^{i}} \right\}} \right)}_{{{{{\mathbf{v}}}_{{f,\delta }}} = \pm \infty }}} = $ = 0, δ = x, y, z. Ниже везде для упрощения записи будем считать, что символ $\gamma _{f}^{i}$ в общем случае означает одновременное задание не только сорта частицы i в узле f , но и более детальную информацию для частицы i – величину $x_{f}^{i}$: $\gamma _{f}^{i} \equiv \gamma _{f}^{i}(x_{f}^{i}) \equiv $ $ \equiv \;\gamma _{f}^{i}({\mathbf{r}}_{f}^{i},{\mathbf{v}}_{f}^{i})$.

Состояние всей решеточной системы из M узлов задается полным набором случайных величин $\left\{ {{{\gamma }_{f}}^{i}} \right\} = \left\langle {\gamma _{1}^{i} \ldots \gamma _{M}^{i}} \right\rangle $, которые представляют детальную информацию о том, частица какого сорта находится в каждом узле решетки. Вероятность нахождения решеточной системы в состоянии, задаваемом набором $\left\{ {\gamma _{f}^{i}} \right\}$, обозначим через $Р \left( {\left\{ {\gamma _{f}^{i}} \right\}} \right)$.

Для сокращенного описания системы используют многочастичные корреляционные функции (или просто корреляторы), определяемые как

(5)
$\theta _{{{{f}_{1}} \ldots {{f}_{m}}}}^{{{{i}_{1}} \ldots {{i}_{m}}}} = {{\left\langle {\gamma _{{{{f}_{1}}}}^{{{{i}_{1}}}}...\gamma _{{{{f}_{m}}}}^{{{{i}_{m}}}}} \right\rangle }_{\tau }} = \sum\limits_{{{i}_{1}} = 1}^s { \ldots \sum\limits_{{{i}_{M}} = 1}^s {\prod\limits_{n = 1}^m {\gamma _{{{{f}_{n}}}}^{{{{i}_{n}}}}} P\left( {\left\{ {\gamma _{f}^{i}} \right\}} \right)} } ,$
где сумма берется по всем состояниям занятости всех узлов решетки; if – сорт частицы в узле f; m – порядок или размерность коррелятора, характеризующего вероятность реализации следующей конфигурации частиц: в узле f1 находится частица i1, в узле f2 – частица i2, и так далее до m-й частицы включительно. Состоянием занятости остальных (М–m) узлов решетки мы не интересуемся, по ним проведено усреднение. В равновесии $P\left( {\left\{ {\gamma _{f}^{i}} \right\}} \right)$ – нормированная функция распределения частиц системы, равная $P\left( {\left\{ {\gamma _{f}^{i}} \right\}} \right)$ = ${\text{exp}}\left[ { - \beta H\left( {\left\{ {\gamma _{f}^{i}} \right\}} \right)} \right]{\text{/}}Q$, где Q – нормировочный сомножитель, называемый статистической суммой системы (3), или суммой по состояниям системы; $H\left( {\left\{ {{{\gamma }_{f}}^{i}} \right\}} \right)$ – полная энергия (гамильтониан) системы (1).

Запись выражения (5) в модифицированной МРГ формально идентична записи для дискретной структуры МРГ с положением частиц в центрах ячеек. Для перехода к ситуации с усредненным значением импульса следует выполнить интегрирование по значениям скоростей частицы

$\gamma _{f}^{i}({\mathbf{r}}_{f}^{i}) = \int\limits_{ - \infty }^\infty {\gamma _{f}^{i}(x_{f}^{i})d{\mathbf{v}}_{f}^{i}} ,$
а для возврата к старым дискретным распределениям по координатам необходимо дополнительно выполнить усреднение по смещениям внутри ячейки
$\begin{gathered} \gamma _{f}^{i} = \int\limits_{d{\mathbf{r}}_{f}^{i} \in {{\omega }_{f}}} {\gamma _{f}^{i}({\mathbf{r}}_{f}^{i})d{\mathbf{r}}_{f}^{i}} = \\ = \int\limits_{d{\mathbf{r}}_{f}^{i} \in {{\omega }_{f}}} {\int\limits_{ - \infty }^\infty {\gamma _{f}^{i}(x_{f}^{i})d{\mathbf{v}}_{f}^{i}d{\mathbf{r}}_{f}^{i}} } . \\ \end{gathered} $
Для простоты записи в интегралах пределы полагаются одинаковыми во всех направлениях (x, y, z), как для скоростей, так и для вектора смещений ${\mathbf{r}}_{f}^{i}$.

Межмолекулярные колебания относят к внутренней (континуальной) шкале размеров, а расстояния между центрами ячеек или расстояние $\left| {r_{{fg}}^{{ij}}} \right|$ между их средними положениями равновесия относят к дискретной шкале [28].

ЭНЕРГЕТИЧЕСКОЕ СОСТОЯНИЕ СИСТЕМЫ

Эффективный гамильтониан в большом каноническом ансамбле запишется как H = H1+ H2 [29], где H1 – так называемый одночастичный вклад от химического потенциала μi молекулы i, а H2 – потенциальная энергия системы, складывающая из всевозможных попарных вкладов взаимодействующих частиц i и j на узлах f и g. Для каждого кластера вводятся величины hf, 1 ≤ f ≤ M, характеризующие вклады в полную энергию системы центральных частиц (кластерные гамильтонианы):

(6)
$\begin{gathered} H = \sum\limits_{f = 1}^M {{{h}_{f}}} ,\quad {{h}_{f}} = \sum\limits_{i = 1}^s {h_{f}^{i}} , \\ h_{f}^{i} = h{{_{f}^{i}}_{{,1}}}(\alpha ) + h{{_{{f,}}^{i}}_{2}},\quad h{{_{{f,}}^{i}}_{2}} = \sum\limits_g {\sum\limits_{j = 1}^s {{{\varepsilon }_{{ij}}}\gamma _{g}^{j}} } \gamma _{f}^{i}, \\ \end{gathered} $
здесь через ${{\varepsilon }_{{ij}}}$ обозначен параметр парного взаимодействия соседних частиц сорта i и j; сумма по j берется по всем узлам решетки, а сумма по g – по всем z соседям узла f; суммы по i и j берутся по всем состояниям занятости узлов решетки.

Будем рассматривать влияние всех окружающих соседей на локальные колебания частицы i [28]; расположение соседних молекул будем характеризовать списком α. Он однозначно связан с набором величин $\gamma _{g}^{j}$. Совокупность значений индексов g, g ∈ zf, и j, 1 ≤ j ≤ s, перечисляет список α расположения соседей вокруг центральной частицы i. Тогда вклад H1 запишется следующим образом:

${{H}_{1}} = \sum\limits_{f = 1}^M {\sum\limits_{i = 1}^s {\sum\limits_\alpha {\mathop H\nolimits_f^i } } } (\alpha ),$
где $H_{f}^{i}(\alpha )$ – кластерный гамильтониан частицы i, находящейся в узле f, вокруг которой состояния занятости j соседних узлов g описываются списком α, или $h{{_{{f,}}^{i}}_{1}}(\alpha )$ = $\sum\nolimits_\alpha {H_{f}^{i}(\alpha )} $. Зависимость hf от $(\alpha )$ определяется зависимостью $h{{_{{f,}}^{i}}_{1}}(\alpha )$. Слагаемые в $h{{_{{f,}}^{i}}_{1}}(\alpha )$ записываются в дискретной и континуальной формах как
(7)
$\begin{gathered} {\text{H}}_{f}^{i}(\alpha ) = \prod\limits_g {\nu _{f}^{i}(x_{f}^{i}{\text{|}}\alpha )\gamma _{g}^{j}(x_{g}^{j})\gamma _{f}^{i}(x_{f}^{i})} \equiv \\ \equiv \;\int\limits_{\omega (f)} {\left\{ {\prod\limits_g {\int\limits_{\omega (g)} {\nu _{f}^{i}(x_{f}^{i}{\text{|}}\alpha )\gamma _{g}^{j}(x_{g}^{j})} } dx_{g}^{j}} \right\}\gamma _{f}^{i}(x_{f}^{i})} dx_{f}^{i}. \\ \end{gathered} $
Здесь явным образом отмечено, что состояния частиц характеризуются координатами и импульсом всех частиц.

Усреднение по импульсам. Процедура усреднения по импульсам приводит в статистической термодинамике к появлению статистических сумм $Q_{f}^{i}({{r}_{f}}^{i}{\text{|}}\alpha )$ [7, 31]. Удобство этих величин особенно наглядно было продемонстрировано для идеальных газов, в которых выделяют поступательное, вращательное и колебательное движения. Те же представления обычно переносят на плотные фазы, хотя в них молекулы постоянно находятся в поле потенциалов соседних частиц (в связанных состояниях).

В общем случае разделение статистических сумм QN = QtranQrotQvib на отдельные компоненты для поступательного, вращательного и колебательного движений, как для газовой фазы, неоднозначно [28]. Оно возможно только в случае аддитивных вкладов каждого из типов движений в полную энергию системы. Взаимное влияние молекул делает такие статистические суммы взаимно зависимыми, точность их разделения определяется удачностью используемых модельных представлений. Вопросы построения Qtran и Qrot обсуждались [29, 30, 32] в связи с обобщением теории абсолютных скоростей реакций на плотные фазы и для задач расчета коэффициентов самодиффузии и сдвиговой вязкости. Такая модель описывает процесс флуктуационного разряжения плотности, при котором может сместиться рассматриваемая молекула. Позднее на этой основе был разработан общий подход к расчету диссипативных коэффициентов в любых плотных системах от газа до твердого тела [30]. Здесь эти вопросы не рассматриваются.

В работах [33–35] колебательные движения были включены в конфигурационную часть статсуммы, но процедура их расчета детально не обсуждалась. Напомним, что учет колебаний в твердом теле связан с усреднением по импульсу через решение уравнений Ньютона, которые определяет классический гамильтониан колебательного движения ${{H}_{{{\text{vib}}}}}$:

(8)
$\begin{gathered} {{H}_{{{\text{vib}}}}}(\{ p,q\} ) = \sum\limits_{i = 1}^N {\sum\limits_{\delta = 1}^3 {p_{{i\delta }}^{2}{\text{/}}(2{{m}_{i}})} } + \\ + \;\sum\limits_{i,j;i \ne j}^N {\sum\limits_{\delta = 1,\chi = 1}^3 {{{a}_{{i\delta ,j\beta }}}{{q}_{{i\delta }}}{{q}_{{j\chi }}}} } , \\ \end{gathered} $
где $p_{{i\delta }}^{2}$ – компонента импульса i-го атома в направлении δ, ${{q}_{{i\delta }}}$ – компонента смещения из положения равновесия i-го атома по декартовой координате δ. Гамильтониану (8) отвечают классические уравнения движения:
(9)
${{\ddot {q}}_{{i\delta }}} = - \sum\limits_{j = 1}^N {\sum\limits_{\chi = 1}^3 {{{a}_{{i\delta ,j\beta }}}{{q}_{{j\chi }}}} } .$
В этих уравнениях ${{a}_{{i\delta ,j\chi }}}$ – функции межатомных силовых констант и масс. Для нормального колебания с циклической частотой ω имеем ${{q}_{{i\delta }}} = {{A}_{{i\delta }}}{{e}^{{i\omega t}}}$, где ${{A}_{{i\delta }}}$ – амплитуда. Уравнения (9) сводятся к линейной системе алгебраических уравнений для частоты ω:
$\begin{gathered} \sum\limits_{j = 1}^{{{N}_{K}}} {\sum\limits_{\chi = 1}^3 {({{a}_{{i\delta ,j\chi }}} - {{\omega }^{2}}{{\delta }_{{i\delta ,j\chi }}}){{A}_{{j\chi }}} = 0} } , \\ i = 1,2,3, \ldots ,N;\quad d = 1,2,3, \\ \end{gathered} $
где ${{\delta }_{{i\delta ,j\chi }}} = 1$, если i = j, δ = χ и ${{\delta }_{{i\delta ,j\chi }}} = 0$ в остальных случаях.

В общем случае для системы из N частиц решение динамической задачи для определения частот гармонических колебаний дает 3N разных частот, 1 ≤ j≤ 3N, которые приводят к следующей статистической сумме колебательных движений ${{Q}_{{{\text{vib}}}}}$:

(10)
$\begin{gathered} {{Q}_{{{\text{vib}}}}} = \left\langle {\exp ( - \beta {{H}_{{{\text{vib}}}}})} \right\rangle = \exp ( - \beta {{E}_{{{\text{pot}}}}}) \times \\ \times \;\prod\limits_{j = 1}^{3N} {\exp ( - \beta h{{\nu }_{j}}{\text{/}}2){\text{/}}[1 - \exp ( - \beta h{{\nu }_{j}})]} . \\ \end{gathered} $
где ${{E}_{{{\text{pot}}}}}$ – потенциальная энергия системы в состоянии, когда все атомы находятся в равновесии. В общем случае наличие пространственного разупорядочения любой природы (дефектность, внешние поля) приводит к усложнениям. Динамическая матрица {${{\alpha }_{{i\delta ,j\chi }}}$} в этом случае не обладает ни простой рекуррентной формой, как в динамике кристаллов, ни малым порядком, как в случае молекулярных колебаний [36]. Поэтому для жидкости такой прямой путь затруднен.

Известно, что в связанном состоянии частицы могут совершать разнообразные колебательные движения (периодические, апериодические и хаотические) [25, 37]. Сложность траекторий резко увеличивается с числом связанных частиц. Следует отметить работы [38, 39], автор которых попытался связать новые результаты [37, 40], полученные в механике сильно нелинейных систем со сложным типом движения молекул в жидкой фазе. Это позволило выразить характерные времена локальных структурных перестроек в жидкостях через “активационную” температурную зависимость (как и в теории переходного состояния). В то же время традиционная энергия активации заменяется на более сложную характеристику динамической системы, что в принципе приводит к изменению понятия самого активационного барьера. Такого рода результаты для сильно нелинейных систем, на первый взгляд, хорошо соотносятся с физической картиной Френкеля [41], однако, следует учитывать, что все результаты [37, 40] относятся к изолированным системам с малым числом степеней свободы. Для реальных флюидов это означает рассмотрение изолированных ансамблей (кластеров). Но для них запрещен обмен как энергией, так и частицами с другими окружающими молекулами, поэтому аналогия с реальной жидкостью возможна только на очень малых интервалах времени – порядка одного столкновения между молекулами. Для плотных фаз это очень малое время.

В качестве альтернативного подхода будем считать, что для каждой молекулы жидкости в ходе ее тепловых движений можно выделить среднее положение центра масс, относительно которого происходят смещения. Внутри каждой ячейки данное распределение считается равномерным, что согласуется с требованием макроскопической однородности жидкости [28]. Такой подход будет аппроксимировать сильные ангармонические смещения молекул друг относительно друга. Его обоснование – экспериментальные данные о том, что время процесса релаксации импульса много меньше, чем время процесса релаксации для массы [42, 43]. Это означает, что процесс смещений молекул в тепловом режиме относительно среднего центра равновесия длится много дольше, чем процесс установления нового положения среднего центра равновесия той же молекулы. Близкая картина была сформулирована Френкелем [41], который относил ее к продолжающей существовать в жидкости кристаллической структуре, тогда как здесь допускается равномерное смещение центра равновесия молекулы внутри области порядка своего размера, что полностью согласуется как с макроскопической трактовкой жидкости, так и с существованием в ней ближнего порядка.

Будем моделировать спектр колебательных движений частиц в виде распределения положений равновесия центров масс соседних молекул, относительно которых происходят колебания, в некотором диапазоне расстояний в пределах от λmin до λmax. Значения λmin и λmax связаны с хорошо известной концепцией исключенного объема [24, 30, 34, 44]. Это позволяет сформулировать разные типы ситуаций с учетом колебательных движений молекул: 1) традиционные колебания гармонического типа, которые однозначно связаны с видом локальных конфигураций α, со статсуммой (10); 2) отсутствие выделенных колебательных движений, когда смещения на любые расстояния приводят к Qvib= 1 для любых конфигураций α; 3) учет распределенности средних равновесных положений r второй частицы связанного осциллятора в диапазоне от от λmin до λmax, согласно парной ФР θAA(r) на шкале времен релаксаций масс. В этом случае формируются статсуммы типа (10) Qvib(α) с измененными силовыми постоянными, приводящие к частотам, зависящим от температуры и плотности, для каждой из конфигураций α.

Формирование локальных статсумм $Q_{f}^{i}({{{\mathbf{r}}}_{i}}{\text{|}}\alpha )$, которые отражают связанные состояния центральных частиц, участвующих в трех типах эффективных движений в жидкости $Q_{f}^{i}({{{\mathbf{r}}}_{i}}{\text{|}}\alpha ) = $ $ = \;Q_{f}^{i}{{({{{\mathbf{r}}}_{i}}{\text{|}}\alpha )}_{{{\text{tran}}}}},\;Q_{f}^{i}{{({{{\mathbf{r}}}_{i}}{\text{|}}\alpha )}_{{{\text{rot}}}}},\;Q_{f}^{i}{{({{{\mathbf{r}}}_{i}}{\text{|}}\alpha )}_{{{\text{vib}}}}}$, завершает процесс усреднения по импульсам. Тогда выражения (7) могут быть представлены в дискретной и континуальной формах записи как

(11)
$\begin{gathered} {\text{H}}_{f}^{i}(\alpha ){\text{ = }}\prod\limits_g {\nu _{f}^{i}(r_{f}^{i}{\text{|}}\alpha )\gamma _{g}^{j}(r_{g}^{j})\gamma _{f}^{i}(r_{f}^{i})} \equiv \\ \equiv \;\int\limits_{\omega (f)} {\left\{ {\prod\limits_g {\int\limits_{\omega (g)} {\nu _{f}^{i}(r_{f}^{i}{\text{|}}\alpha )\gamma _{g}^{j}(r_{g}^{j})} } dr_{g}^{j}} \right\}\gamma _{f}^{i}(r_{f}^{i})} dr_{f}^{i}, \\ \nu _{f}^{i}({\mathbf{r}}_{f}^{i}{\text{|}}\alpha ) = - {{\beta }^{{ - 1}}}{\text{ln}}[a_{f}^{i}({\mathbf{r}}_{f}^{i}{\text{|}}\alpha ){{Р }_{i}}], \\ a_{f}^{i}({\mathbf{r}}_{f}^{i}{\text{|}}\alpha ) = Q_{f}^{i}({{{\mathbf{r}}}_{i}}{\text{|}}\alpha )\beta {\text{/}}Q_{i}^{0}, \\ \end{gathered} $
где $a_{f}^{i}({\mathbf{r}}_{f}^{i}{\text{|}}\alpha )$ – локальная константа удерживания (это константа Генри для задач адсорбции и абсорбции при дополнительном учете потенциала ад- или абсорбента) частицы i в ячейке f. Здесь учтено, что μi – химический потенциал молекулы i: ${{\mu }_{i}} = \mu _{i}^{0}$ + ${{\beta }^{{ - 1}}}\ln [\beta {{P}_{i}}{\text{/}}Q_{i}^{0}]$, связанный с парциальным давлением Pi недиссоциирующейся молекулы i, $\mu _{i}^{0}$ – точка отсчета для химического потенциала: $\mu _{i}^{0}$ = 0 для свободной частицы в газовой фазе или $\mu _{i}^{0}$ = εi для ад- и абсорбированного состояния; $Q_{i}^{0}$ – статсумма частицы в газе. Выражения (11) отражают зависимость внутренних состояний частицы i от конкретного типа расположения всех соседей α. Изменение состояния занятости любого из соседних узлов α меняет потенциал, в котором движется центральная частица i, и соответственно меняются ее три типа движений.

УРАВНЕНИЯ КЛАСТЕРНОГО ПОДХОДА

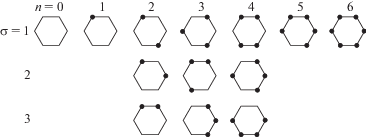
Построенные статсуммы позволяют применить кластерный подход [29, 30], чтобы построить уравнения для ФР, через которые строится вся термодинамика. Ограничимся примером построения кластерных уравнений в случае учета парного взаимодействия между ближайшими соседями бинарной системы. Согласно [29, 30], получим следующие уравнения, связывающие между собой корреляторов первого типа, отличающихся сортом центральной частицы i = А и i = B, и имеющих одинаковое число узлов координационной сферы занятых частицами А (здесь n = nAA и функции ${{\nu }_{i}}(\alpha )$ определены в (11)):

(12)
$\begin{gathered} \theta _{{[n,\sigma ]}}^{B} = M_{{n,\sigma }}^{{AB}}\theta _{{[n,\sigma ]}}^{A}, \\ M_{{n,\sigma }}^{{AB}} = \exp [ - \beta (\nu (\alpha ) + n\omega )], \\ \nu (\alpha ) = {{\nu }_{B}}(\alpha ) - {{\nu }_{A}}(\alpha ) + z({{\varepsilon }_{{AB}}} - {{\varepsilon }_{{BB}}}), \\ \omega = {{\varepsilon }_{{AA}}} + {{\varepsilon }_{{BB}}} - 2{{\varepsilon }_{{AB}}}. \\ \end{gathered} $
По определению корреляторов второго типа, содержащих не менее чем n частиц А в координационной сфере кластера, представим их через корреляторы первого типа как
(13)
$\begin{gathered} \theta _{{n,\sigma }}^{i} = \sum\limits_{k = 0}^{z - n} {\sum\limits_{\sigma (n + k)} {b_{{\sigma (n + k)}}^{{\sigma (n)}}} } \theta _{{[n + k,\sigma ]}}^{i}, \\ \sum\limits_{\sigma (n + k)} {b_{{\sigma (n + k)}}^{{\sigma (n)}} = C_{{z - n}}^{k}} , \\ \end{gathered} $
где $b_{{\sigma (n + k)}}^{{\sigma (n)}}$ – число способов перехода от конфигураций σ(n) к конфигурации σ(n + k), сумма по σ(n + k) берется по всем возможным видам конфигураций при данном числе (n + k) частиц А, которые реализуются при последовательном их добавлении. Величины $b_{{\sigma (n + k)}}^{{\sigma (n)}}$ элементарно подсчитываются по виду конфигураций. На рис. 2 в качестве простейшего примера показаны разные типы “неприводимых” конфигураций соседних частиц на плоской гексагональной решетке z = 6 (они аналогичны неприводимым диаграммам Майера для неидеальных газов [4, 17]). Такие различия между конфигурациями соседей необходимо учитывать в строгом подходе для приближений, более точных, чем использованное ниже квазихимическое приближение (КХП), при учете тройных и более сложных потенциальных функций взаимодействий [29]. В этом случае символ α относится к набору величин σ и n. Коэффициенты $C_{z}^{k}$ представляют собой число сочетаний из z элементов по k: $C_{z}^{k}$ = z!/(k!(z–k)!).

Рис. 2.

Конфигурации частиц А в первой координационной сфере вокруг центрального (не показан) на плоской решетке z = 6; n – число частиц А, σ(n) – тип конфигурации при фиксированном значении n [29, 30].

Последовательный вывод связи между корреляторами второго типа для центральных частиц А и В состоит из следующих шагов: 1) обращение линейной системы уравнений (13), чтобы выразить корреляторы первого типа $\theta _{{[n,\sigma ]}}^{i}$ через корреляторы второго типа $\theta _{{n + k,\sigma }}^{i}$, 2) подстановка корреляторов первого типа в уравнение (12), их связывающее, и 3) решение уравнение относительно $\theta _{{n,\sigma }}^{B}$ через $\theta _{{n + k,\sigma }}^{A}$. Эти преобразования полностью идентичны приведенным в [29], поэтому они не повторяются. Способ замыкания системы уравнений строится путем аппроксимации высших корреляторов через корреляторы меньшей размерности. В КХП все кластерные ФР выражаются через унарные θi и парные θij ФР как в [29, 30]:

(14)
$\theta _{{[n,\sigma ]}}^{i} = {{\theta }_{i}}{{({{t}_{{iA}}})}^{n}}{{({{t}_{{iB}}})}^{{z - n}}},\quad {{t}_{{ij}}} = {{\theta }_{{ij}}}{\text{/}}{{\theta }_{i}},$
где tij – условная вероятность нахождения частицы j рядом с частицей i. В данном приближении способ расположения соседей между собой не играет роли, поэтому отсутствует влияние σ на потенциальную энергию системы, но влияние σ сохраняется за счет учета разного вклада внутренних движений частиц. Это видно при подстановке данного расцепления (14) в уравнение (13), которое используется в уравнениях системы (12). Подставляя данное расцепление в правую часть уравнения (13) для компонентов бинарной системы, получим
(15)
$\begin{gathered} \theta _{{n,\sigma }}^{B} = \sum\limits_{k = 0}^{z - n} {\sum\limits_{\sigma (n + k)} {b_{{\sigma (n + k)}}^{{\sigma (n)}}} } M_{{n + k,\sigma }}^{{AB}}\theta _{{[n + k,\sigma ]}}^{A} = \\ = \;\sum\limits_{k = 0}^{z - n} {\sum\limits_{\sigma (n + k)} {b_{{\sigma (n + k)}}^{{\sigma (n)}}} } M_{{n + k,\sigma }}^{{AB}}{{\theta }_{A}}{{({{t}_{{AA}}})}^{{n + k}}}{{({{t}_{{AB}}})}^{{z - n - k}}}. \\ \end{gathered} $
Для КХП-замыкания системы уравнений необходимы первые два уравнения цепочки $\theta _{0}^{B} \equiv {{\theta }_{B}}$ для n = 0 (вероятность найти узел занятым частицей В) и $\theta _{1}^{B} \equiv {{\theta }_{{BA}}}$ и для n = 1 (вероятность найти рядом пару частиц ВА). Обе функции ${{\theta }_{B}}$ и ${{\theta }_{{BA}}}$ не зависят от способа расположения (конфигураций) соседних частиц, поэтому у них нет символа σ. Хотя зацепление внутренних движений за конфигурационные состояния соседей обусловлены колебательным движением, ниже эти внутренние вклады не расписываются по каждому из типов отдельно. Замкнутые уравнения на унарные ФР имеют вид:
(16)
$\begin{gathered} {{\theta }_{B}} = {{\theta }_{A}}\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \exp [ - \beta \nu (\alpha )] \times \\ \times \;{{({{t}_{{AA}}}\exp [ - \beta \omega ])}^{k}}{{({{t}_{{AB}}})}^{{z - k}}}, \\ \end{gathered} $
подстановка выражения $\nu (\alpha ) = {{\nu }_{B}}(\alpha ) - {{\nu }_{A}}(\alpha )$, где α ↔ k, σ, из (11) дает
$\begin{gathered} {{\theta }_{B}} = {{\theta }_{A}}\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} \left[ {\frac{{{{Q}_{B}}(k,\sigma ){{P}_{B}}Q_{A}^{0}}}{{{{Q}_{A}}(k,\sigma ){{P}_{A}}Q_{B}^{0}}}} \right]} ({{t}_{{AA}}} \times \\ \times \;\exp [\beta ({{\varepsilon }_{{AB}}} - {{\varepsilon }_{{AA}}})]{{)}^{k}}{{({{t}_{{AB}}}\exp [\beta ({{\varepsilon }_{{BA}}} - {{\varepsilon }_{{BB}}})])}^{{z - k}}}. \\ \end{gathered} $
Отсюда следуют две формы записи. В первой форме записи компоненты бинарной системы не связаны с паром, и их химические потенциалы равны нулю (вторая форма записи относится к вакансии в качестве второго компонента – см. ниже). Тогда
(17)
${{\theta }_{B}} = {{\theta }_{A}}\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \frac{{{{Q}_{B}}(k,\sigma )}}{{{{Q}_{A}}(k,\sigma )}}S_{{AA}}^{k}(B)S_{{AB}}^{{z - k}}(B),$
где ${{S}_{{AA}}}(B) = {{t}_{{AA}}}\exp [\beta ({{\varepsilon }_{{AB}}} - {{\varepsilon }_{{AA}}})]$, ${{S}_{{AB}}}(B) = {{t}_{{AB}}} \times $ $ \times \;\exp [\beta ({{\varepsilon }_{{BA}}} - {{\varepsilon }_{{BB}}})]$.

Отношение статсумм разных компонентов включает в себя все типы движений (поступательное, вращательное и колебательное).

Аналогичным образом (как в (16)) можно записать второе уравнение:

(18)
$\begin{gathered} {{\theta }_{{BA}}} = {{\theta }_{{AA}}}\exp [ - \beta \omega ]\sum\limits_{k = 0}^{z - 1} {\sum\limits_{\sigma (1 + k)} {b_{{\sigma (1 + k)}}^{{\sigma (1)}}} \times } \\ \times \;\exp [ - \beta \nu (k + 1,\sigma )]{{({{t}_{{AA}}}\exp [ - \beta \omega ])}^{k}}{{({{t}_{{AB}}})}^{{z - 1 - k}}}. \\ \end{gathered} $
Оно отличается только степенями сомножителей при суммировании разных вкладов от реализуемых конфигураций соседей. Здесь символ $\alpha $ по построению связан с символами $k + 1,\sigma $. Вследствие учета всех внутренних движений компонентов в ячейках вклад от $\nu (k + 1,\sigma )$ не может быть вынесен за знаки суммирования по конфигурациям. С учетом нормировок $\sum\nolimits_{i = 1}^s {} {{\theta }_{i}} = 1$ и $\sum\nolimits_{i,j = 1}^s {} {{\theta }_{{ij}}} = 1$ эти уравнения позволяют найти искомые значения ${{\theta }_{A}}$ и ${{\theta }_{{AA}}}$. Зная значения этих двух функций при заданных величинах температуры и молекулярных параметров системы, можно рассчитать все другие термодинамические характеристики системы.

Учет свойств вакансий. Вторая форма записи уравнений (17), (18) связана с учетом того факта, что второй компонент смеси i = V относится к вакансиям, а для них все молекулярные параметры равны нулю. Этот наиболее важный случай отвечает модели решеточного газа [29]. В нем состояния компонента А связывают условием равенства химического потенциала в паровой фазе, что упрощает выражения

(19)
$\begin{gathered} {{\theta }_{B}} = {{\theta }_{A}}\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \frac{{Q_{A}^{0}}}{{{{Q}_{A}}(\alpha )\beta {{P}_{A}}}} \times \\ \times \;{{[{{t}_{{AA}}}\exp ( - \beta {{\varepsilon }_{{AA}}})]}^{k}}{{[{{t}_{{AB}}}]}^{{z - k}}}. \\ \end{gathered} $
Это позволяет переписать, учитывая нормировку ${{\theta }_{B}} = 1 - {{\theta }_{A}}$, данное уравнение в виде локальной изотермы, связывающей давление РА компоненты А в паровой фазе с плотностью того же компонента в решеточной системе ${{\theta }_{A}}$, в традиционном виде для локальных изотерм адсорбции и сорбции:
(20)
$\begin{gathered} \beta {{P}_{A}}{\text{/}}Q_{A}^{0} = \frac{{{{\theta }_{A}}}}{{1 - {{\theta }_{A}}}}\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \frac{{{{S}_{{AA}}}^{k}{{S}_{{AB}}}^{{z - k}}}}{{{{Q}_{A}}(k,\sigma )}}, \\ {{S}_{{Aj}}} = {{t}_{{Aj}}}\exp ( - \beta {{\varepsilon }_{{Aj}}}). \\ \end{gathered} $
В итоге вопрос свелся к учету влияния каждой из степеней свободы от локального конфигурационного состояния соседей через статсумму ${{Q}_{A}}(k,\sigma )$. В явном виде это отражает влияние вкладов колебательных движений, входящих в статсумму ${{Q}_{A}}(k,\sigma )$, на локальную изотерму и на все равновесные характеристики по сравнению с предыдущими построениями.

Аналогичным образом можно представить уравнение для парных ФР

(21)
$\begin{gathered} {{\theta }_{{BA}}} = {{\theta }_{{AA}}}\exp ( - \beta {{\varepsilon }_{{AA}}})\sum\limits_{k = 0}^{z - 1} {\sum\limits_{\sigma (1 + k)} {b_{{\sigma (1 + k)}}^{{\sigma (1)}}} } \times \\ \times \;\frac{{Q_{A}^{0}{{S}_{{AA}}}^{k}{{S}_{{AB}}}^{{z - 1 - k}}}}{{\beta {{P}_{A}}{{Q}_{A}}(k + 1,\sigma )}}. \\ \end{gathered} $

УЧЕТ БОЛЬШИХ СМЕЩЕНИЙ МОЛЕКУЛ

Усреднения по состояниям узлов соседей включают в себя как смену сорта соседа j, так и смещение $r_{g}^{j}$ его внутри своей ячейки. Смещения соседних молекул вне области локального минимума потенциальной функции учитываются путем усреднения по объемам ячеек. Учитывая условия нормировки для каждого узла системы, запишем

$\theta _{{f{{g}_{1}}...{{g}_{{z - 1}}}}}^{{i{{j}_{1}}...{{j}_{{z - 1}}}}} = \int\limits_{r_{{{{g}_{z}}}}^{{{{j}_{z}}}} \in \omega ({{g}_{z}})} {\sum\limits_{{{j}_{z}} = 1}^s {\theta _{{f{{g}_{1}}...{{g}_{z}}}}^{{i{{j}_{1}}...{{j}_{z}}}}} } dr_{{{{g}_{z}}}}^{{{{j}_{z}}}},$
т.е. усреднение по состоянию занятости узла gz понижает размерность корреляторов, включающих в свою конфигурацию данный узел. Это приводит к тому, что, как и в дискретной версии МРГ размерности корреляторов в цепочке уравнений понижаются, и замкнутые уравнения (16) и (21) перепишутся в виде
${{\theta }_{B}}(r_{f}^{B}) = {{\theta }_{A}}(r_{f}^{A})\sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \prod\limits_A {\prod\limits_B {\exp [ - \beta \nu (\alpha )]} } ,$
(22)
$\prod\limits_A { = \prod\limits_{n = 1}^k {\int\limits_{r_{{{{g}_{n}}}}^{{{{A}_{n}}}} \in \omega ({{g}_{n}})} {dr_{{{{g}_{n}}}}^{{{{A}_{n}}}}} } } \left\{ {{{t}_{{AA}}}(r_{f}^{A},r_{{{{g}_{n}}}}^{A})\exp [ - \beta \omega ]} \right\},$
$\prod\limits_B { = \prod\limits_{n = k + 1}^{z - k} {\int\limits_{r_{{{{g}_{n}}}}^{{{{B}_{n}}}} \in \omega ({{g}_{n}})} {dr_{{{{g}_{n}}}}^{{{{B}_{n}}}}} } } \left[ {{{t}_{{AB}}}(r_{f}^{A},r_{{{{g}_{n}}}}^{B})} \right],$
где показатель экспоненты зависит от переменных в сомножителях А и В.

Как и выше, выражение для $\nu _{f}^{i}({\mathbf{r}}_{f}^{i}{\text{|}}\alpha )$ определено в (11). Изменение состояния занятости любого из соседних узлов α меняет потенциал, в котором движется центральная частица i, и соответственно меняются частоты колебаний. Расположение соседей, задаваемое списком α, также влияет на область поступательного движения частицы i. Ограничиваясь случаем i = V, имеем (при ${{\varepsilon }_{{BA}}} = {{\varepsilon }_{{BB}}} = {{\varepsilon }_{{AB}}} = 0$)

(23)
$\begin{gathered} \beta {{P}_{A}}{\text{/}}Q_{A}^{0} = \\ = \;\frac{1}{{1 - {{\theta }_{A}}}}\int\limits_{r_{f}^{A} \in \omega (f)} {dr_{f}^{A}{{\theta }_{A}}\left( {r_{f}^{A}} \right)} \sum\limits_{k = 0}^z {\sum\limits_{\sigma (k)} {b_{{\sigma (k)}}^{{\sigma (0)}}} } \prod\limits_A {\prod\limits_B {\frac{1}{{{{Q}_{A}}(k,\sigma )}}} } , \\ \end{gathered} $
где
$\begin{gathered} \prod\limits_A = \;\prod\limits_{n = 1}^k {\int\limits_{r_{{{{g}_{n}}}}^{{{{A}_{n}}}} \in \omega ({{g}_{n}})} {dr_{{{{g}_{n}}}}^{{{{A}_{n}}}}} } \left\{ {{{t}_{{AA}}}(r_{f}^{A},r_{{{{g}_{n}}}}^{A})} \right. \\ \left. {\exp [ - \beta {{\varepsilon }_{{AA}}}(r_{f}^{A},r_{{{{g}_{n}}}}^{A})]} \right\}, \\ \end{gathered} $
$\prod\limits_B { = \;} \prod\limits_{n = k + 1}^{z - k} {\int\limits_{r_{{{{g}_{n}}}}^{{{{B}_{n}}}} \in \omega ({{g}_{n}})} {dr_{{{{g}_{n}}}}^{{{{B}_{n}}}}} } {{t}_{{AB}}}(r_{f}^{A},r_{{{{g}_{n}}}}^{B}).$
Аналогично выписывается второе уравнение цепочки для парной ФР

(24)
$\begin{gathered} {{\theta }_{{BA}}}(r_{f}^{B}r_{g}^{A}) = {{\theta }_{{AA}}}(r_{f}^{A}r_{g}^{A})\exp [ - \beta \omega ] \times \\ \times \;\sum\limits_{k = 0}^{z - 1} {\sum\limits_{\sigma (1 + k)} {b_{{\sigma (1 + k)}}^{{\sigma (1)}}} \prod\limits_A {\prod\limits_{n = k + 1}^{z - 1 - k} {\int\limits_{r_{{{{g}_{n}}}}^{{{{B}_{n}}}} \in \omega ({{g}_{n}})} {dr_{{{{g}_{n}}}}^{{{{B}_{n}}}}} } \times } } \\ \times \;[{{t}_{{AB}}}(r_{f}^{A}r_{{{{g}_{n}}}}^{B})\exp [ - \beta \nu (k,\sigma )]. \\ \end{gathered} $

СОПОСТАВЛЕНИЯ С ПРЕЖНИМИ РАБОТАМИ

1. Традиционная МРГ [29] отражала внутримолекулярные колебания, частоты которых резко (до порядка) отличаются от частот межмолекулярных колебаний. Учет межмолекулярных колебаний в уравнениях (16) и (17) имеет конфигурационную природу и влияет на все термодинамические характеристики системы по сравнению с расчетами в исходной МРГ. (С ростом частоты величина Qvib стремится к единице, и чем меньше значения частот, тем больше вклад статсуммы колебательных движений.) Это уточнение происходит за счет модифицированных концентрационных составляющих для унарной и парной ФР, даже для области малых относительных смещений связанных молекул. Обобщение методов дискретного описания компонентов бинарных систем [29] на случай учета влияния межмолекулярных колебательных движений построено в соответствии с данными эксперимента о предварительном установлении равновесия по импульсу перед установлением равновесия по массе. Этот принцип использован также для расширения области применимости предложенных модификаций теории на область существенных смещений связанных молекул за счет выделения средних положений равновесия между этими молекулами.

Учет колебательных движений требует процедуры расчета колебательного спектра. Для ассоциатов в паровой фазе данная задача хорошо известна, и для нее имеются разработанные методы колебательной динамики. Их применение не вызывает принципиальных проблем. Но для объемных фаз даже для твердых тел с заданной структурой кристаллической решетки расчет колебательного спектра требует усилий, особенно в случае разных компонентов. Поэтому для расчета колебательных спектров в разупорядоченной жидкой фазе требуется разработка своих подходов, которые в настоящее время недостаточно хорошо развиты. В качестве грубой оценки учета колебаний может быть использована так называемая квазидимерная модель, отражающая влияние температуры и локальной концентрации соседей [30, 33–35]. Эта модель обобщает модель Ми для жидкой фазы [31], которая в свою очередь является аналогом модели Эйнштейна для твердого тела [19–22]. Квазидимерная модель отражает локальные свойства раствора и может быть использована для оценки частот не только в объемной фазе, но и в неоднородных системах: вблизи поверхностей и на границе раздела пар–жидкость [35].

2. Если пренебречь влиянием величины смещений на величины статсумм в уравнениях (22) и (24), то это исключает колебательные вклады, как и в исходных уравнениях цепочки ББГКИ и ИУ, построенных на ее основе, но сохраняет влияние потенциальной функции на термодинамические функции через больцмановские сомножители в сомножителях $\prod\nolimits_A {} $. Такой же вид уравнений был использован в первой работе [45] по одномерной жидкости. В одномерном случае КХП уравнения относятся к точным решениям конфигурационной задачи, поэтому без учета колебательных движений новые уравнения соответствуют работе [45]. Для простейшего случая однородной объемной фазы с числом соседей z > 2 уравнение (23) перепишется как

$\beta {{P}_{A}}{\text{/}}Q_{A}^{0} = \frac{1}{{1 - {{\theta }_{A}}}}\int\limits_{r_{f}^{A} \in \omega (f)} {dr_{f}^{A}{{\theta }_{A}}(r_{f}^{A})} \times $
(25)
$ \times \;\left[ {\int\limits_{r_{g}^{A} \in \omega (g)} {dr_{g}^{A}} (1 + {{t}_{{AA}}}(r_{f}^{A},r_{g}^{A})} \right. \times $
$ \times \;{{\left. {\{ \exp [ - \beta {{\varepsilon }_{{AA}}}(r_{f}^{A},\mathop {r_{g}^{A}}\limits_{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}^{^{{}}} )] - 1\} )} \right]}^{z}},$
где диапазон изменения расстояния между двумя частицами $r_{g}^{A}$ равен ${{\lambda }_{{\min }}} \leqslant r_{g}^{A} \leqslant {{\lambda }_{{\max }}}$ (более подробно см. в [33, 34]); выражение в фигурных скобках есть функция Майера [17].

Различия между учетом колебаний в обычном их понимании и в виде больших смещений, заложенным во всех теориях жидкого состояния, могут влиять на конечный результат, как через организацию этапа расчета интегрирования ИУ, так и через точность описания взаимной корреляции окружающих соседей. Оба этих момента наглядно показывает уравнение (25), в котором веса конфигураций из k соседей задаются биномиальными коэффициентами $C_{z}^{k}$ в отсутствие колебательных статсумм.

Кроме того, в плотных фазах возникает влияние колебаний на характеристики потенциальных функций, которые включают в себя эффекты ангармонизма [33]. В результате на шкале времен релаксации масс происходит переход от функций Eij(r) или εАА(r) (хорошо известных в литературе и определяемых из экспериментов в газовой фазе [26]) к усредненным параметрам латерального взаимодействия $\tilde {\varepsilon }$ в плотных фазах [27, 33–35].

3. В МРГ второй вириальный коэффициент выражается как $z(1 - \exp ( - \beta {{\varepsilon }_{{AA}}}))$. В континуальной теории он имеет вид $2\pi \int_0^\infty {} {{r}^{2}}[1 - \exp ( - \beta u(r)]dr$ [4, 5, 17], который дают ту же самую температурную зависимость, или, по сути, совпадает с выражением в МРГ . Отличия в числовых коэффициентах связаны с разными способами изменения объема. В новом подходе второй вириальный коэффициент выписывается как $z(1 - \exp ( - \beta {{\varepsilon }_{{AA}}}){\text{/}}{{Q}_{{\dim }}})$, где ${{Q}_{{\dim }}}$ – колебательная статсумма димера. Если ввести обозначение ${{\tilde {\varepsilon }}_{{AA}}} = {{\varepsilon }_{{AA}}} - kT\ln {{Q}_{{\dim }}}$, то формально старое выражение в МРГ сохраняет свой вид: $z(1 - \exp ( - \beta {{\tilde {\varepsilon }}_{{AA}}}))$. Таким образом, из всех экспериментальных измерений, по которым определяют значение парного потенциала межмолекулярного взаимодействия, реально находят величину ${{\tilde {\varepsilon }}_{{AA}}}$. Полученные значения решеточных параметров хорошо отвечают физическому смыслу: величина ε меньше глубины потенциальной ямы для двух атомов аргона (~0.23 ккал/моль) [46]. На это впервые, видимо, обратил внимание Хилл [47]. Позже колебательное движение димера учитывалось в рамках газо-кинетической модели, которая возникла из кинетической теории газов. В кинетической теории стартуют от полного пространства Лиувилля, и в ходе построений импульс не отделяют от координат. Сравнение газо-кинетической модели со старой МРГ показало их полную идентичность в области малых плотностей как для уравнения состояния, так и для сдвиговой вязкости [48]. Однако, уже начиная от третьего вириального коэффициента и выше (до плотной жидкой фазы) вклад колебаний в континуальной теории не учитывается, и это, как указано выше, влияет на величину CV .

Таким образом, предложенный дискретно-континуальный подход для расчета пространственного распределения молекул, который совмещает в себе преимущества двухшкального описания, позволил построить явный учет межмолекулярных колебательных движений, которые не выделяются в обычных ИУ для жидкостных систем, и, в принципе, позволяет дать оценку влияния колебательных движений молекул в жидкости на рассчитываемые термодинамические характеристики.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта № 18-03-00030а).

Список литературы

  1. Боголюбов Н.Н. Проблемы динамической теории в статистической физике. М.: Гостехиздат, 1946. 119 с.

  2. Green H.S. Molecular Theory of Fluids, Amsterdam, 1952.

  3. Фишер И.З. Статистическая теория жидкостей. М.: Физматгиз, 1961. 200 с.

  4. Хилл Т.Л. Статистическая механика. Принципы и избранные приложения. М.: Изд-во иностр. лит., 1960. 485 с.

  5. Крокстон К. Физика жидкого состояния. М.: Мир. 1979. 400 с.

  6. Мартынов Г.А. Классическая статическая физика. Теория жидкостей. Долгопрудный: Интеллект, 2011. 326 с.

  7. Фаулер Р., Гуггенгейм Э. Статистическая термодинамика, М.: Изд-во иностр. лит., 1949.

  8. Guggenheim E.A. Mixtures: The Theory of The Equlibrium Properties of Some Simple Classes of Mixtures Solutions and Alloys. Oxford: Clarendon Press, 1952. 271 p.

  9. Кривоглаз А.Н., Смирнов А.А. Теория упорядочивающихся сплавов. М.: ГИФМЛ, 1958. 388 с.

  10. Пригожин И.Р. Молекулярная теория растворов. М.: Металлургия, 1990. 359 с.

  11. Хачатурян А.Г. Теория фазовых переходов и структура твердых тел. М.: Наука, 1974. 384 с.

  12. Смирнова Н.А. Молекулярные теории растворов. Л.: Химия, 1982. 334 с.

  13. Методы Монте-Карло в статистической физике / под ред. К.М. Биндера. М.: Мир, 1982. 400 с.

  14. Heino P. // Phys. Rev. B. 2005. V. 71. P. 144302.

  15. Turney J.E., Landry E.S., McGaughey A.J.H., Amon C.H. // Phys. Rev. B. 2009. V. 79. P. 064301.

  16. Белащенко Д.К., Сиренко А.Н., Тытик Д.Л. // Российские нанотехнологии. 2009. Т. 4. № 9–10. С. 64.

  17. Майер Дж., Гепперт-Майер М., Статистическая механика. М.: Мир, 1980.

  18. Ferziger J.H., Kaper H.G. Mathematical Theory of Transport Processes in Gases. Amsterdam-London: North-Holland Publishing Company, 1972.

  19. Лейбфрид Г. Микроскопическая теория механических и тепловых свойств кристаллов. М.-Л.: ГИФМЛ, 1963. 313 с.

  20. Борн М., Кунь Х. Динамическая теория кристаллических структур. М.: Изд-во иностр. лит., 1958.

  21. Жирифалько Л. Статистическая теория твердого тела. М.: Мир, 1975. 382 с.

  22. Хир К. Статистическая механика, кинетическая теория и стохастические процессы. М.: Мир, 1976.

  23. Eucken A., Hauck F. // Z. Phys. Chem. A. 1928. V. 134. P. 161.

  24. Мелвин-Хьюз Е.А. Физическая химия. М.: Изд-во иностр. лит., 1962. Кн. 2. 1148 с.

  25. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Механика. Т. 1. М.: Наука, 1965.

  26. Гиршфельдер Дж., Кертис Ч., Берд Р. Молекулярная теория газов и жидкостей. М.: Изд-во иностр. лит., 1961. Т. 929. С. 3.

  27. Базаров И.П. Статистическая теория кристаллического состояния. М.: Изд-во МГУ, 1972. 118 с.

  28. Товбин Ю.К. // Журн. физ. химии. 2006. Т. 80. № 10. С. 1753.

  29. Товбин Ю.К. Тeория физико-химичeских процeссов на границe газ – твeрдоe тeло. М.: Наука, 1990. 288 с.

  30. Товбин Ю.К. Молекулярная теория адсорбции в пористых телах. М.: Физматлит, 2012. 624 с.

  31. Мелвин-Хьюз Е.А. Физическая химия. М.: Изд-во иностр. лит., 1962. Т. 1. Гл. 8.

  32. Товбин Ю.К. // Журн. физ. химии. 1981. Т. 55. № 2. С. 284.

  33. Товбин Ю.К. // Там же. 2013. Т. 87. № 7. С. 1097.

  34. Товбин Ю.К., Рабинович А.Б. // Там же. 2014. Т. 88. № 2. С. 351.

  35. Товбин Ю.К. // Там же. 2015. Т. 89. № 11. С. 1704.

  36. Дин П. // Вычислительные методы в теории твердого тела. М.: Мир, 1975. С. 209.

  37. Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. М.: Мир, 1984. 528 с.

  38. Сырников Ю.П. // Физика многочастичных систем. Киев: Наукова Думка, 1987. Вып. 11. С. 83.

  39. Сырников Ю.П. // Межвуз. сб. науч. тр. “Растворы – электролитные системы”, Иваново, 1988. С. 10.

  40. Заславский Г.М. Стохастичность динамических систем. М.: Наука, 1984. 271 с.

  41. Френкель Я.И. Кинетическая теория жидкостей. М.-Л., 1945.

  42. Пригожин И., Дефэй Р. Химическая термодинамика. Новосибирск: Наука, 1966. 510 с.

  43. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 5. Статистическая физика. М.: Наука, 1964. 568 с.

  44. Товбин Ю.К., Сенявин М.М., Жидкова Л.К. // Журн. физ. химии. 1999. Т. 73. № 2. С. 304.

  45. Gursey F. // Pric. Cambr. Phil. Soc. 1950. V. 46. P. 182.

  46. Товбин Ю.К // Журн. физ. химии. 1998. Т. 72. № 5. С. 775.

  47. Hill T.L. // J. Chem. Phys. 1955. V. 23. P. 617.

  48. Егоров Б.В., Комаров В.Н., Маркачев Ю.Е., Товбин Ю.К. // Журн. физ. химии. 2000. Т. 74. № 5. С. 882.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал