Журнал физической химии, 2019, T. 93, № 9, стр. 1385-1391

Фронтальная динамика сорбции молекул мезопористыми материалами типа МСМ-41

Б. М. Даринский^a, С. И. Карпов^a, *, В. Ф. Селеменев^a, О. О. Крижановская^a, **

^a Воронежский государственный университет
394018 Воронеж, Россия

^* E-mail: karsiv@mail.ru
^** E-mail: o.krizhanovskaya@gmail.com

Поступила в редакцию 27.12.2018
После доработки 27.12.2018
Принята к публикации 19.01.2019

DOI: 10.1134/S0044453719090048

Аннотация

Рассмотрена сорбция молекул наноструктурированными мезопористыми сорбентами МСМ-41 в динамических условиях. Представлена модель динамики сорбции молекул с учетом особенностей транспорта в сорбентах, кинетического параметра, учитывающего соотношение между равновесными концентрациями растворенных молекул в растворе и в фазе адсорбента. Показан эффект влияния соотношения между скоростями и характеристическим временем диффузионных процессов сорбтивов в жидкости и твердом теле на закономерности сорбционного процесса. Отмечена роль природы адсорбента и контактирующей с ним подвижной фазы, а также рассмотрено влияние растворимости и разности в энергии взаимодействий адсорбтива с растворителем и адсорбентом на изменение кинетического параметра К и ширину фронта сорбции. Указаны условия изменения ширины фронта сорбции в зависимости от размера гранул, концентрации примесных молекул в жидкости. Рассмотрены предельные случаи кинетики адсорбции примесных молекул из растворов.

Ключевые слова: мезопористые материалы, сорбция, математическая модель динамики сорбции

Появление нового класса упорядоченных материалов семейства M41S, наибольшее распространение из которого получили материалы типа МСМ-41 [1], благодаря узкому распределению пор по размеру, аномально большой для неорганических материалов удельной площади поверхности (более 1000 м²/г), объему пор (более 1 см³/г). обусловило развитие использования их в катализе, неорганической, супрамолекулярной химии [2]. Последние годы существенный интерес к наноструктурированным материалам обусловлен их перспективными сорбционными свойствами [3–9], находящими применение в медицине [10], в анализе (хроматографии) [11–14].

При прогнозировании процессов сорбционного разделения и концентрирования веществ необходимо рассмотрение математических моделей динамики сорбции. Рассмотрение сорбции в динамических условиях предполагает корректный учет вида изотермы сорбции в широком интервале концентраций и температур. Наиболее часто рассматриваются решения задач динамики сорбции [15, 16], предполагая линейный или нелинейный вид изотерм сорбции, преобладание внутри-, внешнедиффузионной или химической кинетики сорбции веществ [17]. С учетом этого варьируются факторы, определяющие вид хроматограмм, а именно: время (объем) проскока, ширина фронта сорбции, в значительной степени влияющие на возможность разделения близких по природе веществ. Описание выходных кривых с использованием асимптотических решений задач динамики сорбции [18–21] дает возможность учитывать кинетические и равновесные параметры, определяющие движение веществ в сорбционной системе [22–25]. Однако такие решения возможны при больших и малых временах процесса. В настоящей работе представлено решение задачи динамики сорбции веществ пористыми материалами с упорядоченной структурой. Особенностями массопереноса молекул являются ограничения в размере (диаметре) пор, что обуславливает особенности массопереноса молекул и ионов, в том числе органических веществ.

Целью настоящей работы явилось построение модели и нахождение закономерностей сорбции молекул мезопористыми твердотельными материалами в режиме фронтальной хроматографии. Рассмотрение сорбции в динамических условиях предполагает корректный учет вида изотермы сорбции в широком интервале концентраций и температур.

МЕТОДИКА РАСЧЕТА

Будем полагать, что в единице объема жидкости и твердого адсорбента имеется g_L и g_S – число мест, в которых может располагаться растворенная молекула в жидкой фазе и сорбенте, соответственно; n – среднее число молекул, находящихся в разрешенном месте, равное отношению числа молекул растворенного вещества к числу мест в растворе. Разрешенный интервал значений n = (0...1). Аналогичный смысл имеет параметр N для адсорбента.

Поскольку в каждом разрешенном месте может находиться не более одной молекулы, их среднее число в растворе определяется распределением Ферми–Дирака:

(1)

${n = \frac{1}{{\exp \left( {\frac{{{{E}_{L}} - {{\mu }_{L}}}}{{kT}}} \right) + 1}}},$

где E_L – энергия взаимодействия растворенной молекулы с жидкостью; μ_L – химический потенциал молекулы в жидкости.

Аналогичные соотношения могут быть записаны и для среднего числа молекул в сорбенте:

(2)

${N = \frac{1}{{\exp \left( {\frac{{{{E}_{S}} - {{\mu }_{S}}}}{{kT}}} \right) + 1}}},$

где E_S – энергия взаимодействия молекулы с адсорбционным центром в твердом теле; μ_L – химический потенциал молекулы в сорбенте.

В условиях равновесия можно записать:

(3)

${{{\mu }_{L}} = {{\mu }_{S}} = \mu }.$

Отсюда получаем соотношение между средними числами заполнения молекул в разрешенных положениях в жидкости и в твердом теле:

(4)

${p\frac{{1 - n}}{n} = \frac{{1 - N}}{N}},$

где:

(5)

${p = \exp \left( {\frac{{{{E}_{S}} - {{E}_{L}}}}{{kT}}} \right) \ll 1},{\quad {{E}_{S}} < {{E}_{L}} < 0}$

является термодинамическим параметром, определяющим соотношение между равновесными концентрациями растворенных молекул в растворе и адсорбенте.

Решая это уравнение относительно N, получим формулу типа Ленгмюра [8], записанную через равновесные характеристики системы:

(6)

${N = \frac{n}{{n + (1 - n)р}}}.$

Следует полагать, что время установления равновесия между концентрациями растворенных молекул в области контакта жидкость–гранула значительно меньше, чем характерное время процесса сорбции. Поэтому в кинетическом процессе на поверхности контакта выполняется равновесное соотношение между этими концентрациями. В этом случае (4) можно переписать в виде (7):

(7)

${p\frac{{1 - {{n}_{i}}}}{{{{n}_{i}}}} = \frac{{1 - {{N}_{i}}}}{{{{N}_{i}}}}},$

где n_i и N_i – средние числа на поверхности жидкости и твердого тела в области их контакта.

Рассмотрим диффузионную кинетику растворенных молекул при течении жидкого раствора через пористую среду. При обтекании жидкостью частиц адсорбата выполняются условия для ламинарного вязкого течения. Полагая, что на поверхности твердого тела выполняется условие закрепления вещества, находим средний градиент скорости течения:

(8)

${\operatorname{grad} v \cong \frac{V}{r}},$

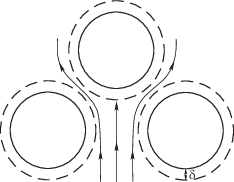
где V – скорость протекания жидкости по каналам между гранулами, которая определяется средним потоком жидкости, превосходя среднюю скорость в потоке в соотношение площади столба к площади каналов. Здесь r – размер каналов, который примем примерно равным размеру гранул. В процессе течения жидкости по “губчатой” среде происходит разбиение потока жидкости на расстояниях отдельных зерен. При этом серединные участки потока жидкости, обогащенные растворенными молекулами, становятся примыкающими к поверхности гранул, как показано на рис. 1. В результате происходит ускорение диффузионного оттока растворенных молекул по сравнению с аналогичными потоками в цилиндрической трубке. С учетом этого эффекта оценим эффективную толщину диффузионного слоя, через который осуществляется доставка растворенных молекул из жидкой фазы в сорбент.

Рис. 1.

Потоки раствора сорбата, примыкающие к поверхности гранул.

Среднее время τ контакта жидкости с гранулой равно:

(9)

${\tau = \frac{r}{{{{V}_{l}}}}}.$

За этот промежуток времени диффузионным путем успевают достичь поверхности гранулы молекулы из слоя толщиной:

(10)

${\delta = \sqrt {{{D}_{L}}\tau } = \sqrt {{{D}_{L}}\frac{r}{{{{V}_{l}}}}} },$

где V_l – скорость жидкости на расстоянии δ от поверхности гранулы, D_L – коэффициент диффузии молекулы в жидкой среде. Эффективная скорость течения жидкости в приповерхностном слое равна:

(11)

${{{V}_{i}} = \operatorname{grad} v\delta = \frac{V}{r}\sqrt {{{D}_{L}}\frac{r}{{{{V}_{l}}}}} }.$

Отсюда находим толщину диффузионного слоя:

(12)

${\delta = {{{\left( {\frac{{{{D}_{L}}{{r}^{2}}}}{V}} \right)}}^{{1/3}}}}.$

Диффузионная плотность потока в этих условиях:

(13)

${{j}_{1}} = \frac{{{{D}_{L}}S}}{\delta }(n - {{n}_{i}}) = \frac{{D_{L}^{{2/3}}{{V}^{{1/3}}}S}}{{{{r}^{{2/3}}}}}(n - {{n}_{i}}).$

Здесь S – площадь поверхности гранул адсорбата, контактирующей с раствором, в единице объема ([S] = 1/L).

Отметим, что для малых скоростей течения ${(\delta = r)}$, ${\tau = \frac{{{{r}^{2}}}}{{{{D}_{L}}}}}$. В этом случае математическая модель кинетики адсорбции может быть представлена в виде следующей системы уравнений:

(14)

${\frac{{\partial n}}{{\partial t}} = - \frac{{{{D}_{L}}S}}{\delta }(n - {{n}_{i}}) - V\frac{{\partial n}}{{\partial z}}},$

(15)

${\frac{{\partial N}}{{\partial t}} = - \frac{{{{D}_{S}}}}{{{{r}^{2}}}}(N - {{N}_{i}})}.$

Здесь ${\frac{{\partial n}}{{\partial t}}}$ – скорость изменения среднего числа растворенных молекул в жидкости, ${\frac{{\partial N}}{{\partial t}}}$ – скорость захвата молекул гранулами сорбента, ${\frac{{\partial n}}{{\partial z}}}$ – изменение концентрации вдоль слоя по координате z.

Второе слагаемое (14) учитывает изменение локальной концентрации жидкости при наличии потока. Уравнение (15) получается предположением, что скорость захвата молекул контролируется диффузией этих молекул от поверхности гранул в ее объем, причем учитывается заключительная стадия этого процесса, в которой он характеризуется временем релаксации:

(16)

${{{\tau }_{S}} = \frac{{{{r}^{2}}}}{{{{D}_{S}}}}}.$

Отметим, что два уравнения ((14) и (15)) объединяются в систему уравнений граничным условием (7), которое отражает равновесие системы молекул в узком приграничном слое.

Другое граничное условие получим из равенства потоков растворенных молекул: входящего из жидкой фазы и выходящего с поверхности гранулы в ее объем:

(17)

${{{g}_{L}}\frac{{S {{D}_{L}}}}{\delta }(n - {{n}_{i}}) = {{g}_{S}}\frac{{{{D}_{S}}}}{{{{r}^{2}}}}(N - {{N}_{i}})}.$

Это соотношение записывается в виде:

(18)

${n - {{n}_{i}} = - K(N - {{N}_{i}})},$

где:

(19)

${K = \frac{{{{g}_{S}}}}{{{{g}_{L}}}}\frac{{{{D}_{S}}}}{{{{D}_{L}}}}\frac{\delta }{{S {{r}^{2}}}}},$

g_L, g_S – количества мест для адсорбируемых молекул в единице объема жидкости и адсорбата, соответственно.

Безразмерный коэффициент К определяет соотношение между скоростями и характеристическим временем τ диффузионных процессов примесных молекул в жидкости и твердом теле. Гельферих и Хуанг [24] показали, что простым критерием отнесения к внешне- или внутридиффузионной кинетике является величина He, характеризующая скорости двух процессов: внешней и внутренней диффузии. Параметр К аналогичен по своему физическому смыслу диффузионному критерию δ*, характеризующему вклад внешней и внутренней диффузии в кинетику сорбции ионов. Для сорбирующей среды, в которой выполняется закон Генри (случай линейной изотермы Г = = dN/dn = const) записывают как критерий Био (Bi) [25, 26]:

(19а)

${Bi = \frac{{\beta {{R}^{2}}}}{{\bar {D}\Gamma }}},$

где β ≡ D_L/d – кинетический коэффициент, характеризующий диффузию в растворе у поверхности сорбента, ${\bar {D}}\; \equiv {{D}_{S}}$ – коэффициент диффузии в фазе сорбента.

В выражении (18) соотношение g_S/g_L может характеризовать константу Генри при линейной изотерме сорбции или производную, характеризуемую величиной коэффициента распределения, при нелинейной изотерме сорбции. В общем случае параметр К в формуле (18) имеет физический смысл аналогичный диффузионному критерию Гельфериха [24, 25] и Био (Bi) [19–21].

Важен учет влияния характера изменения указанного параметра на динамику сорбции, а именно на проскок сорбата на выходных кривых и на ширину фронта сорбции. Малые величины K свидетельствуют об относительной медленности диффузионного процесса внутри твердого тела. Часто решение задачи динамики сорбции проводят в условиях отсутствия внутридиффузионного лимитирования, что упрощает получение аналитического решения. Ниже будет рассматриваться случай, когда K будет иметь достаточно большую величину, то есть, K $ \gg $ p, n₀. Отметим, что поскольку K уменьшается с увеличением скорости протекания раствора (см. уравнение (12)), может произойти смена контролирующего процесса сорбции от диффузии в жидкости к диффузии в твердом теле.

Решение системы (14)–(15) ищут в виде сорбционного фронта, движущегося со скоростью υ в направление потока жидкого раствора. Для этого подставляют:

(20)

${n(t,z) = n\left( {t - \frac{z}{v}} \right)},\quad {N(t,z) = N\left( {t - \frac{z}{v}} \right)}$

в систему (14)–(15). В результате получено выражение:

(21)

${\left( {1 - \frac{V}{v}} \right)\frac{{dn}}{{dt}} = - \frac{{{{D}_{L}}S}}{\delta }(n - {{n}_{i}})},$

(22)

${\frac{{dN}}{{dt}} = \frac{{{{D}_{S}}}}{{{{r}^{2}}}}(N - {{N}_{i}})}.$

Из системы (21)–(22) находят:

(23)

${\frac{{dN}}{{dn}} = \frac{{V - v}}{v}\frac{{g{}_{L}}}{{{{g}_{S}}}}}.$

Решение этого дифференциального уравнения приводит к линейной зависимости во всем интервале концентраций:

(24)

${N = Un}.$

(25)

${U = \frac{{V - v}}{v}\frac{{g{}_{L}}}{{{{g}_{S}}}}}.$

Формулы (24), (25) позволяют найти выражение для скорости движения сорбционного фронта. Для этого, полагая, что вдали от фронта ${\left( {z \to - \infty } \right)}$ возникает равновесное распределение между молекулами адсорбтива в жидкости и адсорбенте, из (7) получают следующие соотношения:

(26)

${p\frac{{1 - {{n}_{0}}}}{{{{n}_{0}}}} = \frac{{1 - U{{n}_{0}}}}{{U{{n}_{0}}}}},$

где n₀ – исходное отношению числа молекул растворенного вещества к числу мест в растворе.

(27)

${U = \frac{1}{{{{n}_{0}} + p - {{n}_{0}}p}}}.$

Подставляя (27) в (25) и разрешая полученное уравнение относительно $v$, находят:

(28)

${v = \frac{{({{n}_{0}} + p){{g}_{L}}}}{{{{g}_{S}} + {{g}_{L}}({{n}_{0}} + p)}}V}.$

Важным случаем в практике разделения веществ является случай малых концентраций растворенных молекул (n₀$ \ll $ 1). Учитывая необходимое для сорбции условие p $ \ll $ 1, из (27) и (28) получают более простые формулы:

(29)

${U = \frac{1}{{{{n}_{0}} + p}}},$

(30)

${v = \frac{{{{g}_{L}}({{n}_{0}} + p)}}{{{{g}_{S}}}}V}.$

Для решения системы (21), (22) находят сначала соотношение между n и n_i, используя (7) и (18):

(31)

${n = {{n}_{i}}\frac{{(p + K + {{n}_{i}})(p + {{n}_{0}})}}{{(p + K + {{n}_{0}})(p + {{n}_{i}})}}}.$

Решение уравнения (31) относительно n_i представляет собой довольно громоздкую функцию, поэтому оно оказывается неудобным для его подстановки в уравнение (21). Поэтому проводят замену переменной в самом уравнении, полагая, что неизвестной функцией будет n_i. В результате получают:

(32)

${\frac{{d{{n}_{i}}}}{{dt}} = \frac{1}{{{{\tau }_{S}}}}\frac{{({{n}_{i}} + p){{n}_{i}}({{n}_{0}} - {{n}_{i}})}}{{(Kp + {{p}^{2}} + 2p{{n}_{i}} + n_{i}^{2})}}}.$

Решение этого уравнения записывается в громоздком, но обозримом виде:

(33)

$\begin{gathered} \frac{t}{{{{\tau }_{S}}}} = \frac{{(K + p)}}{{{{n}_{0}}}}\ln ({{n}_{i}}) - \frac{{(Kp + n_{0}^{2} + 2{{n}_{0}}p + {{p}^{2}})}}{{{{n}_{0}}({{n}_{0}} + p)}} \times \\ \times \;\ln ({{n}_{0}} - {{n}_{i}}) - \frac{K}{{{{n}_{0}} + p}}\ln (p + {{n}_{i}}). \\ \end{gathered} $

Формулы (31) и (33) определяют параметрическую зависимость n(t), в которой в качестве параметра выступает n_i, меняющееся в интервале (0..1).

Рассмотрим предельные случаи кинетики разделения примесных молекул. В случае относительно медленной диффузии в твердофазной среде, т.е. для K $ \ll $ p, n₀, из (31) и (32) находят:

(34)

${n = {{n}_{i}}},{\quad \frac{{dn}}{{dt}} = \frac{1}{{{{\tau }_{S}}}}\frac{{n({{n}_{0}} - n)}}{{p + n}}}.$

Полагая в (34) в качестве характерного времени адсорбционного процесса τ_S и вводя новые переменные:

(35)

${n = {{n}_{0}}f},$

(36)

${\frac{z}{\lambda } \to z},$

(37)

${q = \frac{p}{{{{n}_{0}}}}},$

где λ – ширина фронта; f меняется в интервале (0..1), получим уравнение (34) в следующем виде:

(38)

${\frac{{df}}{{dt}} = \frac{{f(1 - f)}}{{q + f}}}.$

Параметр q, который может меняться в широких пределах, характеризует условие насыщения адсорбента молекулами сорбата. Полагая, что ${N \cong 1 = \frac{{{{n}_{0}}}}{p} = \frac{1}{q}}$, приходим к выводу: условие насыщения выполняется при малых значениях параметра q $ \ll $ 1 (рис. 2а).

Рис. 2.

Расчетные выходные кривые веществ при сорбции для трех различных значений параметра при ln q = –1 (1), 0 (2), 1 (3) при ln K = 1 (а), 0 (б), –1 (в).

Решение уравнения (38) зависит от одного параметра q. При больших величинах этого параметра, что соответствует достаточно малой концентрации примесей в жидкой фазе, уравнение (38) представляется в виде:

(39)

${\frac{{df}}{{dt}} = \frac{{f(1 - f)}}{q}}.$

Решение (39), удовлетворяющее граничным условиям ${f(\infty = {\text{1}})}$, ${f( - \infty ) = {\text{0}}}$, представляется в виде:

(40)

${f = \frac{1}{{1 + \exp \left( {\frac{{ - t}}{{q{{\tau }_{S}}}}} \right)}}}.$

Оно имеет антисимметричный вид с точкой инверсии f = 1/2. В этом случае ширина фронта:

(41)

${\lambda = Vq{{\tau }_{S}}}$

будет увеличиваться при уменьшении концентрации молекул (рис. 2б). С уменьшением q при снижении температуры или увеличении n₀уравнение (39) в пределе при q → 0 принимает простой вид:

(42)

${\frac{{df}}{{dt}} = 1 - f}.$

Можно записать его решение:

(43)

$\begin{gathered} f = 1,\quad t > 0; \\ \exp ( - t{\kern 1pt} /{\kern 1pt} {{\tau }_{S}}),\quad t < 0. \\ \end{gathered} $

Адсорбционный фронт становится экспоненциально спадающим и имеет характеристическую ширину:

(44)

${\lambda = V{{\tau }_{S}}}.$

Таким образом, он становится экспоненциально спадающим и имеет минимальную для рассмотренных условий ширину, которая определяется характерным временем диффузии молекул внутри гранул.

В другом предельном случае больших значений K (рис. 2, кривая 2) из (31) получают:

(45)

${{{n}_{i}} = \frac{{pn}}{{p + {{n}_{0}} - n}}}.$

Подстановка (45) в (21) приводит к уравнению:

(46)

${\frac{{dn}}{{dt}} = \frac{{(p + {{n}_{0}})}}{{{{\tau }_{L}}}}\frac{{n({{n}_{0}} - n)}}{{(p + {{n}_{0}} - n)}}},$

(47)

${{{\tau }_{L}} = \frac{\delta }{{{{D}_{L}}S}} = \frac{{{{r}^{{2/3}}}}}{{{{V}^{{1/3}}}D_{L}^{{2/3}}S}}}.$

Делая замену переменных t/τ_L→ t, получают уравнение:

(48)

${\frac{{df}}{{dt}} = {{n}_{0}}(q + 1)\frac{{f(1 - f)}}{{(q + 1 - f)}}}.$

Характерная ширина фронта в этом случае равна:

(49)

${\lambda = \frac{{V{{\tau }_{L}}}}{{({{n}_{0}} + p)}} = \frac{{{{V}^{{2/3}}}{{r}^{{2/3}}}}}{{({{n}_{0}} + p)D_{L}^{{2/3}}S}}}.$

Таким образом, ширина фронта увеличивается с ростом скорости протекания жидкого раствора и размера гранул по степенному закону. Асимметрия фронта также наращивается с увеличением параметра p.

В переходной области параметров, в которой меняется контролирующий механизм процесса адсорбции от диффузии в гранулах к диффузии в жидкости, необходимо использовать точное решение (33) (рис. 2в).

Таким образом, в настоящей работе представлена модель динамики сорбции молекул с учетом особенностей транспорта в сорбентах, кинетического параметра, определяющего соотношение между равновесными концентрациями растворенных молекул в растворе и адсорбенте. Показано влияние соотношения между скоростями и характеристическим временем τ диффузионных процессов примесных молекул в жидкости и твердом теле.

Анализ соотношений параметра К и влияния растворимости и разности в энергии взаимодействий адсорбтива с растворителем и адсорбентом демонстрирует роль природы адсорбента и подвижной фазы в сорбции адсорбтивов. В статье указаны условия изменения ширины фронта сорбции в зависимости от размера гранул, концентрации примесных молекул в жидкости. Рассмотрены предельные случаи кинетики адсорбции примесных молекул из растворов.

Можно сделать ряд выводов, которые в значительной степени являются общепринятыми и подтверждают правомерность использования предложенной модели для описания адсорбции веществ. А именно:

1. При значительных различиях энергии взаимодействий сорбата с растворителем (жидкостью) и адсорбентом, а также при достаточно малой концентрации примесей в жидкой фазе (малых n), при относительно медленной диффузии в твердофазной среде (K $ \ll $ p, n₀) ширина фронта λ увеличивается при уменьшении концентрации молекул. Этот вывод может соответствовать случаю, когда в качестве подвижной фазы используются неполярные растворители, имеющие малое сродство к адсорбенту (для кремнеземов – гексан, ацетонитрил и др.).

2. При уменьшении температуры или увеличении растворимости (n₀) адсорбционный фронт становится экспоненциально спадающим и имеет минимальную ширину, которая определяется характерным временем диффузии молекул внутри гранул.

Вторая группа выводов в значительной степени демонстрирует преимущества упорядоченных материалов, их структуры, для описания адсорбции органических молекул из растворителей различной природы:

3. При достаточно большой величине K $ \gg $ p и n₀ (при малом различии в энергиях взаимодействий вещества в растворе и адсорбенте, а также при малой растворимости адсорбтива) может произойти смена контролирующего процесса сорбции от диффузии в жидкости к диффузии в твердом теле, поскольку K уменьшается с увеличением скорости протекания раствора. В случае больших K ширина фронта λ увеличивается с ростом скорости протекания жидкого раствора и размера гранул по степенному закону. Асимметрия фронта также наращивается с увеличением параметра p. Этот вывод может соответствовать случаю, когда в качестве растворителя используются протонодонорные и протоноакцепторные растворители, имеющие большее сродство к адсорбенту (этанол, элилацетат и другие – для кремнеземов).

4. В переходной области параметров, в которой меняется контролирующий механизм процесса адсорбции от диффузии в гранулах к диффузии в жидкости, необходимо использовать точное решение, учитывающее равновесные и кинетические параметры сорбции.

Таким образом, в работе получена формула для характеристик процесса сорбции веществ в режиме образования и движения концентрационного фронта. Это аналитическое выражение справедливо во всей области изменений параметров, определяющих условия протекания процесса. Отметим, что следует ожидать существенного изменения кинетического параметра К в условиях относительно быстрой диффузии сорбтивов (в том числе органических молекул) в системе упорядоченных мезопор, которыми обладают мезопористые аналоги МСМ-41 и SBA-15.

Работа выполнена при поддержке Минобрнауки России в рамках базовой части государственного задания вузам в сфере научной деятельности на 2017–2019 годы. Проект № 4.6937.2017/8.9.

Список литературы

Beck J.S., Vartuli J.C., Roth W.J. et al. // J. Am. Chem. Soc. 1992. V. 114. P. 10834. doi.org/.https://doi.org/10.1021/ja00053a020
Ariga K., Vinu A., Hill J.P. et al. // Coordination Chemistry Reviews. 2007. V. 251. P. 2562. doi.org/.https://doi.org/10.1016/j.ccr.2007.02.024
Карпов С.И., Roessner F., Гульбин С.С. и др. // Сорбционные и хроматографические процессы. 2013. Т. 13. Вып. 2. С. 125.
Gokulakrishnan N., Pandurangan A., Somanathan T. et al. // Journal of Porous Materials. 2010. V. 17. № 6. P. 763. doi.org/.https://doi.org/10.1007/s10934-009-9348-6
Seliem Moaaz K., Komarneni Sridhar, Mostafa R. et al. // Microporous and Mesoporous Materials. 2016. V. 224. P. 51. doi.org/.https://doi.org/10.1016/j.micromeso.2015.11.011
Shu Y., Shao Y., Wei X. et al. // Microporous and Mesoporous Materials. 2015. V. 214. № 15 September, P. 88–94. doi.org/.https://doi.org/10.1016/j.micromeso.2015.05.006
Albayati T.M., Alwan G.M., Mahdy O.S. // Korean J. Chem. Eng. 2016. V. 34. № 1. P. 259. doi.org/https://doi.org/10.1007/s11814-016-0231-2
Qin Q., Xu Y. // Microporous and Mesoporous Materials. 2016. V. 232. P. 143. doi.org/.https://doi.org/10.1016/j.micromeso.2016.06.018
Chaudhuri1 H., Dash S., Sarkar A. // J. Porous Mater. 2016. V. 23. № 5. P. 1227. doi.org/.https://doi.org/10.1007/s10934-016-0181-4
Koninti R.K., Palvai S., Satpathi S. et al. // Nanoscale. 2016. V. 8. P. 18436. doi.org/.https://doi.org/10.1039/C6NR06285G
Martínez Pérez-Cejuela H., Ten-Doménech I., El Haskouri J. et al. // Analytical and Bioanalytical Chemistry. 2018. V. 410. № 20: P. 4847. doi.org/.https://doi.org/10.1007/s00216-018-1121-8
Karpov S.I., Roessner F., Selemenev V.F. // J. Porous Mater. 2014. V. 21 P. 449. doi.org/.https://doi.org/10.1007/s10934-014-9791-x
Karpov S.I., Roessner F., Selemenev V.F. // J. Porous Mater. 2016. V. 23. № 2. P. 497. doi.org/.https://doi.org/10.1007/s10934-015-0103-x
Borodina E.V., Karpov S.I., Selemenev V.F. et al. // Nanotechnologies in Russia. 2010. V. 5. № 11–12. P. 808. doi.org/.https://doi.org/10.1134/S1995078010110091
Карпов С.И., Корабельникова Е.О. // Журн. физ. химии. 2015. Т. 89. № 6. С. 1030. doi.org/10.1134/S0036024415060151 Перевод: Karpov S.I., Korabel’nikova E.O. // Russ. J. Phys. Chem. A. V. 89. № 6. P. 1030.
Рачинский В.В. Введение в общую теорию динамики сорбции и хроматографии. М.: Наука, 1964. 135 с.
Венецианов Е.В., Рубинштейн Р.Н. Динамика сорбции из жидких сред. М.: Наука, 1983. 237 с.
Волжинский А.И., Константинов В.А. Регенерация ионитов. Ленинград: Химия, 1990. 240 с.
Шатаева Л.К., Кузнецова Н.Н., Елькин Г.Э. Карбоксильные катиониты в биологии / Под ред. Г.В. Самсонова. Ленинград: Наука, 1979. 286 с.
Кузьминых В.А. // Журн. физ. химии. 1980. Т. 54. № 4. С. 973.
Кузьминых В.А., Мелешко В.П., Голицын Ю.В. // Журн. физ. химии. 1980. № 7. С. 1802.
Langmuir I. // J. Am. Chem. Soc. 1917. V. 39. № 9. P. 1848. doi.org/.https://doi.org/10.1021/ja02254a006
Yoshida H., Kataoka T., Ruthven D.M. // Chemical Engeneering Science. 1984. V. 39. № 10. P. 1489. doi.org/.https://doi.org/10.1016/0009-2509(84)80007-X
Helfferich F.G., Hwang Y.-L. Ion Exchanger. Chapter 6.2. Ion Exchange kinetics. Ed. by K. Dorfner. Walter de Gruyter, Berlin, Germany. 1991. P. 1277.
Кокотов Ю.А., Пасечник В.А. Равновесие и кинетика ионного обмена. Ленинград: Химия, 1970. 336 с.
Хамизов Р.Х. // Сорбционные и хроматографические процессы. 2012. Т. 12. № 1. С. 5.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал