Журнал физической химии, 2019, T. 93, № 9, стр. 1283-1288

ТЕОРИЯ

Фазовая диаграмма изобарно-изотермической пятерной системы, содержащей s соединений, в 4D-пространстве составов представляет собой разбиение выпуклого многогранника с 5 + s вершинами системы на пятифазные комплексы – пентатопы. Их вершины соответствуют компонентам и соединениям, а каждое ребро соединяет две фазы, находящиеся в термодинамическом равновесии друг с другом. Дополнительные элементы диаграммы – трехфазные комплексы в виде треугольных граней и четырехфазные комплексы в виде тетраэдрических гиперграней. Проекция диаграммы на плоскость является непланарным графом. Проблему генерации изобарно-изотермических сечений пятерной системы можно свести к проблеме генерации таких графов с ограничениями, вытекающими из правила фаз.

Симплекс составов. Граф симплекса составов пятикомпонентной системы является проекцией выпуклого пентатопа на плоскость (рис. 1). Отмеченные точками вершины графа соответствуют фазам компонентов k₁, k₂, k₃, k₄, k₅. Каждая из них соединена ребрами со всеми остальными вершинами. Поэтому грани графа – треугольники, а все вершины четырехвалентны. Кроме того, элементами пентатопа являются также тетраэдры (гиперграни). Количество вершин $v$, ребер е, треугольных граней f и тетраэдров t определяется числом сочетаний r элементов из п [11]:

Перечислим элементы симплекса:

вершины $v$ = 5 = {k₁, k₂, k₃, k₄, k₅};

ребра e = 10 = {k₁k₂, k₁k₃, k₁k₄, k₁k₅, k₂k₃, k₂k₄, k₂k₅, k₃k₄, k₃k₅, k₄k₅};

грани f = 10 = {k₁k₂k₃, k₁k₂k₄, k₁k₂k₅, k₁k₃k₄, k₁k₃k₅, k₁k₄k₅, k₂k₃k₄, k₂k₃k₅, k₂k₄k₅, k₃k₄k₅};

гиперграни t = 5 = {k₁k₂k₃k₄, k₁k₂k₃k₅, k₁k₂k₄k₅, k₁k₃k₄k₅, k₂k₃k₄k₅}.

Графы фазовой диаграммы с бинарным соединением. Кроме фаз компонентов в системе могут присутствовать бинарные A, тройные B, четверные C и пятерные D соединения. На рис. 2 приведена фазовая диаграмма с бинарным соединением А состава (k₁)_m(k₂)_{1 –m}. При добавлении вершины А к графу, приведенному на рис. 1, возникает пять новых ребер (k₁А, k₂А, k₃А, k₄А, k₅А) и исчезает ребро k₁k₂, поэтому количество ребер у новой фигуры e = 14. Пентатоп k₁k₂k₃k₄k₅ разделяется на два пентатопа – k₁k₅k₄k₃А и k₂k₃k₄k₅А, имеющих общую гипергрань k₃k₄k₅А (рис. 2). Граф смежности пентатопов позволяет перечислить все тетраэдрические гиперграни и все треугольные грани. При образовании новой фигуры исчезают три тетраэдра с ребром k₁k₂, и возникает семь тетраэдров с вершиной А, следовательно, t = 9. В новой фигуре отсутствуют грани k₁k₂k₃, k₁k₂k₄, k₁k₂k₅, но появляются грани k₁k₃А, k₁k₄А, k₁k₅А, k₂k₃А, k₂k₄А, k₂k₅А, k₃k₄А, k₃k₅А, k₄k₅А. Поэтому на рис. 2 число граней f = 16. Количество пентатопов на фигуре обозначим через q. Перечислим элементы фигуры, изображенной на рис. 2:

$v$ = 6 = {k₁, k₂, k₃, k₄, k₅, A};

e = 14 = {k₁А, k₂А, k₃А, k₄А, k₅А, k₁k₃, k₁k₄, k₁k₅, k₂k₃, k₂k₄, k₂k₅, k₃k₄, k₃k₅, k₄k₅};

f = 16 = {k₁k₃А, k₁k₄А, k₁k₅А, k₂k₃А, k₂k₄А, k₂k₅А, k₃k₄А, k₃k₅А, k₄k₅А, k₁k₃k₄, k₁k₃k₅, k₁k₄k₅, k₂k₃k₄, k₂k₃k₅, k₂k₄k₅, k₃k₄k₅};

t = 9 = {k₁k₃k₄A, k₁k₃k₅A, k₁k₄k₅A, k₂k₃k₄A, k₂k₃k₅A, k₂k₄k₅A, k₃k₄k₅A, k₁k₃k₄k₅, k₂k₃k₄k₅};

q = 2 = {k₁k₅k₄k₃А, k₂k₃k₄k₅А}.

Описанный граф имеет две четырехвалентных и четыре пятивалентных вершины (${{v}_{{\text{4}}}}$ = 2, ${{v}_{{\text{5}}}}$ = 4).

Граф смежности пентатопов, показанный на рис. 2, можно рассматривать как топологическую схему диаграммы с бинарным соединением, так как из него можно определить все элементы диаграммы и порядок их связи между собой. Например, список граней фигуры на рис. 2, эквивалентный списку трехфазных равновесий, несложно составить из перечня тетраэдров. При этом каждая из граней, записанных простым шрифтом, – общая для двух тетраэдров, а грани, записанные жирным шрифтом, – общие для трех тетраэдров. Например, грань k₁k₃А принадлежит тетраэдрам k₁k₃k₄A и k₁k₃k₅A, а грань k₃k₄A – тетраэдрам k₁k₃k₄A, k₂k₃k₄A и k₃k₄k₅A. В списке гиперграней жирным шрифтом выделен внутренний тетраэдр, остальные образуют гиперповерхность фазовой диаграммы.

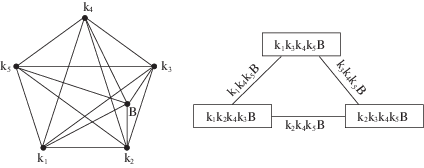
Тройное соединение. На фазовой диаграмме тройное соединение В состава (k₁)_m(k₂)_n (k₃)_{1 – m – n} соответствует вершине, расположенной на грани k₁k₂k₃ (рис. 3). При добавлении вершины В появляются пять новых ребер (Вk₁, Вk₂, Вk₃, Вk₄, Вk₅), поэтому количество ребер новой фигуры e = 15. При этом также исчезает грань k₁k₂k₃ и возникают 10 граней с вершиной В, следовательно, на диаграмме присутствует 19 граней. Тетраэдры k₁k₂k₃k₄ и k₁k₂k₃k₅ также исчезают, но появляются девять тетраэдров с вершиной В, т.е. число тетраэдров равно 12. Симплекс k₁k₂k₃k₄k₅ разделяется на три пентатопа: k₁k₂k₄k₅B, k₁k₃k₄k₅B, k₂k₃k₄k₅B. Два соседних пентатопа имеют общую тетраэдрическую гипергрань. Эти тетраэдры расположены внутри фазовой диаграммы, остальные принадлежат ее гиперповерхности. Граф смежности пентатопов для диаграммы с тройным соединением показан на рис. 3.

Список элементов фазовой диаграммы с тройным соединением имеет следующий вид:

$v$ = 6 = {k₁, k₂, k₃, k₄, k₅, В};

e = 15 = {k₁В, k₂В, k₃В, k₄В, k₅В, k₁k₂, k₁k₃, k₁k₄, k₁k₅, k₂k₃, k₂k₄, k₂k₅, k₃k₄, k₃k₅, k₄k₅};

f = 19 = {k₁k₂В, k₁k₃В, k₁k₄В, k₁k₅В, k₂k₃В, k₂k₄В, k₂k₅В, k₃k₄В, k₃k₅В, k₄k₅В, k₁k₂k₄, k₁k₂k₅, k₁k₃k₄, k₁k₃k₅, k₁k₄k₅, k₂k₃k₄, k₂k₃k₅, k₂k₄k₅, k₃k₄k₅};

t = 12 = {k₁k₂k₄B, k₁k₂k₅B, k₁k₃k₄B, k₁k₃k₅B, k₁k₄k₅B, k₂k₃k₄B, k₂k₃k₅B, k₂k₄k₅B, k₃k₄k₅B, k₁k₂k₄k₅, k₁k₃k₄k₅, k₂k₃k₄k₅};

q = 3 = {k₁k₂k₄k₅B, k₁k₃k₄k₅B, k₂k₃k₄k₅B}.

В полном списке граней девять принадлежит двум, а 10 – трем тетраэдрам.

Все вершины графа пятивалентны, т.е. $v$ = ${{v}_{{\text{5}}}}$ = 6.

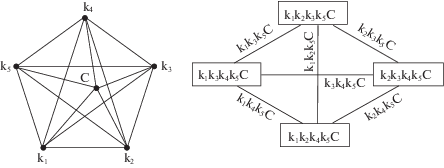
Четверное соединение. На графе фазовой диаграммы, приведенной на рис. 4, четверное соединение С состава (k₁)_m(k₂)_n(k₃)_р(k₄)_{1 – m – n – р} изображено вершиной, расположенной в тетраэдре k₁k₂k₃k₄. При добавлении вершины С на графе появляются четыре ребра внутри этого тетраэдра. Появление еще одного ребра k₅С связано с тем, что граф диаграммы на рис. 4 является полным. Симплекс k₁k₂k₃k₄k₅ разбивается на четыре пентатопа, разделенных шестью внутренними гипергранями. Перечислим элементы диаграммы с четверным соединением:

$v$ = 6 = {k₁, k₂, k₃, k₄, k₅, С};

e = 15 = {k₁С, k₂С, k₃С, k₄С, k₅C, k₁k₂, k₁k₃, k₁k₄, k₁k₅, k₂k₃, k₂k₄, k₂k₅, k₃k₄, k₃k₅, k₄k₅};

f = 20 = {k₁k₂C, k₁k₃C, k₁k₄C, k₁k₅C, k₂k₃C, k₂k₄C, k₂k₅C, k₃k₄С, k₃k₅C, k₄k₅C, k₁k₂k₃, k₁k₂k₄, k₁k₂k₅, k₁k₃k₄, k₁k₃k₅, k₁k₄k₅, k₂k₃k₄, k₂k₃k₅, k₂k₄k₅, k₃k₄k₅};

t = 14 = {k₁k₂k₃C, k₁k₂k₄C, k₁k₂k₅C, k₁k₃k₄С, k₁k₃k₅C, k₁k₄k₅C, k₂k₃k₄C, k₂k₃k₅C, k₂k₄k₅C, k₃k₄k₅С, k₁k₂k₃k₅, k₁k₂k₄k₅, k₁k₃k₄k₅, k₂k₃k₄k₅}

q = 4 = {k₁k₂k₃k₅C, k₁k₂k₄k₅C, k₁k₃k₄k₅C, k₂k₃k₄k₅C}.

В списке граней четыре встречаются по 2 раза, а 16 граней – по 3 раза. Из 14 тетраэдров восемь –внешние и шесть – внутренние. Для графа на рис. 4 $v = {{v}_{{\text{5}}}} = {\text{6}}$. Граф смежности пентатопов – тетраэдр.

Пятерное соединение. Вершина, соответствующая пятерному соединению, находится внутри пентатопа, она соединена конодами с каждой из его вершин.¹¹ Рассматриваемая фазовая диаграмма образована из пяти пентатопов. Перечислим ее элементы:

$v$ = 6 = { k₁, k₂, k₃, k₄, k₅, D};

e = 15 = {k₁D, k₂D, k₃D, k₄D, k₅D, k₁k₂, k₁k₃, k₁k₄, k₁k₅, k₂k₃, k₂k₄, k₂k₅, k₃k₄, k₃k₅, k₄k₅};

f = 20 = {k₁k₂D, k₁k₃D, k₁k₄D, k₁k₅D, k₂k₃D, k₂k₄D, k₂k₅D, k₃k₄D, k₃k₅D, k₄k₅D, k₁k₂k₃, k₁k₂k₄, k₁k₂k₅, k₁k₃k₄, k₁k₃k₅, k₁k₄k₅, k₂k₃k₄, k₂k₃k₅, k₂k₄k₅, k₃k₄k₅};

t = 15 = {k₁k₂k₃D, k₁k₂k₄D, k₁k₂k₅D, k₁k₃k₄D, k₁k₃k₅D, k₁k₄k₅D, k₂k₃k₄D, k₂k₃k₅D, k₂k₄k₅D, k₃k₄k₅D, k₁k₂k₃k₄, k₁k₂k₃k₅, k₁k₂k₄k₅, k₁k₃k₄k₅, k₂k₃k₄k₅};

q = 5 = {k₁k₂k₃k₄D, k₁k₂k₃k₅D, k₁k₂k₄k₅D, k₁k₃k₄k₅D, k₂k₃k₄k₅D}.

Каждая грань принадлежит трем тетраэдрам. Из 15 тетраэдров пять – внешние и 10 – внутренние. Для графа на рис. 5 $v = {{v}_{{\text{5}}}} = {\text{6}}$.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Отметим, что список пентатопов позволяет перечислить все элементы фазовой диаграммы. Однако граф смежности пентатопов более наглядно отражает строение диаграммы. Такие графы удобно использовать для сопоставления разных диаграмм, синтеза новых типов диаграмм и решения ряда других задач. Граф диаграммы, показывающий ее проекцию на плоскость, является более привычным способом демонстрации ее строения.

Построенные выше графы иллюстрируют принципиальные различия между строением изобарно-изотермических фазовых диаграмм четырехкомпонентных систем в 3D-пространстве и пятикомпонентных систем в 4D-пространстве. Симплекс четверной фазовой диаграммы со стехиометрическими фазами является трехмерным тетраэдром, а изобарно-изотермическая фазовая диаграмма представляет собой его разбиение на тетраэдры меньшего размера. Диаграмма в целом или ее фрагменты представляют собой конечное количество тетраэдров, соединенных внутренними гранями. Остальные грани, каждая из которых принадлежит только одному тетраэдру, – внешние и образуют поверхность тетраэдрической конструкции. Рассмотренные выше пятикомпонентные диаграммы представляют собой конструкцию из пентатопов, соединенных тетраэдрическими внутренними гипергранями в четырехмерном пространстве. Диаграмма из пентатопов окружена внешними тетраэдрами, образующими гиперповерхность конструкции из пентатопов. Тетраэдры, принадлежащие гиперповерхности, соединены друг с другом треугольными гранями. Для системы без соединений (рис. 1) эта гиперповерхность состоит из пяти тетраэдров, соединенных десятью гранями. Каждая из треугольных граней принадлежит двум тетраэдрам. Как это ни странно выглядит, в подобной конструкции внешние треугольные грани отсутствуют.

В рассмотренных диаграммах могут присутствовать треугольные грани двух типов – грани первого типа принадлежат двум тетраэдрам, грани второго типа – трем тетраэдрам. Диаграмма без соединения содержит только грани первого типа, диаграмма с пятерным соединением – только грани второго типа. Остальные три диаграммы содержат грани двух типов.

Отметим, что значения основных топологических характеристик однозначно зависят от компонентности соединения r. Для рассматриваемых диаграмм q = r. Тетраэдрические гиперграни делятся на t' внешних, принадлежащих одному пентатопу, (они образуют гиперповерхность диаграммы) и t'' внутренних, принадлежащих двум пентатопам. Количество внутренних тетраэдров равно количеству ребер в графе смежности пентатопов, которое является суммой первых r – 1 членов натурального ряда. Так как каждый пентатоп включает в себя пять тетраэдров, общее количество тетраэдров равно t = 5q – t''. Четырехмерная конструкция диаграммы построена из q пентатопов, каждый из них образован из пяти тетраэдров. Так как один из тетраэдров принадлежит двум соседним пентатопам, общее количество тетраэдров равно t = 5q – t''. Количество ребер определяется из графа диаграммы, а количество граней – из графа смежности полиэдров, строение которых однозначно связано с величиной r.

ЗАКЛЮЧЕНИЕ

Н.С. Курнаков [1] характеризовал сложность концентрационных симплексов диаграмм общим числом геометрических элементов. Сложность рассмотренных выше диаграмм Ω = $v$ + e + f + t + q при изменении r от 1 (система без соединений) до 5 характеризуется следующими величинами: 31, 47, 55, 59, 61. Для сравнения отметим, что для тетраэдра Ω = 15. Очевидно, что наглядное традиционное исчерпывающее геометрическое описание диаграмм высокой сложности в виде совокупности двумерных сечений практически невозможно из-за их разнообразия, а использование таких рисунков для восприятия основных особенностей строения диаграмм нереально. Однако, как показано выше, строение диаграммы удобно описывать в виде ее графа и графа смежности пентатопов, позволяющих перечислить геометрические элементы фазовых диаграмм и определить их относительное расположение в четырехмерном пространстве. Такая информация более наглядна. Ее удобно использовать для понимания строения фрагментов диаграмм, планирования экспериментов по их построению, исследования возможных процессов, сопровождаемых фазовыми превращениями, в таких системах. Очевидна полезность изучения множеств диаграмм с заданными характеристиками, в частности, решения задач перечисления диаграмм, использования субсолидусных диаграмм для построения возможных диаграмм плавкости, а также для решения прикладных задач, требующих знания информации о фазовых соотношениях в многокомпонентных химических системах.

Отметим, что фазовую диаграмму можно рассчитать из термодинамических моделей всех фаз, присутствующих в химической системе [12]. Однако существует множество ситуаций, когда такая информация отсутствует или неполна. Такие задачи решаются с использованием только топологического подхода, либо на основе комбинации такого подхода с термодинамическим моделированием. В настоящей работе продемонстрировано решение задачи генерации фазовых диаграмм пятерных систем, которые принципиально невозможно решать термодинамическими методами.