1. На главную
  2. Электронные версии
  3. Журнал физической химии
  4. T. 94, № 11, 2020

Журнал физической химии, 2020, T. 94, № 11, стр. 1723-1726

Кинетическая модель сопряженных метаболических циклов: орнитинового и лимонной кислоты

Ю. А. Ершов a, К. Д. Лукин b, Т. К. Слонская c, *, М. А. Хачатурян c

a Московский государственный технический университет имени Н.Э. Баумана
Москва, Россия

b Минский филиал РЭУ имени Г.В. Плеханова
Минск, Республика Беларусь

c Первый Московский государственный медицинский университет имени И.М. Сеченова
Москва, Россия

* E-mail: tslonskaya@mail.ru

Поступила в редакцию 27.12.2019
После доработки 27.12.2019
Принята к публикации 21.01.2020

Полный текст (PDF)

Аннотация

На основе кинетического графа и модели биокинетики сопряженных метаболических циклов лимонной кислоты и орнитинового цикла подобраны константы биохимических реакций и решена система из восьми обыкновенных дифференциальных уравнений. Построены зависимости количества метаболитов и продуктов от времени.

Ключевые слова: сопряжение метаболических циклов, кинетика метаболитов, константы биохимических реакций, система обыкновенных дифференциальных уравнений

Существование сопряженных метаболических циклов в организме экспериментально доказано [1]. Изучена кинетика биохимических реакций отдельных стадий метаболических путей [2]. Кинетика сопряженных метаболических циклов изучена недостаточно из-за большого числа параметров, влияющих на протекание биохимических процессов. Воссоздать подобные процессы in vitro для изучения и анализа практически невозможно, поэтому актуальным, а иногда и единственным, остается подход с использованием математического моделирования.

Сложные связи между орнитиновым циклом и циклом лимонной кислоты (рис. 1), с точки зрения химической кинетики, предложено описывать с помощью кинетического графа [2] и моделировать с помощью системы обыкновенных дифференциальных уравнений.

Рис. 1.

Схема сопряжeнных метаболических циклов: цикла лимонной кислоты и орнитинового цикла.

В [3] приводится система обыкновенных дифференциальных уравнений (I), а также формулируются задачи, связанные с этой системой.

(1)
$d{{x}_{0}}{\text{/}}dt = {{{v}}_{0}}--{{k}_{x}}_{{01}}{{x}_{0}},$
(2)
$d{{x}_{1}}{\text{/}}dt = {{k}_{x}}_{{01}}{{x}_{0}} + {{k}_{x}}_{{31}}{{x}_{3}}--{{k}_{x}}_{{12}}{{x}_{1}},$
(3)
$d{{x}_{2}}{\text{/}}dt = {{k}_{x}}_{{12}}{{x}_{1}}--{{k}_{x}}_{{23}}{{x}_{2}} + {{k}_{y}}_{{22}}{{y}_{2}}--{{k}_{y}}_{{21}}{{y}_{2}},$
(I)
$\begin{gathered} \hfill d{{x}_{3}}{\text{/}}dt = {{k}_{x}}_{{23}}{{x}_{2}}--{{k}_{x}}_{{31}}{{x}_{3}}--{{k}_{x}}_{{3p}}{{x}_{3}},\quad \quad \left( 4 \right) \\ \hfill d{{y}_{{\text{1}}}}{\text{/}}dt = {{k}_{y}}_{{21}}{{x}_{2}}--{{k}_{y}}_{{21}}{{y}_{1}},\quad \quad \;\quad \left( 5 \right) \\ \end{gathered} $
(6)
$d{{y}_{2}}{\text{/}}dt = {{k}_{y}}_{{12}}{{y}_{1}}--{{k}_{y}}_{{22}}{{y}_{2}}--{{k}_{y}}_{{2p}}{{y}_{2}},$
(7)
$d{{p}_{x}}{\text{/}}dt = {{k}_{x}}_{{3p}}{{x}_{3}},$
(8)
$d{{p}_{y}}{\text{/}}dt = {{k}_{y}}_{{2p}}{{y}_{2}}.$
Здесь ${{{v}}_{0}}$ – скорость поступления основного субстрата (x0); xi, yi, px, py – количества метаболитов и продуктов; kijk – константы скорости реакций на соответствующих стадиях циклов.

Настоящая работа посвящена построению кинетических кривых зависимости количества метаболитов и продуктов xi, yi, px, py от времени на основе решения системы дифференциальных уравнений (I), а также проведению регуляризации полученных решений для метаболитов и продуктов на основе базы экспериментальных данных для значений констант скорости реакций. Для достижения поставленной цели:

а) проанализированы неизвестные функции системы (I): x0(t), x1(t), x2(t), y1(t), y2(t), px(t), py(t). Все коэффициенты k c индексами – постоянные величины;

б) подобраны значения концентраций субстратов (табл. 1) и констант для решения системы дифференциальных уравнений (табл. 2).

Таблица 1.  

Концентрации субстратов (yi) в метаболических циклах

yi, М t = 10 с t = 360 с t = 600 с
y1 (аргинин сукцинат) 9.31 × 10–7 2.40 × 10–6 2.44 × 10–6
y2 (аргинин) 3.90 × 10–7 8.82 × 10–7 9.04 × 10–7
Орнитин 3.96 × 10–4 2.58 × 10–4 2.56 × 10–4
Цитрулин 4.81 × 10–5 1.84 × 10–4 1.86 × 10–4
Мочевина 1.20 × 10–5 2.20 × 10–3 3.77 × 10–3
х2 (сукцинат) 9.50 × 10–7 9.04 × 10–6 1.09 × 10–5
Таблица 2.  

Значения кинетических констант в уравнениях

ky21, 1/c ky12, 1/c ky2p, 1/c kx23, 1/c
2.04 × 10–3 1.00 × 10–4 1.00 × 10–2 1.6 × 10–3
kx12, 1/c kx3p, 1/c ky22, 1/c kx31, 1/c
2.0 × 10–1 0.9 × 10–3 1.5 × 10–3 1.3 × 10–3

При ${{{v}}_{0}}$ = ${{{v}}_{0}}$(t) уравнение (1) – линейное дифференциальное уравнение первого порядка. Частное решение этого уравнения при начальном условии x0(0) = a:

(II)
${{x}_{0}} = {{{v}}_{0}}{\text{/}}{{k}_{x}}_{{01}}--({{{v}}_{0}}{\text{/}}{{k}_{x}}_{{01}}--a)\exp (--{{k}_{x}}_{{01}}t).$
Подставив это значение для x0 в уравнение (2) системы (I), получаем систему обыкновенных дифференциальных уравнений с постоянными коэффициентами относительно неизвестных функций x1(t), x2(t), y1(t), y2(t), px(t), py(t). Решаем эту систему в пакете Wolfram Mathematica.

При моделировании рассматривали варианты А и Б.

А. Пусть ky22 = ky21. В этом случае система (I) распадается на три подсистемы: (2), (3*), (4); (5), (6) и (7), (8); при этом

(3*)
$d{{x}_{2}}{\text{/}}dt = {{k}_{x}}_{{12}}{{x}_{1}}--{{k}_{x}}_{{23}}{{x}_{2}}.$
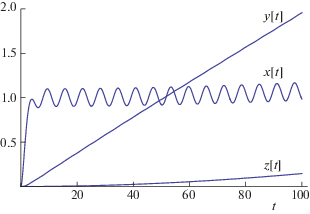
Решаем подсистему (2), (3*), (4), полагая при t = = 0: ${{{v}}_{0}}$ = 0.1, a = 2, xi = y = px = py = 0. Для удобства введены следующие обозначения: x1(t) = x(t), x2(t) = y(t), x3(t) = z(t). Программа для решения этой системы имеет вид
$\begin{gathered} \operatorname{NDSolve} {\kern 1pt} \text{[}\{ x{\kern 1pt} {\text{'}}{\kern 1pt} [t] = = 0.1 - 0.08еxp[ - 0.01t] + \\ + \;0.0013z[t] - 0.21x[t], \\ y{\kern 1pt} {\text{'}}{\kern 1pt} [t] = = 0.21x[t] - 0.0016y[t], \\ z{\kern 1pt} {\text{'}}{\kern 1pt} \left[ t \right] = = 0.0016y[t] - 0.0022z[t], \\ x[0] = = 0,~\;y[0] = = 0,\;z[0] = = 0\} ,\;\{ x,y,z\} ,\;\{ t,0,100\} ]. \\ \end{gathered} $
Графики полученных интегральных кривых приведены на рис. 2.

Рис. 2.

Интегральные кривые функций x(t), y(t), z(t).

Решаем подсистему (5), (6). Так как функция x2 найдена в виде интерполяционного многочлена, то, подставив этот многочлен в подсистему (5), (6). Решаем ее так же, как и подсистему (2), (3*), (4). При этом вводим обозначения y1(t) = Y(t), y2(t) = Z(t). Программа для решения этой подсистемы:

$\begin{gathered} {\text{NDSolve}}{\kern 1pt} \text{[}\{ Y{\kern 1pt} {\text{'}}{\kern 1pt} [t] = = 0.0024(0.000318{{t}^{2}} + \\ + \;0.012558t) - 0.0024Y[t], \\ Z{\kern 1pt} {\text{'}}{\kern 1pt} [t] = = 0.0001Y[t] - 0.0025Z[t], \\ Y[0] = = 0,\;Z[0] = = 0\} ,\;\{ Y,Z\} ,\;\{ t,0,100\} ] \\ \end{gathered} $
Графики функций Y(t), Z(t) представлены на рис. 3.

Рис. 3.

Интегральные кривые функций Y(t), Z(t).

Решаем третью подсистему (7), (8). Функции x3[t] и y2[t] найдены выше в виде интерполяционных многочленов:

${{k}_{x}}_{{3p}}{{x}_{3}}[t] = 317.7 \times {{10}^{{--10}}}{{t}^{2}}--7371 \times {{10}^{{--10}}}t,$
$\begin{gathered} {{k}_{y}}_{{2p}}{{y}_{2}}[t] = 1.85 \times {{10}^{{--12}}}{{t}^{3}}--8.82 \times {{10}^{{--11}}}{{t}^{2}} + \\ + \;105 \times {{10}^{{--11}}}t. \\ \end{gathered} $
Решение системы (7), (8) находится непосредственным интегрированием:

$\begin{gathered} p[t] = {{10}^{{--10}}}(105.9{{t}^{3}}--3685.5{{t}^{2}}), \\ q[t] = {{10}^{{--11}}}(0.0462{{t}^{4}}--2.94{{t}^{3}} + 52.5{{t}^{2}}). \\ \end{gathered} $

Б. Снимая ограничение: ky22 ≠ ky21, решаем исходную систему (I) при следующих значениях констант:

${{K}_{{y21}}} = 2.04 \times {{10}^{{ - 3}}}\;1{\text{/}}c,\quad {{K}_{{y12}}} = {{10}^{{ - 4}}}\;1{\text{/}}c,$
${{K}_{{y2{\text{p}}}}} = = {{10}^{{ - 2}}}\;1{\text{/}}c,\quad {{K}_{{x23}}} = 1,$
${{K}_{{x23}}} = 1.6 \times {{10}^{{ - 3}}}\;1{\text{/}}c,\quad {{K}_{{x31}}} = 1.3 \times {{10}^{{ - 3}}}\;1{\text{/}}c,$
${{K}_{{x12}}} = 2.1 \times {{10}^{{ - 1}}}\;1{\text{/}}c,\quad {{K}_{{x3{\text{p}}}}} = 0.9 \times {{10}^{{ - 3}}}\;1{\text{/}}c,$
${{K}_{{y2{\text{p}}}}} = {{10}^{{ - 3}}}\;1{\text{/}}c,\quad {{K}_{{y22}}} = 1.5 \times {{10}^{{ - 3}}}\;1{\text{/}}c.$
Программа имеет вид:
$\begin{gathered} {\text{NDSolve}}{\kern 1pt} \text{[}\{ x{\kern 1pt} '[t] = = 0.1 - 0.08еxp[ - 0.01t] + \\ + \;0.0013z[t] - 0.21x[t], \\ y{\kern 1pt} '[t] = = 0.21x[t] - 0.0016y[t], \\ \end{gathered} $
$\begin{gathered} z{\kern 1pt} '[t] = = 0.0016y[t] - 0.0022z[t], \\ Y{\kern 1pt} '[t] = = 0.002y[t] - 0.002Y[t], \\ Z{\kern 1pt} '[t] = = 0.0001Y[t] - 0.0025Z[t], \\ p{\kern 1pt} '[t] = = 0.0009z[t],\;q{\kern 1pt} '[t] = = 0.001Z[t], \\ \end{gathered} $
$\begin{gathered} x[0] = = 0,\;y[0] = = 0,\;z[0] = = 0, \\ Y[0] = = 0,\;Z[0] = = 0,\;p[0] = = 0,\;q[0] = = 0\} , \\ \{ x,y,z,Y,Z,p,q\} ,\;\{ t,0,100\} ]. \\ \end{gathered} $
Получены решения функций x(t), y(t), z(t), Y(t), Z(t), p(t), q(t).

При значении kx12 = 2.1 × 10–2 1/c решение этой системы получаем аналогично.

Решение системы (I) существенно зависит от ее первого уравнения. Решение этого уравнения задается формулой (II). При ${{{v}}_{0}}$ = 2 решение первого уравнения принимает вид:

${{x}_{0}} = 2--еxp(--t).$
Решение системы для x0 = 2 – еxp(–t):
$\begin{gathered} {\text{NDSolve}}{\kern 1pt} \text{[}\{ x{\kern 1pt} '[t] = = - x[t] + 0.5z[t] + 2 - еxp[ - t], \\ y{\kern 1pt} '[t] = = x[t] - 1.5y[t] + 0.5Z[t], \\ \end{gathered} $
$\begin{gathered} z{\kern 1pt} '[t] = = 1.5y[t] - z[t],\;Y{\kern 1pt} '[t] = = y[t] - Y[t], \\ Z{\kern 1pt} '[t] = = 0.6Y[t] - 2Z[t],\;p{\kern 1pt} '[t] = = 0.5z[t], \\ q{\kern 1pt} '[t] = = Z[t],\;x[0] = = 0,\;y[0] = = 0,\;z[0] = = 0, \\ \end{gathered} $
$\begin{gathered} Y[0] = = 0,\;Z[0] = = 0,\;p[0] = = 0,\;q[0] = = 0\} , \\ \left\{ {x,y,z,Y,Z,p,q} \right\},\;\left\{ {t,0,20} \right\}]. \\ \end{gathered} $
При периодическом приеме пищи, т.е. при поступлении субстратов, функцию ${{{v}}_{0}}$(t) задают в виде: ${{{v}}_{0}}$(t) = 1 + ${{{v}}_{0}}\sin t$. Решение для x0 в этом случае имеет вид: x0(t) = 1 – 0.9t + 0.1($\sin t - \cos t$). Ниже приводится решение системы (I) для этого случая:
$\begin{gathered} {\text{NDSolve}}{\kern 1pt} \text{[}\{ x{\kern 1pt} '[t] = = - x[t] + 0.5z[t] + 1 - \\ - \;0.9еxp[ - t] + 0.1(\sin [t] - \cos [t]), \\ y{\kern 1pt} '[t] = = 0.21x[t] - 0.0016y[t], \\ \end{gathered} $
$\begin{gathered} z{\kern 1pt} '[t] = = 0.0016y[t] - 0.0022z[t], \\ Y{\kern 1pt} '[t] = = 0.002y[t] - 0.002Y[t], \\ Z{\kern 1pt} '[t] = = 0.0001Y[t] - 0.0025Z[t], \\ p{\kern 1pt} '[t] = = 0.0009z[t],\;q{\kern 1pt} '[t] = = 0.001Z[t], \\ \end{gathered} $
$\begin{gathered} x[0] = = 0,\;y[0] = = 0,\;z[0] = = 0,\;Y[0] = = 0, \\ Z[0] = = 0,\;p[0] = = 0,\;q[0] = = 0\} , \\ \{ x,y,z,Y,Z,p,q\} ,\;\{ t,0,100\} ]. \\ \end{gathered} $
Графики искомых функций x(t), y(t), z(t) приведены на рис. 4. Вид полученных кинетических кривых согласуется с экспериментальными данными.

Рис. 4.

Интегральные кривые функций x(t), y(t), z(t) при поступлении субстратов.

Полученные результаты могут служить базой для количественного прогнозирования при изучении сложных биохимических процессов метаболических циклов в организме человека.

Список литературы

  1. Mogilevskaya E., Demin O., Goryanin I. // J. Biol. Phys. 2006. V. 32. P. 245.

  2. Feng Qi, Xuewen Chen, Beard D.A. // Biochim. Biophys. Acta. 2008. V. 1784(11). P. 1641.

  3. Ершов Ю.А. // Журн. физ. xимии. 2016. Т. 90. № 1. С. 13.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал физической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал