Журнал физической химии, 2020, T. 94, № 2, стр. 301-305
Способ проведения процесса разделения в распределительной системе фракционирования
В. П. Чижков a, В. Н. Бойцов a, *
a Российская академия наук, Институт органической химии им. Н.Д. Зелинского
Москва, Россия
* E-mail: boysoft@list.ru
Поступила в редакцию 09.04.2019
После доработки 09.04.2019
Принята к публикации 14.05.2019
Аннотация
Рассмотрен способ проведения элементарного акта разделения в экстракционной системе жидкость–жидкость. Обсуждены условия и механизмы, позволяющие, по крайней мере в принципе, получить обратимую работу WT = –ΔGT, где ΔGT – изменение энергии Гиббса, определяемое при полной неравновесности процесса.
Известно [1–5], что для разделения веществ, близких по своим физико-химическим свойствам, и изотопов широкое применение находят физико-химические методы, основанные на использовании двухфазных систем и элементарных актов разделения [1, 4, 5], характеризуемых небольшими значениями коэффициента разделения α < 1.5. Примером является ректификация [6] – один из основных методов получения стабильных изотопов легких элементов [1, 4, 5]. Смеси изотопов и некоторых изомеров органических соединений по своим свойствам приближаются к идеализированным растворам. Возможность обратимого перевода совершенного раствора в идеальное газовое состояние и равновесное разделение компонентов газового раствора на ступенях идеального каскада обсуждены в [7–9]. Работа разделения термодинамически идеального каскада оценивалась в [9] с помощью “энтропийного потенциала разделения” [8] при учете данных [6]. Цель настоящего исследования состоит в обосновании способа обратимого проведения элементарного акта разделения в системах жидкость–жидкость [2, 3] при термодинамической интерпретации совершаемой работы с привлечением потенциала Дирака–Пайерлса [1, 5, 9].
Рассмотрим процесс разделения компонентов A и B в системе с двумя растворителями C и D, изображенной на рис. 1, в условиях независимого распределения разделяемых компонентов между двумя несмешивающимися растворителями – экстрагентами [2]. Данная система представляет собой ступень каскада, описанного в [2, 10, 11]. При использовании двух взаимонерастворимых экстрагентов в количествах C0 и D0 молей в систему с одной стороны подаются два бесконечно разбавленных раствора, содержащих разделяемые компоненты A и B в количествах A01 + B01 и A02 + B02 молей, а с другой стороны выводятся два аналогичных раствора, содержащих A1 + B1 и A2 + B2 молей разделяемых компонентов. Однократный акт разделения будем характеризовать параметрами
Коэффициенты $K_{B}^{*}$ и $K_{A}^{*}$ следуют из уравнений
Возможные пути перехода системы жидкость–жидкость из начального состояния (Н) в конечное (К) показаны схематично на рис. 2. Термодинамический эффект разделения заключается в изменении свободной энергии системы и энтропии смешения [5, 6]. Изменение энергии Гиббса, определяемое с привлечением соответствующих химических потенциалов $\mu _{i}^{j}$ [12] для предельно разбавленных растворов, следует из соотношений [11]:
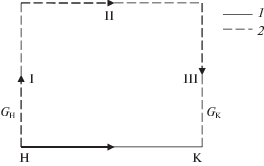
Рис. 2.
Два варианта перехода системы из начального состояния (Н) в конечное (К); 1 – переход в условиях полной неравновесности процесса, 2 – обратимый переход; I – обратимое испарение растворов (C0, A01 + B01 и D0, A02 + B02), II – равновесное разделение компонентов A и B смеси; III – обратимая конденсация паров (C0, A1 + B1 и D0, A2 + B2); GH, GK – энергии Гиббса.
Указанные соотношения можно получить, используя приведенные выше уравнения и применяя приближенные формулы:
В этих формулах (A + B)/С и (A + B)/D – малые числа, и чем меньше их абсолютные значения (чем более разбавлены растворы), тем меньше погрешность каждой формулы. Убыль энергии Гиббса, соответствующая оптимальным условиям разделения при экстракции, следует по данным [11] из уравнения
Здесь и выше q = A0 + B0 (в общем случае A0 ≠ B0), R – газовая постоянная, T – абсолютная температура и
В последнем уравнении энергия GH отвечает начальному состоянию экстракционной системы, а GK – характеризует ее конечное состояние. По данным [11, 12]
Учитывая приведенные уравнения, получим
При α ≤ 1.5 имеем f(α) ≈ 0.25, поэтому для тонкого разделения [1] можно написать равенства
Рассмотрим способ обратимого проведения элементарного акта симметричного разделения, полагая k0 = 1 и используя подход, близкий к применяемому в [14] при термодинамической интерпретации обратимого процесса перегонки растворителя в раствор какого-либо нелетучего вещества. Известно, что существует принципиальная возможность обратимого перевода чистых жидкостей [13, 14] и совершенного раствора [7–9] в идеальное газовое состояние. Возможен подобный обратимый перевод в идеальное газовое состояние и различных бесконечно разбавленных растворов, содержащих летучие вещества. При таком переводе в равных объемах различных газов C и D при одинаковой температуре и одинаковом давлении будет содержаться одинаковое количество молей этих газов (в соответствии с уравнением состояния идеальных газов и законом Авогадро). Учитывая сказанное, переход термодинамической системы из начального положения в конечное (и наоборот) можно представить проходящим через ряд промежуточных состояний [13] по пути осуществления обратимых процессов в соответствии со схемой, изображенной на рис. 2 (пунктирные линии). Неполное равновесное разделение компонентов A и B возможно осуществить с использованием описанных ранее вариантов системы с движущимися полупроницаемыми поршнями [15, 16]. В системе [16] разделение A и B проводится в присутствии инертного газа, свободно проникающего через полупроницаемые поршни. В рассматриваемом переходе инертный газ заменяется в равных объемах системы [15, 16] на C и D. Смешения паров C и D возможно избежать, разделив, например, равные объемы системы [15, 16] неподвижной перегородкой, непроницаемой для C и D и свободно пропускающей A и B.
Перейдем к интерпретации обратимой работы в данном гипотетическом способе однократного равновесного разделения. Подобно тому, как это сделано в [14], представляется необходимым рассматривать в нашем случае следующую сумму работ:
где AI – работа обратимого процесса испарения исходных бесконечно разбавленных растворов (${{C}_{0}} \gg {{A}_{{01}}} + {{B}_{{01}}}$, ${{D}_{0}} \gg {{A}_{{02}}} + {{B}_{{02}}}$), AII = WT – работа, совершаемая в варианте равновесного разделения компонентов A и B в присутствии паров C и D, свободно проникающих через полупроницаемые поршни, AIII – работа обратимого процесса конденсации паров, обогащенных разделяемыми компонентами (${{C}_{0}} \gg {{A}_{1}} + {{B}_{1}}$, ${{D}_{0}} \gg {{A}_{2}} + {{B}_{2}}$). Работа WT предполагается равной максимальной работе, получаемой в обратном процессе. Здесь прослеживается некоторая аналогия с подъемом и опусканием груза [9, 13, 17, 18].С помощью экстракции [2, 3, 17] можно разделить компоненты смеси, различающиеся по своей химической природе, а не по физическим свойствам (например, по величине давления их паров). Учитывая сказанное, принимаем $p_{A}^{{ 0}} = p_{B}^{{ 0}}$, где $p_{A}^{{ 0}}$ и $p_{B}^{{ 0}}$ – давления насыщенных паров чистых A и B. Тогда для рассматриваемых обратимых процессов испарения и конденсации предельно разбавленных растворов возможно, очевидно, написать равенство AI + AII = 0 [14]. По данным [15 , 16] для произвольных значений α соответственно имеем
Следовательно, в указанных условиях проведения процесса AI + AII = 0 и совершается работа WT = –∆GT [11, 13], определяемая с использованием разделительного потенциала [1, 15].
Рассмотренный способ обратимого проведения процесса можно реализовать в принципе на каждой ступени каскада [10, 11]. Тогда для каскада в целом, учитывая результаты, полученные в [11], можно написать
Здесь f(α) ≈ 0.25. Поэтому для значений α ≤ 1.5 возможно принять
где WK характеризует приращение ценности смеси [1, 5, 11] и определяется в [11] из уравненияЗдесь Φ(xp) – разделительный потенциал или функция Дирака–Пайерлса [11].
Таким образом, из полученных данных следует, что для рассмотренного самопроизвольного процесса разделения возможно сконструировать, по крайней мере в принципе, механизмы, позволяющие получить в равновесном процессе обратимую работу WT = –∆GT. Данное равенство вытекает также из уравнений первого и второго законов термодинамики [6] с учетом [12, 17]. Суммарная работа ${{W}_{{T.K}}} = - \Delta {{\tilde {G}}_{T}}$ определяется с привлечением потенциала Φ(xp) и по своей величине не отличается от суммарной работы разделения, совершаемой на ступенях газового каскада [16].
Список литературы
Розен А.М. Теория разделения изотопов в колоннах. М.: Атомиздат, 1960. 440 с.
Трейбал Р. Жидкостная экстракция. М.: Химия, 1966, 722 с.
Экстракционная хроматография / Под ред. Т. Брауна и Г. Гарсини. М.: Мир, 1978. 627 с.
Андреев Б.М., Зельвенский Я.Д., Катальников С.Г. Разделение стабильных изотопов физико-химическими методами. М.: Энергоатомиздат, 1982. 205 с.
Изотопы: свойства, получение, применение / Под ред. В.Ю. Баранова. М.: ИздАТ, 2000. 703 с.
Кириллин В.А., Шейндлин А.Е., Шпильрайн Э.Э. Термодинамика растворов. М.: Энергия, 1980. С. 225.
Голуб А.Е., Ефремов А.А., Аронов А.Р. // Теор. основы хим. технологии. 1980. Т. 14. С. 297.
Чижков В.П., Бойцов В.Н. // Журн. физ. химии. 2017. Т. 91. № 6. С. 1066.
Чижков В.П., Бойцов В.Н. // Там же. 2008. Т. 82. № 7. С. 1397.
Чижков В.П., Бойцов В.Н. // Там же. 2012. Т. 86. № 1. С. 139.
Чижков В.П., Бойцов В.Н., Демин А.В. // Там же. 2011. Т. 85. № 3. С. 565.
Чижков В.П., Бойцов В.Н. // Там же. 2005. Т. 79. № 3. С. 391.
Еремин Е.И. Основы химической термодинамики. М.: Высшая школа, 1974. 340 с.
Жуховицкий А.А., Шварцман Л.А. Физическая химия. М.: Металлургия, 1968. С. 40.
Чижков В.П., Бойцов В.Н., Демин А.В. // Журн. физ. химии. 2010. Т. 84. № 3. С. 585.
Чижков В.П., Бойцов В.Н., Демин А.В. // Там же. 2010. Т. 84. № 10. С. 1943.
Эверет Д. Введение в химическую термодинамику. М.: Изд-во. ин. литер., 1963. 299 с.
Хейвуд Р. Термодинамика равновесных процессов. М.: Мир., 1983. 491 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии



