Журнал физической химии, 2021, T. 95, № 2, стр. 262-271
Конформационные изменения однородно заряженных цепей полиэлектролитов на поверхности поляризованной золотой наночастицы: молекулярно-динамическое моделирование и теория гауссовой цепи в поле
Н. Ю. Кручинин a, *, М. Г. Кучеренко a, П. П. Неясов a
a Оренбургский государственный университет, Центр лазерной и информационной биофизики
Оренбург, Россия
* E-mail: kruchinin_56@mail.ru
Поступила в редакцию 27.03.2020
После доработки 19.05.2020
Принята к публикации 26.05.2020
Аннотация
Методом молекулярной динамики исследованы конформационные изменения однородно заряженных полипептидов, адсорбированных на поверхности поляризованной золотой наночастицы. Рассчитаны зависимости средних угловых распределений и радиальной плотности атомов полиэлектролита на поверхности наночастицы. На поверхности поляризованной золотой наночастицы наблюдалось постепенное смещение звеньев полиэлектролита в полушарие, заряженное противоположно знаку заряда звеньев, а также выраженное разрежение внешнего слоя адсорбированной цепи по сравнению с внутренним в этом полушарии наночастицы. Представлена аналитическая модель конформационных изменений полиэлектролита, основанная на уравнении динамики гауссовой цепи, в потенциальном поле поляризованной наночастицы. Согласно аналитической модели построены картина деформированной опушки полиэлектролита и радиально-угловые зависимости его плотности звеньев на поверхности поляризованной наночастицы.
Использование плазмонных наночастиц с адсорбированными на их поверхностях макромолекулярных цепей полиэлектролитов вызывает большой интерес в связи с задачами создания и улучшения характеристик разнообразных химических сенсоров, а также для использования в качестве нанозондов в биохимических, биофизических и биомедицинских исследованиях [1–5]. Часто для управления характеристиками подобных наносистем используется эффект изменения конформационной структуры адсорбированной полимерной цепи под воздействием электрического поля [6, 7].
Под воздействием электрического поля конформационная структура адсорбированной на твердой поверхности макроцепи, содержащей заряженные звенья, будет изменяться. В работах [8–11] исследовались электрически индуцированные конформационные изменения в целом нейтральных полиамфолитных полипептидов, адсорбированных на поверхностях заряженной золотой подложки и наночастицы, а также поверхности поляризованной наночастицы. При этом наблюдались значительные изменения в конформационной структуре адсорбированного полиамфолита, в том числе связанного с молекулами красителей и атомарными кластерами.
Интерес вызывает исследование изменений в конформационной структуре однородно заряженного полиэлектролита на поверхности металлической, в частности – золотой наночастицы, которая может быть поляризована как в статическом электрическом поле, так и под воздействием электромагнитного излучения. Как известно, во внешнем электрическом поле на поверхности сферической наночастицы заряды распределяются с поверхностной плотностью пропорциональной косинусу угла между направлением вектора E электрического поля и нормали к поверхности наночастицы σ = $3E\cos \theta {\text{/}}(4\pi )$. В случае адсорбции на поверхности поляризованной наночастицы макромолекулы полиэлектролита, которая содержит заряженные звенья одного знака однородно распределенные по макроцепи, изменения его конформационной структуры будут значительно отличаться от случая в целом нейтральной полиамфолитной макромолекулы.
Такие гибридные наносистемы, состоящие из однородно заряженной макроцепи адсорбированной на поверхности металлической наночастицы, могут быть использованы в элементах различных устройств наноэлектроники, нанозондах и сенсорах с управляемыми электрическим полем параметрами, например, таких как сенсоры на основе эффекта гигантского комбинационного рассеяния (ГКР) или поверхностного плазмонного резонанса (ППР). Кроме того, они могут быть включены в состав чувствительного элемента люминесцентно-оптического измерителя концентрации молекулярного (в том числе – синглетного) кислорода [12, 13].
Поэтому целью данной работы является исследование индуцированных электрическим полем изменений конформационной структуры однородно заряженных полипептидов, адсорбированных на поверхности поляризованной золотой наночастицы.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Детали компьютерного эксперимента
Молекулярно-динамическое (МД) моделирование заряженных полипептидов на поверхности поляризованной золотой наночастицы было произведено с использованием программного комплекса NAMD 2.13 [14]. Модель золотой наночастицы была получена путем вырезания шара радиусом 1.5 нм из кристалла золота.
Были рассмотрены четыре заряженных полипептида, состоящих из 400 аминокислотных остатков:
1) полипептид A380D20 (суммарный заряд макроцепи –20e), состоящий из 380 звеньев Ala с равномерно распределенными 20 звеньями Asp (D, заряд –1e) – (A10DA9)20;
2) полипептид A360D40 (суммарный заряд макроцепи –40e), состоящий из 360 звеньев Ala с равномерно распределенными 40 звеньями Asp – (A5DA4)40;
3) полипептид A320D80 (суммарный заряд макроцепи –80e), состоящий из 320 звеньев Ala с равномерно распределенными 80 звеньями Asp – (A2DA2)80;
4) полипептид A340D40R20 (суммарный заряд макроцепи –20e), состоящий из 340 звеньев Ala с равномерно распределенными 40 звеньями Asp и 20 звеньями Arg (R, заряд +1e) – (A5DA4RA4DA4)20.
Для полипептидов было использовано силовое поле CHARMM22 [15]. Нековалентные взаимодействия с золотой наночастицей описывалось потенциалом Леннард-Джонса, параметризованным в работе [16]. Потенциал Ван-дер-Ваальса обрезался на расстоянии 1.2 нм с помощью функции сглаживания между 1.0 и 1.2 нм. Электростатические взаимодействия рассчитывались непосредственно на расстоянии 1.2 нм, а на большем расстоянии использовался метод “частица–сетка” Эвальда (PME) [17] с шагом сетки 0.11 нм. Вся наносистема была помещена в куб с ребрами 20 нм, заполненный молекулами воды TIP3P [18]. Локальное электрическое поле задавалось через изменение зарядов атомов на поверхности сферической наночастицы по закону косинуса, что отвечало ее однородной поляризации. Были получены следующие значения индуцированного дипольного момента наночастицы: p1 ≈ 1.4, p2 ≈ ≈ 2.7, p3 ≈ 5.5 и p4 ≈ 10.9 кД. МД-моделирование производилось при постоянной температуре (термостат Берендсена) при 600 K с последующим снижением до 300 K. Длина временной траектории достигала 15 нс. Для контроля получения равновесных конформаций осуществлялось наблюдение за изменением среднеквадратичного расстояния между атомами полипептида в различных конформациях (RMSD).
На первом этапе были получены стартовые конформационные структуры рассмотренных заряженных полипептидов, которые полностью обволакивали золотую наночастицу. Для этого отрицательно заряженная макроцепь полипептида располагалась в виде неравновесного клубка рядом с положительно заряженной поверхностью золотой наночастицы (поверхностная плотность заряда +3e/нм2). Было рассмотрено по три разных стартовых клубка для каждого полипептида. По результатам МД-моделирования были получены по три конформационные структуры для каждого рассмотренного полипептида, полностью обволакивающих наночастицу. Впоследствии эти структуры были использованы в качестве стартовых конфигураций для МД-моделирования на поверхности нейтральной и поляризованной наночастицы.
По результатам МД-моделирования на конечном стационарном участке траектории по всем полученным конформациям на поверхности наночастицы рассчитывались радиальные распределения средней плотности атомов полипептида. Также были построены зависимости средних угловых распределений атомов полипептида с шагом в 10 градусов (отрицательно заряженному полюсу соответствует угол 180 градусов, экваториальной области – угол 90 градусов, а положительно заряженному полюсу – угол 0 градусов). При этом зависимости угловых распределений атомов адсорбированной макроцепи были нормированы на амплитудные значения атомной плотности в экваториальной области, с учетом различий площади поверхности сферических поясов, ограниченных окружностями различного радиуса: $N({{\theta }_{1}},{{\theta }_{2}}) = n({{\theta }_{1}},{{\theta }_{2}})S(80,90){\text{/}}S({{\theta }_{1}},{{\theta }_{2}})$, где $S(80,90)$ – площадь сферического пояса, ограниченного углами 80 и 90 градусов, $N({{\theta }_{1}},{{\theta }_{2}})$ – нормированное число атомов макроцепи в сферическом поясе, $n({{\theta }_{1}},{{\theta }_{2}})$ – число атомов макроцепи в сферическом поясе, а $S({{\theta }_{1}},{{\theta }_{2}})$ – площадь сферического пояса, ограниченном углами θ1 и θ2.
Математическая модель перестройки конформаций гауссовой цепи, адсорбированной на поляризованной наночастице
При помещении сферической наночастицы в однородное электрическое поле шаровая симметрия системы утрачивается, а потенциал поля в окрестности поляризованной частицы получает зависимость от угловой переменной $\theta $. Ранее, в ряде работ авторов [19–21] для сферически-симметричного случая было показано, что в случае физической – ван-дер-ваальсовой адсорбции адсорбционный потенциал стенок наночастиц может быть эффективно представлен комбинацией простейших модельных потенциалов ${{V}_{1}}(r) = {{V}_{\infty }}(R) - \alpha \delta (r - {{r}_{0}})$ вида “твердая стенка–дельта-функциональная яма” (R – радиус наночастицы). Физически параметр r0 может быть отождествлен с минимумом ван-дер-ваальсова потенциала, и разность r0 – R имеет тот же порядок величины: 0.3–0.4 нм.
Низкочастотное монохроматическое поле $E(t) = {{E}_{0}}\exp ( - i\omega t)$ поляризует наночастицу, и тогда к адсорбционному потенциалу V1(r) добавляется как потенциал $ - e{{E}_{0}}r\cos \theta $ самого поля Е, так и потенциал ${{V}_{P}}(r,\theta )$ поляризованной поверхности глобулы ${{V}_{2}}(r,\theta ) = - e{{E}_{0}}r\cos \theta + {{V}_{P}}(r,\theta )$. В итоге получаем
(1)
$\begin{gathered} V({\mathbf{r}}) = {{V}_{1}}(r) + {{V}_{2}}(r,\theta ) = {{V}_{\infty }}(R) - \\ - \;\alpha \delta (r - {{r}_{0}}) - e{{E}_{0}}r\cos \theta + {{V}_{P}}(r,\theta ), \\ \end{gathered} $(2)
$\begin{gathered} {{V}_{2}}(r,\theta ) = - e{{E}_{0}}r\cos \theta + \\ + \;\frac{{{{\varepsilon }_{1}}(\omega ) - {{\varepsilon }_{2}}}}{{{{\varepsilon }_{1}}(\omega ) + 2{{\varepsilon }_{2}}}}{{R}^{3}}e{{E}_{0}}\frac{{\cos \theta }}{{{{r}^{2}}}}. \\ \end{gathered} $(3)
$\begin{gathered} {{V}_{2}}(r,\theta ) = {{V}_{2}}(r){{P}_{1}}(\cos \theta ) = \\ = - e{{E}_{0}}\left[ {1 - \alpha {\text{'}}(\omega ){{{\left( {\frac{R}{r}} \right)}}^{3}}} \right]r{{P}_{1}}(\cos \theta ). \\ \end{gathered} $Поляризующее наночастицу поле E предполагается считать низкочастотным вплоть до значений ω существенно меньших характерных частот конформационных переходов фрагментов макроцепи ∼1 нс–1. Кроме того, для частиц размером R ∼ 1–10 нм, такое поле можно рассматривать как квазистатическое.
Диэлектрические проницаемости ε1(ω), ε2 в поляризационном потенциале (2) характеризуют металл частицы и окружающую среду, соответственно. Равновесные конформации адсорбированной макроцепи в идеализированной модели, исключающей объемные взаимодействия звеньев, задаются конформационной функцией $\psi ({\mathbf{r}})$, определяющей плотность мономеров $n({\mathbf{r}}) = {{\psi }^{2}}({\mathbf{r}})$, и являющейся решением дифференциального уравнения, изоморфного уравнению шредингеровского типа [22]
(4)
$\frac{{{{a}^{2}}kT}}{6}{{\nabla }^{2}}\psi ({\mathbf{r}}) = [V({\mathbf{r}}) - \zeta ]\psi ({\mathbf{r}}),$Построим зависящие от угла $\theta $ функции $\psi ({\mathbf{r}})$ нулевого приближения, то есть решения уравнения (4) с потенциалом $V(r) = {{V}_{1}}(r)$, без поляризующего поля. Используя для радиальной функции ${{F}_{l}}(r)$ подстановку ${{F}_{l}}(r) = {{f}_{l}}(r){\text{/}}\sqrt r $ для функции ${{f}_{l}}(r)$ получаем уравнение
(5)
$\begin{gathered} f_{l}^{{''}}(r) + \frac{1}{r}f_{l}^{'}(r) - \left[ {\frac{{(l + 1)l + 1{\text{/}}4}}{{{{r}^{2}}}}} \right]{{f}_{l}}(r) = \\ = \frac{6}{{{{a}^{2}}kT}}\left[ {{{V}_{1}}(r) - {{\zeta }_{l}}} \right]{{f}_{l}}(r). \\ \end{gathered} $(6)
$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} F_{l}^{I}(r) = {{A}_{l}}\left[ {\frac{{{{I}_{{l + 1/2}}}({{q}_{l}}r)}}{{\sqrt r }} - \frac{{{{I}_{{l + 1/2}}}({{q}_{l}}R)}}{{{{K}_{{l + 1/2}}}({{q}_{l}}R)}}\frac{{{{K}_{{l + 1/2}}}({{q}_{l}}r)}}{{\sqrt r }}} \right], \hfill \\ R < r < {{r}_{0}}, \hfill \\ \end{gathered} \\ \begin{gathered} F_{l}^{{II}}(r) = {{A}_{l}}\left[ {\frac{{{{I}_{{l + 1/2}}}({{q}_{l}}{{r}_{0}})}}{{{{K}_{{l + 1/2}}}({{q}_{l}}{{r}_{0}})}} - \frac{{{{I}_{{l + 1/2}}}({{q}_{l}}R)}}{{{{K}_{{l + 1/2}}}({{q}_{l}}R)}}} \right] \times \hfill \\ \times \;\frac{{{{K}_{{l + 1/2}}}({{q}_{l}}r)}}{{\sqrt r }},\quad {{r}_{0}} < r < \infty , \hfill \\ \end{gathered} \end{array}} \right.$(7)
${{\left. {\frac{d}{{dr}}F_{l}^{{II}}(r)} \right|}_{{r = {{r}_{0}}}}} - {{\left. {\frac{d}{{dr}}F_{l}^{I}(r)} \right|}_{{r = {{r}_{0}}}}} = - \frac{{6\alpha }}{{{{a}^{2}}kT}}F_{l}^{{II}}({{r}_{0}}).$(8)
$\begin{gathered} \frac{{{{a}^{2}}kT}}{{6\alpha {{r}_{0}}}} = {{I}_{{l + 1/2}}}({{q}_{l}}{{r}_{0}}){{K}_{{l + 1/2}}}({{q}_{l}}{{r}_{0}}) - \\ - \;K_{{l + 1/2}}^{2}({{q}_{l}}{{r}_{0}})\frac{{{{I}_{{l + 1/2}}}({{q}_{l}}R)}}{{{{K}_{{l + 1/2}}}({{q}_{l}}R)}}. \\ \end{gathered} $Теория возмущений второго порядка по полю
Учитывая ортогональность полиномов Лежандра с различными индексами l и структуру угловой зависимости оператора возмущения ${{V}_{2}}(r,\theta )\sim \cos \theta $, замечаем, что вклад в поправки базисного состояния $\psi _{{I,II}}^{{(l = 0)}}(r)$ будут вносить только функции $\psi _{I}^{{(l = 1)}}(r,\theta )$, $\psi _{{II}}^{{(l = 1)}}(r,\theta )$ с l = 1. Исправленное базисное состояние $\psi _{{I,II}}^{{(l = 0)}}(r)$ во втором порядке по малому параметру $\eta = e{{E}_{0}}a{\text{/}}\left| {{{\zeta }_{1}} - {{\zeta }_{0}}} \right|$ может быть записано в виде
(9)
$\left\{ {\begin{array}{*{20}{c}} \begin{gathered} {{\psi }_{I}}(r,\theta ) = \psi _{I}^{{(l = 0)}}(r) + \frac{{\left\langle {\psi _{I}^{{(l = 0)}}\left| {{{V}_{2}}} \right|\psi _{I}^{{(l = 1)}}} \right\rangle }}{{\zeta _{1}^{{(0)}} - \zeta _{0}^{{(0)}}}} \times \hfill \\ \times \;\psi _{I}^{{(l = 1)}}(r,\theta ) - \frac{1}{2}C_{I}^{{(2)}}\psi _{I}^{{(l = 0)}}(r),\quad R < r < {{r}_{0}} \hfill \\ \end{gathered} \\ \begin{gathered} {{\psi }_{{II}}}(r,\theta ) = \psi _{{II}}^{{(l = 0)}}(r) + \frac{{\left\langle {\psi _{{II}}^{{(l = 0)}}\left| {{{V}_{2}}} \right|\psi _{{II}}^{{(l = 1)}}} \right\rangle }}{{\zeta _{1}^{{(0)}} - \zeta _{0}^{{(0)}}}} \times \hfill \\ \times \;\psi _{{II}}^{{(l = 1)}}(r,\theta ) - \frac{1}{2}C_{{II}}^{{(2)}}\psi _{{II}}^{{(l = 0)}}(r),\quad {{r}_{0}} < r < \infty . \hfill \\ \end{gathered} \end{array}} \right.$Выражения для радиально-углового распределения плотности звеньев адсорбированной макроцепи, с учетом указанных упрощений, могут быть записаны в виде
(10)
$\begin{gathered} {{n}_{I}}(r,\theta ) = n_{I}^{{(l = 0)}}(r) + n_{I}^{{(1)}}(r)\cos \theta + \\ + \;n_{I}^{{(2)}}(r){{\cos }^{2}}\theta ,\quad R < r < {{r}_{0}}, \\ \end{gathered} $(11)
$\begin{gathered} {{n}_{{II}}}(r,\theta ) = n_{{II}}^{{(l = 0)}}(r) + n_{{II}}^{{(1)}}(r)\cos \theta + \\ + \;n_{{II}}^{{(2)}}(r){{\cos }^{2}}\theta ,\quad {{r}_{0}} < r < \infty , \\ \end{gathered} $(12)
$\begin{gathered} n_{{I,II}}^{{(1)}}(r) = 2\frac{{\left\langle {\psi _{{I,II}}^{{(l = 0)}}\left| {{{V}_{2}}} \right|\psi _{{I,II}}^{{(l = 1)}}} \right\rangle }}{{\zeta _{1}^{{(0)}} - \zeta _{0}^{{(0)}}}}F_{0}^{{I,II}}(r)F_{1}^{{I,II}}(r), \\ n_{{I,II}}^{{(2)}}(r) = \frac{{{{{\left| {\left\langle {\psi _{I}^{{(l = 0)}}\left| {{{V}_{2}}} \right|\psi _{I}^{{(l = 1)}}} \right\rangle } \right|}}^{2}}}}{{{{{\left| {\zeta _{1}^{{(0)}} - \zeta _{0}^{{(0)}}} \right|}}^{2}}}}{{\left| {F_{1}^{{I,II}}(r)} \right|}^{2}}. \\ \end{gathered} $(13)
$\begin{gathered} \left\langle {\psi _{{I,II}}^{{(l = 0)}}\left| {{{V}_{2}}} \right|\psi _{{I,II}}^{{(l = 1)}}} \right\rangle = \\ = \;\left\{ \begin{gathered} \int\limits_R^{{{r}_{0}}} {F_{0}^{I}(r){{V}_{2}}(r)F_{1}^{I}(r)} {{r}^{2}}dr,\quad I:R < r < {{r}_{0}}, \hfill \\ \int\limits_{{{r}_{0}}}^\infty {F_{0}^{{II}}(r){{V}_{2}}(r)F_{1}^{{II}}(r)} {{r}^{2}}dr,\quad II:{{r}_{0}} < r < \infty , \hfill \\ \end{gathered} \right. \\ \end{gathered} $МД-моделирование однородно заряженных полипептидов на поверхности поляризованной золотой наночастицы
По результатам МД-моделирования по мере увеличения дипольного момента наночастицы происходила такая перестройка конформационной структуры адсорбированного отрицательно заряженного полипептида, при которой макромолекулярная опушка смещалась в положительно заряженное полушарие поляризованной наночастицы (рис. 1) (на рис. 1б и в вектор дипольного момента наночастицы направлен вверх, нижнее полушарие заряжено отрицательно, а верхнее – положительно). Такие конформационные изменения значительно отличаются от случая в целом нейтральной полиамфолитной макромолекулы [9, 10], когда наблюдалось вытягивание макромолекулярной опушки в направлении оси поляризации в равной степени на разных полюсах поляризованной наночастицы.
Рис. 1.
Конформации полипептида A360D40 на поверхности неполяризованной золотой наночастицы (а), поляризованной с дипольным моментом: б) p2, в) p4 (светло-серая трубка – звенья Ala, черным цветом изображены звенья Asp) и 3d-сферическая диаграмма (г) плотности звеньев модельной полиэлектролитной опушки на поверхности наночастицы в поляризующем внешнем поле E0 = 10 мВ/нм. Картина плотности (г) получена в результате расчетов в рамках аналитической модели (10)–(12).
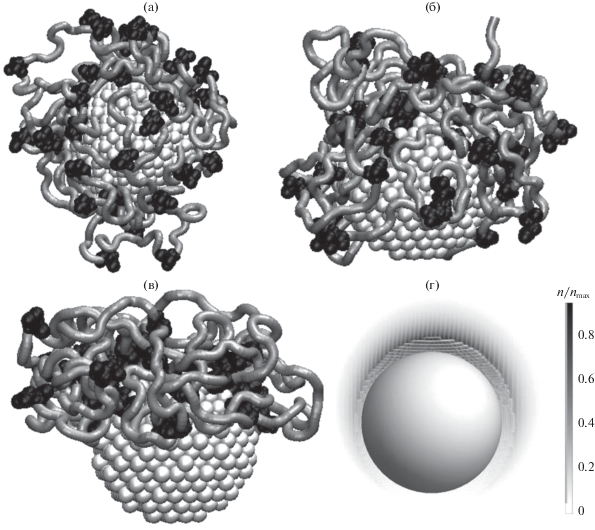
На рис. 1а изображена конформационная структура полипептида A360D40, полученная по окончанию МД-моделирования на неполяризованной наночастице золота, а на рис. 1б и в на поверхности наночастицы, поляризованной с дипольным моментом p2 и p4 соответственно. Видно, что на неполяризованной наночастице полипептид A360D40 полностью ее обволакивает с выталкиванием петель макроцепи в раствор. На рис. 2а изображены радиальные зависимости средней плотности атомов полипептида A360D40 на неполяризованной наночастице. Кривые данных радиальных зависимостей имеют характерный пик около поверхности наночастицы [8] и совпадают в обоих полушариях. На рис. 3а изображены средние угловые распределения атомов полипептида A360D40: на поверхности неполяризованной наночастицы наблюдается в целом равномерное распределение концентрации атомов во всех областях с незначительными флуктуациями.
Рис. 2.
Радиальные зависимости средней плотности атомов полипептида A360D40 (а) на поверхностях положительно (1–3) и отрицательно (4–6) заряженных полушариях поляризованной наночастицы при значениях дипольного момента: 0 (1, 4), p2 (2, 5) и p4 (3, 6). Радиальные зависимости средней плотности атомов полипептидов A380D20 (б, 1), A360D40 (б, 2) и A320D80 (б, 3) на поверхности положительно заряженного полушария наночастицы при ${{p}_{{1.00}}}$.
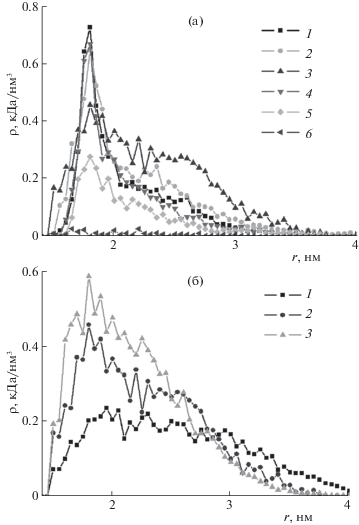
Рис. 3.
Средние угловые распределения атомов полипептида на поверхности поляризованной наночастицы нормированные на экваториальную область для полипептидов: а) A360D40, б) A340D40R20. На рисунке цифрами обозначены значения дипольного момента наночастицы: 1 – 0, 2 – p1, 3 – p2, 4 – p3, 5 – p4.
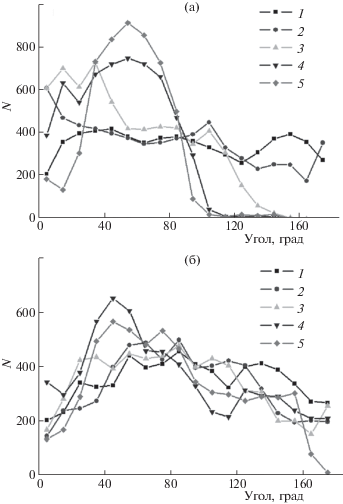
По мере увеличения дипольного момента наночастицы (рис. 1б и 1в) все большая часть звеньев полипептида A360D40 смещалась в положительно заряженное полушарие. Это хорошо видно на графиках угловых распределений атомов макроцепи (рис. 3а). При значении дипольного момента наночастицы равном p1 лишь небольшое число аминокислотных остатков полипептида сместилось в положительно заряженное полушарие наночастицы, при p2 на отрицательно заряженном полюсе наночастицы звенья макроцепи отсутствуют (рис. 1б), а при p3 и p4 практически все аминокислотные остатки находятся в положительно заряженной области, за исключением небольшого количества в слабо заряженной экваториальной области (рис. 1в).
Кривые радиальных зависимостей средней атомарной плотности полипептида A360D40 на поверхности поляризованной наночастицы значительно изменились по сравнению со случаем неполяризованной наночастицы (рис. 2а, кривые 1 и 4). Видно, что для наночастицы с дипольным моментом p2 (кривые 2 и 5) пик кривой распределения средней плотности атомов макроцепи в положительно заряженном полушарии более чем в два раза выше пика кривой радиального распределения в отрицательно заряженном полушарии. Также по сравнению со случаем неполяризованной наночастицы произошло снижение пиков радиального распределения средней плотности атомов полипептида, расположенных как в положительно, так и в отрицательно заряженном полушарии наночастицы. Снижение в отрицательно заряженном полушарии связано со смещением части аминокислотных остатков в положительно заряженное полушарие наночастицы. Однако, при смещении части звеньев в положительно заряженное полушарие (рис. 1б) видно, что концентрация там также незначительно снизилась (рис. 2а, кривая 2).
При значении дипольного момента наночастицы p4 произошло еще большее изменение радиальных зависимостей средней плотности атомов полипептида A360D40 (рис. 2а, кривые 3 и 6). Пик радиального распределения средней плотности атомов полипептида в положительно заряженном полушарии наночастицы еще больше снизился, а профиль этого распределения уширился. При этом плотность атомов полипептида в отрицательно заряженном полушарии имеет околонулевые значения. Это соответствует почти полному смещению звеньев в положительно заряженное полушарие (рис. 1в и 3а).
Такое снижение плотности атомов полипептида в положительно заряженном полушарии поляризованной наночастицы связано с тем, что при увеличении количества аминокислотных остатков в этом полушарии (рис. 3а) происходит набухание макромолекулярной опушки вследствие объемных взаимодействий между звеньями макроцепи в растворе и уменьшении ван-дер-вальсовых взаимодействий с поверхностью наночастицы при уменьшении площади контакта.
Схожие конформационные структуры были получены и для полипептидов A380D20 и A320D80. При этом для полипептида A320D80 с наибольшим количеством отрицательно заряженных аминокислотных остатков Asp большая часть звеньев сместилась в положительное полушарие наночастицы уже при значении дипольного момента равного p2, а для полипептида A380D20 такое смещение происходило при p3.
Для полипептида A380D20 наблюдалось схожее с полипептидом A360D40 набухание макромолекулярной опушки в полярной области по мере увеличения дипольного момента наночастицы. Но при этом опушка у полипептида A380D20 была более рыхлой, а пик кривой радиального распределения при ${{p}_{{1.00}}}$ был примерно в два раза ниже (рис. 2б, кривая 1), чем у полипептида A360D40 (рис. 2б, кривая 2). У полипептида A320D80 с наибольшим количеством отрицательно заряженных аминокислотных остатков Asp напротив пик кривой радиального распределения при p4 был примерно на четверть выше (рис. 2б, кривая 3), чем у полипептида A360D40. Это согласуется с тем, что при увеличении концентрации заряженных звеньев Asp в макроцепи сила притяжения макроцепи к положительному полюсу наночастицы возрастает.
Такой механизм набухания макромолекулярной опушки однородно заряженного полиэлектролита на поверхности поляризованной наночастицы отличается от случая набухания макромолекулярной опушки в целом нейтрального полиамфолита [9, 10] в полярных областях наночастицы, которое было связано со смещением от поверхности одноименно заряженных звеньев по отношению к полюсу наночастицы.
Также был рассмотрен случай, когда макромолекула в целом имела отрицательный суммарный заряд, но при этом содержала также и равномерно распределенные положительно заряженные звенья Arg. В отличие от рассмотренных выше полипептидов часть звеньев полипептида A340D40R20 находилась в области отрицательно заряженного полюса поляризованной наночастицы. Это связано с адсорбцией звеньев Arg в данной области наночастицы. При этом большая часть звеньев полипептида A340D40R20 находится в положительно заряженном полушарии. На рис. 3б изображены средние угловые распределения атомов полипептида A340D40R20 на поверхности поляризованной наночастицы. При увеличении дипольного момента наночастицы все большее количество звеньев полипептида A340D40R20 смещается в положительно заряженное полушарие наночастицы, но при этом в отличие от первых трех рассмотренных полипептидов в отрицательно заряженном полушарии остается часть аминокислотных остатков даже при максимальных рассмотренных значениях дипольного момента наночастицы (рис. 3б).
Расчеты на основе конформационной модели адсорбированной гауссовой цепи
В результате расчетов плотности звеньев адсорбированной гауссовой макроцепи на основе выражений (10), (11) аналитической модели была получена картина деформированной опушки (рис. 1г), переконфигурированной внешним полем и полем поляризованной наночастицы, качественно согласующаяся со структурами МД-моделирования (рис. 1б, 1в). На рис. 4 представлены изменения радиально-углового распределения плотности звеньев однородно заряженной макроцепи полиэлектролита (с положительным знаком заряда сегментов) в диаметральном сечении наночастицы при увеличении амплитуды локального поля
Рис. 4.
Асимметричное перераспределение плотности звеньев опушечного слоя на поверхности поляризованной золотой наночастицы при различных значениях напряженности локального электрического поля $\frac{{{{\varepsilon }_{1}}(\omega ) - {{\varepsilon }_{2}}}}{{{{\varepsilon }_{1}}(\omega ) + 2{{\varepsilon }_{2}}}}{{E}_{0}}$: а – 1, б – 5, в – 10 мВ/нм.
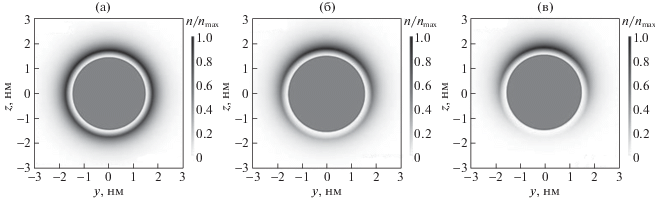
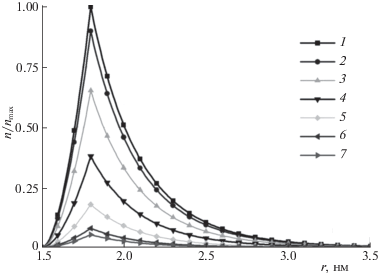
Рис. 5.
Радиальные зависимости плотности звеньев полиэлектролита на поверхности поляризованной золотой наночастицы. Цифрами (1–7) обозначены кривые радиальных зависимостей плотности с шагом по углу в 30 градусов, начиная от верхнего полюса (1) к нижнему (7).
Вместе с тем, необходимо указать и на некоторое отличие в изменении плотности звеньев полиэлектролита в притягивающем полушарии, полученное на основе аналитической модели, от изменений плотности атомов полипептида, полученных методом молекулярной динамики. Оно связано с тем, что в модели идеальной гауссовой цепи не учитываются объемные взаимодействия между звеньями полиэлектролита, тогда как формат МД-расчетов принимает их во внимание.
Таким образом, под воздействием электрического поля поляризованной золотой наночастицы конформационная структура адсорбированного однородно заряженного полиэлектролита значительно изменяется. Она существенно отличается как от случая полиэлектролита, адсорбированного на неполяризованной наночастице, так и от случая адсорбции в целом нейтральных полиамфолитных полипептидов на поверхности поляризованной наночастицы [9, 10].
По мере увеличения степени поляризации наночастицы происходит постепенное смещение аминокислотных остатков однородно заряженного полипептида в заряженное с противоположным знаком по отношению к полипептиду полушарие поляризованной наночастицы. При этом в притягивающем полушарии наночастицы происходит постепенное набухание макромолекулярной опушки, которое сильнее выражено для полиэлектролитов с меньшей концентрацией одноименно заряженных звеньев в макроцепи.
В результате проведенного МД-моделирования однородно заряженного полиэлектролита и моделирования перестройки структуры опушечного слоя адсорбированной макроцепи на основе дифференциального уравнения динамики гауссовой цепи в потенциальном поле получены взаимно согласующиеся результаты. В поле однородно поляризованной наночастицы имеет место асимметричная деформация макроцепной опушки с концентрированием плотности заряженных звеньев цепи на одном полюсе, с зарядом противоположным знаку заряда звеньев, и с разрежением плотности – на другом.
Такие электрически индуцированные изменения конформационной структуры однородно заряженных полиэлектролитов на поверхности поляризованной золотой наночастицы будут оказывать существенное влияние на фотохимические процессы, протекающие в слое макромолекулярной опушки. Это может быть использовано в базовых элементах устройств наноэлектроники, нанозондах и сенсорах с управляемыми параметрами как под воздействием статического электрического поля, так и электромагнитного излучения различной частоты.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований и Оренбургской области в рамках научного проекта № 19-43-560003, а также при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках научного проекта № FSGU-2020-0003.
Список литературы
Zhang P., Chiu Y., Tostanoski L.H., Jewell C.M. // ACS Nano. 2015. V. 9. P. 6465. https://doi.org/10.1021/acsnano.5b02153
Zhang H., Nayak S., Wang W. et al. // Langmuir. 2017. V. 33. P. 12227. https://doi.org/10.1021/acs.langmuir.7b02359
Fuller M.A., Köper I. // Nano Convergence. 2019. V. 6. № 11. https://doi.org/10.1186/s40580-019-0183-4
Qiu T.A., Torelli M.D., Vartanian A.M. et al. // Anal. Chem. 2017. V. 89. P. 1823. https://doi.org/10.1021/acs.analchem.6b04161
Angelatos A.S., Radt B., Caruso F. // J. Phys. Chem. B. 2005. V. 109. P. 3071. https://doi.org/10.1021/jp045070x
Chen Y., Cruz-Chu E.R., Woodard J. et al. // ACS Nano. 2012. V. 6. P. 8847. https://doi.org/10.1021/nn3027408
Cantini E., Wang X., Koelsch P. et al. // Acc. Chem. Res. 2016. V. 49. P. 1223. https://doi.org/10.1021/acs.accounts.6b00132
Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2019. V. 81. № 2. P. 110. https://doi.org/10.1134/S1061933X19020078
Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2020. V. 82. № 2. P. 136.
Кручинин Н.Ю., Кучеренко М.Г. // Биофизика. 2020. Т. 65. № 2. С. 219.
Кручинин Н.Ю., Кучеренко М.Г. // Журн. физ. химии. 2020. Т. 94. № 7. С. 1066.
Kucherenko M.G., Rusinov A.P., Chmereva T.M. et al. // Optics and Spectroscopy. 2009. V. 107. № 3. P. 480. https://doi.org/10.1134/S0030400X0909029X
Kucherenko M.G., Izmodenova S.V., Kruchinin N.Yu., Chmereva T.M. // High Energy Chemistry. 2009. V. 43. № 7. P. 592. https://doi.org/10.1134/S0018143909070169
Phillips J.C., Braun R., Wang W. et al. // J. of Computational Chemistry. 2005. V. 26. P. 1781.https://doi.org/10.1002/jcc.20289
MacKerell A.D., Bashford D., Bellott M. et al. // J. of Phys. Chem. B. 1998. V. 102. P. 3586. https://doi.org/10.1021/jp973084f
Heinz H., Vaia R.A., Farmer B.L., Naik R.R. // J. Phys. Chem. C. 2008. V. 112. P. 17281. https://doi.org/10.1021/jp801931d
Darden T., York D., Pedersen L. // J. Chem. Phys. 1993. V. 98. P. 10089. https://doi.org/10.1063/1.464397
Jorgensen W.L., Chandrasekhar J., Madura J.D. et al. // J. Chem. Phys. 1983. V. 79. P. 926. https://doi.org/10.1063/1.445869
Кучеренко М.Г., Чмерева Т.М. // Вестн. ОГУ. 2008. № 9. С. 177.
Кучеренко М.Г., Кручинин Н.Ю., Чмерева Т.М. // Там же. 2010. № 5. С. 124.
Кучеренко М.Г., Измоденова С.В., Чмерева Т.М. и др. // Там же. 2013. № 9. С. 100.
Гросберг А.Ю., Хохлов А.P. Статистическая физика макромолекул. М.: Наука, 1989.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии


