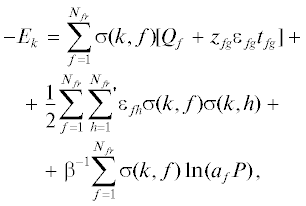Журнал физической химии, 2021, T. 95, № 6, стр. 852-861
Расчет кривых расслаивания в модели решеточного газа модифицированным фрагментным методом
Е. С. Зайцева a, Ю. К. Товбин a, *
a Российская академия наук, Институт общей и неорганической химии им. Н.С. Курнакова
Москва, Россия
* E-mail: tovbinyk@mail.ru
Поступила в редакцию 30.05.2020
После доработки 30.05.2020
Принята к публикации 17.07.2020
Аннотация
Проведено численное исследование влияния роли непрямых корреляций взаимодействующих ближайших частиц на характеристики кривых расслаивания, рассчитываемых в рамках модели решеточного газа, при совместном использовании фрагментного метода (ФМ) и казихимического приближения (КХП). ФМ дает точный расчет статсумм конфигурационных вкладов молекул на малом фрагменте, включающий непрямые корреляции. Влияние частиц, описываемых в КХП, на состояние занятости узлов фрагмента учитывается через локальные внешние поля. Использована версия комбинированного ФМ + КХП-подхода, рассматривающего внешние поля в качестве калибровочной функции, обеспечивающей повышение точности расчета термодинамических функций с учетом непрямых корреляций во всей области плотностей и температур. Получено, что учет непрямых корреляций изменяет вероятности образования малых ассоциатов и уменьшает критическую температуру фазового перехода расслаивания. Расчеты проведены для плоской квадратной решетки, для которой возможно сопоставление критической температуры с точным значением Онсагера, а также для кубической решетки. Результаты расчета сопоставлены с аналогичными кривыми в КХП, в котором учитываются только прямые корреляции.
Проблема корректного расчета свойств неидеальных систем остается одной из наболее сложных задач теории физической химии. Этому вопросу посвящено много работ в статистической термодинамике [1–4]. Среди них особое место занимают работы, в которых получены точные решения, явяющиеся исключительными случаями в задачах многих взаимодействующих тел [2, 5–9]. В основном, приходится использовать приближенные методы учета взаимодействия между частицами, и точные решения служат проверкой их корректности.
В работе [10] дан анализ состояния вопроса по получению квазиточных результатов в рамках модели решеточного газа [2–11] с помощью приближенных методов и главное внимание было уделено фрагментному методу (ФМ) [12–14], который представляет собой прямой расчет статсумм малых систем. Предложенный в [12] путь совместного использования ФМ и квазихимического приближения (КХП) учета взаимодействий между частицами был разработан и представлен как общий метод анализа квазиточных решений. Объединение точного и приближенного методов отталкивается от преимуществ каждого из них (универсальность учета прямых корреляций в КХП и повышение точности учета непрямых корреляций в ФМ). ФМ не позволяет рассматривать большие по размеру системы.
Расширение области системы за счет соседних узлов КХП и повышение точности описания распределения частиц с помощью калибровочных функций направлено на повышение точности расчетов по сравнению с прямыми корреляциями в КХП за счет учета эффектов непрямых корреляций на участках фрагмента. Предложенный ФМ + КХП-подход также ограничен по размерам, как и сам ФМ, тем не менее, даже малые фрагменты позволяют заменить КХП более точными вариантами учета эффектов корреляции. Новый подход может быть использован при описании фазовых переходов и границ раздела фаз, что невозможно в ФМ из-за ограниченности числа узлов системы.
В данной работе впервые излагаются результаты численного анализа комбинированного метода ФМ + КХП учета взаимодействия между частицами. Внимание уделяется двум вопросам: роли непрямых корреляций при описании вероятностей малых ассоциатов/кластеров и кривым расслаивания пар–жидкость. В первом случае ФМ + КХП необходим для анализа расчета свойств малых кластеров, как метод контроля за приближенными методами, также как и в случае макросистем. Во втором случае ФМ + КХП позволяет выйти на исследование фазовых диаграмм.
В обеих ситуациях увеличивается точность учета эффектов корреляции между взаимодействующими частицами. В КХП учитываются только прямые корреляции, что приводит к завышенной оценке величины критической температуры: (βε)с= 1.386 вместо (βε)с = 1.764 в точном решении Онсагера для плоской (d = 2) квадратной решетки с числом ближайших соседей z = 4 [5–7, 9] (здесь β = (kT)–1, ε – параметр взаимодействия ближайших соседей).
Для кубической решетки (d = 3, z = 6) также есть точная оценка [8] (βε)с = 0.886 вместо (βε)с = = 0.810 в КХП. В работе используется только один вариант ФМ + КХП с подключением одного дополнительного узла КХП к Nfr-узлам фрагмента, что можно трактовать как подключение к ФМ калибровочной функции [10]. Роль калибровочных функций состоит в учете дальних корреляций, точное описание которых заменено на аппроксимацию известных точных теоретических или экспериментальных данных [15–17]. В данной работе также излагаются основы алгоритмической реализации метода ФМ + КХП для расчета характеристик равновесно распределенных частиц системы.
МЕТОДИКА АНАЛИЗА
Комбинированный метод ФМ + КХП
Рассматривается система, состоящая из Nfr-узлов фрагмента и одного виртуального распределенного узла, заполнение которого описывается с помощью КХП. Каждый узел фрагмента может быть свободен или занят частицей. Состояние заполнений всех узлов фрагмента рассматривается как одна квазичастица, имеющая конфигурацию k. Это состояние задается функцией $\sigma (k,f)$ равной нулю или единице, если узел f в данной конфигурации k свободен или занят, где $1 \leqslant f \leqslant {{N}_{{fr}}}$ [18]. Всего имеется разных $B = {{2}^{{{{N}_{{fr}}}}}}$, 1 ≤ k ≤ B, конфигураций. Вероятность того, чтобы найти k-ю конфигурацию частиц на фрагменте принимает форму [12–14]
Концепция квазичастиц подразумевает, что смесь квазичастиц идеальна, и все термодинамические и кинетические функции вычислены уравнениями для идеальных смесей [18]. Концентрация квазичастицы определяется как
Все дальнейшие операции усреднения по конфигурациям выражаются через вероятности θk.
Локальная плотность узла θf , 1 ≤ f ≤ ${{N}_{{fr}}}$ и средняя плотность фрагмента θfr запишутся как ${{\theta }_{f}} = \sum\nolimits_{l = 1}^B {\sigma _{{f,l}}^{{}}{{\theta }_{l}}} $ и ${{\theta }_{{fr}}} = \sum\nolimits_k {{{n}_{k}}{{\theta }_{k}}{\text{/}}{{N}_{{fr}}}} $, где через nk обозначено число занятых узлов на фрагменте. Формулу для средней плотности фрагмента θfr можно также записать как ${{\theta }_{{fr}}} = \sum\nolimits_{f = 1}^{{{N}_{{fr}}}} {{{\theta }_{f}}{\text{/}}{{N}_{{fr}}}} $, тогда средняя плотность системы выражается по формуле для обычных неоднородных систем [11, 12] в виде
Эта запись отражает заполнение каждого узла системы. Выражение локальной изотермы для узла g имеют вид:
(1)
$\begin{gathered} {{S}_{{gf}}} = 1 + {{t}_{{gf}}}{{x}_{{gf}}},\quad {{x}_{{gf}}} = \exp ( - \beta {{\varepsilon }_{{gf}}}) - 1, \\ {{t}_{{gf}}} \equiv t_{{gf}}^{{AA}} = \theta _{{gf}}^{{AA}}{\text{/}}\theta _{g}^{A} = 2\theta _{f}^{A}{\text{/}}[{{\delta }_{{gf}}} + {{b}_{{gf}}}], \\ \end{gathered} $Рассматриваемая делокализация узла КХП в случае однородного фрагмента означает, что все локальные плотности фрагмента одинаковые, как и в случае отсутствия данного узла КХП. Поэтому введение такого узла можно считать как введение калибровочной функции, которая позволяет повысить точность описания распределения частиц в широком диапазоне температур и плотностей [10]. Трактовка распределенного узла КХП в качестве калибровочной функции для уравнений совместного применения ФМ + КХП позволяет найти ее параметры по известному точному значению критической температуры. Каждый узел f фрагмента имеет дополнительный вклад в его энергию от узла КХП g. Это вводится через одночастичный вклад в энергию узла – добавляется величина равная ${{\varepsilon }_{{fg}}}{{z}_{{fg}}}{{t}_{{fg}}}$, где энергетический параметр ε имеет свое обычное значение, а число “соседей” zfg можно определить в виде zfg = K/Nfr , где K – некоторый числовой параметр. Если параметр K имеет смысл числа соседей узла КХП (K = z), то zfg = z/Nfr . В общем случае число K можно ассоциировать с эффективным числом соседей отличным от рассматриваемой решетки. Очевидно, если K = 2, то мы имеем аналог одномерной системы, в которой отсутствуют фазовые переходы. При K = 0 вклады КХП-узлов отсутствуют и мы получаем переход к выражениям для исходного ФМ. С учетом этого, выражение для локальной изотермы единственного виртуального узла g выписывается в прежнем виде уравнения (1), в котором функция неидеальности запишется как ${{\Lambda }_{g}} = \prod\nolimits_{f \in {{N}_{{fr}}}} {{{{({{S}_{{gf}}})}}^{{{{z}_{{fg}}}}}}} = {{({{S}_{{gf}}})}^{K}},$ поэтому выражение (1) упрощается. В результате параметрами системы уравнений становятся параметры уравнения КХП (1) – указанный выше параметр К (для числа соседей) и величина энергии связи частицы на узле КХП с решеткой Qg.
Алгоритм и условия расчета
При проведении расчетов функция $\sigma \left( {k,f} \right)$ задавалась в виде массива нулей и единиц по формуле $\sigma \left( {k,f} \right)$ = остаток от деления $\operatorname{int} \{ (k - 1){\text{/}}{{2}^{{f - 1}}}\} $ на 2, где f номер узла фрагмента [19]. При этом k‑я строчка массива определяет состояние занятости узла в конфигурации k. Например, для Nfr = 4 пятая строка массива $\sigma \left( {k,f} \right)$ имеет вид (0010), что означает наличие в конфигурации k = 5 занятого частицей узла f = 3, а остальные узлы – свободны.
Для ускорения расчетов вместо указанной формулы для $\sigma \left( {k,f} \right)$ можно пользоваться двоичным представлением десятичных чисел (k – 1), 1 ≤ k ≤ B, в котором каждая цифра 0 или 1 с порядковым номером f, отсчитываемым справа налево, задает состояние $\sigma \left( {k,f} \right)$. Если в первом случае нам для каждого узла f нужно использовать формулу с выделением остатка, то во втором случае одна операция переводит десятичное число (k – 1) в бинарную строчку, которая содержит ту же информацию, что формула (это программа сделает быстрее). Например, для Nfr = 4 и конфигурации k = 5 двоичное представление десятичного числа (k – 1) = 4 имеет вид (0100), где цифры нумеруем справа налево. Тогда мы также получаем, что в конфигурации k = 5 частицей занят узел f = = 3, а остальные свободны. Преимущество этого описания заключается в том, что можно без перебора узлов f осуществлять операции над значениями $\sigma \left( {k,f} \right)$ сразу для всех узлов f для заданной конфигурации k посредством операций над двоичными числами, являющихся представлением десятичных (k – 1). Метод позволил без больших затрат времени рассчитать фрагменты до Nfr = 30 на обычном персональном компьюторе.
Использованные в работе энергии отсчитаны от связанного состояния атомов, т.е. притяжению отвечает положительный знак, а отталкиванию отрицательный. В представленных ниже результатах потенциал решетки в узлах систем Qf отсчитывался либо от 0, либо от βQf/ε = 22 (что формально отвечает изотермам адсорбции). В последнем случаем изотермы имеют параллельный сдвиг по давлению к меньшим величинам по сравнению с Qf = 0, но фазовые диаграммы не зависят от этого сдвига по давлениям.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА
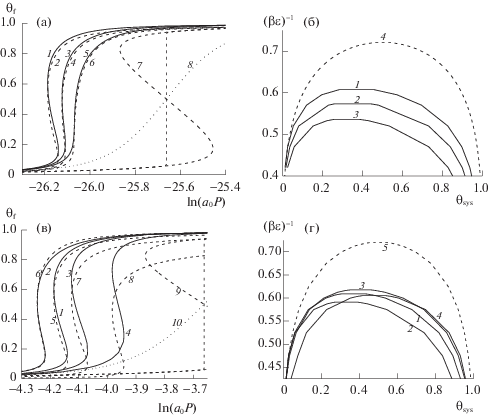
Надкритические температуры. ФМ не позволяет получить расслаивание фаз, поэтому простейшая ситуация для анализа влияния непрямых корреляций соответствует надкритической области температур. На рис. 1 приведены кривые изотерм, а также корреляторы порядка n = 2, 3 и 5 полученные в разных приближениях ФМ и КХП для квадратной решетки z = 4, d = 2 при βQf/ε = 22.
Рис. 1.
Изотермы плотности (а) и корреляторов второго (б), третьего (в) и пятого (г) порядков. Обозначения см. текст.
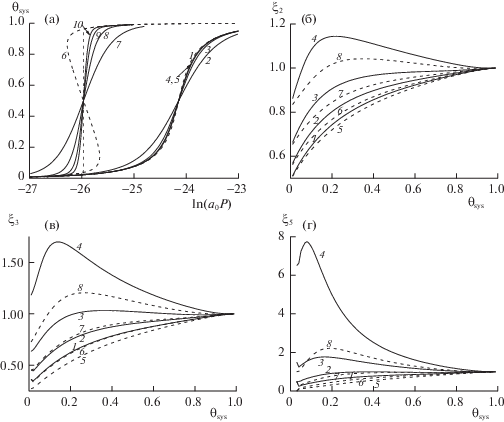
Изотермы на рис. 1а представлены пунктирными кривыми по расчетам в КХП (1, 6) и сплошными кривыми ФМ для фрагментов 2 × 2 (2 и 7), 3 × 3 (3 и 8), 4 × 4 (4 и 9) и 5 × 5 (5 и 10) в широкой области флюида от разреженного пара до плотного флюида для температуры τ = 1.3 (1–5), τ = = T/Tc(КХП), Tc(КХП) – критическая температура в КХП. (Для сопоставления также приведены изотермы в подкритической области при τ = 0.7 (6–10)).
Из рис. 1а видно, что увеличение фрагмента в размере меняет угол наклона γ изотермы в точке θ = 0.5 при неизменном давлении в ней. Для количественного сопоставления изотерм в разных способах расчета воспользуемся величиной тангенса угла наклона изотермы $\operatorname{tg} \gamma $ ≡ $\operatorname{tg} {{(\gamma )}_{{\theta = 0.5}}}$ при плотности θ = 0.5, отчет угла γ идет от наклона к оси плотности. Для кривых на рис. 1а имеем значения $\operatorname{tg} \gamma $ показанные в табл. 1.
Таблица 1.
Тангенс угла наклона γ изотермы в КХП и ФМ для фрагментов m × m
| m × m | $\operatorname{tg} \gamma $ при τ = 0.7 | $\operatorname{tg} \gamma $ при τ = 1.3 |
|---|---|---|
| КХП | –1.04 | 0.68 |
| 2 × 2 | 1.09 | 1.54 |
| 3 × 3 | 0.50 | 1.04 |
| 4 × 4 | 0.29 | 0.88 |
| 5 × 5 | 0.19 | 0.83 |
С ростом размера фрагмента при температуре τ = 1.3 угол наклона изотермы уменьшается и создается впечатление, что он приближается к углу наклона для КХП. Однако эта тенденция обусловлена двумя разными факторами. Увеличение размера фрагмента увеличивает только учет эффектов корреляции, что приводит к уменьшению угла, а для КХП данная область температур уже достаточно близка к критической температуре в данном приближении, что приводит к существенному уменьшение угла вблизи Тc (КХП). Влияние температуры при расчете в ФМ для фрагментов 3 × 3 и 4 × 4 и в КХП на угол наклона показан в табл. 2.
Таблица 2.
Тангенс угла наклона γ изотерм в разных приближениях
| τ | $\operatorname{tg} \gamma $ КХП | $\operatorname{tg} \gamma $ ФМ 3 × 3 | $\operatorname{tg} \gamma $ ФМ 4 × 4 |
|---|---|---|---|
| 2.5 | 2.06 | 2.11 | 2.07 |
| 2.3 | 1.92 | 1.98 | 1.94 |
| 2.1 | 1.75 | 1.83 | 1.78 |
| 1.9 | 1.55 | 1.67 | 1.60 |
| 1.7 | 1.32 | 1.48 | 1.39 |
| 1.5 | 1.04 | 1.27 | 1.16 |
| 1.3 | 0.68 | 1.04 | 0.88 |
| 1.1 | 0.25 | 0.82 | 0.62 |
При высоких температурах три кривые дают достаточно близкие значения углов наклона изотермы в КХП и ФМ 3 × 3 и 4 × 4. Причем $\operatorname{tg} \gamma $ ФМ 3 × 3 > $\operatorname{tg} \gamma $ ФМ 4 × 4 > $\operatorname{tg} \gamma $ КХП. Данная тенденция сохраняется с уменьшением температуры, пока изотерма не входит в область влияния критической точки. Расхождение между $\operatorname{tg} \gamma $ (ФМ 4 × × 4) > $\operatorname{tg} \gamma $ КХП резко увеличивается в области от τ = 1.5 в ходе резкого уменьшения $\operatorname{tg} \gamma $ КХП.
В то же время следует учитывать, что и ФМ является вблизи критической области приближенным методом, в котором могут проявляться дальние корреляции. Это демонстрируют данные для τ = 0.7 в табл. 1. В подкритической области углы наклонов достаточно заметно отличаются от вертикального положения секущей и, тем более, от отрицательного угла наклона изотремы. Здесь даже расчет для фрагмента 5 × 6 приводит к углу $\operatorname{tg} \gamma $ (ФМ 5 × 6) = 0.16.
Более детально отличие эффектов непрямых корреляций от прямых корреляций в КХП представляют собой отношения корреляторов разной размерности. Корреляторы порядка n определяются как средние величины по фрагменту ${{\theta }_{{(n)}}} = \sum\nolimits_{k = 1}^B {N_{{(n)}}^{A}(k){{\theta }_{k}}} {\text{/}}{{N}_{{(n)}}},$ где $N_{{\left( n \right)}}^{A}(k)$ – число групп из n соседних занятых узлов фрагмента для его конфигурации k, ${{N}_{{(n)}}}$ – число групп из n числа соседних узлов во фрагменте. Так как фрагмент однороден, то достаточно рассчитывать корреляторы, построенные на одном центральном узле и на его (n–1) узлах окружения. Когда имеются разные способы расположений соседних узлов вокруг центра (неприводимые конфигурации [11]), то здесь по ним проводится дополнительное усреднение. Так для тройного коррелятора ${{\theta }_{{(3)}}} = \theta _{{fG(f)}}^{{AAA}} = \sum\nolimits_{k = 1}^B {N_{{fG(f)}}^{{AAA}}\left( k \right){{\theta }_{k}}} {\text{/}}6,$ где функция рассчитывается на конкретном центральном узле f и его полном окружении G(f). То есть рассматривается полное окружение центрального узла с двумя соседними узлами, чтобы учесть разное расположение трех соседних узлов системы. Всего вариантов комбинации трех узлов 6, поэтому в знаменателе 6.
Роль размера фрагмента и выявление роли непрямых корреляций в изотермах демонстрируют величины ξn, представляемые в нормированном виде через отношения корреляторов ξn = = θ(n)(ФМ)/θ(n)(КХП) в сопоставляемых приближениях ФМ и КХП.
На рис. 1б,в,г представлены для ФМ изотермы корреляторов парного (рис. 1б), третьего (рис. 1в), и пятого (рис. 1г) порядков, нормированных на соответствующие значения корреляторов в КХП, при τ = 2.5 (1 и 5), 2.1 (2 и 6), 1.7 (3 и 7) и 1.3 (4 и 8) для фрагментов 3 × 3 (сплошные линии 1–4) и 4 × 4 (пунктирные линии 5–8). При высоких температурах τ = 2.5 (1 и 5) и 2.1 (2 и 6) отношение корреляторов ξn монотонно возрастает с ростом плотности, стремясь к единице при полном заполнении системы, когда результаты по КХП и ФМ совпадают. С убыванием температуры отношения ξn растут и при низких температурах τ = 1.7 (3 и 7) и 1.3 (4 и 8) корреляторы изменяются с образованием максимума, сохраняя стремление к единице при больших плотностях, но уже стремление сверху. Чем выше порядок корреляторов, тем выше максимум значения их отношения: на рис. 1г максимум самый большой. Это показывает, как с ростом порядка корреляторов растет расхождение между ФМ и КХП. Данное различие еще больше возрастает при стремлении к критической изотерме сверху (например, при τ = 1.1 максимум на поле 1г будет порядка 32 вместо 8!).
Влияние параметров калибровочных функций
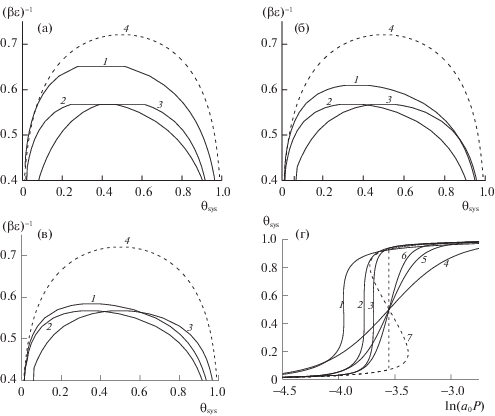
Совместное использование ФМ + КХП позволяет получить петлю на изотерме, которая отвечает кривым типа ван-дер-Ваальса, и из анализа петли можно определить сосуществующие плотности разреженной и плотной фаз. Зная сосуществующие плотности при каждой температуре, построим кривую расслаивания в рамках обсуждаемой модели. Уравнения модели содержат два молекулярных параметра, относящиеся к характеристкам распределенного узла КХП, которые фактически являются параметрами калибровочной функции: величина K (для числа соседей) и величина энергии связи частицы на узле КХП с решеткой Qg (1). На рис. 2 приведены примеры влияния этих параметров на изотермы (поля 2а и 2в) и кривые расслаивания (поля 2б и 2г) для фрагмента 3 × 3. На всех полях приведены аналогичные значения в КХП (пунктирная линия) и аналогичные изотермы в ФМ (точечная линия).
На рис. 2а построены изотермы плотности фрагмента (1–3) (сплошные линии) и плотности виртуального узла (4–6) (пунктирные линии) для ФМ + КХП на фрагменте 3 × 3, полученные при K = 4 (1,4), 3.5 (2, 5) и 3 (3, 6), а также изотерма с секущей в КХП (пунктирная кривая 7) и изотерма ФМ (точечная кривая 8) при βQf/ε = 22. С уменьшением K уменьшается к.ч. виртуального узла, поэтому уменьшаются его заполнения.
На поле 2б показаны соответствующие фазовые диаграммы для ФМ + КХП на фрагменте 3 × × 3 при тех же параметрах K для фргамента 3 × 3 и в КХП (пунктир). Локальные плотности узлов фрагмента и КХП отличаются между собой за счет различий в учете непрямых корреляций. В целом, хотя отличия между локальными плотностями не очень велики, кривые рассливания отличаются по Тс значительно. Отметим, приближенный характер получаемых кривых расслаивания (кривая 3) может иметь темпетатуру выше точного решения Онсагера, которой соответствует величина $(\beta \varepsilon )_{{\text{c}}}^{{ - 1}}$ = 0.567. Поэтому кривая (3), имеющая температуру ниже данной величины, отвечает нефизическому значению.
На рис. 2в показаны изотермы плотности фрагмента (1–4) при Qf = 0 и плотности виртуального узла (5–8) для ФМ + КХП с потенциальной энергией для виртуального узла Qg = 0 (1, 5), 1/3ε (2, 6), –1/3ε (3, 7) и –ε (4, 8), а также КХП (пунктирная кривая с секущей 9) и ФМ (точечная кривая 10), при K = 4.
Локальные плотности узлов фрагмента и виртуального узла отличаются между собой за счет различий в учете непрямых корреляций. В варианте Qg = 1/3ε (2, 6) локальные изотермы для фрагмента и виртуального узла ближе всего между собой. Тогда как для вариантов Qg = 0 (1, 5) и 2/3ε (3, 7) эти отличия более заметны. Здесь следует учитывать, что вклад от виртуального узла быстро уменьшается с ростом размера фрагмента.
На рис. 2г показаны фазовые диаграммы для ФМ + КХП с потенциальной энергией для виртуального узла Qg = 0 (1), 1/3ε (2), –1/3ε (3) и –ε (4), а также КХП (пунктирная кривая 5). Увеличение притяжения Qg > 0 смещает кривую расслаивания влево и увеличивает ее асимметрию за счет уменьшения величины критического заполнения ${{\theta }_{c}}$. Отталкивание между решеткой и частицей Qg < 0 увеличивает ${{\theta }_{c}}$.
Квазиточные кривые расслаивания
На рис. 3а–в показаны кривые расслаивания для трех фрагментов 2 × 2 (рис. 3а), 3 × 3 (рис. 3б) и 4 × 4 (рис. 3в), сопоставляемые с расслаиванием в КХП (пунктирные линии).
На рис. 3а–в кривые расслаивания 1 отвечают K = 4, Qg = 0. С увеличением размера фрагмента величина Тc уменьшается, приближаясь к точному значению: фрагмент 2 × 2 (βε)c = 1.536, θc = = 0.396, фрагмент 3 × 3 (βε)c = 1.642, θc = 0.368, фрагмент 4 × 4 (βε)c = 1.712, θc = 0.355.
Кривые 2 отвечают значениям K = 3.07, θc = = 0.358 (2 × 2), K = 3.39, θc = 0.342 (3 × 3) и K = = 3.69, θc = 0.343 (4 × 4) калиброванным под точное значение (βε)c = 1.764 при Qg = 0. С ростом размера фрагмента величина параметра К стремится к своему значению K = z = 4.
Кривые 3 отвечают калиброванным значениям K и Qg под точное значение (βε)c = 1.764 и под значение критической плотности θc = 0.500 для всех кривых (чтобы сохранить тенденцию к сохранению симметрии кривой расслаивания, которая нарушается в общем случае в ФМ + КХП). Это дает для фрагмента 2 × 2: K = 3.79, Qg = –1.38, для фрагмента 3 × 3: K = 3.61, Qg = –1.23, и для фрагмента 4 × 4: K = 3.72, Qg = –1.19. С ростом размера фрагмента величина K слабо меняется, а величина Qg уменьшается по модулю.
На рис. 3г представлены изотермы для фрагментов 2 × 2 (1, 4), 3 × 3 (2, 5) и 4 × 4 (3, 6) с калибровкой в ФМ + КХП (1–3), без калибровки в ФМ (4–6) и в КХП (пунктирная кривая с расслаиванием 7) при Qf = 0. Критические изотермы ФМ + + КХП (1–3) построены при калибровочных параметрах K и Qg, полученных для кривых 3 на рис. 3а–в, обеспечивающих точное значение (βε)c = = 1.764 и критическую плотность θc = 0.500. С ростом фрагмента для ФМ + КХП получен рост давления: кривая 1 лежит левее всех в области малых давлений, следующие кривые 2 и 3 сдвинуты к большим плотностям. Кривые 1–3 примерно сохраняют симметрию относительно плотности 0.5.
Рисунок 3 демонстрирует, что учет ФМ + КХП понижает критическую температуру, и это понижение тем больше и ближе к точному значению, чем больше размер фрагмента (кривые 1 на рис. 3а–в). С другой стороны, для любого размера фрагмента калибровка позволяет получить точное значение (βε)c = 1.764, и для него можно рассматривать квазиточные значения термодинамических функций.
Наличие двух разных плотностей в системе (узлы фрагмента и узел КХП) вносит искажение в симметрию задачи – кривая расслаивания становится асимметричной и имеет критическую плотность отличную от значения θc = 0.5. При сохранении величин молекулярных параметров системы приближение Тс к точному значению сопровождается смещением от θc = 0.5. Вопрос о целесообразности строгого сохранения симметрии определяется целью использования калибровочных функций. С увеличением размера фрагмента доля вклада от узла КХП в термодинамические функции уменьшается. Процедура калибровки позволяет за счет варьирования двух параметров получить и точное значение (βε)c и θc = 0.5. Это (частично или практически полностью) нивелирует искажение симметрии купола фазовой диаграммы.
Корреляторы ФМ + КХП в надкритической области
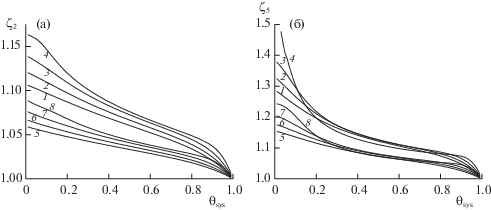
На рис. 4 представлены изотермы корреляторов парного (рис. 4а) и пятого порядка (рис. 4б) в ФМ + КХП без калибровки при K = 4 и Qg = 0, нормированных на аналогичные корреляторы в ФМ, ζn = θ(n)(ФМ + КХП)/θ(n)(ФМ), при τ = 2.5 (1, 5), 2.1 (2, 6), 1.7 (3, 7) и 1.3 (4, 8) для фрагментов 3 × 3 (1–4) и 4 × 4 (5–8).
Согласно рис. 4 корреляторы в ФМ + КХП выше ФМ и с ростом фрагмента они убывают, но это связано исключительно с завышенным координационным числом (к.ч.) для узлов фрагмента по сравнению с z на число K/Nfr, которое убывает с ростом размера фрагмента. Значение отношения корреляторов с ростом плотности убывает, достигая значения единицы, т.е. при полном заполнении системы мы получаем общий результат в ФМ + КХП, ФМ и КХП (отношение ФМ и КХП на рис. 1 также достигало значения единицы при высоких плотностях).
Чем выше порядок корреляторов, тем больше разница между ФМ + КХП и ФМ: на рис. 4а для ζ2 максимальные значения составляют 1.17, а для ζ5 на рис. 4б – 1.5. В пределе разреженного газа все корреляции отсутствуют и все методы дают единицу в точке θ = 0. Рисунок 4 показывает, как с ростом порядка корреляторов растет расхождение между ФМ и ФМ + КХП.
Аналогичные кривые с другой нормировкой были представлены на рис. 1, чтобы подчеркнуть отличия точных расчетов от кривых в КХП, а здесь демонстрируются отличия квазиточных величин от точных. Расчеты показывают, что в методе ФМ + КХП концентрационные зависимости всех корреляторов отражаются достаточно точно – отношения их величин находятся вблизи единицы по сравнению с точными значениями.
Квазиточные кривые расслаивания для кубической решетки
Предложенный подход к комбинированному использованию ФМ + КХП может быть применен к другим двух- и трехмерным решеткам. На рис. 5а показаны фазовые диаграммы для кубической решетки: точечной линией для КХП (1), пунктирными линиями для ФМ + КХП при K = 6, Qg = 0 (без калибровки (2–4)) и сплошными линиями для ФМ + КХП с калибровкой (5–7) для фрагментов 2 × 2 × 2 (2, 5), 2 × 2 × 3 (3, 6) и 2 × 3 × × 3 (4, 7). В КХП (1) в критической точке имеем: (βε)c = 0.812, θc = 0.5.
Так же, как и в двухмерной системе (кривая 3 на поле 2б), в трехмерной системе с увеличением размера фрагмента величина Тc уменьшается, и все они находятся ниже точного значения ((βε)c = = 0.888): фрагмент 2 × 2 × 2 (βε)c = 1.019, θc = = 0.441, фрагмент 2 × 2 × 3 (βε)c = 1.054, θc = 0.433, фрагмент 2 × 3 × 3 (βε)c =1.060, θc = 0.428. Поэтому необходимо использовнаие калибровочных функций.
Кривые 5–7 отвечают калиброванным значениям K = 9.12 и Qg = –0.74 для 2 × 2 × 2, K = 10.60 и Qg = –0.74 для 2 × 2 × 3 и K = 11.74 и Qg = –0.76 для 2 × 3 × 3 под точное значение (βε)c = 1.764 и плотность θc = 0.5. Здесь с ростом размера фрагмента величина параметра K увеличивается, отдаляясь от K = z = 6. Величина Qg уменьшается с ростом размера фрагмента.
На рис. 5б показаны изотермы точечными линиями для КХП (1, 8), пунктирными линиями для ФМ (2, 5, 9, 12), тонкими сплошными линиями для ФМ + КХП без калибровки (3, 6, 10, 13) и толстыми сплошными линиями для ФМ + КХП с калибровкой (4, 7, 11, 14) для фрагментов 2 × 2 × 2 (2–4, 9–11) и 2 × 3 × 3 (5–7, 12–14) при температуре ниже критики τ = 0.7 (1–7) и выше 1.3 (8–14).
Рис. 5б демонстрирует, что изотермы КХП (1, 8) и ФМ (2, 5, 9, 12) при заданной температуре имеют общий центр в точке плотности θ = 0.5 и давления, отвечающего равновесному в КХП при расслаивании. Учет ФМ + КХП (3, 6, 10, 13) уменьшает давление, а учет корреляций (4, 7, 11, 14) еще больше уменьшает давление и уменьшает наклон изотерм в центре к оси плотности. Также давления уменьшаются с ростом фрагмента от 2 × × 2 × 2 (2–4, 9–11) к 2 × 3 × 3 (5–7, 12–14).
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Точные значения термодинамических функций играют важную роль для тестирования методов моделирования. Они позволяют определить корректность и точность используемых приближенных подходов, что особенно важно для неидеальных систем. ФМ представляет собой прямой расчет статсуммы малой системы [12–14, 17]. Рассматриваемый фрагмент представляет собой периодический участок макроскопической поверхности. В нем отсутствуют какие-либо приближения, но в силу малости числа узлов системы он не в состоянии описывать фазовые переходы, которые являются следствием макроскопического числа частиц. Его внутренняя топография для неоднородных систем может быть произвольной.
Комбинированное использование ФМ и КХП в рамках рассмотренного варианта с формальным использованием узла КХП в качестве калибровочной функции существенно расширяет область точного описания физико-химических свойств в широких диапазонах температур и плотностей. ФМ + КХП позволяет использовать известные точные значения для Тcr [5–9], для нахождения квазиточных функций распределений (унарных, парных и корреляторов более высоко порядка) в нужных диапазонах температур и плотностей, и получения квазиточных значений термодинамических функций. В частности, подход ФМ + КХП расширяет возможности калибровочных функций [15–17], которые ранее строились только на основе информации о величинах Тc, на совместное использование величины Тc и точных расчетов в надкритической области.
Возможность калибровки в ФМ + КХП фрагментов практически любого размера на точное значение Тc дает преимущества такого подхода по сравнению вариационным кластерным методом [20, 21] за счет ускорения расчетов (не менее чем на три порядка) и возможностью рассматривать большие по размеру фрагменты, что особенно важно для неоднородных систем.
Предложенный подход расширяет круг систем, для которых повышается точность расчета: это получение точных значений для фрагментов Nfr ≤ 30, возможность описания фазовых переходов до Nfr ≤ 24–25, а также возможность замены КХП в прикладных задачах с включением областей фрагментов порядка Nfr ≤ 10–16. Данные размеры определяют также размеры разных подсистем более общих задач, в которых возможно применение нового подхода ФМ + КХП для расчета или тестирования других численных подходов, что позволяет описывать физико-химические свойства многих реальных задач.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта № 18-03-00030а).
Список литературы
Fowler R.Y., Guggenheim E.A. Statistical Thermodynamics. Cambridge: Cambridge Univer. Press, 1939.
Хилл Т.Л. Статистическая механика. Принципы и избранные приложения. М.: Изд-во. иностр. лит., 1960. 485 с.
Шахпаронов М.И. Введение в молекулярную теорию растворов. М.: ГИТНЛ, 1956. 510 с.
Кривоглаз А.Н., Смирнов А.А. Теория упорядочивающихся сплавов. М.: ГИФМЛ, 1958. 388 с.
Onsager L. // Phys Rev. 1944. V. 65. P. 117.
Domb C. // Adv. Phys. 1960. V. 9. P. 149, 245.
Хуанг К. Статистическая механика. М.: Мир, 1966. 520 с.
Fisher M.E. // J. Math. Phys. 1963. V. 4. P. 278.
Baxter R.J. Exactly Solved Model in Statistical Mechanics, London: Academ. Press, 1982.
Товбин Ю.К. // Журн. физ. химии. 2021. Т. 95. № 5. С. 718.
Товбин Ю.К. Теория физико-химических процессов на границе газ–твердое тело, М.: Наука, 1990. 288 с. (Tovbin Yu.K. Theory of physical chemistry processes at a gas–solid surface processes. Boca Raton, Fl.: CRC Press, 1991.)
Товбин Ю.К. // Журн. физ. химии. 1996. Т. 70. № 4. С. 700.
Товбин Ю.К. // Химическая физика. 1996. Т. 15. № 2. С. 75.
Tovbin Yu.K. // Langmuir. 1997. V. 13. № 5. P. 1979.
Товбин Ю.К. // Журн. физ. химии. 1998. Т. 72. № 12. С. 2254.
Tovbin Yu.K., Rabinovich A.B. // Langmuir. 2004. V. 20. № 12. P. 6041.
Товбин Ю.К. Молекулярная теория адсорбции в пористых телах. М.: Физматлит, 2012. 624 с.
Пригожин И., Дефэй Р. Химическая термодинамика. Новосибирск: Наука, 1966, 510 с.
Товбин Ю.К., Петрова Т.В. // Журн. физ. химии. 1996. Т. 70. № 5. С. 870.
Kikuchi R. // Phys. Rev. 1951. V. 81. P. 988.
Theory and Applications of the Cluster Variation and Path Probability Methods / Eds. J.L. Moran-Lopez and J.M. Sanchez / New York and London: Plenum Press, 1996. P. 237
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии