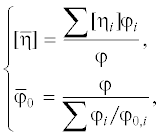Журнал физической химии, 2021, T. 95, № 7, стр. 1131-1134
Сдвиговые напряжения при течении структурированных суспензий
a Bekro Chemie GmbH Industriestraße 104
66802 Überherrn (Saarland, BRD)
* E-mail: Dr.Levinsky@yandex.com
Поступила в редакцию 25.05.2020
После доработки 14.12.2020
Принята к публикации 16.12.2020
Аннотация
Выведено полуэмпирическое уравнение, описывающее зависимость сдвигового напряжения от скорости сдвига при течении однокомпонентной суспензии. Суспензия рассматривается как состоящая из двух фракций: одиночных зерен и их димеров, между которыми устанавливается равновесие, зависящее от скорости сдвига. Уравнение основано на формуле Кригера, обобщенной на случай многокомпонентных суспензий. Выведенное уравнение хорошо аппроксимирует экспериментальные данные и может быть использовано для экстраполяции к нулевой скорости сдвига для определения предела текучести.
ТЕОРИЯ РАСЧЕТА
Известно, что зависимость вязкости суспензии $\eta $ от объемной доли $~\varphi $ диспергированной фазы при постоянной скорости сдвига хорошо описывается формулой Кригера [1, 2]:
(1)
$\eta = {{\eta }_{0}}{{\left( {1 - \frac{\varphi }{{{{\varphi }_{0}}}}} \right)}^{{ - [\eta ]{{\varphi }_{0}}}}},$Формула Кригера является феноменологической и полуэмпирической, и величины $[\eta ]$ и ${{\varphi }_{0}}$ яляются “подстроечными” параметрами, т.е. подбираются таким образом, чтобы график функции (1) наилучшим образом проходил через экспериментальные точки.
В нашей работе [3] в числе прочего было выведено обобщение формулы Кригера на случай многокомпонентных суспензий:
(2)
$\eta = {{\eta }_{0}}{{\left( {1 - \frac{\varphi }{{{{{\bar {\varphi }}}_{0}}}}} \right)}^{{ - [\bar {\eta }]{{{\bar {\varphi }}}_{0}}}}}.$Обобщенную формулу Кригера (2), (3) можно использовать для описания зависимости сдвигового напряжения $\tau $ от скорости сдвига $\dot {\gamma }$, если ввести следующие предположения:
1) однокомпонентную суспензию можно рассматривать как систему, состоящую из двух фракций: одиночных зерен суспензии и их димеров11, причем одиночным зернам и их димерам соответствуют различные значения параметров $[\eta ]$ и ${{\varphi }_{0}}$;
2) димеризацию одиночных зерен можно рассматривать как реакцию с константой скорости ${{k}_{1}}$, распад димеров – как реакцию с константой скорости, линейно зависящей от скорости сдвига $\dot {\gamma }$: $k = {{k}_{2}} + {{k}_{3}}\dot {\gamma }$.
Аналогичные идеи были высказаны в [4], но там они носят качественный характер.
Таким образом, любой скорости сдвига соответствуют свои равновесные концентрации одиночных зерен и димеров, исходя из которых, по формулам (2), (3) можно вычислить вязкость. Последняя является коэффициентом пропорциональности между сдвиговым напряжением $\tau $ и сдвиговой скоростью $\dot {\gamma }$: $\tau = \eta \dot {\gamma }$. Необходимо еще учесть предел текучести ${{\tau }_{0}}$:
(уравнение Шведова–Бингама; ${{\eta }_{{\text{B}}}}$ – пластическая вязкость).Пусть в единице объема суспензии находится n зерен твердой фазы, и пусть средний объем зерна равен ${v}$. Тогда объемная доля твердой фазы равна $\varphi = n{v}$. При заданной скорости сдвига $\dot {\gamma }$ между одиночными зернами и димерами устанавливается равновесие: $2{{n}_{1}} \rightleftarrows {{n}_{2}}$, причем
Умножая левую и правую часть последнего равенства на ${v}$, получим: Константа равновесия K (“константа нестойкости” димеров) равна(7)
$K = \frac{{n_{1}^{2}}}{{{{n}_{2}}}} = \frac{{{{k}_{2}} + {{k}_{3}}\dot {\gamma }}}{{{{k}_{1}}}}.$(10)
$\tau = {{\tau }_{0}} + {{\eta }_{0}}\dot {\gamma }{{\left( {1 - \frac{{{{\varphi }_{1}}}}{{{{\varphi }_{{10}}}}} - \frac{{{{\varphi }_{2}}}}{{{{\varphi }_{{20}}}}}} \right)}^{{ - \frac{{[{{\eta }_{1}}]{{\varphi }_{1}} + [{{\eta }_{2}}]{{\varphi }_{2}}}}{{{{\varphi }_{1}}/{{\varphi }_{{10}}}~ + ~{{\varphi }_{2}}/{{\varphi }_{{20}}}}}}}},$ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для проведения экспериментов использовались жидкие краски для полимерных материалов – суспензии окиси хрома (“зеленые краски”) и алюмосиликата натрия (“синие краски”) в дисперсионной среде, представляющей собой смесь 70% сорбитантриолеата с 30% диоктиладипината. Вязкость дисперсионной среды ${{\eta }_{0}} \approx 0.113~\;{\text{Па с\;}}$, плотность $\rho \approx 930~\;{\text{кг/}}{{{\text{м}}}^{3}}$. Суспензии различных концентраций приготавливались путем смешения пигмента с дисперсионной средой и последующего интенсивного диспергирования в течение 30 мин, затем суспензия разбавлялась дисперсионной средой до нужной концентрации. Геометрические параметры частиц твердой фазы не определялись.
Вязкость суспензий измерялась на ротационном вискозиметре фирмы ThermoHaake с погрешностью не более 5%. Использовалась измерительная ячейка с геометрией конус–плоскость; измерения проводились в режиме контролируемой скорости сдвига, при этом измерялся крутящий момент. Для контроля стационарности течения сканирование по скорости сдвига выполнялось в двух сериях измерений: при росте скорости сдвига и при ее убывании; при этом результаты измерения для обеих серий совпадали в пределах погрешности измерения.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
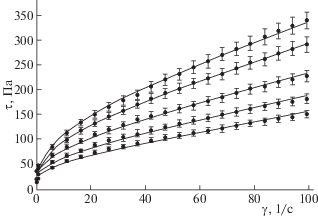
Результаты для дилатантной суспензии (“синяя краска” – дисперсия алюмосиликата натрия) представлены на рис. 1, для псевдопластичной (“зеленая краска” – дисперсия окиси хрома) – на рис. 2 и 3. Точки показывают результаты измерения, кривая – расчет по формулам (8)–(11). Индикатор ошибок показывает 5% разброс. Экстраполяция кривой к нулю скорости сдвига дает предел текучести ${{\tau }_{0}}$.
Рис. 1.
“Синяя краска”. Объемная доля пигмента 38.0%, среднеквадратичное отклонение точек от кривой – 0.34 Па, предел текучести ${{\tau }_{0}} \approx 6.8~\;{\text{Па}}$.
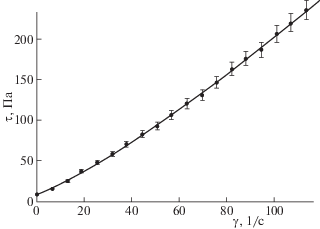
Рис. 2.
“Зеленая краска”.Объемная доля пигмента 31.6%, среднеквадратичное отклонение точек от кривой – 0.24 Па, предел текучести ${{\tau }_{0}} \approx 16.1\;~{\text{Па}}$. Значения параметров: ${{\kappa }_{0}} \approx 0.0665$, ${{\kappa }_{1}} \approx 0.0100$, $[{{\eta }_{1}}] \approx 5.24$, $[{{\eta }_{2}}] \approx 16.1$, ${{\varphi }_{{10}}} \approx 1.0$, ${{\varphi }_{{20}}} \approx 1.0$.
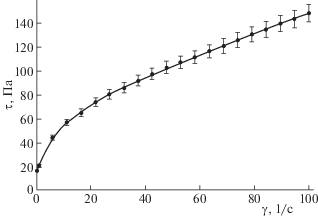
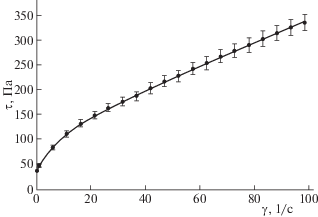
Рис. 3.
“Зеленая краска”. Объемная доля пигмента 39.5%, среднеквадратичное отклонение точек от кривой – 0.25 Па. Предел текучести ${{\tau }_{0}} \approx 41.0~\;{\text{Па}}$. Значения параметров: ${{\kappa }_{0}} \approx 0.390$, ${{\kappa }_{1}} \approx 0.0304$, $[{{\eta }_{1}}] \approx 5.91$, $[{{\eta }_{2}}] \approx 17.6$, ${{\varphi }_{{10}}} \approx 1.0$, ${{\varphi }_{{20}}} \approx 0.988$.
Из рисунков видно, что предлагаемые уравнения демонстрируют исключительно хорошее согласие с экспериментом и могут быть использованы для экстраполяции экспериментальных данных к нулю скорости сдвига с целью определения предела текучести. Это имеет большое значение в особенности для псевдопластичных суспензий, у которых зависимость $\tau (\dot {\gamma })$ в окрестности точки $\dot {\gamma } = 0$ демонстрирует быстрое возрастание.
Представляет также интерес сопоставление точности аппроксимации экспериментальных данных выведенной здесь формулы с наиболее известными уравнениями [5, с. 30]: Гершеля–Балкли $\tau = {{\tau }_{0}} + \eta {{\dot {\gamma }}^{n}}$, Кэссона $\tau = {{(\sqrt {{{\tau }_{0}}} + \sqrt {\eta \dot {\gamma }} )}^{2}}$, Освальда (является частным случаем формулы Гершеля–Балкли при ${{\tau }_{0}} = 0$, поэтому не согласуется с наличием предела текучести и здесь не тестировалась), $\tau = {{\tau }_{0}} + {{\eta }_{1}}\gamma + {{\eta }_{2}}{{\dot {\gamma }}^{n}}$ [5, с. 37].
Это сопоставление было выполнено на примере “зеленой краски” с объемной долей пигмента 31.6%. Оно показало, что всем трем формулам соответствуют кривые, которые в масштабе рис. 2 практически сливаются с кривой для формул (8)–(11). Поэтому соответствующие три кривые не показаны на рис. 2. Тем не менее, формулы (8–11) имеют преимущества по сравнению с формулами Гершеля–Балкли, Кэссона и Сиско: 1) среднеквадратичное отклонение кривой для формул (8)–(11) от экспериментальных точек равно 0.24 Па, тогда как для формулы Гершеля–Балкли оно равно 2.3 Па, для формулы Кэссона – 3.0 Па, для формулы Сиско – 2.0 Па; 2) упомянутые уравнения описывают зависимость сдвигового напряжения лишь от скорости сдвига при заданной концентрации суспензии и не описывают зависимость от концентрации; 3) они являются эмпирическими, и для них отсутствует теоретическое обоснование [5], а входящие в них параметры лишены физического смысла, тогда как выведенные здесь уравнения теоретически обоснованы, а их параметры имеют ясный физический смысл. Также и численные значения параметров лежат в разумных пределах: предельные объемные доли не превышают единицы, характеристические вязкости больше теоретического значения, вытекающего из формулы Эйнштейна ($[\eta ] = 2.5$), но по порядку величины не сильно от него отличаются. При этом известно [2], что $[\eta ] = 2.5$ выполняется только для идеально сферических зерен, а в реальных суспензиях всегда больше.
Вычисление погрешности определения значений параметров не являлось целью работы, тем не менее оно в данном случае представляет определенный интерес. Задача решалась численно на примере “зеленой краски” с объемной долей пигмента 31.6%: численное значение каждого параметра при фиксированных значениях остальных параметров варьировалось таким образом, чтобы кривая оставалась в пределах коридора, ширина которого определялась разбросом в 5%. Результаты: ${{\kappa }_{0}} \in (0.055;$ ${{\kappa }_{0}} \in (0.055;0.080)$, ${{\kappa }_{1}} \in (0.0089;0.012)$, $[{{\eta }_{1}}] \in (5.07;$ $5.36)$, $[{{\eta }_{2}}] \in (15.6;16.6)$, ${{\varphi }_{{10}}} \in (0.9;1)$, ${{\varphi }_{{20}}}\, \in \,(0.8;1)$.
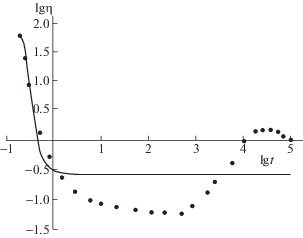
Из литературы известно, что существуют системы, для которых псевдопластичное поведение сменяется дилатантным, например, латексы сополимера стирола и этилакрилата [6]. Из рис. 4 видно, что выведенные здесь уравнения не описывают такое поведение. Вероятно, учет образования тримеров могло бы улучшить качество аппроксимации таких систем; исследование этой возможности могло бы стать темой отдельной работы.
Рис. 4.
Зависимости логарифма вязкости от логарифма напряжения сдвига для латекса сополимера стирола и этилакрилата; объемная доля сополимера 50%. Точки – эксперимент (по данным [6]), кривая – аппроксимация с помощью выведенных формул.
Выведенные здесь уравнения имеют еще один недостаток: параметры уравнения для одной и той же суспензии при разных концентрациях твердой фазы имеют различные значения (см. подписи к рис. 2 и 3). Однако уравнения (8)–(11) описывают зависимость сдвигового напряжения одновременно от двух переменных – концентрации твердой фазы и скорости сдвига: $\tau = \tau (\varphi ;\dot {\gamma })$. Это значит, что одной суспензии при любых концентрациях и скоростях сдвига должен соответствовать один-единственный набор параметров.
Результат описания зависимости $~\tau = \tau (\varphi ;\gamma )$ с помощью универсального набора параметров показан на рис. 5.
Рис. 5.
“Зеленая краска”. Среднеквадратичное отклонение точек от кривых – 0.70 Па. Значения параметров: ${{\kappa }_{0}} \approx 0.0111$, ${{\kappa }_{1}} \approx 0.000933$, $[{{\eta }_{1}}] \approx 5.50$, $[{{\eta }_{2}}] \approx 11.4$, ${{\varphi }_{{10}}} \approx 0.911$, ${{\varphi }_{{20}}} \approx 1.0$.
Теоретические кривые демонстрируют хорошее согласие с экспериментом всюду, за исключением окрестности точки $\dot {\gamma } = 0$. Причиной расхождения является, вероятно, не вполне корректное предположение, что константа скорости “обратной реакции”, т.е. диссоциации димеров, линейно зависит от скорости сдвига (предположение 2 на стр. 1). Более естественно было бы предположить, что она зависит не от скорости сдвига, а от скорости диссипации энергии, т.е. от произведения скорости сдвига и сдвигового напряжения: $k = {{k}_{2}} + {{k}_{3}}\dot {\gamma }\tau $. К сожалению, в этом случае решение получаемых уравнений сталкивается с существенными математическими трудностями: уравнения становятся трансцендентными, и их аналитическое решение невозможно. Однако их можно решать численными методами; исследованию этой возможности будет посвящена следующая работа.
Список литературы
Krieger I.M. // Surfaces and Coatings Related to Paper and Wood. A Symposium, State University College of Forestry at Syracuse University. Syracuse University Press, 1967. P. 25.
Орлов Е.В. // Физика аэродисперсных систем. 2020. № 58. С. 51.
Левинский А.И. // Изв. вузов. Химия и хим. технология. 2005. Т. 48. № 12. С. 22. Levinsky A.I. // Izv. Vyssh. Uchebn. Zaved. Khim. Khim. Tekhnol. 2005. V. 48. № 12. P. 22.
Матвеенко В.Н., Кирсанов Е.А. // Вестн. Моск. ун.-та. Сер. 2. Химия. 2011. Т. 52. № 4. С. 243.
Кирсанов Е.А., Матвеенко В.Н. // Мир химии. М.: Техносфера, 2016. С. 29.
Laun H.M. // Angew. Macromol. Chem. 1984. V. 123. P. 335.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии