Журнал физической химии, 2021, T. 95, № 8, стр. 1284-1294

ДИНАМИКА ЗАСЕЛЕННОСТИ СОСТОЯНИЙ ПОЛНОЙ СИСТЕМЫ

Гамильтониан полной системы из молекулы реагента “$A$”, молекулы продукта “$B$” и квантованного поля излучения представим в виде:

где ${}_{A}H({}_{B}H)$ – гамильтониан молекулы $A(B)$; ${}_{A}{{H}_{f}}({}_{B}{{H}_{f}})$ – гамильтониан поля спонтанной флуоресценции молекулы $A\left( B \right)$; ${}_{A}V = - ({\mathbf{e}}{{{\mathbf{d}}}_{А}})$ и, соответственно, ${}_{B}V = - ({\mathbf{e}}{{{\mathbf{d}}}_{В}})$ – операторы энергии взаимодействия молекулы $A(B)$ с полем излучения; e – напряжённость электрического поля, d_А (d_B) – оператор дипольного момента молекулы $A(B)$. Под оператором $W$ будем подразумевать оператор энергии кулоновского взаимодействия распределения зарядов молекул, приводящего к обмену энергией между молекулами, характеризуемого одной константой $w \equiv {{\hbar }^{{ - 1}}}W$ (см. ниже), аналогично тому, как это принято при моделировании когерентного (без конкретизации его вида) взаимодействия двух кубитов в работе [10]. Например, это может быть диполь-дипольное взаимодействие, учитываемое при рассмотрении динамики заселенности и степени перепутывания состояний двух кубитов во многих работах (см. [11] и приведенную там литературу), или рассматриваемое в [6] взаимодействие близко расположенных друг к другу молекул в разных изомерных формах.

Будем полагать, что молекулы излучают в общий резервуар (коллективный термостат), гамильтониан которого является суммой ${}_{A}{{H}_{f}} + {}_{B}{{H}_{f}}$, а полосы спектральных линий собственного излучения молекулы $A$ и молекулы $B$ практически не перекрываются, как это обычно бывает в случае вторичных фотореакций.

На рис. 1 приведена схема относительного положения отмеченных горизонтальными линиями уровней энергии ${{E}_{n}}{\kern 1pt} \;$ собственных состояний пары молекул $\left| n \right\rangle $ $(n = 1{\kern 1pt} - {\kern 1pt} 4)$. Состояния 1 и 4 относятся к молекуле $A$, а состояния 2 и 3 – к молекуле $B$. Для определенности будем считать, что состояния 1 и 2 – это состояния молекулы $\left| {{{S}_{0}}} \right\rangle $, а состояния 4 и 3 – это возбужденные состояния молекулы $\left| {{{S}_{1}}} \right\rangle $. Для простоты рассмотрения приведены примерно равные значения разности ${{Е}_{4}} - {{E}_{3}} > 0$ и ${{Е}_{2}} - {{E}_{1}} > 0$, но можно полагать, что ${{Е}_{2}} = {{E}_{1}}$, как во многих работах по изучению динамики перепутанности состояний пары двухуровневых наночастиц – литературу см. например, в [11]. Вертикальными линиями обозначены учитываемые радиационные переходы при излучении фотонов флуоресценции, а круговыми кривыми – нерадиационные обратимые переходы между возбужденными состояниями пары молекул, обусловленные отмеченным выше взаимодействием. Предполагается, что можно пренебрегать, как отмечено выше, перекрыванием полосы спектральных линий флуоресценции в области частот ${{\omega }_{{32}}} = {{\hbar }^{{ - 1}}}({{Е}_{3}} - {{E}_{2}})$ с полосой в области частот ${{\omega }_{{41}}} = {{\hbar }^{{ - 1}}}({{Е}_{4}} - {{E}_{1}})$, и что ${{\omega }_{{32}}} \gg {{\gamma }_{3}}$, ${{\omega }_{{41}}} \gg {{\gamma }_{4}}$, где константы ${{\gamma }_{3}}$ и ${{\gamma }_{4}}$, характеризуют радиационную и нерадиационную (см. ниже) ширину уровней ${{E}_{3}}$ и ${{E}_{4}}$. Буква $\sigma $ обозначает “сорт” фотона излучения при переходе 4 → 1 (“$\sigma $-флуоресценция”), а буква $\nu $ – фотона излучения при переходе 3 → 2 (“$\nu $-флуоресценция”).

Время отсчитывается от момента $t = 0$, когда в результате возбуждения ультракоротким импульсом света или столкновения с молекулой окружения молекула $A$ оказалась в состояние $\left| 4 \right\rangle $, так что при $t > 0$ окружающее молекулы поле не содержит фотонов. При этом для описания динамики состояний полной системы можно ограничиться использованием ортонормированного базиса из состояний $\left| {4020} \right\rangle $, $\left| {3010} \right\rangle $, $\left| {102\nu } \right\rangle $ и $\left| {1\sigma 20} \right\rangle $. Здесь к каждой из цифр $1{\kern 1pt} - {\kern 1pt} 4$, обозначающих состояния молекулы, добавлена или цифра $0$, обозначающая состояние поля без фотонов, или буква $\sigma $, или буква $\nu $, обозначающие наличие в поле соответствующего фотона.

Моделирование динамики заселенности состояний полной системы основано на использовании решений уравнения Шредингера для амплитуд ${{b}_{k}}(t)$ заселенности собственных состояний k этой системы:

где i, k, l – индексы приведенных выше базисных состояний; i – индекс начального состояния $\left| {4020} \right\rangle $; k, l–3010, 102ν, 1σ20; энергия, соответственно, E_i, E_k, E_l; δ_ki – символ Кронекера, ${{\delta }_{{ki}}} = 0$ при $k \ne i$ и ${{\delta }_{{ki}}} = 1$ при $k = i$; $\delta (t)$ – функция Дирака.

Для объёма L³ пространства, в котором находится пара молекул и поле излучения имеем, например, для матричного элемента оператора V по состояниям $\left| {1\sigma 20} \right\rangle $ и $\left| {4020} \right\rangle $ выражение ${}_{1}V_{{1\sigma }}^{{40}} = i{{L}^{{ - 3/2}}}\sqrt {2\pi \hbar {{\omega }_{\sigma }}} {{({{d}_{\sigma }})}_{{14}}}$; d₁₄ – матричный элемент оператора дипольного момента d молекулы $A$ по состояниям 1 и 4, ω_σ – частота фотона σ. Матричные элементы W по состояниям $\left| {4020} \right\rangle $ и $\left| {1030} \right\rangle $ обозначим как $\left\langle {4020\left| W \right|1030} \right\rangle $ = $\left\langle {1030\left| W \right|4020} \right\rangle $ ≡ $\hbar w$.

При использовании фурье-представления

где E – энергетическая переменная, решение уравнения Шредингера сводится к решению системы уравнений

Используем обозначения:

где $\zeta (E) = P{\text{/}}E - i\pi \delta (E)$, P/E – главное значение функции 1/E. Под выражениями ${{\gamma }_{m}}$ ($m = 4,3$) можно, как обычно (см., например, в [12]), подразумевать константы которые характеризуют скорости радиационного распада состояния 4 и состояния 3 при излучении фотона $\sigma $ и $\nu $ соответственно.

Однако динамику заселенности возбужденных состояний рассматриваемых двухуровневых молекул можно описывать подобным же образом и в том случае, когда они взаимодействуют и с полем квантованных осцилляторов теплового термостата (фононов) (см. приложение 1 А в [13] и гл. 8 в [14]). При этом можно использовать уравнения и выражения, описывающие появление фононов в тепловом термостате, аналогично приведенным выше уравнениям и выражениям, полученным при описании излучения фотона в радиационный термостат. Имея это в виду, в качестве дополнительного – к радиационным переходам – учета распадов возбужденных состояний молекул с переходом в основное состояние с рождением фононов окружения будем полагать, что константы ${{\gamma }_{3}}$ и ${{\gamma }_{4}}$ учитывают и радиационный и нерадиационный распады возбужденных состояний молекул, как это обычно принято в формализме ОУБ, в котором соответствующие константы называют константами скорости продольной релаксации (приложение 5 .Б в [13]).

Используя введенные обозначения, решаем систему уравнений для ${{G}_{n}}(E)$ и получаем следующие выражения:

С использованием обозначений ${{\gamma }_{3}} + {{\gamma }_{4}} \equiv 2\bar {\gamma }$, ${{\gamma }_{3}} - {{\gamma }_{4}}\, \equiv \,2\tilde {\gamma }$, ${{a}^{2}}\, \equiv \,{{w}^{2}} - {{\tilde {\gamma }}^{2}}$, ${{Е}_{{4020}}}\, - \,{{E}_{{1030}}}$ = $\hbar ({{\omega }_{{43}}} + {{\omega }_{{21}}})$ = = $\hbar ({{\omega }_{{41}}} - {{\omega }_{{32}}}) \equiv 2\hbar \Delta $ и $E - {{E}_{{1030}}} \equiv \hbar x$ нули знаменателей в приведенных выражениях ${{G}_{n}}(E \equiv \hbar x + {{E}_{{1030}}})$ определяются решениями уравнения корни которого имеют следующий вид: где Отметим, что принятое условие $\left| \eta \right| < \bar {\gamma }$ выполняется, например, при тех значениях параметров атомов ${{\gamma }_{3}},\;{{\gamma }_{4}},\;w,\;\Delta $, которые были выбраны в приведенных ниже иллюстрируемых рисунками примерах динамики заселенности состояний системы, образуемой рассматриваемыми атомами (подсистемы полной системы из атомов и полей их флуоресценции).

Применяя теорию вычетов функций ${{G}_{n}}(E)$, вычисляем интегралы их обратных фурье-представлений и получаем выражения для искомых амплитуд:

где ${{\bar {\omega }}_{\nu }} = {{\omega }_{\nu }} - {{\omega }_{{32}}} - \Delta $, ${{\bar {\omega }}_{\sigma }} = {{\omega }_{\sigma }} - {{\omega }_{{41}}} + \Delta $.

Полученные решения уравнения Шредингера могут быть использованы для описания какой-либо одной экспериментальной реализации состояний полной системы, которая соответствует или условной регистрации неизменившегося состояния начального поля излучения (мысленных измерений “необнаружения” фотона флуоресценции – см. в [8, 13, 15]) или регистрации поглощения определенного фотона флуоресценции, которая свидетельствует об окончании спектроскопического перехода [9] соответствующей молекулы (“квантовой траектории” состояния полной системы [8, 13]). Такая регистрация осуществляется при непрерывном поглощении фотонов естественным макроскопическим окружением молекул [8, 15] или специальным детектором счета фотонов.

Динамику заселенности состояний реагирующих молекул определим как зависимости от времени средних – по состояниям поля излучения – значений квадратов модулей полученных выражений для амплитуд заселенности соответствующих состояний полной системы.

ДИНАМИКА СЕЛЕКТИВНОЙ ЗАСЕЛЕННОСТИ СОСТОЯНИЙ МОЛЕКУЛ

При неизменившемся состоянии рассматриваемого начального поля излучения (не содержащего фотонов) имеем:

Здесь введены обозначения ${{\rho }_{{nm,kl}}}$ (n, m, k, l = 1–4).

Эти выражения можно рассматривать как элементы матрицы плотности коллективных состояний $\left| {42} \right\rangle $ и $\left| {13} \right\rangle $ составной системы из молекул (см. далее).

Если эффективность непрерывного поглощения фотонов флуоресценции любого из фотонов одинакова, то при неперекрывающихся полосах спектральных линий $\sigma $- и ν-флуоресценции, заселенности основного состояния молекулы в рассматриваемой паре определяются, соответственно, усреднением выражения ${{\left| {{{b}_{{1\sigma 20}}}(t)} \right|}^{2}}$ по состояниям фотонов $\sigma $, и выражения ${{\left| {{{b}_{{102\nu }}}(t)} \right|}^{2}}$ – по состояниям фотонов ν. Проводя такое усреднение (редуцирование выделенного типа элементов матрицы плотности полной составной системы) при замене суммирования интегрированием по частотам фотонов имеем:

Полученное выражение $\sum\nolimits_\sigma ^{} {{{{\left| {{{b}_{{1\sigma 20}}}(t)} \right|}}^{2}}} \equiv \rho _{{(12,12)}}^{{(A)}}(t)$ очень громоздко, поэтому ограничимся его записью в таком виде:

Непосредственной подстановкой полученных функций $\rho _{{(12,12)}}^{{(A)}}(t)$, $\rho _{{(12,12)}}^{{(B)}}(t)$, ${{\rho }_{{13,13}}}(t)$, ${{\rho }_{{42,42}}}(t)$ и ${{\rho }_{{42,31}}}(t)$ убеждаемся в том, что они являются строгими решениями системы уравнений:

Проверено совпадение функций времени, определенных численным решением этой системы уравнений, с приведенными выше аналитическими функциями ${{\rho }_{{nm,kl}}}$, $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$.

Уравнение для $\dot {\rho }_{{(12,12)}}^{{(A)}}(t)$ отражает изменение вероятности найти в ансамбле молекулы A, оказавшиеся в основном состоянии при поглощении какого-нибудь одного из фотонов $\sigma $, а изменение вероятности найти молекулы B в основном состоянии при поглощении какого-нибудь одного из фотонов ν определяется уравнением для $\dot {\rho }_{{(12,12)}}^{{(B)}}(t)$.

Как следует из приведенного вычисления выражений для амплитуд заселенности состояний полной системы, возможность такого описания динамики относительного числа молекул реагента и молекул продукта в их основных состояниях обусловлена представлением основного состояния рассматриваемой полной системы в виде суперпозиции состояний $\left| {102\nu } \right\rangle $ и $\left| {1\sigma 20} \right\rangle $, которая коллапсирует при проходящей реальной регистрации (поглощении) того или иного ($\nu $ или $\sigma $) фотона, “разбивая” (по [16]) при этом пространство полной системы на изучаемые отдельно подсистемы из одной молекулы и поля ее флуоресценции, отражая при этом переход от представления о динамике заселенности одного “мысленного” коллективного основного состояния пары реагирующих молекул (как суммы заселенностей основного состояния молекулы реагента и основного состояния молекулы продукта), к динамике двух реально осуществляющихся состояний: излучившая какой-то фотон ν молекула продукта в основном состоянии или излучившая какой-то фотон $\sigma $ молекула реагента, вернувшаяся в основное состояние из первоначально возбужденного состояния.

СРАВНЕНИЕ С ДИНАМИКОЙ ПО ОПТИЧЕСКИМ УРАВНЕНИЯМ БЛОХА

Сравним полученную систему уравнений с системой обычно используемых ОУБ для элементов матрицы плотности составной системы из двух двухуровневых молекул при использовании соответствующих базисных коллективных состояний $\left| {42} \right\rangle $, $\left| {13} \right\rangle $, $\left| {12} \right\rangle $.

Гамильтониан этой системы запишем (как, например, в [10]) в виде

где $S_{A}^{ + } = \left| 4 \right\rangle \left\langle 1 \right|$, $S_{A}^{ - } = \left| 1 \right\rangle \left\langle 4 \right|$, $S_{B}^{ + } = \left| 3 \right\rangle \left\langle 2 \right|$ и $S_{B}^{ - } = \left| 2 \right\rangle \left\langle 3 \right|$.

В операторной форме ОУБ для рассматриваемой системы из двух двухуровневых молекул записывают как “управляющее” марковское уравнение Лиувилля с добавлением релаксационных слагаемых по Линдбладу (см. в [1, 13]). При использовании этих слагаемых в том виде, который приведен в [10], для рассматриваемой фотореакции имеем:

где под ${{\gamma }_{A}}$ и ${{\gamma }_{B}}$ следует понимать, соответственно, ${{\gamma }_{4}}$ и ${{\gamma }_{3}}$.

Эта система ОУБ содержит уравнения для ${{\dot {\rho }}_{{13,13}}}(t)$, ${{\dot {\rho }}_{{42,42}}}(t)$ и ${{\dot {\rho }}_{{42,13}}}(t)$, которые совпадают с тремя приведенными выше полученными уравнениями для соответствующих функций, а вместо двух уравнений для $\dot {\rho }_{{(12,12)}}^{{(A)}}(t)$ и $\dot {\rho }_{{(12,12)}}^{{(B)}}(t)$, содержит уравнение

которое описывает динамику заселенности коллективного основного состояния $\left| {12} \right\rangle $, т.е. динамику неселективной заселенности основного состояния рассматриваемой пары молекул в ансамбле. Это отличие отмечено в тезисах доклада результатов этой работы [17].

Приведенное получение описания такой селективной динамики заселенности основных состояний молекул и сопоставление его с описанием неселективной динамики можно рассматривать как пример строгого “распутывания” (“unraveling”) полуклассического диссипативного управляющего уравнения Блоха для пары взаимодействующих частиц за счет учета информации о деталях “траектории” соответствующих волновых функций полной системы из частиц и квантованного поля излучения [9]. Это распутывание – замена уравнения ОУБ для динамики коллективного основного состояния двух молекул двумя уравнениями для динамики основного состояния каждой молекулы – достигнуто за счет отмеченного выше более детального редуцирования матрицы плотности полной составной системы по состояниям фотонов соответствующих неперекрывающихся полос флуоресценции при переходе к матрице плотности молекул по сравнению с обычным редуцированием (см. например, в [5]), которое не ставит задачу о селективном рассмотрении заселенности основного состояния двух молекул. Представляет интерес использовать полученные таким образом “модифицированные уравнения ОУБ” для вычисления динамики степени перепутанности двух взаимодействующих кубитов вместо обычного использования ОУБ с неселективным описанием заселенности основных состояний частиц.

Примеры сравнения полученного описания динамики селективной заселенности основного состояния молекул пары с описанием по ОУБ иллюстрирует рис. 2 для молекул с параметрами ${{\gamma }_{3}} = 3$, $\Delta = 10$, $w = 5$ в единицах ${{\gamma }_{4}}$, и рис. 3 – для молекул с более сильным динамическим взаимодействием: ${{\gamma }_{3}} = 3$, $\Delta = 10$, $w = 20$. Штриховые кривые отображают зависимости $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$, помеченные соответственно цифрами 1 и 2. Суммой цифр 1 + 2 помечена кривая $\rho _{{12,12}}^{{}}(t)$, отражающая равенство $\rho _{{(12,12)}}^{{(A)}}(t)$ + $\rho _{{(12,12)}}^{{(B)}}(t)$ = = $\rho _{{12,12}}^{{}}(t)$, цифрой 3 – кривая, отображающая зависимость $\rho _{{31,31}}^{{}}(t)$, а цифрой 4 – $\rho _{{42,42}}^{{}}(t)$. По оси абсцисс – время в единицах $\gamma _{4}^{{ - 1}}$.

Сравнение зависимостей $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$ позволяет оценить эффективность рассматриваемой реакции в зависимости от значений констант молекул реагента и молекул продукта. Так, рис. 2 иллюстрирует динамику реакции, в результате которой молекул продукта будет в 4 раза меньше молекул реагента, а рис. 3 – реакции, в результате которой молекул продукта будет в 1.7 раза больше молекул реагента.

В общем случае эффективность как “вторичный квантовый выход” рассматриваемой реакции можно характеризовать отношением

Пример зависимости $F(w,\Delta )$ для молекул с константами затухания ${{\gamma }_{3}} = 3{{\gamma }_{4}}$ иллюстрирует рис. 4. Значения $w$ и $\Delta $ отложены в единицах ${{\gamma }_{4}}$.

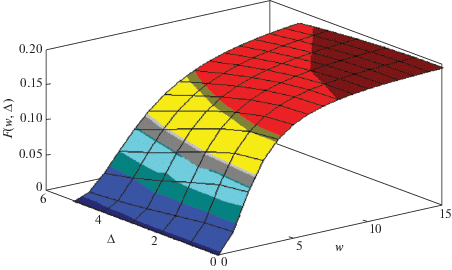
Отметим, что для рассматриваемого примера при всех значениях $w$ и $\Delta $ проверена справедливость неравенства ${{\bar {\gamma }}^{2}} > {{\eta }^{2}}$. Например, при $w = \Delta = 5{{\gamma }_{4}}$ имеем ${{\bar {\gamma }}^{2}} = 4\gamma _{4}^{2}$, а ${{\eta }^{2}} = 0.5\gamma _{4}^{2}$.

Как отмечено выше, полученная система уравнений, учитывающая селективное заселение основного состояния молекул реагента и молекул продукта, позволяет оценить зависимость эффективности рассматриваемой реакции от значений констант продольной релаксации возбужденных состояний этих молекул. Если в этой системе уравнений в дополнение к слагаемому $ - 2\bar {\gamma }{{\rho }_{{42,13}}}(t)$ в правой части ее уравнения для ${{\dot {\rho }}_{{42,13}}}(t)$ ввести слагаемое $ - {{\gamma }_{{ph}}}{\kern 1pt} {{\rho }_{{42,13}}}(t)$, то такая система уравнений – будем отмечать входящие в них матричные элементы статистического оператора как ${{\tilde {\rho }}_{{nm,kl}}}(t)$ – позволит оценивать также зависимость эффективности рассматриваемой реакции от значений констант ${{\gamma }_{{ph}}}$ поперечной (“чисто-фазовой”) релаксации когерентности возбужденных состояний молекул реакционного центра, учитывающей усредненное влияние их упругих соударений между собой и с молекулами окружения (см., например, в гл. 5 [13]). В качестве примера оценки такой зависимости рассмотрим сравнение приведенных на рис. 5 тонких кривых с соответствующими утолщенными кривыми. Тонкими кривыми на этом рисунке приведены зависимости ${{\rho }_{{nm,kl}}}(t)$, $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$ (совпадающие с соответствующими зависимостями на рис. 2) для молекул с параметрами ${{\gamma }_{3}} = 3$, $\Delta = 10$, $w = 5$ и ${{\gamma }_{{ph}}}\, = 0$ (в единицах ${{\gamma }_{4}}$), а утолщенными кривыми – зависимости ${{\tilde {\rho }}_{{nm,kl}}}(t)$, $\tilde {\rho }_{{(12,12)}}^{{(A)}}(t)$ и $\tilde {\rho }_{{(12,12)}}^{{(B)}}(t)$, определенные численными решениями системы уравнений, учитывающей селективное заселение основного состояния молекул реагента и продукта с параметрами ${{\gamma }_{3}} = 3$, $\Delta = 10$, $w = 5$ и ${{\gamma }_{{ph}}}\, = 30$. Штриховые тонкие кривые, отмеченные цифрами 1 и 2, отображают соответственно зависимости $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$, а утолщенные штриховые кривые отмеченные цифрами I и II, отображают соответственно зависимости $\tilde {\rho }_{{(12,12)}}^{{(A)}}(t)$ и $\tilde {\rho }_{{(12,12)}}^{{(B)}}(t)$. Суммой цифр 1 + 2 помечена зависимость решения $\rho _{{12,12}}^{{}}(t)$ соответствующего уравнения системы ОУБ, цифрой 3 – кривая, отображающая зависимость $\rho _{{31,31}}^{{}}(t)$ , а цифрой 4 – $\rho _{{42,42}}^{{}}(t)$. Суммой цифр I + II помечена утолщенная кривая ${{\tilde {\rho }}_{{12,12}}}(t)$, определяемая решением системы соответствующих уравнений ОУБ с ${{\gamma }_{{ph}}}\, = 30$, цифрой III – кривая, отображающая зависимость ${{\tilde {\rho }}_{{31,31}}}(t)$, а цифрой IV – зависимость ${{\tilde {\rho }}_{{42,42}}}(t)$. По оси абсцисс – время в единицах $\gamma _{4}^{{ - 1}}$.

В результате сравнения вида приведенных на рис. 5 утолщенных кривых с соответствующими тонкими кривыми, следует вывод, что в то время как система ОУБ отражает лишь сглаживание временных изменений динамики заселенности состояний молекулы реагента и молекулы продукта вследствие отмеченных их упругих соударений, система уравнений, учитывающая селективное заселение основных состояний молекул, отражает увеличение заселенности конечных основных состояний молекул продукта при соответствующем уменьшении заселенности основного состояния молекулы реагента, т.е. повышение эффективности рассматриваемой реакции при упругих соударениях молекул. Такой же вывод был сделан в результате проведения подобных вычислений для молекул с другими параметрами по сравнению с параметрами, принятыми для отмеченных выше молекул.

Систему уравнений для описания селективной динамики основных состояний многоуровневых моделей молекул реагента и продукта вторичной фотореакции можно получить аналогичным разделением уравнения для динамики коллективного основного состояния этих молекул в системе соответствующих ОУБ на два уравнения для динамики заселенности основного состояния каждой из молекул.

Заметим, что полученные функции ${{\rho }_{{nm,kl}}}(t)$, $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$ не меяют вид, когда под состояниями молекул $\left| n \right\rangle $ $(n = 1{\kern 1pt} - {\kern 1pt} 4)$ подразумеваются соответствующие вибронные состояния при переобозначении, соответственно, матричных элементов операторов $V$ и $W$ с учетом зависимости их от координат ядер молекул, а также зависимости $W$ от расстояния между молекулами. При выборе конкретных молекул, значения параметров ${{\gamma }_{4}},\;{{\gamma }_{3}},\;\Delta $ определяются по результатам регистрации интенсивности полос их флуоресценции, и зная взятые их значения, можно найти параметр $w$ по результату измерения вторичного квантового выхода, используя его определение $F({{\gamma }_{4}},{{\gamma }_{3}},\Delta ,w)$. Для близко расположенных друг к другу молекул, величину w можно определять степенью перекрывания соответствующих вибронных волновых функций молекулы реагента и молекулы продукта по [6].

Отметим, что для описания динамики заселенности состояний молекул при структурной изомеризации авторами монографии [6] предложена система кинетических уравнений, которые отражают замену пары возбужденных состояний молекул c одинаковыми значениями энергии единым “смешанным изомер-изомерным состоянием” (стр. 295 в [6]) с волновой функцией в виде суперпозиции волновых функций этих “резонансных” состояний с дополнительными, так подобранными множителями (зависящими от времени), что квадрат модуля этой суперпозиционной функции отражает квантовые биения “переходных изомер-изомерных состояний” (стр. 296 в [6]). В этих кинетических уравнениях учитывались распады возбужденных состояний молекул путем введения феноменологических констант их спонтанного экспоненциального затухания. Авторы работы [18] отмечают, что использование этих уравнений позволяет перейти к количественному описанию кинетики рассматриваемой реакции, которое невозможно было получить при применении общей теории фотохимических реакций, состояние которой отражено в монографиях и обзорах от 1987 г. до 2011 г. (приведен список из 17-ти наименований этих работ).

В многочисленных работах авторов [6] с соавторами, выполненных в 2004–2017 годы, при рассмотрении динамики распада отмеченного суперпозиционного состояния модельных – в том числе двухуровневых – молекул диенового ряда при превращении их в циклические изомеры, сделаны выводы, что результаты расчетов при использовании отмеченных выше кинетических уравнений качественно и количественно хорошо согласуются с соответствующими экспериментальными данными. Например, в [19] приведены зависимости от времени заселенности резонансного состояния и основных состояний двухуровневых моделей взаимодействующих молекул: 2,3-диметил-бутадиен-1,3 и диметилциклобутен (рис. 3 в [19]). Вид этих зависимостей подобен виду функций ${{\rho }_{{nm,kl}}}(t)$, $\rho _{{(12,12)}}^{{(A)}}(t)$ и $\rho _{{(12,12)}}^{{(B)}}(t)$, приведенных на рис. 2 настоящей работы. Отметим также, что в [20] при использовании отмеченных кинетических уравнений с применением двухуровневых моделей (см. рис. 3 в [20] или рис. 8.13 на стр. 302 в [6]), приведен расчет зависимости квантового выхода фотопревращения молекулы цис-бутадиен в 1,3-циклобутен от величины константы их взаимодействия. Для параметров молекул – в принятых выше обозначениях – использовались следующие значения: ${{\gamma }_{4}} \cong 2 \times {{10}^{{10}}}$ c^–1, ${{\gamma }_{3}} \cong 3 \times {{10}^{{10}}}$ c^–1, $\Delta = 0$, $w \approx {{10}^{{11}}}$ c^–1.

Как уже отмечено, в основу вывода системы кинетических уравнений в [6] положено представление об излучении парой молекул из “смешанного изомер-изомерного состояния” молекул c одинаковыми значениями энергии при феноменологическом отражении квантовых биений “переходных изомер-изомерных состояний”, в то время как модифицированная система ОУБ в настоящей работе получена на основе последовательного использования строгого решения уравнения Шредингера при описании динамики заселенности состояний системы из квантованного поля спонтанного излучения двух взаимодействующих между собой двухуровневых молекул. Таким образом, использованный при выводе этих сисем уравнений формализм различается как в отношении принятия некоторых существенных аспектов физического смысла механизма рассматриваемой реакции, так и техники учета его особенностей. Поэтому представляет интерес провести сравнение результатов интерпретации экспериментальных данных относительно динамики какой-нибудь конкретной вторичной фотохимической реакции, которые получены при использовании каждой из этих систем уравнений. Как показал результат предварительного такого сравнения, оно требует специального отдельного рассмотрения, которое выходит за рамки постановки задачи, поставленной в настоящей работе.

ЗАКЛЮЧЕНИЕ

Приведен строгий вывод уравнений динамики заселенности состояний молекул реакционного комплекса бимолекулярной вторичной фотохимической реакции, которые в отличие от оптических уравнений Блоха, описывающих динамику заселенности коллективного основного состояния молекул комплекса, селективно описывают динамику заселенности молекулы реагента и молекулы продукта реакции. Приведенные примеры использования решений полученной системы уравнений и ее обобщения на случай учета, наряду с продольной, также и поперечной релаксации возбужденных состояний молекул, иллюстрируют преимущества применения полученных уравнений по сравнению с применением соответствующих оптических уравнений Блоха в отношении описания эффективности изучаемой вторичной фотореакции.