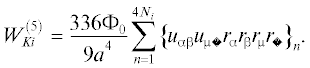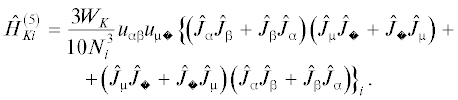Физика металлов и металловедение, 2019, T. 120, № 3, стр. 227-238

Макромагнитный расчет намагниченности деформированного ферромагнетика

В. К. Игнатьев^a, Н. Г. Лебедев^a, *, А. В. Никитин^a, А. А. Орлов^a

^a Волгоградский государственный университет
400062 Волгоград, пр. Университетский, 100, Россия

Поступила в редакцию 05.02.2018
После доработки 21.08.2018
Принята к публикации 09.10.2018

DOI: 10.1134/S0015323019030069

Аннотация

Проведено исследование динамики намагниченности деформированного ферромагнетика во внешнем переменном магнитном поле. Предложена микроскопическая модель деформированного магнитомягкого ферромагнетика на примере кристалла α-железа, учитывающая зеемановскую энергию, энергию взаимодействия с кристаллическим полем и магнито-дипольного взаимодействия доменов. Параметры модельных гамильтонианов согласованы с экспериментальными данными по магнитострикции железа. Минимизация функционала плотности энергии кристалла варьированием намагниченности образца позволила получить выражение для равновесной намагниченности ферромагнетика в квадратичном по деформации приближении. На основе численного решения динамического уравнения Блоха получено решение, имеющее характерный вид петли гистерезиса, основные параметры которой зависят от величины относительной деформации образца. Проведено сравнение полученных численных результатов с экспериментальными данными.

Ключевые слова: модельный гамильтониан, зеемановская энергия, кристаллическое поле, магнитная анизотропия, эквивалентные операторы, гистерезис, коэрцитивная сила

ВВЕДЕНИЕ

Микромагнитный теоретический расчет намагниченности ферромагнетиков различной структуры является одним из основных направлений мировых исследований свойств магнитных материалов, особенно когда нельзя получить аналитическое решение уравнений движения, описывающих процессы намагничивания или перемагничивания изучаемого образца. В рамках такого подхода, как правило, решаются задачи исследования статических магнитных характеристик различных сред, изучение доменной структуры, расчет параметров петель гистерезиса и др. [1].

Физика магнитного гистерезиса является одной из хорошо изученных областей физики магнитоупорядоченных материалов [2, 3], но несмотря на свою вековую историю и многочисленные экспериментальные и теоретические достижения в этой области, до сих пор остается актуальным направлением исследования. Основными причинами магнитного гистерезиса считаются необратимые процессы вращения, задержка роста зародышей перемагничивания (инверсия) и особенности динамики доменных границ [2]. Строгое аналитическое описание данных процессов наталкивается на существенные трудности, которые преодолеваются с помощью построения математических моделей, например, модели Стонера–Вольфарта, Джилеса–Атертона, Хаузера и др., основанных на решении нелинейных дифференциальных уравнений [4]. Нелинейные слагаемые вводятся в уравнения моделей, как правило, феноменологически, основным критерием достоверности такой процедуры является воспроизведение петли гистерезиса. Широкое распространение при численном моделировании магнитных сред получила модель на основе дискретно-дипольной аппроксимации [1]. В соответствии с этой моделью, дискретная среда рассматривается как совокупность магнитных диполей (моментов), под которыми в зависимости от уровня детализации и решаемой задачи могут пониматься как отдельные спины, так и магнитные моменты ячеек, на которые разбивается среда. На основе численного моделирования распределения магнитных моментов в тонких пленках наноструктурированных кристаллов показано, что гистерезис может быть вызван одноосной анизотропией, введенной в модель феноменологически.

Помимо фундаментального значения построение феноменологических моделей магнитного гистерезиса имеет и практическое значение, например, для расчета магнитных полей в элементах магнитных систем ускорителей заряженных частиц [5]. Параметры предложенной авторами модели выбирали в соответствии с экспериментальной кривой гистерезиса конструкционной стали. Численные решения модельных уравнений удовлетворительно аппроксимируют также и несимметричные петли гистерезиса.

Экспериментальное и теоретическое изучение магнитного отклика образца на его деформацию (эффект Виллари) является объектом активного научного исследования уже более века. В работе [6] автор экспериментально изучил зависимость параметров петли магнитного гистерезиса стали от величины относительной деформации. В частности, показана нелинейная зависимость коэрцитивной силы исследуемых образцов от величины одноосной деформации. В современной работе [7] методом локальных измерений на сканирующем спектрометре ферромагнитного резонанса обнаружены и исследованы сложные распределения величины и угла направления поля одноосной магнитной анизотропии по площади неоднородно напряженных пермаллоевых пленок. Феноменологический расчет распределения величины и направления эффективной одноосной магнитной анизотропии по площади пленок показал хорошее согласие с экспериментом.

Одним из подходов в теоретических исследованиях магнитных свойств ферромагнетиков, в том числе гистерезиса, является минимизация функционала магнитостатической энергии [8, 9] методом релаксации или градиентного спуска. Однако даже при рассмотрении моделей с относительно небольшим количеством элементов наличие большого числа метастабильных состояний и нелинейности системы приводит к тому, что вычислительные процедуры крайне неустойчивы, могут иметь плохую сходимость или даже расходиться. Более перспективный подход, успешно использованный в работе [1] для расчета двумерного равновесного распределения магнитных моментов тонких пленок со случайным распределением по площади одноосной магнитной анизотропии, заключается в построении уравнений Лагранжа.

Интересным подходом в построении модели магнитомеханических взаимодействий в ферромагнитных диэлектриках явилась ранняя работа [10]. В рамках приближения сплошной среды и спинового континуума автор получил систему связанных дифференциальных уравнений и граничные условия для описания макроскопического поведения непроводящих насыщенных ферромагнетиков, подверженных сильным деформациям.

В данной работе развита методика анализа распределения макроскопической намагниченности в деформированном магнитно-мягком ферромагнетике на примере α-железа с тремя случайно ориентированными осями легкого намагничивания. Усреднение вектора микроскопической намагниченности с постоянным модулем по кристаллиту выполняется аналитически. В результате для вектора макроскопической намагниченности нет условия постоянства модуля, что существенно облегчает численное моделирование.

МОДЕЛЬНЫЙ ГАМИЛЬТОНИАН

В магнитно-мягких материалах толщина блоховских стенок между доменами составляет несколько тысяч постоянных решетки, а их энергия очень мала (менее 10^–3 Дж/м²) [2, 3]. При движении эти стенки почти не тормозятся на дефектах решетки атомных размеров и на примесях. Энергия образования зародыша нового домена также очень мала. Поэтому в первом приближении можно пренебречь вкладом доменных стенок в магнитные свойства мягкого ферромагнетика по сравнению с естественной и наведенной анизотропией. Намагниченность кристаллита в зарелеевской области меняется из-за изменения ориентации доменов. Энергия обменного взаимодействия в кристаллите при этом не меняется. Поэтому эффективный гамильтониан ${{\hat {H}}_{i}}$ i-го домена объемом v_i можно построить как сумму гамильтонианов кристаллического поля ${{\hat {H}}_{K}},$ магнитно-дипольного ${{\hat {H}}_{{\text{m}}}}$ и зеемановского ${{\hat {H}}_{{\text{Z}}}}$ взаимодействия:

(1)

${{\hat {H}}_{i}} = {{\hat {H}}_{{{\text{Z}}i}}} + {{\hat {H}}_{{Ki}}} + {{\hat {H}}_{{{\text{m}}i}}}.$

Здесь ${{\hat {H}}_{{{\text{Z}}i}}}$ – оператор энергии зеемановского взаимодействия i-го домена с внешним магнитным полем, который имеет стандартный вид [2]

(2)

${{\hat {H}}_{{{\text{Z}}i}}} = - g{{\mu }_{{\text{B}}}}{{\mu }_{0}}{{{\mathbf{\hat {J}}}}_{i}}{{{\mathbf{{\rm H}}}}_{e}},$

где ${{\mu }_{{\text{B}}}} = {{e\hbar } \mathord{\left/ {\vphantom {{e\hbar } {2m}}} \right. \kern-0em} {2m}}$ – магнетон Бора, μ₀ – магнитная постоянная, g – фактор Ланде, H_e – напряженность внешнего магнитного поля, ${{{\mathbf{\hat {J}}}}_{i}}$ – оператор полного механического момента i-го домена.

Соответственно, ${{\hat {H}}_{{Ki}}}$ – оператор энергии кристаллического поля кристалла кубической сингонии [11, 12] с учетом с тетрагонального возмущения, обусловленного явлением магнитострикции:

(3)

$\begin{gathered} {{{\hat {H}}}_{{Ki}}} = - e\sum\limits_{n = 1}^{4{{N}_{i}}} {{{\Phi }_{n}}} \approx - \frac{{8\sqrt 2 {{\Phi }_{0}}}}{{{{a}^{2}}}}f(a,c)\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {3{{z}^{2}} - {{r}^{2}}} \right)}}_{n}}} - \\ - \,\,\frac{{140{{\Phi }_{0}}}}{{9{{a}^{4}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {{{x}^{4}} + {{y}^{4}} + {{z}^{4}} - \frac{3}{5}{{r}^{4}}} \right)}}_{n}}} , \\ \end{gathered} $

где a = 2.86 Å – параметр ОЦК-решетки кристалла α-Fe [13], ε₀ – электрическая постоянная, e – элементарный заряд, N_i = v_i/a³ – число элементарных ячеек в домене, и введены следующие обозначения:

${{\Phi }_{0}} = \frac{{{{e}^{2}}}}{{4\pi {{\varepsilon }_{0}}a}} \approx 5.04\,{\text{eV,}}$

$f(a,c) = {{\left[ {5 - {{{\left( {{{2a} \mathord{\left/ {\vphantom {{2a} c}} \right. \kern-0em} c}} \right)}}^{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {5 - {{{\left( {{{2a} \mathord{\left/ {\vphantom {{2a} c}} \right. \kern-0em} c}} \right)}}^{2}}} \right]} {{{{\left[ {1 + {{{\left( {{{2a} \mathord{\left/ {\vphantom {{2a} c}} \right. \kern-0em} c}} \right)}}^{2}}} \right]}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}.}}} \right. \kern-0em} {{{{\left[ {1 + {{{\left( {{{2a} \mathord{\left/ {\vphantom {{2a} c}} \right. \kern-0em} c}} \right)}}^{2}}} \right]}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}.}}$

Отношение c/a называется тетрагональностью и характеризует величину относительной деформации кубической решетки, обусловленной действием тетрагонального возмущения кристаллического поля [14].

Последнее слагаемое в (1) ${{\hat {H}}_{{{\text{m}}i}}}$ – гамильтониан магнитно-дипольного взаимодействия i-го домена в кристалле [2]:

(4)

$\begin{gathered} {{{\hat {H}}}_{{{\text{m}}i}}} = \frac{{{{g}^{2}}\mu _{{\text{B}}}^{2}{{\mu }_{0}}}}{{8\pi }} \times \\ \times \,\,\sum\limits_{j \ne l} {\frac{{{{{{\mathbf{\hat {J}}}}}_{i}}{{{{\mathbf{\hat {J}}}}}_{j}}{{{\left| {{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}} \right|}}^{2}} - 3\left( {{{{{\mathbf{\hat {J}}}}}_{i}}\left( {{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}} \right)} \right)\left( {{{{{\mathbf{\hat {J}}}}}_{j}}\left( {{{{\mathbf{r}}}_{l}} - {{{\mathbf{r}}}_{j}}} \right)} \right)}}{{{{{\left| {{{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}} \right|}}^{5}}}}} . \\ \end{gathered} $

Согласно методу эквивалентных операторов, координаты электрона x, y, z в выражении (3) заменяются компонентами оператора полного механического момента j_x, j_y, j_z соответственно следующим образом [11, 12]:

(5)

$\begin{gathered} \left( {3{{z}^{2}} - {{r}^{2}}} \right) = \left( {2{{z}^{2}} - {{x}^{2}} - {{y}^{2}}} \right) \to \\ \to \alpha \left\langle {{{r}^{2}}} \right\rangle \left( {3\hat {j}_{z}^{2} - j(j + 1)} \right) = \\ = \alpha \left\langle {{{r}^{2}}} \right\rangle \left( {2\hat {j}_{z}^{2} - \hat {j}_{x}^{2} - \hat {j}_{y}^{2}} \right), \\ \left( {{{x}^{4}} + {{y}^{4}} + {{z}^{4}} - {{3{{r}^{4}}} \mathord{\left/ {\vphantom {{3{{r}^{4}}} 5}} \right. \kern-0em} 5}} \right) \to \\ \to \beta \left\langle {{{r}^{4}}} \right\rangle \left( {\hat {j}_{x}^{4} + \hat {j}_{y}^{4} + \hat {j}_{z}^{4} - j\left( {j + 1} \right)} \right. \times \\ \times \,\,\left. {{{\left( {3{{j}^{2}} + 3j - 1} \right)} \mathord{\left/ {\vphantom {{\left( {3{{j}^{2}} + 3j - 1} \right)} 5}} \right. \kern-0em} 5}} \right), \\ \end{gathered} $

где α = –2/21 и β = 2/63 – коэффициенты пропорциональности, которые находят прямым вычислением диагонального матричного элемента оператора кристаллического поля в состоянии $\left| {j,j} \right\rangle ,$ $\left\langle {{{r}^{2}}} \right\rangle $ и $\left\langle {{{r}^{4}}} \right\rangle $ – средние значения r² и r⁴ в 3d-состоянии, которые можно оценить, например, с помощью водородоподобной атомной орбитали [15]:

(6)

$\begin{gathered} \left\langle {{{r}^{2}}} \right\rangle = \int\limits_0^\infty {{{r}^{2}}R_{{3d}}^{2}{{r}^{2}}dr} = 126{{\left( {\frac{{{{a}_{{\text{B}}}}}}{Z}} \right)}^{2}}, \\ \left\langle {{{r}^{4}}} \right\rangle = \int\limits_0^\infty {{{r}^{4}}R_{{3d}}^{2}{{r}^{2}}dr} = 7!{{\left( {\frac{{3{{a}_{{\text{B}}}}}}{{2Z}}} \right)}^{4}}, \\ {{R}_{{3d}}} = \frac{4}{{81\sqrt {30} }}{{\left( {\frac{Z}{{{{a}_{{\text{B}}}}}}} \right)}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}{{r}^{2}}\exp \left( { - \frac{{Zr}}{{3{{a}_{{\text{B}}}}}}} \right), \\ \end{gathered} $

где R_3d – радиальная волновая функция 3d-состояния, a_B = 0.53 Å – боровский радиус, Z – порядковый номер атома.

Производя замену j_n = J/(4N), где J – полный механический момент домена, оставляя наиболее значащие слагаемые, пренебрегая слагаемыми, дающими постоянный вклад, и переходя к операторам домена в приближении LS-связи [16], эффективный гамильтониан кристаллического поля для 3d-электронов в недеформированном кристаллите можно представить в виде

(7)

$\begin{gathered} \hat {H}_{{Ki}}^{{\left( 0 \right)}} \approx \frac{{8\sqrt 2 {{\Phi }_{0}}}}{{{{a}^{2}}}}f(a,c)\frac{2}{{21}}\left\langle {{{r}^{2}}} \right\rangle \times \\ \times \,\,\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {3\hat {j}_{z}^{2} - j\left( {j + 1} \right)} \right)}}_{n}}} - \frac{{140{{\Phi }_{0}}}}{{9{{a}^{4}}}}\frac{2}{{63}}\left\langle {{{r}^{4}}} \right\rangle \times \\ \times \,\,\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {\hat {j}_{x}^{4} + \hat {j}_{y}^{4} + \hat {j}_{z}^{4} - {{j\left( {j + 1} \right)\left( {3{{j}^{2}} + 3j - 1} \right)} \mathord{\left/ {\vphantom {{j\left( {j + 1} \right)\left( {3{{j}^{2}} + 3j - 1} \right)} 5}} \right. \kern-0em} 5}} \right)}}_{n}}} \approx \\ \approx 72\sqrt 2 {{\Phi }_{0}}f(a,c){{\left( {\frac{{{{a}_{{\text{B}}}}}}{{Za}}} \right)}^{2}}\frac{{\hat {J}_{z}^{2}}}{{{{N}_{i}}}} - \frac{{1575{{\Phi }_{0}}}}{8}{{\left( {\frac{{{{a}_{{\text{B}}}}}}{{Za}}} \right)}^{4}} \times \\ \times \,\,\frac{{\left( {\hat {J}_{x}^{4} + \hat {J}_{y}^{4} + \hat {J}_{z}^{4}} \right)}}{{{{N}_{i}}^{3}}} \approx {{W}_{T}}(a,c)\frac{{\hat {J}_{z}^{2}}}{{{{N}_{i}}}} - \\ - \,\,{{W}_{K}}\frac{{\left( {\hat {J}_{x}^{4} + \hat {J}_{y}^{4} + \hat {J}_{z}^{4}} \right)}}{{{{N}_{i}}^{3}}}, \\ \end{gathered} $

где введены обозначения:

(8)

$\begin{gathered} {{W}_{T}}(a,c) = 102{{\Phi }_{0}}f(a,c){{\left( {\frac{{{{a}_{{\text{B}}}}}}{{Za}}} \right)}^{2}} = f(a,c) \times 26\,\,{\text{meV}}, \\ {{W}_{K}} = 197{{\Phi }_{0}}{{\left( {\frac{{{{a}_{{\text{B}}}}}}{{Za}}} \right)}^{4}} = 2.5\;\mu {\text{eV}} \\ \end{gathered} $

– тетрагональная и кубическая константы кристаллического поля в приближении ближайших соседей.

Для большинства мартенситных сталей максимальная тетрагональность решетки, обусловленная растворением атомов углерода, составляет величину c/a = 1.08 [14]. В этом случае функция f(a, c) = 0.038 и тетрагональная константа кристаллического поля принимает значение W_T ≈ ≈ 972 мкэВ.

МОДЕЛЬ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ФЕРРОМАГНЕТИКА

Деформированное состояние образца в общем случае характеризуется тензором дисторсии, симметричная часть которого называется тензором деформаций u_αβ (α, β = x, y, z) [3, 17]. Произвольная точка кристалла с координатами (x, y, z) смещается новое положение с координатами (x', y', z'), связанными с исходными известным соотношением [3]:в

(9)

$\begin{gathered} {\mathbf{r}}{\text{'}} = {\mathbf{r}} + {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}},\,\,r_{{\alpha }}^{'} = {{r}_{{\alpha }}} + {{u}_{{{\alpha \beta }}}}{{r}_{{\beta }}} = {{r}_{{\alpha }}} + {{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}}} \right)}_{{\alpha }}}; \\ r_{{\alpha }}^{{'2}} = r_{{\alpha }}^{2} + 2{{u}_{{{\alpha \beta }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}} + {{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}{{r}_{{\beta }}}{{r}_{{\gamma }}}, \\ r{\text{'}} = {{\left( {{{r}^{2}} + 2{{u}_{{{\alpha \beta }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}} + {{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}{{r}_{{\beta }}}{{r}_{{\gamma }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

где α, β, γ = x, y, z. В результате деформации образца ферромагнетика изменяется кристаллическое поле, потенциал которого содержит степенные функции координат электронов. Учет нелинейных слагаемых по деформации второго порядка приведет к следующим преобразованиям:

(10)

$\begin{gathered} {{\left( {r_{{\alpha }}^{'}} \right)}^{4}} \approx r_{{\alpha }}^{4} + 4r_{{\alpha }}^{3}{{u}_{{{\alpha \beta }}}}{{r}_{{\beta }}} + 6r_{{\alpha }}^{2}{{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}{{r}_{{\beta }}}{{r}_{{\gamma }}} = \\ = r_{{\alpha }}^{4} + 4r_{{\alpha }}^{3}{{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}}} \right)}_{{\alpha }}} + 6r_{{\alpha }}^{2}\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}}} \right)_{{\alpha }}^{2}, \\ {{\left( {r{\text{'}}} \right)}^{4}} \approx {{r}^{4}} + 4{{r}^{2}}{{u}_{{{\alpha \beta }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}} + 2{{r}^{2}}{{u}_{{{\alpha \beta }}}}{{u}_{{{\beta \gamma }}}}{{r}_{{\alpha }}}{{r}_{{\gamma }}} + \\ + \,\,4{{u}_{{{\alpha \beta }}}}{{u}_{{{\mu \nu }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}}{{r}_{{\mu }}}{{r}_{{\nu }}} = {{r}^{4}} + 4{{r}^{2}}{\mathbf{r\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}} + \\ + \,\,2{{r}^{2}}{{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}}} \right)}^{2}} + 4{{\left( {{\mathbf{r\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} r}}} \right)}^{2}}. \\ \end{gathered} $

Оставляя квадратичные по деформации слагаемые, энергия домена в кристаллическом поле (8) деформированного кристаллита с учетом преобразования (10) принимает вид

$\begin{gathered} {{W}_{{Ki}}} = - \frac{{0.304\sqrt 2 {{\Phi }_{0}}}}{{{{a}^{2}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {3{{z}^{{'2}}} - {{r}^{{'2}}}} \right)}}_{n}}} - \\ - \,\,\frac{{140{{\Phi }_{0}}}}{{9{{a}^{4}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left( {{{x}^{{'4}}} + {{y}^{{'4}}} + {{z}^{{'4}}} - \frac{3}{5}{{r}^{{'4}}}} \right)}}_{n}}} = \\ = W_{{Ki}}^{{(0)}} + W_{{Ki}}^{{\left( 1 \right)}} + W_{{Ki}}^{{\left( 2 \right)}} + W_{{Ki}}^{{\left( 3 \right)}} + W_{{Ki}}^{{\left( 4 \right)}} + W_{{Ki}}^{{\left( 5 \right)}}, \\ \end{gathered} $

где $W_{{Ki}}^{{\left( 0 \right)}}$ – энергия домена в недеформированном кристаллите вида (8), $W_{{Ki}}^{{\left( 1 \right)}},$ $W_{{Ki}}^{{\left( 2 \right)}},$ $W_{{Ki}}^{{\left( 3 \right)}},$ $W_{{Ki}}^{{\left( 4 \right)}}$ и $W_{{Ki}}^{{\left( 5 \right)}}$ – составляющие магнитоупругой энергии домена:

(11)

$W_{{Ki}}^{{(1)}} = - \frac{{0.608\sqrt 2 {{\Phi }_{0}}}}{{{{a}^{2}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left\{ {3{{u}_{{z{\beta }}}}z{{r}_{{\beta }}} - {{u}_{{{\alpha \beta }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}}} \right\}}}_{n}}} ;$

(12)

$W_{{Ki}}^{{(2)}} = - \frac{{0.304\sqrt 2 {{\Phi }_{0}}}}{{{{a}^{2}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {\left( {3{{u}_{{z{\beta }}}}{{u}_{{z{\gamma }}}} - {{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}} \right){{{\left\{ {{{r}_{{\beta }}}{{r}_{{\gamma }}}} \right\}}}_{n}}} ;$

(13)

$W_{{Ki}}^{{\left( 3 \right)}} = - \frac{{560{{\Phi }_{0}}}}{{9{{a}^{4}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {{{{\left\{ {{{r}_{{\alpha }}}^{3}{{u}_{{{\alpha \beta }}}}{{r}_{{\beta }}} + \frac{3}{2}r_{{\alpha }}^{2}{{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}{{r}_{{\beta }}}{{r}_{{\gamma }}}} \right\}}}_{n}}} ;$

(14)

$W_{{Ki}}^{{\left( 4 \right)}} = \frac{{336{{\Phi }_{0}}}}{{9{{a}^{4}}}}\sum\limits_{n = 1}^{4{{N}_{i}}} {r_{n}^{2}{{{\left\{ {{{u}_{{{\alpha \beta }}}}{{r}_{{\alpha }}}{{r}_{{\beta }}} + \frac{1}{2}{{u}_{{{\alpha \beta }}}}{{u}_{{{\beta \gamma }}}}{{r}_{{\alpha }}}{{r}_{{\gamma }}}} \right\}}}_{n}}} ;$

(15)

После применения метода эквивалентных операторов [11, 12] и перехода к операторам домена в приближении LS-связи формулы (11)–(15) можно представить в виде соответствующих операторов:

(16)

$\begin{gathered} \hat {H}_{{Ki}}^{{\left( 1 \right)}} = \\ = \frac{{{{W}_{T}}}}{{6{{N}_{i}}}}{{\left\{ {3{{u}_{{z{\beta }}}}\left( {{{{\hat {J}}}_{z}}{{{\hat {J}}}_{{\beta }}} + {{{\hat {J}}}_{{\beta }}}{{{\hat {J}}}_{z}}} \right) - {{u}_{{{\alpha \beta }}}}\left( {{{{\hat {J}}}_{{\alpha }}}{{{\hat {J}}}_{{\beta }}} + {{{\hat {J}}}_{{\beta }}}{{{\hat {J}}}_{{\alpha }}}} \right)} \right\}}_{i}}; \\ \end{gathered} $

(17)

$\hat {H}_{{Ki}}^{{\left( 2 \right)}} = \frac{{{{W}_{T}}}}{{6{{N}_{i}}}}\left( {3{{u}_{{z{\beta }}}}{{u}_{{z{\gamma }}}} - {{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}} \right){{\left( {{{{\hat {J}}}_{{\gamma }}}{{{\hat {J}}}_{{\beta }}} + {{{\hat {J}}}_{{\beta }}}{{{\hat {J}}}_{{\gamma }}}} \right)}_{i}};$

(18)

$\begin{gathered} \hat {H}_{{Ki}}^{{\left( 3 \right)}} = \\ = - \frac{{2{{W}_{K}}}}{{N_{i}^{3}}}{{\left\{ {{{u}_{{{\alpha \beta }}}}\left( {\hat {J}_{{\alpha }}^{3}{{{\hat {J}}}_{{\beta }}} + {{{\hat {J}}}_{{\beta }}}\hat {J}_{{\alpha }}^{3}} \right) + 3{{u}_{{{\alpha \beta }}}}{{u}_{{{\alpha \gamma }}}}\left( {\hat {J}_{{\alpha }}^{2}{{{\hat {J}}}_{{\beta }}}{{{\hat {J}}}_{{\gamma }}}} \right)} \right\}}_{i}}; \\ \end{gathered} $

(19)

$\begin{gathered} \hat {H}_{{Ki}}^{{\left( 4 \right)}} = \frac{{1152{{W}_{K}}}}{{20{{N}_{i}}}}\left\{ {2{{u}_{{{\alpha \beta }}}}\left( {{{{\hat {J}}}_{{\alpha }}}{{{\hat {J}}}_{{\beta }}} + {{{\hat {J}}}_{{\beta }}}{{{\hat {J}}}_{{\alpha }}}} \right) + } \right. \\ {{\left. { + \,\,{{u}_{{{\alpha \beta }}}}{{u}_{{{\beta \gamma }}}}\left( {{{{\hat {J}}}_{{\alpha }}}{{{\hat {J}}}_{{\gamma }}} + {{{\hat {J}}}_{{\gamma }}}{{{\hat {J}}}_{{\alpha }}}} \right)} \right\}}_{i}}; \\ \end{gathered} $

(20)

Выражения (16)–(20) представляют собой операторы магнитоупругой энергии i-го домена ферромагнетика в рамках описанных выше приближений.

ПЕРЕХОД К МАКРОСКОПИЧЕСКОЙ МОДЕЛИ

Определим равновесную намагниченность m(r) магнитомягкого ферромагнетика D из условия минимума его энергии во внешнем магнитном поле, которое вблизи тела D вне источников поля является потенциальным H_e(r) = gradφ_e(r). Намагничивающееся тело D создает магнитное поле [18]

${{{\mathbf{h}}}_{m}}\left( {\mathbf{r}} \right) = \frac{1}{{4\pi }}\iiint\limits_{{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d}} {\left\{ {\frac{{3\left( {\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right){\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{5}}}} - \frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}} \right\}{{d}^{3}}r{\text{'}}}$

с магнитным потенциалом

${{\phi }_{m}}\left( {\mathbf{r}} \right) = - \frac{1}{{4\pi }}\iiint\limits_{{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d}} {\frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}{{d}^{3}}r{\text{'}}}.$

Здесь d – шаровой вырез диаметром порядка размера домена с центром в точке r ∈ D, введенный для исключения самовоздействия.

При d → 0 существует предел этих интегралов в смысле главного значения несобственных интегралов [19]:

(21)

$\begin{gathered} {{{\mathbf{h}}}_{m}}\left( {\mathbf{r}} \right) = \\ = \,\,\frac{1}{{4\pi }}\iiint\limits_D {\left\{ {\frac{{3\left( {\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right){\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{5}}}} - \frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}} \right\}{{d}^{3}}r{\text{'}}}, \\ \end{gathered} $

(22)

${{\phi }_{m}}\left( {\mathbf{r}} \right) = - \frac{1}{{4\pi }}\iiint\limits_D {\frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}{{d}^{3}}r{\text{'}}},$

(23)

$\begin{gathered} {{{\mathbf{h}}}_{m}}\left( {{\mathbf{r}} \in D} \right) = \frac{{\partial {{\phi }_{m}}\left( {\mathbf{r}} \right)}}{{\partial {\mathbf{r}}}} + \frac{1}{3}{\mathbf{m}}\left( {\mathbf{r}} \right), \hfill \\ {{{\mathbf{h}}}_{m}}\left( {{\mathbf{r}} \in \bar {D}} \right) = \frac{{\partial {{\phi }_{m}}\left( {\mathbf{r}} \right)}}{{\partial {\mathbf{r}}}}. \hfill \\ \end{gathered} $

Здесь h_m(r) и m(r) – микроскопические магнитное поле и намагниченность, соответственно, существенно меняющиеся внутри тела D на расстоянии порядка размера домена.

Как отмечалось выше, можно пренебречь вкладом доменных стенок в магнитные свойства магнитомягкого ферромагнетика по сравнению с естественной и наведенной анизотропией. Поэтому полную энергию образца можно рассматривать как сумму зеемановской энергии доменов во внешнем магнитном поле, магнитостатической энергии диполь-дипольного взаимодействия и энергии взаимодействия домена с кристаллическим полем:

(24)

$W = \iiint\limits_D {\left\{ {{{w}_{m}}\left( {\mathbf{r}} \right) + {{w}_{a}}\left( {\mathbf{r}} \right) - {{\mu }_{0}}{{{\mathbf{H}}}_{e}}\left( {\mathbf{r}} \right){\mathbf{m}}\left( {\mathbf{r}} \right)} \right\}{{d}^{3}}r},$

где

(25)

$\begin{gathered} {{w}_{m}}\left( {{\mathbf{r}} \in D} \right) = \frac{{{{\mu }_{0}}}}{{8\pi }}\iiint\limits_{{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d}} {\frac{{{\mathbf{m}}\left( {\mathbf{r}} \right){\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right){{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{2}}}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{5}}}}{{d}^{3}}r{\text{'}}} - \\ - \,\,\frac{{{{\mu }_{0}}}}{{8\pi }}\iiint\limits_{{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d}} {\frac{{3\left( {{\mathbf{m}}\left( {\mathbf{r}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)} \right)\left( {{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{5}}}}{{d}^{3}}r{\text{'}}} \\ \end{gathered} $

плотность магнитостатической энергии, величина w_a (r ∈ D) – плотность энергии магнитной анизотропии, обусловлена взаимодействием домена с кристаллическим полем и выражается формулами (7), (16)–(20).

Для перехода к макроскопической модели введем следующие величины: ${{{\mathbf{м }}}_{i}} = - g{{\mu }_{{\text{B}}}}\left\langle {{{{{\mathbf{\hat {J}}}}}_{i}}} \right\rangle $ – магнитный момент i-го домена, v_i – его объем, ${{{\mathbf{m}}}_{i}} = {{{{{\mathbf{м }}}_{i}}} \mathord{\left/ {\vphantom {{{{{\mathbf{м }}}_{i}}} {{{v}_{i}}}}} \right. \kern-0em} {{{v}_{i}}}}$ – его намагниченность и ${{M}_{S}} = {{2g{{\mu }_{{\text{B}}}}{{N}_{i}}} \mathord{\left/ {\vphantom {{2g{{\mu }_{{\text{B}}}}{{N}_{i}}} {{{v}_{i}}}}} \right. \kern-0em} {{{v}_{i}}}}$ – намагниченность насыщения домена с учетом величины момента J = 2N. Тогда, усредняя суммы операторов (7), (16)–(20) по состоянию с наибольшим спиновым моментом, т.е. намагниченности насыщения, и пренебрегая дисперсией оператора полного момента, выражение для плотности энергии анизотропии, обусловленной взаимодействием домена с кристаллическим полем деформированного кристаллита, можно представить в виде

(26)

$\begin{gathered} {{w}_{a}} = \frac{{{{\mu }_{0}}{{M}_{T}}}}{{{{M}_{S}}}}{{\left( {{\mathbf{mc}}} \right)}^{2}} + \\ + \,\,\frac{{{{\mu }_{0}}{{M}_{T}}}}{{3{{M}_{S}}}}\left\{ {3{{{\mathbf{m}}}_{z}}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}} - {\mathbf{m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}} + 3\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)_{z}^{2} - {{{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)}}^{2}}} \right\} - \\ - \,\,\frac{{{{\mu }_{0}}{{M}_{K}}}}{{4M_{S}^{3}}}\left\{ {{{{\left( {{\mathbf{ma}}} \right)}}^{4}} + {{{\left( {{\mathbf{mb}}} \right)}}^{4}} + {{{\left( {{\mathbf{mc}}} \right)}}^{4}}} \right\} - \\ - \,\,\frac{{{{\mu }_{0}}{{M}_{K}}}}{{M_{S}^{3}}}\left\{ {{{{\mathbf{m}}}^{{\left( 3 \right)}}}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}} + \frac{3}{2}m_{{\alpha }}^{2}\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)_{{\alpha }}^{2} - \frac{3}{5}{{{\left( {{\mathbf{m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)}}^{2}}} \right\} + \\ + \,\,\frac{{29{{\mu }_{0}}{{M}_{K}}}}{{2{{M}_{S}}}}\left\{ {{\mathbf{m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}} + \frac{1}{2}{{{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)}}^{2}}} \right\}, \\ \end{gathered} $

где для удобства введены обозначения m⁽³⁾ – вектор с компонентами $\left\{ {m_{x}^{3},m_{y}^{3},m_{z}^{3}} \right\}$ и

(27)

${{M}_{T}} = \frac{{2{{W}_{T}}}}{{{{\mu }_{0}}g{{\mu }_{{\text{B}}}}}},\,\,\,{{M}_{K}} = \frac{{32{{W}_{K}}}}{{{{\mu }_{0}}g{{\mu }_{{\text{B}}}}}}$

тетрагональный и кубический параметры кристаллического поля соответственно.

Оси координат направлены вдоль осей легкого намагничивания a, b, c, совпадающих с кристаллографическими осями [100], [010] и [001] α-Fe, направления которых постоянны в пределах кристаллита, но меняются случайным образом при переходе от кристаллита к кристаллиту.

Первое и третье слагаемые в формуле (26) описывают плотность энергии естественной анизотропии, остальные – наведенной анизотропии, обусловленной магнитоупругой энергией. Поскольку |m| ≤ M_S, четвертым слагаемым в правой части формулы (26) можно пренебречь по сравнению с последним. Соответственно, можно пренебречь вкладом операторов (18) и (20) в полный гамильтониан домена. Для деформированного кристаллита плотность его магнитоупругой энергии можно приближенно записать в виде [3]

(28)

$\begin{gathered} {{w}_{{ME}}} = \frac{{{{W}_{T}}{{{\left( {2N} \right)}}^{2}}}}{{3{{N}^{2}}v}}\left( {3{{u}_{{z{\beta }}}}{{c}_{z}}{{c}_{{\beta }}} - {{u}_{{{\alpha \beta }}}}{{c}_{{\alpha }}}{{c}_{{\beta }}}} \right) + \\ + \,\,\frac{{1152{{W}_{K}}{{{\left( {2N} \right)}}^{2}}}}{{5{{N}^{2}}v}}{{u}_{{{\alpha \beta }}}}{{c}_{{\alpha }}}{{c}_{{\beta }}} = \\ = \left( {\frac{{9{{W}_{K}}{{2}^{9}}}}{{5{{a}^{3}}}} - \frac{{4{{W}_{T}}}}{{3{{a}^{3}}}}} \right){{u}_{{{\alpha \beta }}}}{{c}_{{\alpha }}}{{c}_{{\beta }}} + \frac{{4{{W}_{T}}}}{{{{a}^{3}}}}{{u}_{{z{\beta }}}}{{c}_{z}}{{c}_{{\beta }}} \approx \\ \approx \,\,{{W}_{M}}{{u}_{{{\alpha \beta }}}}{{c}_{{\alpha }}}{{c}_{{\beta }}}, \\ \end{gathered} $

где c_α,β – направляющие косинусы вектора намагниченности, W_M – константа магнитострикции:

${{W}_{M}} = \frac{{27{{W}_{K}}{{2}^{9}} - 20{{W}_{T}}}}{{15{{a}^{3}}}} \approx \frac{{9{{W}_{K}}{{2}^{9}}}}{{5{{a}^{3}}}} \approx \frac{{922{{W}_{K}}}}{{{{a}^{3}}}}.$

В результате деформации в кристалле возникает упругая энергия, и деформация прекращается, когда кристалл перейдет в равновесие, т.е. суммарная магнитоупругая и упругая энергия станет минимальной. Минимизируя функционал плотности энергии:

(29)

$\begin{gathered} w = {{w}_{{ME}}} + {{w}_{E}} = \\ = \,\,{{W}_{M}}\sum\limits_{{\alpha ,\beta } = 1}^3 {{{u}_{{{\alpha \beta }}}}{{c}_{{\alpha }}}{{c}_{{\beta }}}} + \frac{{{{C}_{{11}}}}}{2}\sum\limits_{{\alpha } = 1}^3 {{{u}_{{{\alpha \alpha }}}}^{2}} + \\ + \,\,{{C}_{{12}}}\sum\limits_{{\alpha ,\beta = 1}}^3 {{{u}_{{{\alpha \alpha }}}}{{u}_{{{\beta \beta }}}}\left( {1 - {{\delta }_{{{\alpha \beta }}}}} \right)} + \frac{{{{C}_{{44}}}}}{2}\sum\limits_{{\alpha ,\beta = 1}}^3 {u_{{{\alpha \beta }}}^{2}\left( {1 - {{\delta }_{{{\alpha \beta }}}}} \right)} , \\ \end{gathered} $

где С₁₁ = 2.41 × 10¹¹ Пa, С₁₂ = 1.46 × 10¹¹ Пa и С₄₄ = = 1.12 × 10¹¹ Пa – модули упругости кубического кристалла железа при комнатной температуре. По деформациям кристалла, из условия ${{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial {{u}_{{{\alpha \beta }}}}}}} \right. \kern-0em} {\partial {{u}_{{{\alpha \beta }}}}}} = 0,$ можно получить выражения для равновесных деформаций [3]:

(30)

$\begin{gathered} {{u}_{{{\alpha \alpha }}}} = {{W}_{M}}\frac{{\left[ {{{C}_{{12}}} - c_{{\alpha }}^{2}\left( {{{C}_{{11}}} + 2{{C}_{{12}}}} \right)} \right]}}{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)\left( {{{C}_{{11}}} + 2{{C}_{{12}}}} \right)}}, \\ {{u}_{{{\alpha \beta }}}} = - \frac{{{{W}_{M}}}}{{{{C}_{{44}}}}}{{c}_{{\alpha }}}{{c}_{{\beta }}}. \\ \end{gathered} $

В результате подстановки (30) в (29) выражение для плотности полной упругой энергии можно преобразовать к виду

(31)

$\begin{gathered} w = {{w}_{0}} + \frac{{W_{M}^{2}}}{2}\left[ {\frac{{{{C}_{{11}}}}}{{{{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}^{2}}}} - \frac{1}{{2{{C}_{{44}}}}}} \right] \times \\ \times \,\,\sum\limits_{{\alpha ,\beta = 1}}^3 {c_{{\alpha }}^{2}c_{{\beta }}^{2}\left( {1 - {{\delta }_{{{\alpha \beta }}}}} \right)} . \\ \end{gathered} $

Сравнивая полученное выражение (31) с выражением для равновесной плотности упругой энергии, приведенным в [3]

${{w}_{{\exp }}} = \frac{1}{2}\left[ {\frac{{B_{1}^{2}}}{{{{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}^{2}}}} - \frac{{B_{2}^{2}}}{{2{{C}_{{44}}}}}} \right]\sum\limits_{{\alpha ,\beta = 1}}^3 {c_{{\alpha }}^{2}c_{{\beta }}^{2}\left( {1 - {{\delta }_{{{\alpha \beta }}}}} \right)} ,$

можно оценить константу W_M через экспериментальные параметры магнитострикции кристалла железа (B₁ = –2.9 × 10⁶ Дж/м³ и B₂ = 3.2 × 10⁶ Дж/м³):

(32)

$\begin{gathered} W_{M}^{2}\left[ {\frac{{{{C}_{{11}}}}}{{{{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}^{2}}}} - \frac{1}{{2{{C}_{{44}}}}}} \right] = \frac{{B_{1}^{2}}}{{{{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}^{2}}}} - \frac{{B_{2}^{2}}}{{2{{C}_{{44}}}}}; \\ W_{M}^{2} = \frac{{2{{C}_{{44}}}B_{1}^{2} - B_{2}^{2}\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}{{2\left[ {{{C}_{{44}}}{{C}_{{11}}} - {{{\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right)}}^{2}}} \right]}}\left( {{{C}_{{11}}} - {{C}_{{12}}}} \right). \\ \end{gathered} $

Из выражения (32) следует оценка величины W_M = 1.55 × 10⁶ Дж/м³, тогда константа кристаллического поля, согласованная с экспериментальными данными по магнитострикции, принимает значение $W = {{W}_{M}}{{{{a}^{3}}} \mathord{\left/ {\vphantom {{{{a}^{3}}} {921}}} \right. \kern-0em} {921}} \approx 0.25\;{\mu e}V{\text{,}}$ на порядок меньшее теоретической оценки (8). Соответственно, из формулы (21) получаем оценку кубического параметра кристаллического поля M_K ≈ 4 × 10⁴ A/м.

Найдем равновесное распределение микроскопической намагниченности, доставляющее минимум функционалу энергии. Вычисляя стандартным образом первую вариацию функционала (24) по намагниченности, переходя к пределу d → 0, с учетом формулы (21) получим

(33)

$\delta W = - {{\mu }_{0}}\iiint\limits_D {{{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right)\delta {\mathbf{m}}\left( {\mathbf{r}} \right){{d}^{3}}r},$

где

(34)

${{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right) = {{{\mathbf{H}}}_{e}}\left( {\mathbf{r}} \right) + {{{\mathbf{h}}}_{m}}\left( {\mathbf{r}} \right) + {{{\mathbf{h}}}_{K}}\left( {\mathbf{r}} \right),$

(35)

$\begin{gathered} {{{\mathbf{h}}}_{K}} = \frac{{{{M}_{K}}}}{{M_{S}^{3}}}\left( {{{{\left( {{\mathbf{ma}}} \right)}}^{3}}{\mathbf{a}} + {{{\left( {{\mathbf{mb}}} \right)}}^{3}}{\mathbf{b}} + {{{\left( {{\mathbf{mc}}} \right)}}^{3}}{\mathbf{c}}} \right) - \\ - \,\,\frac{{2{{M}_{T}}}}{{{{M}_{S}}}}\left( {{\mathbf{mc}}} \right){\mathbf{c}} - \frac{{{{M}_{A}}}}{{{{M}_{S}}}}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}} - \frac{{{{M}_{T}}}}{{{{M}_{S}}}}{\mathbf{c}}\left( {{\mathbf{c}}\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)} \right) - \\ - \,\,\frac{{{{M}_{T}}}}{{{{M}_{S}}}}\left( {{\mathbf{mc}}} \right){\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} c}} - \frac{{{{M}_{B}}}}{{{{M}_{S}}}}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right) - \frac{{2{{M}_{T}}}}{{{{M}_{S}}}}\left( {{\mathbf{c}}\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} m}}} \right)} \right){\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} c}} \\ \end{gathered} $

напряженность кристаллического поля, в котором находится домен,

(36)

${{M}_{A}} = 29{{M}_{K}} - \frac{{2{{M}_{T}}}}{3},\,\,\,{{M}_{B}} = \frac{{29{{M}_{K}}}}{2} - \frac{{2{{M}_{T}}}}{3}.$

Ферромагнетик в полях, слабых по сравнению с полем насыщения, можно считать состоящим из отдельных доменов, намагниченных до насыщения. Это значит, что

(37)

$\left| {{\mathbf{m}}\left( {\mathbf{r}} \right)} \right| = {{M}_{S}}\left( {\mathbf{r}} \right).$

Из формулы (37) следует, что с точностью до второго порядка малости

(38)

$2{\mathbf{m}}\left( {\mathbf{r}} \right)\delta {\mathbf{m}}\left( {\mathbf{r}} \right) + {{\left( {\delta {\mathbf{m}}\left( {\mathbf{r}} \right)} \right)}^{2}} = 0.$

Тогда условие равенства нулю первой вариации (33), линейной по вариации намагниченности, имеет вид

(39)

${{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right) = f\left( {\mathbf{r}} \right){\mathbf{m}}\left( {\mathbf{r}} \right),$

где f(r) – произвольная функция. Из уравнений (37) и (39) получаем

(40)

$f\left( {\mathbf{r}} \right) = \pm \frac{{\left| {{{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right)} \right|}}{{{{M}_{S}}\left( {\mathbf{r}} \right)}}.$

Для определения устойчивых распределений намагниченности m(r), доставляющий условный минимум функционалу (24) рассмотрим его вторую вариацию. При выполнении условия (39), когда первая вариация равна нулю, вариация (33) с учетом условия (37) имеет вид

(41)

$\begin{gathered} \delta W = - {{\mu }_{0}}\iiint\limits_D {f\left( {\mathbf{r}} \right){\mathbf{m}}\left( {\mathbf{r}} \right)\delta {\mathbf{m}}\left( {\mathbf{r}} \right){{d}^{3}}r} = \\ = \frac{{{{\mu }_{0}}}}{2}\iiint\limits_D {f\left( {\mathbf{r}} \right){{{\left( {\delta {\mathbf{m}}\left( {\mathbf{r}} \right)} \right)}}^{2}}{{d}^{3}}r}. \\ \end{gathered} $

Вариация (41), квадратичная по вариации намагниченности, является второй вариацией. Необходимым и достаточным условием ее положительности при произвольной вариации намагниченности является строгая положительность функции f(r) для всех r ∈ D. Таким образом, для того чтобы распределение намагниченности с учетом условия (37) было равновесным, необходимо и достаточно, чтобы функция f(r) была положительно определенной. Тогда

(42)

${\mathbf{m}}\left( {\mathbf{r}} \right) = {{M}_{S}}\left( {\mathbf{r}} \right)\frac{{{{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right)}}{{\left| {{{{\mathbf{h}}}_{{ef}}}\left( {\mathbf{r}} \right)} \right|}}.$

Уравнения (21), (34) и (35) совместно с уравнением (42) описывают намагниченность в заданном внешнем поле H_e(r).

Рассмотрим внутри тела D медленно меняющиеся макроскопические поля и намагниченность как средние значения по физически малому объему V, содержащему большое число доменов:

$\begin{gathered} {\mathbf{M}}\left( {\mathbf{r}} \right) = \left\langle {{\mathbf{m}}\left( {\mathbf{r}} \right)} \right\rangle = \frac{1}{V}\iiint\limits_V {{\mathbf{m}}\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right){{d}^{3}}r{\text{'}}}; \\ {{{\mathbf{H}}}_{m}}\left( {\mathbf{r}} \right) = \left\langle {{{{\mathbf{h}}}_{m}}\left( {\mathbf{r}} \right)} \right\rangle = \frac{1}{V}\iiint\limits_V {{{{\mathbf{h}}}_{m}}\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right){{d}^{3}}r{\text{'}}} \\ \end{gathered} $

и соответствующие флуктуационные составляющие:

(43)

$\begin{gathered} {\mathbf{\tilde {m}}}\left( {\mathbf{r}} \right) = {\mathbf{m}}\left( {\mathbf{r}} \right) - {\mathbf{M}}\left( {\mathbf{r}} \right),\quad {{{{\mathbf{\tilde {h}}}}}_{m}}\left( {\mathbf{r}} \right) = {{{\mathbf{h}}}_{m}}\left( {\mathbf{r}} \right) - {{{\mathbf{H}}}_{m}}\left( {\mathbf{r}} \right); \\ \left\langle {{\mathbf{\tilde {m}}}\left( {\mathbf{r}} \right)} \right\rangle = 0,\quad \left\langle {{{{{\mathbf{\tilde {h}}}}}_{m}}\left( {\mathbf{r}} \right)} \right\rangle = 0; \\ \left\langle {{{{\left| {{\mathbf{\tilde {m}}}\left( {\mathbf{r}} \right)} \right|}}^{2}}} \right\rangle = M_{S}^{2}\left( {\mathbf{r}} \right) - {{M}^{2}}\left( {\mathbf{r}} \right). \\ \end{gathered} $

Медленно меняющаяся намагниченность M(r) в соответствии с формулой (23) создает в центре домена регулярное поле

(44)

${{{\mathbf{H}}}_{m}}\left( {\mathbf{r}} \right) = - \frac{1}{{4\pi V}}\frac{\partial }{{\partial {\mathbf{r}}}}\iiint\limits_V {{{\phi }_{m}}\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right){{d}^{3}}r{\text{'}}} + \frac{{{\mathbf{M}}\left( {\mathbf{r}} \right)}}{3},$

а флуктуационная составляющая намагниченности ${\mathbf{\tilde {m}}}\left( {\mathbf{r}} \right)$ создает случайное поле ${\mathbf{\tilde {h}}}\left( {\mathbf{r}} \right)$ соответственно. Пусть тело D состоит из доменов объемом v_i с центром в точке r_i и магнитным моментом p_i = m(r_i)${{v}_{i}}$, модуль которого постоянен и равен M_S${{v}_{i}}$. Тогда, в соответствии с формулой (21):

$\begin{gathered} {{{{\mathbf{\tilde {h}}}}}_{j}} = {{{{\mathbf{\tilde {h}}}}}_{m}}\left( {{{{\mathbf{r}}}_{j}} \in D} \right) = \\ = \frac{1}{{4\pi }}\sum\limits_{i \ne j} {\left\{ {\frac{{3\left( {\left( {{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}} \right){{{{\mathbf{\tilde {p}}}}}_{i}}} \right)\left( {{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}} \right)}}{{{{{\left| {{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}} \right|}}^{5}}}} - \frac{{{{{{\mathbf{\tilde {p}}}}}_{i}}}}{{{{{\left| {{{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}} \right|}}^{3}}}}} \right\}} . \\ \end{gathered} $

Если тело D далеко от насыщения, то ${{\left| {{\mathbf{M}}\left( {\mathbf{r}} \right)} \right|}^{2}} \ll $ $ \ll \left\langle {{{{\left| {{\mathbf{\tilde {m}}}\left( {\mathbf{r}} \right)} \right|}}^{2}}} \right\rangle $ = $M_{S}^{2}\left( {\mathbf{r}} \right)$ и можно считать, что случайные величины p_i не коррелированны. Случайные величины ${{{\mathbf{\tilde {h}}}}_{j}}$ при этом являются суммой большого числа случайных некоррелированных величин, и их распределение близко к нормальному

(45)

$w\left( {\mathbf{h}} \right) = \frac{1}{{{{{\left( {2\pi } \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\sigma }^{3}}}}\exp \left( { - \frac{{{{h}^{2}}}}{{2{{\sigma }^{2}}}}} \right)$

с дисперсией ${{\sigma }^{2}} = \left\langle {{{{\left| {{{{{\mathbf{\tilde {h}}}}}_{j}}} \right|}}^{2}}} \right\rangle .$

Однородно намагниченное до насыщения тело в соответствии с формулой (44) создает в центре каждого домена поле, для которого ${{\left| {{{{\mathbf{h}}}_{j}}} \right|}^{2}} = {{M_{S}^{2}} \mathord{\left/ {\vphantom {{M_{S}^{2}} 9}} \right. \kern-0em} 9},\,\,\,\,\left\langle {{{{\left| {{{{{\mathbf{\tilde {h}}}}}_{j}}} \right|}}^{2}}} \right\rangle = 0.$ Тело с нулевой средней намагниченностью M можно рассматривать как три случайно ориентированные подрешетки с намагниченностью M_S/3. Тогда $\left\langle {{{{\left| {{{{{\mathbf{\tilde {h}}}}}_{j}}} \right|}}^{2}}} \right\rangle = {{M_{S}^{2}} \mathord{\left/ {\vphantom {{M_{S}^{2}} {27}}} \right. \kern-0em} {27}}.$ С учетом формулы (38), можно принять

(46)

${{\sigma }^{2}} = {{\left( {M_{S}^{2} - {{M}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {M_{S}^{2} - {{M}^{2}}} \right)} {27}}} \right. \kern-0em} {27}}.$

Перепишем формулу (42) с учетом флуктуаций поля:

(47)

$\begin{gathered} {\mathbf{m}}\left( {\mathbf{r}} \right)\sqrt {{{H}^{2}}\left( {\mathbf{r}} \right) + 2{\mathbf{H}}\left( {\mathbf{r}} \right){{{{\mathbf{\tilde {h}}}}}_{m}}\left( {\mathbf{r}} \right) + \tilde {h}_{m}^{2}\left( {\mathbf{r}} \right)} = \\ = {{M}_{S}}\left( {{{{{\mathbf{\tilde {h}}}}}_{m}}\left( {\mathbf{r}} \right) + {\mathbf{H}}\left( {\mathbf{r}} \right)} \right), \\ \end{gathered} $

где обозначено H(r) = H_e(r) + H_m(r) + h_K(r).

Макроскопическую намагниченность кристаллита можно найти усреднением формулы (47) по случайным ориентациям осей легкого намагничивания и по полю размагничивания. По формуле (21) поле h_m(r) зависит от намагниченности во всех точках, кроме точки r. Поле же h_K(r) по формуле (35) определяется намагниченностью в точке r и ориентацией осей легкого намагничивания в этой же точке. Поэтому случайная величина h_m(r) не зависит от h_K(r) и от m(r), и усреднение по намагниченности, полю размагничивания и по ориентациям осей легкого намагничивания можно производить последовательно. Усредним выражение (47) с учетом распределения (45) для одного кристаллита, учитывая, что в пределах кристаллита направления осей легкого намагничивания постоянны:

$\begin{gathered} \frac{{{{{\mathbf{m}}}_{l}}}}{{{{{\left( {2\pi } \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\sigma }^{3}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\sqrt {H_{{}}^{2} + 2{\mathbf{Hh}} + {{h}^{2}}} } } } \times \\ \times \,\,\exp \left( { - \frac{{{{h}^{2}}}}{{2{{\sigma }^{2}}}}} \right){{d}^{3}}h = {{M}_{S}}{\mathbf{H}}, \\ \end{gathered} $

где m_l средняя намагниченность l-го кристаллита, поля берутся в центре l-го кристаллита.

Перейдем к сферической системе координат, направив полярную ось вдоль вектора H. Тогда

(48)

$\begin{gathered} \frac{{2\pi {{{\mathbf{m}}}_{l}}}}{{{{{\left( {2\pi } \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\sigma }^{3}}}}\int\limits_0^{\pi } {\int\limits_0^\infty {\sqrt {{{H}^{2}} + 2{\mathbf{Hh}} + {{h}^{2}}} {{h}^{2}}\theta } } \times \\ \times \,\,\sin \theta \exp \left( { - \frac{{{{h}^{2}}}}{{2{{\sigma }^{2}}}}} \right)dhd\theta = {{M}_{S}}{\mathbf{H}}. \\ \end{gathered} $

Параметрический интеграл в левой части формулы (48) не вычисляется аналитически, численный расчет показывает, что в диапазоне 0 ≤ H/σ ≤ ≤ 100 он хорошо аппроксимируется функцией

${{\sigma }^{4}}\sqrt {6\pi + 2\pi {{{{H}^{2}}} \mathord{\left/ {\vphantom {{{{H}^{2}}} {{{\sigma }^{2}}}}} \right. \kern-0em} {{{\sigma }^{2}}}}} .$

Тогда

(49)

$\begin{gathered} {{{\mathbf{m}}}_{l}}\sqrt {3{{\sigma }^{2}} + H_{{ef}}^{2} + 2{{{\mathbf{H}}}_{{ef}}}{{{\mathbf{h}}}_{K}} + h_{K}^{2}} = \\ = \,\,{{M}_{S}}\left( {{{{\mathbf{h}}}_{K}} + {{{\mathbf{H}}}_{{ef}}}} \right), \\ \end{gathered} $

где введено обозначение H_ef = H_e + H_m.

Из формул (36) и (37) следует, что $h_{K}^{2} \leqslant M_{K}^{2}$ + + $M_{T}^{2}.$ Для магнитомягкого ферромагнетика при условии M_T, M_K $ \ll $ M_S получаем $h_{K}^{2} \ll 3{{\sigma }^{2}} + H_{{ef}}^{2},$ и левую часть формулы (49) можно разложить в ряд Тейлора, ограничившись линейным по h_K слагаемым. С учетом формулы (46), опуская индекс l, получаем:

(50)

$\begin{gathered} {\mathbf{m}}\left( {M_{S}^{2} + 6{\mathbf{Hm}} + 9{{H}^{2}}} \right) + 9{\mathbf{m}}\left( {{\mathbf{H}}{{{\mathbf{h}}}_{K}}} \right) + 3{\mathbf{m}}\left( {{\mathbf{m}}{{{\mathbf{h}}}_{K}}} \right) = \\ = {{M}_{S}}\left( {3{{{\mathbf{h}}}_{K}} + 3{\mathbf{H}} + {\mathbf{m}}} \right)\sqrt {M_{S}^{2} + 6{\mathbf{Hm}} + 9{{H}^{2}}} , \\ \end{gathered} $

где

${\mathbf{H}}\left( {\mathbf{r}} \right) = {{{\mathbf{H}}}_{e}}\left( {\mathbf{r}} \right) + {{{\mathbf{H}}}_{1}}\left( {\mathbf{r}} \right),$

(51)

${{{\mathbf{H}}}_{1}}\left( {\mathbf{r}} \right) = \frac{\partial }{{\partial {\mathbf{r}}}}{{\phi }_{m}}\left( {\mathbf{r}} \right) = \frac{1}{{4\pi }}\frac{\partial }{{\partial {\mathbf{r}}}}\iiint\limits_{{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d}} {\frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}{{d}^{3}}r{\text{'}}}$

– напряженность поля размагничивания.

Формулу (50) можно переписать в виде m(r) = = m^e(r), где

(52)

$\begin{gathered} {{{\mathbf{m}}}^{e}} = {{M}_{S}}\frac{{3{\mathbf{H}} + {\mathbf{m}} + 3{{{\mathbf{h}}}_{K}}}}{{M_{S}^{2} + 9{{H}^{2}} + 9{\mathbf{H}}{{{\mathbf{h}}}_{K}}}} \times \\ \times \,\,\sqrt {M_{S}^{2} + 6{\mathbf{Hm}} + 9{{H}^{2}}} - \\ - \,\,3{\mathbf{m}}\frac{{{\mathbf{m}}\left( {{{{\mathbf{h}}}_{K}} + 2{\mathbf{H}}} \right)}}{{M_{S}^{2} + 9{{H}^{2}} + 9{\mathbf{H}}{{{\mathbf{h}}}_{K}}}}. \\ \end{gathered} $

Тогда уравнение релаксации макроскопической намагниченности m(r) к равновесной намагниченности m^e(r) принимает классический вид уравнения Блоха:

(53)

$\frac{{\partial {\mathbf{m}}}}{{\partial t}} = - \frac{{{\mathbf{m}} - {{{\mathbf{m}}}^{e}}}}{{{{T}_{1}}}},$

где T₁ – время продольной релаксации, являющееся свободным параметром модели.

Подобное феноменологическое описание спиновой релаксации в ферромагнитном диэлектрике с использованием общего подхода Бломбергена позволил авторам работы [20] получить уравнения движения намагниченности образцов. В работе рассматривается высокодисперсионная среда, описываемая многомодовыми спиновыми волнами. Для каждой спиновой моды вводится время релаксации. Полученные уравнения определенным образом трансформируются в уравнения Блоха, Каллена и Ландау–Лифшица.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Верификация теоретически полученных выражений (52) и (53) на экспериментальных данных осуществлена численным моделированием зависимостей средней по объему намагниченности от внешнего поля H_e и анализом их характерных особенностей. Численное моделирование осуществляли прямым решением уравнения (53) методом Рунге–Кутты 4-го порядка [21].

Для расчета равновесной намагниченности, входящей в уравнение (52), разработаны эффективные алгоритмы, основанные на методах линейной алгебры, успешно апробированные на двумерной дискретной модели [1]. При этом отмечено, что для трехмерной модели с большим количеством взаимодействующих диполей, целесообразно применять другие методы, например, спектральный метод, реализованный в известном пакете по микромагнитному моделированию MuMax3 [22].

Если намагниченное тело занимает конечный объем, выберем параллелепипед L со сторонами L_x, L_y и L_z, полностью охватывающий тело, и доопределим функцию m(r) нулевыми значениями вне этого тела. Выберем начало координат в одном из углов параллелепипеда, тогда спектр магнитного потенциала (22) будет иметь вид:

$\begin{gathered} {{{\tilde {\phi }}}_{m}}\left( {\mathbf{k}} \right) = - \frac{1}{{4\pi }}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_0^{{{L}_{x}}} {\int\limits_0^{{{L}_{y}}} {\int\limits_0^{{{L}_{z}}} {\frac{{{\mathbf{m}}\left( {{\mathbf{r}}{\text{'}}} \right)\left( {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right)}}{{{{{\left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}} \right|}}^{3}}}}} } } } } } \times \\ \times \,\,\exp \left( { - j{\mathbf{kr}}} \right){{d}^{3}}r{\text{'}}{{d}^{3}}r = \\ = \left( { - \frac{1}{{4\pi }}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\frac{{\mathbf{r}}}{{{{r}^{3}}}}\exp \left( { - j{\mathbf{kr}}} \right){{d}^{3}}r} } } } \right) \times \\ \times \,\,\left( {\int\limits_0^{{{L}_{x}}} {\int\limits_0^{{{L}_{y}}} {\int\limits_0^{{{L}_{z}}} {{\mathbf{m}}\left( {\mathbf{r}} \right)\exp \left( { - j{\mathbf{kr}}} \right){{d}^{3}}r} } } } \right) = \\ = j\frac{{{\mathbf{k\tilde {m}}}\left( {\mathbf{k}} \right)}}{{{{k}^{2}}}},\,\,\,\,{{{\tilde {\phi }}}_{m}}\left( 0 \right) = 0, \\ \end{gathered} $

где

(54)

${\mathbf{\tilde {m}}}\left( {\mathbf{k}} \right) = \int\limits_0^{{{L}_{x}}} {\int\limits_0^{{{L}_{y}}} {\int\limits_0^{{{L}_{z}}} {{\mathbf{m}}\left( {\mathbf{r}} \right)\exp \left( { - j{\mathbf{kr}}} \right){{d}^{3}}r} } } $

– пространственный спектр намагниченности. Соответственно,

(55)

$\begin{gathered} {{{{\mathbf{\tilde {H}}}}}_{1}}\left( {\mathbf{k}} \right) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\mathbf{H}}}_{1}}\left( {\mathbf{r}} \right)\exp \left( { - j{\mathbf{kr}}} \right){{d}^{3}}r} } } = \\ = j{\mathbf{k}}{{{\tilde {\phi }}}_{m}}\left( {\mathbf{k}} \right) = - \frac{{{\mathbf{k\tilde {m}}}\left( {\mathbf{k}} \right)}}{{{{k}^{2}}}}{\mathbf{k}} \\ \end{gathered} $

– пространственный спектр поля H₁(r) вида (51).

Если при численном моделировании параллелепипед L разбивается на ячейки со сторонами Δ_x, Δ_y и Δ_z, для построения регуляризированного почти решения носитель спектра (49) следует ограничить областью K [–π/Δ_x ≤ k_x ≤ π/Δ_x, –π/Δ_y ≤ ≤ k_y ≤ π/Δ_y, –π/Δ_z ≤ k_z ≤ π/Δ_z] и взвесить компоненты спектров ${\mathbf{\tilde {m}}}\left( {\mathbf{k}} \right)$ и ${\mathbf{\tilde {H}}}\left( {\mathbf{k}} \right)$ окном W_K(k) [23], например, окном Ханна [24]. Тогда

(56)

$\begin{gathered} {{{\mathbf{H}}}_{1}}\left( {\mathbf{r}} \right) = \\ = \,\,\int\limits_{ - {{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{x}}}}} \right. \kern-0em} {{{\Delta }_{x}}}}}^{{{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{x}}}}} \right. \kern-0em} {{{\Delta }_{x}}}}} {\int\limits_{ - {{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{y}}}}} \right. \kern-0em} {{{\Delta }_{y}}}}}^{{{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{y}}}}} \right. \kern-0em} {{{\Delta }_{y}}}}} {\int\limits_{ - {{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{z}}}}} \right. \kern-0em} {{{\Delta }_{z}}}}}^{{{\pi } \mathord{\left/ {\vphantom {{\pi } {{{\Delta }_{z}}}}} \right. \kern-0em} {{{\Delta }_{z}}}}} {{{W}_{K}}\left( {\mathbf{k}} \right){{{{\mathbf{\tilde {H}}}}}_{1}}\left( {\mathbf{k}} \right)\exp \left( {j{\mathbf{kr}}} \right)\frac{{{{d}^{3}}k}}{{8{{\pi }^{3}}}}} } } . \\ \end{gathered} $

Поскольку интегралы в выражениях (54) и (56) собственные, они могут вычисляться с помощью прямого и обратного дискретного преобразования Фурье, соответственно, для которого существуют эффективные алгоритмы БПФ, допускающие распараллеливание вычислений [25–27].

При численном моделировании в качестве объекта исследования использовали параллелепипед из однородного ферромагнетика размером L_x × L_y × L_z, т.е. объем измерения совпадал с объемом параллелепипеда. Задавали компоненты постоянного внешнего поля H_e, компоненты постоянного тензора деформации u_λσ (λ, σ = x, y, z) и случайным образом формировались оси легкого намагничивания доменов a, b и c, введенные в выражении (26)

${\mathbf{a}}\left( {\mathbf{r}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \left( \alpha \right)\cos \left( \gamma \right) - \sin \left( \alpha \right)\cos \left( \beta \right)\sin \left( \gamma \right)} \\ {\sin \left( \alpha \right)\cos \left( \gamma \right) + \cos \left( \alpha \right)\cos \left( \beta \right)\sin \left( \gamma \right)} \\ {\sin \left( \beta \right)\sin \left( \gamma \right)} \end{array}} \right],$

${\mathbf{b}}\left( {\mathbf{r}} \right) = \left[ {\begin{array}{*{20}{c}} { - \cos \left( \alpha \right)\sin \left( \gamma \right) - \sin \left( \alpha \right)\cos \left( \beta \right)\cos \left( \gamma \right)} \\ { - \sin \left( \alpha \right)\sin \left( \gamma \right) + \cos \left( \alpha \right)\cos \left( \beta \right)\cos \left( \gamma \right)} \\ {\sin \left( \beta \right)\cos \left( \gamma \right)} \end{array}} \right],$

${\mathbf{с }}\left( {\mathbf{r}} \right) = \left[ {\begin{array}{*{20}{c}} {\sin \left( \alpha \right)\sin \left( \beta \right)} \\ { - \cos \left( \alpha \right)\sin \left( \beta \right)} \\ {\cos \left( \beta \right)} \end{array}} \right],$

где 0 ≤ α(r) < π, 0 ≤ β(r) < 2π, 0 ≤ γ(r) < 2π – случайные углы Эйлера, а также задавали значение критерия окончания итераций δ. В качестве начального использовали случайное распределение намагниченности с нулевым средним.

На каждом шаге итераций очередное распределение намагниченности m′(r) определяли путем численного решения уравнения (53). Величину m^e(r) рассчитывали по формуле (52), а входящее в него поле h_K(r) – по формуле (36). Поле H₁(r), необходимое для вычисления полного поля H(r), определяли спектральным методом с помощью выражений (54)–(56) и алгоритма БПФ. Затем проверяли критерий окончания итераций

$\varepsilon = \frac{1}{V}\iiint\limits_V {\frac{{{{{\left| {{\mathbf{m}}{\text{'}}\left( {\mathbf{r}} \right) - {\mathbf{m}}\left( {\mathbf{r}} \right)} \right|}}^{2}}}}{{{{m}^{{'2}}}\left( {\mathbf{r}} \right) + {{m}^{2}}\left( {\mathbf{r}} \right)}}{{d}^{3}}r} < \delta ,$

при невыполнении которого полагали m(r) = m'(r) и осуществляли переход к очередному шагу итераций. При ε < δ вычисляли среднюю по объему намагниченность образца:

${\mathbf{M}} = \frac{1}{V}\iiint\limits_V {{\mathbf{m}}\left( r \right){{d}^{3}}r}.$

Моделирование макроскопической намагниченности проводили для прямоугольного тела размером L_x = 430 мм, L_y = 15 мм, L_z = 15 мм и намагниченностью насыщения M_S = 1.6 × 10⁶ A/м, характерной для магнитомягкой стали. Область моделирования разбивали на N_x = 256, N_y = 8, N_z = 8 ячеек. В начальном состоянии в каждой ячейке задавали вектор намагниченности с модулем $\left| {\mathbf{M}} \right| = \sqrt {M_{S}^{2} - 9M_{K}^{2}} $ и ориентированным в случайном направлении.

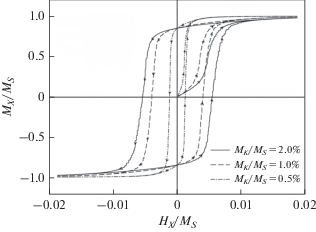
На рис. 1 приведены зависимости относительной намагниченности M_X/M_S недеформированного ферромагнетика от относительной напряженности внешнего поля H_X/M_S при различных значениях параметра M_K/M_S. Видно, что при уменьшении величины кристаллического поля M_K ширина петли гистерезиса уменьшается. Зависимость коэрцитивной силы H_C/M_S от параметра M_K/M_S имеет незначительную нелинейность и проходит через начало координат.

Рис. 1.

График зависимости намагниченности M_X/M_S недеформированного ферромагнетика от относительной напряженности внешнего поля H_X/M_S при различных значениях параметра M_K/M_S.

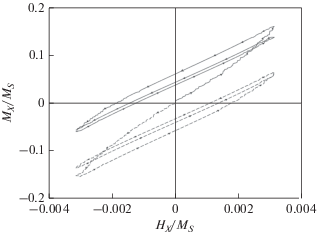
На рис. 2 приведена зависимость намагниченности M_X/M_S недеформированного ферромагнетика от относительной напряженности внешнего поля H_X/M_S в релеевской области при M_K/M_S = = 0.26 × 10^–3. Видно, что гистерезис проявляется и в этом случае, но петля имеет гораздо меньшую площадь. Если из начального состояния увеличивать напряженность внешнего магнитного поля, то полученная петля гистерезиса располагается выше начала координат, если уменьшать – ниже начала координат. Эти результаты также согласуются с экспериментом [3].

Рис. 2.

График зависимости намагниченности M_X/M_S недеформированного ферромагнетика от относительной напряженности внешнего поля H_X/M_S в релеевской области при M_K/M_S = 2.6 × 10^–3.

На рис. 3 приведены экспериментальная зависимость относительной коэрцитивной силы H_C/M_S деформированного ферромагнетика (образцы стали Durehete 1055 и AS1548-7-46OR) от приложенного продольного давления p = σ_xx [6] (сплошная линия) и зависимость, полученная в результате численного моделирования при заданных параметрах модели M_S = 1.6 × 10⁶ A/м, M_K = 4500 A/м, M_T = = 30M_K, M_A = 118M_K, M_B = –72 000M_K, E = 2 × 10¹¹ Пa, σ = 0.28 (пунктирная линия). Для оценки влияния тетрагонального параметра кристаллического поля приведена зависимость, полученная при M_T = 0.

Рис. 3.

График зависимости коэрцитивной силы H_C от приложенного давления при M_K/M_S = 2.8 × 10^–3. Сплошной линией показаны экспериментальные данные из работы [6], пунктирными линиями – результаты моделирования при M_T = 0 и 30 M_K.

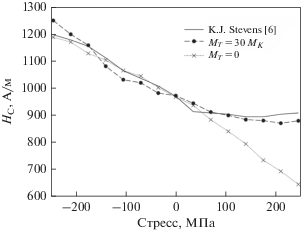
Аналогичное сравнение экспериментальной зависимости относительной коэрцитивной силы H_C/M_S деформированного ферромагнетика (образец стали Х70 [28]) от приложенного продольного давления и модельных результатов приведено на рис. 4. Численное моделирование проводили при заданных параметрах M_S = 1.6 × × 10⁶ A/м, M_K = 22 000 A/м, M_T = 27M_K, M_A = = 265M_K, M_B = –95 500M_K.

Рис. 4.

График зависимости коэрцитивной силы H_C от приложенного давления. Сплошной линией показаны экспериментальные данные из работы [28], пунктирной линией – результаты моделирования при M_T = 27M_K.

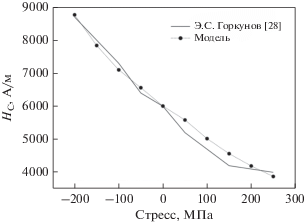
На рис. 5 показаны экспериментальная зависимость относительной коэрцитивной силы H_C/M_S деформированного ферромагнетика (образец стали 11ХН3Д [29]) от приложенного продольного давления и результаты численного моделирования, которое проводили при заданных параметрах M_S = 1.6 × 10⁶ A/м, M_K = 3400 A/м, M_T = = 11M_K, M_A = 191M_K, M_B = –235 300M_K.

Рис. 5.

График зависимости коэрцитивной силы H_C от приложенного давления. Сплошной линией показаны экспериментальные данные из работы [29], пунктирной линией – результаты моделирования при M_T = 11 M_K.

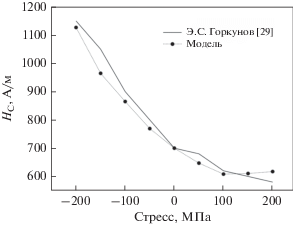
Из приведенных графиков видно, что влияние тетрагонального возмущения кристаллического поля на коэрцитивную силу деформированного ферромагнетика мало при отрицательных деформациях и существенно при положительных. Численно изучена зависимость коэрцитивной силы образца от внешней нагрузки, получено качественное и количественное согласие модельных результатов с экспериментальными данными для образцов стали, используемой для производства болтов и сосудов высокого давления.

ЗАКЛЮЧЕНИЕ

На основе метода модельных гамильтонианов, учитывающих зеемановскую энергию, энергию взаимодействия с кристаллическим полем и магнито-дипольного взаимодействия доменов, предложена микроскопическая модель деформированного магнитомягкого ферромагнетика на примере кристалла α-железа. Параметры модельных гамильтонианов согласованы с экспериментальными данными по магнитострикции железа. Минимизация функционала плотности энергии кристалла варьированием намагниченности образца позволила получить выражение для равновесной намагниченности ферромагнетика в квадратичном по деформации приближении. На основе численного решения динамического уравнения Блоха получено решение, имеющее характерный вид петли гистерезиса, основные параметры которой зависят от величины деформации образца.

Таким образом, в работе показано, что петля гистерезиса может быть получена решением динамического уравнения типа Блоха с учетом только процессов вращения векторов намагниченностей доменов и диполь-дипольного взаимодействия между доменами.

Результаты работы можно использовать для расчета и оптимизации характеристик феррозондовых магнитометров, в частности, магнитометра на резонансных микрополосковых преобразователях с тонкими магнитными пленками [30].

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 15-19-00028).

Список литературы

Беляев Б.А., Изотов А.В., Лексиков А.А. Микромагнитный расчет равновесного распределения магнитных моментов тонких пленок // ФТТ. 2010. Т. 52. Вып. 8. С. 1549–1556.
Вонсовский С.В. Магнетизм. М.: Наука, 1971. 1032 с.
Кринчик Г.С. Физика магнитных явлений. М.: Изд-во Моск. ун-та, 1976. 367 с.
Cardelli E. Advances in Magnetic Hysteresis Modeling // In Handbook of Magnetic Materials. 2015. V. 24. P. 323–409.
Винокуров Н.А., Шевченко О.А., Середняков С.С., Щеглов М.А., Рояк М.Э., Ступаков И.М., Кондратьева Н.С. Учет гистерезиса при расчете поля в элементах магнитных систем ускорителей // Письма в ЖТФ. 2016. Т. 42. Вып. 13. С. 96–102.
Stevens K.J. Stress dependence of ferromagnetic hysteresis loops for two grades of steel // NDT&E International. 2000. V. 33. P. 111–121.
Беляев Б.А., Изотов А.В. Исследование влияния упругих напряжений на анизотропию магнитных пленок методом ферромагнитного резонанса // ФТТ. 2007. Т. 49. Вып. 9. С. 1651–1659.
Maicas M., Lopez E., Sanchez M.C., Aroca C., Sanchez P. Magnetostatic energy calculations in two- and three-dimensional arrays of ferromagnetic prisms // IEEE transactions on magnetic. 1998. V. 34. Iss. 3. P. 601–607.
Carey R., Beg M., Albert M., Bisotti M.-A., Cortés-Ortuño D., Vousden M., Wang W., Hovorka O., Fangohr H. Hysteresis of nanocylinders with Dzyaloshinskii-Moriya interaction // Appl. Phys. Letters. 2016. V. 109. 122401.
Tiersten H.F. Coupled Magnetomechanical Equations for Magnetically Saturated Insulators // J. Mathematical Physics. 1964. V. 5. P. 1298–1318.
Абрагам А., Блини Б. Электронный парамагнитный резонанс переходных ионов. Т. 2. М.: Мир, 1973. 351 с.
Лоу В. Парамагнитный резонанс в твердых телах. М.: ИИЛ, 1962. 242 с.
Ашкрофт Н., Мермин Н. Физика твердого тела. Т 1. М.: Мир, 1979. 400 с.
Гуляев А.П. Металловедение. М.: Металлургия, 1986. 544 с.
Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул. Ростов-на-Дону: Феникс, 1997. 560 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. III. Квантовая механика. Нерелятивистская теория. М.: Физматлит, 2004. 800 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VII. Теория упругости. М.: ФИЗМАТЛИТ, 2003. 264 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VIII. Электродинамика сплошных сред. М.: ФИЗМАТЛИТ, 2005. 656 с.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1966. 754 с.
Fletcher R.C., LeCraw R.C., Spencer E.G. Electron Spin Relaxation in Ferromagnetic Insulators // Phys. Review. 1960. V. 117. Num. 4. P. 955–963.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: БИНОМ. Лаборатория знаний, 2008. 636 с.
Vansteenkiste A., Leliaert J., Dvornik M., Helsen M., Garcia-Sanchez F., Van Waeyenberge B. The design and verification of MuMax3 // AIP Advances. 2014. V. 4. Iss. 10. 107133.
Василенко Г.И., Тараторин А.М. Восстановление изображений. М.: Радио и связь, 1986. 304 с.
Марпл-мл С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 584 с.
Frigo M., Johnson S.G. The Design and Implementation of FFTW3 // Proceedings IEEE. 2005. V. 93. Iss. 2. P. 216–231.
Khan F.G., Montrucchio B., Jan B, Khan A.N., Jadoon W., Shamshirband S., Chronopoulos A.T., Khan I.A. An optimized magnetostatic field solver on GPU using open computing language // Concurrency Computat.: Pract. Exper. 2017. V. 29. Iss. 5. e3981.
Электронный ресурс http://www.fftw.org/.
Горкунов Э.С., Задворкин С.М., Путилова Е.А., Саврай Р.А. Влияние структуры и напряженного состояния на магнитные свойства металла в различных зонах сварных труб большого диаметра // ФММ. 2014. Т. 115. № 10. С. 1011–1018.
Горкунов Э.С., Якушенко Е.И., Задворкин С.М., Мушников А.Н. Влияние упругих деформаций на магнитные характеристики хромоникелевых сталей // ФММ. 2015. Т. 116. № 2. С. 156–164.
Бабицкий А.Н., Беляев Б.А., Боев Н.М., Скоморохов Г.В., Изотов А.В., Галеев Р.Г. Магнитометр слабых квазистационарных и высокочастотных полей на резонансных микрополосковых преобразователях с тонкими магнитными пленками // Приборы и техника эксперимента. 2016. № 3. С. 96–104.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал