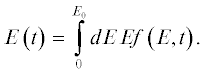Физика металлов и металловедение, 2019, T. 120, № 8, стр. 892-896

Модель развития каскада выбитых атомов в твердом теле

Е. В. Метелкин^a, *, А. Н. Манвелов^a, А. Я. Пономарев^a, В. И. Шмырев^a

^a Российский государственный социальный университет
129226 Москва, ул. Вильгельма Пика, 4, стр. 1, Россия

Поступила в редакцию 20.11.2018
После доработки 20.11.2018
Принята к публикации 21.01.2019

DOI: 10.1134/S001532301906007X

Аннотация

На основе решения кинетического уравнения Больцмана определяется нестационарная функция распределения, описывающая энергетическое распределение каскада движущихся атомов с учетом их размножения. Развитие каскада рассматривается в материалах, состоящих из одинаковых атомов, без учета энергия связи атомов в узлах решетки. Предполагается, что рассеяние движущихся атомов является упругим и сферически симметричным в системе центра инерции, а сечение взаимодействия является величиной, обратно пропорциональной скорости. Использование перечисленных приближений позволяет получить простые аналитические формулы для нестационарной функции распределения каскада замедляющихся атомов и проанализировать ее основные характерные особенности. С другой стороны, на основе полученных результатов можно оценивать точность различных приближенных решений.

Ключевые слова: кинетическое уравнение, столкновения, каскад атомов, замедление атомов, сечение взаимодействия

ВВЕДЕНИЕ

Создание ядерных реакторов и проектирование будущих термоядерных установок тесно связано с проблемой выбора для них радиационно-стойких материалов, поскольку их корпуса и отдельные элементы должны выдерживать продолжительное воздействие радиации. Радиационно-индуцированное охрупчивание материалов ректоров накладывает существенные ограничения на срок их службы.

Облучение твердых тел быстрыми частицами (особенно нейтронами) приводит к тому, что атомы кристаллической решетки, получившие от налетающей частицы энергию, большую некоторой пороговой величины, вылетают из своих равновесных положений. Дальнейший обмен энергией между движущимися атомами и атомами, находящимися в узлах кристаллической решетки, приводит к появлению новых поколений выбитых атомов. В результате возникает так называемый каскад атомных столкновений. В результате развития каскада в твердом теле образуются точечные дефекты – вакансии и междоузельные атомы, определяющие степень повреждения материала [1, 2]. В связи с этим большой интерес представляет исследование энергетического распределения каскада атомных столкновений и его развитие во времени.

Исследованию развития каскадов атомных столкновений в твердом теле посвящено достаточно большое количество работ [3–9]. В работе [3] с помощью построенной модельной индикатрисы рассеяния получено приближенное стационарное энергетическое распределение каскада движущихся атомов для произвольных потенциалов межатомного взаимодействия. В работах [4, 5] проанализирована возможность образования субкаскадов – ряда неперекрывающихся между собой областей в процессе развития каскада атомных столкновений. Оценка пороговой энергии образования субкаскадов проведена в работе [6]. В работе [7] разработана теоретическая модель для исследования образования каскадов и субкаскадов атомных столкновений в облучаемых твердых телах, основанная на использовании линейного кинетического уравнения Больцмана. На основе расширенного толкования понятия первично выбитый атом (ПВА) сформулирован критерий для определения пороговой энергии образования субкаскадов в твердом теле и получены формулы для определения средних размеров и их числа в зависимости от энергии ПВА. На основе результатов, представленных в [7], в работе [8] проведены численные расчеты для конкретных материалов.

Следует отметить, что в работе [7] была найдена функция распределения, описывающая стационарное энергетическое распределение каскада движущихся атомов с учетом их размножения для наиболее простого частного случая упругого, сферически симметричного рассеяния в системе центра масс без учета энергии связи атомов в узлах решетки. В работе [9] на основе решения кинетического уравнения Больцмана рассчитана функция распределения по энергиям, описывающая стационарное энергетическое распределение каскада движущихся атомов при степенном потенциале взаимодействия (U ~ 1/r ⁿ [10]) с учетом энергии связи атомов в узлах решетки.

Кроме этого, на основе представлений, развитых в [7], в работе [11] определены пространственные и временные характеристики первично выбитых релятивистских электронов (ПВЭ), замедляющихся в веществе за счет ионизационных потерь: зависимость энергии ПВЭ от времени, зависимость энергии замедляющегося ПВЭ от пройденного пути и зависимость пути, проходимого ПВЭ, от времени замедления. В работе [12] эти представления были использованы для вычисления стационарного энергетического распределения релятивистских электронов, замедляющихся в веществе за счет ионизационных потерь, с учетом их размножения.

В настоящей работе на основе решения кинетического уравнения Больцмана определяется нестационарная функция распределения, описывающая замедление каскада движущихся атомов, с учетом их размножения. Решение носит модельный характер, поскольку предполагается, что рассеяние движущихся атомов является упругим и сферически симметричным в системе центра инерции, а сечение взаимодействия обратно пропорционально их скорости.

Преимущество использования перечисленных приближений состоит в том, что в этом случае удается найти точное решение кинетического уравнения и получить простые аналитические формулы для нестационарной функции распределения каскада замедляющихся атомов. На основе полученного решения можно проанализировать основные особенности его развития. Кроме того, с помощью полученных результатов можно оценивать точность различных приближенных решений.

ПОСТАНОВКА ЗАДАЧИ

В настоящей работе будем рассматривать твердое тело, состоящее из атомов одного сорта, энергией связи которых в узлах решетки будем пренебрегать. Кинетическое уравнение, описывающее нестационарное энергетическое распределение движущихся атомов от мгновенного равномерно распределенного по пространству моноэнергетического источника, имеет следующий вид [13]:

(1)

$\begin{gathered} \frac{1}{v}\frac{{\partial \Phi \left( {E,t} \right)}}{{\partial t}} + \Sigma \left( E \right)\Phi \left( {E,t} \right) = \\ = \int\limits_E^{{{E}_{0}}} {dE{\kern 1pt} 'P} \quad\left( {E{\kern 1pt} ' \to E} \right)\Sigma \left( {E{\kern 1pt} '} \right)\Phi \left( {E{\kern 1pt} ',t} \right) + \\ + \,\,\int\limits_E^{{{E}_{0}}} {dE{\kern 1pt} 'P} \quad\left( {E{\kern 1pt} ' \to E{\kern 1pt} ' - E} \right)\Sigma \left( {E{\kern 1pt} '} \right)\Phi \left( {E{\kern 1pt} ',t} \right) + \\ + \,\,{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)\delta \left( t \right), \\ \end{gathered} $

где $f(E,t)dE$ – число атомов с энергией E в интервале dE в момент времени t в единице объема; ${\Phi }\left( {E,t} \right) = vf\left( {E,t} \right)$ – поток движущихся атомов; $v$ – их скорость; $P\left( {E{\kern 1pt} {\text{'}} \to E} \right)$ = ${{{\Sigma }\left( {E{\kern 1pt} {\text{'}} \to E} \right)} \mathord{\left/ {\vphantom {{{\Sigma }\left( {E{\kern 1pt} {\text{'}} \to E} \right)} {{\Sigma }\left( {E{\kern 1pt} {\text{'}}} \right)}}} \right. \kern-0em} {{\Sigma }\left( {E{\kern 1pt} {\text{'}}} \right)}}$ – индикатриса рассеяния (вероятность того, что движущийся атом с энергией $E{\kern 1pt} {\text{'}}$ в результате соударения перейдет в единичный интервал энергий вблизи значения E); ${\Sigma }\left( {E{\kern 1pt} {\text{'}} \to E} \right)$ и ${\Sigma }\left( {E{\kern 1pt} {\text{'}}} \right)$ – дифференциальное и полное макроскопические сечения рассеяния атомов; δ(x) – дельта-функция Дирака; E₀ – начальная энергия движущихся атомов; N₀ – их полное число, испущенное в единицу объема.

Первый интеграл, стоящий в правой части кинетического уравнения (1), описывает переход движущегося атома с энергией E ' в состояние с энергией E. При этом выбитый атом получает кинетическую энергию $\left( {E{\kern 1pt} {\text{'}} - E} \right).\quad$ Второй интеграл описывает образование выбитого атома с энергией E, когда движущийся атом перешел в состояние с энергией $\left( {E{\kern 1pt} {\text{'}} - E} \right).$

В случае упругого, сферически симметричного рассеяния в системе центра инерции индикатриса рассеяния имеет следующий вид [13]:

(2)

$P\left( {E{\kern 1pt} {\text{'}} \to E} \right) = {1 \mathord{\left/ {\vphantom {1 {E{\kern 1pt} {\text{'}}}}} \right. \kern-0em} {E{\kern 1pt} {\text{'}}}}.$

С учетом этого обстоятельства уравнение (1) принимает следующий вид:

(3)

$\begin{gathered} \frac{1}{{v\Sigma \left( E \right)}}\frac{{\partial \Psi \left( {E,t} \right)}}{{\partial t}} + \Psi \left( {E,t} \right) = \\ = 2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} '}}{{E{\kern 1pt} {\text{'}}}}} \Psi \left( {E{\kern 1pt} {\text{'}},t} \right) + {{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)\delta \left( t \right), \\ \end{gathered} $

где $\Psi \left( {E,t} \right) = \Sigma \left( E \right)\Phi \left( {E,t} \right)$ – плотность столкновений движущихся атомов.

РЕШЕНИЕ КИНЕТИЧЕСКОГО УРАВНЕНИЯ

Применяя к обеим частям уравнения (3) преобразование Лапласа по времени [14]

(4)

$\tilde {\Psi }\left( {E,p} \right) = \int\limits_0^\infty {\exp } \left( { - pt} \right)\Psi \left( {E,t} \right)dt$

и предполагая, что сечение рассеяния имеет следующий вид:

(5)

$\Sigma \left( E \right) = {{{{\Sigma }_{0}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{0}}} v}} \right. \kern-0em} v},\,\,\,\,\quad{{\Sigma }_{0}} = {\text{const,}}$

получим:

(6)

$\begin{gathered} \left( {\frac{p}{{{{\Sigma }_{0}}}} + 1} \right)\tilde {\Psi }\left( {E,p} \right) = \\ = 2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} {\text{'}}}}{{E{\kern 1pt} {\text{'}}}}\quad} \tilde {\Psi }\left( {E{\kern 1pt} {\text{'}},p} \right) + {{N}_{0}}\delta \left( {E - {{E}_{0}}} \right). \\ \end{gathered} $

Выделим в решении уравнения (6) нерассеянное излучение:

(7)

$\tilde {\Psi }\left( {E,p} \right) = {{\tilde {\Psi }}_{0}}\left( {E,p} \right) + \frac{{{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)}}{{\left( {\frac{p}{{{{\Sigma }_{0}}}} + 1} \right)}}.$

Подставив (7) в (6), получим уравнение для определения функции ${{\tilde {\Psi }}_{0}}\,:$

(8)

$\begin{gathered} \left( {\frac{p}{{{{\Sigma }_{0}}}} + 1} \right){{{\tilde {\Psi }}}_{0}}\left( {E,p} \right) = \\ = 2\int\limits_E^{{{E}_{0}}} {\frac{{dE{\kern 1pt} {\text{'}}}}{{E{\kern 1pt} {\text{'}}}}} {{{\tilde {\Psi }}}_{0}}\left( {E{\kern 1pt} {\text{'}},p} \right) + \quad\quad\frac{{2{{N}_{0}}}}{{{{E}_{0}}\left( {\frac{p}{{{{\Sigma }_{0}}}} + 1} \right)}}. \\ \end{gathered} $

Продифференцировав уравнение (8) по энергии, получим дифференциальное уравнение для функции ${{\tilde {\Psi }}_{0}}\left( {E,p} \right)$

(9)

$\frac{{\partial {{{\tilde {\Psi }}}_{0}}\left( {E,p} \right)}}{{\partial E}} = - \frac{1}{E}\frac{2}{{\left( {1 + \frac{p}{{{{\Sigma }_{0}}}}} \right)}}{{\tilde {\Psi }}_{0}}\left( {E,p} \right),$

решение которого, исходя из (8), должно удовлетворять следующему начальному условию:

(10)

${{\tilde {\Psi }}_{0}}\left( {{{E}_{0}},p} \right) = \frac{{2{{N}_{0}}}}{{{{E}_{0}}{{{\left( {\frac{p}{{{{\Sigma }_{0}}}} + 1} \right)}}^{2}}}}.$

Интегрируя (9) с учетом (10), найдем:

(11)

${{\tilde {\Psi }}_{0}}\left( {E,p} \right) = \frac{{2{{N}_{0}}\Sigma _{0}^{2}}}{{{{E}_{0}}{{{\left( {p + {{\Sigma }_{0}}} \right)}}^{2}}}}{{\left( {\frac{{{{E}_{0}}}}{E}} \right)}^{{\frac{{2{{\Sigma }_{0}}}}{{\left( {p + {{\Sigma }_{0}}} \right)}}}}}.$

Заметим, что при $p = 0$ выражение (11) совпадает с решением соответствующей стационарной задачи, представленным в [7].

Для образа Лапласа функции распределения получим (см (7)):

(12)

$\begin{gathered} \tilde {f}\left( {E,p} \right) = \frac{{\tilde {\Psi }\left( {E,p} \right)}}{{{{\Sigma }_{0}}}} = \\ = \frac{{2{{N}_{0}}{{\Sigma }_{0}}}}{{{{E}_{0}}{{{\left( {p + {{\Sigma }_{0}}} \right)}}^{2}}}}{{\left( {\frac{{{{E}_{0}}}}{E}} \right)}^{{\frac{{2{{\Sigma }_{0}}}}{{\left( {p + {{\Sigma }_{0}}} \right)}}}}} + \frac{{{{N}_{0}}\delta \left( {E - {{E}_{0}}} \right)}}{{\left( {p + {{\Sigma }_{0}}} \right)}}. \\ \end{gathered} $

Применяя к (12) обратное преобразование Лапласа [14], для функции распределения получим следующий окончательный результат:

(13)

$\begin{gathered} f\left( {E,t} \right) = {{N}_{0}}\exp \left( { - \tau } \right)\delta \left( {E - {{E}_{0}}} \right) + \\ + \,\,\frac{{{{N}_{0}}}}{{{{E}_{0}}\ln \left( {\frac{1}{\varepsilon }} \right)}}\exp \left( { - \tau } \right)\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} {{I}_{1}}\left( {2\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} } \right), \\ \end{gathered} $

где ${{I}_{1}}\left( z \right)$ – модифицированная функция Бесселя первого порядка [15]; $\tau = {{{\Sigma }}_{0}}t$ – безразмерное время; $\varepsilon = \left( {{E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}}} \right)$ – безразмерная энергия.

АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Проанализируем полученный результат (13). Рассмотрим сначала законы сохранения числа частиц и энергии в каскаде движущихся атомов.

Найдем изменение со временем полного числа атомов в каскаде:

(14)

$N\left( t \right) = \int\limits_0^{{{E}_{0}}} {dEf} \left( {E,t} \right).$

Для этого найдем его образ Лапласа:

(15)

$\tilde {N}\left( p \right) = \int\limits_0^{{{E}_{0}}} {dE\tilde {f}} \left( {E,p} \right).$

Подставив (12) в (15), получим:

(16)

$\tilde {N}\left( p \right) = \frac{{{{N}_{0}}}}{{\left( {p - {{\Sigma }_{0}}} \right)}}.$

Используя обратное преобразование Лапласа [14] получим:

(17)

$N\left( t \right) = {{N}_{0}}\exp \left( {{{\Sigma }_{0}}t} \right).$

Из (17), как и следовало ожидать, вытекает, что число движущихся атомов в каскаде со временем нарастает. Причем в данном случае этот рост не ограничен, так как мы не учитываем энергию связи покоящихся атомов.

Теперь найдем изменение со временем полной энергии частиц в каскаде:

(18)

Поступая аналогичным образом, получим:

(19)

$E\left( t \right) = {{N}_{0}}{{E}_{0}} = {\text{const}}{\text{.}}$

Из (19) вытекает, что несмотря на рост числа движущихся атомов, их полная энергия сохраняется. Это объясняется тем, что мы не учитываем энергию связи покоящихся атомов.

Поэтому энергия, с которой начал двигаться после соударения покоящийся атом, целиком равна энергии, переданной ему движущимся атомом.

Проанализируем подробнее функцию распределения (13) и ее особенности, связанные с увеличением числа атомов в каскаде. При малых значениях аргумента

(20)

$\tau \ll \frac{1}{{8{\text{ln}}\left( {\frac{1}{\varepsilon }} \right)}}$

функция Бесселя принимает вид [15]:

${{I}_{1}}\left( z \right) \simeq \frac{z}{2}\,\,\,\,{\text{и л и }}$

(21)

${{I}_{1}}(2\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} \simeq \sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} .$

В этом случае функция распределения (13) при E < E₀ будет равна

(22)

$f\left( {E,t} \right) = \frac{{2{{N}_{0}}}}{{{{E}_{0}}}}\tau \exp \left( { - \tau } \right).$

При τ = 1 она достигает максимума, равного

(23)

${{f}_{{\max }}} = \frac{{2{{N}_{0}}}}{{e{{E}_{0}}}}.$

Это значение не зависит от энергии, поскольку приближение (22) справедливо при энергиях, близких к энергии источника (см. (20)).

При больших значениях аргумента

(24)

$\tau \gg \frac{1}{{8\ln \left( {\frac{1}{\varepsilon }} \right)}}.$

функция Бесселя принимает вид [15]:

${{I}_{1}}\left( z \right) \simeq \frac{{\exp \left( z \right)}}{{\sqrt {2\pi z} }}\,\,\,\,{\text{и л и }}$

(25)

${{I}_{1}}\left( {2\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} } \right) \simeq \frac{{\exp \left( {2\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} } \right)}}{{2\sqrt \pi {{{\left( {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}.$

Функция распределения (13) при E < E₀ в этом случае будет равна

(26)

$\begin{gathered} f\left( {E,t} \right) = \frac{{{{N}_{0}}}}{{2\sqrt \pi {{E}_{0}}\ln \left( {\frac{1}{\varepsilon }} \right)}}{{\left( {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}} \times \\ \times \,\,\exp \left( { - \tau + 2\sqrt {2\tau \ln \left( {\frac{1}{\varepsilon }} \right)} } \right). \\ \end{gathered} $

Рассмотрим изменение этой функции при фиксированной энергии. Из (26) следует, что со временем она нарастает, достигая максимума при

${{\tau }_{m}} \simeq 2\ln \left( {\frac{1}{\varepsilon }} \right) = 2\ln \left( {\frac{{{{E}_{0}}}}{E}} \right)$

и затем убывает. Из (27) вытекает, что с уменьшением энергии максимум смещается в сторону больших времен, поскольку, чем меньше энергия, тем позже достигнут ее атомы при замедлении. Значение функции в максимуме будет равно

(28)

$\begin{gathered} f\left( {E,{{\tau }_{m}}} \right) = \frac{{{{N}_{0}}}}{{\sqrt {2\pi } {{E}_{0}}}}\frac{1}{{{{\varepsilon }^{2}}\sqrt {\ln \left( {\frac{1}{\varepsilon }} \right)} }} = \\ = \frac{{{{N}_{0}}}}{{\sqrt {2\pi } {{E}_{0}}}}\frac{1}{{\sqrt {\ln \left( {\frac{{{{E}_{0}}}}{E}} \right)} }}{{\left( {\frac{{{{E}_{0}}}}{E}} \right)}^{2}}. \\ \end{gathered} $

Видно, что с уменьшением энергии значение функции в максимуме быстро нарастает, за счет увеличения со временем числа атомов в каскаде.

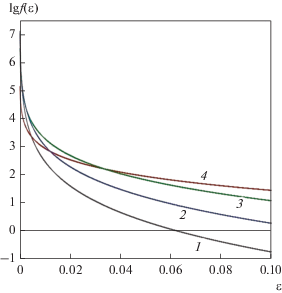
На рис. 1 представлены изменения функции распределения ($f{\text{'}} = {{f{{E}_{0}}} \mathord{\left/ {\vphantom {{f{{E}_{0}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$) со временем при различных значения энергии, построенные в результате расчетов по формуле (26). Видно, что выводы, сделанные выше о характере изменения функции распределения, целиком согласуются с результатами расчетов, при этом формулы (27) и (28) с хорошей точностью описывают соответствующие величин.

Рис. 1.

Зависимость функции распределения от времени τ при различных значениях энергии ε (1 – 0.1; 2 – 0.01; 3 – 0.001; 4 – 0.0001).

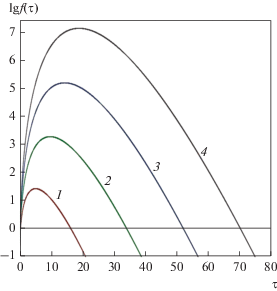
Теперь проанализируем изменение функции (26) с энергией в различные фиксированные моменты времени. Результаты соответствующих расчетов представлены на рис. 2. Видно, что с увеличением времени атомы за счет замедления переходят в области более низких энергий. Следует отметить, что площадь под каждой из кривых на рис. 2 будет при увеличении времени возрастать согласно выражению (16), что обусловлено увеличением со временем числа движущихся атомов в каскаде.

Рис. 2.

Зависимость функции распределения от энергии ε в различные моменты времени τ (1 – 20; 2 – 15; 3 – 10; 4 – 5).

ЗАКЛЮЧЕНИЕ

В работе исследовано развитие каскада атомных столкновений в твердом теле. Предполагали, что твердое тело состоит из одинаковых атомов, энергия связи которых не учитывали, рассеяние движущихся атомов является упругим и сферически симметричным в системе центра инерции, а сечение взаимодействия является величиной, обратно пропорциональной скорости (см. (5)). Сделанные предположения позволили получить строгое решение кинетического уравнения Больцмана, описывающее нестационарное энергетическое распределение каскада замедляющихся атомов с учетом их размножения (см. (13)).

На основе полученного решения были проанализированы особенности, присущие функции распределения, обусловленные ростом числа атомов в каскаде, имеющие общий характер. Кроме того, с помощью полученных результатов можно оценивать точность различных приближенных решений.

Список литературы

Лейман К. Взаимодействие излучения с твердым телом и образование элементарных дефектов. М.: Атомиздат, 1979. 297 с.
Вас Гэри С. Основы радиационного материаловедения. Металлы и сплавы М.: ТЕХНОСФЕРА, 2014. 992 с.
Ryazanov A.I., Metelkin E.V. Concerning the theory of radiation cascades of atomic collisions in a solid with an arbitrary interatomic interaction potential // Radiation Effects and Defects in Solids, 1980. V. 52. № 1–2. P. 15–23.
Sato Y., Kojimo S., Yoshiie T., Kiritani M. Criterion of subcascade formation in metals from atomic collision calculation // J. Nucl. Mater. 1991. № 179–181. P. 901–904.
Sato Y., Yoshiie T., Kiritani M. Binary collision calculation of subcascade structure and its correspondence to observe subcascade defects in 14 MeV neutron irradiated copper // J. Nuclear Mater. 1992. № 191–194. P. 1101–1104.
Метелкин Е.В., Рязанов А.И. Пороговая энергия образования субкаскадов // Атомная энергия. 1997. Т. 83. В. 3. С. 183–189.
Метелкин Е.В., Рязанов А.И., Семенов Е.В. Разработка новых теоретических моделей для исследования образования каскадов и субкаскадов атомных столкновений в облучаемых твердых телах // ЖЭТФ. 2008. Т. 134. Bып. 3(9). С. 469–480.
Ryazanov A.I., Metelkin E.V., Semenov E.V. Modeling of cascade and sub-cascade formation at high PKA energies in irradiated fusion structural materials // J. Nucl. Mater. 2009. № 386–388. P. 132–134.
Александров А.А., Акатьев В.А., Метелкин Е.В., Барышева Е.Ю. Разработка модели исследования энергетического распределения каскадов атомных столкновений // Вестник МГТУ им. Н.Э. Баумана, серия “Естественные науки”. 2018. (в печати)
Lindhard J., Vibeke Nielsen, Scharff M. Approximation Method in Classical Scattering by Screened Coulomb Fields // Det Kongelige Danske Videnskabernes Selskab Matematisk-fysiske Meddelelser. 1968. V. 36. № 10. P. 1–32.
Акатьев В.А., Метелкин Е.В., Савинов А.М. Пространственно-временные характеристики релятивистских электронов, замедляющихся в веществе // Атомная энергия. 2017. Т. 122. Bып. 5. С. 295–298.
Метелкин Е.В., Лебедева М.В., Черняев А.В. Энергетическое распределение релятивистских электронов, замедляющихся в веществе // Атомная энергия. 2018. Т. 125. Bып. 3. С. 184–186.
Исаков А.И., Казарновский М.В., Медведев Ю.А., Метелкин Е.В. Нестационарное замедление нейтронов. Основные закономерности и некоторые приложения. М.: Наука, 1984, 264 с.
Бейтман Г., Эрдейи А. Таблицы интегральных преобразований. Т. 1. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969, 343 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971, 1108 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал