Физика металлов и металловедение, 2020, T. 121, № 11, стр. 1162-1186
Моделирование эволюции микроструктуры металлических материалов в процессе горячей пластической деформации и термической обработки
А. Ю. Чурюмов a, *, А. В. Поздняков a
a Национальный исследовательский технологический университет “МИСиС”
119991 Москва, Ленинский пр., 4, Россия
* E-mail: churyumov@misis.ru
Поступила в редакцию 01.04.2020
После доработки 04.07.2020
Принята к публикации 14.07.2020
Аннотация
Развитие современных вычислительных методов и техники позволяют производить высокоточные расчеты сложных промышленных процессов, в том числе и в металлургической промышленности. В обзорной работе проведена систематизация основных физико-математических моделей формирования структуры при термической и деформационной обработке. Проведен анализ модели Кокса–Мекинга–Эстрина, описывающей дислокационную структуру на начальном этапе горячей пластической деформации, рассмотрены модели кинетики динамической, метадинамической и статической рекристаллизации на основе уравнения Джонсона–Мела–Аврами–Колмогорова. Дан обзор моделей кинетики фазовых превращений при нагреве и охлаждении стали, а также рассмотрена модель Кампмана–Вагнера, описывающая распад пересыщенного твердого раствора при старении алюминиевых сплавов. Рассмотрены основные численные методы расчета эволюции микроструктуры, такие как метод “клеточных автоматов”, Монте-Карло и многофазного поля. Показана их высокая точность при расчете процессов рекристаллизации и фазовых превращений. Систематизация существующих моделей эволюции структуры показала возможность создания комплексных моделей, позволяющих реализовать сквозной расчет полного цикла термической и деформационной обработки металлических материалов, и их применения для оптимизации и разработки новых технологий.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ СТРУКТУРЫ ПРИ ГОРЯЧЕЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
1.1. Динамический наклеп и возврат
1.2. Динамическая рекристаллизация
1.3. Метадинамическая рекристаллизация
1.4. Статическая рекристаллизация
1.5. Рост зерен в процессе отжига
2. МОДЕЛИРОВАНИЕ КИНЕТИКИ ФАЗОВЫХ ПРЕВРАЩЕНИЙ В СТАЛЯХ
2.1. Образование аустенита при нагреве
2.2. Процессы превращения аустенита при охлаждении
3. МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ СТРУКТУРЫ ПРИ РАСПАДЕ ПЕРЕСЫЩЕННОГО ТВЕРДОГО РАСТВОРА
4. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА ЭВОЛЮЦИИ СТРУКТУРЫ
4.1. Метод “клеточных автоматов”
4.2. Метод Монте-Карло
4.3. Метод многофазного поля
ЗАКЛЮЧЕНИЕ
ВВЕДЕНИЕ
В настоящее время современные вычислительные методы и техника позволяют производить высокоточные расчеты сложных промышленных процессов, в том числе и в металлургической промышленности. Основным требованием к качеству продуктов металлургической промышленности является формирование необходимой микроструктуры и определяемого ею уровня свойств. Микроструктура металлических материалов формируется в основном конечными этапами металлургического передела, а именно деформационной и термической обработкой. В связи с этим высокую актуальность приобретает создание систематизированной базы данных по физико-математическим моделям формирования микроструктуры при пластической деформации и термической обработке.
К настоящему времени для моделирования эволюции структуры в процессе горячей пластической деформации наибольшее распространение получили модели связи характеристик микроструктуры (объемная доля и размер рекристализованных зерен) с параметрами деформации, основанные на уравнениях типа Аврами–Колмогорова. Они показывают высокую предсказательную способность, хотя и требуют большого количества экспериментальных данных для определения неизвестных констант. Изначально математические уравнения связи характеристик микроструктуры с параметрами термодеформационного воздействия были применены для жаропрочных сплавов типа Waspalloy [1] и Inconel [2] и впоследствии были распространены на широкий круг металлических материалов. Однако модели, основанные на уравнениях такого типа, могут прогнозировать параметры микроструктуры только у сплавов, деформация которых проходит в однофазной области. Для сплавов, в которых в интервале горячей пластической деформации происходят фазовые превращения, требуется дополнение уравнений типа Аврами–Колмогорова уравнениями, описывающими фазовые превращения. Определение констант в этих уравнениях для конкретных материалов требует дополнительных дилатометрических и микроструктурных исследований, а также сложных расчетов [3–6], однако существенно расширяет возможности прогнозирования структуры материалов после многоэтапной деформационной и термической обработки. Такие модели построены для низкоуглеродистых [7, 8] и заэвтектоидных хромсодержащих сталей [9]. Кроме этого, особого внимания заслуживает математическое описание процессов распада пересыщенного твердого раствора с образованием метастабильных модификаций упрочняющих фаз (продуктов старения в алюминиевых сплавах, карбидных и карбонитридных фаз в сталях [10, 11] и др.), так как они существенным образом влияют на конечные свойства изделий.
Альтернативными способами моделирования структурообразования являются численные методы расчета структуры, такие как метод “клеточных автоматов”. Этот метод заключается в разбиении исследуемого участка структуры на отдельные элементы (ячейки), состояние которых определяется не только внешними факторами (температура, скорость деформации, степень накопленной деформации), но и состоянием соседних ячеек. В результате расчета создается полная картина эволюции структурных характеристик в моделируемом участке материала в течение всего процесса деформации и термической обработки. Несмотря на большой объем структурных исследований, необходимый для точного расчета, этот метод является перспективным для моделирования структуры в современном материаловедении, о чем свидетельствует большое количество посвященных ему публикаций. Метод “клеточных автоматов” был применен для моделирования эволюции структуры стали AISI 304L [12], для описания динамической рекристаллизации стали 42CrMo [13], для описания фазовых превращений при нагреве двухфазных сталей и моделирования других процессов структурообразования в процессе деформации и термической обработки.
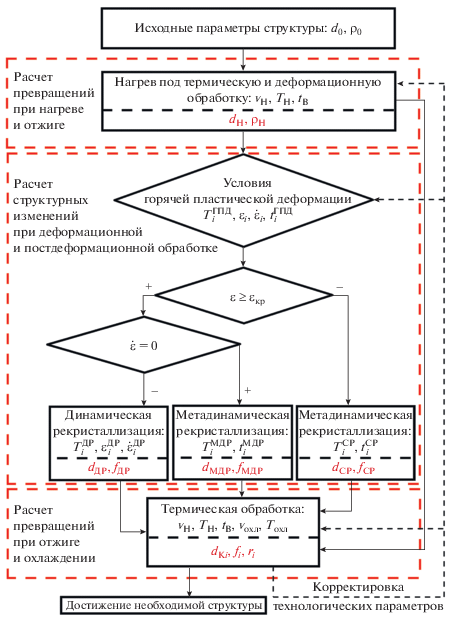
Таким образом, целью настоящей обзорной статьи является систематизация современных физико-математических моделей и численных методов моделирования эволюции структуры, позволяющая создать теоретический базис для разработки интеллектуальных производственных технологий пластической деформации и термической обработки металлических материалов. Упрощенный алгоритм расчета и управления параметрами микроструктуры металлических материалов в процессе термической и деформационной обработки представлен на рис. 1. Возможность алгоритмизации физико-математических и численных моделей позволяет использовать их совместно с методами конечноэлементного моделирования, что позволяет существенно сократить временные и материальные затраты на оптимизацию существующих и разработку новых производственных технологий.
1. МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ СТРУКТУРЫ ПРИ ГОРЯЧЕЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
1.1. Динамический наклеп и возврат
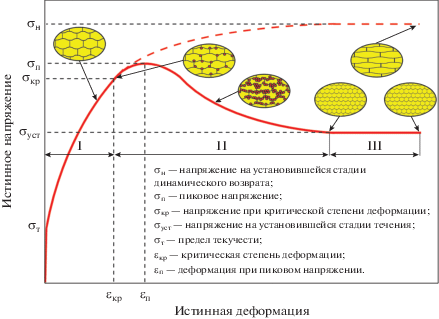
Первые существенные структурные изменения при пластической деформации как при комнатной, так и при повышенных температурах связаны с процессами динамического наклепа и динамического возврата (стадия I на рис. 2). Эта стадия хорошо описывается моделями, предложенными Коксом, Мекингом, Эстриным [14–16] и Несом [17–19]. Согласно этим моделям, эволюция дислокационной структуры описывается следующим законом:
(1)
$\frac{{d\rho }}{{d\varepsilon }} = \frac{{d{{\rho }^{ + }}}}{{d\varepsilon }} + \frac{{d{{\rho }^{ - }}}}{{d\varepsilon }},$Рис. 2.
Схема структурных изменений и зависимость напряжение–деформация при горячей пластической деформации металлических материалов [21]. I – Динамический возврат, II – динамическая рекристаллизация, III – стадия установившегося течения.
Первое слагаемое в уравнении (1) представляет собой атермическое накопление дислокаций, которое для однофазных крупнозернистых материалов можно определить по уравнению [16]:
(2)
$\frac{{d{{\rho }^{ + }}}}{{d\varepsilon }} = \frac{2}{{{{b}_{{\text{B}}}}L}} = {{k}_{1}}\sqrt \rho ,$а для многофазных материалов и сплавов с микрозеренной структурой:
где bB – вектор Бюргерса, м; L – среднее расстояние, которое проходит дислокация до полной остановки, м, ${{k}_{1}}~$ и k – константы, определяющие деформационное упрочнение. Значение констант зависит от природы и концентрации легирующих элементов в твердом растворе, объемной доли фаз и др. и определяется на основе экспериментальных данных. Второе слагаемое описывает динамический возврат. Скорость возврата обычно определяется уравнением реакции первого порядка (вопрос о том, почему она пропорциональна первой степени плотности дислокаций леса, является предметом дискуссий [20], однако такая зависимость согласуется с экспериментальными данными): где ${{k}_{2}}$ – константа, зависящая от многих факторов (температуры, концентрации легирующих элементов, энергии активации диффузии, энергии дефекта упаковки и др.). Значение коэффициента ${{k}_{2}}$ рассчитать достаточно сложно и оно для конкретных сплавов определяется на основе экспериментальных данных. Авторами [21] было показано, что для Армко-железа значение константы ${{k}_{2}}$ изменяется в пределах 5.8–42.5 в зависимости от температуры и скорости деформации. Степенная зависимость этой константы от параметра Зинера–Холломона Z = $\dot {\varepsilon }{\text{exp}}\left( {\frac{{602100}}{{RT}}} \right)$ была также выявлена для титанового сплава TA15 [22]:${\mathbf{\dot {\varepsilon }}}$ – скорость деформации, с–1, T – температура, K, R – универсальная газовая постоянная.
Эволюция дислокационной структуры в процессе динамического возврата при деформации при повышенных температурах в большинстве случаев приводит к формированию субзеренной микроструктуры. На стадии насыщения в случае подавления динамической рекристаллизации за счет быстрого протекания процессов динамического возврата средний размер субзерен, угол их разориентировки и средняя плотность дислокаций внутри субзерен остаются постоянными. Таким образом, по значению плотности дислокаций, рассчитанному по уравнению (1), и при условии, что плотность дислокаций внутри субзерен значительно меньше средней плотности дислокаций, можно определить средний размер субзерен (dS):
где ${\varphi }$ – угол разориентировки между субзернами. Угол разориентивки между субзернами ${\varphi }$ на стадии насыщения обычно составляет 1.5°–2°.На практике определение значений неизвестных коэффициентов ${{k}_{1}}$ и ${{k}_{2}}$ не требует проведения глубоких структурных исследований. Их значение и зависимости от скорости и температуры можно определить по начальному участку кривой деформации, зная соотношение между напряжением течения и плотностью дислокаций [23]:
где ${{{\sigma }}_{0}}$ – напряжение течения, не связанное сопротивлением вновь сгенерированных дислокаций (примерно соответствует пределу текучести), ${\alpha }$ – постоянный коэффициент (${\alpha } \approx 1$), $G$ – модуль сдвига, МПа. Таким образом, можно с достаточной точностью определить параметры субструктуры материалов по начальной стадии кривой деформации до достижения критической степени деформации.1.2. Динамическая рекристаллизация
После достижения критической степени деформации к разупрочнению за счет динамического возврата добавляется процесс зарождения новых зерен с совершенной структурой, которые также в процессе деформации подвергаются наклепу, что может приводить к формированию новых зерен внутри них. Этот процесс получил название динамическая рекристаллизация.
Известно, что кинетика фазовых и структурных превращений хорошо описывается моделью Джонсона–Мела–Аврами–Колмогорова (JMAK) [24–26]:
где X – доля превращенного вещества, $t$ – время, с, ${\beta }$ и $n$ – константы.Уравнение (8) в случае динамической рекристаллизации можно привести к следующему виду:
(9)
${{X}_{{{\text{DRX}}}}} = 1 - {\text{exp}}\left[ { - \beta {{{\left( {{{\left( {\varepsilon - {{\varepsilon }_{{{\text{кр}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - {{\varepsilon }_{{{\text{кр}}}}}} \right)} {({{\varepsilon }_{{0.5}}} - {{\varepsilon }_{{{\text{кр}}}}})}}} \right. \kern-0em} {({{\varepsilon }_{{0.5}}} - {{\varepsilon }_{{{\text{кр}}}}})}}} \right)}}^{{{{k}_{{\text{d}}}}}}}} \right],$(10)
${{\varepsilon }_{{{\text{кр}}}}} = {{a}_{1}}d_{0}^{{{{n}_{1}}}}{{\dot {\varepsilon }}^{{{{m}_{1}}}}}{\text{exp}}\left[ {\frac{{{{Q}_{1}}}}{{RT}}} \right],$${{{\varepsilon }}_{{0.5}}}$ – степень деформации, при которой в структуре формируется 50% рекристаллизованных зерен. Эта величина обычно определяется по степени разупрочнения при динамической рекристаллизации и примерно соответствует значению напряжения течения:
где ${{{\sigma }}_{{\text{п}}}}$ – пиковое значение напряжения течения, МПа, ${{{\sigma }}_{{{\text{уст}}}}}$ – напряжение на установившейся стадии течения, МПа.Эмпирически показано, что величина ${{{\varepsilon }}_{{0.5}}}$ также зависит от исходного размера зерна и параметра Зинера–Холломона:
(12)
${{\varepsilon }_{{0.5}}} = {{a}_{2}}d_{0}^{{{{n}_{2}}}}{{\dot {\varepsilon }}^{{{{m}_{2}}}}}{\text{exp}}\left[ {\frac{{{{Q}_{2}}}}{{RT}}} \right],$Размер динамически рекристаллизованных зерен на стадии установившегося течения практически не зависит от степени деформации и определяется только исходным размером зерна, скоростью и температурой деформации:
(13)
${{d}_{{{\text{DRX}}}}} = {{a}_{3}}d_{0}^{{{{n}_{3}}}}{{\dot {\varepsilon }}^{{{{m}_{3}}}}}\exp \left( {\frac{{{{Q}_{3}}}}{{RT}}} \right),$Таблица 1.
Математические модели эволюции структуры в процессе динамической рекристаллизации
| Материал | Объемная доля динамически рекристаллизованных зерен | Размер динамически рекристаллизованного зерна dDRX, мкм | Источник |
|---|---|---|---|
| ЭП666 | kd = 1.76, ${{\varepsilon }_{{{\text{кр}}}}} = 0.014{{\dot {\varepsilon }}^{{0.06}}}\exp \left[ {\frac{{28\,930}}{{RT}}} \right]$, ${{\varepsilon }_{{0.5}}} = 0.053{{\dot {\varepsilon }}^{{0.05}}}\exp \left[ {\frac{{27\,200}}{{RT}}} \right]$ |
$8826{{\dot {\varepsilon }}^{{ - 0.01}}}\exp \left( {\frac{{69\,800}}{{RT}}} \right)$ | [39] |
| AISI 316 | ${{k}_{{\text{d}}}} = 0.029{{\dot {\varepsilon }}^{{ - 0.04}}}\exp \left[ { - \frac{{16\,550}}{{RT}}} \right],{\text{\;}}$ ${{\varepsilon }_{{{\text{кр}}}}} = 1.97{{\dot {\varepsilon }}^{{0.06}}}\exp \left[ {\frac{{23\,590}}{{RT}}} \right]$ ${{\varepsilon }_{{0.5}}} = 71{{\dot {\varepsilon }}^{{0.124}}}\exp \left[ {\frac{{51\,300}}{{RT}}} \right]$ |
$0.3{{\dot {\varepsilon }}^{{ - 0.123}}}\exp \left( {\frac{{50\,900}}{{RT}}} \right)$ | [40] |
| AISI 310S | kd = 1.78, ${{\varepsilon }_{{{\text{кр}}}}} = 0.0175{{\dot {\varepsilon }}^{{0.063}}}\exp \left[ {\frac{{33\,390}}{{RT}}} \right]$, ${{\varepsilon }_{{0.5}}} = 0.05{{\dot {\varepsilon }}^{{0.056}}}\exp \left[ {\frac{{28\,900}}{{RT}}} \right]$ |
$3062{{\dot {\varepsilon }}^{{ - 0.067}}}\exp \left( {\frac{{60\,970}}{{RT}}} \right)$ | [41] |
| 15Х2НМФА | ${{k}_{{\text{d}}}} = 3.42,$${{\varepsilon }_{{{\text{кр}}}}} = 0.022d_{0}^{{0.029}}{{\dot {\varepsilon }}^{{0.13}}}\exp \left[ {\frac{{26900}}{{RT}}} \right],$ ${{\varepsilon }_{{0.5}}} = 0.022d_{0}^{{0.076}}{{\dot {\varepsilon }}^{{0.1}}}\exp \left[ {\frac{{32600}}{{RT}}} \right]$ |
$314\,302d_{0}^{{ - 0.01}}{{\dot {\varepsilon }}^{{ - 0.1}}}\exp \left( {\frac{{111\,400}}{{RT}}} \right)$ | [42] |
| 30ХН3М2ФА | ${{k}_{{\text{d}}}} = 3.74,$${{\varepsilon }_{{{\text{кр}}}}} = 0.076d_{0}^{{0.019}}{{\dot {\varepsilon }}^{{0.048}}}\exp \left[ {\frac{{10\,900}}{{RT}}} \right],$ ${{\varepsilon }_{{0.5}}} = 0.19{{\dot {\varepsilon }}^{{0.44}}}\exp \left[ {\frac{{7900}}{{RT}}} \right]$ |
$63\,900d_{0}^{{ - 0.01}}{{\dot {\varepsilon }}^{{ - 0.09}}}\exp \left( {\frac{{96\,000}}{{RT}}} \right)$ | [42] |
Существуют также частные модели определения размера зерна для разных типов динамической рекристаллизации: непрерывной, прерывистой и геометрической. Так для геометрической динамической рекристаллизации (термин предложен МакКвином с соавт. в [27, 28]) размер динамически рекристаллизованного зерна описывается моделью Т. Петтерсен с соавт. [29]. Согласно модели, изменение размера зерна в процессе деформации описывается следующим дифференциальным уравнением:
(14)
$\frac{{d{{d}_{{{\text{DRX}}}}}}}{{d\varepsilon }} = \frac{{dd_{{{\text{DRX}}}}^{ + }}}{{d\varepsilon }} + \frac{{dd_{{{\text{DRX}}}}^{ - }}}{{d\varepsilon }},$(15)
$\frac{{dd_{{{\text{DRX}}}}^{ + }}}{{d\varepsilon }} = \frac{{{{K}_{{\text{G}}}}}}{{Z{{d}_{{{\text{DRX}}}}}}},$(16)
$\frac{{dd_{{{\text{DRX}}}}^{ - }}}{{d\varepsilon }} = \left[ {1 - \left( {\frac{1}{4}\varepsilon + 1} \right){{e}^{{ - 2{\varepsilon }}}}} \right]nA{{d}_{{{\text{DRX}}}}}{{\left( {\frac{{{{d}_{{{\text{DRX}}}}}}}{d}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}},$Кроме того, на кинетику динамической рекристаллизации и рост зерна оказывают существенное влияние наноразмерные частицы вторых фаз [30], приводя к уменьшению коэффициента ${\beta }$ в уравнении (8) согласно зависимости:
где ${{P}_{{\text{d}}}}$ – движущая сила роста зерен при рекристаллизации в матричной фазе, не содержащей частицы, Pz – сила сопротивления частиц движению границ зерен.(18)
${{P}_{{\text{d}}}} = \frac{{Gb_{{\text{B}}}^{2}}}{2}\left( {{{\rho }_{{{\text{def}}}}} - {{\rho }_{0}}} \right) + \frac{{4\gamma }}{{{{d}_{{{\text{DRX}}}}}}},$где ${{{\rho }}_{{{\text{def}}}}},$ ${{{\rho }}_{0}}$ – плотность дислокаций в деформированных и рекристаллизованных зернах, ${\gamma }$ – удельная энергия границ зерен,$~r$ и f – радиус и объемная доля частиц второй фазы соответственно.
Разработаны также модели формирования зеренной структуры в материалах, содержащих частицы второй фазы микронного размера. Наиболее общий подход заключается в применении модели Зинера–Смита [31], получившей развитие в работах Гладмана [32], Нишизавы [33] и др. Общий вид уравнения связи размера зерна с параметрами частиц вторых фаз имеет вид:
где A, n – константы материала. Эта модель показала хорошие результаты при расчете размеров зерен микролегированной стали [34] и двухфазных алюминиевых сплавов [35].Одна из сложностей расчета процесса динамической рекристаллизации заключается в определении критической степени деформации. Основываясь на термодинамике необратимых процессов, Поляк и Джонас определили, что момент начала образования зародышей соответствует точке перегиба на зависимости коэффициента деформационного упрочнения (∂σ/∂ε) от напряжения течения (σ) [36]. Другой метод определения момента начала динамической рекристаллизации, основанный на определении критического градиента плотности дислокаций, предлагают Имран и Бамбах [37].
Этот метод позволяет учесть неравномерность распределения дислокаций при деформации вблизи границ и в теле зерен. Эволюция дислокационной структуры отдельно описывается для подвижных и закрепленных дислокаций. Зарождение новых зерен начинается только при достижении критического значения градиента плотности дислокаций. Однако, в практическом применении чаще всего используют эмпирическую зависимость критической степени деформации от значения пиковой деформации [38]: ${{\varepsilon }_{{{\text{кр}}}}} = {5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-0em} 6}{{\varepsilon }_{{\text{п}}}}.$
1.3. Метадинамическая рекристаллизация
Процесс метадинамической рекристаллизации (МДР) начинается после остановки процесса деформации при достижении критической степени ${{\varepsilon }_{{{\text{кр}}}}}.$ Фактически процесс МДР заключается в росте зерен (зародышей), появившихся в результате динамической рекристаллизации. Поэтому этот процесс происходит без инкубационного периода, характерного для статической рекристаллизации деформированного металла.
Кинетика метадинамической рекристаллизации может быть также описана моделью JMAK [43–45]:
(21)
${{X}_{{{\text{MRX}}}}} = 1 - {\text{exp}}\left[ { - \beta {{{\left( {{{\left( t \right)} \mathord{\left/ {\vphantom {{\left( t \right)} {({{t}_{{0.5}}})}}} \right. \kern-0em} {({{t}_{{0.5}}})}}} \right)}}^{{{{k}_{{\text{m}}}}}}}} \right],$(22)
${{t}_{{0.5}}} = {{a}_{4}}d_{0}^{{{{n}_{4}}}}{{\dot {\varepsilon }}^{{{{m}_{4}}}}}{\text{exp}}\left[ {\frac{{{{Q}_{4}}}}{{RT}}} \right],$(23)
${{d}_{{{\text{MRX}}}}} = {{a}_{5}}d_{0}^{{{{n}_{5}}}}{{\dot {\varepsilon }}^{{{{m}_{5}}}}}\exp \left( {\frac{{{{Q}_{5}}}}{{RT}}} \right),$(24)
$d_{{{\text{MRX}}}}^{t} = d_{{{\text{MRX}}}}^{0} + \left( {{{d}_{{{\text{MRX}}}}} - d_{{{\text{MRX}}}}^{0}} \right)(1 - \exp \left( { - {{k}_{{{\text{MRX}}}}}t)} \right),$Рис. 3.
Зависимость размера зерна от времени метадинамической рекристаллизации стали 300 М после деформации со скоростью 0.01 с–1 при температуре 1000°С [44].
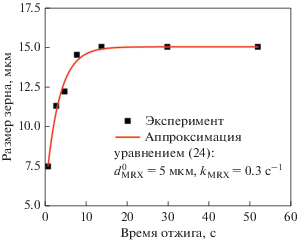
Однако в большинстве случаев практического применения модель (23) дает удовлетворительные результаты. Значения констант, определяющих поведение некоторых материалов при МДР представлены в табл. 2.
Таблица 2.
Математические модели кинетики и изменения размера зерна в процессе МДР
| Материал | Объемная доля метадинамически рекристаллизованных зерен | Размер метадинамически рекристаллизованного зерна dMRX, мкм | Источник |
|---|---|---|---|
| Сталь SA508-III | km = 0.508, ${{t}_{{0.5}}} = 9.8 \times {{10}^{{ - 5}}}{{\dot {\varepsilon }}^{{ - 0.335}}}\exp \left[ {\frac{{116\,210}}{{RT}}} \right]$ | $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} 472.8{{{\dot {\varepsilon }}}^{{ - 0.205}}}\exp \left( {\frac{{ - 23\,800}}{{R \cdot T}}} \right),~ \hfill \\ {\text{если}}\,\,~{{d}_{0}} \geqslant 120~\,\,{\text{мкм}}~ \hfill \\ \end{gathered} \\ \begin{gathered} 12.5{{{\dot {\varepsilon }}}^{{ - 0.23}}}d_{0}^{{0.758}}\exp \left( {\frac{{ - 23\,800}}{{RT}}} \right),~ \hfill \\ {\text{если}}~\,\,{{d}_{0}} < 120~\,\,{\text{мкм}}~ \hfill \\ \end{gathered} \end{array}} \right.$ | [47] |
| Сталь Fe–C–Mn | km = 1.5, ${{t}_{{0.5}}} = 1.1{{\dot {\varepsilon }}^{{ - 0.8}}}\exp \left[ { - \frac{{10\,000}}{{RT}}} \right]$ | $26\,000{{\dot {\varepsilon }}^{{ - 0.23}}}\exp \left( {\frac{{ - 69\,000}}{{RT}}} \right)$ | [43, 48] |
| Сталь 300M | km = 1.21, ${{t}_{{0.5}}} = 0.049{{\dot {\varepsilon }}^{{0.039}}}\exp \left[ { - \frac{{49\,770}}{{RT}}} \right]$ | $62.36{{\dot {\varepsilon }}^{{0.076}}}\exp \left( {\frac{{ - 11\,535}}{{RT}}} \right)$ | [45] |
| Сталь 316 | km = 0.237, ${{t}_{{0.5}}} = 2.14 \times {{10}^{{ - 9}}}{{d}_{0}}{{\dot {\varepsilon }}^{{ - 0.85}}}\exp \left[ {\frac{{155\,000}}{{RT}}} \right]$ | $1.57d_{0}^{{0.99}}{{\dot {\varepsilon }}^{{ - 0.033}}}\exp \left( {\frac{{ - 5115}}{{RT}}} \right)$ | [40] |
| Сталь 30Cr2Ni4MoV | km = 0.31, ${{t}_{{0.5}}} = 1.27 \times {{10}^{{ - 9}}}{{\dot {\varepsilon }}^{{ - 0.44}}}\exp \left[ {\frac{{217\,800}}{{RT}}} \right]$ | $\left\{ {\begin{array}{*{20}{c}} \begin{gathered} 4059{{{\dot {\varepsilon }}}^{{ - 0.22}}}\exp \left( {\frac{{ - 47\,900}}{{RT}}} \right),~ \hfill \\ {\text{если}}\,\,~{{d}_{0}} \geqslant 225.4~\,\,{\text{мкм}}~ \hfill \\ \end{gathered} \\ \begin{gathered} 0.28{{{\dot {\varepsilon }}}^{{ - 0.22}}}d_{0}^{{1.77}}\exp \left( {\frac{{ - 47\,900}}{{RT}}} \right),~ \hfill \\ {\text{если}}\,\,~{{d}_{0}} < 225.4~\,\,{\text{мкм}}~ \hfill \\ \end{gathered} \end{array}} \right.$ | [49] |
1.4. Статическая рекристаллизация
Если в результате горячей пластической деформации критическая степень не достигнута, однако накопленной внутренней энергии достаточно для образования зародышей новых зерен, протекает статическая рекристаллизация (СР). По аналогии с метадинамической рекристаллизацией, основными характеристиками, определяющими кинетику протекания процесса, являются показатель степени ${{k}_{{\text{s}}}}$ и время, при котором в структуре формируется 50% рекристаллизованных зерен ${{t}_{{0.5}}}{\text{:}}$
(25)
${{X}_{{{\text{SRX}}}}} = 1 - {\text{exp}}\left[ { - \beta {{{\left( {{{\left( t \right)} \mathord{\left/ {\vphantom {{\left( t \right)} {({{t}_{{0.5}}})}}} \right. \kern-0em} {({{t}_{{0.5}}})}}} \right)}}^{{{{k}_{{\text{s}}}}}}}} \right].$Несмотря на наличие инкубационного периода, необходимого для образования зародышей, уравнения, описывающие зависимость t0.5 и ks, подобны уравнениям, используемым для описания МДР, однако в случае статической рекристаллизации накопленная деформация играет значительную роль [50]:
(26)
${{t}_{{0.5}}} = {{a}_{6}}d_{0}^{{{{n}_{6}}}}{{\dot {\varepsilon }}^{{{{m}_{6}}}}}{{\varepsilon }^{{{{h}_{6}}}}}{\text{exp}}\left[ {\frac{{{{Q}_{6}}}}{{RT}}} \right],$(27)
${{d}_{{{\text{SRX}}}}} = {{a}_{7}}d_{0}^{{{{n}_{7}}}}{{\dot {\varepsilon }}^{{{{m}_{7}}}}}{{\varepsilon }^{{{{h}_{7}}}}}\exp \left( {\frac{{{{Q}_{7}}}}{{RT}}} \right),$Таблица 3.
Модели кинетики и изменения размера зерна в процессе статической рекристаллизации
| Материал | Объемная доля статически рекристаллизованных зерен | Размер статически рекристаллизованного зерна dSRX, мкм | Источник |
|---|---|---|---|
| Сталь 300M | ks = 0.114, ${{t}_{{0.5}}} = 5.4{{\dot {\varepsilon }}^{{ - 0.181}}}\exp \left[ {\frac{{32\,200}}{{RT}}} \right]$ | $2378{{\dot {\varepsilon }}^{{0.233}}}\exp \left( {\frac{{ - 53130}}{{R \cdot T}}} \right)$ | [51] |
| Сталь 316 | ks = 0.31, ${{t}_{{0.5}}} = 3.72 \times {{10}^{{ - 8}}}{{\varepsilon }^{{ - 2.2}}}{{\dot {\varepsilon }}^{{ - 0.66}}}\exp \left[ {\frac{{137\,000}}{{RT}}} \right]$ | $0.57{{d}_{0}}{{\left( {{{t}_{{0.5}}}} \right)}^{{0.042}}}$ | [40] |
| Сталь Ti–Nb-HSLA | ks = 0.6, ${{t}_{{0.5}}} = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} 1.18 \times {{10}^{{ - 11}}}{{\varepsilon }^{{ - 1.31}}}{{{\dot {\varepsilon }}}^{{ - 1.07}}}d_{0}^{{0.353}}\exp \left( {\frac{{240\,000}}{{RT}}} \right), \hfill \\ ~{\text{если}}~\,\,T < 1150~^\circ {\text{C}}~ \hfill \\ \end{gathered} \\ \begin{gathered} 3.81 \times {{10}^{{ - 4}}}{{\varepsilon }^{{ - 1.31}}}{{{\dot {\varepsilon }}}^{{ - 1.07}}}d_{0}^{{0.353}}\exp \left( {\frac{{35\,400}}{{RT}}} \right),~ \hfill \\ {\text{если}}~\,\,T \geqslant 1150~^\circ {\text{C}} \hfill \\ \end{gathered} \end{array}} \right.$ | $8.49{{\varepsilon }^{{ - 0.872}}}d_{0}^{{0.33}}\exp \left( {\frac{{ - 10\,600}}{{RT}}} \right)$ | [52] |
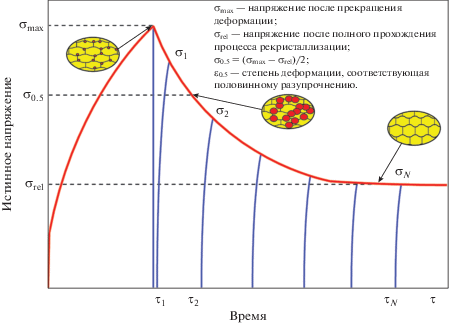
Для определения значений неизвестных констант требуется большое количество структурных исследований, при этом возможно определение размера рекристаллизованного зерна in-situ с использованием лазерного микроскопа [53] и лазерного ультразвукового измерения [53–56]. Для уменьшения количества структурных исследований применяют специальные методики, позволяющие отслеживать кинетику рекристаллизации по степени разупрочнения после деформации. Этот метод предполагает аддитивное влияние на напряжение течения деформированных и рекристаллизованных участков материала. При этом определение времени достижения половины рекристаллизованного объема при МДР и СР возможно двумя способами (рис. 4) [57, 58]. Первый способ предполагает проведение дополнительного нагружения и деформацию на незначительную величину (до достижения предела текучести) через определенные промежутки времени τ1, τ2, τN и определение отклика материала на данное воздействие. Второй способ предполагает непрерывное измерение кривой релаксации напряжений после деформации. Время половинного снижения напряжения течения σ0.5 должно соответствовать времени рекристаллизации половины объема материала (${{t}_{{0.5}}}$). Оба метода имеют существенный недостаток, так как на начальном этапе релаксации существенную роль играют процессы возврата, влияние которых необходимо учитывать согласно методике, предложенной Карьялайненом [57]. Кроме того, даже незначительная дополнительная деформация при многократном нагружении может оказывать влияние на правильность определения кинетических параметров.
1.5. Рост зерен в процессе отжига
Стремление системы к уменьшению внутренней энергии, в том числе и за счет снижения количества дефектов, приводит к росту зерна в металлических материалах при повышенных температурах вне зависимости от наличия внутренних дефектов. Этот процесс также иногда называется собирательной рекристаллизацией. Основными факторами, влияющими на скорость роста и, как следствие, конечный размер зерна являются время и температура отжига. При этом общепринятой считается зависимость следующего вида:
(28)
${{d}^{{{{n}_{8}}}}} = d_{0}^{{{{n}_{8}}}} + {{k}_{{{\text{gg}}}}}t{\text{exp}}\left( {\frac{{ - {{Q}_{8}}}}{{RT}}} \right),$Результаты расчетов по моделям, описывающим эволюцию структуры в результате горячей пластической деформации, могут быть использованы в качестве входных параметров для расчета структуры материалов на окончательных этапах термической и деформационной обработки.
2. МОДЕЛИРОВАНИЕ КИНЕТИКИ ФАЗОВЫХ ПРЕВРАЩЕНИЙ В СТАЛЯХ
2.1. Образование аустенита при нагреве
Превращения в углеродистых и легированных сталях при нагреве и охлаждении являются определяющими при формировании структуры и свойств. Известно, что при нагреве феррито-перлитной смеси выше точки AC1 происходит образование аустенита, зародыши которого в основном формируются на границах ферритных зерен и перлитных колоний. Кинетика образования аустенита может быть описана классической теорией образования и роста зародышей. Согласно Лю с соавт. [60] при наличии перегрева скорость формирования зародышей описывается законом Аррениуса:
где ${{Q}_{N}}$ – энергетический барьер для перехода атомов через межфазную границу. Предэкспоненциальный множитель ${{N}_{0}}$ зависит от большого количества факторов, таких как скорость нагрева, размер перлитной колонии и ферритного зерна. Так, для фиксированной исходной микроструктуры стали 22MnB5 скорость образования зародышей аустенита может иметь вид [61]:(30)
$N = \left( {{{A}_{0}} + {{A}_{1}}{{{v}}^{{{{m}_{A}}}}}} \right){\text{exp}}\left( { - \frac{{{{Q}_{N}}}}{{RT}}} \right),$Скорость роста зародышей при наличии перегрева также в основном определяется диффузией и описывается следующим уравнением:
где ${{Q}_{{v}}}$ – эффективная энергия активация роста, ${{{v}}_{0}}$ – предэкспоненциальный множитель. Объединяя уравнения (30) и (31), скорость роста объемной доли (f) аустенитной фазы можно описать следующим образом: где t – время, с.Несмотря на простоту модели существенное количество допущений сильно ограничивают ее применение. Во-первых, в модель необходимо искусственно вводить ограничения по прекращению формирования зародышей (например, при превышении объемной доли аустенита над объемной долей перлита [61]), кроме того модель не ограничивает предельное значение объемной доли и затухание ее роста. В связи с этим, требуется приведение указанной модели к форме, учитывающей уменьшение реакционного объема (JMAK-модель):
где ${{f}^{R}}$ – реальная объемная доля аустенита.Данная модель значительно усложняется, если принять во внимание, что аустенизация может происходить не полностью, и если учитывать геометрию растущих зерен аустенита [62]. Рассматривая рост зерен как радиальный, уравнение (32) можно преобразовать к виду:
где ${{R}_{{\gamma }}}$ – радиус аустенитного зерна (при условии неограниченного роста). Рост фазы определяется подвижностью атомов на границе раздела α/γ (Mαγ) и движущей силой α → γ превращения ΔGγ:Mαγ может быть описана уравнением Аррениуса:
(36)
${{M}^{{{\alpha \gamma }}}} = M_{0}^{{{\alpha \gamma }}}{\text{exp}}\left( { - \frac{{{{Q}_{{\gamma }}}}}{{RT}}} \right),$Движущая сила превращения пропорциональна-равновесной объемной доли аустенита ${{f}_{{{\text{eq}}}}}$
(37)
$\Delta {{G}^{{\gamma }}} = {\Delta }G_{0}^{{\gamma }}\left( {{{f}_{{{\text{eq}}}}} - f} \right),$(38)
$\begin{gathered} \frac{{df}}{{dt}} = {{\left( {36\pi \smallint Ndt} \right)}^{{\frac{1}{3}}}}{{f}^{{\frac{2}{3}}}}M_{0}^{{{\alpha \gamma }}}\Delta G_{0}^{{\gamma }} \times \\ \times \,\exp \left( { - \frac{{{{Q}_{{\gamma }}}}}{{RT}}} \right)\left( {{{f}_{{{\text{eq}}}}} - f} \right). \\ \end{gathered} $Определение параметров модели возможно с использованием прежде всего дилатометрических исследований. Так, в работе [63] были построены модели аустенизации стали 55CrMo при изохронном нагреве и изотермической выдержке.
Кроме этого, существуют эмпирические модели определения размера аустенитного зерна (${{d}_{{\gamma }}}$) после нагрева и выдержки при определенной температуре [64]:
(39)
${{d}_{{\gamma }}} = {{A}_{{\gamma }}}{{t}^{{{{C}_{{\gamma }}}}}}{\text{exp}}\left( { - \frac{{{{b}_{{\gamma }}}}}{T}} \right),$Модели формирования аустенита при нагреве, совмещенные с расчетом роста зерна при собирательной рекристаллизации имеют большое практическое применение для измельчения аустенитного зерна перед окончательной термической обработкой.
2.2. Процессы превращения аустенита при охлаждении
Моделирование структурообразования при распаде аустенита является важным этапом при выборе оптимальных технологических параметров термической обработки стали. Формирование феррита, перлита и бейнита при охлаждении стали, происходящее по диффузионному механизму, зависит от температуры и времени протекания процесса и хорошо описывается моделью JMAK (8). При этом показатель Аврами составляет ~1 для образования феррита, ~2 – для перлита и ~4 – для бейнита [65]. Для условий непрерывного охлаждения Камамото [66] предложил использовать вместо времени в уравнении (8) безразмерный параметр τ:
где ${{T}_{{\text{H}}}},$ ${{T}_{{\text{K}}}}$ – температуры начала и окончания процесса.Распад аустенита по диффузионному механизму также обычно описывается моделью образования и роста зародышей, рассмотренной при моделировании кинетики формирования аустенита при нагреве. Однако при этом необходимо учитывать, что в процессе распада образуется несколько видов его продуктов. Джонс и Бхадеша предложили модель, описывающую возможность одновременного выделения феррита и перлита при распаде переохлажденного аустенита [67]. В этом случае кинетика выделения обеих фаз будет зависеть от объемной их доли:
(41)
$\begin{gathered} {{f}^{{\alpha }}} = \left( {\frac{1}{{1 + K}}} \right) \times \\ \times \,\,\left[ {1 - \exp \left( { - \frac{1}{3}\left( {1 + K} \right)\pi {{{\left( {\frac{{d{{R}_{{\alpha }}}}}{{dt}}} \right)}}^{3}}{{N}_{{\alpha }}}{{t}^{4}}} \right)} \right], \\ \end{gathered} $(42)
$\begin{gathered} {{f}^{{\text{p}}}} = \left( {\frac{K}{{1 + K}}} \right) \times \\ \times \,\,\left[ {1 - \exp \left( { - \frac{1}{3}\left( {\frac{{1 + K}}{K}} \right)\pi {{{\left( {\frac{{d{{R}_{{\text{p}}}}}}{{dt}}} \right)}}^{3}}{{N}_{{\text{p}}}}{{t}^{4}}} \right)} \right], \\ \end{gathered} $(43)
$K = \frac{{{{{\left( {\frac{{d{{R}_{{\text{p}}}}}}{{dt}}} \right)}}^{3}}{{N}_{{\text{p}}}}}}{{{{{\left( {\frac{{d{{R}_{{\alpha }}}}}{{dt}}} \right)}}^{3}}{{N}_{{\alpha }}}}}.$Для анализа фазовых превращений при охлаждении аустенита обычно используются диаграммы изотермического превращения (TTT-диаграммы) и диаграммы, полученные при непрерывном охлаждении (CCT-диаграммы). В связи с этим возможность их расчета позволит прогнозировать микроструктуру стали после разных режимов охлаждения. В общей форме TTT-диаграммы можно описать уравнением, предложенным Зинером [68] и Хиллертом [69]:
(44)
$t\left( {f,T} \right) = \frac{{F\left( {Comp,d} \right)}}{{{\Delta }{{T}^{n}}\exp \left( { - \frac{Q}{{RT}}} \right)}}S\left( f \right),$(45)
$S\left( f \right) = \int\limits_0^f {\frac{{df}}{{{{f}^{{0.4\left( {1 - f} \right)}}}{{{\left( {1 - f} \right)}}^{{0.4f}}}}}} .$Мартенситное превращение определяется в основном только температурой. Койстинен и Марбургер предложили следующий вид модели для описания бездиффузионного превращения [71]:
(46)
$X\left( T \right) = 1 - {\text{exp}}\left[ { - {{{\beta }}_{m}}\left( {{{M}_{{\text{s}}}} - T} \right)} \right],$(47)
$\frac{{d{{f}_{m}}}}{{dT}} = \alpha {{\left( {{{M}_{{\text{s}}}} - T} \right)}^{n}}f_{m}^{{{{{\varphi }}_{m}}}}{{\left( {1 - {{f}_{m}}} \right)}^{{{{{\psi }}_{m}}}}},$Рассмотренные модели были успешно применены при расчете фазовых превращений при охлаждении аустенита для сталей BR1500HS [73], HC380WD [6], 22MnB5 [74] и 1045 [75]. Кроме того, они нашли широкое применение при расчете упрочнения стальных деталей при охлаждении с использованием программных средств, реализующих метод конечных элементов, таких как Deform и Abaqus [76, 77].
3. МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ СТРУКТУРЫ ПРИ РАСПАДЕ ПЕРЕСЫЩЕННОГО ТВЕРДОГО РАСТВОРА
Процесс распада пересыщенного твердого раствора является одним из конечных этапов формирования структуры и свойств дисперсионно твердеющих сплавов. При этом для достижения максимальных прочностных свойств необходимо добиться равномерного распределения наноразмерных частиц по всему объему материала. Для этого полезным является использование предварительного моделирования структуры с целью выбора оптимальных условий термической обработки. Старинк с соавт. [78] предложили модель зарождения и роста частиц при отжиге, близкую к модели Джонсона–Мела–Аврами–Колмогорова, согласно которой кластер объемом ${{V}_{{\text{p}}}}$ растет в соответствие с уравнением:
(48)
${{V}_{{\text{p}}}} = {{A}_{{\text{p}}}}{{\left[ {G\left( {t - \zeta } \right)} \right]}^{{{{m}_{{\text{p}}}}}}},$Авторы работы [84] адаптировали уравнение Зенера–Хиллерта для расчета скорости роста иглообразных выделений метастабильной модификации β-фазы:
(49)
$\frac{{dl}}{{dt}} = 1.5\frac{{{{D}_{{{\text{Mg}}}}}}}{{2{{r}_{{\text{p}}}}}}\frac{{{{X}_{{{\text{Mg}}}}} - X_{{{\text{Mg}}}}^{i}}}{{{\alpha }X_{{{\text{Mg}}}}^{{\text{p}}} - X_{{{\text{Mg}}}}^{i}}} = 1.5\frac{{{{D}_{{{\text{Si}}}}}}}{{2{{r}_{p}}}}\frac{{{{X}_{{{\text{Si}}}}} - X_{{{\text{Si}}}}^{i}}}{{\alpha X_{{{\text{Si}}}}^{{\text{p}}} - X_{{{\text{Si}}}}^{i}}},$1. Зарождение частиц гомогенное и не учитывает упругую энергию, связанную с формированием частицы. Это приводит к следующей закономерности скорости зарождения:
(50)
$\frac{{dN}}{{dt}} = {{N}_{0}}Z{\beta }{\kern 1pt} {\text{*exp}}\left( {\frac{{G{\kern 1pt} *}}{{{{k}_{b}}T}}} \right)\left( {1 - {\text{exp}}\left( { - \frac{t}{\tau }} \right)} \right),$2. Фактор формы частиц остается постоянным независимо от абсолютного размера частиц и равен 11.
По значениям структурных параметров модель была откалибрована и показала высокую точность при расчете не только параметров частиц β‑фазы, но и при определении предела текучести в алюминиевом сплаве 6061.
Модели формирования и роста частиц показали хорошую точность и при расчете образования дисперсоидов в структуре алюминиевых сплавов. Робсон и Прагнелл [85] предложили модель, описывающую кинетику выделения и распределение частиц метастабильной фазы L12 Al3Zr в зависимости от концентрации циркония и режима гомогенизационного отжига. Модель также базируется на методологии Кампмана и Вагнера и учитывает внутрикристаллитную ликвацию циркония при кристаллизации, однако также содержит допущения:
1. Метастабильные выделения имеют точную стехиометрию фазы Al3Zr и являются единственной цирконий-обогащенной фазой. В связи с этим модель применима для сплавов 7ХХХ серии.
2. Выделения однородно распределены, скорость их зарождения зависит от локальной концентрации циркония. Гетерогенное зарождение, возможное только на границах зерен, исключено.
3. Рост частиц контролирует диффузия циркония на границе матрица/частица.
4. Атомы циркония равномерно распределяются между растущими частицами в зонах диффузионного перекрытия.
Скорость зарождения частиц описывается классическим уравнением [86]:
где $J$ – скорость зарождения на единицу объема, ${{N}_{0}}$ – плотность выделений (для гомогенного зарождения – число атомов циркония на единицу объема), $Q$ – энергия активации диффузии циркония в алюминии. Параметр $G{\text{*}}$ рассчитывается по уравнениюВ соответствии c моделью, критический размер зародыша рассчитывается по уравнению Гиббса–Томсона для твердых растворов. При этом концентрация на границе равна средней концентрации в матрице, и отсутствует градиент на границе зерна. $r{\text{*}}$ рассчитывают по уравнению:
(53)
$r* = \frac{{2{\sigma }{{V}_{{\text{a}}}}}}{{kT{\text{ln}}\frac{c}{{c_{\infty }^{{\alpha }}}}}}~,$Для сферических частиц L12 фазы уравнение роста выглядит следующим образом:
(54)
$\frac{{{\text{d}}r}}{{{\text{d}}t}} = \frac{D}{r}\frac{{c - c_{r}^{{\alpha }}}}{{{{c}^{{{\alpha }{\kern 1pt} {\text{'}}}}} - c_{r}^{{\alpha }}}}~,$(55)
$c_{r}^{{\alpha }} = ~c_{\infty }^{{\alpha }}{\text{exp}}\left( {\frac{{2\sigma {{V}_{{\text{a}}}}}}{{kT}}\frac{1}{r}} \right).$Ликвация циркония может оказывать сильное влияние на однородность распределения частиц в матрице. При этом особенно интересно влияние состава и режима термической обработки на ширину зон, свободных от выделений.
Уравнение Шайля показывает, что концентрация циркония в твердой фазе (${{c}_{{\text{s}}}}$) зависит от объемной доли твердых фаз (${{f}_{{\text{s}}}}$) в процессе кристаллизации [88].
(56)
${{c}_{{\text{s}}}} = k\bar {c}{{\left( {1 - {{f}_{{\text{s}}}}} \right)}^{{\left( {k - 1} \right)}}},$Аналогичная модель предложена для гомогенного и гетерогенного зарождения и роста частиц Al3Sc [89]. Объединение двух полученных моделей представлено в работе [90] на примере моделирования упрочнения высокопрочного алюминиевого сплава, легированного скандием и цирконием.
Клое с соавторами предложили другой подход к моделированию кинетики образования дисперсоидов Al3Zr и Al3Sc [91], основанный на кластерной динамике, которая позволяет описывать разные стадии гомогенного зарождения и роста дисперсоидов с использованием только значений коэффициентов диффузии и свободной энергии межфазных границ. В данной модели скорость зарождения выделений описывается следующей системой уравнений:
(57)
${{{\beta }}_{{{{n}_{X}}}}} = 4\pi \frac{{{{D}_{X}}}}{{\Omega }}{{r}_{{{{n}_{X}}}}}{{C}_{1}}\frac{{1 + k{{r}^{{{\text{ext}}}}}}}{{1 + k\left( {{{r}^{{{\text{ext}}}}} - {{r}_{{{{n}_{X}}}}}} \right)}},~\,\,\,\,{{r}_{{{{n}_{X}}}}} \leqslant {{r}^{{{\text{ext}}}}},$(58)
${{{\beta }}_{{{{n}_{X}}}}} = 4\pi \frac{{{{D}_{X}}}}{{\Omega }}{{r}_{{{{n}_{X}}}}}{{C}_{1}}\left( {1 + k{{r}_{{{{n}_{X}}}}}} \right),\,\,\,\,{{r}_{{{{n}_{X}}}}} \geqslant {{r}^{{{\text{ext}}}}},$Таким образом, к настоящему моменту разработаны высокоточные модели, позволяющие рассчитывать объемную долю и средний размер продуктов распада пересыщенного твердого раствора, что в свою очередь позволяет прогнозировать прочность алюминиевых сплавов с высокой точностью [92, 93].
4. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА ЭВОЛЮЦИИ СТРУКТУРЫ
Благодаря развитию вычислительных технологий было разработано значительное количество численных методов расчета микроструктуры. Наиболее распространенными среди них являются метод “клеточных автоматов” [94–98], метод Монте-Карло [99–103], метод многофазного поля [104, 105]. Эти методы позволяют не только рассчитывать количественные характеристики микроструктуры, как это делают представленные выше физико-математические модели, но и предоставлять информацию о наиболее вероятном распределении тех или иных элементов микроструктуры по фазово-структурному состоянию и размерам, благодаря большому объему анализируемых элементов.
4.1. Метод “клеточных автоматов”
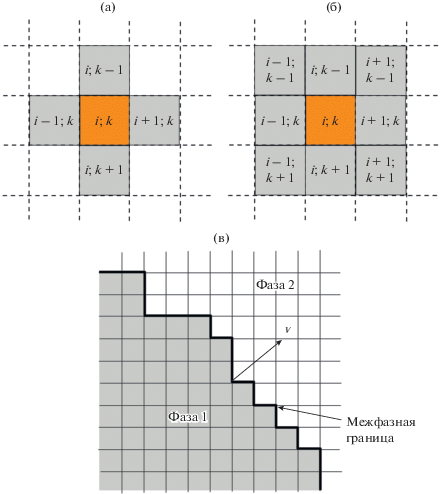
Основной принцип метода “клеточных автоматов” заключается в дискретизации пространства и времени, при этом физические величины, такие как плотность дефектов, характеристики структурно-фазового состояния и др. принимают набор значений в каждой ячейке – отдельном элементе микроструктуры. Состояние ячеек и связь между ними в каждый момент времени описывается физическими и вероятностными соотношениями. При этом состояние каждой из ячеек, то есть набор количественных значений, характеризующих структурно-фазовое состояние, определяется внешними условиями, предыдущим состоянием ячейки и ее соседей. Примеры расположения соседних ячеек приведены на рис. 5а, 5б, при этом могут учитываться состояния не только непосредственных соседей, но и соседей из второго, третьего и т.д. рядов. Эти значения обновляются одновременно в процессе моделирования на основе набора предварительно определенных правил преобразования, что приводит к изменению состояния всей системы, например, к смещению межфазной границы (рис. 5в). Метод “клеточных автоматов” описывает эволюцию микроструктуры во временном и пространственном масштабе. Так, например, в случае моделирования эволюции микроструктуры в процессе горячей деформации состояние каждого элемента может определяться следующими параметрами: плотность дислокаций, кристаллографическая ориентация, идентификатор принадлежности к определенному зерну и др. Кроме того должны быть описаны правила взаимодействия между отдельными элементами сетки, которые определяют кинетику зарождения и роста зерен [106].
Рис. 5.
Схема расположения соседей описываемой ячейки по Нейману (а) и по Муру (б). Схема движения межфазной (межзеренной) границы при расчете методом “клеточных автоматов” [108].
Общий алгоритм построения эволюции микроструктуры методом “клеточных автоматов” состоит из следующих стадий:
1. Моделируемый объем разделяется на N элементов, называемых ячейками.
2. Каждой ячейке присваиваются начальные значения параметров ее состояния и определяются ее соседей.
3. При переходе на следующий временной шаг вычисляется новое состояние ячейки, исходя из состояний ее соседей.
4. Итерацией состояний всех ячеек моделируемого объема материала определяется новое состояние системы и происходит переход к следующему шагу по времени.
Простота алгоритма позволяет реализовывать расчеты с применением этого метода совместно с расчетами методом конечных элементов, что значительно расширяет его функциональность, позволяя моделировать как статические, так и динамические процессы структурообразования. Основной сложностью реализации метода является нахождение физических и вероятностных закономерностей взаимодействия между ячейками.
В работе [107] разработана модель статической рекристаллизации для малоуглеродистой стали 0.14C–0.2Si–0.4Mn. Скорость образования зародышей N описывали следующим уравнением:
где ${{Q}_{{\text{a}}}}$ – энергия активации образования зародышей. Значение коэффициента ${{M}_{N}}$ определяется уравнением где ${{С}_{0}}$ – константа, ${{H}_{i}}$ – количество запасенной энергии в ячейке, ${{H}^{{\text{c}}}}$ – критическое количество энергии, необходимое для образования зародыша, зависящее от критической степени деформации (${{{\varepsilon }}_{{\text{с}}}})$ и энергии малоугловых границ ${{{\gamma }}_{{{\text{lab}}}}},$ со значением ~0.2 Дж/м2:(61)
${{H}^{{\text{c}}}} = \frac{{{{\varepsilon }_{{\text{с}}}}}}{{a{{\varepsilon }_{{\text{с}}}} + b}}{{\gamma }_{{{\text{lab}}}}},$Рассмотренный подход расчета вероятности зарождения является универсальным, однако возможен более простой вероятностный подход, согласно которому скорость зарождения не зависит от запасенной энергии, а зарождение происходит на границах зерен случайным образом, пропорционально площади свободных от зародышей границ. Такой подход был реализован при расчете статической рекристаллизации жаропрочного никелевого сплава [110].
Скорость роста зародыша рекристаллизации можно описать уравнением
где p – движущая сила рекристаллизации, а М – подвижность границ зерен, определяемая диффузионной подвижностью атомов на границе где D – коэффициент зернограничной диффузии, bB – вектор Бюргерса, k – константа Больцмана.Движущая сила зависит от двух факторов: разности между плотностью дислокаций (Δρ в зародыше и нерекристаллизованной матрице:
где $G$ – модуль касательной упругости, и зернограничной энергии, зависящей от кривизны границы (${\kappa }$): где ${{{\gamma }}_{{{\text{hagb}}}}}$ – энергия высокоугловой границы (~0.6 Дж/м2):(67)
${{{\gamma }}_{{{\text{hagb}}}}} = \left\{ {\begin{array}{*{20}{c}} {{\gamma }_{{{\text{hagb}}}}^{0},\,\,\,\,\theta \geqslant {{{\theta }}_{0}}} \\ {{\gamma }_{{{\text{hagb}}}}^{0}\frac{{\theta }}{{{{{\theta }}_{0}}}}\left( {1 - \ln \left( {\frac{{\theta }}{{{{{\theta }}_{0}}}}} \right)} \right)~\theta < {{{\theta }}_{0}}} \end{array}} \right.,$(68)
${\gamma }_{{{\text{hagb}}}}^{0} = \frac{{G{{b}_{{\text{B}}}}{{{\theta }}_{0}}}}{{4{\pi }\left( {1 - \nu } \right)}},$В результате расчетов авторами [107] показана хорошая сходимость результатов с расчетами по модели JMAK и экспериментальными данными [111]. Высокая точность прогнозирования эволюции структуры в процессе статической рекристаллизации в интервале температур 970–1040°С после горячей пластической деформации продемонстрирована для жаропрочного никелевого сплава [110, 112], а также для холоднодеформированной феррито-перлитной малолегированной стали [113].
В случае моделирования процесса динамической рекристаллизации к рассмотренному алгоритму добавляется предварительный шаг по определению возможности образования зародыша рекристаллизации, т.е. достижения критического значения плотности дислокаций (в общем случае суммарной плотности дислокаций в границах и внутри субзерен) в отдельных ячейках. Зависимость плотности дислокаций от параметров горячей пластической деформации описывается моделью Кокса–Мекинга–Эстрина (уравнения (1)–(4)), а определение критической степени деформации возможно по модели Поляка и Джонаса [36]. В интегрированном виде эволюция плотности дислокаций на стадии динамического возврата описывается следующей формулой:
(70)
$\rho = \left[ {\frac{{{{k}_{1}}}}{{{{k}_{2}}}} - \frac{{{{k}_{1}}}}{{{{k}_{2}}}}\exp \left( { - \frac{{{{k}_{1}}}}{{{{k}_{2}}}}\varepsilon } \right) + \sqrt {{{\rho }_{0}}} \exp \left( { - \frac{{{{k}_{1}}}}{2}\varepsilon } \right)} \right],$Кроме того, для процесса динамической рекристаллизации в уравнение расчета скорости образования зародышей ( 59) вводится влияние скорости деформации [114]:
(72)
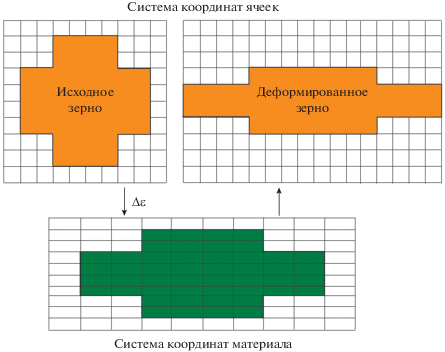
$N = {{C}_{1}}{{\dot {\varepsilon }}^{m}}{\text{exp}}\left( { - \frac{{{{Q}_{{\text{a}}}}}}{{RT}}} \right),$Основной сложностью при моделировании процесса динамической рекристаллизации является изменение формы зерен, что естественно сказывается на образовании и росте зародышей. В связи с этим необходима процедура перехода от координат материала к координатам ячеек после каждой итерации вычислений. Схема такого перехода представлена на рис. 6. В результате такого преобразования границы зерен изменяют свое положение согласно деформации материала по следующему закону [115]:
(73)
$\left( {\begin{array}{*{20}{c}} {{{{\mathbf{v}}}_{1}}} \\ {{{{\mathbf{v}}}_{2}}} \\ {{{{\mathbf{v}}}_{3}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{e}_{{11}}}}&{{{e}_{{12}}}}&{{{e}_{{13}}}} \\ {{{e}_{{21}}}}&{{{e}_{{22}}}}&{{{e}_{{23}}}} \\ {{{e}_{{31}}}}&{{{e}_{{32}}}}&{{{e}_{{33}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{{\mathbf{u}}}_{2}}} \\ {{{{\mathbf{u}}}_{3}}} \end{array}} \right),$Рис. 6.
Схема перехода от системы координат материала к системе координат ячеек после деформации [116].
Несмотря на значительные упрощения и допущения, метод “клеточных автоматов” показал высокую точность расчета и хорошую предсказательную способность при моделировании динамической рекристаллизации широкого спектра металлических материалов. Так, Фей с сотр. [116] показал, что на измельчение зерна при горячей пластической деформации аустенитной нержавеющей стали 316LN основное влияние оказывает исходный размер зерна. При исходном размере зерна 450 мкм объемная доля рекристаллизованных зерен составила всего 43% даже после истинной деформации 3 ($\dot {\varepsilon }$ = 1 с–1, t = 950°C). Лю с сотр. [117] смоделировал измельчение зерна при деформации жаропрочного никелевого сплава, показав хорошее соответствие между расчетными и экспериментальными значениями размера зерна, а также определил тот факт, что на начальном этапе деформации динамическая рекристаллизация протекает гетерогенно и становится гомогенной только после достижения определенной степени деформации. Чен с сотр. [13] улучшили точность расчета процесса динамической рекристаллизации стали 42CrMo, введя в зависимости скорости образования зародышей N (72) и подвижности границ зерен (64) степенную зависимость от исходного размера зерна. С применением метода “клеточных автоматов” и определением параметров модели JMAK была описана кинетика динамической рекристаллизации инструментальной стали Cr12MoV [118], среднеуглеродистой стали 36Cr2Ni2Mo [119], чистой меди [120] и магниевого сплава AZ80 [121].
Кроме динамической рекристаллизации, метод “клеточных автоматов” нашел применение для моделирования других процессов термомеханической обработки. В работе [122] Яздипур и Ходгсон рассчитали процесс разупрочнения аустенитной нержавеющей стали 304 после горячей пластической деформации в результате статической и метадинамической рекристаллизаций. Входными параметрами модели были величина накопленной в результате деформации энергии, объемная доля и размер динамически рекристаллизованных зерен, температура, степень и скорость деформации. Авторами показано существенное замедление процесса разупрочнения в случае начала динамической рекристаллизации, вследствие чего уменьшается время половинного разупрочнения при увеличении степени, скорости и температуры деформации.
Метод конечных элементов также применим для описания фазовых превращений. Хорошее соответствие между расчетом и экспериментом было показано при моделировании распада аустенита в малолегированной стали [123], в том числе и после деформации [124]. Используя в уравнении для определения подвижности границ зерен феррита термодинамические данные о распределении углерода между ферритом и аустенитом, авторы определили с высокой точностью кинетику образования феррита и средний размер его зерна при охлаждении со скоростями в интервале 1–58°C/с. Однако в результате расчета форма зерен оказалась равноосной, в то время как реальная форма зерен являлась вытянутой [125]. Моделирование процесса аустенизации стали 1070 было проведено Янгом с соавт. [126] при нагреве со скоростями 0.5–5°C/с, и предложен метод, позволяющий устранять искусственную анизотропию зерен, возникающую при расчете. Авторами [127] методом “клеточных автоматов” было показано существенное влияние температуры отжига и размера зерна на выделение хромсодержащих карбидов при отжиге аустенитных сталей AISI 304 и 316. Кроме того, данный метод позволяет проводить расчет объемной доли, формы и размера бейнитной и мартенситной фаз в зависимости от скорости охлаждения рекристаллизованного или деформированного аустенита [95].
4.2. Метод Монте-Карло
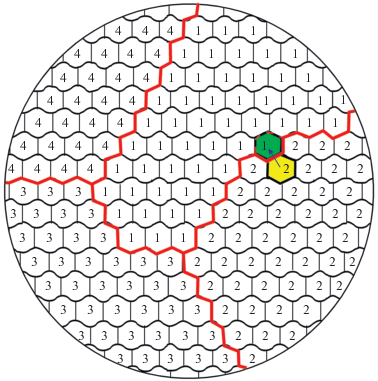
По аналогии с методом “клеточных автоматов” в методе Монте-Карло производится разбиение структуры на сетку отдельных элементов. Этим элементам задается начальная конфигурация, исходя из проблематики решаемой задачи. Основным принципом расчета методом Монте-Карло является минимизация общей энергии системы за счет перебора локальных состояний отдельных элементов. Общая энергия системы описывается Гамильтонианом [128]:
(74)
$E = \frac{J}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^m {\left( {1 - {{\delta }_{{{{S}_{i}}{{S}_{j}}}}}} \right)} } + \sum\limits_{i = 1}^N {{{H}_{{{{S}_{i}}}}}} ,$(75)
${{\delta }_{{{{S}_{i}}{{S}_{j}}}}}~ = \left\{ {\begin{array}{*{20}{c}} {1,\,\,\,\,{\text{если}}\,\,\,\,{{S}_{i}} = {{S}_{j}}} \\ {0,\,\,\,\,{\text{если}}\,\,\,\,{{S}_{i}} \ne {{S}_{j}}} \end{array}} \right.,$Рис. 7.
Схема распределения гексагональных элементов по ориентировкам при расчете методом Монте-Карло.
N – общее количество элементов в системе, m – количество соседних элементов, ${{H}_{{{{S}_{i}}}}}$ – внутренняя энергия каждого из элементов. Так, в случае моделирования процесса рекристаллизации внутренняя энергия связана прежде всего с плотностью дислокаций и определяется формулой [129]:
В первую очередь энергия системы рассчитывается для начального состояния. После этого одному из элементов изменяют состояние на состояние его соседа и определяют следующее значение энергии системы. В зависимости от разности полученных значений энергии, определяют вероятность изменения состояния выбранного элемента, как
(77)
$P~~ = \left\{ {\begin{array}{*{20}{l}} {1,\,\,\,\,{\text{если}}\,\,\,\,\Delta E \leqslant 0} \\ {{\text{exp}}\left( { - \frac{{\Delta E}}{{kT}}} \right),\,\,\,\,{\text{если}}\,\,\,\,\Delta E > 0} \end{array}} \right..$В случае, если переход вероятен, т.е. $P$ не меньше случайного числа от 0 до 1, то элемент меняет свою ориентировку (рис. 7).
Несмотря на то, что метод Монте-Карло носит вероятностный характер, в большинстве опубликованных работах он дает хорошие результаты при моделировании структурных изменений в материалах. Это связано с тем, что начальный этап и кинетика превращений зависит от энергии системы, которая определяется параметрами структуры (например, плотности дислокаций), определение которых требует некоторых физических закономерностей, таких как уравнение Кокса–Мекинга–Эстрина (1)–(4). Авторы [128] показали, что параметры микроструктуры при горячей прокатке молибденсодержащей стали, рассчитанные с использованием этого метода, сопоставимы с результатами моделирования по уравнению JMAK и экспериментальными данными. Моделирование процесса статической рекристаллизации для этой стали [99] показало, что изменение количества элементов в сетке разбиения с 40 000 до 160 000 не влияет существенно на значения рассчитанных параметров структуры, изменяя только визуальное представление результатов расчета. При этом в обоих случаях наблюдается хорошее соответствие с экспериментальными данными. Применение метода Монте-Карло позволило рассчитать характеристики текстуры, возникающей в процессе статической рекристаллизации в α-уране [100], а также спрогнозировать кинетику выделений частиц меди в α‑железе при отжиге в интервале температур 250–500°C [101]. Однако основным из недостатков данного метода является отсутствие, в отличие от метода “клеточных автоматов”, физических ограничений при движении межзеренных границ, что может привести к нетипичной для реальных процессов рекристаллизации дендритной форме рекристаллизованных зерен [107].
4.3. Метод многофазного поля
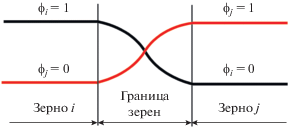
Еще одним дискретным методом моделирования структурообразования является метод многофазного поля. Однако в отличие от двух рассмотренных ранее подходов дискретизация пространства и времени происходит не при задании начальных состояний, а на стадии решения дифференциальных уравнений, описывающих процесс эволюции структуры. Само же состояние системы описывается суперпозицией фазовых полей ${{\phi }_{i}},$ отвечающих отдельным структурным составляющим [130]. В случае поликристалла, содержащего N зерен, каждому i-тому зерну будет соответствовать фазовое поле ${{\phi }_{i}},$ которое принимает значение 1 внутри зерна i, значение 0 за его пределами и значение 0 < ${{\phi }_{i}}$ < 1 на границе зерен (рис. 8).
Функция ${{\phi }_{i}}$ не является независимой и ограничена выражением:
Общее состояние системы описывает функционал в следующем виде:
(79)
$F = \int {\left[ {\sum\limits_{i = 1}^N {\sum\limits_{j = i + 1}^N {\left( { - \frac{{a_{{ij}}^{2}}}{2}\nabla {{\phi }_{i}} \cdot \nabla {{\phi }_{j}} + {{W}_{{ij}}}{{\phi }_{i}}{{\phi }_{j}}} \right)} } + {{f}_{e}}} \right]} dV,$${{W}_{{ij}}}$ – высота энергетического барьера
${{f}_{e}}$ – плотность свободной энергии внутри зерен.
Количество зерен N в уравнении (79) можно заменить значением $n = \sum\nolimits_i^N {{{{\sigma }}_{i}}} ,$ где ${{{\sigma }}_{i}} = 1,$ если 0 < < ${{\phi }_{i}}$ ≤ 1 и ${{{\sigma }}_{i}} = 0$ в противном случае.
Изменение фазового поля во времени описывается функцией [131]
(82)
$\frac{{\partial {{\phi }_{i}}}}{{\partial t}} = \sum\limits_{j = 1}^n {\frac{{2M_{{ij}}^{\phi }}}{n}\left( {\frac{{\partial F}}{{\partial {{\phi }_{i}}}} - \frac{{\partial F}}{{\partial {{\phi }_{j}}}}} \right)} ,$Производная функционала (79) по отдельным функциям фазового поля имеет вид:
(84)
$\frac{{\partial F}}{{\partial {{\phi }_{i}}}} = \sum\limits_{k = 1}^n {\left( {{{W}_{{ij}}}{{\phi }_{k}} + \frac{{a_{{ij}}^{2}}}{2}{{\nabla }^{2}}{{\phi }_{k}}} \right)} + \frac{{\partial {{f}_{e}}}}{{\partial {{\phi }_{i}}}}.$Принимая во внимание, что движущей силой является разница:
(85)
$\frac{{\partial {{f}_{e}}}}{{\partial {{\phi }_{i}}}} - \frac{{\partial {{f}_{e}}}}{{\partial {{\phi }_{j}}}} = - \frac{8}{\pi }\sqrt {{{\phi }_{i}}{{\phi }_{j}}} {\Delta }{{E}_{{ij}}},$(86)
$\begin{gathered} \frac{{\partial {{\phi }_{i}}}}{{\partial t}} = - \sum\limits_{j = 1}^n {\frac{{2M_{{ij}}^{\phi }}}{n}} \times \\ \times \,\,\left[ {\sum\limits_{k = 1}^n {\left\{ {({{W}_{{ik}}} - {{W}_{{jk}}}){{\phi }_{k}} + \frac{1}{2}\left( {a_{{ik}}^{2} - a_{{jk}}^{2}} \right){{\nabla }^{2}}{{\phi }_{k}}} \right\}} - } \right. \\ \left. { - \,\,\frac{8}{\pi }\sqrt {{{\phi }_{i}}{{\phi }_{j}}} \Delta {{E}_{{ij}}}} \right]. \\ \end{gathered} $В работе [104] метод многофазного поля был применен для моделирования динамической рекристаллизации путем реализации следующего алгоритма:
1. Начальная поликристаллическая структура была смоделирована согласно [130].
2. Задано начальное значение плотности дислокаций.
3. С использованием модели Кокса–Мекинга–Эстрина по кривой сжатия было определено значение плотности дислокаций после приращения степени деформации на величину Δε.
4. Если плотность дислокаций превышала критическую, то на границе зерен создавался зародыш рекристаллизации.
5. Процесс роста зерен рассчитывался решением системы уравнений (86).
Шаги 3–5 повторяли до достижения заданной степени деформации. В результате авторами были определены оптимальные значения параметров в уравнении (86) и показана достаточно хорошая сходимость с результатами расчета методом “клеточных автоматов” [132]. Авторы [4] продемонстрировали высокую функциональность данного подхода при моделировании процесса формирования бейнита и мартенсита в процессе охлаждения аустенита двухфазной стали DP600. Показано, что при учете в расчете упругих составляющих нет необходимости в указании мест зарождения фаз. При этом предпочтительными для зарождения являлись плоскости перпендикулярные плоскости габитуса мартенсита. Применение данного метода позволило с высокой точностью смоделировать формирование аустенита, включая его морфологию и распределение легирующих элементов, при изотермической выдержке мартенситной стали состава Fe–9.6Ni–7.1Mn в интервале температур 510–600°С [133]. Киношита с соавт. применил этот метод для описания аномального роста зерен в науглероженном слое ниобий содержащей стали [134]. Также с использованием этого метода, совмещенного с термодинамическими и диффузионными расчетами, было объяснено аномальное расхождение пластин в перлитных колониях при распаде аустенита в стали Fe–C–Mn [135].
Несмотря на достаточно сложный математический аппарат реализации метода многофазного поля, он является достаточно перспективным для моделирования процессов структурообразования благодаря большой вариативности влияющих на функцию фазового поля факторов.
ЗАКЛЮЧЕНИЕ
1. Разработанные к настоящему времени физико-математические модели эволюции структуры в процессе горячей пластической деформации, основанные на уравнениях Джонса–Мел–Аврами–Колмогорова и Кокса–Мекинга–Эстрина, позволяют с высокой точностью прогнозировать структурные параметры металлических материалов. Простые аналитические закономерности, реализуемые данными моделями, позволяют их успешно интегрировать в современные вычислительные системы расчета промышленных процессов обработки металлов давлением. Однако большое число неизвестных констант требует значительное количество механических испытаний и структурных исследований для построения полноценной модели, охватывающей процессы динамического наклепа, возврата и рекристаллизации. Вследствие этого, перспективным направлением исследования является создание in-situ методов определения параметров микроструктуры в процессе горячей пластической деформации и термической обработки.
2. К настоящему времени создан значительный теоретический базис для расчета кинетики структурных превращений при нагреве и охлаждении стали, а также при распаде пересыщенного твердого раствора. Основываясь на теории образования и роста зародышей, разработанные модели показывают не только высокую точность при определении объемной доли и размеров продуктов фазовых превращений, но и возможность применения этих моделей для определения механических свойств.
3. Наиболее перспективными в настоящий момент представляются численные методы расчета закономерностей эволюции структуры. Несмотря на минимальный набор необходимых экспериментальных данных, методы “клеточных автоматов”, Монте-Карло и многофазного поля демонстрируют высокую точность при расчете процессов рекристаллизации и фазовых превращений.
Таким образом, существует полноценный базис для создания комплексных адаптируемых моделей, позволяющих реализовать сквозной расчет полного цикла термической и деформационной обработки металлических материалов, с возможностью рекурсивной оптимизации технологических параметров с целью достижения заданной структуры. Ключевую роль в таких моделях должны играть численные методы расчета, являющиеся наиболее универсальными и адаптируемыми к использованию совместно с конечно-элементными методами моделирования.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-79-10153).
Список литературы
Shen G., Semiatin S.L., Shivpuri R. Modeling microstructural development during the forging of Waspaloy // Metall. Mater. Trans. A 1995. V. 26. P. 1795–1803.
Guo Q.M., Li D.F., Guo S.L. Microstructural models of dynamic recrystallization in hot-deformed inconel 625 superalloy // Mater. Manuf. Process. 2012. V. 27. P. 990–995.
Mecozzi M.G., Bos C., Sietsma J. A mixed-mode model for the ferrite-to-austenite transformation in a ferrite/pearlite microstructure // Acta Mater. 2015. V. 88. P. 302–313.
Schoof E., Schneider D., Streichhan N., Mittnacht T., Selzer M., Nestler B. Multiphase-field modeling of martensitic phase transformation in a dual-phase microstructure // Int. J. Solids Struct. 2018. V. 134. P. 181–194.
Li Z., Wen Z., Su F., Zhang R., Zhou Z. Modeling research on pearlite-to-austenite transformation in hypereutectoid steel containing Cr // J. Alloys Compd. 2017. V. 727. P. 1050–1056.
Hippchen P., Lipp A., Grass H., Craighero P., Fleischer M., Merklein M. Modelling kinetics of phase transformation for the indirect hot stamping process to focus on car body parts with tailored properties // J. Mater. Process. Technol. 2016. V. 228. P. 59–67.
Yin F., Hua L., Mao H., Han X., Qian D., Zhang R. Microstructural modeling and simulation for GCr15 steel during elevated temperature deformation // Mater. Des. 2014. V. 55. P. 560–573.
Jin Z., Li K., Wu X., Dong H. Modelling of Microstructure Evolution during Thermoplastic Deformation of Steel by a Finite Element Method // Mater. Today Proc. 2015. V. 2. P. S460–S465.
Elwazri A.M., Essadiqi E., Yue S. Kinetics of Metadynamic Recrystallization in Microalloyed Hypereutectoid Steels // ISIJ Int. 2004. V. 44. P. 744–752.
Popov V.V., Gorbachev I.I. Computer Simulation for the Prediction of Phase Composition and Structure of Low-Alloyed Steels with Carbonitride Hardening // Phys. Met. Metallogr. 2018. V. 119. P. 1333–1337.
Горбачев И.И., Пасынков А.Ю., Попов В.В. Моделирование эволюции карбонитридных частиц сложного состава при горячей деформации низколегированной стали // Физика металлов и металловедение. 2018. Т. 119. № 8. С. 817–826.
Łach Ł., Nowak J., Svyetlichnyy D. The evolution of the microstructure in AISI 304L stainless steel during the flat rolling – modeling by frontal cellular automata and verification // J. Mater. Process. Technol. 2018. V. 255. P. 488–499.
Chen M.S., Yuan W.Q., Lin Y.C., Li H. Bin, Zou Z.H. Modeling and simulation of dynamic recrystallization behavior for 42CrMo steel by an extended cellular automaton method // Vacuum. 2017. V. 146. P. 142–151.
Estrin Y., Mecking H. A unified phenomenological description of work hardening and creep based on one-parameter models // Acta Metall. 1984. V. 32. P. 57–70.
Kocks U.F., Mecking H. Physics and phenomenology of strain hardening: The FCC case // Prog. Mater. Sci. 2003.V. 48. P. 171–273.
Mecking H., Kocks U.F. Kinetics of flow and strain-hardening // Acta Metall. 1981. V. 29. P. 1865–1875.
Nes E., Marthinsen K., Brechet Y. On the mechanisms of dynamic recovery // Scr. Mater. 2002. V. 47. P. 607–611.
Nes E. Modelling of work hardening and stress saturation in FCC metals // Prog. Mater. Sci. 1997. V. 41. P. 129–193.
Nes E., Marthinsen K. Modeling the evolution in microstructure and properties during plastic deformation of f.c.c.-metals and alloys – An approach towards a unified model // Mater. Sci. Eng. A. 2002. V. 322. P. 176–193.
Sevillano J.G. Flow Stress and Work Hardening / in Mater. Sci. Technol. Wiley-VCH Verlag GmbH & Co. KGaA, 2006. P. 21–88.
Zhang Y., Fan Q., Zhang X., Zhou Z., Xia Z., Qian Z. Avrami kinetic-based constitutive relationship for armco-type pure iron in hot deformation // Metals (Basel). 2019. V. 9. P. 365
Guo J., Zhan M., Wang Y.Y., Gao P.F. Unified modeling of work hardening and flow softening in two-phase titanium alloys considering microstructure evolution in thermomechanical processes // J. Alloys Compd. 2018. V. 767. P. 34–45.
Haghdadi N., Martin D., Hodgson P. Physically-based constitutive modelling of hot deformation behavior in a LDX 2101 duplex stainless steel // Mater. Des. 2016. V. 106. P. 420–427.
Johnson W.A., Mehl R.T. Reaction kinetics in processes of nucleation and growth // Trans AIME 1939. V. 185. P. 416–442.
Avrami M. Kinetics of phase change. II Transformation-time relations for random distribution of nuclei // J. Chem. Phys. 1940. V. 8. P. 212–224.
Kolmogorov A.N. On the Statistical Theory of Crystallization of Metals // Izv. Akad. Nauk SSSR, Ser. Mat. 1937. V. 3. P. 355–359.
McQueen H.J., Solberg J.K., Ryum N., Nes E. Evolution of flow stress in aluminium during ultra-high straining at elevated temperatures. Part II // Philos. Mag. A Phys. Condens. Matter, Struct. Defects Mech. Prop. 1989. V. 60. P. 473–485.
Solberg J.K., McQueen H.J., Ryum N., Nes E. Influence of ultra-high strains at elevated temperatures on the microstructure of aluminium. Part I // Philos. Mag. A Phys. Condens. Matter, Struct. Defects Mech. Prop. 1989. V. 60. P. 447–471.
Pettersen T., Holmedal B., Nes E. Microstructure development during hot deformation of aluminum to large strains // Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2003. V. 34. P. 2737–2744.
Горбачев И.И., Пасынков А.Ю., Попов В.В. Моделирование влияния горячей деформации на размер аустенитного зерна низколегированных сталей с карбонитридным упрочнением. Физика металлов и металловедение. 2018. Т. 119. № 6. С. 582–589.
Zener C. Private communication to C.S.Smith // Trans. Am. Inst. Min. Engrs. 1949. V. 175. P. 15.
Gladman T. On the theory of the effect of precipitate particles on grain growth in metals // Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1966. V. 294. P. 298–309.
Nishizawa T., Ohnuma I., Ishida K. Examination of the Zener relationship between grain size and particle dispersion // Mater. Trans. JIM. 1997. V. 38. P. 950–956.
Горбачев И.И., Пасынков А.Ю., Попов В.В.. Прогнозирование размера аустенитного зерна микролегированных сталей на основе моделирования эволюции карбонитридных выделений // Физика металлов и металловедение. 2015. Т. 116. № 11. С. 1184.
Чурюмов А.Ю., Михайловская А.В., Котов А.Д., Базлов А.И., Портной В.К. Разработка математических моделей связи показателей сверхпластичности с параметрами структуры алюминиевых сплавов системы Al–Mg–Si // Физика металлов и металловедение. 2013. Т. 114. № 3. С. 297–304.
Poliak E.I., Jonas J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization // Acta Mater. 1996. V. 44. P. 127–136.
Imran M., Bambach M. A new model for dynamic recrystallization under hot working conditions based on critical dislocation gradients // Procedia Eng. 2017. V. 207. P. 2107–2112.
Sun W.P., Hawbolt E.B. Comparison between static and metadynamic recrystallization - An application to the hot rolling of steels // ISIJ Int. 1997. V. 37. P. 1000–1009.
Хомутов М.Г., Чурюмов А.Ю., Поздняков А.В., Войтенко А.Г., Черешнева А.А. Моделирование кинетики динамической рекристаллизации сплава ХН55МБЮ-ВД в процессе горячей деформации. Металловедение и термическая обработка металлов. 2018. Т. 9(759). С. 52–56.
Kim S. Il, Lee Y., Jang B.L. Modeling of recrystallization and austenite grain size for AISI 316 stainless steel and its application to hot bar rolling // Mater. Sci. Eng. A. 2003. V. 357. P. 235–239.
Чурюмов А.Ю., Поздняков А.В., Чурюмова Т.А., Чеверикин В.В. Горячая пластическая деформация жаропрочной аустенитной стали AISI 310S: 1. Mоделирование напряжения течения и динамической рекристаллизации // Черные металлы. 2020. № 8 (в печати).
Dub V., Churyumov A., Rodin A., Belikov S., Barbolin A. Prediction of grain size evolution for low alloyed steels // Results Phys. 2018. V. 8. P. 584–586.
Zufía Á., Llanos J.M. Mathematical simulation and controlled cooling in an EDC conveyor of a wire rod rolling mill // ISIJ Int. 2001. V. 41. P. 1282–1288.
Manohar P.A., Lim K., Rollett A.D., Lee Y. Computational exploration of microstructural evolution in a medium C-Mn steel and applications to rod mill // ISIJ Int. 2003. V. 43. P. 1421–1430.
Zhao M., Huang L., Zeng R., Su H., Wen D., Li J. In-situ observations and modeling of metadynamic recrystallization in 300M steel // Mater. Charact. 2020. V. 159. P. 109997.
He D.G., Lin Y.C., Wang L.H. Microstructural variations and kinetic behaviors during metadynamic recrystallization in a nickel base superalloy with pre-precipitated δ phase // Mater. Des. 2019. V. 165. P. 107584
Dong D., Chen F., Cui Z. Investigation on metadynamic recrystallization behavior in SA508-Ш steel during hot deformation // J. Manuf. Process. 2017. V. 29. P. 18–28.
Majta J., Lenard J.G., Pietrzyk M. Modelling the Evolutlon of the Microstructure of a Nb Steel // ISIJ Int. 1996. V. 36. P. 1094–1102.
Chen F., Cui Z., Sui D., Fu B. Recrystallization of 30Cr2Ni4MoV ultra-super-critical rotor steel during hot deformation. Part III: Metadynamic recrystallization // Mater. Sci. Eng. A 2012. V. 540. P. 46–54.
Ma B., Peng Y., Jia B., Liu Y.F. Static recrystallization kinetics model after hot deformation of low-alloy steel Q345B // J. Iron Steel Res. Int. 2010. V. 17. P. 61–66.
Zhao M., Huang L., Zeng R., Wen D., Su H., Li J. In-situ observations and modeling of static recrystallization in 300 M steel // Mater. Sci. Eng. A 2019. V. 765. P. 138300
Nakata N., Militzer M. Modelling of microstructure evolution during hot rolling of a 780 MPa high strength steel // ISIJ Int. 2005. V. 45. P. 82–90.
Yogo Y., Tanaka K., Nakanishi K. In-situ observation of grain growth of steel at high temperature // Mater. Trans. 2009. V. 50. P. 280–285.
Dubois M., Militzer M., Moreau A., Bussière J.F. New technique for the quantitative real-time monitoring of austenite grain growth in steel // Scr. Mater. 2000. V. 42. P. 867–874.
Toozandehjani M., Matori K.A., Ostovan F., Mustapha F., Zahari N.I., Oskoueian A. On the correlation between microstructural evolution and ultrasonic properties: a review // J. Mater. Sci. 2015. V. 50. P. 2643–2665.
Garcin T., Schmitt J.H., Militzer M. In-situ laser ultrasonic grain size measurement in superalloy INCONEL 718 // J. Alloys Compd. 2016. V. 670. P. 329–336.
Karjalainen L.P. Stress relaxation method for investigation of softening kinetics in hot deformed steels // Mater. Sci. Technol. (United Kingdom) 1995. V. 11. P. 557–565.
Cheng L., Chang H., Tang B., Kou H., Li J. Characteristics of metadynamic recrystallization of a high Nb containing TiAl alloy // Mater. Lett. 2013. V. 92. P. 430–432.
Hodgson B., Gibbs R.K. A Mathematical Hot Rolled C‒Mn Model to Predict and Microalloyed the Mechanical Properties ot Steels // ISIJ Int. 1992. V. 32. P. 1329–1338.
Liu F., Sommer F., Bos C., Mittemeijer E.J. Analysis of solid state phase transformation kinetics: Models and recipes // Int. Mater. Rev. 2007. V. 52. P. 193–212.
Li N., Lin J., Balint D.S., Dean T.A. Modelling of austenite formation during heating in boron steel hot stamping processes // J. Mater. Process. Technol. 2016. V. 237. P. 394–401.
Bellavoine M., Dumont M., Dehmas M., Stark A., Schell N., Drillet J., Hébert V., Maugis P. Ferrite recrystallization and austenite formation during annealing of cold-rolled advanced high-strength steels: In situ synchrotron X-ray diffraction and modeling // Mater. Charact. 2019. V. 154. P. 20–30.
Li H., Gai K., He L., Zhang C., Cui H., Li M. Non-isothermal phase-transformation kinetics model for evaluating the austenization of 55CrMo steel based on Johnson–Mehl–Avrami equation // Mater. Des. 2016. V. 92. P. 731–741.
De Andres M.P., Carsí M. Hardenability: an alternative to the use of grain size as calculation parameter // J. Mater. Sci. 1987. V. 22. P. 2707–2716.
Tamura I., Sekine H., Tanaka T. Thermomechanical Processing of High-Strength Low-Alloy Steels. Butterworth-Heinemann, 1988; ISBN 9781483164052.
Kamamoto S., Nishimori T., Kinoshita S. Analysis of residual stress and distortion resulting from quenching in large low-alloy steel shafts // Mater. Sci. Technol. (United Kingdom) 1985. V. 1. P. 798–804.
Johns S.J., Bhadeshia H.K.D.H. Kinetics of the Simultaneous Decomposition of Austenite into Several Transformation Products // Acta Metallurg. Mater. 1997. V. 45. P. 2911–2920.
Zener C. Kinetics of the decomposition of austenite // Trans. Aime. 1946. V. 167. P. 550–595.
Hillert M. The role of interfacial energy during solid-state phase transformations // Jernkontorets Ann. 1957. V. 141. P. 757–789.
Victor Li M., Niebuhr D. V., Meekisho L.L., Atteridge D.G. A computational model for the prediction of steel hardenability // Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 1998. V. 29. P. 661–672.
Koistinen D.P., Marburger R.E. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels // Acta Metall. 1959. V. 7. P. 59–60.
Lee S.J., Lee Y.K. Finite element simulation of quench distortion in a low-alloy steel incorporating transformation kinetics // Acta Mater. 2008. V. 56. P. 1482–1490.
Zhao H., Hu X., Cui J., Xing Z. Kinetic Model for the Phase Transformation of High-Strength Steel Under Arbitrary Cooling Conditions // Met. Mater. Int. 2019. V. 25. P. 381–395.
Venturato G., Bruschi S., Ghiotti A., Chen X. Numerical modeling of the 22MnB5 formability at high temperature // Procedia Manuf. 2019. V. 29. P. 428–434.
Lee S.J., Pavlina E.J., Van Tyne C.J. Kinetics modeling of austenite decomposition for an end-quenched 1045 steel // Mater. Sci. Eng. A 2010. V. 527. P. 3186–3194.
Chen W., Xu L., Zhao L., Han Y., Jing H., Zhang Y., Li Y. Thermo-mechanical-metallurgical modeling and validation for ferritic steel weldments // J. Constr. Steel Res. 2020. V. 166. P. 105948.
Wang Q., Liu X.S., Wang P., Xiong X., Fang H.Y. Numerical simulation of residual stress in 10Ni5CrMoV steel weldments // J. Mater. Process. Technol. 2017. V. 240. P. 77–86.
Starink M.J., Zahra C.Y., Zahra A.M. Analysis of precipitation in Al-based alloys using a novel model for nucleation and growth reactions // J. Therm. Anal. Calorim. 1998. V. 51. P. 933–942.
Myhr O.R., Grong, Fjær H.G., Marioara C.D. Modelling of the microstructure and strength evolution in Al–Mg–Si alloys during multistage thermal processing // Acta Mater. 2004. V. 52. P. 4997–5008.
Wagner R., Kampmann R., Voorhees P.W. Homogeneous Second-Phase Precipitation // Mater. Sci. Technol. 2013. P. 309–407. https://doi.org/10.1002/9783527603978.mst0388
Simar A., Bréchet Y., de Meester B., Denquin A., Pardoen T. Sequential modeling of local precipitation, strength and strain hardening in friction stir welds of an aluminum alloy 6005A-T6 // Acta Mater. 2007. V. 55. P. 6133–6143.
Perez M., Dumont M., Acevedo-Reyes D. Implementation of classical nucleation and growth theories for precipitation // Acta Mater. 2008. V. 56. P. 2119–2132.
da Costa Teixeira J., Cram D.G., Bourgeois L., Bastow T.J., Hill A.J., Hutchinson C.R. On the strengthening response of aluminum alloys containing shear-resistant plate-shaped precipitates // Acta Mater. 2008. V. 56. P. 6109–6122.
Bardel D., Perez M., Nelias D., Deschamps A., Hutchinson C.R., Maisonnette D., Chaise T., Garnier J., Bour-lier F. Coupled precipitation and yield strength modelling for non-isothermal treatments of a 6061 aluminium alloy // Acta Mater. 2014. V. 62. P. 129–140.
Robson J.D., Prangnell P.B. Dispersoid precipitation and process modelling in zirconium containing commercial aluminum alloys // Acta Mater. 2001. V. 49. P. 599–613.
Christian J.W. The Theory of Transformations in Metals and Alloys. 1st Editio. Pergamon, 2002; ISBN 9780080440194.
Saunders N. Calculated stable and metastable phase equilibria in Al–Li–Zr alloys // Zeitschrift fuer Met. 1989. V. 80. P. 894–903.
Porter D.A., Easterling K.E. Phase transformations in metals and alloys; Chapman & Hall, Ed., 1992.
Robson J.D., Jones M.J., Prangnell P.B. Extension of the N-model to predict competing homogeneous and heterogeneous precipitation in Al-Sc alloys // Acta Mater. 2003. V. 51. P. 1453–1468.
Robson J.D. A new model for prediction of dispersoid precipitation in aluminium alloys containing zirconium and scandium // Acta Mater. 2004. V. 52. P. 1409–1421.
Clouet E., Barbu A., Laé L., Martin G. Precipitation kinetics of Al3Zr and Al3Sc in aluminum alloys modeled with cluster dynamics // Acta Mater. 2005. V. 53. P. 2313–2325.
Золоторевский В.С., Поздняков А.В., Чурюмов А.Ю. Поиск перспективных композиций для создания новых многофазных литейных сплавов на основе матрицы Al–Zn–Mg с использованием термодинамических расчетов и математического моделирования // Физика металлов и металловедение. 2014. Т. 115. № 3. С. 305.
Золоторевский В.С., Поздняков А.В., Чурюмов А.Ю. Поиск перспективных композиций для создания новых многофазных литейных сплавов на основе матрицы Al–Cu–Mg с использованием термодинамических расчетов и математического моделирования // Физика металлов и металловедение. 2012. Т. 113. № 11. С. 1–10.
Svyetlichnyy D.S., Nowak J., Łach Ł. Modeling of recrystallization with recovery by frontal cellular automata / In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). 2012. V. 7495 LNCS, P. 494–503.
Seppälä O., Pohjonen A., Kaijalainen A., Larkiola J., Porter D. Simulation of bainite and martensite formation using a noval cellular automata method // Procedia Manuf. 2018. V. 15. P. 1856–1863.
Kundu S., Dutta M., Ganguly S., Chandra S. Prediction of phase transformation and microstructure in steel using cellular automaton technique // Scr. Mater. 2004. V. 50. P. 891–895.
Zhang J., Li Z., Wen K., Huang S., Li X., Yan H., Yan L., Liu H., Zhang Y., Xiong B. Simulation of dynamic recrystallization for an Al–Zn–Mg–Cu alloy using cellular automaton // Prog. Nat. Sci. Mater. Int. 2019. V. 29. P. 477–484
Sitko M., Pietrzyk M., Madej L. Time and length scale issues in numerical modelling of dynamic recrystallization based on the multi space cellular automata method // J. Comput. Sci. 2016. V. 16. P. 98–113.
Hore S., Das S.K., Banerjee S., Mukherjee S. Computational modelling of static recrystallization and two dimensional microstructure evolution during hot strip rolling of advanced high strength steel // J. Manuf. Process. 2015. V. 17. P. 78–87.
Steiner M.A., McCabe R.J., Garlea E., Agnew S.R. Monte Carlo modeling of recrystallization processes in α-uranium // J. Nucl. Mater. 2017. V. 492. P. 74–87.
Molnar D., Niedermeier C., Mora A., Binkele P., Schmauder S. Activation energies for nucleation and growth and critical cluster size dependence in JMAK analyses of kinetic Monte-Carlo simulations of precipitation // Contin. Mech. Thermodyn. 2012. V. 24. P. 607–617.
Rasti J. Study of the Grain Size Distribution during Preheating Period Prior to the Hot Deformation in AISI 316L Austenitic Stainless Steel // Phys. Met. Metallogr. 2019. V. 120. P. 584–592.
Gorbatov O.I., Gornostyrev Y.N., Korzhavyi P.A., Ruban A. V. Ab initio modeling of decomposition in iron based alloys // Phys. Met. Metallogr. 2016. V. 117. P. 1293–1327.
Takaki T., Hirouchi T., Hisakuni Y., Yamanaka A., Tomita Y. Multi-phase-field model to simulate microstructure evolutions during dynamic recrystallization // Mater. Trans. 2008. V. 49. P. 2559–2565.
Zhang J., Zheng C.W., Li D.Z. A multi-phase field model for static recrystallization of hot deformed austenite in a C–Mn steel // Acta Metall. Sin. (English Lett). 2018. V. 31. P. 208–215.
Janssens K.G.F. An introductory review of cellular automata modeling of moving grain boundaries in polycrystalline materials // Math. Comput. Simul. 2010. V. 80. P. 1361–1381.
Sieradzki L., Madej L. A perceptive comparison of the cellular automata and Monte Carlo techniques in application to static recrystallization modeling in polycrystalline materials // Comput. Mater. Sci. 2013. V. 67. P. 156–173.
Hallberg H. Approaches to modeling of recrystallization // Metals (Basel). 2011. V. 1. P. 16–48.
Song X., Rettenmayr M. Modeling recrystallization in a material containing fine and coarse particles // Comput. Mater. Sci. 2007. V. 40. P. 234–245.
Lin Y.C., Liu Y.X., Chen M.S., Huang M.H., Ma X., Long Z.L. Study of static recrystallization behavior in hot deformed Ni-based superalloy using cellular automaton model // Mater. Des. 2016. V. 99. P. 107–114.
Doherty R.D., Hughes D.A., Humphreys F.J., Jonas J.J., Juul Jensen D., Kassner M.E., King W.E., McNelley T.R., McQueen H.J., Rollett A.D. Current issues in recrystallization: A review // Mater. Sci. Eng. A. 1997. V. 238. P. 219–274.
Liu Y.X., Lin Y.C., Zhou Y. 2D cellular automaton simulation of hot deformation behavior in a Ni-based superalloy under varying thermal-mechanical conditions // Mater. Sci. Eng. A. 2017. V. 691. P. 88–99.
Madej L., Sitko M., Perzynski K., Sieradzki L., Radwanski K., Kuziak R. Multi scale cellular automata and finite element based model for cold deformation and annealing of a ferritic-pearlitic microstructure // Multiscale Mater. Model. Approaches to Full Multiscaling. 2016. V. 77. P. 235–254.
Ding R., Guo Z.X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization // Acta Mater. 2001. V. 49. P. 3163–3175.
Chen F., Cui Z., Liu J., Chen W., Chen S. Mesoscale simulation of the high-temperature austenitizing and dynamic recrystallization by coupling a cellular automaton with a topology deformation technique // Mater. Sci. Eng. A. 2010. V. 527. P. 5539–5549.
Chen F., Qi K., Cui Z., Lai X. Modeling the dynamic recrystallization in austenitic stainless steel using cellular automaton method // Comput. Mater. Sci. 2014. V. 83. P. 331–340.
Liu Y.X., Lin Y.C., Li H. Bin, Wen D.X., Chen X.M., Chen M.S. Study of dynamic recrystallization in a Ni-based superalloy by experiments and cellular automaton model // Mater. Sci. Eng. A. 2015. V. 626. P. 432–440.
Sun F., Zhang D.Q., Cheng L., Zheng P., Liao D.M., Zhu B. Microstructure Evolution Modeling and Simulation for Dynamic Recrystallization of Cr12MoV Die Steel During Hot Compression Based on Real Metallographic Image // Met. Mater. Int. 2019. V. 25. P. 966–981.
Zhang C., Zhang L., Xu Q., Xia Y., Shen W. The kinetics and cellular automaton modeling of dynamic recrystallization behavior of a medium carbon Cr–Ni–Mo alloyed steel in hot working process // Mater. Sci. Eng. A. 2016. V. 678. P. 33–43.
Zhang H., Wang J., Chen Q., Shu D., Wang C., Chen G., Zhao Z. Study of dynamic recrystallization behavior of T2 copper in hot working conditions by experiments and cellular automaton method // J. Alloys Compd. 2019. V. 784. P. 1071–1083.
Li X., Li X., Zhou H., Zhou X., Li F., Liu Q. Simulation of dynamic recrystallization in AZ80 magnesium alloy using cellular automaton // Comput. Mater. Sci. 2017. V. 140. P. 95–104.
Yazdipour N., Hodgson P.D. Modelling post-deformation softening kinetics of 304 austenitic stainless steel using cellular automata // Comput. Mater. Sci. 2012. V. 54. P. 56–65.
Lan Y.J., Li D.Z., Li Y.Y. Modeling austenite decomposition into ferrite at different cooling rate in low-carbon steel with cellular automaton method // Acta Mater. 2004. V. 52. P. 1721–1729.
Lan Y.J., Li D.Z., Li Y.Y. Mesoscale simulation of ferrite transformation from deformed austenite during continuous cooling in a C–Mn steel using a cellular automaton method // Comput. Mater. Sci. 2005. V. 32. P. 147–155.
Militzer M., Pandi R., Hawbolt E.B. Ferrite nucleation and growth during continuous cooling // Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1996. V. 27. P. 1547–1556.
Yang B.J., Chuzhoy L., Johnson M.L. Modeling of reaustenitization of hypoeutectoid steels with cellular automaton method // Comput. Mater. Sci. 2007. V. 41. P. 186–194.
Yu X., Chen S. A simulation of Cr depletion in austenitic stainless steel with cellular automaton // Comput. Mater. Sci. 2009. V. 45. P. 899–904.
Hore S., Das S.K., Banerjee S., Mukherjee S. A multiscale coupled Monte Carlo model to characterize microstructure evolution during hot rolling of Mo-TRIP steel // Acta Mater. 2013. V. 61. P. 7251–7259.
Kazeminezhad M. On the modeling of the static recrystallization considering the initial grain size effects // Mater. Sci. Eng. A. 2008. V. 486. P. 202–207.
Krill C.E., Chen L.Q. Computer simulation of 3-D grain growth using a phase-field model // Acta Mater. 2002. V. 50. P. 3057–3073.
Steinbach I., Pezzolla F. A generalized field method for multiphase transformations using interface fields // Phys. D Nonlinear Phenom. 1999. V. 134. P. 385–393.
Kugler G., Turk R. Modeling the dynamic recrystallization under multi-stage hot deformation // Acta Mater. 2004. V. 52. P. 4659–4668.
Zhang X., Shen G., Li C., Gu J. Phase-field simulation of austenite reversion in a Fe–9.6Ni–7.1Mn (at %) martensitic steel governed by a coupled diffusional/displacive mechanism // Mater. Des. 2020. V. 188. P. 108426.
Kinoshita T., Ohno M. Phase-field simulation of abnormal grain growth during carburization in Nb-added steel // Comput. Mater. Sci. 2020. V. 177. P. 109558.
Mushongera L.T., Amos P.G.K., Nestler B., Ankit K. Phase-field simulations of pearlitic divergence in Fe–C–Mn steels // Acta Mater. 2018. V. 150. P. 78–87.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение