Физика металлов и металловедение, 2020, T. 121, № 5, стр. 454-457

ВВЕДЕНИЕ

Одним из впечатляющих проявлений самосборки в неживой природе можно считать наблюдаемые в магнитоупорядоченных средах процессы целенаправленного (спонтанного или вынужденного) изменения симметрии, формы, или типа доменных структур (ДС) под действием внешних факторов и даже в их отсутствие. Такие процессы могут быть как статическими, так и динамическими (в этом случае говорят о самоорганизации).

ПРЕДЫСТОРИЯ

Существование статической самосборки ДС было обнаружено сразу же после разработки в 30-е годы прошлого века первого способа визуализации доменов, получившего название метода порошковых фигур или метода магнитной суспензии [1–3]. Оказалось, что расположение доменов в магнетиках не является случайным, а имеет тенденцию к образованию вполне определенных конфигураций. Многочисленные фотографии ДС, полученные указанным методом, приведены в статьях и тематических сборниках того же периода времени. Интерес к наблюдению, описанию и классификации различных проявлений статической самосборки породил в 60-е годы прошлого века и другие методы визуализации доменов (магнитооптические: на эффектах Керра [4], Фарадея [5] и магнитного двулучепреломления [6], с использованием электронной микроскопии [7, 8], датчиков Холла [9] и др.). Дополнительный импульс к изучению данной проблемы придали эксперименты по динамической самоорганизации, выполненные уральскими физиками Кандауровой Г.С. и Свидерским А.Э., которые в тонких квазиодноосных эпитаксиальных пленках ферритов-гранатов наблюдали преобразование лабиринтной ДС в спиральные и кольцевые домены под действием внешнего низкочастотного магнитного поля [10, 11]. Позже ими же было показано, что в сходных условиях реализуются и другие типы динамически индуцируемых ДС [12, 13]. Формирование строго упорядоченных массивов цилиндрических магнитных доменов с образующими в форме эллипса, бумеранга, восьмерки, гантели и др. при специальном выборе параметров переменного магнитного поля наблюдали авторы работ [14–17].

Анализ многочисленных изображений, возникающих при статической и динамической самосборке ДС, показывает, что в целом ряде случаев в них присутствуют фрагменты, обладающие иерархической структурой и приближенным (топологическим) самоподобием, что позволяет производить их описание в рамках фрактальной идеологии. Образование подобных агрегатов, наблюдаемое в различных структурированных средах при диффузионном характере движения их частей, носит название фрактальной кластеризации (см., напр., [18]). Размер фрагментов, определяемый множеством факторов, в том числе степенью однородности магнетика и качества поверхности, на которой наблюдается ДС, может колебаться в значительных пределах. Найти полную аналогию с известными типами геометрических фракталов, как правило, не удается, поэтому во всех рассматриваемых случаях следует употреблять термин “фракталоподобные ДС”, как это было сделано в [19].

Если для классификации абстрактных фракталов (геометрических, алгебраических и стохастических) используют принцип персонификации (снежинка Коха, ковер Серпинского, множество Мандельброта и т.п.), то для фракталоподобных ДС обращаются, как правило, к наглядному описанию, выделяя классы древовидных, мозаичных, сетчатых, ромбических, клиновидных, зигзагообразных, ветвящихся и других конфигураций. Для изучения возможности практического использования таких структур необходимо нахождение их адекватных моделей и алгоритмов их конструирования.

ОПИСАНИЕ ПРЕДЛАГАЕМОЙ МОДЕЛИ

Конфигурация возникающих при самосборке ДС может быть достаточно сложной, поэтому их модели стараются создавать, опираясь на хорошо известные геометрические фракталы, напр., ковер Серпинского [20, 21]. Довольно часто при этом используют и различные его модификации, чему в немалой степени способствует и то обстоятельство, что именно такие фрактальные структуры находят применение в магнонных, фононных и фотонных кристаллах для микро- и наноэлектроники [22‒24]. Модели кластеров со структурой ковра Серпинского использовали для оценки влияния фрактальной размерности на кривые намагничивания материалов, состоящего из обменно-связанных наночастиц со случайно ориентированными осями легкого намагничивания [25].

Авторы [26] для описания правильной ромбической формы замыкающих доменов на плоскости (010) монокристаллов FeB использовали модель, показанную на рис. 1. По существу, эта модель представляет собой паркетную укладку в шахматном порядке двух типов предфракталов, которые можно рассматривать, как модификации ковра Серпинского. Предфракталы двух типов, соседствующие друг с другом, переходят друг в друга при инверсии цвета.

Рис. 1.

Модель структуры замыкающих доменов на плоскости (010) ромбического монокристалла FeB [26].

Для моделирования часто наблюдаемой в высокоанизотропных одноосных монокристаллах cложной приповерхностной ДС со “звездочками” (рис. 2), нами предложено использовать модификацию квадратного ковра Серпинского с однотипной деформацией границ всех квадратных элементов в каждом из поколений фрактала. Другие примеры можно найти в обзоре [12] и в работах Пастушенкова Ю.Г. с сотрудниками [28].

Рис. 2.

Сложная приповерхностная ДС со “звездочками” на базисной плоскости (001) монокристалла ErFe₁₁Ti [27].

Процесс создания модели включает два этапа. На первом этапе формируется промежуточная модификация обычного ковра по алгоритму, который поясняет рис.3. В верхнем ряду приведены последовательные стадии построения предфракталов первых трех поколений классического ковра Серпинского. На первом шаге большой черный квадрат со сторонами L делится на девять равновеликих со сторонами L/3, и средний квадрат выбрасывается; далее процедура производится с каждым из восьми черных квадратов, окаймляющих центральный “белый” квадрат, который остается без изменений. Далее процесс повторяется для шестидесяти четырех квадратов со сторонами L/9 и т.д.

Рис. 3.

Последовательные стадии построения начальных поколений предфракталов классического (верхний ряд) и модифицированного (нижний ряд) ковра Серпинского.

Построение промежуточной модификации ковра (см. нижний ряд на рис. 3) начинается также с большого черного квадрата со сторонами L, из которого удален центральный квадрат со сторонами L/3, однако на втором шаге, в отличие от классического ковра Серпинского, в центр фигуры вставляется черный квадрат со сторонами L/9. На третьем шаге (последнее изображение в нижнем ряду) используется разбиение квадрата сеткой с шагом L/9 на 81 квадрат с последующим размещением в центре каждого из них квадрата со сторонами L/27 противоположного цвета (черный в белом и наоборот). Этот процесс можно продолжать до бесконечности. Для достижения итеративности предлагаемого алгоритма моделирования выбранной ДС отсчет поколений описанного модифицированного ковра Серпинского следует начинать со второго шага.

Этот ковер обладает всеми признаками фрактала: при изменении масштаба в 3 раза не меняется как его вид, так и создаваемая им дифракционная картина в дальней зоне. В отличие от классического ковра Серпинского, который представляет собой связанное топологическое множество, этот модифицированный ковер связностью не обладает. Хаусдорфова размерность для него равна 2 (у ковра Серпинского она составляет ln8/ln3 = = 1.89), а коэффициенты масштабирования у обеих фракталов равны 3.

На втором этапе формирования модели для приближенной имитации реальной формы доменов на каждом шаге построения модифицированного ковра Серпинского стороны всех квадратов (белых и черных) заменяются симметричными трехзвенными ломаными с одинаковой длиной звеньев (верхняя часть рис.4). Нетрудно убедиться, что отношение k длины звеньев ломаной к длине заменяемой стороны квадрата, определяется формулой

Рис. 4.

Результаты замены трехзвенными ломаными всех отрезков прямых линий для трех поколений предфракталов модифицированного ковра Серпинского.

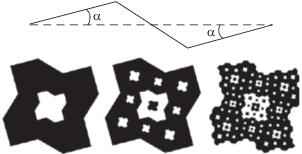
Здесь α – угол отклонения крайних звеньев ломаной от стороны квадрата, который не может превышать 30°. Далее мы использовали значение α = 15°. Применяя описанную процедуру к промежуточной модификации ковра (нижний ряд на рис. 3) при обходе сторон квадратов в направлении против часовой стрелки, получаем структуры, изображенные в нижнем ряду рис. 4.

Замена всех отрезков прямых линий полученного на первом этапе модифицированного ковра Серпинского трехзвенными ломаными приводит к преобразованию внешней границы, а также всех границ между “черными” и “белыми” внутренними элементами топологического множества во фрактальные кривые в виде замкнутых многозвенных ломаных (см. рис. 4). Необходимо заметить, что такая модификация ковра Серпинского является принципиально новой и ранее в литературе не описывалась.

ЗАКЛЮЧЕНИЕ

Совокупность модифицированных ковров, соединенных в цепочку или образующих шахматный порядок с коврами противоположной “полярности”, может служить грубой, но достаточно адекватной моделью сложных ДС. Предложенная принципиально новая фрактальная модель является гибкой и позволяет добиваться максимального сходства ее изображения с реальной формой моделируемых ДС путем варьирования угла α и номера поколения модифицированного ковра Серпинского. При этом следует иметь в виду, что любые геометрические модели, оперирующие невзаимодействующими объектами в “пустом” пространстве, не в состоянии полностью отражать поведение реальных фракталов, составные части которых, как правило, взаимодействуют и влияют друг на друга. По этой причине при использовании для моделирования высоких поколений предфракталов происходит сдвиг внутренних областей, а также изменение их размеров.

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме 0030-2019-0014.