1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 122, № 10, 2021

Физика металлов и металловедение, 2021, T. 122, № 10, стр. 1013-1021

Сечения поглощения и рассеяния электромагнитного излучения ансамблями металлических наночастиц разной формы

А. В. Коротун a, *, Н. И. Павлище a

a Национальный университет “Запорожская политехника”
69063 Запорожье, ул. Жуковского, 64, Украина

* E-mail: andko@zntu.edu.ua

Поступила в редакцию 26.01.2021
После доработки 31.05.2021
Принята к публикации 07.06.2021

Полный текст (PDF)

Аннотация

С помощью предельных переходов из общих соотношений для скоростей поверхностной релаксации и радиационного затухания в вытянутой и сплюснутой эллипсоидальной наночастице получены соответствующие выражения для частиц в форме стержня и диска. Рассчитаны частотные зависимости статистически усредненных эффективностей поглощения и рассеяния электромагнитного излучения наночастицами различной формы. Вычисления проведены для наноструктур Au, Ag, Cu и Pt. Проанализировано влияние формы и материала наночастицы на количество, положение максимумов и эффективность поглощения и рассеяния. Установлено, что наличие двух максимумов частотной зависимости эффективности рассеяния для нанодисков связано с проявлением продольного и поперечного поверхностного плазмонного резонанса.

Ключевые слова: сечение поглощения, сечение рассеяния, ансамбль, скорость релаксации, эффективность поглощения, эффективность рассеяния, частотная зависимость

ВВЕДЕНИЕ

В настоящее время наблюдается повышенный интерес ученых и практиков к изучению оптических свойств наночастиц и вещества в дисперсной фазе [1–8]. Этот интерес вызван прежде всего с тем фактом, что оптические свойства указанных объектов существенно отличаются от аналогичных свойств объемных материалов. Кроме того, эти уникальные свойства имеют широкое использование в квантовой микро- и оптоэлектронике, материаловедении, медицине, биологии и других областях науки и техники [9–12]. Существуют предпосылки для использования необычных оптических свойств наночастиц для создания диэлектриков с регулируемыми диэлектрическими свойствами [13], элементов градиентной оптики [14] и плазмонной фотовольтаики [15], новых видов электронных устройств [9–11], средств для фототермической терапии злокачественных опухолей и других медицинских применений [16].

Следует отметить, что быстрое развитие аналитических и численных методов в последние годы [17, 18] обусловило значительный прогресс в понимании процессов взаимодействия света с наночастицами. Однако сказанное выше относится к частицам сферической, цилиндрической и эллипсоидальной формы [18–21]. В работах [22, 23] было исследовано влияние квантово-размерных эффектов на оптические свойства единичных металлических наноструктур цилиндрической и сферической формы.

На практике часто приходится иметь дело не с отдельными частицами, а с их ансамблями. При этом частицы в ансамблях, как правило, отличаются размерами, формой и составом, могут непрерывно изменять свою ориентацию и положение в пространстве. Еще одним усложняющим фактором может быть необходимость учета многократного рассеяния (взаимной поляризации частиц). Понятно, что все эти обстоятельства значительно усложняют изучение закономерностей взаимодействия света с ансамблями частиц. В большинстве случаев необходимо знание эффективных (усредненных по ансамблю) характеристик рассеяния (поглощения), таких как эффективное интегральное сечение или индикатриса рассеяния вместо характеристик отдельных частиц. Расчет указанных величин, а также поляризационных характеристик рассеянного света, в свою очередь, является очень сложной задачей и часто требует применения численных методов.

В длинноволновом приближении эффективная диэлектрическая функция любого ансамбля малых частиц может быть представлена в интегральной форме с ядром, представляющим собой поляризуемость сфероида [24]. Это означает, что длинноволновые линейные оптические свойства любой дисперсной среды такие же, как и у некоторого формораспределенного ансамбля невзаимодействующих сфероидов.

Поэтому целью данной работы является исследование усредненных по ансамблю частотных зависимостей сечения поглощения и рассеяния электромагнитного излучения наночастицами различной геометрии (сфера, стержень, диск), изготовленных из различных металлов с учетом поверхностного и радиационного рассеяния электронов.

УСРЕДНЕННЫЕ СЕЧЕНИЯ ПОГЛОЩЕНИЯ И РАССЕЯНИЯ

Рассмотрим ансамбль металлических наночастиц, имеющих хаотическую ориентацию и расположенных в диэлектрической среде с проницаемостью ${{\epsilon }_{{\text{m}}}}.$

Применим к такому ансамблю статистическое усреднение [24], когда можно рассматривать рассеяние от некоторой “эффективной” частицы, характеристики которой имеют статистическую природу. Преимущество такого подхода заключается в следующем. Картина рассеяния и поглощения электромагнитного излучения отдельной частицей может быть весьма сложной и содержать множество деталей. При усреднении же по размерам и ориентациям большинство деталей сглаживаются. Таким образом, статистический подход позволяет избавиться от необходимости рассчитывать детали тонкой структуры спектров поглощения и рассеяния.

Усредненные по ансамблю сечения поглощения и рассеяния электромагнитного излучения наночастицами даются выражениями [24]:

(1)
$\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle = \frac{\omega }{c}\sqrt {{{\epsilon }_{{\text{m}}}}} \left\langle {\operatorname{Im} \alpha } \right\rangle ;$
(2)
$\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle = \frac{1}{{6\pi }}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}\epsilon _{{\text{m}}}^{2}{{\left| {\left\langle \alpha \right\rangle } \right|}^{2}},$
где

(3)
$\left\langle {\operatorname{Im} \alpha } \right\rangle = \frac{1}{3}\operatorname{Im} \left( {{{\alpha }_{1}} + {{\alpha }_{2}} + {{\alpha }_{3}}} \right);$
(4)
${{\left| {\left\langle \alpha \right\rangle } \right|}^{2}} = \frac{{{{{\left| {{{\alpha }_{1}}} \right|}}^{2}} + {{{\left| {{{\alpha }_{2}}} \right|}}^{2}} + {{{\left| {{{\alpha }_{3}}} \right|}}^{2}}}}{3}.$

Компоненты диагонального тензора поляризуемости

$\alpha = \left( {\begin{array}{*{20}{c}} {{{\alpha }_{1}}}&0&0 \\ 0&{{{\alpha }_{2}}}&0 \\ 0&0&{{{\alpha }_{3}}} \end{array}} \right),$
задаются соотношением

(5)
${{\alpha }_{i}} = V\frac{{{{\epsilon }^{{\left( i \right)}}} - {{\epsilon }_{{\text{m}}}}}}{{{{\epsilon }_{{\text{m}}}} + {{\mathcal{L}}_{i}}\left( {{{\epsilon }^{{\left( i \right)}}} - {{\epsilon }_{{\text{m}}}}} \right)}}.$

Здесь $V$ – объем наночастицы; ${{\mathcal{L}}_{i}}$ – фактор деполяризации ($i = 1,\,\,2,\,3$); ${{\epsilon }^{{\left( i \right)}}}$ – компоненты диагонального диэлектрического тензора

$\epsilon = \left( {\begin{array}{*{20}{c}} {{{\epsilon }^{{\left( 1 \right)}}}}&0&0 \\ 0&{{{\epsilon }^{{\left( 2 \right)}}}}&0 \\ 0&0&{{{\epsilon }^{{\left( 3 \right)}}}} \end{array}} \right).$

Конкретизируем выражения (1) и (2) для ансамблей наночастиц, имеющих форму сферы, стержня и диска.

1. Сфера (${{\mathcal{L}}_{1}} = {{\mathcal{L}}_{2}} = {{\mathcal{L}}_{3}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$), поэтому диэлектрический тензор вырождается в скаляр ${{\epsilon }^{{\left( 1 \right)}}} = {{\epsilon }^{{\left( 2 \right)}}} = {{\epsilon }^{{\left( 3 \right)}}} = \epsilon \left( \omega \right) = {{\epsilon }_{1}} + \operatorname{i} {{\epsilon }_{2}}{\kern 1pt} :$

(6)
${{\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{sphere}}}}} = \frac{\omega }{c}\frac{V}{{\sqrt {{{\epsilon }_{{\text{m}}}}} }}\frac{{27{{\epsilon }_{2}}\epsilon _{{\text{m}}}^{2}}}{{{{{\left( {{{\epsilon }_{1}} + 2{{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{2}}};$
(7)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{sphere}}}}} = \frac{{81}}{{2\pi }}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}{{V}^{2}}\epsilon _{{\text{m}}}^{2} \times \\ \times \,\,\frac{{{{{\left[ {\frac{1}{3}\left( {{{{\left( {{{\epsilon }_{1}} - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{2}} \right) + {{\epsilon }_{{\text{m}}}}\left( {{{\epsilon }_{1}} - {{\epsilon }_{{\text{m}}}}} \right)} \right]}}^{2}} + \epsilon _{{\text{m}}}^{2}\epsilon _{2}^{2}}}{{{{{\left( {{{\epsilon }_{1}} + 2{{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{2}}}. \\ \end{gathered} $

Используя модифицированную теорию Друде–Зоммерфельда, выражения для действительной и мнимой частей диэлектрической функции металлической наночастицы можно записать в виде:

(8)
${{\epsilon }_{1}}\left( \omega \right) = {{\epsilon }^{\infty }} - \frac{{\omega _{p}^{2}}}{{{{\omega }^{2}} + \gamma _{{{\text{eff}}}}^{2}}},\,\,\,\,{{\epsilon }_{2}}\left( \omega \right) = \frac{{\omega _{p}^{2}{{\gamma }_{{{\text{eff}}}}}}}{{\omega \left( {{{\omega }^{2}} + \gamma _{{{\text{eff}}}}^{2}} \right)}}.$

Здесь ${{\epsilon }^{\infty }}$ – вклад ионного остова; $\omega _{p}^{2} = {{{{e}^{2}}{{n}_{e}}} \mathord{\left/ {\vphantom {{{{e}^{2}}{{n}_{e}}} {{{\epsilon }_{0}}m{\kern 1pt} *}}} \right. \kern-0em} {{{\epsilon }_{0}}m{\kern 1pt} *}},$ $e$ и ${{n}_{e}}$ – заряд и концентрация электронов, соответственно (${{n}_{e}} = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}\pi r_{s}^{3},$ ${{r}_{s}}$ – среднее расстояние между электронами), ${{\epsilon }_{0}}$ – электрическая постоянная, $m{\kern 1pt} *$ – эффективная масса электронов; ${{\gamma }_{{{\text{eff}}}}}$ – эффективная скорость релаксации.

2. Стержень (${{\mathcal{L}}_{1}} = {{\mathcal{L}}_{2}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, ${{\mathcal{L}}_{3}} = 0$). С учетом того, что

(9)
${{\epsilon }^{{\left( 1 \right)}}} = {{\epsilon }^{{\left( 2 \right)}}} = {{\epsilon }^{ \bot }} = \epsilon _{1}^{ \bot } + \operatorname{i} \epsilon _{2}^{ \bot },\,\,\,\,{{\epsilon }^{{\left( 3 \right)}}} = {{\epsilon }^{\parallel }} = \epsilon _{1}^{\parallel } + \operatorname{i} \epsilon _{2}^{\parallel }$
и можно записать:

(10)
${{\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{rod}}}}} = \frac{1}{3}\frac{\omega }{c}V\sqrt {{{\epsilon }_{{\text{m}}}}} \left[ {\frac{{8{{\epsilon }_{{\text{m}}}}\epsilon _{2}^{ \bot }}}{{{{{\left( {\epsilon _{1}^{ \bot } + {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}}} + \frac{{\epsilon _{2}^{\parallel }}}{{{{\epsilon }_{{\text{m}}}}}}} \right];$
(11)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{rod}}}}} = \frac{1}{{18{{\pi }^{2}}}}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}{{V}^{2}}\epsilon _{{\text{m}}}^{2} \times \\ \times \,\,\left\{ {8\frac{{{{{\left[ {{{{\left( {\epsilon _{1}^{ \bot }} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}} - \epsilon _{{\text{m}}}^{2}} \right]}}^{2}} + 4\epsilon _{{\text{m}}}^{2}{{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}}}{{{{{\left[ {{{{\left( {\epsilon _{1}^{ \bot } + {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}} \right]}}^{2}}}}} \right. + \\ + \,\,\left. {\frac{{{{{\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{\parallel }} \right)}}^{2}}}}{{\epsilon _{{\text{m}}}^{2}}}} \right\}. \\ \end{gathered} $

3. Диск. Используя выражения для факторов деполяризации [25]:

(12)
$\begin{gathered} {{\mathcal{L}}_{1}} = {{\mathcal{L}}_{2}} = {{\mathcal{L}}_{ \bot }} = \frac{\pi }{4}\frac{H}{D};\, \\ {{\mathcal{L}}_{3}} = {{\mathcal{L}}_{\parallel }} = 1 - \frac{\pi }{2}\frac{H}{D}, \\ \end{gathered} $
где $H$ и $D$ – высота и диаметр диска, а также выражения (9), получим:

(13)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{disk}}}}} = \frac{1}{3}\frac{\omega }{c}\epsilon _{{\text{m}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{\epsilon }_{2}}V \times \\ \times \,\,\left\{ {\frac{2}{{{{{\left[ {{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot } + \left( {1 - {{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{ \bot }^{2}{{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}}}} \right. + \\ + \,\,\left. {\frac{1}{{{{{\left[ {{{\mathcal{L}}_{\parallel }}\epsilon _{1}^{\parallel } + \left( {1 - {{\mathcal{L}}_{\parallel }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{\parallel }^{2}{{{\left( {\epsilon _{2}^{\parallel }} \right)}}^{2}}}}} \right\}; \\ \end{gathered} $
(14)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{disk}}}}} = \frac{1}{{6\pi }}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}{{V}^{2}}\epsilon _{{\text{m}}}^{2} \times \\ \times \,\,\left\{ {\frac{2}{3}\frac{{{{{\left[ {{{\mathcal{L}}_{ \bot }}\left( {{{{\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}} \right) + {{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)} \right]}}^{2}}}}{{{{{\left\{ {{{{\left[ {{{L}_{ \bot }}\epsilon _{1}^{ \bot } + \left( {1 - {{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{ \bot }^{2}{{{\left( {\epsilon _{2}^{ \bot }} \right)}}^{2}}} \right\}}}^{2}}}}} \right. + \\ + \,\,\left. {\frac{1}{3}\frac{{{{{\left[ {{{\mathcal{L}}_{\parallel }}\left( {{{{\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + {{{\left( {\epsilon _{2}^{\parallel }} \right)}}^{2}}} \right) + {{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)} \right]}}^{2}}}}{{{{{\left\{ {{{{\left[ {{{\mathcal{L}}_{\parallel }}\epsilon _{1}^{\parallel } + \left( {1 - {{L}_{\parallel }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{\parallel }^{2}{{{\left( {\epsilon _{2}^{\parallel }} \right)}}^{2}}} \right\}}}^{2}}}}} \right\}. \\ \end{gathered} $

Поскольку

$\mathcal{L}_{ \bot }^{2} = \left( {\frac{\pi }{4}\frac{H}{D}} \right) \ll 1\,\,{\text{и}}\,\,{{\left( {1 - {{\mathcal{L}}_{\parallel }}} \right)}^{2}} = {{\left( {\frac{\pi }{4}\frac{H}{D}} \right)}^{2}} \ll 1,$
то соотношения (13), (14) можно упростить. В этом случае:
$\begin{gathered} {{\left[ {{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot } + \left( {1 - {{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}}} \right]}^{2}} + \mathcal{L}_{ \bot }^{2}\epsilon _{2}^{{ \bot 2}} \simeq \\ \simeq \,\,{{\epsilon }_{{\text{m}}}}\left( {{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot } + {{\mathcal{L}}_{\parallel }}{{\epsilon }_{{\text{m}}}}} \right); \\ \end{gathered} $
$\begin{gathered} {{\left[ {{{\mathcal{L}}_{\parallel }}\epsilon _{1}^{\parallel } + \left( {1 - {{\mathcal{L}}_{\parallel }}} \right){{\epsilon }_{{\text{m}}}}} \right]}^{2}} + \mathcal{L}_{\parallel }^{2}\epsilon _{2}^{{\parallel 2}} \simeq \\ \simeq \,\,\left( {1 - 4{{\mathcal{L}}_{ \bot }}} \right)\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}} - {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }} \right) + {{\mathcal{L}}_{\parallel }}{{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }, \\ \end{gathered} $
так как $\mathcal{L}_{\parallel }^{2} = {{\left( {1 - 2{{\mathcal{L}}_{ \bot }}} \right)}^{2}} \simeq 1 - 4{{\mathcal{L}}_{ \bot }}.$ Поэтому формула для усредненного сечения поглощения принимает вид:

(15)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{disk}}}}} = \frac{1}{3}\frac{\omega }{c}\epsilon _{{\text{m}}}^{{3/2}}{{\epsilon }_{2}}V\left\{ {\frac{2}{{{{\epsilon }_{{\text{m}}}}\left( {{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot } + {{\mathcal{L}}_{\parallel }}{{\epsilon }_{{\text{m}}}}} \right)}}} \right. + \\ + \,\,\left. {\frac{1}{{\left( {1 - 4{{\mathcal{L}}_{ \bot }}} \right)\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}} - {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }} \right) + {{\mathcal{L}}_{\parallel }}{{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }}}} \right\}. \\ \end{gathered} $

Учитывая, что

$\begin{gathered} {{\left\{ {{{{\left[ {{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot } + \left( {1 - {{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{ \bot }^{2}\epsilon _{2}^{{ \bot 2}}} \right\}}^{2}} \simeq \\ \simeq \epsilon _{{\text{m}}}^{3}\left( {\left( {1 - 4{{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}} + 2{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot }} \right); \\ \end{gathered} $
$\begin{gathered} {{\left\{ {{{{\left[ {{{\mathcal{L}}_{\parallel }}\epsilon _{1}^{\parallel } + \left( {1 - {{\mathcal{L}}_{\parallel }}} \right){{\epsilon }_{{\text{m}}}}} \right]}}^{2}} + \mathcal{L}_{\parallel }^{2}\epsilon _{2}^{{\parallel 2}}} \right\}}^{2}} \simeq \\ \simeq \left( {1 - 8{{L}_{ \bot }}} \right){{\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}} \right)}^{2}} + 4{{\mathcal{L}}_{ \bot }}\epsilon _{{\text{m}}}^{2}\epsilon _{1}^{{\parallel 2}}; \\ \end{gathered} $
$\begin{gathered} {{\left\{ {{{\mathcal{L}}_{ \bot }}\left( {{{{\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{{ \bot 2}}} \right) + {{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)} \right\}}^{2}} \simeq \\ \simeq {{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)\,\, \times \\ \times \,\,\left[ {{{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right) + 2{{\mathcal{L}}_{ \bot }}\left( {{{{\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{{ \bot 2}}} \right)} \right], \\ \end{gathered} $
получим формулу для усредненного сечения рассеяния электромагнитного излучения ансамблем нанодисков:

(16)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{disk}}}}} = \frac{1}{{6\pi }}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}\epsilon _{{\text{m}}}^{2}{{V}^{2}} \times \\ \times \,\,\left\{ {\frac{2}{3}\frac{{\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)\left[ {{{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right) + 2{{\mathcal{L}}_{ \bot }}\left( {{{{\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{{ \bot 2}}} \right)} \right]}}{{\epsilon _{{\text{m}}}^{2}\left( {\left( {1 - 4{{\mathcal{L}}_{ \bot }}} \right){{\epsilon }_{{\text{m}}}} + 2{{\mathcal{L}}_{ \bot }}\epsilon _{1}^{ \bot }} \right)}} + } \right.\frac{1}{3}\left. {\frac{{{{{\left[ {{{\mathcal{L}}_{\parallel }}\left( {{{{\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} + \epsilon _{2}^{{\parallel 2}}} \right) + {{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)} \right]}}^{2}}}}{{\left( {1 - 8{{\mathcal{L}}_{ \bot }}} \right){{{\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}} \right)}}^{2}} + 4{{\mathcal{L}}_{ \bot }}\epsilon _{{\text{m}}}^{2}\epsilon _{1}^{{\parallel 2}}}}} \right\}. \\ \end{gathered} $

Сохраняя в соотношениях (15) и (16) слагаемые, линейные по ${{\mathcal{L}}_{ \bot }}$, получим

(17)
${{\left\langle {{{C}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{disk}}}}} \cong \frac{1}{3}\frac{\omega }{c}\epsilon _{{\text{m}}}^{{3/2}}{{\epsilon }_{2}}V\,\left\{ {\frac{2}{{\epsilon _{{\text{m}}}^{2}}} + \frac{1}{{\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}}} + 2{{\mathcal{L}}_{ \bot }}\left[ {\frac{{{{2}^{{^{{^{{}}}}}}}}}{{\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}}}} \right.} \right.\,\,\left. {\left. {\left( {1 - \frac{{{{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }}}{{2\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}} \right)}}} \right) - \frac{1}{{\epsilon _{{\text{m}}}^{2}}}\left( {\frac{{\epsilon _{1}^{ \bot }}}{{{{\epsilon }_{{\text{m}}}}}} - 2} \right)} \right]} \right\};$
(18)
$\begin{gathered} {{\left\langle {{{C}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{disk}}}}} \simeq \frac{1}{{6\pi }}\frac{{{{\omega }^{4}}}}{{{{c}^{4}}}}\epsilon _{{\text{m}}}^{2}{{V}^{2}}\left\{ {\frac{2}{3}\frac{{\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}}}{{\epsilon _{{\text{m}}}^{3}}}\left[ {{{\epsilon }_{{\text{m}}}}\left( {\epsilon _{1}^{ \bot } - {{\epsilon }_{{\text{m}}}}} \right)} \right.} \right. + \\ + \,\,\left. {2{{\mathcal{L}}_{ \bot }}\left( {\epsilon _{2}^{{ \bot 2}} - \epsilon _{{\text{m}}}^{2} + {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{ \bot }} \right)} \right] + \frac{1}{3}\frac{{\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}} - {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{{\parallel 2}}}}{{{{{\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}} \right)}}^{2}}}} \times \\ \times \,\,\left[ {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}} - {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel } + 4{{\mathcal{L}}_{ \bot }} \times } \right. \\ \times \,\,\left( {2\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}} - {{\epsilon }_{{\text{m}}}}\epsilon _{1}^{\parallel }} \right)\left( {1 - \frac{{\epsilon _{{\text{m}}}^{2}\epsilon _{1}^{{\parallel 2}}}}{{2\left( {\epsilon _{1}^{{\parallel 2}} + \epsilon _{2}^{{\parallel 2}}} \right)}}} \right) - } \right. \\ - \,\,\left. {\left. {\left. {{{{\left( {\epsilon _{1}^{\parallel } - {{\epsilon }_{{\text{m}}}}} \right)}}^{2}} - \epsilon _{2}^{{\parallel 2}}} \right)} \right]} \right\}. \\ \end{gathered} $

В дальнейшем формулы (6), (7), (10), (11), (17) и (18) используются для расчетов частотных зависимостей сечений поглощения и рассеяния.

ЭФФЕКТИВНАЯ СКОРОСТЬ РЕЛАКСАЦИИ

Величина эффективной скорости релаксации представляет собой сумму вкладов от объемного и поверхностного рассеяния электронов, а также радиационного затухания [26]

(19)
$\gamma _{{{\text{eff}}}}^{{ \bot \left( \parallel \right)}} = {{\gamma }_{{{\text{bulk}}}}} + \gamma _{{\text{s}}}^{{ \bot \left( \parallel \right)}} + \gamma _{{{\text{rad}}}}^{{ \bot \left( \parallel \right)}},$
где ${{\gamma }_{{{\text{bulk}}}}}$ – скорость релаксации в 3D-металле.

В отличие от ${{\gamma }_{{{\text{bulk}}}}},$ скорости радиационного затухания и поверхностной релаксации являются размерно-зависящими, а поэтому зависят от формы частиц. Так, в случае сферической частицы выражения для ${{\gamma }_{{{\text{rad}}}}}$ и ${{\gamma }_{{\text{s}}}}$ имеют, соответственно, вид [27, 28]:

(20)
${{\gamma }_{{{\text{rad}}}}} = \frac{1}{{24\pi }}\frac{{{{V}_{0}}}}{{\sqrt {{{\epsilon }_{{\text{m}}}}\left( {2{{\epsilon }_{{\text{m}}}} + {{\epsilon }^{\infty }}} \right)} }}{{\left( {\frac{{{{\omega }_{p}}}}{c}} \right)}^{3}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}}\frac{{{{v}_{{\text{F}}}}}}{R},$
(21)
${{\gamma }_{{\text{s}}}} = \mathcal{A}\left( {\omega ,\,\,R} \right)\frac{{{{v}_{{\text{F}}}}}}{R},$
где ${{v}_{{\text{F}}}} = \sqrt {2{{\varepsilon }_{{\text{F}}}}{\text{/}}m{\kern 1pt} *} $ – скорость электронов на поверхности Ферми, ${{\varepsilon }_{{\text{F}}}}$ – энергия Ферми; $\mathcal{A}\left( {\omega ,\,\,R} \right)$ – эффективный параметр, описывающий степень потери когерентности при рассеянии электрона на поверхности, который в общем случае зависит от радиуса наночастицы и частоты [27]:

(22)
$\begin{gathered} \mathcal{A}\left( {\omega ,R} \right) = \frac{1}{4}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}} \times \\ \times \,\,\left[ {1 - \frac{{2{{\nu }_{s}}}}{\omega }\sin \frac{\omega }{{{{\nu }_{s}}}} + \frac{{2\nu _{s}^{2}}}{{{{\omega }^{2}}}}\left( {1 - \cos \frac{\omega }{{{{\nu }_{s}}}}} \right)} \right]. \\ \end{gathered} $

Найдем теперь выражения для $\gamma _{{{\text{rad}}}}^{{ \bot \left( \parallel \right)}}$ и $\gamma _{{\text{s}}}^{{ \bot \left( \parallel \right)}}$ в случае стержня и диска. С этой целью воспользуемся соответствующими формулами для вытянутых и сплюснутых эллипсоидов вращения [27, 28]

(23)
$\gamma _{{{\text{rad}}}}^{{ \bot \left( \parallel \right)}} = \frac{2}{{9{{\epsilon }_{0}}\sqrt {{{\epsilon }_{{\text{m}}}}} }}{{\left( {\frac{{{{\omega }_{p}}}}{c}} \right)}^{3}}\frac{{{{R}_{\parallel }}R_{ \bot }^{2}{{\mathcal{L}}^{{ \bot \left( \parallel \right)}}}{{\sigma }_{{ \bot \left( \parallel \right)}}}\left( \omega \right)}}{{\sqrt {{{\epsilon }^{\infty }} + \left( {\frac{1}{{{{\mathcal{L}}^{{ \bot \left( \parallel \right)}}}}} - 1} \right){{\epsilon }_{{\text{m}}}}} }};$
(24)
$\gamma _{s}^{{ \bot \left( \parallel \right)}} = \frac{{{{\mathcal{L}}^{{ \bot \left( \parallel \right)}}}{{\sigma }_{{ \bot \left( \parallel \right)}}}\left( \omega \right)}}{{{{\epsilon }_{0}}\left[ {{{\epsilon }_{{\text{m}}}} + {{\mathcal{L}}^{{ \bot \left( \parallel \right)}}}\left( {1 - {{\epsilon }_{{\text{m}}}}} \right)} \right]}},$
где ${{R}_{{ \bot \left( \parallel \right)}}}$ – полуоси эллипсов, являющихся поперечными сечениями эллипсоидов вращения; ${{\sigma }_{{ \bot \left( \parallel \right)}}}\left( \omega \right)$ – диагональные компоненты тензора проводимости, которые определяются выражениями [27]:

(25)
$\begin{gathered} {{\sigma }_{ \bot }}\left( \omega \right) = \frac{{9n{{e}^{2}}}}{{4m\omega }}{{\left( {\frac{\omega }{{\nu _{s}^{ \bot }}}} \right)}^{2}}\frac{{e_{p}^{2} - 1}}{{e_{p}^{3}}}\int\limits_{\frac{\omega }{{\nu _{s}^{ \bot }}}}^{\frac{\omega }{{\nu _{s}^{\parallel }}}} {\frac{{dx}}{{{{x}^{4}}}}\frac{{1 - {{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {\nu _{s}^{\parallel }x}}} \right. \kern-0em} {\nu _{s}^{\parallel }x}}} \right)}}^{2}}}}{{{{{\left[ {1 - {{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {\nu _{s}^{ \bot }x}}} \right. \kern-0em} {\nu _{s}^{ \bot }x}}} \right)}}^{2}}} \right]}}^{{1/2}}}}}} \times \\ \times \,\,\left[ {1 - \frac{2}{x}{\kern 1pt} \sin {\kern 1pt} x + \frac{2}{{{{x}^{2}}}}\left( {1 - \cos {\kern 1pt} x} \right)} \right]; \\ {{\sigma }_{\parallel }}\left( \omega \right) = \frac{{9n{{e}^{2}}}}{{2m\omega }}{{\left( {\frac{\omega }{{\nu _{s}^{ \bot }}}} \right)}^{2}}\frac{1}{{e_{p}^{3}}}\int\limits_{\frac{\omega }{{\nu _{s}^{ \bot }}}}^{\frac{\omega }{{\nu _{s}^{\parallel }}}} {\frac{{dx}}{{{{x}^{4}}}}{{{\left[ {1 - {{{\left( {{\omega \mathord{\left/ {\vphantom {\omega {\nu _{s}^{ \bot }x}}} \right. \kern-0em} {\nu _{s}^{ \bot }x}}} \right)}}^{2}}} \right]}}^{{1/2}}}} \times \\ \times \,\,\left[ {1 - \frac{2}{x}{\kern 1pt} \sin {\kern 1pt} x + \frac{2}{{{{x}^{2}}}}\left( {1 - \cos {\kern 1pt} x} \right)} \right]. \\ \end{gathered} $

В формулах (25) введены такие обозначения: $e_{p}^{2} = \left| {1 - {{R_{ \bot }^{2}} \mathord{\left/ {\vphantom {{R_{ \bot }^{2}} {R_{\parallel }^{2}}}} \right. \kern-0em} {R_{\parallel }^{2}}}} \right|$ – эксцентриситет; $\nu _{s}^{{ \bot \left( \parallel \right)}} = {{{{v}_{{\text{F}}}}} \mathord{\left/ {\vphantom {{{{v}_{{\text{F}}}}} {2{{R}_{{ \bot \left( \parallel \right)}}}}}} \right. \kern-0em} {2{{R}_{{ \bot \left( \parallel \right)}}}}}$ – частоты индивидуальных осцилляций в направлениях, перпендикулярном и параллельном оси симметрии эллипсоида вращения; $x$ – переменная интегрирования.

В случае стержня ${{R}_{ \bot }} = R,$ ${{R}_{\parallel }} = {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}$ ($R$ и $l$ – радиус и длина стержня), коэффициенты деполяризации ${{\mathcal{L}}^{\parallel }} = 0,$ ${{\mathcal{L}}^{ \bot }} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ Подставляя соотношения (25) в (23) и (24), и учитывая, что $R{\text{/}}l \ll 1,$ получаем:

(26)
$\gamma _{{{\text{rad}}}}^{ \bot } = \frac{3}{{128}}\frac{V}{{\sqrt {{{\epsilon }_{{\text{m}}}}\left( {{{\epsilon }^{\infty }} + {{\epsilon }_{{\text{m}}}}} \right)} }}{{\left( {\frac{{{{\omega }_{p}}}}{c}} \right)}^{3}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}}\frac{{{{v}_{{\text{F}}}}}}{R};$
(27)
$\gamma _{{\text{s}}}^{ \bot } = \frac{{27\pi }}{{128\left( {{{\epsilon }_{{\text{m}}}} + 1} \right)}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}}\frac{{{{v}_{{\text{F}}}}}}{R},$
(28)
$\gamma _{{{\text{rad}}}}^{\parallel } = \gamma _{{\text{s}}}^{\parallel } = 0,$
где $V = \pi {{R}^{2}}l$ – объем стержня.

В случае диска ${{R}_{ \bot }} = D{\text{/}}2,$ ${{R}_{\parallel }} = {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2},$ а коэффициенты деполяризации определяются формулами (12). Подставляя соотношения (25) в (23) и (24), с учетом $H{\text{/}}D \ll 1,$ будем иметь:

(29)
$\begin{gathered} \gamma _{{{\text{rad}}}}^{\parallel } = \frac{V}{{2\sqrt {{{\epsilon }^{\infty }}{{\epsilon }_{{\text{m}}}}} }}{{\left( {\frac{{{{\omega }_{p}}}}{c}} \right)}^{3}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}} \times \\ \times \,\,\frac{D}{H}\frac{{{{v}_{{\text{F}}}}}}{H}\left( {1 + \left( {\frac{{{{\epsilon }_{{\text{m}}}}}}{{2{{\epsilon }^{\infty }}}} - 1} \right)\frac{\pi }{2}\frac{H}{D}} \right); \\ \end{gathered} $
(30)
$\begin{gathered} \gamma _{{{\text{rad}}}}^{ \bot } = \frac{{{{\pi }^{{\frac{3}{2}}}}V}}{{32{{\epsilon }_{{\text{m}}}}}}{{\left( {\frac{{{{\omega }_{p}}}}{c}} \right)}^{3}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}} \times \\ \times \,\,{{\left( {\frac{H}{D}} \right)}^{{\frac{3}{2}}}}\frac{{{{v}_{{\text{F}}}}}}{H}\left( {1 - \frac{\pi }{8}\frac{{{{\epsilon }^{\infty }}}}{{{{\epsilon }_{{\text{m}}}}}}\frac{H}{D}} \right); \\ \end{gathered} $
(31)
$\gamma _{{\text{s}}}^{\parallel } = \frac{9}{8}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}}\frac{D}{H}\frac{{{{v}_{{\text{F}}}}}}{H}\left( {1 + \left( {{{\epsilon }_{{\text{m}}}} - 2} \right)\frac{\pi }{2}\frac{H}{D}} \right);$
(32)
$\gamma _{{\text{s}}}^{ \bot } = \frac{{9\pi }}{{64}}{{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}}\frac{H}{D}\frac{{{{v}_{{\text{F}}}}}}{H}\left( {1 + \left( {{{\epsilon }_{{\text{m}}}} - 1} \right)\frac{\pi }{4}\frac{H}{D}} \right),$
где $V = {{\pi {{D}^{2}}H} \mathord{\left/ {\vphantom {{\pi {{D}^{2}}H} 4}} \right. \kern-0em} 4}$ – объем диска.

Подставляя выражение (19) с учетом соотношений (20)–(22) и (26)–(32) в формулу (8), можно определить действительную и мнимую части диэлектрической функции, а соответственно, и рассчитать частотные зависимости усредненных сечений поглощения и рассеяния электромагнитного излучения ансамблями наночастиц различной формы.

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ И ОБСУЖДЕНИЕ

Расчеты были проведены для наночастиц Ag, Cu, Au и Pt, находящихся в тефлоне (${{\epsilon }_{{\text{m}}}} = 2.3$). Параметры металлов приведены в табл. 1. Вычисляли эффективности поглощения и рассеяния – соответствующие сечения, нормированные на геометрическую площадь поперечного сечения эквивалентной сферы ${{\left\langle {{{Q}_{{{\text{abs}}\,\left( {{\text{sca}}} \right)}}}} \right\rangle = \left\langle {{{C}_{{{\text{abs}}\,\left( {{\text{sca}}} \right)}}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{Q}_{{{\text{abs}}\,\left( {{\text{sca}}} \right)}}}} \right\rangle = \left\langle {{{C}_{{{\text{abs}}\,\left( {{\text{sca}}} \right)}}}} \right\rangle } {\pi R_{{{\text{eff}}}}^{2}}}} \right. \kern-0em} {\pi R_{{{\text{eff}}}}^{2}}}$ (см. табл. 2 ).

Таблица 1.  

Параметры металлов

Металл Cu [7] Au [7] Ag [7] Pt [29]
${{{{r}_{s}}} \mathord{\left/ {\vphantom {{{{r}_{s}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ 2.11 3.01 3.02 3.27
${{m{\kern 1pt} *} \mathord{\left/ {\vphantom {{m{\kern 1pt} *} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$ 1.49 0.99 0.96 0.54
$~{{\epsilon }^{\infty }}$ 12.03 9.84 3.70 4.42
${{\gamma }_{{{\text{bulk}}}}},\,\,{{10}^{{13}}}\,\,{{{\text{c}}}^{{ - 1}}}$ 3.70 3.45 2.50 10.52

Таблица 2.  

Эффективные радиусы эквивалентной сферы для наночастиц разной формы

Объект Reff
Сфера R
Стержень $\sqrt[3]{{\frac{3}{4}{{R}^{2}}l}}$
Диск $\frac{1}{2}\sqrt[3]{{\frac{3}{2}{{D}^{2}}H}}$
На рис. 1 приведены частотные зависимости усредненных эффективностей поглощения и рассеяния электромагнитного излучения ансамблем сферических наночастиц Ag. С увеличением радиуса максимальное значение эффективности поглощения увеличивается (рис. 1а), а сам максимум незначительно сдвигается в область меньших частот. По аналогии с этим случаем максимальные значения эффективности рассеяния излучения ансамблем сферических наночастиц Ag с увеличением их радиуса также возрастают (рис. 1б), испытывая незначительный “красный” сдвиг. Однако в этом случае максимум выражен сильнее, чем для эффективности поглощения, что связано с быстрым ростом $\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle $ при увеличении объема наночастицы.

Рис. 1.

Частотные зависимости усредненных эффективностей поглощения (а) и рассеяния (б) ансамбля сферических наночастиц Ag различного радиуса.

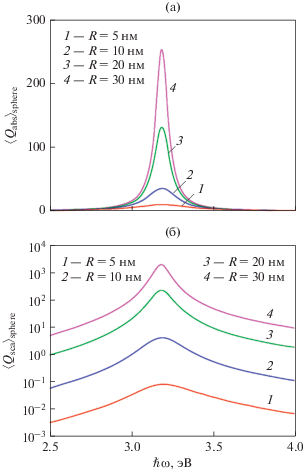
Аналогичные зависимости усредненных эффективностей поглощения и рассеяния для ансамбля наностержней Ag изображены на рис. 2. Качественно кривые $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle \left( \omega \right)$ и $\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle \left( \omega \right)$ подобны аналогичным зависимостям для ансамблей сферических частиц, однако максимальные значения на порядок меньше. Это связано с тем, что $R_{{{\text{eff}}}}^{{{\text{rod}}}} > R_{{{\text{eff}}}}^{{{\text{sphere}}}},$ причем $l \gg R.$

Рис. 2.

Частотные зависимости усредненных эффективностей поглощения (а) и рассеяния (б) ансамбля наностержней Ag длиной $l = 200$ нм различного радиуса.

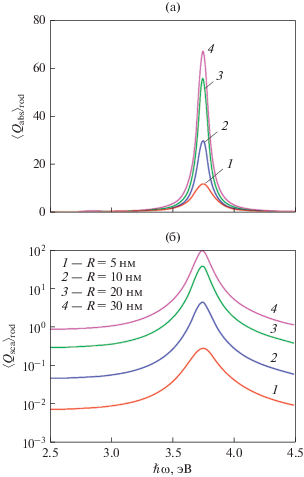
На рис. 3 представлены частотные зависимости усредненных эффективностей поглощения и рассеяния ансамблем нанодисков Ag. Как видно из рисунка, с увеличением высоты дисков растут максимальные значения ${{\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle }_{{\max }}}$ и ${{\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle }_{{\max }}}.$ Однако сдвиг максимумов $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle ,$ в отличие от сфер и стержней, уже “синий” и достаточно существенный ($\sim {\kern 1pt} 0.5$ эВ), а зависимость $\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle \left( \omega \right)$ имеет два максимума (рис. 3б), соответствующих случаям двух плазмонных резонансов в нанодисках

$\epsilon _{1}^{{ \bot \left( \parallel \right)}} = - \frac{{1 - {{\mathcal{L}}_{{ \bot \left( \parallel \right)}}}}}{{{{\mathcal{L}}_{{ \bot \left( \parallel \right)}}}}}{{\epsilon }_{{\text{m}}}}.$
Рис. 3.

Частотные зависимости усредненных эффективностей поглощения (а) и рассеяния (б) ансамбля нанодисков Ag диаметром $D = 100$ нм различной высоты.

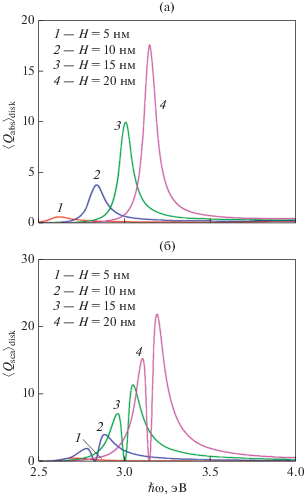
Разное количество максимумов на частотных зависимостях ${{\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle }_{{{\text{disk}}}}}$ и ${{\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle }_{{{\text{disk}}}}}$ связано с большей шириной пиков эффективности поглощения и наличием слабого минимума, находящегося между близко расположенными максимумами, что приводит к их слиянию, в отличие от максимумов эффективности рассеяния, разделенных глубоким минимумом.

Частотные зависимости эффективностей поглощения электромагнитного излучения ансамблями наноструктур различной геометрии из разных металлов приведены на рис. 4. Следует отметить, что для ансамблей наночастиц любой формы наибольшими будут максимальные значения $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle $ для Ag и Pt. При этом для всех металлов $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{sphere}}}}^{{\max }} > \left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{rod}}}}^{{\max }} > \left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{disk}}}}^{{\max }}$, и если $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{rod}}}}^{{\max }}$ и $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{disk}}}}^{{\max }}$ отличаются слабо, то $\left\langle {{{Q}_{{{\text{abs}}}}}} \right\rangle _{{{\text{sphere}}}}^{{\max }}$ превышает эффективности поглощения стержня и диска на порядок. В свою очередь, разное спектральное положение максимумов усредненной эффективности поглощения для нанообъектов различной геометрии из одного и того же металла можно объяснить существенным изменением частоты поверхностного плазмонного резонанса при изменении формы наночастицы.

Рис. 4.

Частотные зависимости усредненных эффективностей поглощения ансамблей сферических наночастиц (а), наностержней (б) и нанодисков (в) различных металлов.

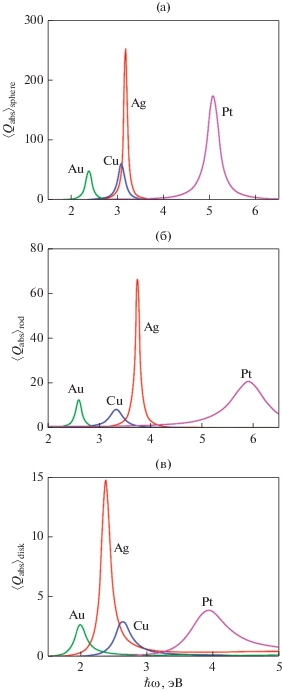
На рис. 5 изображены частотные зависимости эффективностей рассеяния для ансамблей наноструктур различной формы из разных металлов. По аналогии со случаем эффективностей поглощения $\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle _{{{\text{sphere}}}}^{{\max }} > \left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle _{{{\text{rod}}}}^{{\max }} > \left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle _{{{\text{disk}}}}^{{\max }}$, а наибольшими являются максимальные значения $\left\langle {{{Q}_{{{\text{sca}}}}}} \right\rangle $ для Ag и Pt, независимо от формы наночастиц, что объясняется различиями величин ${{\epsilon }^{\infty }}$ и ${{\omega }_{p}}$ для рассматриваемых металлов.

Рис. 5.

Частотные зависимости усредненных эффективностей рассеяния ансамблей сферических наночастиц (а), наностержней (б) и нанодисков (в) различных металлов.

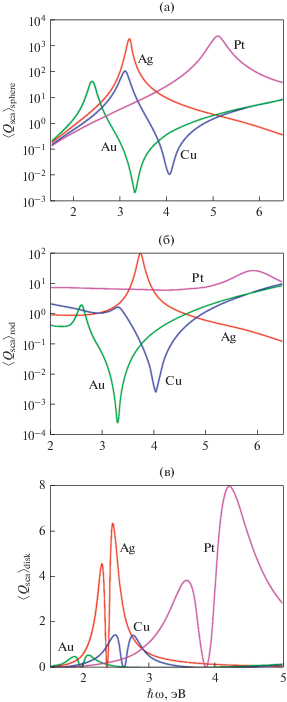
Следует отметить, что в случае ансамблей сфер и стержней эффективность рассеяния имеет один максимум, соответствующий поверхностному плазмонному резонансу, тогда как для ансамбля нанодисков этих максимумов два. Это связано с тем, что у наностержней $l \gg R$ и ${{\mathcal{L}}^{\parallel }} = 0,$ а значит продольный поверхностный резонанс не проявляется. В случае дисков ${{\mathcal{L}}^{{ \bot \left( \parallel \right)}}} \ne 0,$ поэтому могут возбуждаться как продольный, так и поперечный резонансы.

ЗАКЛЮЧЕНИЕ

Получены соотношения для скоростей поверхностной и радиационной релаксации электронов для наночастиц в форме стержня и диска как предельные случаи соответствующих выражений для вытянутого и сплюснутого эллипсоидов вращения.

Исследованы частотные зависимости усредненных эффективностей поглощения и рассеяния электромагнитного излучения ансамблями наночастиц предельной геометрии.

Установлено, что для наночастиц Ag различной формы увеличение максимальных значений усредненных эффективностей поглощения и рассеяния электромагнитного излучения происходит с увеличением латерального размера частицы (радиуса сферы, радиуса поперечного сечения стержня и толщины диска). При этом смещение самих максимумов в область больших или меньших частот зависит как от материала, так и от формы наночастиц.

Показано, что для ансамблей наночастиц из рассмотренных металлов максимальные эффективности поглощения и рассеяния наибольшие для сфер, а для дисков и стержней они близки по величине, что связано с увеличением площади поперечного сечения эквивалентной сферы в ряду сферы → стержни → диски.

Продемонстрировано качественное отличие результатов для ансамбля дисков различных металлов (наличие двух максимумов на кривых эффективности рассеяния), связанное с учетом частотной зависимости соответствующих скоростей релаксации и проявлением как продольного, так и поперечного плазмонного резонанса.

Список литературы

  1. Филатов Л.Д., Санников Д.Г., Семенцов Д.И., Евсеев Д.А. Плазмон-поляритонные поверхностные волны на границе диэлектрика и нанокомпозита с металлическими включениями // ФТТ. 2014. Т. 56. № 7. С. 1372–1378.

  2. Коротун А.В. О влиянии квантово-размерных эффектов на оптическое поглощение металлического композита // ФММ. 2014. Т. 115. № 5. С. 451–454.

  3. Battie Y., Resano-Garcia A., Chaoui N., En Naciri A. Optical properties of plasmonic nanoparticles distributed in size determined from a modified Maxwell-Garnett-Mie theory // Phys. Status Solidi C. 2014. V. 12. No 1–2. P. 1–5.

  4. Vieaud J., Merchiers O., Rajaoarivelo M., Warenghem M., Borensztein Y., Ponsinet V., Aradian A. Effective medium description of plasmonic couplings in disordered polymer and gold nanoparticle composites // Thin Solid Films. 2016. https://doi.org/10.1016/j.tsf.2016.02.022

  5. Lozovski V., Razumova M. Influence of inclusion shape on light absorption in thin Au/Teflon nanocomposite films // J. Opt. Soc. Amer. B. 2016. V. 33. № 1. P. 8–16.

  6. Levin V., Markov M., Mousatov A., Kazatchenko E., Pervago E. Effective electro-magnetic properties of microheterogeneous materials with surface phenomena // Eur. Phys. J. B. 2017. V. 90. P. 192 (1–16).

  7. Коротун А.В., Коваль А.А., Рева В.И., Титов И.Н. Оптическое поглощение композита на основе биметаллических наночастиц. Классический подход // ФММ. 2019. Т. 120. № 11. С. 1136–1142.

  8. Magnozzi M., Brasse Y., König T.A.F., Bisio F., Bittrich E., Fery A., Canepa M. Plasmonics of Au/Polymer Core/Shell Nanocomposites for Thermoresponsive Hybrid Metasurfaces // ACS Appl. Nano Mater. 2020. V. 3. P. 1674−1682.

  9. Maier S.A. Plasmonics: Fundamentals and Applications. New York, 2007. 245 p.

  10. Nanocolloids: A Meeting Point for Scientists and Technologists / Ed. by M. Sanchez-Dominguez, C. Rodriguez-Abreu. Amsterdam: Elsevier, 2016. 538 p.

  11. Балыкин В.И., Мелентьев П.Н. Оптика и спектроскопия единичной плазмонной наноструктуры // УФН. 2018. Т. 188. № 2. С. 143–168.

  12. Dykman L., Khlebtsov N. Gold Nanoparticles in Biomedical Applications. CRC Press, 2018. 332 p.

  13. Виноградов А.П. Электродинамика композитных материалов. М.: Эдиториал УРСС, 2001. 208 с.

  14. Duncan T.M. Gradient-index optics: a review // Appl. Opt. 1980. V. 19. № 7. P. 1035–1038.

  15. Миличко В.А., Шалин А.С., Мухин И.С., Ковров А.Э., Красилин А.А., Виноградов А.В., Белов П.А., Симовский К.Р. Солнечная фотовольтаика: современное состояние и тенденции развития // УФН. 2016. Т. 186. № 8. С. 801–852.

  16. Farokhnezhad M., Esmaeilzadeh M. Graphene coated gold nanoparticles: an emerging class of nanoagents for photothermal therapy applications // Phys. Chem. Chem. Phys. 2019. V. 21. P. 18352–18362.

  17. Ruiz M. Mathematical analysis of plasmonics resonances for nanoparticles and applications. Plasmas. Université Paris sciences et lettres, 2017. 217 p.

  18. Moradi A. Canonical Problems in the Theory of Plasmonics. From 3D to 2D Systems. Springer-Verlag, 2020 XVII+349 p.

  19. Amendola V., Pilot R., Frasconi M., Maragò O.M., Iatì M.A. Surface plasmon resonance in gold nanoparticles: a review // J. Phys.: Condens. Matter. 2017. V. 29. id. 03002.

  20. Debela S., Mesfin B., Senbeta T. Surface plasmon resonances in ellipsoidal bimetallic nanoparticles // Photon. & Nanostruct. Fundamentals and Applications. 2019. V. 33. P. 48–54.

  21. Figueiredo N.M., Cavaleiro A. Dielectric properties of shape-distributed ellipsoidal particle systems // Plasmonics. 2020. V. 15. P. 379–397.

  22. Коротун А.В., Коваль А.А. Диэлектрический тензор металлической нанопроволочки с эллиптическим сечением // ФММ. 2019. Т. 120. № 7. С. 675–680.

  23. Коваль А.А., Коротун А.В. Диэлектрическая функция металлической наночастицы // ФММ. 2021. Т. 122. № 3. С. 248–254.

  24. Dmitruk N.L., Goncharenko A.V., Venger E.F. Optics of small particles and composite media. Kyiv: Naukova Dumka, 2009. 386 p.

  25. Zorić I., Zäch M., Kasemo B., Langhammer C. Gold, Platinum, and Aluminum Nanodisk Plasmons: Material Independence, Subradiance, and Damping Mechanisms // ACS Nano. 2011. V. 5. № 4. P. 2535–2546.

  26. Bohren C.F., Huffman D.R. Absorption and scattering of light by small particles. John Wiley & Sons, 2008. 530 p.

  27. Grigorchuk N.I., Tomchuk P.M. Optical and transport properties of spheroidal metal nanoparti-cles with account for the surface effect // Phys. Rev. B. 2011. V. 84. № 8. id. 085448.

  28. Grigorchuk N.I. Radiative damping of surface plasmon resonance in spheroidal metallic nanoparticle embedded in a dielectric medium // J. Opt. Soc. Am. B. 2012. V. 29. № 12. P. 3404–3411.

  29. Коротун А.В., Погосов В.В. К расчету оптических характеристик и размерных сдвигов частоты поверхностных плазмонов биметаллических наносфер // ФТТ. 2021. Т. 63. № 1. С. 120–131.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал