Физика металлов и металловедение, 2021, T. 122, № 7, стр. 675-683
Особенности магнитокалорического эффекта вблизи точки фазового перехода II рода в ферромагнетике с биквадратичным обменом
Е. Е. Кокорина a, *, М. В. Медведев a, **
a Институт электрофизики УрО РАН
620016 Екатеринбург, ул. Амундсена, 106, Россия
* E-mail: kokorina@iep.uran.ru
** E-mail: medvedev@iep.uran.ru
Поступила в редакцию 29.10.2020
После доработки 02.02.2021
Принята к публикации 10.02.2021
Аннотация
Исследован магнитокалорический эффект (изменение магнитной энтропии при изотермическом намагничивании ${{\Delta }}{{S}_{M}}\left( H \right)$) в модели ферромагнетика с билинейным ($I > 0$) и биквадратичным ($K > 0$) обменными взаимодействиями между ближайшими магнитными соседями для той области отношений параметров обмена $I$ и $K,$ в которой переход из парамагнитного состояния в магнитоупорядоченное является переходом II рода. В приближении среднего поля получен термодинамический потенциал магнитоупорядоченного состояния, который характеризуется двуми параметрами порядка – дипольным (относительной намагниченностью) ${{\sigma }_{Z}}$ и квадрупольным ${{q}_{0}},$ и рассмотрено температурное и полевое поведение параметров порядка этого ферроквадрупольного состояния вблизи точки Кюри ${{T}_{{\text{C}}}}.$ Установлено, что показатели степенных зависимостей изменения магнитной энтропии от магнитного поля $H$ совпадают с показателями степенной зависимости изменения энтропии обычного ферромагнетика только с одним билинейным обменом, т.е. изменение энтропии ${{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{{\text{\;C}}}}},H} \right)$ в точке Кюри ${{T}_{{\text{C}}}}$ пропорционально $ - {{H}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},$ несколько ниже ${{T}_{{\text{C}}}}$ будет ${{\Delta }}{{S}_{{\text{M}}}}(T < {{T}_{{\text{C}}}},H)\sim - H$ и выше ${{T}_{{\text{C}}}}$ имеет место ${{\Delta }}{{S}_{{\text{M}}}}(T > {{T}_{{\text{C}}}},H)\sim - {{H}^{2}}.$ В то же время коэффициенты перед этими степенными множителями в энтропии существенно зависят от отношений параметров обмена $I$ и $K$ – они минимальны при $K = 0$ и заметно увеличиваются по абсолютной величине при возрастании отношения ${K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I},$ отражая усиление понижения энтропии по мере усиления вклада от биквадратичного обмена.
1
Магнитокалорические эффекты (МКЭ) в ферро- и ферримагнетиках имеют максимальную величину вблизи температур фазового перехода либо II, либо I рода между магнитоупорядоченным и парамагнитным состояниями [1–3]. Эти эффекты привлекают сейчас большое внимание в связи с перспективами создания охлаждающих устройств без использования жидких хладоносителей [4].
С теоретической точки зрения полевые и температурные зависимости МКЭ – изменения магнитной энтропии при изотермическом намагничивании и изменения температуры при адиабатическом намагничивании – в случаях фазовых переходов II рода довольно хорошо описываются в рамках моделей билинейного гейзенберговского обмена между локализованными магнитными моментами вида $I{{S}_{1}}{{S}_{2}}$ [3], где $I > 0$ – параметр ферромагнитного обменного взаимодействия между спинами ${{S}_{1}}$ и ${{S}_{2}}.$ В то же время в рамках модели билинейного обмена на несжимаемой кристаллической решетке не удается получить магнитный фазовый переход I рода типа “порядок–беспорядок”, который экспериментально наблюдается в ряде магнетиков, и поэтому не удается описать связанные с этим переходом изменения термодинамических характеристик, включая и особенности МКЭ.
Проблема объяснения причин появления фазового перехода I рода в магнетиках была отчасти решена Бином и Родбеллом [5], которые предложили дополнительно учесть взаимодействие магнитной подсистемы со сжимаемой кристаллической решеткой и зависимость величины обменных взаимодействий от межатомных расстояний. Дальнейшее развитие этого подхода в применении к МКЭ позволило описать полевые и температурные закономерности поведения МКЭ в случае магнитного фазового перехода I рода на сжимаемой решетке (см., напр., [6, 7]).
Существует и другая физическая причина возникновения фазового перехода I рода в ферромагнетиках, она имеет чисто магнитную природу и связана с существованием биквадратичного обменного взаимодействия в магнетиках с локализованными спиновыми моментами в случаях величин спинов $S \geqslant 1$. Заметим, что идея существования биквадратичного обмена вида $K{{({{S}_{1}}{{S}_{2}})}^{2}},$ где $K$ – параметр обмена, была впервые высказана Шрёдингером еще в 1941 г., а в последующем она получила микроскопическое обоснование в работе Андерсона [8] и Хуанга и Орбаха [9].
При этом сам параметр биквадратичного обмена $K$ может быть и положительным, и отрицательным. К настоящему времени заметное влияние биквадратичного обменного взаимодействия на физические свойства магнетиков установлено как в магнитных соединениях с невысокими или умеренными температурами магнитных переходов (например, в халькогенидах европия [10], в мультиферроике ${\text{YMn}}{{{\text{O}}}_{3}}$ [11], в сверхпроводящих ферропниктидах [12], в многослойных магнитных гетероструктурах [13], в многочисленных солях и халькогенидах переходных металлов [14]), так и даже в ОЦК-железе с высокотемпературной точкой Кюри ${{T}_{{\text{C}}}}$ [15].
Дальнейшие исследования магнитных фазовых состояний в модели с одновременным существованием изотропных билинейных и биквадратичных обменов показали, что в зависимости от соотношения параметров билинейного $(I > 0)$ и биквадратичного $(K > 0)$ обменов при понижении температуры в магнетике возникает либо ферромагнитное (точнее говоря, ферро-квадрупольное, так как наличие двух разных механизмов обмена приводит к появлению двух разных параметров порядка – дипольному и квадрупольному), либо чисто квадрупольное упорядочение [16–26]. При этом ферроквадрупольное состояние с конечной намагниченностью, в свою очередь, в зависимости от отношения параметров обмена ${K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I},$ при понижении температуры может возникать как путем фазового перехода II рода, так и I рода. В целом, общая картина фазовых магнитных состояний [16–26] в этой модели обменных взаимодействий изучена достаточно хорошо, однако вопросы изменения магнитной энтропии в магнитном поле вблизи точек фазовых переходов не были исследованы. Таким образом, модель магнетика с одновременным наличием билинейного и биквадратичного обмена дает возможности изучить и сравнить особенности МКЭ в случаях фазового перехода как II, так и I рода в рамках единого модельного подхода.
В настоящей работе в рамках приближения среднего поля получено выражение для термодинамического потенциала магнетика с билинейным и биквадратичным обменом между ближайшими магнитными соседями, которое учитывает появление дипольного и квадрупольного параметров порядка, и рассмотрена возможность перехода в такое ферроквадрупольное состояние путем фазового перехода II рода. Затем вблизи точки фазового перехода II рода (точка Кюри ${{T}_{{\text{C}}}}$) исследовано температурное и полевое поведение параметров порядка и на основе этого изучено изменение магнитной энтропии в магнитном поле.
2
Гамильтониан магнетика с билинейным и биквадратичным обменным взаимодействием между ближайшими магнитными соседями имеет вид:
(1)
$\begin{gathered} \tilde {H} = - \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{{{\Delta }} = 1}^z {\left[ {I{{S}_{n}}{{S}_{{n + {{\Delta }}}}} + K{{{\left( {{{S}_{n}}{{S}_{{n + {{\Delta }}}}}} \right)}}^{2}}} \right]} } - \\ - \,\,{{\mu }_{0}}H\sum\limits_{n = 1}^N {{{S}_{{Zn}}}} . \\ \end{gathered} $Здесь $I > 0$ и $K > 0,$ сумма по ${{\Delta }}$ переходит по $z$ ближайшим магнитным соседям, $H$ – магнитное поле вдоль оси OZ, ${{\mu }_{0}} \equiv g{{\mu }_{{\text{B}}}}$ ($g$ – фактор Ланде).
Для дальнейших расчетов биквадратичное произведение спинов ${{\left( {{{S}_{n}}{{S}_{{n + {{\Delta }}}}}} \right)}^{2}}$ преобразуем к произведению квадрупольных операторов ${{Q}_{n}},$ вводя их следующим образом [19, 26]:
(2)
$\begin{gathered} {{Q}_{{0n}}} = 3S_{{Zn}}^{2} - S\left( {S + 1} \right),\,\,\,{{Q}_{{2n}}} = S_{{Xn}}^{2} - S_{{Yn}}^{2}, \\ Q_{{2n}}^{{{{\alpha \gamma }}}} = {{S}_{{{{\alpha }}n}}}{{S}_{{{{\gamma }}n}}} + {{S}_{{{{\gamma }}n}}}{{S}_{{{{\alpha }}n}}},\,\,\,\left( {\alpha \gamma = XY,YZ,ZX} \right). \\ \end{gathered} $Гамильтониан $\tilde {H}$ (1) после такого преобразования примет форму [19]:
(3)
$\begin{gathered} \tilde {H} = - \frac{1}{6}NKz{{[S\left( {S + 1} \right)]}^{2}} - {{\mu }_{0}}H\sum\limits_{n = 1}^N {{{S}_{{Zn}}}} - \\ - \,\,\frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{{{\Delta }} = 1}^z {\left[ {\left( {I - - \frac{1}{2}K} \right){{S}_{n}}{{S}_{{n + {{\Delta }}}}} + \frac{1}{2}K\left( {\frac{1}{3}{{Q}_{{0n}}}{{Q}_{{0,n + {{\Delta }}}}} + } \right.} \right.} } \\ \left. {\left. { + \,\,{{Q}_{{2n}}}{{Q}_{{2,n + {{\Delta }}}}} + \sum\limits_{{{\alpha \gamma }} = XY,YZ,ZX} {Q_{{2n}}^{{{{\alpha \gamma }}}}Q_{{2,n + {{\Delta }}}}^{{{{\alpha \gamma }}}}} } \right)} \right]. \\ \end{gathered} $Заметим, что при таком переходе от ${{\left( {{{S}_{n}}{{S}_{{n + {{\Delta }}}}}} \right)}^{2}}$ к квадрупольным операторам дополнительно выделяется билинейный член ${{S}_{n}}{{S}_{{n + {{\Delta }}}}},$ и поэтому параметр билинейного обмена перенормируется по сравнению с гамильтонианом (1).
Исследуем термодинамику модели, вводя приближение среднего поля. Если не конкретизировать магнитную структуру упорядоченного состояния, то, применив процедуру введения среднего поля ко всем парным произведениям спиновых и квадрупольных операторов соседних узлов, получим гамильтониан среднего поля в виде:
(4)
$\begin{gathered} {{{\tilde {H}}}^{{MF}}}\, = \tilde {C} - {{\mu }_{0}}H\sum\limits_{n = 1}^N {{{S}_{{Zn}}}} - \left( {I - \frac{1}{2}K} \right)z\sum\limits_{n = 1}^N {\sum\limits_{{{\alpha }} = X,Y,Z} {{{\sigma }_{{{\alpha }}}}{{S}_{{{{\alpha }}n}}}} } - \\ - \,\frac{1}{2}{\kern 1pt} Kz\sum\limits_{n = 1}^N {\left( {\frac{1}{3}{{q}_{0}}{{Q}_{{0n}}} + {{q}_{2}}{{Q}_{{2n}}} + \sum\limits_{{{\alpha \gamma }} = XY,YZ,ZX} {q_{{2n}}^{{{{\alpha \gamma }}}}Q_{{2n}}^{{{{\alpha \gamma }}}}} } \right)} , \\ \end{gathered} $(5)
$\begin{gathered} \tilde {C} = Nz\left\{ { - \frac{1}{6}K{{{[S\left( {S + 1} \right)]}}^{2}} + \frac{1}{2}\left( {I - \frac{1}{2}K} \right)} \right. \times \\ \times \,\,\left( {\sigma _{{X~}}^{2} + \sigma _{Y}^{2} + \sigma _{Z}^{2}} \right) + \frac{1}{4}K\left. {\left[ {\frac{1}{3}q_{0}^{2} + q_{2}^{2} + \sum\limits_{{{\alpha \gamma }}} {{{{\left( {q_{2}^{{{{\alpha \gamma }}}}} \right)}}^{2}}} } \right]} \right\}. \\ \end{gathered} $При этом термодинамические средние одноузельных дипольных ${{\sigma }_{{{\alpha }}}}$ и квадрупольных ${{q}_{0}},$ ${{q}_{2}}$ и $q_{2}^{{{{\alpha ,\gamma }}}}$ операторов выступают в роли параметров порядка, характеризующих магнитные структуры всех возможных упорядоченных фаз:
(6)
$\begin{gathered} {{\sigma }_{{{\alpha }}}} = \left\langle {{{S}_{{{{\alpha }}n}}}} \right\rangle ,\,\,\,{{q}_{0}} = \left\langle {{{Q}_{{0n}}}} \right\rangle , \\ {{q}_{2}} = \left\langle {{{Q}_{{2n}}}} \right\rangle ,\,\,\,q_{2}^{{{{\alpha \gamma }}}} = \left\langle {Q_{{2n}}^{{{{\alpha \gamma }}}}} \right\rangle . \\ \end{gathered} $Рассмотрим теперь только случай ферромагнитного упорядочения вдоль оси 0Z по направлению магнитного поля и ограничимся в дальнейшем случаем спина $S = 1.$ Тогда волновая функция основного ферромагнитного состояния $\left| {{{{{\Psi }}}_{f}}} \right\rangle $ с параллельным выстраиванием всех спинов вдоль оси 0Z будет иметь вид:
(7)
${{\left| {{{{{\Psi }}}_{f}} \geqslant \prod\limits_{n = 1}^N 1 } \right\rangle }_{n}},\,\,\,{\text{где}}\,\,\,{{S}_{{Zn}}}{{\left| 1 \right\rangle }_{n}} = {{\left| 1 \right\rangle }_{n}}.$Поэтому в основном состоянии при $T = 0$ из всех возможных параметров порядка (6) будут отличны от нуля только два:
(8)
$\begin{gathered} {{\sigma }_{Z}}\left( {T = 0} \right) = \left\langle {{{{{\Psi }}}_{f}}\left| {{{S}_{{Zn}}}} \right|{{{{\Psi }}}_{f}}} \right\rangle = 1, \\ {{q}_{0}}\left( {T = 0} \right) = \left\langle {{{{{\Psi }}}_{f}}\left| {{{Q}_{{0n}}}} \right|{{{{\Psi }}}_{f}}} \right\rangle = \\ = \,\,\left\langle {{{{{\Psi }}}_{f}}\left| {3S_{{Zn}}^{2} - 2} \right|{{{{\Psi }}}_{f}}} \right\rangle = 1. \\ \end{gathered} $Тогда будем считать, что такое магнитное упорядочение и при конечных температурах $T \ne 0$ характеризуется только двумя параметрами порядка – дипольным ${{\sigma }_{Z}}$ и квадрупольным ${{q}_{0}},$ а все остальные термодинамические средние (6) равны нулю. Нетрудно также видеть, что параметр порядка ${{\sigma }_{Z}} = \left\langle {{{S}_{{Zn}}}} \right\rangle $ по своему физическому смыслу является относительной намагниченностью ферромагнитного состояния (на один узел) для спиновой системы с $S = 1.$
В результате гамильтониан (4) для ферромагнитной фазы становится равным
(9)
$\begin{gathered} \tilde {H}_{f}^{{MF}} = \sum\limits_{n = 1} {\tilde {H}_{f}^{{MF}}\left( n \right)} = \\ = \,\,\sum\limits_n {\left( {{{{\tilde {C}}}_{f}}\left( n \right) - {{h}_{f}}{{S}_{{Zn}}} - {{h}_{{q0}}}{{Q}_{{0n}}}} \right)} , \\ \\ \end{gathered} $(10)
${{\tilde {C}}_{f}}\left( n \right) = z\left[ { - \frac{2}{3}K + \frac{1}{2}\left( {I - \frac{1}{2}K} \right)\sigma _{Z}^{2} + \frac{1}{{12}}Kq_{0}^{2}} \right]$и где для краткости обозначено
(11)
${{h}_{f}} = {{\mu }_{0}}H + \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}},\,\,\,{{h}_{{q0}}} = \frac{1}{6}Kz{{q}_{0}}.$Тогда термодинамический потенциал (ТДП) магнетика будет равен (на один магнитный атом):
(12)
$\begin{gathered} {{F}_{f}} = - {{\beta }^{{ - 1}}}{\text{ln}}Sp{\text{exp}}\left( { - \beta \tilde {H}_{f}^{{MF}}\left( n \right)} \right) = \\ = \,\,\,{{{\tilde {C}}}_{f}}\left( n \right) - {{\beta }^{{ - 1}}}{\text{ln[}}2{\text{exp}}\left( {\beta {{h}_{{q0}}}} \right){\text{ch}}\left( {\beta {{h}_{f}}} \right) + \\ + \,\,{\text{exp}}\left( { - 2\beta {{h}_{{q0}}}} \right)],\,\,\,\,\beta = {1 \mathord{\left/ {\vphantom {1 {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}, \\ \end{gathered} $и магнитная энтропия ${{S}_{M}}$ равна
(13)
$\begin{gathered} {{S}_{{\text{M}}}} = {{\left[ {\left\langle {\tilde {H}_{f}^{{MF}}\left( n \right)} \right\rangle - {{F}_{f}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\left\langle {\tilde {H}_{f}^{{MF}}\left( n \right)} \right\rangle - {{F}_{f}}} \right]} T}} \right. \kern-0em} T} = \\ = \,\,{{k}_{{\text{B}}}}\{ {\text{ln[}}2{\text{exp}}\left( {\beta {{h}_{{q0}}}} \right){\text{ch}}\left( {\beta {{h}_{f}}} \right) + \\ + \,\,{\text{exp}}\left( { - 2\beta {{h}_{{q0}}}} \right)] - \beta \left( {{{h}_{f}}{{\sigma }_{Z}} + {{h}_{{q0}}}{{q}_{0}}} \right)\} . \\ \end{gathered} $Уравнения для определения положений точек экстремумов ${{F}_{f}}$ в пространстве переменных ${{\sigma }_{Z}}$ и ${{q}_{0}}$
(14)
$\frac{{\partial {{F}_{f}}}}{{\partial {{\sigma }_{Z}}}} = 0,\,\,\,\,\frac{{\partial F}}{{\partial {{q}_{0}}}} = 0$дают два самосогласованных уравнения для определения значений ${{\sigma }_{Z}}$ и ${{q}_{0}}{\text{:}}$
(15)
$\begin{gathered} {{\sigma }_{Z}} = \frac{{2{\text{sh}}\left\{ {\left[ {{{\mu }_{0}}H + \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}}} \right]} \right\}}}{{2{\text{ch}}\left\{ {\beta \left[ {{{\mu }_{0}}H + \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}}} \right]} \right\} + {\text{exp}}\left( { - \frac{1}{2}\beta Kz{{q}_{0}}} \right)}}, \\ {{q}_{0}} = \frac{{2{\text{ch}}\left\{ {\beta \left[ {{{\mu }_{0}}H + \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}}} \right]} \right\} - 2{\text{exp}}\left( { - \frac{1}{2}\beta Kz{{q}_{0}}} \right)}}{{2{\text{ch}}\left\{ {\beta \left[ {{{\mu }_{0}}H + \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}}} \right]} \right\} + {\text{exp}}\left( { - \frac{1}{2}\beta Kz{{q}_{0}}} \right)}}. \\ \end{gathered} $Чтобы выяснить, соответствуют ли значения ${{\sigma }_{Z}}$ и ${{q}_{0}},$ находимые из (15), точкам локальных минимумов или максимумов ТДП ${{F}_{f}}$ при заданных $T$ и $H,$ необходимо исследовать знаки вторых производных ${{F}_{f}}$ по ${{\sigma }_{Z}}$ и ${{q}_{0}}.$ Условия минимума требуют, чтобы выполнялись неравенства:
(16)
$\begin{gathered} \frac{{{{\partial }^{2}}{{F}_{f}}}}{{\partial \sigma _{Z}^{2}}} = \left( {I - \frac{1}{2}K} \right)z\left\{ {1 - 2\beta \left( {I - \frac{1}{2}K} \right)} \right.; \\ z\left. {\frac{{2 + {\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right){\text{ch}}\left( {\beta {{h}_{f}}} \right)}}{{{{{[2{\text{ch}}\left( {\beta {{h}_{f}}} \right) + {\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right)]}}^{2}}}}} \right\} > 0; \\ {{\Delta }}\left( {{{\sigma }_{Z}},{{q}_{0}}} \right) \equiv \frac{{{{\partial }^{2}}{{F}_{f}}}}{{\partial \sigma _{Z}^{2}}}\frac{{{{\partial }^{2}}{{F}_{f}}}}{{\partial q_{0}^{2}}} - {{\left( {\frac{{{{\partial }^{2}}{{F}_{f}}}}{{\partial {{q}_{0}}\partial {{\sigma }_{Z}}}}} \right)}^{2}} = \\ = \,\, - \frac{1}{6}K\left( {I - \frac{1}{2}K} \right){{z}^{2}}[2{\text{ch}}\left( {\beta {{h}_{f}}} \right) + \\ + \,\,{\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right){{]}^{{ - 3}}}D > 0, \\ \end{gathered} $(17)
$\begin{gathered} D = {{[2{\text{ch}}\left( {\beta {{h}_{f}}} \right) + {\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right)]}^{3}} - \beta z \times \\ \times \,\,\left[ {4I - 2K + \left( {2I + 4K} \right){\text{ch}}\left( {\beta {{h}_{f}}} \right){\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right)} \right. \times \\ \left. { \times \,\,2{\text{ch}}\left( {\beta {{h}_{f}}} \right) + {\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right)} \right] + \\ + \,\,6{{\beta }^{2}}{{z}^{2}}K\left( {I - \frac{1}{2}K} \right){\text{exp}}\left( { - 3\beta {{h}_{{q0}}}} \right). \\ \end{gathered} $Очевидно, что условие ${{\Delta }}\left( {{{\sigma }_{Z}},{{q}_{0}}} \right) = 0,$ решаемое совместно с уравнением (15) для ${{\sigma }_{Z}}\left( {T,H} \right)$ и ${{q}_{0}}\left( {T,H} \right)$ при фиксированных $H,$ будет на кривых температурных зависимостей ${{\sigma }_{Z}}\left( {T,H} \right)$ и ${{q}_{0}}\left( {T,H} \right)$ определять границу между термодинамически устойчивыми значениями ${{\sigma }_{Z}}\left( {T,H} \right)$ и ${{q}_{0}}\left( {T,H} \right),$ отвечающими локальным минимумам ТДП, и термодинамически неустойчивым значениям этих же параметров, отвечающих максимумам ТДП.
3
Исследуем поведение параметров порядка ${{\sigma }_{Z}}$ и ${{q}_{0}},$ предполагая, что магнитное упорядочение возникает путем фазового перехода II рода. При высоких температурах, считая ${{\sigma }_{Z}} \ll 1$ и ${{q}_{0}} \ll 1,$ получим разложение ТДП ${{F}_{f}}$ (12) в ряд как
(18)
$\begin{gathered} {{F}_{f}} \approx - {{\beta }^{{ - 1}}}{\text{ln}}3 - \frac{2}{3}Kz + \frac{1}{2}\left( {I - \frac{1}{2}K} \right) \times \\ \times \,\,z\left[ {1 - ~~\frac{2}{3}\beta \left( {I - \frac{1}{2}K} \right)z} \right] \times \\ \times \,\,\sigma _{Z}^{2} + \frac{1}{{12}}Kz\left( {1 - \frac{1}{3}\beta Kz} \right)q_{0}^{2} + \\ + \,\,\frac{1}{{36}}{{\beta }^{3}}{{\left( {I - \frac{1}{2}K} \right)}^{4}}{{z}^{4}}\sigma _{Z}^{4} - \\ - \,\,\frac{1}{{18}}{{\beta }^{2}}K{{\left( {I - \frac{1}{2}K} \right)}^{2}}{\text{\;}}{{z}^{3}}{{q}_{0}}\sigma _{Z}^{2} - \frac{2}{3}\beta \left( {I - \frac{1}{2}K} \right)z{{\sigma }_{Z}}{{\mu }_{0}}H. \\ \end{gathered} $Из (18) видно, что температура Кюри ${{T}_{C}}$ определяется как
(19)
$\beta _{C}^{{ - 1}} \equiv {{k}_{{\text{B}}}}{{T}_{{\text{c}}}} = \frac{2}{3}\left( {I - \frac{1}{2}K} \right)z.$Ограничиваясь температурами, близкими к ${{T}_{{\text{C}}}},$ и рассматривая относительное отклонение температуры $T$ от точки Кюри ${{T}_{{\text{C}}}}$ в виде t = = ${{\left( {{{T}_{{\text{C}}}} - T} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{{\text{C}}}} - T} \right)} {{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{T}_{{\text{C}}}}}} \ll 1$ как параметр малости, приведем ${{F}_{f}}$ (18) к виду
(20)
$\begin{gathered} {{F}_{f}} \approx - {{\beta }^{{ - 1}}}{\text{ln}}3 - \frac{2}{3}Kz - \frac{1}{2}\left( {I - \frac{1}{2}K} \right)zt\sigma _{{Z~}}^{{2{\text{\;}}}} + \\ + \,\,\frac{3}{{32}}\left( {I - \frac{1}{2}K} \right)z\sigma _{Z}^{4} + \frac{{K\left( {I - K} \right)}}{{6\left( {2I - K} \right)}}zq_{0}^{2} - \\ - \,\,\frac{1}{8}Kz{{q}_{0}}\sigma _{Z}^{2} - {{\mu }_{0}}H{{\sigma }_{Z}}. \\ \end{gathered} $Условия ${{\partial {{F}_{f}}} \mathord{\left/ {\vphantom {{\partial {{F}_{f}}} {\partial {{\sigma }_{Z}}}}} \right. \kern-0em} {\partial {{\sigma }_{Z}}}} = 0,$ ${{\partial {{F}_{f}}} \mathord{\left/ {\vphantom {{\partial {{F}_{f}}} {\partial {{q}_{0}}}}} \right. \kern-0em} {\partial {{q}_{0}}}} = 0$ дают уравнение для определения ${{\sigma }_{Z}}$ и ${{q}_{0}}$ вблизи ${{T}_{{\text{C}}}}{\text{:}}$
(21)
$\left( {\begin{array}{*{20}{l}} {\left( {I - \frac{1}{2}K} \right)z\left( { - t{{\sigma }_{Z}} + \frac{3}{8}\sigma _{Z}^{3}} \right) - \frac{1}{4}Kz{{q}_{0}}{{\sigma }_{Z}} - {{\mu }_{0}}H = 0} \\ {\frac{{I - K}}{{3\left( {2I - K} \right)}}{{q}_{0}} - \frac{1}{8}\sigma _{Z}^{2} = 0.} \end{array}} \right.$В случае $H = 0$ решения (21) описывают следующие спонтанные состояния:
1) парамагнитное состояние с
которое, как можно убедиться из соотношений (16), термодинамически устойчиво при температурах выше точки Кюри $T > {{T}_{{\text{C}}}}$ и соотношениях параметров обмена $I > K.$
2) магнитное состояние с ненулевыми параметрами порядка
(23)
$\begin{gathered} \sigma _{Z}^{2}\left( {H = 0} \right) = \frac{{16}}{3}\left( {\frac{{I - K}}{{2I - 3K}}} \right)\left( {1 - \frac{T}{{{{T}_{{\text{C}}}}}}} \right), \\ {{q}_{0}} = 2\frac{{\left( {2I - K} \right)}}{{\left( {2I - 3K} \right)}}\left( {1 - \frac{T}{{{{T}_{{\text{C}}}}}}} \right), \\ \end{gathered} $которое термодинамически устойчиво при $T < {{T}_{{\text{C}}}}$ и соотношении параметров обмена ${K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I} < \frac{2}{3}.$
Заметим, что для области значений параметров обмена $I > K,$ $3K > 2I$ (т.е. $1 > {K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I} > \frac{2}{3}$) также существуют решения с вещественными значениями параметров порядка
(24)
$\begin{gathered} \sigma _{Z}^{2}\left( {H = 0} \right) = \frac{{16}}{3}\left( {\frac{{I - K}}{{3K - 2I}}} \right)\left( {\frac{T}{{{{T}_{C}}}} - 1} \right) > 0, \\ {\text{\;}}{{q}_{0}} = 2\frac{{\left( {2I - K} \right)}}{{\left( {3K - 2I} \right)}}\left( {\frac{T}{{{{T}_{{\text{C}}}}}} - 1} \right) > 0. \\ \end{gathered} $Однако эти решения подразумевают нефизическую картину существования магнитного упорядочения в области температур $T > {{T}_{{\text{C}}}}$ выше точки Кюри и увеличение параметров порядка при повышении температуры. Можно убедиться, что эти решения отвечают точкам максимумов ТДП и поэтому являются термодинамически неустойчивыми. Таким образом, условия $0 < {K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I} < {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ ограничивают область фазовых переходов II рода в ферромагнетике с биквадратичным обменом, а значение ${K \mathord{\left/ {\vphantom {K I}} \right. \kern-0em} I} = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ дает трикритическую точку на шкале отношений параметров обмена.
В случае конечного магнитного поля $H \ne 0$ из уравнений (21) следует кубическое уравнение для ${{\sigma }_{Z}}{\text{:}}$
(25)
$\sigma _{Z}^{3} - \frac{{16}}{3}\left( {\frac{{I - K}}{{2I - 3K}}} \right)t{{\sigma }_{Z}} - \frac{{32}}{9}\left( {\frac{{I - K}}{{2I - 3K}}} \right)\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}} = 0.$Отсюда при $t = 0$ (т.е. $T = {{T}_{{\text{C}}}}$) получим
(26)
$\begin{gathered} {{\sigma }_{Z}}\left( {{{T}_{{\text{C}}}},H} \right) = 2{{\left[ {\frac{4}{9}\left( {\frac{{I - K}}{{2I - 3K}}} \right)\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \\ {{q}_{0}}\left( {{{T}_{{\text{C}}}},H} \right) = \frac{{3\left( {2I - K} \right)}}{{8\left( {I - K} \right)}}\sigma _{Z}^{2}\left( {{{T}_{{\text{C}}}},H} \right) = \\ = \,\,{{\left( {\frac{2}{3}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\frac{{\left( {2I - K} \right)}}{{{{{(I - K)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{{(2I - 3K)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{\left( {\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Далее, при $t < 0$ (т.е. $T > {{T}_{{\text{C}}}}$) точное решение кубического уравнения (25) имеет довольно сложный вид (см. [27]):
(27)
$\begin{gathered} {{\sigma }_{Z}} = {{\left( {\frac{f}{3}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left\{ {{{{\left[ {{{{\left( {\frac{f}{3}{{{\left| t \right|}}^{3}} + {{g}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + g} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - } \right. \\ \left. { - \,\,{{{\left[ {{{{\left( {\frac{f}{3}{{{\left| t \right|}}^{3}} + {{g}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - g} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right\}, \\ \end{gathered} $В пределе ${{\left| t \right|}^{3}} \ll {{({{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}})}^{2}}$ решение (27) можно приближенно представить в виде
(28)
$\begin{gathered} {{\sigma }_{Z}} \simeq 2{{\left[ {\frac{4}{9}\left( {\frac{{I - K}}{{2I - 3K}}} \right)\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} - \\ - \,\,\frac{4}{3}{{\left[ {\frac{2}{3}{{{\left( {\frac{{I - K}}{{2I - 3K}}} \right)}}^{2}}\frac{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}{{{{\mu }_{0}}H}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left| t \right| + ..., \\ \end{gathered} $что при $\left| t \right| \to 0$ переходит в результат (26). В противоположном пределе ${{\left| t \right|}^{3}} \gg {{({{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}})}^{2}}$ из (27) получается стандартный результат для σZ, пропорциональный линейной восприимчивости:
(29)
$\begin{gathered} {{\sigma }_{Z}}\left( {T > {{T}_{{\text{C}}}}} \right) \simeq \frac{2}{3}\left( {\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right) \times \frac{1}{{\left| t \right|}} = \frac{2}{3}\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}\left( {{{T}_{{\text{C}}}} - T} \right)}}; \\ {{q}_{0}}(T > {{T}_{{\text{C}}}}) \simeq \frac{1}{6}\left( {\frac{{2I - K}}{{I - K}}} \right){{\left[ {\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}\left( {{{T}_{{\text{C}}}} - T} \right)}}} \right]}^{2}}. \\ \end{gathered} $Наконец, в области магнитного упорядочения при $t > 0$ увеличение ${{\sigma }_{Z}}$ в поле $H$ добавляется к величине спонтанной намагниченности ${{\sigma }_{{Z0}}}\left( T \right).$ Тогда представим ${{\sigma }_{Z}}\left( {H,T} \right)$ в виде ряда по степеням $H$ как
(30)
$\begin{gathered} {{\sigma }_{Z}}\left( {T,H} \right) = {{\sigma }_{{Z0}}}\left( T \right) + \frac{d}{{dH}}{{\sigma }_{Z}}{{\left. {\left( {T,H} \right)} \right|}_{{H = 0}}}H + ... = \\ = {{\sigma }_{{Z0}}}\left( T \right) + {{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) \\ \end{gathered} $и ограничимся вычислением поправки ${{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) \simeq $ $ \simeq \frac{d}{{dH}}{{\sigma }_{Z}}{{\left. {\left( {T,H} \right)} \right|}_{{H = 0}}}H,$ линейной по магнитному полю $H$. Дифференцируя уравнение (25) по $H$ и переходя к пределу $H \to 0,$ найдем dσZ(H)/dH|H = 0. В результате получим
(31)
$\begin{gathered} {{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) \simeq {{\left. {\frac{{d{{\sigma }_{Z}}\left( {T,H} \right)}}{{dH}}} \right|}_{{H = 0}}}H \simeq \\ \simeq \,\,\frac{1}{3}\left( {\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right) \times \frac{1}{t} = \frac{{{{\mu }_{0}}H}}{{3{{k}_{{\text{B}}}}\left( {{{T}_{{\text{C}}}} - T} \right)}}. \\ \end{gathered} $Аналогичным образом, учитывая взаимосвязь ${{q}_{0}}$ и $\sigma _{Z}^{2}\left( {T,H = 0} \right)$ (23), можно получить увеличение квадрупольного параметра порядка ${{\Delta }}{{q}_{0}}$ в магнитном поле при $T < {{T}_{{\text{C}}}}{\text{:}}$
(32)
$\begin{gathered} {{\Delta }}{{q}_{0}}\left( {T < {{T}_{{\text{C}}}},H} \right) \approx \frac{3}{4}\left( {\frac{{2I - K}}{{I - K}}} \right){{\sigma }_{Z}}\left( {T,H = 0} \right) \times \\ \times \,\,{{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) = \frac{{2I - K}}{{{{{[3\left( {I - K} \right)\left( {2I - 3K} \right)]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \times \\ \times \,\,\left[ {\frac{{{{\mu }_{0}}H}}{{{{k}_{{\text{B}}}}\sqrt {{{T}_{{\text{C}}}}\left( {{{T}_{{\text{C}}}} - T} \right)} }}} \right]. \\ \end{gathered} $Учитывая, что разложение ${{\sigma }_{Z}}\left( {T,H} \right)$ (30) в ряд (для области температур $T < {{T}_{{\text{C}}}}$) подразумевает использование соотношения ${{\sigma }_{{Z0}}} \gg {{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) \simeq $ $ \simeq \frac{d}{{dH}}{\kern 1pt} {{\sigma }_{Z}}{{\left. {\left( {T,H} \right)} \right|}_{{H = 0}}}{\kern 1pt} H,$ получим условие ${{t}^{3}} \gg $ $ \gg \,\,{{({{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}})}^{2}}$ на область применимости результата (31), аналогичное условию применимости соотношения (29) для ${{\sigma }_{Z}}\left( {T,H} \right)$ в области температур $T > {{T}_{{\text{C}}}}.$
4
Рассчитаем изменение магнитной энтропии ${{\Delta }}{{S}_{M}}\left( {T,{{H}_{f}}} \right)$ (на один магнитный атом) при изотермическом намагничивании от начального поля ${{H}_{i}} = 0$ до конечного поля ${{H}_{f}}$ [3]:
(33)
$\begin{gathered} {{\Delta }}{{S}_{M}}\left( {T,{{H}_{f}}} \right) = \int\limits_0^{{{H}_{f}}} {{{{\left( {\frac{{dm\left( {T,H} \right)}}{{dT}}} \right)}}_{H}}dH} = \\ = {{\mu }_{0}}\int\limits_0^{{{H}_{f}}} {{{{\left( {\frac{{d{{\sigma }_{Z}}\left( {T,H} \right)}}{{dT}}} \right)}}_{H}}dH} . \\ \end{gathered} $Для $T = {{T}_{{\text{C}}}},$ предварительно продифференцировав кубическое уравнение (25) по $T,$ получим
(34)
$\frac{{d{{\sigma }_{Z}}}}{{dT}} = \frac{{{{\sigma }_{Z}}}}{{{{T}_{{\text{C}}}} - T - \frac{9}{{16}}\left( {\frac{{2I - 3K}}{{I - K}}} \right){{T}_{{\text{C}}}}\sigma _{Z}^{2}\left( {T,H} \right)}},$что при $T \to {{T}_{{\text{C}}}}$ дает
(35)
$\begin{gathered} {{\left. {\frac{{d{{\sigma }_{Z}}}}{{dT}}} \right|}_{{T = {{T}_{{\text{C}}}}}}} = - \frac{{16}}{9}\left( {\frac{{I - K}}{{2I - 3K}}} \right)\frac{1}{{{{T}_{{\text{C}}}}{{\sigma }_{Z}}\left( {{{T}_{{\text{C}}}},H} \right)}} = \\ = - \frac{2}{T}{{\left[ {\frac{{4\left( {I - K} \right)}}{{9\left( {2I - 3K} \right)}}} \right]}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\left( {\frac{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}{{{{\mu }_{0}}H}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Отсюда получаем
(36)
${{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}},{{H}_{f}}} \right) = - 3{{k}_{{\text{B}}}}{{\left[ {\frac{{4\left( {I - K} \right)}}{{9\left( {2I - 3K} \right)}}\frac{{{{\mu }_{0}}{{H}_{f}}}}{{{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right]}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$В области $T > {{T}_{{\text{C}}}},$ используя (28) и (31), найдем
(37)
$\begin{gathered} \frac{{d{{\sigma }_{Z}}(T > {{T}_{C}})}}{{dT}} = - \frac{{2{{\mu }_{0}}H}}{{3{{k}_{{\text{B}}}}{{{(T - {{T}_{{\text{C}}}})}}^{2}}}}, \\ {{\Delta }}{{S}_{{\text{M}}}}(T > {{T}_{{\text{C}}}},{{H}_{f}}) = \\ = - \frac{1}{3}{{k}_{{\text{B}}}}{{\left[ {\frac{{{{\mu }_{0}}{{H}_{f}}}}{{{{k}_{{\text{B}}}}\left( {T - {{T}_{{\text{C}}}}} \right)}}} \right]}^{2}}. \\ \end{gathered} $Наконец, в ферромагнитной области при T < < TC, где в интервале относительных температур выполняется условие ${{t}^{3}} \gg {{({{{{\mu }_{0}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}{{H}_{f}}} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}})}^{2}}$ и где увеличение намагниченности в поле описывается поправкой, линейной по магнитному полю (31), имеет место
(38)
$\begin{gathered} \frac{{d{{\sigma }_{z}}(T < {{T}_{{\text{C}}}})}}{{dT}} = \frac{d}{{dT}}{{\sigma }_{{Z0}}}\left( T \right) + \\ + \,\,\frac{d}{{dT}}{{\Delta }}{{\sigma }_{Z}}\left( {T,H} \right) = \\ = - 2{{\left[ {\frac{{I - K}}{{3\left( {2I - 3K} \right){{T}_{{\text{C}}}}\left( {{{T}_{{\text{C}}}} - T} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \frac{{{{\mu }_{0}}H}}{{3{{k}_{{\text{B}}}}{{{({{T}_{{\text{C}}}} - T)}}^{2}}}}. \\ \end{gathered} $Тогда изменение магнитной энтропии будет состоять из двух вкладов с противоположными знаками
(39)
$\begin{gathered} {{\Delta }}{{S}_{{\text{M}}}}\left( {T < {{T}_{{\text{C}}}},{{H}_{f}}} \right) = {{k}_{{\text{B}}}}\left\{ { - 2{{{\left[ {\frac{{I - K}}{{3\left( {2I - 3K} \right)}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right. \times \\ \left. { \times \,\,\left( {\frac{{{{\mu }_{0}}{{H}_{f}}}}{{{{k}_{{\text{B}}}}{{{[{{T}_{{\text{C}}}}\left( {{{T}_{{\text{C}}}} - T} \right)]}}^{{1/2}}}}}} \right) + \frac{1}{6}{{{\left[ {\frac{{{{\mu }_{0}}{{H}_{f}}}}{{{{k}_{{\text{B}}}}\left( {{{T}_{{\text{C}}}} - T} \right)}}} \right]}}^{2}}} \right\} \approx \\ \approx \,\, - 2{{k}_{{\text{B}}}}{{\left[ {\frac{{I - K}}{{3\left( {2I - 3K} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {\frac{{{{\mu }_{0}}{{H}_{f}}}}{{{{k}_{{\text{B}}}}{{{[{{T}_{{\text{C}}}}\left( {{{T}_{{\text{C}}}} - T} \right)]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right), \\ \end{gathered} $причем в этой области температур положительным вкладом, квадратичным по магнитному полю, можно пренебречь вследствие вышеупомянутого условия малости ${{({{{{\mu }_{0}}{{H}_{f}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}{{H}_{f}}} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}})}^{2}} \ll {{t}^{3}}$ = ${{\left( {1 - \frac{T}{{{{T}_{{\text{C}}}}}}} \right)}^{3}}.$
Таким образом, в ферроквадрупольное упорядочение в магнетике с дополнительным биквадратичным обменом и двумя параметрами порядка (относительной намагниченностью и квадрупольным) дает те же критические степенные показатели в полевых и температурных зависимостях намагниченности и магнитной энтропии, что получается в теории фазовых переходов II рода в приближении среднего поля для обычного ферромагнетика с одним билинейным гейзенберговским обменом и одним дипольным параметром порядка. Однако важно отметить, что коэффициенты, стоящие в выражениях для намагниченности или энтропии перед полевыми или температурными переменными в степенном виде, теперь существенно зависят от соотношений параметров билинейного $I$ и биквадратичного обменов $K$ – они увеличиваются по мере роста отношения $K{\text{/}}I$ от минимального значения при $K{\text{/}}I = 0$ и становятся сингулярными в трикритической точке $K{\text{/}}I = 2{\text{/}}3,$, что знаменует переход в область фазовых переходов I рода.
5
Если с помощью численных расчетов уравнения (15) проследить спонтанное поведение параметров порядка ${{\sigma }_{{Z0}}}$ и ${{q}_{0}}\left( {H = 0} \right)$ для всего интервала температур от $T = 0$ до точки Кюри ${{T}_{{\text{C}}}}$ (19) при разных соотношениях параметров обмена $K{\text{/}}I,$ то видно следующее. С одной стороны, увеличение параметра биквадратичного обмена $K$ при фиксированном параметре билинейного обмена $I$ приводит к понижению температуры Кюри ${{T}_{{\text{C}}}}$ (19). С другой стороны, в области высоких относительных температур $t = T{\text{/}}{{T}_{{\text{C}}}} \geqslant 1{\text{/}}2$ увеличение отношения $K{\text{/}}I$ ведет к заметному увеличению параметров порядка ${{\sigma }_{{Z0}}}$ и ${{q}_{0}}\left( {H = 0} \right)$ по сравнению со случаем только одного билинейного обмена ($K = 0$). Это видно из рис. 1, где представлены расчеты ${{\sigma }_{{Z0}}}\left( t \right)$ для трех случаев: $K{\text{/}}I = 0$ – отсутствие биквадратичного обмена, $K{\text{/}}I = {\text{1/}}3$ и $K{\text{/}}I = 2{\text{/}}3$ (для трикритической точки на шкале отношений $K{\text{/}}I$).
Рис. 1.
Температурная зависимость спонтанной относительной намагниченности на шкале относительных температур $t = {T \mathord{\left/ {\vphantom {T {{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{T}_{{\text{C}}}}}}$ (где ${{k}_{{\text{B}}}}{{T}_{{\text{C}}}} = \frac{2}{3}\left( {I - \frac{1}{2}K} \right)z$) для случаев $K{\text{/}}I = 0$ (кривая 1), $K{\text{/}}I = 1{\text{/}}3$ (кривая 2) и $K{\text{/}}I = 2{\text{/}}3$ (кривая 3).

Если говорить о роли квадрупольных параметров порядка в термодинамике магнитных систем, то надо иметь в виду, что, вообще говоря, квадрупольный параметр порядка ${{q}_{0}} = 3\left\langle {S_{Z}^{2}} \right\rangle $ – $S\left( {S + 1} \right)$ существует и в обычной гейзенберговском ферромагнетике с билинейным обменом в случаях спинов $S \geqslant 1.$ Однако в отсутствие биквадратичного обмена ($K = 0$) этот параметр не связан динамическим взаимодействием с гамильтонианом магнитной системы, и поэтому он не дает никакого вклада в термодинамику магнетика.
Заметим также, что аналитические результаты для поведения параметров порядка ${{q}_{0}}$ и ${{\sigma }_{Z}}$ (формулы (23) и (26)) и соответственно изменения энтропии ${{\Delta }}{{S}_{M}}$ (36), (39) получены путем разложения термодинамического потенциала ${{F}_{f}}$ (12) в ряд по малым значениям ${{\sigma }_{0}} \ll 1$ и ${{q}_{0}} \ll 1,$ вследствие чего самосогласованные уравнения для ${{\sigma }_{Z}}$ и ${{q}_{0}}$ (15) были заменены на приближенные кубические уравнения (21) и (25). Поэтому полученные фомулы справедливы только в небольшом интервале $\left( {{{T}_{{\text{C}}}} - T} \right) \ll {{T}_{{\text{C}}}}$ температурных отклонений от точки Кюри ${{T}_{{\text{C}}}}.$ Кроме того, даже в этом температурном интервале появляются ограничения на допустимый диапазон отношений параметров обмена $K{\text{/}}I,$ так как коэффициенты кубического уравнения (25) и соответственно выражения для ${{\sigma }_{Z}}$ и ${{q}_{0}}$ (23) и (26) содержат опасный множитель ${{(2I - 3K)}^{{ - 1}}}.$ Это ведет к расходимости результатов при $K{\text{/}}I \to 2{\text{/}}3$ и к безусловному нарушению вблизи трикритической точки $K{\text{/}}I = 2{\text{/}}3$ исходных ограничений на малость параметров ${{\sigma }_{Z}} \ll 1$ и ${{q}_{0}} \ll 1$ даже при $T \approx {{T}_{{\text{C}}}}.$ Поэтому представляет интерес выяснить в более широком интервале температур и для всего диапазона отношений параметров обмена $K{\text{/}}I,$ допускающих переход II рода, общий характер дополнительного влияния квадрупольного параметра порядка ${{q}_{0}}$ и параметра биквадратичного обмена $K$ на физические свойства магнетика по сравнению со случаем ферромагнетика только с билинейным обменом ($I \ne 0$).
На рис. 2 представлен результат численного расчета температурной зависимости магнитной энтропии ${{{{S}_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{M}}}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}$ в области спонтанного магнитного упорядочения $0 < T < {{T}_{{\text{C}}}},$ вычисленной по формуле (13) с использованием предварительно рассчитанных параметров порядка ${{\sigma }_{Z}}$ и ${{q}_{0}}$ из (15) для тех же значений $K{\text{/}}I,$ что были использованы при расчете спонтанной намагниченности на рис. 1. Видно, что если сравнить ферромагнитное состояние в случае только билинейного обмена ($K = 0,$ $I \ne 0$) и ферроквадрупольные состояния с дополнительным биквадратичным обменом ($K \ne 0,$ $I \ne 0$) при одинаковой температуре Кюри ${{T}_{{\text{C}}}},$ то при одинаковом удалении по температуре от ${{T}_{{\text{C}}}}$ ферро-квадрупольные состояния будут более упорядочены – они имеют более низкую магнитную энтропию.
Рис. 2.
Зависимость магнитной энтропии ${{{{S}_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{M}}}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}$ в случаях спонтанного упорядочения от относительной температуры ${T \mathord{\left/ {\vphantom {T {{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{T}_{{\text{C}}}}}}$ для трех значений отношений $K{\text{/}}I,$ а именно, кривая 1 – для $K{\text{/}}I = 0$ (отсутствие биквадратичного обмена), кривая 2 – для $K{\text{/}}I = 1{\text{/}}3$ и кривая 3 – для $K{\text{/}}I = 2{\text{/}}3$ (трикритическая точка фазовых переходов на шкале отношений $K{\text{/}}I$).

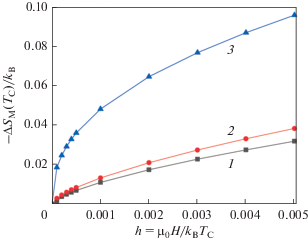
Наконец, рис. 3 демонстрирует полевую зависимость изменения магнитной энтропии ${{{{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}},H} \right)} \mathord{\left/ {\vphantom {{{{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}},H} \right)} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}$ в точке Кюри ${{T}_{{\text{C}}}},$ вычисленную из выражения (13) с использованием ${{\sigma }_{Z}}\left( {{{T}_{{\text{C}}}},H \ne 0} \right)$ и ${{q}_{0}}\left( {{{T}_{{\text{C}}}},H \ne 0} \right)$ из уравнения (15). Видно, что наличие биквадратичного обмена $K \ne 0$ и квадрупольного параметра порядка ${{q}_{0}} \ne 0$ заметно увеличивает абсолютную величину изменения энтропии
Рис. 3.
Зависимость изменения магнитной энтропии ${{ - {{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}}} \right)} \mathord{\left/ {\vphantom {{ - {{\Delta }}{{S}_{{\text{M}}}}\left( {{{T}_{{\text{C}}}}} \right)} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}}$ в точке Кюри ${{T}_{{\text{C}}}}$ от безразмерного магнитного поля $h = {{{{\mu }_{0}}H} \mathord{\left/ {\vphantom {{{{\mu }_{0}}H} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}{{T}_{{\text{C}}}}}}$ для трех случаев отношений параметров обмена: 1) кривая 1 – для $K{\text{/}}I = 0$ (отсутствие биквадратичного обмена), 2) кривая 2 – для $K{\text{/}}I = 1{\text{/}}3$ (середина интервала отношений $K{\text{/}}I,$ допускающего фазовый переход II рода), 3) кривая 3 – для $K{\text{/}}I = 2{\text{/}}3$ (переход в трикритической точке, на границе интервала отношений $K{\text{/}}I$ для переходов II рода).
Работа частично поддержана проектом РФФИ № 18-02-00281 А.
Список литературы
Tishin A.M., Spichkin Y.I. The magnetocaloric effect and its applications // Institute of Physics Publishing, Bristol and Philadelphia. 2003. 480 p.
Gschneider K.A.Jr., Pecharsky V.K., Tsokol A.O. Recent developments in magnetocaloric materials // Rep. Progr. Phys. 2005. V. 68. P. 1479–1539.
Oliveira N.A., von Ranke P.J. Theoretical aspects of the magnetocaloric effect // Phys. Reports. 2010. V. 489. P. 89–153.
Ram N.R., Prakash M., Naresh U., Kumar N.S., Sarmash T.S., Subbarao T., Kumar R.J., Kumar G.R., Naidu K.C.B. Review on magnetocaloric effect and materials // J. Supercond. Nov. Magn. 2018. V. 31. P. 1971–1979.
Bean C.P., Rodbell D.S. Magnetic disorder as a first-order phase transformation // Phys.Rev. 1962. V. 126. P. 104–115.
Валиев Э.З. Энтропия и магнитотепловые эффекты в ферромагнетиках с фазовыми переходами первого и второго рода // ЖЭТФ. 2009. Т. 135. С. 314–321.
Валиев Э.З. О соотношении Максвелла в ферромагнетиках и ферримагнетиках // ФММ. 2020. Т. 121. С. 789–793.
Anderson P.W. New approach to the theory of superexchange interactions // Phys. Rev. 1959. V. 115. P. 2–11.
Huang N.L., Orbach R. Biquadratic superexchange // Phys. Rev. Lett. 1964. V. 12. P. 275–277.
Kobler U., Mueller R., Smardz L., Maier D., Fisher K., Olefs B., Zinn W. Biquadratic exchange interaction in the Europium monochalcogenides // Z. Phys. B. 1996. V. 100. P. 497–506.
Novak P., Chaplygin I., Seifert G., Gemming S., Lasowski R. Ab-initio calculation of exchange interactions in YMnO3 // Computational Mater. Sci. 2008. V. 44. P. 79–81.
Wysocki A.I., Beloshchenko K.D., Ke L., van Schilfgarde M., Antropov V.P. Biquadratic magnetic interaction in parent ferropnictides // J. Phys.: Conf. Series. 2013. V. 449. O12024.
Slonzewski J.C. Origin of biquadratic exchange in magnetic multilayers (invited) // J. Appl. Phys. 1993. V. 73. P. 5957–5962.
Kartsev A., Augustin M., Evans R.F.L., Novoselov K.S., Santes E.J.G. Biquadratic exchange interactions in two-dimensional magnets // NPY: Comp. Mater. 2020. 150.
Spisak D., Hafner J. Theory of bilinear and biquadratic exchange interactions in iron: bulk and surface // JMMM. 1997. V. 168. P. 257–268.
Brown H.A. Heisenberg ferromagnet with biquadratic exchange // Phys. Rev. B. 1971. V. 4. P. 115–121.
Sivardiere J., Blume M. Dipolar and quadrupolar ordering in S = 3/2 Ising systems // Phys. Rev. B. 1972. V. 5. P. 1126–1134.
Nauciel-Bloch M., Sarma G., Castets A. Spin-one Heisenber ferromagnet in the presence of biquadratic exchange // Phys. Rev. B. 1972. V. 5. P. 4603–4609.
Chen H.H., Levy P.M. Dipole and quadrupole phase transitions in spin-1 models // Phys. Rev. B. 1973. V. 7. P. 4267–4284.
Матвеев В.М. Квантовый квадрупольный магнетизм и фазовые переходы в присутствии биквадратичного обмена // ЖЭТФ. 1974. Т.65. P. 1626–1636.
Матвеев В.М. Неколлинеарные структуры, фазовые переходы и метамагнитизм при биквадратичном обмене // ФТТ. 1974. Т. 16. P. 1635–1643.
Барьяхтар В.Г., Ганн В.В., Яблонский Д.А. К теории магнитоупорядоченных кристаллов с биквадратичным обменным взаимодействием // ФТТ. 1975. Т. 17. P. 1744–1748.
Brown H.A.Biquadratic exchange and first-order ferromagnetic phase transitions // Phys. Rev. B. 1975. V. 11. P. 4725–4727.
Chakraborty K.G. Phase transitions in a Heisenberg ferromagnet in the presence of biquadratic exchange: isotropic case // J. Phys. C: Solid St. Phys. 1976. V. 9. P. 1499–1509.
Матвеев В.М. Перестройка квантового квадрупольного упорядочения в магнитном поле // ФТТ. 1983. Т. 25. С. 3655–3664.
Вальков В.В., Мацулева Г.Н., Овчинников С.Г. Влияние сильного кристаллического поля на спектральные свойства магнетиков с биквадратичным обменом // ФТТ. 1989. Т. 31. С. 60–67.
Корн Г., Корн Т. Справочник по математике. М.: Наука. Физматлит. 1973, 632 с.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение


