Физика металлов и металловедение, 2022, T. 123, № 4, стр. 414-419
Низкотемпературные особенности магнитных и магнитокалорических свойств системы Mn1 – xCoxNiGe (0.05 ≤ x ≤ 0.4)
В. И. Митюк a, Г. С. Римский a, В. И. Вальков b, *, А. В. Головчан b, А. В. Маширов c, В. В. Коледов c
a ГО “НПЦ НАН Беларуси по материаловедению”
220072 Беларусь, ул. П. Бровки, 19, Минск
b ГУ “Донецкий физико-технический институт им. А.А. Галкина”
283072 Донецк, ул. Р. Люксембург, 72, ДНР
c Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, корп. 7, Россия
* E-mail: valkov09@gmail.com
Поступила в редакцию 28.10.2021
После доработки 12.12.2021
Принята к публикации 22.12.2021
- EDN: WEYMRC
- DOI: 10.31857/S0015323022040088
Аннотация
Анализ экспериментальных результатов, полученных при исследовании магнитоструктурных и магнитокалорических свойств системы Mn1– xCoxNiGe (0.05 ≤ x ≤ 0.80) позволил выделить ряд особенностей, одной из которых является появление необратимых спонтанных и индуцированных магнитным полем низкотемпературных переходов, сопровождающихся относительно резким увеличением намагниченности. Эти переходы наиболее отчетливо наблюдаются в области концентраций 0.15 ≤ x ≤ 0.40 при температурах, значительно более низких чем характерные температуры изоструктурных переходов 2-го рода из парамагнитного гексагонального в ферромагнитное гексагональное состояние. Основной целью настоящей работы является теоретический анализ низкотемпературных особенностей при учете наблюдаемых особенностей всего диапазона концентраций 0.05 ≤ x ≤ 0.40. Феноменологическое описание экспериментальных результатов проведено на основе концепции мягкой моды для структурных переходов между гексагональной и ромбической кристаллическими структурами при использовании в гамильтониане Гейзенберга внутреннего ортогонального поля, воздействующего на ортогональную спиновую компоненту. В рамках приближения молекулярного поля для спиновой подсистемы и приближения смещенного гармонического осциллятора для структурной подсистемы получено, что в зависимости от соотношения между ортогональным полем и обменно-структурными вкладами, которые описывают взаимодействие спиновой и структурной подсистем, может реализоваться ряд особенностей сопоставимых с экспериментально наблюдаемыми случаями характерными для 0.05 ≤ x ≤ 0.1 и 0.1 < x ≤ 0.4.
ВВЕДЕНИЕ
Четырехкомпонентные твердые растворы германидов на основе MnNiGe–CrNiGe [1], MnNiGe–CoNiGe [2–4] при различных комбинациях замещений 3d-элементов активно исследуют в рамках поиска оптимальных магнитокалорических функциональных материалов. Это связано с наличием в этих системах структурных и магнитных фазовых переходов, сопровождающихся относительно большим магнитокалорическим эффектом (МКЭ). Структурный вклад возникает вследствие изменения кристаллической симметрии при структурном фазовом переходе 1-го рода из гексагональной (hex) структуры типа Ni2In (группа симметрии P63/mmc) в ромбическую(orth) решетку типа TiNiSi (группа симметрии Pnma). Магнитный вклад возникает вследствие изменения магнитной симметрии при возникновении магнитного порядка. Как правило, магнитоупорядоченному ферромагнитному (FM) или геликоидальному (HM) состояниям соответствует ромбическая решетка TiNiSi. Магнитонеупорядоченное парамагнитное (PM) состояние может стабилизироваться как в ромбической TiNiSi, так и в гексагональной Ni2In решетках. В последнем случае магнитное разупорядочение может реализоваться как магнитоструктурный переход 1-го рода FM/HM(orth) ↔ ↔ PM(hex) и изменение магнитного поля вблизи температуры перехода приводит к максимальному МКЭ. Это обусловлено тем, что понижение магнитной симметрии при возникновении магнитного порядка сопровождается понижением кристаллографической симметрии и, напротив, повышение магнитной симметрии при исчезновении магнитного порядка происходит на фоне повышения структурной симметрии.
В системе Mn1 –xCoxNiGe при 0.05 ≤ x ≤ 0.1 магнитное упорядочение является результатом магнитоструктурных переходов 1-го рода HM(orth) ↔ ↔ PM(hex). Кроме упомянутого выше, к основным особенностям магнитоструктурных свойств исследуемой системы можно отнести следующее
1. Отсутствие самостоятельно существующего высокотемпературного парамагнитного структурного перехода PM(orth) ↔ PM(hex) (рис. 1).
Рис. 1.
T–x, σ–x диаграммы системы Mn1–xCoxNiGe. Тt1, Тt2, Tt4 – температуры лабильности PM(hex), HM1(orth) и HM2(orth) состояний; HM1, HM2 – высокотемпературные, низкотемпературные гелимагнитные структуры с ромбической решеткой; переход при Tt4 можно наблюдать при нагреве после охлаждения образца в поле B = 0 (режиме ZFCdown).
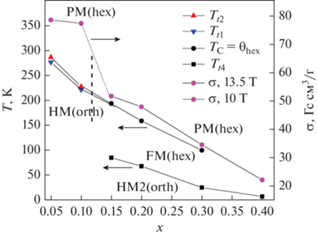
2. Изменение характера магнитного разупорядочения от фазовых переходов 1-го рода PM(hex)-HM1(orth), сопровождающихся температурным гистерезисом Δ = Тt2–Тt1 и резким увеличением намагниченности насыщения (рис. 2) до безгистерезисных фазовых переходов 2-го рода PM(hex)–FM(hex) с плавным изменением намагниченности [3] (см. рис. 2) при температуре Кюри ТС = Θhex, которое происходит при увеличении концентрации x от 0.1 до ≥0.15.
Рис. 2.
Температурные зависимости намагниченности, демонстрирующие магнитоструктурные и изоструктурные переходы в системе Mn1 –xCoxNiGe в сильном и слабом магнитном поле.
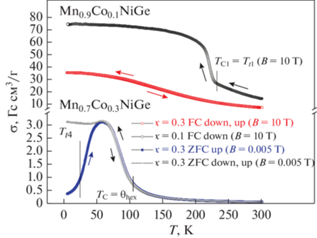
3. Уменьшение намагниченности насыщения спиновой системы в относительно узком диапазоне 0.1 ≤ x ≤ 0.15 концентраций Co и изменение типа и характера стабилизации магнитного порядка (см. рис. 1, 2). Магнитные фазовые переходы, сопровождающие установление ферромагнетизма (FM) при ТС, становятся плавными безгистерезисными изоструктурными переходами 2-го рода FM(hex) ↔ PM(hex) (см. рис. 2).
4. Чувствительность температурных зависимостей намагниченности σ(Т) к режимам ZFC, FC образцов с 0.15 ≤ x ≤ 0.8 в слабых магнитных полях, рис. 2.
5. Существование низкотемпературных (Т = 5 K) необратимо индуцированных магнитным полем переходов в сильных магнитных полях (0.15 ≤ x ≤ ≤ 0.8), сопровождающихся увеличением намагниченности насыщения (рис. 3).
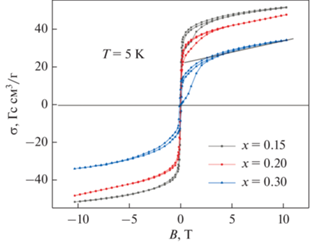
Рис. 3.
Полевые зависимости намагниченности, демонстрирующие необратимые индуцированные магнитным полем переходы [3] в области гелиевых температур.
На рис. 2 зависимости для x = 0.1 FC down (B = = 10 Tл) и для x = 0.3 ZFC up (B = 0.005 Tл) соответствуют магнитоструктурным переходам 1-го рода PM(hex) → HM1(orth) и HM2(orth) → FM(hex). Все остальные зависимости соответствуют изоструктурному поведению намагниченности в сильном и слабом магнитных полях. HM1(orth) для х = 0.1 в поле 10 Тл близко к ферромагнитному состоянию FM(orth), поэтому в поле 10 Тл магнитоструктурный переход 1-го рода PM(hex) → → HM1(orth) трансформируется в переход 1-го рода PM(hex) → FM(orth).
В настоящей работе предложена модель магнитоструктурных переходов, учитывающая основные особенности магнитных и структурных свойств системы Mn1 –xCoxNiGe.
АНАЛИЗ МАГНИТОСТРУКТУРНЫХ ПЕРЕХОДОВ В СИСТЕМЕ Mn1 –xCoxNiGe
При теоретическом анализе особенностей экспериментальных результатов исходим из следующих предположений:
совмещение магнитного и структурного переходов для образцов с x < 0.15 напрямую связано с характером фазовых переходов порядок–беспорядок;
существенное уменьшение намагниченности насыщения спиновой системы за пределами диапазона 0.05 ≤ x ≤ 0.1 обусловлено не только уменьшением концентрации Mn, но и различием в ее формировании в ромбическом и гексагональном состояниях;
изменения намагниченности при температуре Tt4 при нагреве предварительно охлажденных в режиме ZFC образцов, соответствуют магнитоструктурным переходам 1-го рода HM2(orth) → FM(hex). Геликоидальные структуры HM1, HM2 при этом могут совпадать или отличаться.
При описании структурных переходов будем опираться на модель структурных переходов типа смещения, в которой используется концепция замораживания локальных оптических колебаний ионов Ni, соответствующих размягчению z-компоненты мягкой локальной моды ${{Q}_{{nz}}}$ для Ni [1, 4]. Согласно [1, 4], термодинамический потенциал (ТП) структурноупругой системы имеет вид:
(1)
$\begin{gathered} \Omega {}_{Q}\, \equiv \Omega \left( {{{Q}_{0}},\sigma } \right) = \frac{{{{N}_{0}}}}{2}{{V}_{0}}\left( {Q_{0}^{2} + \sigma } \right) + \\ + \,\,\frac{{{{N}_{0}}}}{4}\left( {\gamma Q_{0}^{4} + 6Q_{0}^{2}\sigma + 3{{\sigma }^{2}}} \right) + \frac{{{{N}_{0}}}}{6}\Gamma \times \\ \times \,\,\left( {Q_{0}^{6} + 15Q_{0}^{4}\sigma + 45Q_{0}^{2}{{\sigma }^{2}} + 15{{\sigma }^{3}}} \right) - \frac{1}{2}{{N}_{0}}Q_{0}^{2}{{v}_{0}} \times \\ \times \,\,\left( {1 + {{L}_{1}}{{e}_{1}} + {{L}_{2}}{{e}_{2}}} \right) - T\frac{{{{k}_{B}}}}{2}{{N}_{0}}\ln \sigma + {{\tfrac{1}{2}e_{1}^{2}} \mathord{\left/ {\vphantom {{\tfrac{1}{2}e_{1}^{2}} {{{\kappa }_{1}}}}} \right. \kern-0em} {{{\kappa }_{1}}}} + \\ + \,\,{{\tfrac{1}{2}{{{\left( {{{e}_{2}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{\tfrac{1}{2}{{{\left( {{{e}_{2}}} \right)}}^{2}}} {{{\kappa }_{2}}}}} \right. \kern-0em} {{{\kappa }_{2}}}} + Р{{e}_{1}} - T\left( {{{\alpha {{e}_{1}}} \mathord{\left/ {\vphantom {{\alpha {{e}_{1}}} {{{\kappa }_{1}}}}} \right. \kern-0em} {{{\kappa }_{1}}}}} \right). \\ \end{gathered} $Здесь Q0 = 〈Qn〉 – среднее тепловое значение локальной нормальной координаты мягкой моды Qn, вычислено в приближении смещенного гармонического осциллятора [5] и описывает замороженное коллективное смещение ионов Ni1, Ni2$\left\langle {U_{{nz}}^{{{\text{Ni}}1,2}}} \right\rangle $ в n-той элементарной ячейке [1] при структурном переходе PM(hex) ↔ PM(orth). Данный переход сопровождается изменением симметрии P63/mmc(Q0 = 0) ↔ Pnma(Q0 ≠ 0); Q0 – является параметром структурного порядка; $\sigma = \left\langle {{{{[{{Q}_{n}} - \left\langle {{{Q}_{n}}} \right\rangle ]}}^{2}}} \right\rangle $ – дисперсия; N0 – число исходных гексагональных элементарных ячеек в единице объема. Зависимость фурье-компоненты парного взаимодействия между мягкими модами различных ячеек ${{v}_{0}}({{e}_{1}},{{e}_{2}}) = \sum\nolimits_{n{\kern 1pt} '} {{{v}_{{nn{\kern 1pt} '}}}} $ = ${{v}_{0}}\left( {1 + {{L}_{1}}{{e}_{1}} + {{L}_{2}}{{e}_{2}}} \right)$ от объемных (e1) и ромбических (e2) деформаций учитывает связь фононной подсистемы со статическими деформациями кристалла.
Для описания спиновой подсистемы, допускающей гелимагнитное упорядочение с волновым вектором магнитной структуры ${\mathbf{q}} = \left[ {{\text{0,0,}}{{q}_{a}}} \right]$ и изменение магнитного момента насыщения при постоянном значении спина S = 3/2, используем модельный гамильтониан [3]:
(2)
$\hat {H}\left( s \right) = - \sum\limits_{nk,n{\kern 1pt} 'k{\kern 1pt} '} {J_{{nn{\kern 1pt} '}}^{{kk{\kern 1pt} '}}} {\mathbf{\hat {s}}}_{n}^{k}{\mathbf{\hat {s}}}_{{n{\kern 1pt} {\text{'}}}}^{{k{\kern 1pt} {\text{'}}}} - 2{{\mu }_{B}}{{{\mathbf{H}}}_{0}}\sum\limits_{ni} {{\mathbf{\hat {s}}}_{n}^{k}} - \sum\limits_{ni} {{\mathbf{{\rm O}}}_{n}^{k}{\mathbf{\hat {s}}}_{n}^{k}} ,$(3)
${\mathbf{w}}_{n}^{k} = \left\lfloor {\sin ({\mathbf{qR}}_{n}^{k}),\,\, - \cos ({\mathbf{qR}}_{n}^{k}),\,\,0} \right\rfloor .$В приближении среднего поля (2) можно привести к виду ${{\hat {H}}_{{\mathbf{h}}}}(s)$ [3]:
(4a)
${{\hat {H}}_{{\mathbf{h}}}}(s) = - \sum\limits_{nk} {{\mathbf{\Delta }}_{n}^{k}{\mathbf{\hat {s}}}_{n}^{k}} ;$(4б)
$\begin{gathered} {\mathbf{\Delta }}_{n}^{k} = {\mathbf{h}}_{n}^{k} + {\mathbf{{\rm O}}}_{n}^{k} = \Delta {\mathbf{V}}_{n}^{k} \equiv \left| {\left( {{\mathbf{h}}_{n}^{k} + {\mathbf{{\rm O}}}_{n}^{k}} \right)} \right|{\mathbf{V}}_{n}^{k} \equiv \\ \equiv \left( {\sqrt {{{h}^{2}} + {{{\rm O}}^{2}}} } \right){\mathbf{V}}_{n}^{k};\,\,\,\,{\mathbf{h}}_{n}^{k} = h{\mathbf{u}}_{n}^{k}. \\ \end{gathered} $При ${\mathbf{{\rm O}}}_{n}^{k}{\mathbf{h}}_{n}^{k} = \left( {{\mathbf{w}}_{n}^{k}{\mathbf{u}}_{n}^{k}} \right){\rm O}h = 0,$ где ${\mathbf{w}}_{n}^{k},{\mathbf{u}}_{n}^{k}$ – единичные векторы; ${\rm O} \equiv {\rm O}(x,{{Q}_{0}});$ ${\mathbf{V}}_{n}^{k}$ – единичный вектор в направлении двухкомпонентного среднего поля ${\mathbf{\Delta }}_{n}^{k}.$ Согласно [4], для используемых $\hat {H}\left( s \right),{{\hat {H}}_{{\mathbf{h}}}}(s){\text{:}}$
(5)
$h = 2\left[ {J({{q}_{a}}) - \Delta Jco{{s}^{2}}(\vartheta )} \right]sy + 2{{\mu }_{B}}{{H}_{0}}\cos \left( \theta \right).$Тогда термодинамический потенциал спиновой системы имеет вид:
(7)
$\begin{gathered} X = \frac{{\sqrt {{{{(hs)}}^{2}} + {{s}^{2}}{{{\rm O}}^{2}}} }}{{{{k}_{B}}T}}; \\ z(X) = {{\left[ {sh\left( {1 + {{{\left( {2s} \right)}}^{{ - 1}}}} \right)X} \right]} \mathord{\left/ {\vphantom {{\left[ {sh\left( {1 + {{{\left( {2s} \right)}}^{{ - 1}}}} \right)X} \right]} {sh\left[ {{{{\left( {2s} \right)}}^{{ - 1}}}X} \right]}}} \right. \kern-0em} {sh\left[ {{{{\left( {2s} \right)}}^{{ - 1}}}X} \right]}}; \\ \end{gathered} $(8б)
$J({\text{0}}) \approx {{J}_{0}} + {{J}_{1}} + {{J}_{2}},\,\,\,\,\Delta J \equiv J({{q}_{a}}) - J(0).$Здесь $y = {m \mathord{\left/ {\vphantom {m s}} \right. \kern-0em} s} \leqslant 1,$ $m = \left\langle {\hat {s}_{n}^{k}u_{n}^{k}} \right\rangle \equiv {{\left\langle {\hat {m}_{n}^{k}} \right\rangle }_{h}}$ – среднее значение проекции спина $\hat {m}_{n}^{k}$ на направление локальной оси квантования ${\mathbf{u}}_{n}^{k} = [сos\left( {{\mathbf{qR}}_{n}^{k}} \right)\sin \left( \vartheta \right),$ $\sin \left( {{\mathbf{qR}}_{n}^{k}} \right)\sin \left( \vartheta \right),\cos \left( \vartheta \right)],$ вычисленное в приближении среднего поля $\Psi = {{{{q}_{a}}{{c}_{{{\text{hex}}}}}} \mathord{\left/ {\vphantom {{{{q}_{a}}{{c}_{{{\text{hex}}}}}} 2}} \right. \kern-0em} 2},$ $2\Psi = {{q}_{a}}{{c}_{{{\text{hex}}}}}$ – параметры геликоидальной структуры, описываемой волновым вектором qa; оптимальные значения этих параметров определяются из уравнения ${{\partial J(q)} \mathord{\left/ {\vphantom {{\partial J(q)} {\partial q}}} \right. \kern-0em} {\partial q}} = 0,$ конкурирующими решениями которого при ${{J}_{1}} \equiv {{J}_{1}}({{Q}_{0}},{{e}_{1}}) > 0,$ ${{J}_{2}} \equiv {{J}_{2}}({{{\text{Q}}}_{{\text{0}}}}{\text{,}}{{e}_{{\text{1}}}}) < 0$ будут только геликоидальное (при cosΨ = = ${{{{J}_{1}}({{Q}_{{\text{0}}}}{\text{,}}{{e}_{{\text{1}}}})} \mathord{\left/ {\vphantom {{{{J}_{1}}({{Q}_{{\text{0}}}}{\text{,}}{{e}_{{\text{1}}}})} {4\left| {{{J}_{2}}({{Q}_{{\text{0}}}}{\text{,}}{{e}_{{\text{1}}}})} \right|}}} \right. \kern-0em} {4\left| {{{J}_{2}}({{Q}_{{\text{0}}}}{\text{,}}{{e}_{{\text{1}}}})} \right|}}$ = $\delta \left( {{{Q}_{0}},{{e}_{1}}} \right) < 1$) c более высоким значением величины $J(q)$ и ферромагнитное (при $\Psi = 0$) с более низким значением величины $J(0)$ [3], $\vartheta $ – угол между направлением локальной оси квантования ${\mathbf{h}}_{n}^{k} = h{\mathbf{u}}_{n}^{k}$ (обменного поля) и направлением внешнего поля ${{H}_{0}};$ ${{k}_{{\text{B}}}}$ – постоянная Больцмана. ${{J}_{0}} \equiv {{J}_{0}}\left( {{{Q}_{0}},{{e}_{1}}} \right)$ – обменные интегралы между атомами Mn внутри слоев, перпендикулярных направлению волнового вектора q; ${{J}_{1}} \equiv {{J}_{1}}({{Q}_{0}},{{e}_{1}})$ и ${{J}_{2}} \equiv {{J}_{2}}({{Q}_{0}},{{e}_{1}},)$ – обменные интегралы между атомами Mn, которые находятся в ближайших и следующих за ближайшими слоями на расстояниях chex/2 и сhex (сhex – параметр гексагональной ячейки вдоль направления волнового вектора q).
Для каждого из сплавов системы Mn1 –xCoxNiGe и набора аналитических выражений для величин $\cos \Psi ,$ ${\kern 1pt} \cos \vartheta \equiv \varepsilon ,{{e}_{1}},{{e}_{2}},\sigma ,$ полученных из решения уравнений ${{\partial J(q)} \mathord{\left/ {\vphantom {{\partial J(q)} {\partial q}}} \right. \kern-0em} {\partial q}} = 0,$ ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial \vartheta }}} \right. \kern-0em} {\partial \vartheta }} = 0,$ ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial {{e}_{1}}}}} \right. \kern-0em} {\partial {{e}_{1}}}} = 0,$ ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial {{e}_{2}}}}} \right. \kern-0em} {\partial {{e}_{2}}}} = 0,$ ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial \sigma }}} \right. \kern-0em} {\partial \sigma }} = 0$ $(\Omega = {{\Omega }_{Q}} + {{\Omega }_{S}})$ для равновесных значений параметров структурного и магнитного порядков ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial {{Q}_{0}}}}} \right. \kern-0em} {\partial {{Q}_{0}}}} = 0,$ ${{\partial \left( \Omega \right)} \mathord{\left/ {\vphantom {{\partial \left( \Omega \right)} {\partial y}}} \right. \kern-0em} {\partial y}} = 0,$ приводятся к виду соответственно:
(9a)
$ - {{y}^{2}}\left( {{{\partial {{h}_{m}}} \mathord{\left/ {\vphantom {{\partial {{h}_{m}}} {\partial {{Q}_{0}}}}} \right. \kern-0em} {\partial {{Q}_{0}}}}} \right) + \left( {{{\partial \Omega ({{Q}_{0}},\sigma )} \mathord{\left/ {\vphantom {{\partial \Omega ({{Q}_{0}},\sigma )} {\partial {{Q}_{0}}}}} \right. \kern-0em} {\partial {{Q}_{0}}}}} \right) = 0;$(9б)
$y - {{B}_{s}}\left( X \right)\frac{{({{2a} \mathord{\left/ {\vphantom {{2a} {{{a}_{3}}}}} \right. \kern-0em} {{{a}_{3}}}}){{h}_{m}}y + 2{{\mu }_{0}}{{H}_{0}}\varepsilon }}{{\sqrt {{{{\left( {({{2a} \mathord{\left/ {\vphantom {{2a} {{{a}_{3}}}}} \right. \kern-0em} {{{a}_{3}}}}){{h}_{m}}y + 2{{\mu }_{0}}s{{H}_{0}}\varepsilon } \right)}}^{2}} + {{s}^{2}}{{{\rm O}}^{2}}} }} = 0.$Здесь Bs(X) – функция Бриллюэна:
(10)
${{B}_{s}}\left( X \right) = \left( {\frac{1}{{2s + 1}}} \right)\operatorname{cth} \frac{1}{{2s + 1}}X - \left( {\frac{1}{{2s}}} \right)\operatorname{cth} \frac{1}{{2s}}X;$(11)
$X = {{\left\lfloor {\sqrt {{{{\left( {({{2a} \mathord{\left/ {\vphantom {{2a} {{{a}_{3}}}}} \right. \kern-0em} {{{a}_{3}}}}){{h}_{m}}y + 2{{\mu }_{0}}s{{H}_{0}}\varepsilon } \right)}}^{2}} + {{s}^{2}}{{{\rm O}}^{2}}} } \right\rfloor } \mathord{\left/ {\vphantom {{\left\lfloor {\sqrt {{{{\left( {({{2a} \mathord{\left/ {\vphantom {{2a} {{{a}_{3}}}}} \right. \kern-0em} {{{a}_{3}}}}){{h}_{m}}y + 2{{\mu }_{0}}s{{H}_{0}}\varepsilon } \right)}}^{2}} + {{s}^{2}}{{{\rm O}}^{2}}} } \right\rfloor } {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}};$Зависимость обменных интегралов от параметров структурного порядка ${{Q}_{0}}$ и объемных деформаций ${{e}_{1}}$ определяет связь между спиновой и магнитоупругой решеточной подсистемами:
(12)
$\frac{{J({{q}_{a}})}}{{{{J}_{{00}}}}} = \left[ {{{r}_{{AF}}} + Q_{0}^{2}\left( {{{\lambda }_{{AF}}} + {{\lambda }_{{1AF}}}{{e}_{1}}} \right)2 + 2\lambda Q_{0}^{4}} \right];$(13)
$\begin{gathered} \frac{{\Delta J({{q}_{a}})}}{{{{J}_{{00}}}}} = \left[ {1 + 2Q_{0}^{2}\left( {{{\lambda }_{{20}}} + {{\lambda }_{{21}}}{{e}_{1}}} \right)} \right] \times 2z\left( {\cos \Psi - 1} \right) \times \\ \times \,\,\left( {2\delta \left( {{{Q}_{0}}} \right) - \cos \Psi - 1} \right); \\ \end{gathered} $(14)
${{r}_{{AF}}} = 1 + z\left[ {4\delta \left( {Q{}_{0}} \right)\cos \Psi - 2{{{\cos }}^{2}}\Psi + 1} \right];$(15)
${{\lambda }_{{AF}}} = {{\lambda }_{{00}}} + z{{\lambda }_{{20}}}\left[ {4\delta \left( {Q{}_{0}} \right)\cos \Psi - 2{{{\cos }}^{2}}\Psi + 1} \right];$(16)
${{\lambda }_{{1AF}}} = {{\lambda }_{{01}}} + z{{\lambda }_{{21}}}\left\lfloor {4\delta ({{Q}_{0}})\cos \Psi - 2{{{\cos }}^{2}}\Psi + 1} \right\rfloor ;$(17)
${{J}_{{00}}} = {{J}_{0}}({{Q}_{0}} = 0,\,\,{{e}_{1}} = 0) = ({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}){{{{T}_{0}}{{k}_{{\text{B}}}}} \mathord{\left/ {\vphantom {{{{T}_{0}}{{k}_{{\text{B}}}}} {s(s + 1)}}} \right. \kern-0em} {s(s + 1)}};$Первые два уравнения ${{\partial J(q)} \mathord{\left/ {\vphantom {{\partial J(q)} {\partial q}}} \right. \kern-0em} {\partial q}} = 0,$ ${{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial \vartheta }}} \right. \kern-0em} {\partial \vartheta }} = 0$ определяют условия существования гелимагнитной структуры вне зависимости от внешнего магнитного поля (19a) и во внешнем магнитном поле ${{H}_{0}} = [0,0,{{H}_{0}}]$ (19б)
(19a)
$\cos \Psi = \left\{ \begin{gathered} \delta ({{Q}_{0}})\,\,\,{\text{при}}\,\,\left| {\delta ({{Q}_{0}})} \right| < 1 \hfill \\ 1\,\,{\text{в}}\,\,{\text{противном}}\,\,{\text{случае}} \hfill \\ \end{gathered} \right.,$(19б)
$\begin{gathered} \cos \vartheta = \\ = \,\,\left\{ \begin{gathered} \frac{{2{{H}_{0}}{{\mu }_{0}}}}{{(J({{q}_{a}}) - J(0))y}}\,\,\,{\text{при}}\,\,\,\left| {\delta ({{Q}_{0}}) < 1} \right| \\ \frac{{2{{H}_{0}}{{\mu }_{0}}}}{{(J({{q}_{a}}) - J(0))y}}\,\,\,{\text{при}}\,\,\,\left| {\frac{{2{{H}_{0}}{{\mu }_{0}}}}{{(J({{q}_{a}}) - J(0))y}}} \right| < 1 \\ \,\,\,\,\,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{в}}\,\,{\text{противном}}\,\,{\text{случае}} \\ \end{gathered} \right.. \\ \end{gathered} $АНАЛИЗ РЕШЕНИЙ УРАВНЕНИЙ СОСТОЯНИЯ
Решения уравнений (9) определяют температурные зависимости параметров структурного Q0 и магнитного y порядков, которые позволяют получить экспериментально измеряемые зависимости обратной парамагнитной восприимчивости ${{\chi }^{{ - 1}}}(T) \equiv {{\chi }^{{ - 1}}}({{Q}_{0}}(T),T)$ [3] и намагниченности $M\left( T \right)$ [3]:
(20)
$M\left( T \right) = {{M}_{0}}\left( x \right)\varepsilon \left( {y(T),{{Q}_{0}}(T),{{H}_{0}}} \right)y(T),$(21)
$\begin{gathered} {{M}_{0}}(x) = {{(1 - x)2s\mu } \mathord{\left/ {\vphantom {{(1 - x)2s\mu } {A\left( x \right)}}} \right. \kern-0em} {A\left( x \right)}} = \\ = \,\,1.116906s \times 10\,000 \times {{(1 - x)} \mathord{\left/ {\vphantom {{(1 - x)} A}} \right. \kern-0em} A}. \\ \end{gathered} $Здесь $A$ – атомный вес одной формульной единицы сплава.
Согласно [3], анализ решений (9) показал, что когда парные межъячеечные структурные и магнитоструктурные взаимодействия достаточно велики (${{v}_{0}} \geqslant 43$) и (${{\lambda }_{{AF}}} \geqslant 68$), а ${{{\rm O}s} \mathord{\left/ {\vphantom {{{\rm O}s} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}} \leqslant 382,$ температурные зависимости параметров структурного и магнитного порядков описывают магнитоструктурные переходы 1-го рода PM(hex) ↔ HM(orth), характерные для х < 0.15. Скачкообразное появление (исчезновение) намагниченности при этом происходит при температурах Tt1(Tt2), совпадающих с температурами появления (исчезновения) параметра структурного порядка Q0. При этом намагниченность насыщения в сильном магнитном поле в ромбическом состоянии приближается к соответствующему максимуму M0 (см. рис. 1, 2) и значительно превосходит расчетную величину М (Т = 0) в гексагональной фазе. Менее исследованными в работе [3] оказались случаи, когда межъячеечные структурные и магнитоструктурные взаимодействия уменьшаются (ν0 ≤ 38) и (λAF ≤ 5.6), а модуль ортогонального поля увеличивается (Os/kB > 485). Эти случаи характерны для образцов с х ≥ 0.15, в которых упорядочение в ферромагнитное состояние реализуется как изоструктурный переход 2-го рода FM(hex) ↔ PM(hex) при температуре Кюри TC, совпадающей с парамагнитной температурой θhex (рис. 4). В рамках рассматриваемого подхода для этого случая удается объяснить низкотемпературное поведение намагниченности в режимах ZFC, FC на рис. 4 и 5.
Рис. 4.
Совмещенные экспериментальные (σ-символы) и теоретические (M, χ–1, Q0-линии) магнитные характеристики применительно к образцу с х = 0.3. σi(B), Miorth(B) соответствует намагниченности геликоидального ромбического состояния в магнитном поле B.
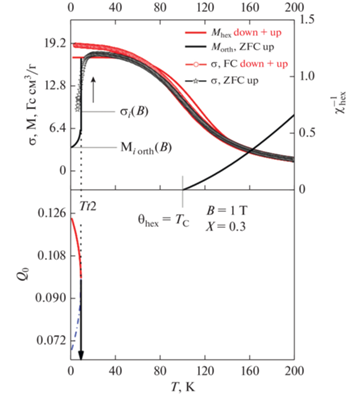
Рис. 5.
Влияние магнитного поля на изменение энергии ромбического Ωorth (|Q0| > 0) и гексагонального Ωhex (Q0 = 0) состояний при понижении температуры.
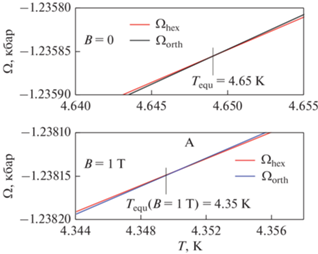
Согласно модели, ромбическое состояние при T > 0 является метастабильным, однако при понижении температуры в режиме ZFC до T ≤ Tequ(B = 0) энергия ромбического состояния Ωorth, |Q0| > 0 становится ниже энергии гексагонального состояния Ωhex, Q0 = 0 (рис. 5) и возможен переход в ромбичекую фазу с относительно малой намагниченностью Morth $ \ll $ Mhex. Повышение температуры до температуры лабильности ромбического состояния Tt4 приводит к скачкообразному магнитоструктурному переходу HM(orth) → FM(hex) (рис. 4) в гексагональное высокомагнитное состояние с последующим его исчезновением при температуре ТС = θhex в результате плавного изоструктурного перехода FM(hex) ↔ PM(hex). При понижении температуры в магнитном поле (в режиме FC) переход в ромбическое состояние может не произойти, поскольку с ростом магнитного поля температура Tequ(B) может значительно понизиться (см. рис. 5) вплоть до температур ниже гелиевых. Эта ситуация может лежать в основе понимания механизмов особой чувствительности к эффектам ZFC, FC измерений в слабых полях, наблюдаемых в образцах с х < 0.1.
В заключение отметим, что предварительный анализ на основе модели позволил объяснить необратимые “скачки” намагниченности (см. рис. 3) при 5 К как необратимые индуцированные магнитным полем магнитоструктурные переходы 1‑го рода HM(orth) → FM(orth) → FM(hex). Согласно теории, эти переходы сопровождаются увеличением намагниченности насыщения FM фазы от Morth(Q0,B) до Mhex(0,B) > Morth(Q0,B). Разница между Morth(Q0,B) и Mhex(0,B) обусловлена присутствием ортогонального поля ${\rm O}$. Из уравнения (9b) легко видеть, что при ${\rm O} = 0$ имеем $T \to 0,$ $y \to 1$ вне зависимости от величины параметра ${{Q}_{0}}$ и поэтому, согласно (20), намагниченность насыщения гексагонального и ромбического состояний будет одинакова.
Явление необратимости переходов Morth(Q0, B) → Mhex(0, B) (сохранение индуцированного состояния Mhex(0, B) при уменьшении поля вплоть до перемагничивания) при 5 К можно объяснить отсутствием температуры лабильности Tt3 состояния FM (hex). Действительно, согласно рис. 4, при 5 К система находится в области температурного гистерезиса, ΔТ(В) = Tt4(В) – Tt3(В) магнитоструктурных переходов HM(orth) → → FM(orth) → FM(hex). При этом согласно рис. 4 при В = 0 температура Тequ(В), сопоставляемая с температурой лабильности Тt1(В) (исчезновения состояния FM(hex)), остается ниже 5 К < < Tt4(0) < θhex. Поэтому при перемагничивании конечное индуцированное магнитным полем состояние (FM(hex)) сохраняет устойчивость, как в отношении низкотемпературного FM(hex) → HM(orth), так и высокотемпературного FM(hex) → PM(hex)-переходов.
Исследование выполнено при финансовой поддержке БРФФИ и РФФИ в рамках научного проекта № Т20Р-204 и № 20-58-00059 соответственно.
Список литературы
Вальков В.И., Головчан А.В., Коледов В.В., Тодрис Б.М., Митюк В.И. Скачкообразные процессы магнитного разупорядочения, стимулированные магнитным полем в системах со структурной неустойчивостью // ФТТ. 2020. Т. 62. С. 710–718.
Liu E.K., Zhang H.G., Xu G.Z., Zhang X.M., Ma R.S., Wang W.H., Chen J.L., Zhang H.W., Wu G.H., Feng L., Zhang X.X. Giant magnetocaloric effect in isostructural MnNiGe–CoNiGe system by establishing a Curie-temperature window // Appl. Phys. Lett. 2013. V. 102. P. 122405.
Митюк В.И., Римский Г.С., Янушкевич К.И., Коледов В.В., Маширов А.В., Вальков В.И., Головчан А.В., Ковалев О.Е. Магнито-структурные особенности фазовых переходов в системе Mn1 – xCoxNiGe. Часть 1. Экспериментальные результаты // ФTТ. 2021. Т. 63. № 12. С. 2073–2081.
Митюк В.И., Римский Г.С., Коледов В.В., Маширов А.В., Вальков В.И., Головчан А.В., Ковалев О.Е. Магнитоструктурные особенности фазовых переходов в системе Mn1 –xCoxNiGe. Часть 2. Анализ // ФTТ. 2021. Т. 63. № 12. С. 2082–2095.
Блинц Р., Жекш Б. Сегнетоэлектрики и антисегнетоэлектрики. Динамика решетки. М.: Мир, 1975. 398 с.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение


