Физика металлов и металловедение, 2022, T. 123, № 7, стр. 716-752

2.1. Фазовое расслоение в манганитах

Ярким примером сильно коррелированных электронных систем, в которых наблюдается явление электронного фазового расслоения, являются манганиты – соединения на основе оксида марганца [1, 3, 7]. Манганиты обладают достаточно богатой фазовой диаграммой, включающей в себя различные магнитные фазы, а также фазы с зарядовым и орбитальным упорядочением.

В литературе рассматриваются различные типы неоднородных состояний, характерных для этих соединений. Недопированные манганиты являются антиферромагнитными диэлектриками с орбитальным упорядочением. При малом допировании для манганитов характерно возникновение т.н. магнитных поляронов (ферронов) – ферромагнитных капель нанометровых размеров, находящихся в антиферромагнитной матрице [8‒12]. Такой тип фазового расслоения был впервые предложен Нагаевым [8]. В работах [13–17] были подробно исследованы электронные и магнитные свойства магнитных поляронов. Теоретически механизм возникновения магнитных поляронов объясняется самолокализацией носителей заряда: электрон “вырывает” себе потенциальную яму, образуя ферромагнитную область в антиферромагнитном окружении, и локализуется в ней. Характерные размеры магнитных поляронов составляют несколько периодов решетки.

Существуют и другие типы фазового расслоения в манганитах. Так, в некоторых случаях наблюдаются ферромагнитные капли с размерами порядка 100–1000 Å [18, 19]. Как уже указывали во введении, при уровне допирования вблизи половинного заполнения могут возникать ферроны, находящиеся в зарядово- и орбитально упорядоченной диэлектрической матрице [20]. Взаимодействие спиновых, зарядовых и орбитальных степеней свободы может приводить также к формированию страйповых структур [21–23]. В манганитах такие структуры приводят к сильным искажениям решетки [24] и могут экспериментально наблюдаться с помощью электронной дифракции или малоуглового нейтронного рассеяния.

В данном разделе мы рассмотрим теоретическую модель манганитов, учитывающую ян-теллеровскую природу магнитных ионов Mn³⁺, приводящую к локализации носителей заряда и искажению решетки. Мы вводим этот эффект в модель двойного обмена. Заметим, что в манганитах эффект Яна‒Теллера широко обсуждается в литературе [1, 25, 26], он является существенным для понимания их фазовой диаграммы (см. рис. 1). Мы построим фазовую диаграмму манганитов в плоскости допирование–температура (x – T) с учетом фазового расслоения, а также рассмотрим эффекты, связанные с приложением постоянного магнитного поля.

2.1.1. Модельный гамильтониан манганитов

Рассмотрим допированные манганиты, имеющие химическую формулу $(\operatorname{Re} _{{1 - x}}^{{3 + }}{\text{Mn}}_{{1 - x}}^{{3 + }})$${\text{(A}}_{x}^{{2 + }}{\text{Mn}}_{x}^{{4 + }}){\text{O}}_{3}^{{2 - }},$ где Re обозначает трехвалентный (редкоземельный) элемент, A – двухвалентный (щелочноземельный) элемент. Ионы марганца Mn³⁺ и Mn⁴⁺ обладают 3d⁴- и 3d³-электронным конфигурациями, соответственно. Рассматриваемые соединения имеют кристаллическую структуру перовскита, в которой ионы марганца находятся в окружении кислородных октаэдров. В случае идеального неискаженного октаэдра кристаллическое поле расщепляет пятикратно вырожденный 3d-уровень ионов марганца на трехкратно вырожденный t_2g-уровень (d_xy, d_yz, d_zx) и на имеющий более высокую энергию двукратно вырожденный e_g-уровень (${{d}_{{{{x}^{2}} - {{y}^{2}}}}},$ ${{d}_{{3{{z}^{2}} - {{r}^{2}}}}}$).

Ионы марганца характеризуются сильным внутриатомным (хундовским) обменным взаимодействием J_H, которое стремится выстроить спины d-электронов параллельно друг другу. В результате спины t_2g электронов формируют локальный спин S = 3/2. В случае идеального MnO₆ октаэдра ионы марганца Mn³⁺ имеют один электрон на двукратно вырожденном e_g-уровне. Согласно теореме Яна и Теллера такая конфигурация неустойчива, и вырождение e_g-уровня снимается путем искажения кислородного октаэдра. Ион Mn⁴⁺ не является ян-теллеровским ионом, и в нулевом приближении (без учета влияния со стороны соседних октаэдров) октаэдр Mn⁴⁺O₆ остается неискаженным, а энергия e_g-уровня не меняется. В то же время искажение Mn³⁺O₆ октаэдра приводит к понижению энергии e_g-электрона на величину ${{\epsilon }_{{{\text{JT}}}}}$ и его локализации. В то же время в допированных манганитах e_g-электрон может перескакивать с иона Mn³⁺ на ион Mn⁴⁺, что приводит к выигрышу в кинетической энергии электрона. Следовательно, e_g-электрон может либо понизить свою энергию за счет искажений октаэдра (и при этом локализоваться), либо за счет формирования энергетической зоны. Таким образом, в системе существует конкуренция между локализацией и делокализацией, и возможно существование двух типов e_g-электронов (зонных b и локальных l) [27–29]. Отметим также, что сильная хундовская константа связи J_H вынуждает делокализованный e_g-электрон двигаться только при параллельной ориентации локальных спинов ионов Mn³⁺ и Mn⁴⁺. Это и есть широко известный механизм двойного обмена, обусловливающий ферромагнитное взаимодействие локальных спинов [30, 31].

При выводе эффективного гамильтониана для манганитов мы стартуем со следующей модели, учитывающей все обсуждаемые свойства системы [32]:

В этих выражениях $a_{{{\mathbf{n}}a\sigma }}^{\dag }$ и a_naσ – операторы рождения и уничтожения e_g-электронов на узле n с орбитальным индексом a (3z²–r² или x²–y²) и проекцией спина σ, n_naσ = $a_{{{\mathbf{n}}a\sigma }}^{\dag }{{a}_{{{\mathbf{n}}a\sigma }}},$ S_n – локальный спин t_2g-электронов на узле n, который мы будем рассматривать как классический вектор. Далее, σ – матрицы Паули, Q_2n, Q_3n – нормальные моды тетрагональных искажений MnO₆ октаэдра, приводящих к расщеплению e_g-уровня. Член H_el в гамильтониане (1) включает в себя кинетическую энергию e_g-электронов, а также слагаемое, описывающее обменное (хундовское) взаимодействие между e_g- и t_2g-электронами. Слагаемое H_AF описывает антиферромагнитное сверхобменное взаимодействие (J' > 0) между локальными спинами. Слагаемое H_JT определяет взаимодействие между e_g-состояниями и колебательным модами MnO₆ октаэдров, где K – упругая константа, соответствующая Q_2n и Q_3n модам, g – константа электрон–решеточного взаимодействия. Наконец, последнее слагаемое в (1), H_el-el, описывает электрон-электронное взаимодействие e_g-электронов, где черта над a или σ значит, соответственно, не a или не σ.

Далее мы рассмотрим предел J_H → ∞. В этом случае спин e_g-электрона на узле n всегда параллелен локальному спину S_n, и в результате мы можем перейти от операторов a_naσ к операторам c_na, описывающим e_g-электроны с проекцией спина +1/2 на направление S_n. Такое преобразование приводит к преобразованию амплитуд перескока вида [33]: $t_{{{\mathbf{nm}}}}^{{ab}}$ → $t_{{{\mathbf{nm}}}}^{{ab}}$cos(ν_nm/2), где cosν_nm = S_nS_m/S². Кроме того, мы будем считать, что $t_{{{\mathbf{nm}}}}^{{\left( l \right)}}$ → 0 для “локализованных” e_g-электронов (l-электронов), которые создают максимальные искажения кислородных октаэдров, приводя к выигрышу в энергии $\epsilon _{{{\text{JT}}}}^{{(0)}}$ = –g²/2K, в то время как “зонные” e_g-электроны (b-электроны) имеют ненулевую амплитуду перескока, но создают значительно меньшие искажения кислородных октаэдров. Величина $\epsilon _{{{\text{JT}}}}^{{(0)}}$ получается путем минимизации гамильтониана H_JT по Q_2n и Q_3n при равном единице числе e_g-электронов, приходящихся на один узел решетки. В результате эффективный гамильтониан модели можно записать в виде:

где n_bn = $b_{{\mathbf{n}}}^{\dag }{{b}_{{\mathbf{n}}}}$ и n_ln = $l_{{\mathbf{n}}}^{\dag }{{l}_{{\mathbf{n}}}}$ – операторы числа b и l электронов на узле n, $b_{{\mathbf{n}}}^{\dag },$ b_n и $l_{{\mathbf{n}}}^{\dag },$ l_n – соответствующие операторы рождения и уничтожения электронов. Первые три слагаемых в H_eff описывают, соответственно, кинетическую энергию b-электронов, выигрыш в энергии локализованных электронов с энергией ${{\epsilon }_{{{\text{JT}}}}}$ ∼ –g²/2K, и, наконец, член, описывающий отталкивание b и l электронов на одном узле. Легко заметить, что эта часть эффективного гамильтониана соответствует модели Фаликова‒Кимбалла [34]. Эта модель, сформулированная первоначально для соединений с тяжелыми фермионами, описывает взаимодействие между электронами в сравнительно широкой зоне проводимости и электронами, локализованными на некотором энергетическом уровне. Здесь, в отличие от стандартной модели Фаликова‒Кимбалла, амплитуда перескока зонных электронов между узлами n и m зависит от взаимной ориентации локальных спинов в этих узлах. Последнее слагаемое в H_eff описывает сверхобменное (через ионы кислорода) антиферромагнитное взаимодействие локальных спинов. Характерные значения энергетических параметров эффективной модели равны [1]:

Таким образом, рассматриваемая эффективная модель манганитов представляет собой расширенную модель Фаликова‒Кимбалла, в которой введены дополнительные степени свободы – локальные спины магнитных ионов. Известно, что модель Фаликова‒Кимбалла неустойчива к расслоению на фазы в некоторой области параметров [35]. Уже одно это обстоятельство указывает на то, что рассматриваемая модель манганитов может быть неустойчива по отношению к фазовому расслоению. Мы покажем ниже, что это действительно так, причем безотносительно неустойчивости непосредственно самой модели Фаликова‒Кимбалла.

В качестве исходных соединений мы будем рассматривать соединения типа ReMnO₃. В таких манганитах электронная конфигурация ионов марганца соответствует одному e_g-электрону на узле. При замещении редкоземельного элемента Re щелочноземельным элементом A на e_g-уровне образуется дырка. Таким образом, связь между средним числом локализованных и зонных электронов c уровнем допирования x имеет вид: n_b + n_l = = 1 – x. Надо отметить, что параметры эффективной модели (2), такие как t и ${{\epsilon }_{{{\text{JT}}}}}$, могут зависеть, вообще говоря, от температуры, например, за счет уменьшения амплитуды перескока t с ростом температуры из-за эффекта поляронного сужения зоны [36, 37], который может быть достаточно сильным для манганитов.

При исследовании эффективного гамильтониана (2) мы воспользуемся приближением типа среднего поля, которое позволит расцепить магнитные (связанные с локальными спинами) и электронные степени свободы. Процедура расцепления выглядит следующим образом. В (2) величины $b_{{\mathbf{n}}}^{\dag }{{b}_{{\mathbf{m}}}}$ и ϑ_nm ≡ $\sqrt {{{\left( {{{S}^{2}} + {{S}_{n}}{{S}_{m}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{S}^{2}} + {{S}_{n}}{{S}_{m}}} \right)} {2{{S}^{2}}}}} \right. \kern-0em} {2{{S}^{2}}}}} = \sqrt {{{(1 + {{e}_{n}}{{e}_{m}})} \mathord{\left/ {\vphantom {{(1 + {{e}_{n}}{{e}_{m}})} 2}} \right. \kern-0em} 2}} $ могут быть записаны в виде:

где угловые скобки означают усреднение по температуре, S_n = Se_n, e_n – единичный вектор, описывающий направление локального спина на узле n (напомним, что мы рассматриваем локальный спин S = 3/2 как классический вектор). Пренебрегая слагаемыми, пропорциональными $\delta \left( {b_{{\mathbf{n}}}^{\dag }{{b}_{{\mathbf{m}}}}} \right)\delta {{\vartheta }_{{{\mathbf{nm}}}}},$ можно записать эффективный гамильтониан в виде суммы “электронной” и “магнитной” частей: где $\bar {t} = t\left( T \right)\sqrt {{{(1 + {{e}_{n}}{{e}_{m}})} \mathord{\left/ {\vphantom {{(1 + {{e}_{n}}{{e}_{m}})} 2}} \right. \kern-0em} 2}} $ ‒ эффективный интеграл перескока, зависящий от температуры и угла между локальными спинами (температурная зависимость t определяется поляронным сужением зоны), μ ‒ химический потенциал. Как видно из (5), электронная часть эффективного гамильтониана, H_el, представляет собой гамильтониан модели Фаликова‒Кимбалла, в котором амплитуда перескока зонных электронов зависит от температуры и магнитной структуры, которую образуют локальные спины.

2.1.2. Однородные состояния (ферромагнитное состояние)

В ферромагнитном состоянии мы имеем ⟨e_ne_m⟩ ≈ ≈ 1 при температурах, много меньших температуры Кюри T_C. Рассмотрим сначала электронную часть эффективного гамильтониана. Взаимодействие зонных и локализованных электронов приводит к возникновению двух хаббардовских подзон b-электронов, разделенных щелью порядка U. Закон дисперсии подзон имеет вид:

В этом выражении ε(k) – затравочный спектр b-электронов, $~\varepsilon \left( k \right) = \bar {w}\zeta \left( k \right),$

где $\bar {w}$ – полуширина зоны свободных электронов, которая зависит как от температуры, так и от магнитной структуры, образованной локальными спинами.

Поскольку допирование в рассматриваемых манганитах является дырочным, n_b + n_l = 1 – x < 1, то верхняя хаббардовская подзона всегда остается пустой. В этом случае мы можем перейти к пределу U → ∞. Ширина нижней хаббардовской подзоны b-электронов равна W = 2(1 – n_l)$~\bar {w}$, а ее заполнение равно 1 – n_l. Зависимости n_b и n_l от уровня допирования x представлены на рис. 2.

При малом допировании b-электроны отсутствуют, n_l = 1 – x, а ширина нижней хаббардовской подзоны равна W = $2x\bar {w}.$ При критической концентрации допирования x₁(T) = ${{{{\epsilon }_{{{\text{JT}}}}}} \mathord{\left/ {\vphantom {{{{\epsilon }_{{{\text{JT}}}}}} {\bar {w}}}} \right. \kern-0em} {\bar {w}}}$(T), когда дно нижней хаббардовской подзоны достигает уровня $ - {{\epsilon }_{{{\text{JT}}}}}$, в системе начинают появляться зонные электроны, которые сосуществуют с локализованными, вплоть до второй критической концентрации x₂(T), при которой n_l = 0. Поскольку $\bar {w}$ уменьшается с температурой как за счет разрушения ферромагнитного порядка, так и за счет поляронного сужения зоны, то обе критические концентрации, x₁ и x₂, изменяются с ростом температуры (обе увеличиваются). Отметим, что возникновение ферромагнитного порядка возможно только при x > x₁, когда в системе имеются b-электроны.

Рассмотрим теперь магнитную часть гамильтониана (5). Мы будем исследовать H_m в приближении среднего поля. Следуя стандартной процедуре вывода среднеполевого гамильтониана [38], мы заменяем единичный вектор e_m = {sinθ_mcosϕ_m, sinθ_msinϕ_m, cosθ_m} в выражении для H_m на его среднее значение {0, 0, σ}, где σ = ⟨cosθ_m⟩ – среднее значение локального спина, рассчитанное в единицах S = 3/2. В результате H_m разбивается на сумму независимых одноузельных гамильтонианов, H_m = ΣnH_m0(cosθ_n), где

w(T) = zt(T), J = zJ’S² (z = 6 – число ближайших соседей для кубической решетки), а функция B ответственна за взаимосвязь с электронной частью гамильтониана. Первое слагаемое в правой части этого выражения, имеющее минимум при θ = 0, описывает ферромагнитное взаимодействие локальных спинов за счет механизма двойного обмена. Второе слагаемое описывает антиферромагнитное сверхобменное взаимодействие. Равновесное значение σ при конечной температуре определяется из соответствующего условия самосогласования. Кроме того, необходимо учесть условие самосогласования для величины $\bar {w},$ которая зависит от среднего cos θ. Соответствующий анализ позволяет выявить особенности магнитных фазовых переходов в рассматриваемой системе.

Отметим, что переход из ферромагнитного (FM) в парамагнитное (PM) состояние не означает, что в системе исчезают b-электроны. Как обсуждалось ранее, n_b ≠ 0 при x > x₁(T), и значение x₁ увеличивается с ростом температуры. При определенной температуре T*, x₁(T) достигает уровня допирования x. Ясно, что T* > T_C, поскольку ферромагнитное состояние может существовать только при n_b ≠ 0. Таким образом, в нашей модели в дополнении к магнитному фазовому переходу должен существовать еще переход, при котором в системе исчезают зонные электроны. Температура T* такого перехода определяется из условия x₁(T*) = x.

2.1.3. Однородные состояния (антиферромагнитное и подкошенное состояния)

Рассматриваемая модель допускает другие типы однородных состояний, конкурирующих с ферро- и парамагнетизмом, а именно антиферромагнитное, и т.н. скошенное состояние (или скошенное антиферромагнитное (CAF) состояние, см. рис. 1). В скошенной фазе так же, как и в антиферромагнитной, имеются две магнитные подрешетки, угол ν между направлениями магнитных моментов которых (угол подкоса) отличен как от 0 (ферромагнитная фаза), так и от π (антиферромагнитная фаза). Скошенная фаза может возникать благодаря конкуренции между ферромагнитным взаимодействием локальных спинов, возникающим за счет двойного обмена, и их антиферромагнитным сверхобменным взаимодействием. Впервые подкошенная фаза в манганитах была рассмотрена, по-видимому, Де Женом [33], а впоследствии более подробно проанализирована Нагаевым [39]. Мы рассмотрим антиферромагнитное и подкошенные состояния G-типа, когда каждый узел в одной магнитной подрешетке имеет ближайшими соседями узлы, принадлежащие другой подрешетке.

Угол подкоса ν определяется как cosν = 〈e₀e_Δ〉. В приближении среднего поля это среднее равно 〈e₀e_Δ〉 = 〈e₀〉〈e_Δ〉, где Δ ‒ номера ближайших соседей заданного узла 0. Таким образом, для скошенной фазы мы также можем ввести параметр σ, который связан с углом подкоса как σ² = cosν если ν < π/2 или σ² = –cosν, если ν > π/2. В этой ситуации рассмотрение проводится практически так же, как и для ферромагнитной фазы. Отметим однако, что в скошенной фазе σ < 1 даже при T = 0.

Так же, как и ферромагнитное состояние, подкошенное состояние существует только при наличии в системе b-электронов. При уровне допирования x < x₁(T) мы имеем n_b = 0, и система находится в антиферромагнитном (AF) состоянии. При этом если x < x₁(0), то n_b = 0 при любой температуре. В этом случае температура Нееля не зависит от x. При большем допировании может возникать переход из антиферромагнитного в парамагнитное состояние с n_b ≠ 0, и температура Нееля T_N в этом случае определяется путем сравнения свободных энергий антиферромагнитного и парамагнитного состояний. Переход в парамагнитную фазу в этом случае является переходом первого рода. В области допирования, соответствующего этому сценарию, антиферромагнитное состояние оказывается энергетически более выгодным, чем подкошенное. При больших x существует область допирования, в которой реализуется температурный переход первого рода из антиферромагнитного в ферромагнитное состояние. При еще большем допировании более выгодной становится ферромагнитная фаза. При этом фазовая диаграмма модели имеет тройную AF–FM–PM точку при x = x₃. Таким образом, в нашей модели подкошенная фаза не реализуется при x < 0.5. Подкошенное состояние может реализовываться вблизи x = 1, при x₄ < x < 1, где отсутствуют локализованные электроны, но число b-электронов недостаточно, чтобы стабилизировать ферромагнитное состояние.

Фазовая диаграмма модели в плоскости x–T представлена на рис. 3. Она более или менее адекватно воспроизводит экспериментальную фазовую диаграмму манганитов (AF- и FM-фазы при x < 0.5, скошенную антиферромагнитную фазу при 1 – x $ \ll $ 1), представленную на рис. 1, за исключением области 0.5 < x < x₄, где теоретическая модель предсказывает ферромагнитную металлическую фазу, в то время как в этой области экспериментально наблюдается антиферромагнитная диэлектрическая фаза. Это, по-видимому, связано с тем, что при больших x необходимо более аккуратно учитывать орбитальные степени свободы. Кроме того, в рассматриваемой модели никак не учитывается дальнодействующее кулоновское отталкивание электронов, которое может приводит к зарядовому упорядочению, наблюдаемому в этой области допирования (см. рис. 1).

2.1.4. Особенности фазового расслоения в манганитах

До сих пор мы рассматривали только однородные состояния системы, однако, как обсуждали выше, есть указания на то, что рассматриваемая модель может быть неустойчива к фазовому расслоению. Мы будем исследовать возможность возникновения фазового расслоения в рассматриваемой модели манганитов путем анализа зависимости свободной энергии однородного состояния от допирования. В рассматриваемой модели возможны различные типы фазового расслоения: расслоение на антиферромагнитную (AF) и ферромагнитную (FM) фазы или на парамагнитную (PM) и ферромагнитную (FM) фазы, каждая из фаз характеризуется своим числом носителей заряда. Возможно также и расслоение на две PM-фазы с различным числом носителей.

Мы сфокусируемся на области допирования x < 0.5, где фазовая диаграмма модели качественно соответствует наблюдаемой, и поэтому не будем анализировать устойчивость скошенной фазы при x, близким к единице.

На рис. 4 показаны зависимости свободной энергии наиболее выгодного однородного состояния, F_hom = min(F_fm, F_af, F_pm, F_cant), от допирования, рассчитанные при нескольких различных температурах. Кривые F_hom(x) имеют два минимума, один при x = 0, а второй вблизи x = x₂(T). При T = 0 кривая имеет излом (который сглаживается при конечной температуре) в точке перехода из антиферромагнитного в ферромагнитное состояние. Кривая F_fm(x) имеет отрицательную кривизну от точки излома до x ≈ x₂(T), что указывает на неустойчивость ферромагнитного состояния в этой области. Однако это обстоятельство не столь важно в рассматриваемом случае. Более важным является наличие излома на кривой F_hom(x): благодаря ему фазовое расслоение существует в области 0 < x $ \lesssim $ x₂, система расслаивается на антиферромагнитную (или парамагнитную при T > > T_N) диэлектрическую фазу с n_b = 0 и концентраций электронов x_A = 0 и ферромагнитную (или парамагнитную) металлическую фазу с n_l ≈ 0 и концентрацией электронов x_B ≈ x₂(T). Концентрация x₂ находится из построения Максвелла [41].

Обозначим объемную долю металлической фазы через p. Тогда в силу закона сохранения заряда величина p находится из соотношения px_B + + (1– p)x_A = x. Свободная энергия фазово-расслоенного (PS) состояния при этом равна F_PS = = pF_hom(x_B) + (1 – p)F_hom(x_A).

Отметим, что свободная энергия F_PS и область концентраций, в которой существует фазовое расслоение, были получены в приближении полностью вырожденной электронной компоненты системы. Учет температурных поправок приводит к уменьшению области фазовой диаграммы, в которой существует фазовое расслоение.

Однако более важным фактором, влияющим на фазовое расслоение, является то обстоятельство, что концентрация электронов в фазах A и B различна. Поэтому при расчете энергии неоднородного состояния необходимо включить в модель дальнодействующее кулоновское отталкивание электронов, которое существенно уменьшает область существования неоднородного состояния, и может даже сделать его невыгодным при любых концентрациях допирования (подробнее см. в [32]).

Здесь мы приведем окончательный результат для фазовой диаграммы модели, рассчитанной с учетом влияния дальнодействующего кулоновского отталкивания на фазовое расслоение. Она представлена на рис. 5. Фазовое расслоение существует в области концентраций 0 $ \lesssim $ x $ \lesssim $ 0.5, а по температуре область фазового расслоения ограничена кривой T_PS(x), которая оказывается порядка температуры Кюри ферромагнитной фазы. Поскольку концентрации x_A и x_B практически не зависят от уровня допирования, то температуры магнитных фазовых переходов в каждой из фаз тоже почти не зависят от x. Температура Нееля антиферромагнитной компоненты неоднородного состояния можно считать равной $T_{{\text{N}}}^{0}$ = J/3, в то время как температура Кюри ферромагнитной компоненты примерно соответствует максимальной температуре Кюри однородного ферромагнитного состояния (см. горизонтальные штриховые линии на рис. 5).

Рассмотрим теперь переход по температуре из неоднородного в однородное состояние. Поскольку x_A ≈ 0, x_B ≈ x₂(_T), то объемная доля металлической фазы p равна p(T) ≈ x/x₂(T). В зависимости от соотношений между температурами T_PS, T_C, T_N и T*, система может переходить из фазово-расслоенного в однородное FM (p = 1), AF (p = 0) или PM (с n_b ≠ 0 или n_b = 0) состояние. Во всех случаях равновесное число зонных электронов n_b претерпевает скачок при переходе в однородное состояние.

2.1.5. Влияние магнитного поля

В связи с тем, что манганиты характеризуются эффектом колоссального магнитосопротивления, представляется чрезвычайно интересным рассмотреть вопрос о влиянии магнитного поля на свойства системы. Мы не будем исследовать здесь транспортные характеристики, а ограничимся лишь рассмотрением изменения термодинамических величин при приложении магнитного поля. Однако уже этого достаточно, чтобы сделать качественные выводы о поведении проводимости системы в магнитном поле. Отметим также, что транспортные свойства (проводимость, магнитосопротивление, 1/f шум) в фазово-расслоенных манганитах были подробно исследованы в работах [42–44].

При рассмотрении влияния магнитного поля H мы будем учитывать только взаимодействие поля с локальными спинами, пренебрегая как парамагнитным, так и диамагнитными слагаемыми в электронном гамильтониане H_el, появляющимися в ненулевом H. Это соответствует пределу большого локального спина S $ \gg $ 1. Таким образом, в ненулевом магнитном поле мы добавляем только одно слагаемое в полный гамильтониан модели (6), равное –μ_BgΣ_nS_nH, где μ_B – магнетон бора, g – фактор Ланде, который, вообще говоря, может сильно отличаться от двойки. В результате модифицируется только магнитная часть гамильтониана (5), где под знаком суммы появляется дополнительное слагаемое e_nh (h = μ_BgSH).

В ферромагнитном состоянии, в приближении среднего поля, среднее значение σ = ${{\left\langle {S_{0}^{z}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {S_{0}^{z}} \right\rangle } S}} \right. \kern-0em} S}$ находится путем решения системы уравнений согласования с видоизмененным гамильнонианом. При T < T_C поправка к свободной энергии в присутствии магнитного поля δF ∼ –h, в то время как в парамагнитной фазе δF ∼ –h²/T_C. В антиферромагнитной и скошенной фазах результат зависит от взаимной ориентации магнитного поля H и вектора антиферромагнетизма l = (〈e₀〉 – 〈e_Δ〉)/2. Минимум свободной энергии (мы полностью пренебрегаем здесь магнитной анизотропией) достигается, когда h ⊥ l. Поэтому мы рассмотрим именно такую конфигурацию. Пусть вектор l направлен вдоль оси z, а магнитное поле направлено вдоль оси x. Тогда направления векторов локальных спинов в двух магнитных подрешетках равны ⟨e₀⟩ = {σ, 0, l} и 〈e_Δ〉 = {σ, 0, –l}.

В полях h/J $ \ll $ 1 соответствующая система уравнений самосогласования может решаться по теории возмущений по магнитному полю. При этом поправка к свободной энергии в антиферромагнитном состоянии δF ∼ –h²/T_N при температурах как выше, так и ниже T_N, что связано с отсутствием спонтанной намагниченности при H = 0. В то же время в ферромагнитном состоянии мы имеем δF ∼ –h при T < T_С. Таким образом, внешнее магнитное поле делает более выгодным ферромагнитное состояние. В частности, оно приводит к уменьшению температуры перехода из AF- в FM- фазу, который существует в некоторой области допирования (см. рис. 3). Магнитное поле приводит также к увеличению эффективного обменного интеграла и увеличению числа b-электронов при заданной температуре. Кроме того, магнитное поле изменяет температуру перехода из неоднородного в однородное состояние, при этом разница ΔT_PS = = T_PS(H) – T_PS(0) ∼ h.

Как отмечали ранее, число зонных электронов n_b меняется существенно при переходе из неоднородного в однородное состояние. Соответственно, сдвиг температуры T_PS в магнитном поле приводит к существенному изменению числа b-электронов при заданной температуре вблизи T_PS. Температурная зависимость изменения относительной концентрации [n_b(H)–n_b(0)]/n_b(0) показана на рис. 6. Мы видим, что магнитное поле приводит к возникновению узкого пика относительной концентрации при температурах вблизи перехода в однородное состояние. Поскольку число зонных электронов определяет проводимость системы, то существование такого пика может быть связано с эффектом колоссального магнитосопротивления, наблюдаемого в манганитах.

2.1.6. Заключительные замечания к разделу о манганитах

Таким образом, в этом разделе мы описали эффективную электронную модель манганитов и исследовали ее свойства. Модель предполагает конкуренцию между локализацией электронов за счет ян-теллеровских искажений решетки и делокализацией. Гамильтониан модели учитывает основную специфику манганитов: сильное электрон‒решеточное и электрон‒электронное взаимодействия, включая сильную хундовскую связь d-электронов марганца, а также сверхобменное взаимодействие локальных спинов. Такой подход, в частности, позволяет объяснить несоответствие между числом зонных электронов n_b и уровнем допирования [27–29, 32].

Мы показали, что наша модель предсказывает существование фазового расслоения в широкой области температур и допирования. Полученные результаты хорошо согласуются с экспериментальными данными о фазовом расслоении в манганитах. Так, в области малых концентраций допирования эксперименты [45, 46] по упругому и неупругому рассеянию нейтронов в манганитах показали наличие небольших ферромагнитных капель в антиферромагнитной матрице. Эксперименты по ядерному магнитному резонансу (ЯМР) также свидетельствуют в пользу этой картины: авторы работы [47] наблюдали в манганитах два резонансных пика, один из которых соответствовал ферромагнитной, а другой – антиферромагнитной фазе; следов наличия подкошенного состояния обнаружено не было. О наличии ферромагнитных металлических капель свидетельствуют также эксперименты [48] по малоугловому нейтронному рассеянию.

Имеются также четкие экспериментальные указания, что фазовое расслоение характерно не только для магнитоупорядоченных фаз, но существует и в парамагнитной области [49, 50]. В области оптимальных концентраций (x ∼ 0.3) в системе La_{1 –x}Ca_xMnO₃ авторы работы [51] с помощью сканирующей туннельной микроскопии наблюдали маленькие ферромагнитные металлические кластеры в парамагнитной матрице выше температуры Кюри.

Обработка экспериментальных данных по проводимости, магнитосопротивлению и магнитной восприимчивости различных манганитов в парамагнитной фазе [52–55] с помощью модели, в которой электронный транспорт осуществляется путем туннелирования электронов между металлическими каплями с сильными ферромагнитными корреляциями [43], показывает хорошее согласие между теорией и экспериментом.

Здесь мы не рассматриваем геометрию (капли, страйпы и пр.) и характерные размеры неоднородностей. Это будет сделано в разд. 4. Отметим только, что геометрия фазово-расслоенного состояния может существенно влиять на транспортные свойства системы. Так, в случае капельной структуры неоднородностей (ферроны в диэлектрической матрице), изменение концентрации ферромагнитной металлической фазы за счет допирования или приложения магнитного поля приводит к перколяционному переходу металл–диэлектрик, что, по-видимому, имеет непосредственное отношение к явлению колоссального магнитосопротивления.

Отметим, что рассмотренная здесь модель слишком грубо учитывает орбитальные степени свободы манганитов. Это оставляет за рамками рассмотрения такое существенное свойство манганитов, как орбитальное упорядочение, существующее при малых концентрациях допирования, а также вблизи половинного заполнения. Возможность фазового расслоения при орбитальном упорядочении (“орбитальные” ферроны), подробно рассматривали в работах [56, 57].

2.2. Кобальтиты. Эффективный гамильтониан для систем со спиновыми переходами

Среди оксидов переходных металлов существуют соединения, содержащие ионы кобальта или железа, в которых возможно изменение спинового состояния иона при изменении температуры, давления или допирования. Как уже указывали выше, в октаэдрическом окружении кристаллическое поле расщепляет пятикратно вырожденный d-уровень переходного метала на трехкратно вырожденный t_2g-уровень (d_xy, d_yz, d_zx) и двукратно вырожденный e_g-уровень $\left( {{{d}_{{{{x}^{2}} - {{y}^{2}}}}},{{d}_{{3{{z}^{2}} - {{r}^{2}}}}}} \right).$

Переходы с изменением спинового состояния становятся возможными, когда энергия расщепления d-уровня в кристаллическом поле Δ сравнима с хундовской константой связи J_H. Примерами таких систем являются соединения, содержащие ионы Co³⁺ (типичный представитель – LaCoO₃ [58–61], см. также обзор [62]), которые могут находиться в низкоспиновом (LS) состоянии со спином S = 0 $\left( {t_{{2g}}^{6}} \right),$ промежуточном состоянии (IS) со спином S = 1 $\left( {t_{{2g}}^{5}e_{g}^{1}} \right),$ и высокоспиновом (HS) состоянии $\left( {t_{{2g}}^{4}e_{g}^{2}} \right)$ с S = 2. Близость энергий этих состояний и может приводить к переходам при изменении температуры, давления или при допировании. Кроме того, существует возможность упорядочения ионов с различным полным спином [63, 64], наподобие орбитального или спинового упорядочения. Таким образом, в системах со спиновыми переходами в дополнение к зарядовым, орбитальным и спиновым (связанными с проекцией спина) степеням свободы добавляется еще одна, связанная с величиной спина иона переходного металла. Взаимодействие этой последней степени свободы с остальными в принципе может приводить к возникновению неоднородных состояний, аналогично тому, как это происходит в других сильно коррелированных системах, например, манганитах, рассмотренных в предыдущем разделе.

Как уже упоминали выше, спиновые переходы, наблюдаемые в соединениях, содержащих ионы Co³⁺ и Fe²⁺, могут возникать при изменении температуры или давления, а также при допировании. Мы сфокусируемся на последнем случае, в котором необходимо учитывать конкуренцию между одноузельными эффектами и кинетической энергией носителей заряда, возникающих при допировании. Мы рассмотрим возможность возникновения неоднородных состояний в кобальтитах в рамках модели, во многих отношениях сходной с той, что рассматривали в предыдущем разделе.

Одним из основных параметров модели является отношение расщепления d-уровня в кристаллическом поле Δ к хундовской константе связи J_H. Мы построим фазовые диаграммы модели в плоскости Δ/J_H–x при различных значениях других параметров модели.

Прежде чем приступить к описанию предлагаемой электронной модели систем со спиновыми переходами и исследованию ее свойств, мы хотели бы качественно обсудить, почему, на наш взгляд, естественно ожидать возникновения фазового расслоения в таких системах. На поведение систем со спиновыми переходами существенное влияние оказывает т.н. эффект спиновой блокады [65]. Поясним здесь суть этого явления на примере материалов с ионами кобальта Co³⁺, находящимися в низкоспиновом состоянии, S = 0. При электронном допировании таких систем ионы кобальта Co²⁺ оказываются в высокоспиновом состоянии, S = 3/2. В этом случае когерентный электронный транспорт оказывается невозможным (или сильно подавленным), поскольку невозможно произвести обмен между состояниями Co³⁺ с S = 0 и Co²⁺ с S = 3/2 посредством перемещения одного электрона. Движение электрона в этом случае приводит к появлению шлейфа “неправильных” ионов Co³⁺, находящихся в промежуточном спиновом состоянии с S = 1, что в конечном счете приводит к локализации электрона, подобно тому, как это происходит в модели Хаббарда [66]. Эту ситуацию можно “исправить” путем изменения спиновых состояний ионов Co³⁺ вблизи рассматриваемого электрона. В результате электрон оказывается запертым в небольшой области из “неправильных” ионов Co³⁺. Это, очевидно, является аналогом магнитных поляронов, неоднородных состояний, обсуждаемых в начале предыдущего раздела.

2.2.1. Спиновые состояния ионов кобальта

Рассмотрим системы со спиновыми переходами на примере дырочно допированных кобальтитов, которые имеют структуру перовскита (например, La_{1 –x}Sr_xCoO₃). В этом случае мы имеем два вида ионов кобальта в системе, Co³⁺ и Co⁴⁺. Каждый ион кобальта находится в окружении кислородных октаэдров, что приводит к расщеплению d-уровня иона кобальта на t_2g и e_g уровни. Обозначим в данном разделе энергию расщепления этих уровней как Δ. Перечислим сначала интересующие нас спиновые состояния ионов Co³⁺ и Co⁴⁺ в октаэдрическом окружении, их электронные конфигурации и энергии. Ион Co³⁺ может находиться в низкоспиновом (LS) состоянии с S = 0 и электронной конфигурацией $t_{{2g}}^{6}e_{g}^{0},$ промежуточном состоянии (IS) $t_{{2g}}^{5}e_{g}^{1},$ S = 1, и высокоспиновом состоянии (HS) с электронной конфигурацией $t_{{2g}}^{4}e_{g}^{2}$ и спином S = 2. Энергии этих состояний равны, соответственно, $E_{{{\text{LS}}}}^{{\left( {3 + } \right)}}$ = E₀, $E_{{{\text{IS}}}}^{{\left( {3 + } \right)}}$ = E₀ + Δ – J_H и $E_{{{\text{HS}}}}^{{\left( {3 + } \right)}}$ = E₀ + 2Δ – 4J_H, где J_H – хундовская константа связи. Ион кобальта Co⁴⁺ также может находиться в низкоспиновом ($t_{{2g}}^{5}e_{g}^{0},$ S = 1/2), промежуточном ($t_{{2g}}^{4}e_{g}^{1},$ S = 3/2) и высокоспиновом ($t_{{2g}}^{3}e_{g}^{2},$ S = 5/2) состояниях, которые отличаются от соответствующих состояний Co³⁺ удалением одного электрона с t_2g уровня. Энергии этих состояний равны $E_{{{\text{LS}}}}^{{\left( {4 + } \right)}}$ = E₁, $E_{{{\text{IS}}}}^{{\left( {4 + } \right)}}$ = E₁ + Δ – 2J_H и $E_{{{\text{HS}}}}^{{\left( {4 + } \right)}}$ = E₁ + 2Δ – 6J_H. Здесь мы ввели E₀ и E₁ как некие реперные значения энергий ионов Co³⁺ и Co⁴⁺, соответственно. Хотя эти величины могут значительно отличаться друг от друга, мы покажем ниже, что результат практически не зависит от значений E₀ и E₁. Для большей ясности все перечисленные состояния ионов кобальта и их характеристики сведены на рис. 7.

Каким будет основное состояние ионов Co³⁺ и Co⁴⁺, зависит от соотношения между Δ и J_H. Можно легко показать, что если Δ > 3J_H, то низкоспиновое состояние имеет наименьшую энергию как для Co³⁺, так и для Co⁴⁺.

В случае, когда 2J_H < Δ < 3J_H, иону Co³⁺ по-прежнему выгодно находиться в низкоспиновом состоянии, в то время как иону Co⁴⁺ становится выгодно иметь высокоспиновую конфигурацию. Наконец, при Δ < 2J_H, высокоспиновое состояние является основным состоянием для обоих ионов. Таким образом, мы видим, что в случае изолированных ионов промежуточное состояние никогда не реализуется.

Ситуация становится более сложной, когда мы учтем возможность перескока электронов между ионами кобальта. Заметим, во-первых, что так же, как и в случае с манганитами, интегралы перескока t_2g-электронов значительно меньше таковых для e_g-электронов. Поэтому в дальнейшем мы ими пренебрежем и будем рассматривать только перескоки e_g-электронов. Во-вторых, мы будем рассматривать только одноэлектронные процессы переноса заряда от Co³⁺ и Co⁴⁺, т.е. такие процессы, при которых спин ионов кобальта при перескоке электрона меняется на 1/2. Вероятность остальных процессов будет сильно подавлена: это и есть обсуждавшийся выше эффект спиновой блокады.

В результате в допированных кобальтитах остаются только два наиболее вероятных процесса переноса заряда: (i) переходы между IS Co³⁺ и LS Co⁴⁺, а также (ii) переходы между HS Co³⁺ и IS Co⁴⁺ (см. рис. 7).

Следовательно, для того чтобы получить выигрыш в кинетической энергии электронов, необходимо, чтобы в системе имелись ионы кобальта в промежуточном (IS) спиновом состоянии. Такая ситуация может возникнуть, когда изолированные ионы Co⁴⁺ находятся в LS-состоянии, или когда изолированные ионы Co³⁺ находятся HS-состоянии. В первом случае, реализуемом при Δ > 3J_H, часть LS-Co³⁺ может перейти в IS-состояние. Во втором случае, соответствующем Δ < 2J_H, часть HS-Co⁴⁺ переходит в IS-состояние. Когда 2J_H < Δ < < 3J_H, электронный транспорт возможен лишь, если часть из обоих типов ионов, Co³⁺ и Co⁴⁺, будет переведена из основного (для изолированных ионов) в возбужденные состояния. Такого типа двойные возбуждения представляются маловероятными. Ниже мы рассмотрим сначала наиболее реалистичный (для соединений типа La_{1 –x}Sr_xCoO₃) случай Δ > 3J_H.

Сконструируем эффективный электронный гамильтониан системы, учитывающий ее основные свойства, описанные выше, и проанализируем его основное состояние с учетом возможности фазового расслоения. Затем, аналогично, рассмотрим случай Δ < 2J_H. После этого мы построим фазовую диаграмму предложенной модели в плоскости x –‒ Δ/J_H и обсудим ее соответствие эксперименту. Надо заметить, что если уровень допирования x определяется процентным замещением редкоземельного элемента R в соединениях RCoO₃ щелочноземельным элементом A, то величина Δ контролируется радиусом r_R редкоземельного иона; чем больше r_R, тем меньше Δ, и наоборот.

2.2.2. Эффективный гамильтониан в случае низкоспинового основного состояния изолированных ионов

Мы рассматриваем системы с кристаллической структурой перовскита, в которой ионы кобальта образуют простую кубическую решетку. Относительное число ионов Co⁴⁺ и Co³⁺ равно, соответственно, x и 1 – x, где x – уровень допирования. Здесь мы считаем, что основное состояние изолированных ионов является низкоспиновым (Δ > > 3J_H); это является типичной ситуацией для дырочно-допированных кобальтитов типа R_1 – xA_xCoO₃ для R=La или ионов с меньшим ионным радиусом r_R [79]. Мы можем получить выигрыш в кинетической энергии электронов, если часть ионов Co³⁺ перевести в промежуточное спиновое состояние. При этом, однако, мы будем терять в одноузельной энергии, которая в пересчете на один такой ион равна: $E_{{{\text{IS}}}}^{{\left( {3 + } \right)}}--E_{{{\text{LS}}}}^{{(3 + )}}$ = Δ – J_H.

Сконструируем теперь эффективный гамильтониан системы. Для этого выберем LS-состояние иона Co³⁺, |Co³⁺ LS⟩ в качестве вакуумного состояния |0⟩ и введем операторы рождения и уничтожения электрона на e_g-уровне в узле n, $a_{{\mathbf{n}}}^{\dag }$ и a_n, а также операторы рождения и уничтожения дырки на t_2g-уровне в узле n, $c_{{\mathbf{n}}}^{\dag }$ и c_n. Действие этих операторов на вакуумное состояние определяется следующими правилами (см. также рис. 7):

Таким образом, промежуточное спиновое состояние иона Co³⁺ получается одновременным действием оператора рождения дырки на t_2g-уровне и оператора рождения электрона на e_g-уровне. Суммируя по всем возможным конфигурациям, мы получаем для одноузельной части гамильтониана [67]

где $n_{{\mathbf{n}}}^{e}$ = $a_{{\mathbf{n}}}^{\dag }{{a}_{{\mathbf{n}}}}$ и $n_{{\mathbf{n}}}^{h}$ = $c_{{\mathbf{n}}}^{\dag }{{c}_{{\mathbf{n}}}}$ – операторы числа электронов и дырок, U = U' + E₁ – Δ + J_H – 2E₀. Суммируя по всем узлам и добавляя слагаемое, описывающее перескоки e_g-электронов между ближайшими соседями, мы получим эффективный гамильтониан кобальтитов в виде (с учетом химпотенциала μ):

где Δ₁ = Δ – J_H.

Отметим, что рассматриваемый эффективный гамильтониан кобальтитов является достаточно упрощенным, поскольку не учитывает орбитальных и спиновых степеней свободы введенных квазичастиц. Действительно, в IS-состоянии иона Co³⁺, например, имеется один электрон на двукратно вырожденном e_g-уровне, что делает, вообще говоря, этот ион ян-теллеровским и может приводить к локальным деформациям решетки. Что касается спиновых степеней свободы, то так же, как и в случае манганитов, в пределе сильной хундовской связи, J_H → ∞, мы можем рассматривать бесспиновые фермионы, подразумевая, что амплитуда перескока e_g-электронов в гамильтониане (9) зависит от взаимной ориентации спинов ионов как t = t₀cosν_nm/2. Ниже мы будем подразумевать ферромагнитное состояние, так что cosν_nm/2 ≈ 1.

В защиту рассматриваемой упрощенной модели скажем, что нашей задачей здесь является учесть физику, обусловленную наличием переходов с изменением спинового состояния, которая и учитывается гамильтонианом (9). Усложнение модели безусловно сделало бы ее более подходящей для описания реальных систем, однако привело бы к существенному усложнению расчетов.

Средние числа e_g-электронов, $\left\langle {n_{{\mathbf{n}}}^{e}} \right\rangle $ = n^e, и t_2g дырок, $\left\langle {n_{{\mathbf{n}}}^{h}} \right\rangle $ = n^h, приходящихся на один узел решетки, удовлетворяют равенству n^h – n^e = x, где x – уровень допирования. Следовательно, энергию, приходящуюся в среднем на один узел, можно записать как

E_LS = E₀(1 – x) + E₁x + 〈H₁〉/N, где N – число узлов в решетке, а

Индекс LS в энергии E_LS означает, что мы рассматриваем низкоспиновое состояние иона Co³⁺ в качестве основного состояния.

Гамильтониан H₁ аналогичен гамильтониану в модели Фаликова‒Кимбалла [34]. Как и в предыдущем разделе, мы будем исследовать его в приближении среднего поля. Средние числа ионов кобальта в различных состояниях надо выразить через средние от операторов $n_{{\mathbf{n}}}^{e},$ $n_{{\mathbf{n}}}^{h}$ и их произведения. Если на узле n находится как дырка на t_2g-уровне, так и электрон на e_g-уровне, то ион кобальта на этом узле находится в состоянии IS Co³⁺ [см. (7) и рис. 7]. Следовательно, среднее число ионов IS Co³⁺ (в расчете на один узел) равно ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ = $\left\langle {n_{{\mathbf{n}}}^{h}n_{{\mathbf{n}}}^{e}} \right\rangle .$ Если в узле n имеется только дырка на t_2g-уровне, то этот узел занимает ион LS Co⁴⁺, т.е. ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{4 + }}}}}}$ = = $\left\langle {n_{{\mathbf{n}}}^{h}\left( {1--n_{{\mathbf{n}}}^{e}} \right)} \right\rangle .$ Если же на узле n находится только e_g-электрон, то такой узел находится в состоянии Co²⁺, и среднее число таких ионов равно ${{n}_{{{\text{C}}{{{\text{o}}}^{{{\text{2 + }}}}}}}}$ = = $\left\langle {n_{{\mathbf{n}}}^{e}\left( {1--n_{{\mathbf{n}}}^{h}} \right)} \right\rangle .$ Среднее число ионов LS Co³⁺ тогда равно ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ = 1 – ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ – ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{4 + }}}}}}$ – ${{n}_{{{\text{C}}{{{\text{o}}}^{{{\text{2 + }}}}}}}}$ = 1 – n^e – ‒ n^h + $\left\langle {n_{{\mathbf{n}}}^{h}n_{{\mathbf{n}}}^{e}} \right\rangle .$ Отметим, что параметр U в гамильтониане (10), приблизительно равный энергии одноцентрового кулоновского отталкивания d-электронов на ионе кобальта, имеет величину порядка нескольких электронвольт. Для кобальтитов так же, как и для манганитов, мы можем считать выполненным неравенство U $ \gg $ t. В этом случае число ионов Co²⁺ будет сильно подавлено. В пределе U → ∞ тогда будем иметь $\left\langle {n_{{\mathbf{n}}}^{h}n_{{\mathbf{n}}}^{e}} \right\rangle $ ≈ n^e и, следовательно, ${{n}_{{{\text{C}}{{{\text{o}}}^{{{\text{2 + }}}}}}}}$ ≈ 0, ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ ≈ n_e, ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{4 + }}}}}}$ ≈ n^h – n^e = x и ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ = 1 – n^h. Эти средние, а также энергию системы мы можем рассчитывать аналогично тому, как это было сделано в предыдущем разделе. Однако надо иметь в виду, что для рассматриваемой системы возможна также еще одна фаза, в которой все ионы Co³⁺ промотированы в IS-состояние, т.е. в этом случае мы имеем (в пределе U → ∞) n^h = 1, n^e = 1 – x. На языке зонных и локализованных электронов модели Фаликова‒Кимбалла такое состояние соответствует пустому локальному уровню, лежащему ниже уровня Ферми частично заполненной зоны проводимости. В рассматриваемом случае локализованный уровень по определению исчезает после того, как все ионы Co³⁺ переведены из LS в IS-состояние.

Обозначим состояние, в котором могут сосуществовать LS- и IS-ионы Co³⁺, как состояние 1. Состояние, в котором имеются только IS-ионы Co³⁺, мы обозначим как состояние 2. Свободные энергии (при T = 0) этих состояний как функции допирования представлены на рис. 8. Состояние 2 становится энергетически выгодным при x > x₂. Отметим, что состояния 1 и 2 становятся фактически эквивалентными при x > x₃, когда в обоих состояниях отсутствуют ионы LS-Co³⁺. В случае x < x₁, при котором реализуется состояние 1, в системе отсутствуют ионы IS-Co³⁺, и система является диэлектриком из-за спиновой блокады.

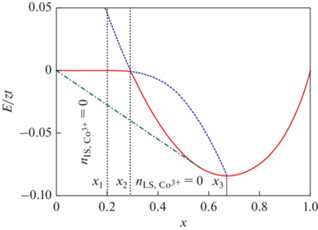
При x > x₁ число e_g-электронов растет. Если не принимать во внимание состояние 2, этот рост продолжался бы вплоть до x = x₃, когда все ионы Co³⁺ были бы переведены в промежуточное спиновое состояние. Однако при x = x₂ состояние 2 становится энергетически невыгодно, и происходит переход 1-го рода в состояние 1. Зависимости числа LS- и IS-ионов кобальта от допирования показаны на рис. 9.

Свободная энергия основного (однородного) состояния системы как функция допирования показана на рис. 8 сплошной линией. Видно, что кривая свободной энергии имеет излом при переходе из состояния 1 в состояние 2. Это обусловливает то, что однородное состояние является неустойчивым в области допирования 0 < x < x* ≈ x₃. В этой области, определяемой построением Максвелла, система разваливается на две фазы с концентрациями электронов x = 0 и x = x*. В первой фазе мы имеем ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ = 0, а во второй ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$ = 0.

Зависимость n^e от допирования x определяет поведение магнитного момента системы. Действительно, магнитный момент ионов кобальта в низкоспиновом состоянии равен нулю. Допирование приводит, во-первых, к появлению ионов LS-Co⁴⁺ со спином S = 1/2, а во-вторых, к появлению ионов кобальта в промежуточном спиновом состоянии с S = 1. Таким образом, данные, приведенные на рис. 9, могут быть перестроены в терминах магнитного момента, приходящегося на один допант (или, другими словами, на один ион Co⁴⁺). Результаты расчета представлены на рис. 10. Если мы будем рассматривать только однородные состояния системы, то упоминавшийся выше фазовый переход из состояния 1 в состояние 2 приведет, очевидно, к скачку намагниченности.

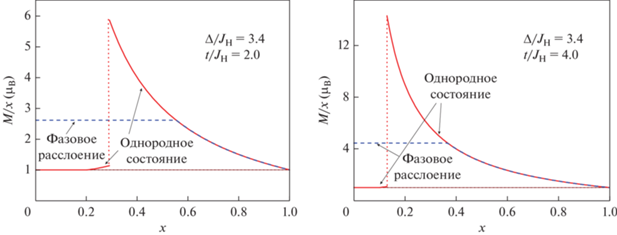
В то же время, в фазово-расслоенном состоянии магнитный момент, приходящийся на один ион Co⁴⁺, остается постоянным, т. к. и количество IS-ионов Co³⁺, и число ионов Co⁴⁺ пропорционально x. Магнитный момент системы, приходящийся на один ион Co⁴⁺ (так же, как и величина скачка магнитного момента в однородном состоянии), существенно зависит от параметров модели и особенно от амплитуды перескока e_g-электронов.

Из сравнения графиков на рис. 10 мы видим, что увеличение t вдвое приводит к существенному росту магнитного момента. Отметим, что обсуждаемые здесь величины магнитного момента в неоднородном состоянии соответствуют макроскопическому фазовому расслоению, при котором размеры неоднородностей много больше периода решетки. Такого типа неоднородного состояния можно ожидать при достаточно большом уровне допирования. При малых x, однако, естественно предположить, что неоднородности имеют капельную структуру, при которой каждый отдельный ион Co⁴⁺ окружен некоторым количеством IS-ионов Co³⁺. В этом случае магнитным момент, приходящийся на один ион Co⁴⁺, должен быть больше, чем в случае крупномасштабного фазового расслоения. Именно такая ситуация может иметь место в случае слабо легированного La_{1 –x}Sr_xCoO₃, экспериментально исследованного в работе [68], в которой наблюдали магнитные поляроны с моментом, примерно равным 13μ_B. Из упомянутых выше качественных соображений следует ожидать, что магнитным момент, приходящийся на один ион Co⁴⁺, должен несколько уменьшаться с допированием.

Таким образом, мы показали, что спиновые переходы в дырочно-допированых кобальтитах могут быть описаны в рамках модели, учитывающей сосуществование и конкуренцию зонных и локализованных электронов. Такая модель допускает возможность скачкообразного перехода ионов Co³⁺ из LS- в IS-состояние. При малом допировании, однако, более предпочтительным является состояние фазового расслоения, в котором только часть ионов Co³⁺ промотирована в промежуточно-спиновое состояние, при этом носители заряда, появляющиеся при допировании, оказываются в окружении IS- ионов Co³⁺. Экспериментальные данные по соединению La_{1 –x}Sr_xCoO₃ [68–73] свидетельствуют в пользу такой картины.

2.2.3. Эффективный гамильтониан для высокоспинового основного состояния изолированных ионов

Рассмотрим теперь область параметров Δ < 2J_H, когда изолированные ионы Co³⁺ и Co⁴⁺ находятся в высокоспиновом состоянии. Перенос заряда в этом случае возможен, только если мы переведем часть ионов Co⁴⁺ в промежуточное состояние. При этом у нас возникает дырка на e_g-уровне.

Итак, теперь вместо переноса электрона с IS- иона Co³⁺ на LS-ион Co⁴⁺, мы имеем перескок электрона с HS-иона Co³⁺ на IS-ион Co⁴⁺, или, что то же самое, перескок дырки с IS-иона Co⁴⁺ на HS-ион Co³⁺. Используя эту аналогию, мы выберем HS-состояние иона Co⁴⁺ в качестве нового вакуумного состояния и напишем соотношения, аналогичные (7), в виде (см. рис. 7):

где мы ввели операторы рождения и уничтожения электрона на t_2g-уровне в узле n, и â_n, а также операторы рождения и уничтожения дырки на e_g-уровне, $\hat {c}_{{\mathbf{n}}}^{\dag }$ и ĉ_n.

Соответствующий одноузельный гамильтониан может быть получен путем следующей замены в (8): E₀, E₁, E₂, U → Ê₀, Ê₁, Ê₂, Û, а также $n_{{\mathbf{n}}}^{e}$ → $\sim n _{{\mathbf{n}}}^{h},$ $n_{{\mathbf{n}}}^{h}$ → $\sim n _{{\mathbf{n}}}^{e}.$ Для полного гамильтониана системы

где Δ₂ = 4J_H – Δ > 0 – разница в энергии ионов Co⁴⁺ в IS- и HS-состояниях.

Теперь средние числа электронов и дырок, приходящихся на один узел решетки, связаны с уровнем допирования соотношением ñ^e – ñ^h = 1 – x. В этом случае для энергии системы, рассчитанной на один узел решетки, вместо (10) будем иметь

где

Индекс HS в энергии E_HS означает, что мы рассматриваем высокоспиновое состояние иона Co⁴⁺ в качестве основного состояния. Отметим, что разность E_HS–E_LS не зависит от E₀ и E₁. Таким образом, фазовая диаграмма модели, получаемая путем сравнения энергий различных фаз, не будет зависеть от этих параметров. Поскольку эффективные гамильтонианы кобальтитов (10) и (13) являются схожими, то зависимости энергии системы, а также средних ñ^e и ñ^h от допирования будет схожи с теми, что представлены на рис. 8 и 9.

Более конкретно, на этих рисунках мы должны сделать замены n^h → ñ^e, n^e → ñ^h и x → 1 – x, т.е. плотности ионов Co³⁺ в IS (n^e = ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$) и LS (1 – ‒ n^h = ${{n}_{{{\text{LS}},{\text{C}}{{{\text{o}}}^{{3 + }}}}}}$) состояниях заменяются на плотности ионов Co⁴⁺ в IS (ñ^h = ${{n}_{{{\text{IS}},{\text{C}}{{{\text{o}}}^{{4 + }}}}}}$) и HS (1 – ñ^e = = ${{n}_{{{\text{HS}},{\text{C}}{{{\text{o}}}^{{4 + }}}}}}$) состояниях. Отметим также, что подобная аналогия между двумя случаями (LS‒LS и HS‒HS) есть следствие того факта, что мы рассматриваем модель с бесспиновыми фермионами. Таким образом, существует электрон‒дырочная симметрия между пустым e_g-уровнем иона LS Co³⁺ и наполовину заполненным e_g-уровнем (два электрона с параллельными спинами) иона HS Co³⁺.

2.2.4. Фазовая диаграмма

Полученные выше результаты могут быть объединены в фазовую диаграмму модели в плоскости x ‒ Δ/J_H. Вид этой диаграммы существенно зависит от интеграла перескока t. Типичные фазовые диаграммы, рассчитанные при двух значениях t, показаны на рис. 11.

При достаточно малых t (t/J_H = 1, левая часть рис. 11) мы видим хорошо определенные области фазовой диаграммы, отвечающие случаям Δ > 3J_H и Δ < 2J_H (обсуждали в разделах 2.2.2 и 2.2.3, соответственно). В каждой из этих областей изменение допирования (от 0 до 1 и наоборот) приводит к последовательным переходам от фазы с локализованными носителями к фазе, в которой появляются зонные электроны, и наконец к фазе, в которой все носители заряда делокализованы. Эти две области с Δ $ \gtrsim $ 3J_H и Δ $ \gtrsim $ 2J_H разделены фазой, в которой система состоит из смеси LS (S = 0) ионов Co³⁺ и HS (S = 5/2) ионов Co⁴⁺. Эта фаза является диэлектрической при любом допировании из-за эффекта спиновой блокады [65]. При достаточно больших t (t/J_H$ \gtrsim $ 1, правая часть рис. 11) указанная диэлектрическая фаза коллапсирует в промежуточной области допирования.

Вид фазовой диаграммы меняется, если мы примем во внимание возможность фазового расслоения. Соответствующие фазовые диаграммы, построенные при двух различных значениях t/J_H, показаны на рис. 12.

Мы видим, что вместо фаз с частично или полностью делокализованными носителями на фазовой диаграмме появляются области расслоения на фазы с полностью локализованными и полностью делокализованными носителями.

Опять, при малых t (t/J_H$ \lesssim $ 1, левая часть рис. 12) мы имеем промежуточную область с локализованными носителями при любом допировании (фаза с LS ионами Co³⁺ и HS-ионами Co⁴⁺ соответственно). Эта промежуточная область становится уже с ростом t, и при t/J_H ≈ 1.24 разделяется на две отдельных области. При дальнейшем росте t эти промежуточные области продолжают сокращаться и полностью исчезают при t/J_H ≈ 1.44 (правая часть рис. 12).

2.3.5. Заключительные замечания к разделу о кобальтитах

Итак, в этом разделе мы построили простую электронную модель соединений со спиновыми переходами и проанализировали ее свойства на примере дырочно-допированных кобальтитов. Спиновые состояния изолированных ионов переходного металла определяются соотношением между расщеплением d-уровня в кристаллическом поле Δ и хундовской константой связи J_H.

При этом электронный транспорт за счет носителей, появляющихся при допировании, может быть сильно подавлен за счет эффекта спиновой блокады [65]. В этом случае может оказаться выгодным изменить спиновое состояние некоторого количества ионов переходного металла для получения выигрыша в кинетической энергии носителей. Таким образом, в системе возникает конкуренция между локализацией за счет спиновой блокады и делокализацией, которая может приводить к фазовому расслоению.

Анализ эффективной модели показывает существование двух типов фазового расслоения, которые отличаются спиновыми состояниями ионов переходного металла. Фазовое расслоение типа I существует в области при x $ \lesssim $ 0.5 и Δ $ \gtrsim $ 2.5J_H фазовой диаграммы в плоскости x – Δ и характеризуется низкоспиновыми состояниями ионов. Фазовое расслоение типа II зеркально первому, область его существования качественно определяется неравенствами x $ \gtrsim $ 0.5 и Δ $ \lesssim $ 2.5J_H, а ионы переходного металла преимущественно находятся в высокоспиновых состояниях (рис. 12).

Существование неоднородных состояний в некоторых допированных кобальтитах, например, в La_{1 –x}Sr_xCoO₃, подтверждается в различных экспериментах [60, 68–73]. Так магнитные измерения, выполненные в работе [60] при малом (дырочном) допировании x < 1%, показали, что магнитный момент, приходящийся на одну дырку, оказывается значительно выше, чем тот, который бы создавал ион Co⁴⁺ в низкоспиновом состоянии с S = 1/2. Вместо этого авторы наблюдали появление магнитных примесей с необычайно большим спином S = 10–16, что ясно сигнализирует о том, что ион Co⁴⁺ оказывается окруженным облаком соседних ионов Co³⁺, находящихся в более высоком, чем S = 0, спиновом состоянии. Эксперименты по нейтронному рассеянию, а также ЭПР- и ЯМР-исследования, выполненные для схожих систем в работе [80], позволяют оценить размер и форму таких магнитных кластеров. Во всех перечисленных работах неоднородные состояния наблюдали при малых x, а основное состояние ионов Co³⁺ являлось низкоспиновым (т.е. можно считать, что Δ $ \gtrsim $ 3J_H), что качественно согласуется с рассчитанной фазовой диаграммой.

Отметим, что сконструированный модельный гамильтониан является во многом переупрощенным, поскольку не учитывает орбитальных и спиновых (связанных с проекцией спина) степеней свободы, однако он корректно воспроизводит физику, обусловленную наличием спиновых переходов, которая, по нашему мнению, и ответственна за возникновение неоднородных состояний. Для более тщательного исследования и количественного сравнения теории с экспериментом безусловно необходимо расширение модели, которое может быть различным в каждом конкретном случае.

3.1. Волна спиновой плотности и фазовое расслоение в модели со слабонеидеальным нестингом. Общее рассмотрение

В данном разделе мы проанализируем модель [82], предложенную Райсом для описания волны спиновой плотности в хроме (см. также обзор [96]).

3.1.1. Модель Райса: основные уравнения

Зонная структура модели включает одну электронную (a) и одну дырочную (b) зоны, которые выходят на уровень Ферми. Предполагается, что ферми-поверхности электронных и дырочных зон ‒ сферические (мы рассматриваем здесь 3D-случай), со слегка отличающимися радиусами (неидеальный нестинг). Поверхность Ферми зоны a центрирована на импульсе k = 0, тогда как поверхность Ферми дырочной зоны центрирована на импульсе k = Q₀. Кроме того, имеется еще одна зона (c), выходящая на уровень Ферми, но не участвующая в формировании магнитного порядка (т.н. электронный резервуар). Из всех возможных попарных межэлектронных взаимодействий учитывается только отталкивание a и b электронов, поскольку именно оно приводит к возникновению волны спиновой плотности.

Гамильтониан модели имеет вид:

где $a_{{{\mathbf{k}}\sigma }}^{\dag },$ a_kσ ($b_{{{\mathbf{k}}\sigma }}^{\dag },$ b_kσ) ‒ операторы рождения и уничтожения электрона в зоне a (b), $n_{{{\mathbf{k}}\sigma }}^{\alpha }$ ‒ операторы числа частиц типа α импульсом k и проекцией спина σ, $\mathcal{V}$ ‒ объем образца, U ‒ константа взаимодействия a и b электронов, которое предполагается точечным.

Мы предположим здесь, что зоны a и b имеют квадратичную дисперсию. Кроме того, мы включим химпотенциал в определение ε^α. Тогда выражения для ε^a,b(k) будут иметь вид:

Условия идеального нестинга означают, что при некотором значении μ = μ₀ поверхности Ферми зон a и b совпадают при трансляции на вектор Q₀, и что обе ферми-сферы характеризуются одним и тем же радиусом k_F. В случае электрон‒дырочной симметрии, когда m_a = m_b = m и $\varepsilon _{{{\text{max}}}}^{b}$ = $ - \varepsilon _{{{\text{min}}}}^{a},$ будем иметь μ₀ = 0. Вблизи поверхности Ферми энергетические спектры зон a и b тогда имеют вид:

где k_F = (k_Fa + k_Fb)/2 и μ = v_F(k_Fa ‒ k_Fb)/2. Плотность состояний электронов на поверхности Ферми (при μ = 0) в зоне a (как b в зоне b), рассчитанная на единицу объема и одну проекцию спина, равна N_m = ${{k_{{\text{F}}}^{2}} \mathord{\left/ {\vphantom {{k_{{\text{F}}}^{2}} {2{{\pi }^{2}}{{v}_{{\text{F}}}}}}} \right. \kern-0em} {2{{\pi }^{2}}{{v}_{{\text{F}}}}}}.$

Рассмотрим здесь предел слабой связи, когда UN_m $ \ll $ 1. В этом случае интересующие нас изменения химпотенциала μ и импульсов Ферми k_Fa и k_Fb будут незначительны по сравнению с энергией Ферми ε_F = v_Fk_F (при μ = 0), и поэтому можно считать плотность состояний N_m при этих изменениях постоянной.

Отметим, что для простоты здесь считаем скорости Ферми v_F электронной и дырочной зон одинаковыми. Можно показать, что различие в скоростях Ферми для зон a и b не принципиально для получаемых ниже результатов. Далее, предположение о квадратичности дисперсии при всех импульсах также не существенно: для нас здесь важна лишь форма поверхности Ферми и ее изменение при изменении химпотенциала.

Что касается зоны резервуара (c), то мы не будем делать конкретных предположений о законе ее дисперсии. Мы будем лишь считать, что у нее имеется конечная плотность состояний на уровне Ферми, которую мы обозначим здесь как 2N_r$\mathcal{V}$ (N_r ‒ плотность состояний на один спин, на единицу объема), и что эта плотность состояний слабо меняется при изменении химпотенциала.

Мы будем рассматривать гамильтониан (14) в приближении среднего поля, которое является адекватным приближением в пределе слабого взаимодействия, UNm $ \ll $ 1. Отправной точкой нашего рассмотрения является случай идеального нестинга, когда μ = 0. В этом случае радиусы Ферми электронной и дырочной зон совпадают. Замена оператора взаимодействия на его аналог в приближении среднего поля в общем случае производится фактически тем же образом, как и в случае манганитов. В результате второе слагаемое в гамильтониане (14) становится квадратичным по электронным операторам и приобретает вид:

где мы ввели параметр порядка ${{\Delta }_{0}} = \left( {\frac{U}{\mathcal{V}}} \right)$ × × $\sum\nolimits_k {\left\langle {a_{{k\sigma }}^{\dag }{{b}_{{k{\text{ + }}{{Q}_{0}} - \sigma }}}} \right\rangle } ,$ который соответствует антиферромагнетизму. При этом мы предполагали, что средние от произведений операторов отличны от нуля только при q = Q₀ и σ' = ‒σ. Величина Δ₀ определяет щель в спектре, возникающую за счет электрон-электронного взаимодействия. Она определяется минимизацией термодинамического потенциала Ω. В случае, когда $\varepsilon _{{{\text{max}}}}^{b}$ = ‒$\varepsilon _{{{\text{min}}}}^{a}$ ≈ ε_F, мы в результате будем иметь

Эта формула аналогична выражению для сверхпроводящей щели в теории БКШ, в которой энергия Ферми играет роль энергии Дебая. Параметр порядка Δ₀ связывает электроны с неравными импульсами. Следовательно, в реальном пространстве такой параметр порядка описывает вращение намагниченности (в плоскости xy) с волновым вектором Q₀. Поскольку обычно карманы a и b располагаются в высоко-симметричных точках зоны Бриллюэна, вектор Q₀ оказывается соизмеримым с периодом решетки. То есть, в этом случае рассматриваемый параметр порядка соответствует антиферромагнитному состоянию, в котором можно ввести несколько (в простейшем случае две) магнитных подрешеток.

Рассмотрим теперь случай ненулевого μ. В такой ситуации ферми-сферы электронной и дырочной зон имеют различные радиусы. Однако разница в радиусах мала, пока μ мало. Несмотря на это, состояние со щелью может быть по-прежнему устойчивым и, по крайней мере, метастабильным и в случае ненулевого химпотенциала. Однако можно попробовать минимизировать энергию еще больше, если рассматривать трансляции на вектор Q₁ = Q₀ + Q, который также можно считать вариационным параметром. Новый параметр порядка тогда имеет вид $\Delta = \left( {\frac{U}{\mathcal{V}}} \right)\sum\nolimits_k {\left\langle {a_{{k\sigma }}^{\dag }{{b}_{{k{\text{ + }}{{Q}_{1}} - \sigma }}}} \right\rangle } .$ В противоположность Q₀, абсолютная величина которого порядка величины вектора обратной решетки, вектор Q мал: |Q| ~ |Δ|/v_F$ \ll $ |Q₀|.

Таким образом, параметр порядка Δ описывает несоизмеримую волну спиновой плотности, в которой вектор антиферромагнетизма медленно меняется в пространстве с длиной волны, равной 2π/|Q|. Отметим, что рассматриваемая фаза аналогична фазе Фулде‒Феррела‒Ларкина‒Овчинникова (ФФЛО) для сверхпроводника в магнитном поле [122, 123].

Равновесные характеристики системы могут быть получены путем вычисления термодинамического потенциала Ω = ‒Tln[Tr(exp(‒H '/T)]. В приближении среднего поля гамильтониан (14) является квадратичным по электронным операторам, что дает возможность достаточно легко найти спектр квазичастиц и вычислить термодинамический потенциал. Минимизация Ω позволяет вычислить Δ и Q как функции химпотенциала и температуры при заданном уровне допирования x. Нам также понадобится дополнительный параметр r =N_r/2N_m, характеризующий соотношение между плотностью состояний электронов резервуара (c) и зон a и b.

Также мы определяем температуру Нееля T_N(x) при заданном x как минимальную температуру, при которой Δ = 0. Кроме того, путем исследования зависимости Q(x, T), мы определяем кривую T_Q(x), которая разделяет соизмеримую и несоизмеримую антиферромагнитные фазы. В результате, мы получаем фазовую диаграмму модели в плоскости x‒Т.

Фактически вид фазовой диаграммы зависит от единственного безразмерного параметра r, который определяет долю электронов резервуара от полного числа электронов на уровне Ферми. При r ≠ 0 фазовая диаграмма схематически представлена на рис. 13. При r = 0, кривая T_Q(x) начинается в точке (x = 0, T = 0), т.е. в отсутствие немагнитных электронов при нулевой температуре несоизмеримая антиферромагнитная фаза становится выгодной при сколь угодно малом допировании.

3.1.2. Неустойчивость однородного состояния

Проведем теперь анализ устойчивости однородного состояния, рассматривая свободную энергию системы как функцию допирования. Типичная кривая F(x, T = 0)/${{\mathcal{F}}_{0}}$, где ${{\mathcal{F}}_{0}}$ = N_mΔ²$\mathcal{V}{\text{,}}$ рассчитанная при r = 0.3, представлена на рис. 14, где также показаны зависимости Δ(x, 0) и Q(x, 0).

Расчеты показывают, что при r $ \lesssim $ 0.4 переход по концентрации между антиферромагнитными фазами с Q = 0 и Q ≠ 0 является переходом второго рода, и функции Δ(х, 0) и Q(х, 0) непрерывны. При этом свободная энергия имеет отрицательную кривизну (∂²F/∂x² < 0) в некоторой области допирования, что свидетельствует о неустойчивости однородного состояния. При r ≳ 0.4 переход между упорядоченными фазами с Q = 0 и Q ≠ 0 является переходом первого рода, функции Δ(х, 0) и Q(х, 0) претерпевают разрыв в некоторой точке x*, а кривая свободной энергии имеет излом в этой точке. В этом случае однородное состояние также является неустойчивым в некоторой области допирования, содержащей в себе точку х*. При любом значении r расслоение происходит на соизмеримую АФМ-фазу с концентрацией носителей x₁ и несоизмеримую АФМ-фазу с концентрацией x₂. Значения концентраций x₁ и x₂ определяются построением Максвелла [41].

С ростом температуры область фазового расслоения x₁ < x < x₂ постепенно уменьшается и сходит на нет выше некоторого критического значения T*. Фазовые диаграммы модели с учетом фазового расслоения, рассчитанные при двух различных значениях r, представлены на рис. 15. Область фазового расслоения ограничена на этих фазовых диаграммах штриховой кривой T_PS(x).

3.1.3. Обсуждение результатов раздела 3.1

Мы продемонстрировали выше, что состояние с волной спиновой плотности в модели Райса [82] неустойчиво к расслоению на фазы. Это обстоятельство имеет существенные последствия для множества различных материалов, в которых нестинг поверхности Ферми ответственен за возникновение магнитного порядка. Такими материалами являются, например, сплавы хрома [96], пниктиды железа [100], двухслойный AA графен [124] и др. В заключение этого раздела мы хотели бы обсудить полученные результаты и сравнить их с опубликованными в других работах.

Выше мы упоминали о соответствии несоизмеримой волны спиновой плотности в модели Райса фазе ФФЛО в сверхпроводниках. Однако обычно фазовое расслоение не упоминается на фазовой диаграмме сверхпроводника с фазой ФФЛО. Это имеет простое объяснение: такие фазовые диаграммы строятся в координатах температура‒магнитное поле (которое является аналогом химического потенциала для несоизмеримой волны спиновой плотности). Магнитное поле, являясь интенсивным термодинамическим параметром, не допускает фазового расслоения. Вместо этого система претерпевает фазовый переход первого рода по магнитному полю [122]. Однако в таких системах, как холодные атомы в оптической ловушке, оказывается возможным контролировать полную спиновую поляризацию, которая является экстенсивным параметром (аналог допирования). В этом случае в системе предсказывается возникновение фазового расслоения [125].

Помимо рассматриваемого здесь параметра порядка, в литературе рассматриваются также различные пространственно-неоднородные (по абсолютной величине) параметры порядка [126‒129]. Один из них обсуждали в работе [126], в которой численные результаты для двумерного ФФЛО сверхпроводника с параметром порядка типа Ларкина‒Овчинникова [130] были использованы для исследования модели Райса. Предполагали [126], что при малом допировании параметр порядка в реальном пространстве формирует доменные стенки. В доменных стенках параметр порядка локально обнуляется, что делает их предпочтительным местом для аккумуляции заряда, возникающего при допировании.

В реальных системах баланс между различными типами упорядочения может быть сдвинут за счет факторов, не учитываемых в рассматриваемой модели (например, анизотропии, дальнодействующего кулоновского взаимодействия и т.д.). Таким образом, возможность фазового расслоения за счет рассматриваемого здесь механизма должна приниматься во внимание при анализе экспериментальных данных.

Проделанные здесь расчеты предсказывают расслоение на две антиферромагнитные фазы. В то же время надо отметить, что свободная энергия несоизмеримой АФМ-фазы чрезвычайно близка к энергии парамагнитного состояния. В реальной ситуации существует множество факторов, которые могут привести к разрушению магнитного порядка в несоизмеримой фазе. Одним из таких механизмов является рассеяние на примесях. Действительно, широко известно, что состояние ФФЛО, аналогом которого (с математической точки зрения) является несоизмеримая АФМ-фаза, чрезвычайна чувствительна к беспорядку [131]. Расчеты показывают, что в случае, если магнитный порядок в несоизмеримой фазе будет разрушен, то фазовое расслоение тем не менее сохранится, но будет происходить между соизмеримой антиферромагнитной и парамагнитной фазами.

Имеет смысл кратко упомянуть несколько усложняющих факторов, которые не рассматриваются в настоящей модели, но характерны для практически любых реальных систем, и которые несомненно будут существенно влиять на результирующую фазовую диаграмму. В эксперименте форма Ферми поверхности отличается от сферической, и кроме того, электронные и дырочные карманы имеют различные скорости Ферми. Влияние этих факторов на фазовое расслоение требует отдельного исследования.

При рассмотрении пниктидов железа в следующем разделе мы будем учитывать эллиптичность электронных карманов и разницу в скоростях Ферми электронных и дырочных зон. Помимо этого, упомянем здесь также, что любое фазово-расслоенное состояние обладает определенной геометрией (капли, страйпы и пр.) и характеризуется определенными размерами неоднородностей. Рассматриваемая здесь модель не позволяет сделать никаких предсказаний относительно этих характеристик. В простейшем случае структура неоднородного состояния регулируется соотношением между дальнодействующим кулоновским взаимодействием электронов и поверхностной энергией границы раздела фаз. Этот вопрос будет проанализирован в разд. 4.

3.2. Фазовое расслоение в пниктидах железа

Пниктиды железа, являющиеся частным случаем железосодержащих сверхпроводников, в настоящее время представляют огромный интерес для исследователей как в связи с их высокой температурой сверхпроводящего перехода [132‒134], так и благодаря богатой физике их электронной подсистемы (см., напр., обзоры [110, 135, 136]). К пниктидам железа относятся несколько семейств соединений, сходных по химическому составу и кристаллической структуре. Это такие соединения, как RFeAsO, где R = La, Ce, Sm, Pr и др. (в литературе для них используется краткое обозначение 1111), AFe₂As₂ (A = Ba, Sr, Ca, обозначаются как 122) и наконец, NaFeAs, LiFeAs и пр. (соединения типа 111). Объединяющим элементом для всех типов структур является наличие плоскостей FeAs, разделенных плоскостями, образованными различными атомами или группами атомов. Таким образом, как и сверхпроводящие купраты, пниктиды являются слоистыми материалами.

Исходные соединения пниктидов, упомянутые выше, могут быть допированы путем частичного или полного замещения какого-либо атома атомом с другой или той же валентностью. В результате слои FeAs приобретают дырки (например, в соединениях LaO_{1 –x}F_xFeAs [132] или Ba_{1 –x}K_xFe₂As₂ [133]) или электроны (например, BaFe_{2 –x}Co_xAs₂ [104] или BaFe_2 – xNi_xAs₂ [105]). В случае изовалентного замещения (в частности, при замене Fe на Ru [137, 138]), дополнительных носителей не возникает, однако изменение электронной структуры и типа основного состояния все равно происходит.

Фазовая диаграмма пниктидов во многом схожа с таковой для купратов. Родительские соединения 1111 (например, LaFeAsO) и 122 (типа BaFe₂As₂) являются антиферромагнитными металлами. При допировании температура Нееля уменьшается, и антиферромагнитное основное состояние сменяется сверхпроводящим. На фазовой диаграмме можно отметить наличие несоизмеримого антиферромагнетизма в области электронного допирования, а также несоизмеримых спиновых флуктуаций в области дырочного допирования.

Зонная структура пниктидов активно исследуется методом фотоэлектронной спектроскопии с угловым разрешением (ARPES) [139, 140]. Эти исследования показывают, что пниктиды обладают многокомпонентной поверхностью Ферми. Исходные соединения имеют несколько дырочных и электронных карманов, расположенных вблизи высокосимметричных точек зоны Бриллюэна. Схожие результаты дают и первопринципные расчеты [141–143]. Так, на рис. 16 представлена поверхность Ферми пниктида типа 122 [142].

Видно, что поверхность Ферми является квазидвумерной ‒ ее форма слабо зависит от компоненты импульса, перпендикулярной слоям железа. Всего имеется 5 карманов: 3 дырочных, 2 из которых расположены вблизи точки (0, 0), один – вблизи точки (в единицах 1/а, a ‒ постоянная решетки) (π, π), и 2 электронных кармана, расположенных близи точек (π, 0) и (0, π).

Отметим, что представленная поверхность Ферми изображена в т.н. расширенной зоне Бриллюэна, которая соответствует элементарной ячейке, содержащей один атом железа (пунктирные линии на рис. 16a). Реальная элементарная ячейка пниктидов в два раза больше по объему и содержит 2 атома железа (штрих-пунктирная линия).

При описании пниктидов теоретики используют в основном два различных подхода (помимо первопринципных расчетов), один из которых можно условно назвать феноменологическим [87, 88, 90, 98], а другой – микроскопическим [89, 93, 144]. В феноменологическом подходе рассматриваются модели пниктидов, в которых считаются заданными поверхность Ферми и скорости Ферми для всех карманов. При этом чаще всего пренебрегают зависимостью поверхности Ферми от импульса, перпендикулярного слоям FeAs, а компоненты поверхности Ферми аппроксимируются простыми фигурами типа круга и/или эллипса. Именно такой подход будет здесь использоваться нами. В микроскопическом подходе чаще всего используют многозонные модели Хаббарда, в которых основными компонентами являются d-электроны железа. Параметры моделей, такие как амплитуды перескоков, хаббардовское U и параметр Хунда J_H, подбирают так, чтобы рассчитанная поверхность Ферми соответствовала экспериментально наблюдаемой.

При любом подходе роль нестинга в формировании антиферромагнетизма в пниктидах считается общепризнанной. В пользу этого прежде всего свидетельствует то, что данный механизм правильно предсказывает тип антиферромагнетизма исходных пниктидов. Еще одним аргументом является экспериментальное наблюдение несоизмеримой фазы в некоторых допированных соединениях. Наконец, в отличие, например, от купратов или манганитов, исходные соединения которых являются моттовскими диэлектриками, недопированные пниктиды являются металлами, это говорит о том, что электрон‒электронное взаимодействие в них не является сильным (см., однако, обсуждение по этому поводу в работе [110]). Это, в свою очередь, свидетельствует об адекватности использования моделей типа Райса для данных соединений.

3.2.1. Модельный гамильтониан пниктидов

Сформулируем теперь электронную модель пниктидов. Прежде всего мы пренебрежем зависимостью энергий квазичастиц от импульса, перпендикулярного слоям FeAs, т.е. будем рассматривать двумерную модель. Поверхность Ферми состоит из трех дырочных и двух электронных карманов. Мы будем считать, что дырочные компоненты имеют форму круга, а электронные – эллипса (см. рис. 17), что в достаточно хорошей степени соответствует эксперименту [144]. В расширенной зоне Бриллюэна два дырочных кармана центрированы вокруг Γ = (0, 0) точки, а один карман расположен вокруг точки Γ' = (π/а, π/а). Электронные компоненты Ферми поверхности расположены вокруг точек (0, π/а) и (π/а, 0).

Как и раньше, запишем гамильтониан модели в виде суммы H = H₀ + H_int, где одночастичная часть имеет вид:

Здесь $a_{{{\mathbf{k}}\lambda \sigma }}^{\dag },$ a_kλσ ($b_{{{\mathbf{k}}s\sigma }}^{\dag },$ b_ksσ) ‒ операторы рождения и уничтожения квазичастиц в дырочных (электронных) зонах λ = 1, 2, 3 (s = 1, 2) с дисперсиями $\varepsilon _{{\lambda {\mathbf{k}}}}^{h}$ $\left( {\varepsilon _{{s{\mathbf{k}}}}^{e}} \right).$

Мы предполагаем, что вблизи поверхности Ферми все зоны обладают квадратичной дисперсией. Электронные компоненты поверхности Ферми эллиптические. Примем, что вблизи поверхности Ферми дисперсия электронных зон имеет вид $\varepsilon _{{1{\mathbf{k}} + {\mathbf{Q}}0}}^{e}$ = ε(k_x, ky), $\varepsilon _{{2{\mathbf{k}} + {\mathbf{Q}}{\kern 1pt} '0}}^{e}$ = ε(k_y, kx), где

Здесь $v_{{\text{F}}}^{e}$ ‒ скорости Ферми для электронных зон, усредненных по поверхности Ферми. Центры электронных карманов находятся в точках Q₀ = (π/а, 0) и ${\mathbf{Q}}_{0}^{'}$ = (0, π/а). Отметим, что в общем случае скорости Ферми неодинаковы для различных листов. Параметр α определяет эллиптичность электронных карманов. Положительные α соответствуют рис. 17. В этом случае главные оси эллипсов направлены к точке Г = (0, 0). Если α < 0, то эллипсы должны быть повернуты на 90° вокруг своих центров.

В силу многокомпонентной структуры поверхности Ферми, гамильтониан взаимодействия H_int в общем случае должен включать множество членов, описывающих попарное взаимодействие между носителями заряда в различных зонах. Однако, поскольку мы интересуемся только свойствами волны спиновой плотности, то большинство этих членов мы можем отбросить, ибо они не ответственны за возникновение антиферромагнитного фазового перехода. Поэтому мы сразу можем отбросить члены, описывающие взаимодействие как электронных компонент друг с другом, так и дырочных компонент друг с другом.

Из эксперимента известно [110], что магнитный порядок в пниктидах имеет полосчатую, страйповую, структуру, такую, что магнитный момент осциллирует вдоль одной кристаллической оси, оставаясь неизменным вдоль другой оси. В общем случае носители заряда в каждой дырочной зоне взаимодействуют с таковыми в каждой электронной зоне. Однако для того чтобы воспроизвести страйповую магнитную структуру, достаточно связать одну дырочную зону с одной электронной [87]. Например, осцилляции магнитного момента вдоль оси x возникают при взаимодействии квазичастиц в дырочной зоне 1 с квазичастицами в электронной зоне 1, или квазичастиц в дырочной зоне 3 с квазичастицами в электронной зоне 2 (см. сплошные и пунктирные стрелки на рис. 16). В обоих случаях векторы нестинга будут слабо отличаться друг от друга и будут примерно (точно, в случае соизмеримой АФМ фазы) равны Q₀ = (π/а, 0). Мы будем считать для простоты, что только одна электронная и одна дырочная зоны формируют АФМ-порядок. Положим, что это зоны $\varepsilon _{1}^{h}$ и $\varepsilon _{1}^{e},$ и взаимодействие между ними является существенным для формирования магнитного порядка. Остальными членами в операторе взаимодействия можно пренебречь. Как мы покажем ниже, даже такая простая модель пниктидов позволяет правильно описать экспериментальные данные по соизмеримой и несоизмеримой АФМ-фазе, а также фазовое расслоение.

Исходя из этих соображений, для нас теперь будет удобней разбить полный гамильтониан модели на магнитную часть H_m и немагнитную часть (“резервуар”) H_r. В результате будем иметь H = H_m + H_r:

В этих уравнениях N ‒ число атомов Fe в одном слое, V₁ > 0 ‒ константа взаимодействия между зонами $\varepsilon _{{1{\mathbf{k}}}}^{e}$ и $\varepsilon _{{1{\mathbf{k}}}}^{h}$ (мы рассматриваем предел сильно экранированного кулоновского взаимодействия, когда V₁ не зависит от импульса). Ниже мы будем называть эти зоны магнитными. Зоны $\varepsilon _{{2{\mathbf{k}}}}^{h}$, $\varepsilon _{{3{\mathbf{k}}}}^{h}$ и $\varepsilon _{{2{\mathbf{k}}}}^{e}$ мы будем называть немагнитными, поскольку в рассматриваемой модели они не дают вклада в формирование магнитного порядка.

Модель (20) является обобщением модели Райса, которую рассматривали в предыдущем разделе. Единственное существенное отличие данной модели от гамильтониана Райса (14) заключается в том, что Ферми поверхность одной из магнитных зон является эллиптической, что делает невозможным идеальный нестинг при любом допировании.

3.2.2. Несоизмеримая АФМ-фаза

Мы будем исследовать гамильтониан (20) в приближении среднего поля, действуя так же, как и в предыдущем разделе. Условием применимости приближения является неравенство Δ/ε_F$ \ll $ 1. АФМ-параметр порядка имеет вид:

вектор нестинга Q равен Q = Q₀ + q. Когда q = 0, АФМ-фаза является соизмеримой. Если q мало, но отлично от нуля, мы имеем несоизмеримую АФМ-фазу, при которой вектор антиферромагнетизма медленно поворачивается в пространстве.

Отметим, что различные компоненты Ферми поверхности имеют, вообще говоря, различный орбитальный состав (суперпозиции p-электронов As и d-электронов Fe) [139, 142]. Более выгодным является спаривание тех частей поверхности Ферми, орбитальный состав которых является схожим. В нашем подходе это обстоятельство может быть эффективно учтено, если сделать константу связи зависящей от импульса. Такое обобщение привело бы к ярко выраженной зависимости параметра порядка от импульса, что могло бы повлиять на температуру магнитного перехода, а также на структуру несоизмеримой фазы. Однако надежный расчет такой импульсной зависимости V₁ является сложной задачей, далеко выходящей за рамки настоящего рассмотрения. Более того, до тех пор, пока вариации V₁ не слишком большие, они не смогут качественно повлиять на фазовое расслоение ‒ основной предмет нашего исследования. Поэтому мы будем считать здесь V₁ константой.

Вектор намагниченности, соответствующий АФМ-параметру порядка Δ, лежит в плоскости xy. В случае соизмеримой фазы, в реальном пространстве наблюдается страйповая структура. Именно направление векторов намагниченности атомов железа в узлах решетки остается неизменным на линии, перпендикулярной вектору нестинга Q₀. Однако при движении вдоль Q₀ направление намагниченности меняется на противоположное при переходе от одного соседнего атому к другому. Для несоизмеримой фазы такая страйповая структура медленно вращается в плоскости xy: полярный угол φ(R), описывающий направление намагниченности на узле R, равен (qR), см. рис. 18.

Дальнейшее рассмотрение проводится в приближении среднего поля в соответствии с той же процедурой, которую использовали выше для модели Райса. В частности, посредством минимизации термодинамического потенциала Ω находятся выражения для параметра порядка Δ и вектора нестинга Q при фиксированном уровне допирования x. Так же, как и выше, можно ввести параметры x₀ и r: x₀ определяет характерный уровень допирования, разрушающий антиферромагнитный порядок, параметр r есть отношение плотностей состояний электронов в немагнитных и магнитных зонах.

Проведенный анализ выявил, что уравнения самосогласования имеют решения только при параметре эллиптичности α, меньшем некоторого критического значения α₀.

Кривые Δ(x) и q(x), вычисленные при r = 1 и двух различных значениях α, показаны на рис. 19. При |x| < $x_{{\text{1}}}^{*},$ где критическое допирование $x_{{\text{1}}}^{*}$ зависит от параметров модели, весь дополнительный заряд, появляющийся при допировании, уходит в немагнитные зоны. В результате параметр порядка не зависит от x, Δ(x) = Δ₀, q(x) = 0. В таком режиме система находится в соизмеримой АФМ-фазе. Когда |x| = $x_{{\text{1}}}^{*},$ химпотенциал касается дна (верха, если x < 0) верхней (нижней) магнитной зоны. При дальнейшем допировании, электроны (дырки) появляются в зоне $E_{{\mathbf{k}}}^{{\left( 2 \right)}}$ $\left( {E_{{\mathbf{k}}}^{{(1)}}} \right).$ Антиферромагнитный параметр порядка становится несоизмеримым [118, 122], q ≠ 0. Переход в несоизмеримую фазу может быть как первого, так и второго рода, в зависимости от параметров α и r.

Электронное допирование (x > 0) во многих отношениях схоже с дырочным (x < 0) благодаря электрон‒дырочной симметрии. При этом функции Δ(x) и q(x) не зависят от знака α. Однако направление вектора q(x) зависит как от знака α, так и от типа допирования. Когда α > 0, вектор q(x) параллелен оси x при электронном допировании и оси y в случае дырочного допирования. В случае α < 0 ситуация прямо противоположная (см. рис. 18).

3.2.3. Особенности фазового расслоения в пниктидах

Как и для модели Райса, мы проводим исследование устойчивости однородного состояния путем анализа зависимости свободной энергии системы от допирования. При этом соответствующие кривые в целом аналогичны изображенным на рис. 14 и демонстрируют возможность фазового расслоения в определенной области параметров модели.

Область допирования, в которой существует фазовое расслоение, максимальна при α = 0. В этом случае рассматриваемая модель аналогична двумерной модели Райса [82], трехмерный аналог которой рассматривали выше. Область существования фазового расслоения непрерывно сужается с ростом α и полностью исчезает при некотором критическом значении α.

Полученные результаты проиллюстрированы на фазовой диаграмме модели в плоскости (x, $\bar {\alpha }$) (рис. 20). Эта диаграмма рассчитана при r = 1. Она остается качественно такой же при любых r ≠ 0.

Отметим здесь неожиданное поведение границы раздела антиферромагнитной и парамагнитной (ПМ) фаз. А именно, линия раздела между несоизмеримой АФМ-фазой и ПМ-фазой (переход второго рода, сплошная кривая на рис. 20) тянется слева направо, тогда как все остальные границы раздела ведут себя противоположным образом. Иными словами, область допирования, в которой существует антиферромагнетизм, увеличивается с ростом параметра эллиптичности α. Чтобы понять эту особенность, нужно иметь в виду, что качество нестинга контролируется не только параметром α, но также и параметром μ (или x). Параметр α определяет форму электронного кармана, в то время как μ (или допирование) определяет относительный размер дырочных и электронных карманов. Таким образом, при большем допировании относительные размеры электронных и дырочных карманов сильно разнятся, но в то же время они могут лучше совмещаться при большей эллиптичности электронной компоненты поверхности Ферми.

3.2.4. Обсуждение результатов раздела о пниктидах

Итак, основным результатом, полученным в этом разделе, является предсказание электронного фазового расслоения в пниктидах железа в определенной области допирования. Неоднородное состояние является смесью соизмеримой и несоизмеримой АФМ-фаз с различными концентрациями электронов. Фазовое расслоение в железосодержащих сверхпроводниках экспериментально наблюдали во множестве работ [101‒104, 106]. Например, неоднородное состояние, являющееся смесью соизмеримых антиферромагнитных и немагнитных (сверхпроводящих при низких температурах) доменов с характерными размерами ~65 нм наблюдали в соединениях Ba_{1 –x}K_xFe₂As₂ (дырочное допирование) в работе [101]. Наше рассмотрение показывает, что второй фазой должная быть несоизмеримая АФМ-фаза, а не парамагнитная фаза. Однако предложенный механизм фазового расслоения в целом может соответствовать наблюдениям, описанным в работе [101]. Как мы упоминали выше, свободные энергии несоизмеримой АФМ и парамагнитной фаз близки друг к другу. Несоизмеримая АФМ-фаза может быть разрушена по различным причинам, которые не учитываются в рассматриваемой модели, например, из-за наличия беспорядка. В этом случае фазовое расслоение будет возникать между соизмеримой АФМ и парамагнитной фазами.

Мы не исследовали здесь механизмы, определяющие геометрию неоднородностей и их характерные размеры. Этот вопрос будет рассмотрен в следующем разделе. Отметим только, что электронные концентрации в расслоенных фазах различны. Следовательно, неоднородности должны быть заряжены, и необходимо учитывать дальнодействующее кулоновское отталкивание. Характерные размеры неоднородностей могут определяться конкуренцией между кулоновской энергией и поверхностной энергией раздела фаз. В простейшем случае структура неоднородностей соответствует каплям одной фазы, помещенным в матрицу другой фазы. Однако, в зависимости от свойств системы, возможны и другие геометрии, такие как чередующиеся слои различных фаз, страйповые структуры, и т.д. [145‒148]. Наличие беспорядка также влияет на структуру неоднородного состояния.

Как это следует из фазовой диаграммы, представленной на рис. 20, чем меньше параметр эллиптичности электронных карманов α, тем шире область фазового расслоения. Щель Δ₀ увеличивается с ростом константы взаимодействия V₁. Следовательно, чем сильнее взаимодействие дырочных и электронных компонент поверхности Ферми, тем шире область фазового расслоения, поскольку $\bar {\alpha }~$ ∼ α/Δ₀.

Несоизмеримая АФМ-фаза с вектором q, перпендикулярным Q₀, была экспериментально обнаружена в соединениях Ba(Fe_{1 –x}Co_x)₂As₂ (электронное допирование) в работах [149‒151]. Измеренное значение |q| было порядка 0.02‒0.03 (в единицах 1/a) при концентрациях 0.056 < x < < 0.06. Такие значения x и |q|, а также направление вектора q (соответствующее α < 0 в нашей модели) хорошо описываются рассматриваемой здесь теорией.

Ближний несоизмеримый АФМ-порядок был описан в работе [152], исследующей электронно-допированные соединения BaFe_{2 –x}Ni_xAs₂. В целом надо быть осторожными при интерпретации этого эксперимента в рамках нашей модели, поскольку в работе [152] наблюдали короткодействующие антиферромагнитные корреляции, тогда как мы имеем дело с дальним порядком. Отметим, однако, что измеренный вектор q был перпендикулярен Q₀, что соответствует отрицательным α. Спиновые флуктуации со сдвоенным пиком на значениях импульса Q = Q₀ ± q были экспериментально измерены в работах [153, 154] при исследовании дырочно-допированных соединений Ba_{1 –x}K_xFe₂As₂ в широкой области допирования. В этих измерениях вектор q оказался параллелен Q₀, что, опять-таки, соответствует α < 0 в нашей модели.

Отметим, что в общем случае все электронные и все дырочные компоненты поверхности Ферми взаимодействуют друг с другом. Каждая i-ая пара таких взаимодействующих карманов характеризуется своим вектором нестинга Q_i, константой взаимодействия V_i и параметром “денестинга” α_i. Однако i-ое взаимодействие дает вклад в формирование АФМ порядка, только если V_i превосходит некоторое критическое значение. Все остальные карманы не дают вклада в “магнитное” взаимодействие и формируют резервуар. Вполне вероятно, что среди различных пниктидов железа существуют системы с такими резервуарами. Однако существование резервуара не является необходимым условием для формирования несоизмеримой АФМ-фазы и фазового расслоения.

Мы ограничились рассмотрением только одного типа взаимодействия, но показали, что даже такой упрощенный сценарий способен описать экспериментально наблюдаемый тип АФМ-порядка, как соизмеримого, так и несоизмеримого типа. “Включение” дополнительных взаимодействий может быть рассмотрено в будущем, если несоизмеримая АФМ-фаза с другим типом симметрии будет обнаружена в эксперименте. Отметим, однако, что полученные здесь результаты качественно останутся неизменными.

Итак, мы продемонстрировали, что достаточно простая модель пниктидов (упрощенная форма Ферми поверхности, не учитываются орбитальные степени свободы и т.д.) оказывается способной описать существование фазового расслоения в этих соединениях в режиме слабого взаимодействия, т.е. в отсутствие сильных электронных корреляций. Это является важным выводом для интерпретации экспериментальных данных о неоднородных состояниях в пниктидах железа: доказывает, что чисто электронные модели с умеренной константой взаимодействия оказываются способными объяснить явление фазового расслоения в этих соединениях.

4.1. Геометрия неоднородностей

В этом разделе рассмотрим, как меняются правила Максвелла для определения равновесных концентраций расслоенных фаз при учете дальнодействующего кулоновского отталкивания между неоднородностями. Будем следовать здесь работам [146, 147] и учитывать результаты расчетов поверхностной энергии раздела фаз в каждом конкретном случае [32, 40, 145, 157].

Предположим, что нам известна свободная энергия системы как функция числа частиц N и объема V. В термодинамическом пределе мы можем написать F = Vf(n), где n = N/V ‒ концентрация электронов, f ‒ свободная энергия единицы объема. В неоднородном состоянии система состоит из фазы 1 с концентрацией n₁ и объемом V₁, и фазы 2 с концентрацией n₂ и занимающей объем V₂ = V ‒ V₁. Пусть объемная доля фазы 2 равна p = V₂/V. Тогда концентрации n₁, n₂ и n связаны между собой соотношением (1 ‒ p)n₁ + pn₂ = n. Свободная энергия фазово-расслоенного состояния, приходящаяся на единицу объема, равна

где e_int ‒ плотность энергии, которая определяется взаимодействием фаз 1 и 2 друг с другом. Ее можно представить в виде суммы e_int = e_c + e_s, где e_c ‒ кулоновская энергия взаимодействия фаз, e_s ‒ поверхностная энергия. Последнюю можно представить в виде e_s = σS/V, где S ‒ общая площадь раздела фаз, σ ‒ поверхностное натяжение. Рассмотрим сначала кулоновский вклад в e_int.

4.1.1. Кулоновская энергия неоднородного состояния в приближении Вигнера‒Зейтца

Кулоновская энергия существенно зависит от геометрии неоднородностей в фазово-расслоенном состоянии. Во многих случаях в системе имеются конечного размера домены одной из фаз, находящиеся в окружении другой фазы. Пусть для определенности это будут домены фазы 2. В изотропном случае естественно моделировать такие домены в виде сфер, упорядоченно расположенных в матрице из фазы 1. Число таких сфер N_s и их радиус R связаны с полным объемом фазы 2 соотношением 4πR³/3 = V₂/N_s. Следуя работам [146, 147], мы рассчитываем кулоновскую энергию системы в приближении Вигнера‒Зейтца [158].

В этом приближении плотность кулоновской энергии неоднородной системы равна плотности энергии сферической ячейки Вигнера‒Зейтца. Последняя состоит из двух вложенных одна в другую сфер, с центрами в начале координат. Внутренняя сфера соответствует фазе 2 и имеет радиус R. Пространство, ограниченное внутренней и внешней сферами, заполнено фазой 1. Радиус внешней сферы (ячейки Вигнера‒Зейтца) выбирается так, чтобы ее объем равнялся объему всей системы, поделенному на N_s: 4πR_WS³/3 = V/N_s. Нетрудно видеть, что радиусы R и R_WS связаны между собой соотношением R = p^1/3R_WS.

Плотность заряда в фазе 2 равна р₂ = ‒e(n₂ ‒ n) = = ‒e(1 ‒ p)(n₂ ‒ n₁), где мы учли заряд, создаваемый положительно заряженными ионами, который мы считаем равномерно распределенным по всему образцу. Аналогично, для плотности заряда в фазе 1 имеем р₁ = ‒e(n₁ ‒ n) = ep(n₂ ‒ n₁). Нетрудно убедиться в том, что полный заряд в ячейке Вигнера‒Зейтца, как и должно быть, равен нулю. Заряд, помещенный в рассматриваемую неоднородную систему, будет экранироваться. При этом будем считать, что системе в целом можно приписать некоторую диэлектрическую проницаемость ϵ, которую будем считать пространственно однородной [146, 147] и одинаковой как в фазе 1, так и в фазе 2. Кроме того, будем считать, что заряд в фазах 1 и 2 распределен равномерно. Последнее предположение оправданно, если характерный размер неоднородностей не сильно превышает характерную длину экранировки заряда. Можно показать, в частности, что для манганитов величина R составляет 1‒3 периода решетки. При этом длина экранировки есть величина того же порядка, так что предположение об однородном распределении заряда внутри неоднородностей является оправданным.

В случае, когда заряд внутри фаз 1 и 2 распределен равномерно, нетрудно рассчитать создаваемое им поле E внутри ячейки Вигнера−Зейтца, решая уравнения Пуассона. Интегрируя ϵE²/8π по объему ячейки, получаем в результате выражение для плотности кулоновской энергии

Плотность поверхностной энергии равна e_s = = 3pσ/R. Характерный размер неоднородностей R определяется минимизацией полной энергии взаимодействия фаз e_tot = e_C + e_s. Это дает:

где черта над R и e_tot означает, что соответствующая величина соответствует минимуму энергии, а функция u(p) равна

Аналогично можно рассчитать энергию взаимодействия фаз и для других возможных геометрий фазово-расслоенного состояния. Рассмотрим здесь еще две возможности: домены фазы 2 неограниченные в одном и в двух направлениях. В первом случае домены моделируются цилиндрами радиуса R, упорядоченно расположенными в матрице из фазы 1. Ячейка Вигнера−Зейтца в этом случае представляет собой два центрированных цилиндра с радиусами R и R_WS = R/p^1/2. Во втором случае мы имеем чередующиеся плоские слои с толщинами 2R (фаза 2) и 2R_WS = 2R/p (фаза 1). В обоих случаях плотность энергии взаимодействия фаз можно представить в виде (24), но с различным видом функции u(p). Для цилиндрических доменов и слоев имеем, соответственно:

При этом оптимальный радиус цилиндра и оптимальная полуширина слоя фазы 2 равны

Формула (24) дает нам выражения для плотности энергии взаимодействия фаз как функцию концентраций n₁ и n₂. При этом мы предполагаем, что поверхностное натяжение σ как функция n₁ и n₂ нам известна. Соответствующие вычисления можно найти в [157]. Отметим здесь, что функция σ(n₁, n₂) довольно слабо зависит от своих аргументов. Тогда сами концентрации электронов в расслоенных фазах находятся путем минимизации полной свободной энергии.

Во всех вышеприведенных формулах предполагается, что фаза 2 разбивается на ограниченные области, помещенные в фазу 1. В случае когда объемная доля фазы 2, p > 0.5, естественно предположить обратное: фаза 1 находится в конечного размера доменах, помещенных в фазу 2. В этом случае в формулах p → 1 − p. Изменение геометрии неоднородностей в зависимости от p проиллюстрировано на рис. 21.

4.2. Фазовое расслоение, фрустрированное дальнодействующим кулоновским отталкиванием

Исследуем теперь вопрос о том, как дальнодействующее кулоновское отталкивание влияет на область существования фазового расслоения. Продемонстрируем это для наглядности на основе модели манганитов, которую мы рассматривали в разделе 2. Как указывали там, эффективная модель манганитов допускает несколько типов магнитного упорядочения в качестве основного состояния. В частности, для ферромагнитного и антиферромагнитного состояний, энергия основного состояния выражается через число носителей заряда (на один узел решетки) локализованных, n_l, и зонных, n_b, связанных с уровнем (дырочного) допирования x соотношением n_l + n_b = = 1 ‒ x. При заданном x концентрации n_l и n_b находили самосогласованно.

В неоднородном состоянии у нас имеется антиферромагнитная фаза с уровнем допирования x_a и ферромагнитная фаза с уровнем допирования x_f > x_a. Пусть объемная доля ферромагнитной фазы есть p. Тогда мы имеем px_f + (1 ‒ p)x_a = x. Относительно геометрии неоднородностей мы будем предполагать, что при p < 0.5, имеются ферромагнитные капли в антиферромагнитной матрице, а при p > 0.5, наоборот, антиферромагнитные капли в ферромагнитной матрице. При малых x такая геометрия соответствует эксперименту [11, 12]. Свободная энергия неоднородного состояния, приходящаяся на один узел решетки, равна

где ${{\bar {e}}_{{{\text{tot}}}}}$ дается формулой (24), в которой надо заменить n₂ ‒ n₁ → (x_f ‒ x_a)/d³ (d ‒ постоянная решетки).

Оптимальные концентрации x_f и x_a определяются минимизацией свободной энергии. При этом надо знать поведение поверхностной энергии σ как функции x_f и x_a. Согласно [157], основной вклад в поверхностную энергию обусловлен размерным квантованием электронных состояний в неоднородностях, т.е. он связан с наличием зонных электронов. В антиферромагнитной фазе они либо отсутствуют полностью, n_b = 0, либо их концентрация чрезвычайно мала, n_b $ \ll $ 1. Поэтому мы можем считать, что σ = σ(x_f).

Минимизируя свободную энергию при заданном уровне допирования x, мы получаем зависимость F_PS(х), которую мы сравниваем с энергией однородного состояния F_hom(х) = min[F_fm(х), F_af(х)]. Фазовое расслоение существует в области допирования, где F_PS(х) < F_hom(х). Зависимости F_PS(х), рассчитанные при некоторых значениях характерной кулоновской энергии u = e²/($\epsilon $d), показаны на рис. 22. Энергия однородной фазы также показана на этом рисунке. Мы видим, что фазовое расслоение существует в области допирования х₁ < х < х₂, где х₁ и х₂ определяются как точки, в которых F_PS(х₁) = F_af(х₁) и F_PS(х₂) = F_fm(х₂). При заданном х концентрации х_а и x_f близки к значениям х₁ и х₂, соответственно, но, вообще говоря, не совпадают с ними.

Область фазового расслоения уменьшается при увеличении кулоновского отталкивания u = e²/($\epsilon $d), При u выше некоторого критического значения u_c фазовое расслоение невыгодно ни при каком допировании. Для рассмотренной модели манганитов мы имеем u_c ≈ 2.5w₀. Из простых оценок следует, что если диэлектрическая проницаемость $\epsilon $ не слишком велика, то можно ожидать, что u ~ w₀. В этом случае характерный размер неоднородностей, рассчитанный по формуле (23), оказывается порядка R/d ~ 1.5‒3.

Итак, на примере эффективной модели манганитов, мы показали, что дальнодействующее кулоновское отталкивание сужает область электронного фазового расслоения. Модель учитывает наличие локализованных и зонных электронов, а также взаимодействие последних с локальными спинами S = 3/2 посредством механизма двойного обмена. Аналогичные расчеты можно провести для кобальтитов, поскольку предложенная в разделе 2.2 модель этих соединений во многих отношениях сходна с моделью Фаликова‒Кимбалла, использовавшейся для манганитов. Подобный подход применим и для систем с неидеальным нестингом, таких как пниктиды.