1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 124, № 11, 2023

Физика металлов и металловедение, 2023, T. 124, № 11, стр. 1122-1128

Магнитокалорический эффект сплавов Mn2YSn (Y = Sc, Ti, V)

В. В. Соколовский a, М. А. Загребин a, *, В. Д. Бучельников a

a Челябинский государственный университет
454001 Челябинск, ул. Братьев Кашириных, 129, Россия

* E-mail: miczag@mail.ru

Поступила в редакцию 05.07.2023
После доработки 07.08.2023
Принята к публикации 07.08.2023

Полный текст (PDF)

Аннотация

Рассмотрены структурные, магнитные и термодинамические свойства сплавов Mn2YSn (Y = Sc, Ti, V) в зависимости от приложенного давления, используя теорию функционала плотности и метод Монте-Карло. Показано, что для каждого соединения существуют два магнитных состояния с низким и высоким магнитным моментом при меньшем и большем объеме элементарной ячейки, разделенные энергетическим барьером. Величина барьера зависит от приложенного внешнего давления. Две фазы становятся практически равными по энергии при критических давлениях 3.4, –2.9 и –3.25 ГПа для Mn2ScSn, Mn2TiSn и Mn2VSn соответственно. Смоделированы температурные зависимости намагниченности и магнитокалорических характеристик для исследуемых фаз при различных давлениях. Учет давления приводит к пониманию механизма повышения магнитокалорического эффекта в фазе с высоким магнитным моментом. Наибольший эффект (∆Sмаг ≈ 0.158 Дж/моль К и ∆Tад ≈ 1.1 К) предсказан для Mn2TiSn при давлении –2.9 ГПа и изменении магнитного поля от 0 до 2 Тл.

Ключевые слова: сплавы Гейслера на основе Mn, фазовые переходы, ab initio расчеты, моделирование методом Монте-Карло

ВВЕДЕНИЕ

Полуметаллические ферро- и ферримагнитные сплавы представляют собой класс материалов, в которых одна из спиновых подзон имеет металлический, а другая – полупроводниковый характер. В связи с этим электроны одной спиновой подзоны участвуют в электронно-транспортных свойствах и проявляют 100% спиновую поляризацию на уровне Ферми. Это говорит о возможности создания такого электронного устройства, в котором не только заряд, но и спин электрона могут играть важную роль в передаче сигнала и, таким образом, он свободен от омической диссипации [1–5].

В последние годы сплавы Гейслера на основе Mn2 особенно привлекательны из-за их полуметаллических свойств и потенциальных применений в области спинтроники и спиновой калоритроники. Их можно использовать в качестве спиновых инжекторов для магнитной оперативной памяти, а также устройств переноса спинового магнитного момента [6–12].

Интерес к сплавам Гейслера на основе Mn2 обусловлен наличием двух подрешеток Mn, ориентированных ферримагнитно, что приводит к малой полной намагниченности и высокой температуре Кюри. В результате может быть достигнуто уменьшение потока рассеяния и компенсация энергии.

За последние несколько десятилетий было проведено большое количество теоретических и экспериментальных исследований металлических сплавов Mn2YZ, содержащих 3d, 4d и 5d-переходные металлы Y, с целью найти и предсказать новые функциональные полуметаллические соединения. Некоторыми репрезентативными примерами сплавов Гейслера на основе Mn2 являются Mn2VAl и Mn2VSi [6], Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) [8], Mn2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb) [13], Mn2CrZ (Z = Al, Ga, Si, Ge, Sb) [7], Mn2TiZ (Z = Al, As, Bi, Ga, Ge, Sb, Si, Sn) [9], Mn2ZrZ (Z = = Ga, Ge, Si) [14, 15], Mn2RuZ (Z = Sn, Si) [16], Mn2RhZ (Z = Al, Ga, In, Si, Ge, Sn, Sb) [17]. Большинство этих исследований посвящено изучению электронной структуры, магнитных, механических и полуметаллических свойств сплавов Гейслера с регулярной L21 и инверсной XA-структурами в рамках ab initio расчетов и обобщенного градиентного приближения (General gradient approximation – GGA) для обменно-корреляционного функционала. В то же время многие из них теоретически предсказаны как полуметаллы с псевдощелью в одном из двух спиновых каналов, что делает их пригодными для технических приложений. Данная работа посвящена теоретическим исследованиям структурных, магнитных и магнитокалорических свойств сплавов Гейслера Mn2YSn (Y = Sc, Ti и V) в рамках первопринципных расчетов и моделирования методом Монте-Карло (МК).

ДЕТАЛИ ВЫЧИСЛЕНИЙ

В настоящей работе исследования при 0 K выполнены на основе теории функционала плотности и метода присоединенных проекционных плоских волн (Projector augmented wave – PAW), реализованного в программном пакете VASP (Vienna Ab initio Simulation Package) [18, 19]. В качестве приближения для обменно-корреляционного функционала выбрано приближение GGA в параметризации Пердью–Бурке–Эрнцерхофа [20]. В PAW потенциалах рассмотрены следующие конфигурации валентных электронов: 3s23p64s23d5 для Mn, 3s23p64s23d1 для Sc, 3s23p64s23d2 для Ti, 3s23p64s23d3 для V и 3d104s24p2 для Sn. Энергия обрезания базиса плоских волн составляла 450 эВ. Для интегрирования по зоне Бриллюэна использована сетка, построенная по методу Монхорста–Пака размером 11 × 11 × 11. Геометрическая оптимизация кубической 16-ти атомной ячейки типа L21 выполнена с использованием релаксации положений атомов при постоянном объеме и форме ячейки с критериями сходимости для энергий и сил, равными 10−6 эВ и 10−2 эВ/Å соответственно.

Моделирование температурных зависимостей намагниченности и магнитокалорических характеристик при конечных температурах реализовано с помощью классического метода МК и гамильтониана Гейзенберга при учете параметров обменного взаимодействия, полученных ранее из первопринципных расчетов [21]:

(1)
$H = - \sum\limits_{i \ne j} {{{J}_{{ij}}}} {{{\mathbf{S}}}_{i}}{{{\mathbf{S}}}_{j}} - g{{{{\mu }}}_{0}}{{{{\mu }}}_{{\text{Б}}}}{{H}_{z}}\sum\limits_{i = 0} {S_{i}^{z}.} $
Здесь i, j – индексы i-го и j-го узлов, Si – единичный спиновый вектор, указывающий направление локального магнитного момента на узле i, Jij – параметр обменного взаимодействия между магнитными атомами, расположенными на узлах i и j. Обменные взаимодействия Jij между атомами Mn−Mn и Mn−Y учтены в шести и трех координационных сферах соответственно. μ0 – магнитная проницаемость вакуума, μБ – магнетон Бора, Hz – z компонента магнитного поля.

Моделирование МК выполнено на кубической решетке размером 7 × 7 × 7 элементарных ячеек, состоящих из 16 атомов, и учетом периодических граничных условий. Таким образом, модельная решетка состояла из 5488 атомов (2744 атома Mn, 1372 атома Y и Sn). В качестве алгоритма выбран алгоритм Метрополиса. За единицу времени был выбран один шаг МК, заключающийся в N изменении спиновых переменных Si, где N соответствует количеству магнитных атомов в решетке. Полное количество шагов МК, приходящихся на одно значение температуры, составляло 105 с учетом 104 шагов для установления теплового равновесия в системе. Для каждой температуры термодинамические величины усредняли по 225 конфигурациям на каждые 400 шагов МК.

Выражение для вычисления магнитного параметра порядка:

(2)
${{m}^{{{\alpha }}}}{\text{ }} = {\text{ }}\frac{{\text{1}}}{{{{N}^{{{\alpha }}}}}}\sum\limits_i {\sqrt {{{{\left( {S_{i}^{{{{\alpha }},x}}} \right)}}^{2}} + {{{\left( {S_{i}^{{{{\alpha }},y}}} \right)}}^{2}} + {{{\left( {S_{i}^{{{{\alpha }},z}}} \right)}}^{2}}} } ,$
где α соответствует атомам Mn и Y = Ti, V, Sc. Nα – полное число α атомов, суммирование идет по всем соответствующим узлам подрешеток атомов α.

Полная намагниченность сплавов Mn2YSn определяется суммой:

(3)
$M{\text{ }} = 2{{{{\mu }}}_{{{\text{Mn}}}}}{{m}^{{{\text{Mn}}}}} + {{{{\mu }}}_{Y}}{{m}^{Y}}.$

Температурные зависимости магнитного вклада теплоемкости Cмаг и энтропии Sмаг в нулевом и магнитном поле вычислены, исходя из поведения усредненных значений магнитной части внутренней энергии εмаг, следующим образом:

(4)
${{С}_{{{\text{маг}}}}}\left( {T,{{{{\mu }}}_{0}}H} \right) = \frac{1}{{{{k}_{{\text{B}}}}{{T}^{2}}}}\left[ {\left\langle {{{\varepsilon }_{{{\text{маг}}}}}^{2}} \right\rangle - {{{\left\langle {\varepsilon _{{{\text{маг}}}}^{{}}} \right\rangle }}^{2}}} \right],$
(5)
${{S}_{{{\text{маг}}}}}\left( {T,{{{{\mu }}}_{0}}H} \right) = \int\limits_{{{T}_{1}}}^{{{T}_{2}}} {\frac{{{{C}_{{{\text{маг}}}}}\left( {T,{{{{\mu }}}_{0}}H} \right)}}{T}dT.} $

Магнитокалорические характеристики ΔSмаг и ΔTад можно выразить в форме:

(6)
$\Delta {{S}_{{{\text{маг}}}}}\left( T \right) = {{S}_{{{\text{маг}}}}}\left( {T,{{{{\mu }}}_{0}}H} \right) - {{S}_{{{\text{маг}}}}}\left( {T,0} \right),$
(7)
$\Delta {{T}_{{{\text{ад}}}}}\left( T \right) = - \frac{T}{{C\left( {T,{{{{\mu }}}_{0}}H} \right)}}\Delta {{S}_{{{\text{маг}}}}}\left( T \right).$
Здесь C – полная теплоемкость с учетом магнитного и решеточного вклада. Решеточный вклад учтен в рамках модели Дебая.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В недавней нашей работе [21] представлены теоретические исследования структурных, магнитных и электронных свойств основного состояния сплавов Гейслера Mn2YSn в зависимости от приложенного внешнего давления. Мы показали, что для каждого соединения возможны два магнитных состояния с малым целым и высоким дробным магнитным моментом μполн при меньшем и большем объеме кристаллической структуры L21. Состояние с низкой намагниченностью (low magnetic state – LMS) характеризуется полуметаллическими свойствами, тогда как состояние с высоким магнитным моментом (high magnetic state – HMS) – металлическими свойствами.

Рассмотрим сначала результаты проведения геометрической оптимизации кубической кристаллической структуры сплавов Mn2YSn, выполненной при нормальном давлении. На рис. 1а приведены профили энергетических кривых в зависимости от параметра решетки, демонстрирующие наличие глобального и локального минимумов энергии. Для соединений Mn2VSn и Mn2TiSn глобальный минимум энергии, соответствующий фазе LMS, приходится на меньший равновесный параметр решетки (a0 ≈ 6.016 и 6.128 Å соответственно) по сравнению с локальным минимумом, соответствующим фазе HMS, при большем a0 (6.216 и 6.252 Å соответственно). Отметим, что в данном случае локальный минимум ввиду его неявности получен расчетом кривой энергии методом фиксированного момента [22, 23]. Напротив, для соединения Mn2ScSn глобальный минимум энергии наблюдается при большем значении a0 = 6.47 Å (фаза HMS) по сравнению с локальным минимумом при a0 = 6.306 Å (фаза LMS).

Рис. 1.

Изменение энтальпии ΔH как функции параметра решетки при атмосферном давлении (а) и как функции приложенного давления (б) для соединений Mn2YSn. ΔH построено относительно минимума энергии при меньшем объеме. На рис. (а) энтальпия (H) соответствует внутренней энергии (E) при P = 0 ГПа. На рис. (б) отрицательное и положительное давление соответствует всестороннему растяжению и сжатию кристаллической решетки соответственно; числа над символами указывают на значения полного магнитного момента; в скобках на линии ΔH = 0 указаны магнитные моменты метастабильного состояния.

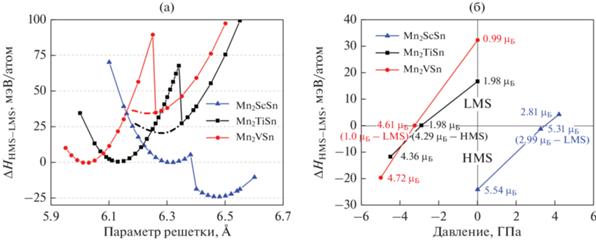
Наши расчеты показывают, что воздействие внешнего давления на кристалл приводит к изменению разницы энергий между фазами HMS и LMS и позволяет достичь вырожденного по энергии состояния. На рис. 1б представлена фазовая диаграмма в координатах “Изменение энтальпии–Давление”. В данном случае ΔHHMS−LMS < 0 указывает на энергетически выгодную металлическую фазу HMS с высоким дробным значением μполн, и, напротив, ΔHHMS−LMS > 0 говорит об устойчивости полуметаллической фазы LMS с низким и практически целым значением μполн, согласующимся с правилом Слейтера–Полинга. Данное правило связывает магнитный момент и число валентных электронов Nve в полуметаллических соединениях Гейслера как μполн = Nve − 24. Приложение внешнего давления приводит к тому, что две магнитные фазы с низким и высоким магнитным моментом становятся практически равными по энергии при критических давлениях 3.4, −2.9 и −3.25 ГПа для Mn2ScSn, Mn2TiSn и Mn2VSn соответственно.

Это означает, что фазы LMS и HMS будут равны по энергии и могут переходить друг в друга при трехосном сжатии кристаллической решетки Mn2ScSn на ≈6.5% и ее расширении для Mn2TiSn и Mn2VSn на ≈7.8 и ≈13% соответственно. Отметим, что отрицательное давление или химическое расширение объема может быть реализовано экспериментально путем добавления атомов небольшого размера, таких как H, B, C и N в междоузельные позиции [24, 25].

На рис. 2 приведены результаты моделирования МК температурных зависимостей намагниченности M и магнитной части теплоемкости Cмагн для LMS- и HMS-фаз на примере сплава Mn2TiSn. Учет давления реализован посредством использования параметров обменного взаимодействия в ур. (1), рассчитанных для конечных значений всестороннего давления [21].

Рис. 2.

Температурная зависимость намагниченности (а, б) и магнитного вклада в теплоемкость (в, г) для LMS- и HMS-фаз сплава Mn2TiSn при давлении 0 и −4.5 ГПа в магнитных полях 0 и 2 Тл.

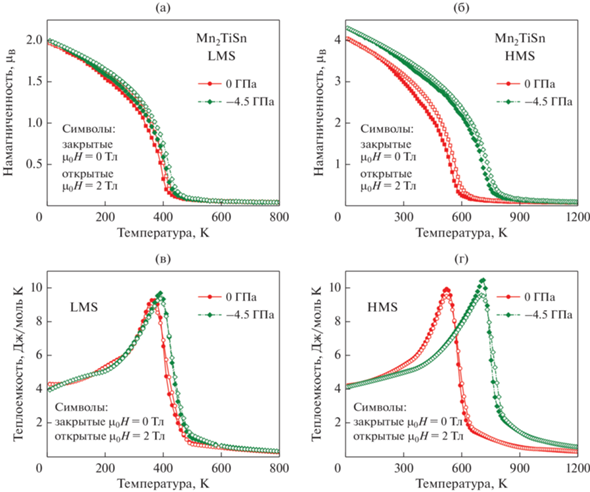
Как видно из рис. 2а, 2б, кривые M(T) демонстрируют ферро-парамагнитное поведение с температурой Кюри TC = 390 и 539 К для фаз LMS и HMS при нормальном давлении и в отсутствие магнитного поля. Меньшая температура TC и намагниченность насыщения для фазы LMS обусловлена слабыми обменными взаимодействиями между парами атомов Mn−Mn и Mn−Ti. Плавное поведение намагниченности и пиков теплоемкости в окрестностях TC указывает на магнитный фазовый переход второго рода.

Приложение внешнего давления приводит к сдвигу TC в область более высоких значений. Однако сдвиг TC для LMS-фазы существенно меньше (dTC/dP ≈ 3.77 K/ГПа) по сравнению с фазой HMS (dTC/dP ≈ 40.8 K/ГПа). Это свидетельствует о том, что ферромагнитная металлическая HMS-фаза может существовать в более широком температурном интервале при внешнем давлении, чем полуметаллическая LMS-фаза. Высокая чувствительность температуры Кюри к внешней нагрузке для HMS фазы обусловлена сильным изменением параметров обменного взаимодействия между ближайшими атомами Mn–Mn (11 и 17 мэВ для 0 и −4.5 ГПа соответственно) [21]. Приложение магнитного поля приводит к незначительному смещению кривые намагниченности и пиков теплоемкости, делая их большими и меньшими по величине, соответственно, в сторону больших температур.

В табл. 1 приведены значения температуры Кюри для всех исследуемых соединений Mn2YSn в фазах LMS и HMS. В целом для всех соединений фаза HMS характеризуется более высокой TC по сравнению с фазой LMS. Большие значения TC объясняются большим μполн и большими параметрами магнитного обмена Jij. Из таблицы видно, TC увеличивается с ростом атомного номера Y (Sc → Ti → V) от ≈300 до 620 K. Характерной особенностью сплавов Mn2TiSn и Mn2VSn в LMS-фазе является слабая зависимость dTC/dP при всестороннем расширении кристаллической решетки по сравнению с фазой HMS. Напротив, сжатие решетки в соединении Mn2ScSn приводит к росту TC в обеих фазах.

Таблица 1.  

Температуры Кюри TC (в K) для состояний LMS- и HMS-сплавов Mn2YSn (Y = Sc, Ti и V) при атмосферном и приложенном давлении P

P, ГПа TC
LMS HMS
Mn2ScSn
0 62 298
3.5 256 388
4.2 243 270
Mn2TiSn
0 390 539
–2.9 388 723
–4.5 407 723
Mn2VSn
0 226 628
–3.25 226 843
–5.0 258 911

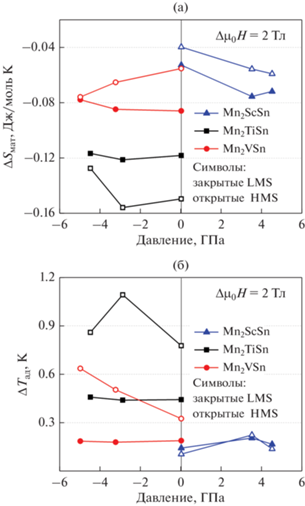
На рис. 3 представлены результаты моделирования магнитокалорических характеристик ΔSмаг и ΔTад для Mn2TiSn в LMS- и HMS-фазах при давлении 0, −2.9 и −4.5 ГПа и изменении магнитного поля от 0 до 2 Тл. Из рисунка видно, что для данного сплава наблюдается прямой МКЭ (ΔSмаг < 0, ΔTад > 0) вследствие магнитного перехода между ФиМ и ПМ-фазой в кубической аустенитной структуре. Такой переход является переходом второго рода и, в отличие от мартенситного перехода, не сопровождается гистерезисом.

Рис. 3.

Температурная зависимость ΔSмаг (а) и ΔTад (б) для LMS- и HMS-фаз сплава Mn2TiSn при давлении 0, –2.9 и –4.5 ГПа и изменении магнитного поля от 0 до 2 Тл.

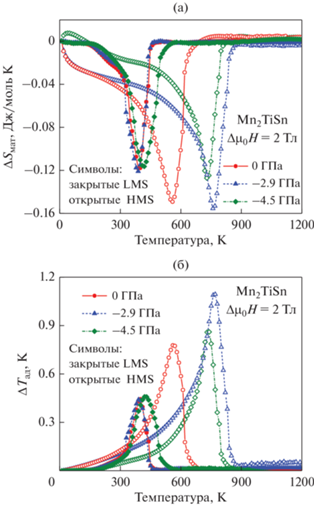
Наши расчеты показывают, что величины МКЭ (ΔSмаг и ΔTад) для полуметаллической фазы LMS практически не зависят от величины приложенного давления и составляют ≈−0.12 Дж/моль K и 0.45 K. В случае металлической фазы HMS МКЭ примерно в 1.8 раз больше, чем для LMS-фазы вследствие большей величины μполн. Приложение внешнего давления приводит к смещению пиков МКЭ в область высоких температур, а также к росту МКЭ. Наибольший МКЭ (ΔTад ≈ 1.1 K) предсказан при давлении −2.9 ГПа, т.е. при всестороннем расширении решетки на 7.8%. Попутно отметим, что МКЭ для Mn2TiSn в HMS-фазе является также наибольшим среди всех исследуемых соединений в обоих магнитных состояниях. Данный результат следует из зависимостей МКЭ от приложенного давления, представленных на рис. 4. Напротив, соединение Mn2ScSn обладает наименьшим и схожим МКЭ в обеих фазах, который слабо зависит от приложенного давления. Это может быть связано с малой величиной и слабым изменением параметров обменного взаимодействия между ближайшими атомами в зависимости от степени сжатия кристаллической решетки. Наши расчеты показывают, что величина ΔTад как в полуметаллической, так и металлической фазе для сплавов Mn2YSn варьируется в интервале от ≈0.18 до 1.1 K в зависимости от знака приложенного давления (сжатие или расширение).

Рис. 4.

Зависимость ΔSмаг (а) и ΔTад (б) от приложенного давления для соединений Mn2YSn при изменении магнитного поля от 0 до 2 Тл.

ЗАКЛЮЧЕНИЕ

В представленной работе проведены теоретические исследования структурных, магнитных и магнитокалорических свойств сплавов Гейслера Mn2YSn (Y = Sc, Ti и V) в рамках первопринципных расчетов и моделирования методом МК.

Первопринципные расчеты предсказывают наличие двух магнитных фаз с разной величиной магнитного момента и электронной структурой при разных объемах кристаллической решетки исследуемых соединений. Фаза с меньшим объемом решетки проявляет полуметаллические свойства (фаза LMS), тогда фаза при большем объеме решетки − металлические свойства (фаза HMS).

Показано, что в основном состоянии две фазы разделены энергетическим барьером порядка ≈25 мэВ/атом для каждого из соединений. Однако приложение внешнего давления позволяет существенно снизить величину барьера и сделать две фазы вырожденными по энергии. Это говорит о возможности механизма переключения полуметаллических и металлических свойств вследствие перестройки электронной структуры фаз LMS и HMS на уровне Ферми при определенном критическом давлении. Критическое давление составляет 3.4, –2.9 и –3.25 ГПа для Mn2ScSn, Mn2TiSn и Mn2VSn, что, в свою очередь, соответствует трехосному сжатию кристаллической решетки Mn2ScSn на ≈6.5% и ее расширению на ≈7.8 и ≈13% для Mn2TiSn и Mn2VSn соответственно. Мы полагаем, что всестороннее расширение кристаллической структуры (приложение отрицательного давления) возможно реализовать путем внедрения примесей небольшого размера, таких как H, B, C и N.

В рамках моделирования методом МК и модели Гейзенберга получены температурные зависимости намагниченности и магнитокалорических характеристик для двух фаз (LMS и HMS) при различных давлениях. Показано, что для всех соединений температура Кюри TC и МКЭ для LMS-фазы в несколько раз меньше по сравнению с HMS-фазой. Приложение внешнего давления оказывает слабое влияние на TC и МКЭ для LMS-фазы и увеличивает эти характеристики для HMS-фазы. Наибольший МКЭ (ΔSмаг ≈ 0.158 Дж/моль K и ΔTад ≈ 1.1 K) предсказан соединения Mn2TiSn в HMS-фазе при давлении –2.9 ГПа и изменении магнитного поля от 0 до 2 Тл.

Мы предполагаем, что барический механизм переключения между полуметаллическим и металлическим состоянием с различной намагниченностью, температурой Кюри и МКЭ может представлять интерес для дальнейших фундаментальных и экспериментальных исследований и стать материальной платформой для разработки устройств спинтроники и калоритроники.

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-12-20032, https://rscf.ru/project/22-12-20032/, ФГБОУВО Челябинский государственный университет, Челябинская обл.).

Нет конфликта интересов.

Список литературы

  1. Fert A. Nobel Lecture: Origin, development, and future of spintronics // Rev. Mod. Phys. 2008. V. 80. P. 1517.

  2. Bhatti S., Sbiaa R., Hirohata A., Ohno H., Fukami S., Piramanayagam S.N. Spintronics based random access memory: A review // Mater. Today. 2017. V. 20. P. 530–548.

  3. Zhang H., Kang W., Cao K., Zhao W. Spintronic processing unit in spin transfer torque magnetic random access memory // IEEE Trans. Electron Devices. 2019. V. 66. P. 2017–2022.

  4. Puebla J., Kim J., Kondou K., Otani Y. Spintronic devices for energy-efficient data storage and energy harvesting // Commun. Mater. 2020. V. 1. P. 1–9.

  5. Hirohata A., Yamada K., Nakatani Y., Prejbeanu I.-L., Diény B., Pirro P., Hillebrands B. Review on spintronics: Principles and device applications // J. Magn. Magn. Mater. 2020. V. 509. P. 166711.

  6. Galanakis I., Özdoğan K., Şaşıoğlu E., Aktaş B. Doping of Mn2VAl and Mn2VSi Heusler alloys as a route to half-metallic antiferromagnetism // Phys. Rev. B. 2007. V. 75. P. 092407.

  7. Luo H., Zhu Z., Liu G., Xu S., Wu G., Liu H., Qu J., Li Y. Prediction of half-metallic properties for the Heusler alloys Mn2CrZ (Z = Al, Ga, Si, Ge, Sb): A first-principles study // J. Magn. Magn. Mater. 2008. V. 320. P. 421–428.

  8. Luo H.Z., Zhang H.W., Zhu Z.Y., Ma L., Xu S.F., Wu G.H., Zhu X.X., Jiang C.B., Xu H.B. Half-metallic properties for the Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) Heusler alloys: a first-principles study // J. Appl. Phys. 2008. V. 103. P. 083 908.

  9. Zenasni H., Faraoun H.I., Esling C. First-principle prediction of half-metallic ferrimagnetism in Mn-based full-Heusler alloys with highly ordered structure // J. Magn. Magn. Mater. 2013. V. 333. P. 162–168.

  10. Nayak A.K., Nicklas M., Chadov S., Khuntia P., Shekhar C., Kalache A., Baenitz M., Skourski Y., Guduru V.K., Puri A., Zeitler U., Coey J.M.D., Felser C. Design of compensated ferrimagnetic Heusler alloys for giant tunable exchange bias // Nat. Mater. 2015. V. 14. P. 679–684.

  11. Felser C., Wollmann L., Chadov S., Fecher G.H., Parkin S.S.P. Basics and prospective of magnetic Heusler compounds // APL Mater. 2015. V. 3. P. 041518.

  12. Marchenkov V.V., Irkhin V.Yu., Semiannikova A.A. Unusual kinetic properties of usual Heusler alloys // J. Supercond. Nov. Magn. 2022. V. 35. P. 2153–2168.

  13. Liu Z., Yu S., Yang H., Wu G., Liu Y. Phase separation and magnetic properties of Co–Ni–Al ferromagnetic shape memory alloys // Intermetallics. 2008. V. 16. P. 447–452.

  14. Abbas Emami S.A., Amirabadizadeh A., Nourbakhsh Z., Baizaee S.M., Alavi Sadr S.M. Study of the Structural, Electronic, Magnetic, and Optical Properties of Mn2ZrGa Full-Heusler Alloy: First-Principles Calculations // J. Supercond. Nov. Magn. 2018. V. 31. P. 127–134.

  15. Abada A., Amara K., Hiadsi S., Amrani B. First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe // J. Magn. Magn. Mater. 2015. V. 388. P. 59–67.

  16. Jiang D., Ye Y., Liu H., Gou Q., Wu D., Wen Y., Liu L. First-principles calculations of electronic, acoustic and anharmonic properties of Mn2RuZ (Z = Si and Ge) Heusler compounds // J. Magn. Magn. Mater. 2018. V. 458. P. 268–276.

  17. Ren Z., Liu Y., Li S., Zhang X., Liu H. Site preference and electronic structure of Mn2RhZ (Z = Al, Ga, In, Si, Ge, Sn, Sb): a theoretical study // Mater. Sci.-Pol. 2016. V. 34. P. 251–259.

  18. Kresse G., Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set // Phys. Rev. B. 1996. V. 54. P. 11169–11186.

  19. Kresse G., Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method // Phys. Rev. B. 1999. V. 59. P. 1758.

  20. Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple // Phys. Rev. Lett. 1996. V. 77. P. 3865–3868.

  21. Sokolovskiy V., Zagrebin M., Baigutlin D., Buchelnikov V. Ab initio prediction of coexistence of two magnetic states in Mn2YSn (Y = Sc, Ti, and V) Heusler alloys under applied pressure // Comput. Mater. Sci. 2023. V. 228. P. 112 365.

  22. Schwarz K., Mohn P. Itinerant metamagnetism in YCo2 // J. Phys. F. 1984. V. 14. P. L129.

  23. Moruzzi V.L., Marcus P.M., Schwarz K., Mohn P. Ferromagnetic phases of bcc and fcc Fe, Co, and Ni // Phys. Rev. B. 1986. V. 34. P. 1784.

  24. Kitagawa J., Sakaguchi K., Hara T., Hirano F., Shirakawa N., Tsubota M. Interstitial atom engineering in magnetic materials // Metals. 2020. V. 10. P. 1644.

  25. Tian L.Y., Eriksson O., Vitos L. Pressure effect on the order–disorder transformation in L10−FeNi // Sci. Rep. 2020. V. 10. P. 14766.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал