1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 124, № 7, 2023

Физика металлов и металловедение, 2023, T. 124, № 7, стр. 622-634

Изменение радиуса первой координационной сферы в аморфных сплавах при деформировании

Г. Е. Абросимова a, *, В. В. Астанин b, Н. А. Волков a, Д. В. Гундеров c, Е. Ю. Постнова a, А. С. Аронин a

a Институт физики твердого тела им. Ю.А. Осипьяна РАН
142432 Черноголовка, ул. академика Осипьяна, 2, Россия

b Уфимский университет науки и технологий
450000 Уфа, ул. Заки Валиди, 32, Россия

c Институт физики молекул и кристаллов Уфимского федерального исследовательского центра РАН
450075 Уфа, проспект Октября, 151, Россия

* E-mail: gea@issp.ac.ru

Поступила в редакцию 30.03.2023
После доработки 15.05.2023
Принята к публикации 15.05.2023

Полный текст (PDF)

Аннотация

Методами рентгенографии и сканирующей электронной микроскопии исследованы изменения структуры аморфных сплавов при деформировании методами кручения под высоким давлением, многократной прокатки и барической обработки. Показано, что при всех способах деформирования в аморфных сплавах формируются полосы сдвига, представляющие собой области более низкой плотности по сравнению с окружающей недеформированной аморфной матрицей. Полосы сдвига являются зонами повышенного свободного объема, образование полос приводит к появлению ступенек на поверхности образцов. Количество полос сдвига и морфология поверхности деформированных аморфных сплавов определяются видом деформации и физическими свойствами материала.

Ключевые слова: аморфные сплавы, деформация, полосы сдвига, свободный объем

ВВЕДЕНИЕ

Аморфные металлические сплавы (металлические стекла) обладают необычной для сплавов структурой и рядом великолепных физических свойств [1–4]. Некоторые из этих свойств могут быть повышены путем создания композитной аморфно-нанокристаллической структуры [5–7], состоящей из нанокристаллов, распределенных в аморфной матрице. Параметры такой структуры (размер нанокристаллов, их расположение, доля кристаллической составляющей) существенно зависят от условий формирования нанокристаллов. Основными способами создания аморфно-нанокристаллической структуры является термообработка или деформация (и их сочетание) исходной аморфной фазы. Формирующаяся структура зависит от способа воздействия на аморфную фазу. Так, например, если нанокристаллы сформировались в деформированном образце, их размер оказывается меньше, а доля больше по сравнению с нанокристаллами, образующимися в процессе термообработки [8, 9]. Для выяснения причин такого различия необходимы исследования изменений структуры аморфной фазы, происходящих в процессе деформации.

Деформация аморфной фазы является сильно локализованной. Пластическая деформация при низких температурах и умеренных нагрузках осуществляется в узких зонах – полосах сдвига (зонах локализации пластической деформации), практически не затрагивая основную часть аморфной фазы. В этих полосах структура, естественно, изменяется. Согласно литературным данным [10] полосы сдвига ориентированы под углом 55° ± 5° к направлению деформации. Важной особенностью пластической деформации аморфных сплавов является увеличение количества свободного объема в полосах сдвига, т.е. увеличение среднего расстояния между атомами [11–13]. Толщина полос сдвига составляет 5–20 нм [14–16]. Деформация часто приводит к ветвлению полос сдвига [17, 18]. Исследования показали, что структура полос сдвига и их окрестностей является сложной и изменения структуры аморфной фазы могут распространяться на большие расстояния от полосы сдвига; вплоть до 200 нм. Степень изменений структуры в полосе сдвига зависит от условий деформирования. На поверхности пластическая деформация проявляется в виде ступенек, представляющих собой места выхода полосы сдвига на поверхность. Количественные характеристики таких ступенек после деформации методами кручения под высоким давлением и многократной прокатки исследовались в ряде работ [5, 19–22]. Структура в полосах сдвига отличается от структуры недеформированной части аморфной фазы. Образование нанокристаллов начинается в полосах сдвига и их окрестностях. Было установлено, что в полосах сдвига коэффициент диффузии при комнатной температуре на 5–6 порядков выше, чем в окружающей аморфной матрице [23]. Обычно при обсуждении ускоренной диффузии в полосах сдвига рассматривают либо локальное сильное, но непродолжительное (~30 пс) повышение температуры в области локализации деформации [24–28], либо уменьшение плотности материала в полосе сдвига [17, 29–31]. В принципе, в каждом конкретном случае превалирующим может быть любой из указанных факторов. В настоящее время ускорение диффузии в этих областях связывают с увеличением доли свободного объема [17, 29, 31]. Фактически это означает, что в результате деформации формируется своеобразное наностекло: структура состоит из аморфных областей, различающихся по плотности [32]: аморфной фазы в полосах сдвига (областях с повышенной долей свободного объема) и неизменившейся аморфной матрицы в основной части образца. Следует отметить, что понятие “свободный объем” широко используется и для описания ряда свойств аморфных материалов [33–37]. Концепция свободного объема была выдвинута в работах [33, 38, 39], в которых свободный объем рассматривается как увеличенное пространство между атомами в неупорядоченной структуре. В настоящее время для определения наличия свободного объема используется метод рентгенографии [37].

Было показано [15, 40], что свойства аморфной фазы (например, микротвердость) меняются на заметном удалении от полосы деформации [5]. Очевидно, что полосы сдвига играют важную роль в процессах формирования нанокристаллов. Несмотря на большое число работ, посвященных исследованию полос сдвига в аморфной фазе [5, 12, 17–19, 41–45], четких представлений о структуре этих областей, их зависимости от условий деформирования, связи с формированием нанокристаллов в настоящее время нет. Имеется группа работ, авторы которых предпринимали попытки исследовать изменения структуры аморфной фазы при деформации. Одним из первых таких исследований является изучение структуры прокатанных лент сплава Pd80Si20 (1975 г. [46]); после прокатки на рентгенограммах аморфных образцов наблюдалось смещение первого пика структурного фактора в сторону меньших углов. В то время специальных исследований изменения структуры при деформации не проводилось, тем не менее, полученный результат, несомненно, указывает на изменение радиуса первой координационной сферы, как минимум, в некоторых областях образца. Исследования эволюции структуры аморфных сплавов на основе циркония непосредственно в процессе деформации [47–49] позволили обнаружить изменения структуры, происходящие при упругой деформации. В указанных работах наблюдали различие в положении первого диффузного максимума при рентгеноструктурных исследованиях вдоль и поперек направления растяжения. Исследования проводились in-situ в процессе деформирования в области упругих напряжений; полученные результаты однозначно свидетельствовали об эллиптическом характере первой координационной “сферы”. Таким образом, авторы показали, что в отсутствии пластической деформации растяжение приводит к изменению расстояния между атомами в аморфной структуре, причем эти изменения зависят от ориентации приложенного напряжения. При пластической деформации аморфного сплава Pd40Ni40P20 [50] наблюдалось формирование анизотропной аморфной структуры.

Имеющиеся в литературе данные указывают на важность изменений структуры и, в частности, плотности аморфной фазы в полосах деформации. Поскольку именно эти области и их окрестности являются местами зарождения нанокристаллов, а параметры наноструктуры, формирующейся при деформации, определяют свойства материала, исследования изменений структуры при деформации оказываются принципиально важными. Работ, посвященных таким исследованиям сравнительно немного. В частности, было показано, что увеличение свободного объема в полосах сдвига способствует ускорению процесса кристаллизации [43, 51, 52]. Одним из способов оценки изменений структуры при деформации может быть анализ кривых рассеяния рентгеновских лучей деформированными образцами в сочетании с исследованием их поверхности (ступенек, отражающих места выхода полос сдвига на поверхность образца). Сдвиг основного диффузного максимума свидетельствует об изменении расстояния между атомами в аморфной фазе, а присутствие ступенек на поверхности деформированного образца, их количество, расположение и другие характеристики могут позволить оценить долю деформированного материала. Целью настоящей работы было исследование изменений структуры в металлических стеклах разного химического состава (на базе металлов с разными упругими характеристиками).

МЕТОДИКА ЭКСПЕРИМЕНТА

Исследования проводили на широкой группе сплавов систем Al–Y, Al–TM–RE (TM = Ni, Co; RE = Y, Gd, La), Fe–Si–B, Co–Si–B–Fe–Nb, Pd–Ni–P, Zr–Cu–Al–Fe. Аморфные сплавы в виде лент были получены методом скоростной закалки расплава на быстровращающийся диск. Слитки сплавов номинального состава готовили дуговой плавкой в очищенном аргоне, после чего расплавляли и подвергали закалке по одновалковой схеме. Скорость охлаждения при закалке составляла около 106 град/с. Аморфные ленты имели толщину 30–50 мкм и ширину 10–15 мм. Массивные аморфные сплавы (bulk metallic glasses, BMG) Zr55Cu30Al15Ni5 и Zr62,5Cu22,5Al10Fe5 были получены расплавлением во взвешенном состоянии и закалкой в медную изложницу. Они представляли собой стержни диаметром 8 мм. Химический состав всех образцов контролировали методом локального рентгеноспектрального анализа на приставке к сканирующему электронному микроскопу ZeissSupra 50VP.

Для деформирования образцов использовали три разных метода: кручение под высоким давлением, многократную прокатку и барическую обработку. Для деформирования методом кручения под высоким давлением образцы массивных сплавов разрезали на диски толщиной 0.5 мм и полировали перед началом деформации. Аморфные сплавы, полученные в виде лент, разрезали на отрезки соответствующего размера. Деформирование методом кручения под давлением осуществляли по стандартной методике [53]. Для деформации образец помещали между двух наковален и подвергали воздействию сжимающей силы в несколько ГПа и деформации сдвигом за счет вращения нижней наковальни. Разная степень деформации обеспечивалась разным количеством оборотов. Деформирование проводили при давлении 4–6 ГПа при комнатной температуре. Деформирование прокаткой проводили на четырехвалковом стане VEB Schwermaschinenbau с числом проходов 50–150.

Истинную деформацию при кручении под высоким давлением и прокатке рассчитывали по формуле (1) [54–56]:

(1)
$e = \ln {{\left( {1 + {{{\left( {\frac{{\varphi r}}{h}} \right)}}^{2}}} \right)}^{{0.5}}} + {\text{\;}}\ln \left( {\frac{{{{h}_{0}}}}{h}} \right),~$
где r – радиус образца, φ – угол поворота пуансона, h0 – начальная толщина образца, h – толщина образца после деформации.

При барической обработке образцы последовательно закладывали в ячейку высокого давления; средой, передающей давление, служил порошок гексагонального нитрида бора или прокладки из тефлона. При этих условиях воздействия были близкими к гидростатическим. Барическую обработку проводили при давлениях Р = 5–8 ГПа в течение 30–60 мин. После выдержки под давлением давление стравливали, а ячейку разбирали.

Выбор разных способов деформирования обусловлен влиянием способа нагружения на изменение структуры аморфных сплавов. При деформировании методом кручения под давлением величина деформации меняется по радиусу образца: центральная часть является практически недеформированной, а наибольшая истинная деформация оказывается на периферии. При прокатке величина деформации меняется по глубине образца, наиболее деформированными являются приповерхностные области. При барической обработке условия деформации являются квазигидростатическими. Следует отметить, что надежного способа определения величины деформации при барической обработке в настоящее время нет.

Структуру сплавов исследовали методами рентгенографии на рентгеновском дифрактометре SIMENSD-500 с использованием CоKα- и CuKα-излучений, шаг при съемке составлял 0.05° или 0.02°. В ряде случаев проводили съемку с эталоном. При обработке спектров использовали специальные программы, позволяющие проводить сглаживание, коррекцию фона, разделение перекрывающихся максимумов и др. Морфологию поверхности исходных и деформированных образцов исследовали на сканирующем электронном микроскопе. При исследовании поверхности основное внимание уделялось измерению высоты и ширины ступенек, образующихся при выходе полос сдвига на поверхность. Оценку доли свободного объема ΔV проводили по формуле:

(2)
$\Delta V = {\text{ }}(R_{{{\text{деф}}}}^{3}--R_{{{\text{исх}}}}^{3}){\text{/}}R_{{{\text{исх}}}}^{3} \times {\text{ }}100\% ,$
где Rдеф и Rисх – радиусы первой координационной сферы деформированного и исходного образцов соответственно.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Основным методом исследования структуры аморфных сплавов является рентгеноструктурный анализ. Интенсивность рассеяния рентгеновских лучей аморфной фазой определяется формулой:

(3)
$\begin{gathered} ~I\left( {\mathbf{S}} \right) = N{{F}^{2}}\left( {\mathbf{S}} \right) \times \\ \times \left\{ {1 + \int\limits_0^\infty {4\pi {{R}^{2}}[\rho (R) - {{\rho }_{0}}]\left( {\left( {\sin {\mathbf{S}}R} \right){\text{/}}{\mathbf{S}}R} \right)dR~} } \right\}, \\ \end{gathered} $
где N – полное число атомов в единице объема, F(S) – амплитуда рассеяния, ρ(R) – число атомов в единице объема, находящихся на расстоянии R от выбранного атома, ρ0 – среднее число атомов в единице объема, S – волновой вектор [57]. Последовательность максимумов функции I(S) определяется последовательностью максимумов функции sin(SR)/SR. Эта функция имеет максимумы при значениях SR, равных 7.73, 14.06, 20.46 и т.д. Легко определить, что радиус первой координационной сферы (кратчайшее расстояние между атомами):

(4)
${{R}_{1}} = 7.73{\text{/}}{{{\mathbf{S}}}_{1}} = 14.06{\text{/}}{{{\mathbf{S}}}_{2}} = 20.46{\text{/}}{{{\mathbf{S}}}_{3}} \ldots ~.~~~~$

Таким образом, радиус первой координационной сферы может быть определен по значению волнового вектора, соответствующему любому максимуму кривой интенсивности рассеяния. Значение R1 определяют, используя уравнение Эренфеста [57]:

(5)
$2{{R}_{1}}\sin {{\theta }} = 1.23{{\lambda ,}}$
где λ – длина волны используемого излучения, θ – дифракционный угол.

Поскольку первый максимум кривой является наиболее интенсивным, его положение, как правило, и используется для определения радиуса первой координационной сферы.

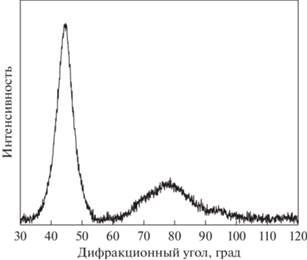
На рис. 1 показана рентгенограмма аморфного сплава Al90Y10 непосредственно после закалки. Такая картина является типичной: интенсивный первый диффузный максимум и последующие диффузные максимумы существенно меньшей интенсивности. В дальнейшем будут приведены части рентгенограмм, соответствующие области первого диффузного максимума. Радиус первой координационной сферы аморфного сплава Al90Y10, определенный по формуле (5), R1 = 2.906 Ǻ. После деформирования методом кручения под высоким давлением наблюдается небольшое смещение диффузного максимума в область меньших углов. После деформирования прокаткой радиус первой координационной сферы составляет R1 = = 2.914 Ǻ.

Рис. 1.

Рентгенограмма закаленного аморфного сплава Al90Y10.

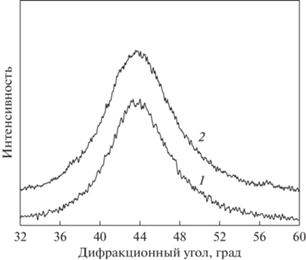
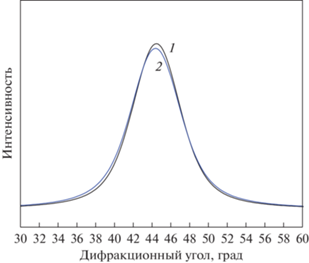
На рис. 2 показаны результаты аппроксимации диффузных максимумов исходного (1) и деформированного (2) образцов. Видно, что смещение пика мало, но результаты воспроизводимы при повторных съемках.

Рис. 2.

Результат аппроксимации первых диффузных максимумов на рентгенограммах исходного (1) и деформированного (2) образцов аморфного сплава Al90Y10.

На изображениях поверхности образцов (приведены ниже в разделе “Исследование морфологии поверхности деформированных образцов”) видны ступеньки, являющиеся местами выхода полос сдвига на поверхность. Такая морфология поверхности свидетельствует, что в результате деформирования в образце образовались полосы сдвига, и структура образца стала неоднородной. Как отмечалось выше, деформированный образец представляет собой наностекло, состоящее из аморфных областей с неизменившейся при деформации аморфной фазой и аморфных областей пониженной плотности (полос сдвига). Это означает, что определенный выше радиус первой координационной сферы является усредненным и составляет:

(6)
${{R}_{1}} = (а{{R}_{{1{\text{образца}}}}} + b{{R}_{{1{\text{полос сдвига}}}}})~{\kern 1pt} ,$
где а и b – объемные доли неизменившейся аморфной фазы и полос сдвига, соответственно. Поскольку объемная доля полос сдвига невелика, изменение среднего радиуса первой координационной сферы
(7)
${{R}_{1}} = \Delta {{R}_{{{\text{1деформ}}}}} - \Delta {{R}_{{1{\text{исходный}}~}}}$
должно быть небольшим, что и наблюдается экспериментально. Для приведенного выше образца Al90Y10 это изменение составляет ΔR1 = 0.008 Ǻ. Оценка изменения радиуса первой координационной сферы дает величину ~0.3%. Это соответствует увеличению свободного объема ΔV примерно на 0.9%, что согласуется с известными данными об изменении структуры аморфных сплавов при кручении под высоким давлением.

Насколько типично такое изменение при деформации? Для ответа на этот вопрос исследовали группу аморфных сплавов, полученных в виде тонких лент или стержней (массивные металлические стекла) и подвергнутых деформации разного типа: кручению под высоким давлением (КВД), многократной прокатке и барической обработке.

Кручение под высоким давлением

Исследование изменений структуры при деформации методом КВД проводили на массивных аморфных образцах и образцах, полученных в виде лент. Массивные сплавы на основе циркония составов Zr55Cu30Al10Ni5 и Zr62.5Cu22.5Al10Fe5 деформировали при комнатной температуре. Радиус первой координационной сферы аморфного сплава Zr55Cu30Al10Ni5R1 = 2.989Ǻ. После деформации (давление 6 ГПа, 1 оборот) наблюдается небольшое смещение диффузного максимума в область меньших углов. На рис. 3 приведены рентгенограммы сплава Zr55Cu30Al10Ni5 до (1) и после (2) деформации (область первого диффузного максимума). Кривые для наглядности смещены вдоль оси ординат. Рассчитанное по кривой рассеяния значение радиуса первой координационной сферы деформированного образца составляет R1 = = 3.014 Ǻ. Увеличение радиуса первой координационной сферы составляет ΔR1 = 0.025 Ǻ.

Рис. 3.

 Рентгенограммы  массивного  сплава Zr55Cu30Al10Ni5 до (1) и после (2) деформации методом КВД.

Для исходного аморфного сплава Zr62,5Cu22,5Al10Fe5R1 = 2.998 Ǻ, значение радиуса R1 после деформации (6 ГПа, 5 оборотов) увеличивается, R1 = 3.003 Ǻ, и это увеличение составляет ΔR1 = 0.005 Ǻ.

Исследования соответствующих изменений на лентах проводили для аморфных сплавов системы Fe–B–Si (разного состава), Zr62,5Cu22,5Al10Fe5, а также приведенного выше сплава Al90Y10. В результате исследований были получены следующие данные:

исходный аморфный сплав Zr62,5Cu22,5Al10Fe5: R1 = 3.003 Ǻ, деформированный при комнатной температуре (6 ГПа, 30 оборотов) R1 = 3.028 Ǻ, и ΔR1 = 0.025 Ǻ. При деформировании лент того же сплава при 150°C, ΔR1 = 0.014 Ǻ [13].

На рис. 4 приведены рентгенограммы сплава Fe76B11Si13 до (1) и после (2) деформации (область первого диффузного максимума). Рассчитанные по рентгенограммам значения радиуса первой координационной сферы составляют R1 = 2.488 Ǻ для исходного аморфного сплава и R1 = 2.492 Ǻ для деформированного образца (4 ГПа, 1 оборот) Таким образом, рассчитанное по смещению диффузного максимума значение составляет ΔR1 = = 0.004 Ǻ.

Рис. 4.

Рентгенограммы сплава Fe76B11Si13 до (1) и после (2) деформации методом КВД.

Увеличение истинной деформации (путем увеличения количества оборотов наковальни) приводит к большему изменению радиуса первой координационной сферы. При увеличении количества оборотов наковальни от 1 до 5 изменение радиуса первой координационной сферы в сплаве Fe77Si13B9 увеличивается до ΔR1 = 0.007 Ǻ. После такой обработки образцы оставались аморфными. Подобные результаты наблюдались и при прокатке для сплавов на основе циркония [58].

Таким образом, деформирование методом КВД способствует увеличению кратчайшего расстояния между атомами и в массивных аморфных сплавах, и в аморфных лентах.

Многократная прокатка

Аналогичные изменения наблюдались и при деформировании методом многократной прокатки. Изменение радиуса первой координационной сферы, естественно, зависят от степени деформации, а также от упругих констант материала. Так, например, для сплава Fe77Si13B9, после деформации методом КВД ΔR1 = 0.007 Ǻ, после прокатки ΔR1 = 0.001 Ǻ. В многокомпонентном аморфном сплаве после прокатки Al85Ni6.1Co2Gd6Si0.9 ΔR1 = = 0.007 Ǻ.

Важно отметить, что в случае прокатки наблюдается неодинаковое изменение структуры по глубине образца. Так для образцов аморфного сплава Pd40Ni20P20 изменение радиуса первой координационной сферы в приповерхностной области составляло ΔR1 = 0.020 Ǻ и уменьшалось примерно вдвое в центральной по толщине части ленты. Наблюдаемое различие обусловлено неоднородностью распределения степени деформации по глубине образца. Как отмечалось выше, при прокатке наиболее деформированными оказываются приповерхностные области.

Определенные сложности вызывает исследование обсуждаемых изменений в аморфных сплавах систем Al–Ni–RE (RE = Y, La, Gd). Проблема исследования этих сплавов связана с тем, что при деформировании аморфной фазы в сплавах этой группы образование полос сдвига сопровождается химическим расслоением, приводящим к образованию аморфных областей, обогащенных/обедненных никелем и/или редкоземельным компонентом [23, 59–61]. Это, естественно, влияет на вид кривых рассеяния. Результаты, полученные для деформированных прокаткой сплавов (до появления заметного химического расслоения), составляют ΔR1= 0.010 Ǻ для сплава Al88Ni10Y2 и ΔR1 = 0.023 Ǻ для сплава Al87Ni8Y5. Поскольку химическое расслоение происходит и при термообработке, для сравнения были получены соответствующие данные для отожженного образца, содержащего 2 аморфные фазы: ΔR1 = ~0.55 Ǻ. Это изменение значительно больше изменений, наблюдаемых при деформировании. На рис. 5 приведена рентгенограмма аморфного сплава Al87Ni8La5 после отжига при 150°С [60]. На рентгенограмме кривая 1 соответствует экспериментальному спектру, кривые 3 и 4 – двум аморфным фазам разного химического состава, а кривая 2 является суммарной кривой (кривые 3 + 4).

Рис. 5.

Рентгенограмма аморфного сплава Al87Ni8La5 после отжига при 150°C в течение 15 ч (1 – экспериментальный спектр, 3 и 4 – две аморфные фазы, 2 – сумма кривых 3 + 4).

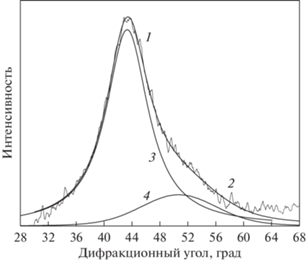
На рисунке хорошо видно, что помимо смещения пика (положение кривых 1 и 3) наблюдается искажение формы диффузного гало (появление плеча со стороны больших углов). Поскольку в сплавах систем Al-Ni-RE наиболее крупным атомом является атом редкоземельного металла (La в обсуждаемом сплаве, RLa = 1.877 Å), то в аморфной фазе, обогащенной этим компонентом, расстояния между атомами будут больше, чем в исходной аморфной фазе. Это означает, что левый субпик (кривая 3) соответствует аморфной фазе, обогащенной лантаном. Соответственно, правый субпик (кривая 4) соответствует аморфной фазе, обогащенной никелем (RNi = 1.246 Å). Важно отметить тот факт, что смещение диффузного максимума при химическом расслоении существенно больше смещения, наблюдаемого при деформации.

Барическая обработка

В качестве еще одного способа деформирования использовали барическую обработку в камере высокого давления. Как отмечалось выше, при этом условия воздействия были близкими к гидростатическим, однако не полностью. В качестве среды, передающей давление, использовали либо порошок BN, либо тефлоновые прокладки. Можно было ожидать, что использование порошка BN будет приводить к более гидростатическим условиям, однако заметной разницы в случае применения BN или тефлоновых прокладок мы не обнаружили. Изменение положения диффузного гало зависело от величины давления (Р), ниже приведены сравнительные данные по изменению радиуса первой координационной сферы в зависимости от приложенного давления:

$\begin{gathered} {\text{F}}{{{\text{e}}}_{{{\text{90}}}}}{{{\text{B}}}_{{\text{2}}}}{\text{S}}{{{\text{i}}}_{{\text{8}}}},\,\,\,\,Р = {\text{ }}5{\text{ и 8 ГПа}}{\kern 1pt} :{{R}_{{1\left( {Р = 5} \right)}}} = 2.486{\text{ }}{\AA}, \\ {{R}_{{1\left( {Р = 8} \right)}}} = 2.509{\text{ }}{\AA},\,\,\,\,{{R}_{{1\left( 8 \right)}}}--{{R}_{{1\left( 5 \right)}}} = 0.023{\text{ }}{\AA} \\ \end{gathered} $
(здесь и далее R1(Р) – радиус первой координационной сферы после барической обработки при давлении Р ГПа);

$\begin{gathered} {\text{C}}{{{\text{o}}}_{{{\text{70}}}}}{\text{S}}{{{\text{i}}}_{{{\text{12}}}}}{{{\text{B}}}_{{\text{9}}}}{\text{F}}{{{\text{e}}}_{{\text{7}}}}{\text{N}}{{{\text{b}}}_{{\text{2}}}},\,\,\,\,Р = 5,\,\,6.5{\text{ и }}7.5{\text{ ГПа}}{\kern 1pt} : \\ {{R}_{{1\left( {Р = 5} \right)}}} = 2.454\,\,{\AA},~\,\,\,\,{{R}_{{1\left( {Р = 6.5} \right)}}} = 2.460{\text{ }}{\AA}, \\ {{R}_{{1\left( {Р = 7.5} \right)}}} = 2.466{\text{ }}{\AA},{{R}_{{1\left( {7.5} \right)}}}--{{R}_{{1\left( {6.5} \right)}}} = 0.006{\text{ }}{\AA}, \\ {{R}_{{1\left( {7.5} \right)}}}--{{R}_{{1\left( 5 \right)}}} = 0.012{\text{ }}{\AA}; \\ \end{gathered} $
$\begin{gathered} {\text{C}}{{{\text{o}}}_{{{\text{67}}}}}{\text{S}}{{{\text{i}}}_{{{\text{12}}}}}{{{\text{B}}}_{{\text{9}}}}{\text{F}}{{{\text{e}}}_{{\text{7}}}}{\text{N}}{{{\text{b}}}_{{\text{5}}}},\,\,\,\,Р = {\text{5}}\,\,{\text{и}}\,\,{\text{6}}{\text{.5}}\,\,{\text{ГПа}}{\kern 1pt} : \\ {{R}_{{1(}}}{{_{Р}}_{{ = 5)}}} = 2.478{\text{ }}{\AA},\,\,\,\,{{R}_{{1(}}}{{_{Р}}_{{ = 6.5)}}} = 2.485{\text{ }}{\AA}, \\ {{R}_{{1(6.5)}}}--{{R}_{{1(5)}}} = 0.007{\text{ }}{\AA}; \\ \end{gathered} $
$\begin{gathered} {\text{A}}{{{\text{l}}}_{{{\text{88}}}}}{\text{N}}{{{\text{i}}}_{{\text{8}}}}{{{\text{Y}}}_{{\text{6}}}},\,\,\,\,Р = {\text{5}}\,\,{\text{и}}\,\,{\text{8}}\,\,{\text{ГПа}}{\kern 1pt} :{{R}_{{1(}}}_{{Р = 5)}} = 2.878{\text{ }}{\AA},~~ \\ {{R}_{{1(}}}{{_{Р}}_{{ = 8)}}} = 2.903{\text{ }}{\AA},\,\,\,\,{{R}_{{1(8)}}}--{{R}_{{1(5)}}} = 0.025{\text{ }}{\AA}. \\ \end{gathered} $

Следует также отметить, что при использовании всех способов деформирования, как правило, наблюдается небольшое уширение диффузного гало, что также отражает существование областей двух типов, с разным кратчайшим расстоянием между атомами: основной аморфной фазы и полос сдвига.

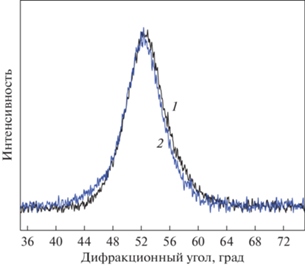
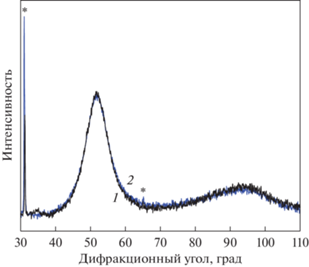
Величина смещения зависит от химического состава сплава и может быть незначительной. На рис. 6 показаны рентгенограммы сплава Co77Zr11Cr12 после барической обработки при 3 (кривая 1) и 5 (кривая 2) ГПа в BN (положение отражений от порошка BN показаны звездочками). Никакого изменения положения гало в зависимости от величины давления обнаружено не было.

Рис. 6.

Рентгенограммы аморфного сплава Co77Zr11Cr12 после барической обработки при 3 (кривая 1) и 5 ГПа (кривая 2).

В табл. 1 суммированы все наблюдаемые изменения радиуса первой координационной сферы для образцов, деформированных разными методами. В таблице приведены также рассчитанные по формуле (2) значения разницы объема до и после обработки материала (оценка изменения средней плотности или избыточного свободного объема). Полученные результаты хорошо согласуются с имеющимися в литературе данными о смещении диффузного гало на рентгенограммах за счет “закачки” свободного объема в процессе деформирования методами кручения под высоким давлением и прокатки [13, 58, 62].

Таблица 1.  

Изменение радиуса первой координационной сферы ΔR1 при деформации

Состав Тип образца Условия деформирования ΔR1, Ǻ ΔV = ($R_{{{\text{деф}}}}^{3}$ – $R_{{{\text{исх}}}}^{3}$)/$R_{{{\text{исх}}}}^{3}$ × 100%
КВД
Zr55Cu30Al10Ni5 BMG 6 ГПа, RT, N = 1 0.025 2.53
Zr62,5Cu22,5Al10Fe5 BMG 6 ГПа, RT, N = 5 0.005 0.50
Zr52.5Cu17.9Ni14.6Al10Ti5 BMG 6 ГПа, RT, N = 5 0.018 1.84 [13]
Zr52.5Cu17.9Ni14.6Al10Ti5 BMG 6 ГПа, RT, N = 30 0.026 4.54 [13]
Zr62,5Cu22,5Al10Fe5 Лента 6 ГПа,RT, N = 30 0.025 2.51
Fe76B11Si13 Лента 4 ГПа, RT, N = 1 0.004 0.48
Fe79B9Si12 Лента 4 ГПа, RT, N = 1 0.006 0.72
Fe77Si13B10 Лента 4 ГПа, RT, N = 5 0.007 0.84
Al90Y10 Лента 5 ГПа, RT, N = 0.5 0.008 0.83
Прокатка
Fe77Si13B10 Лента Прокатка 0.001 0.12
Al85Ni6.1Co2Gd6Si0.9 Лента Прокатка 0.007 0.72
Pd40Ni20P20, приповерхностная область Лента Прокатка 0.020 3.99
Pd40Ni20P20, в объеме образца Лента Прокатка 0.010 1.15
Al88Ni10Y2 Лента Прокатка 0.010 1.05
Al87Ni8Y5 Лента Прокатка 0.023 2.41
Al87Ni8La5, аморфный, расслоение Лента Отжиг 150°С 15 часов 0.550  
Барическая обработка
Fe76Si13B11 Лента Р = 5 и 8 ГПа R1(8) – R1(5) = 0.023 2.48
Co70Si12B9Fe7Nb2 Лента Р = 5, 6.5, 7.5 ГПа R1(7.5) – R1(6.5) = 0.006, 0.73
  R1(7.5) – R1(5) = 0.012 1.47
Co67Si12B9Fe7Nb5 Лента Р = 5 и 6.5 ГПа R1(6.5) – R1(5) = 0.007 0.85
Al88Ni8Y6 Лента Р = 5 и 8 ГПа R1(8) – R1(5) = 0.025 2.63
Co77Zr11Cr12 Лента Р = 3 и 5 ГПа ΔR1 = 0 0

* RT – комнатная температура, N – число оборотов.

Величина смещения диффузного гало, естественно, зависит от условий деформирования. В процессе деформирования происходит “закачка” свободного объема в область полос сдвига, величина которого зависит от степени деформации. Изменение структуры обусловлено не только способом и степенью деформации, но и продолжительностью процесса деформирования. При прокатке или кручении под давлением степень деформации больше, чем при барической обработке (давлении без кручения), однако при КВД процесс деформации продолжается 1–10 мин (стандартная скорость кручения составляет 1 оборот в минуту). При прокатке собственно деформирование продолжается также несколько минут. При использованной нами барической обработке процесс проводился в течение нескольких часов (около 2 ч подъем давления, 30–60 мин выдержка и около 2 ч стравливание давления).

Образование полос сдвига при разных способах деформации зависит также от упругих констант материала. В табл. 2 приведены значения модулей Юнга (Е) и сдвига (G) некоторых аморфных и кристаллических материалов.

Таблица 2.  

Значения модулей Юнга (Е) и сдвига (G) некоторых аморфных и кристаллических материалов

Материал Е, ГПа G, ГПа Ссылка
Al87Ni8Y5 36 – [63]
Al87Ni8Gd5 20 – [63]
Al87Ni4Fe4Gd5 18 – [63]
La–Al–Ni–Cu 43 – [64]
Ce70Al10Ni10Cu10 30.3 11.5 [65]
Fe78Si10B12 120 – [66]
Fe63Cr3Mo12P10C7B5 183 68.8 [67]
Co70Fe6B20 179 68 [68]
Co73Si15B12 90 – [68]
Zr50Cu40Al10 93 23.0 [69]
Zr52.5Cu17.9Ni14.6Al10Ti5 89 32.4 [69]
Pd79Cu6Si10P5 82 – [70]
Кристаллический Al 72 26.5 [71]
Кристаллическое Fe 205 80 [71]
Кристаллический Co 206 78.5 [71]

Изменение расстояния между атомами (радиуса первой координационной сферы) при нагреве, деформации и просто вылеживании зависит и от условий получения аморфного сплава. При скоростной закалке расплава структуры аморфной фазы (и доля закаленного объема) зависят и от состава сплава, и от температуры расплава перед закалкой (соответственно, плотности расплава), и от скорости охлаждения. Все эти параметры могут оказывать влияние на величину свободного объема в образцах непосредственно после получения. Важным является факт изменения величины свободного объема в аморфных сплавах при разных воздействиях и, в частности, при деформации разного типа.

Исследование морфологии поверхности деформированных образцов

Как упоминалось выше, при пластической деформации на поверхности образца появляются ступеньки, соответствующие выходу полос сдвига на поверхность. Было показано [22], что увеличение степени деформации приводит к росту шероховатости поверхности. Авторами [22] было обнаружено, что морфология поверхности может различаться очень сильно, отражая степень девитрификации аморфной фазы. Было также установлено, что высота ступенек в деформированных образцах зависит от изменения структуры сплава. Так, например, в аморфных сплавах на основе Со [21] в образцах с большой высотой ступенек наблюдалась частичная кристаллизация с образованием нанокристаллов, а сплавы с малой высотой ступенек остались аморфными. Данные работы [22] и других исследований морфологии поверхности аморфных сплавов [5, 19–21] указывают на необходимость систематического исследования поверхности деформированных металлических стекол. Полученные нами результаты свидетельствуют, что состояние поверхности коррелирует с изменением структуры сплава.

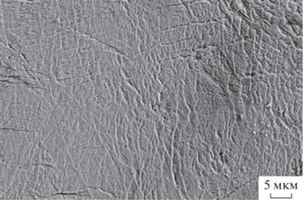
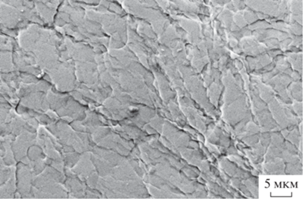
На рис. 7 приведено изображение поверхности деформированного сплава Fe77Si13B10 после обработки методом КВД, а на рис. 8 – изображение поверхности прокатанного сплава Fe77Si13B10, полученные методом сканирующей электронной микроскопии.

Рис. 7.

Изображение поверхности деформированного сплава Fe77Si13B10 (КВД).

Рис. 8.

Изображение поверхности прокатанного сплава Fe77Si13B10.

На поверхности прокатанного образца наблюдаются немногочисленные ступеньки, отвечающие полосам сдвига. В отличие от этих изображений, на рис. 9, 10 присутствуют многочисленные ступеньки, характеризующие более значительные изменения структуры. Эти результаты согласуются с данными об изменении средней плотности материалов, приведенными в табл. 1.

Рис. 9.

Изображение поверхности сплава Al88Ni10Y2 после барической обработки при 8 ГПa.

Рис. 10.

 Изображение  поверхности  сплава Zr55Cu30Al15Ni5, деформированного методом кручения под давлением.

Результаты исследования морфологии поверхности деформированных аморфных сплавов показывают, что число полос сдвига растет с увеличением степени деформации. Чем больше полос сдвига, тем, естественно, больше доля материала с бо́льшим значением радиуса первой координационной сферы (кратчайшего расстояния между атомами). Необходимо еще раз подчеркнуть, что данные по изменению радиусов координационных сфер и изменению плотности (или избыточного свободного объема, определенного по формуле (2)) являются средними значениями. Значения коэффициентов а и b, характеризующих объемные доли неизменившейся аморфной фазы (а) и полос сдвига (b), различаются существенно: а $ \gg $ b. Это означает, что реальные изменения структуры непосредственно в полосах сдвига много больше наблюдаемых используемыми в настоящей работе методами. Именно такие большие изменения и приводят к повышению коэффициента диффузии в этих областях, отмеченному в [23], на несколько порядков величины. Для определения реального вклада областей полос сдвига в изменение структуры деформированных аморфных сплавов необходима информация об объемной доле полос сдвига, что требует дальнейших исследований.

По полученным изображениям поверхности сплава Zr55Cu30Al15Ni5, деформированного методом кручения под давлением, была проведена оценка плотности расположения ступенек на поверхности. Для этого были получены серии изображений с увеличением 10 000 крат. Размер кадра, в котором измеряли длину полос сдвига, составлял 33.75 мкм × 22 мкм = 742.5 мкм2. Первоначально было получено 50 изображений по направлению от края образца к центру. Изображения следовали друг за другом без наложения и без зазоров. Таким образом были получены изображения с полоски образца длиной 33.75 × 50 = = 1687.5 мкм. Далее были получены серии из 10 изображений от центральной части образца, и областей, находящихся на расстоянии 0.5, 1, 1.5, 2 мм от края образца. График зависимости длины ступенек при перемещении от края образца к его центру представлены на рис. 11 Видно, что длина ступенек, приходящаяся на единицу площади поверхности образца, остается примерно постоянной. Она составляет приблизительно 1000 мкм на площади 740 мкм2 (на одном изображении). Если считать, что каждой ступеньке соответствует полоса сдвига толщиной 20 нм [14, 16, 22] и она проходит через весь образец без ветвления и достигает противоположной поверхности, то объем материала в полосах сдвига в участке образца площадью 740 мкм2 составляет приблизительно 1000 × 0.02 × × h = 20 мкм2 × h (h – толщина образца). Тогда объемная доля материала в полосах сдвига будет равна приблизительно 20 мкм2 × h/ 740мкм2 × h = = 0.0270.

Рис. 11.

Зависимость длины ступенек от расстояния от края образца сплава Zr55Cu30Al15Ni5, деформированного методом КВД.

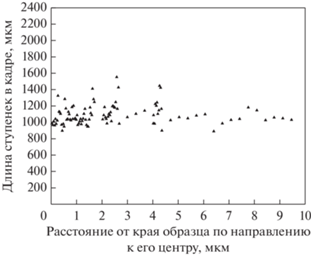
Если в соответствии с [17, 20] полагать, что плотность аморфной фазы в полосах сдвига меньше плотности аморфной фазы в остальной матрице на 10%, то средняя плотность аморфного деформированного образца будет оставлять 0.973 + + 0.024 = 0.997 плотности недеформированного образца. Разница между плотностью деформированного и недеформированного образца составляет приблизительно 0.3%. Эта величина меньше, чем значение, полученное из рентгеновских данных. Однако здесь считалось, что ступенька соответствует единичной полосе сдвига толщиной 20 нм. В то же время наши исследования тонкой структуры полос с помощью атомно-силовой микроскопии [22], показали, что ступеньки, которые мы видим с помощью сканирующей электронной микроскопии, имеют сложную структуру. Они образуются в результате действия нескольких единичных полос сдвига. В этом случае доля материала, находящегося в полосах сдвига, будет в несколько раз больше, и будет наблюдаться соответствие между экспериментальными данными, полученными разными методами.

ЗАКЛЮЧЕНИЕ

Исследования влияния деформации на изменение структуры аморфных сплавов систем Al–Y, Al–TM–RE (TM = Ni, Co; RE = Y, Gd, La), Fe–Si–B, Co–Si–B–Fe–Nb, Pd–Ni–P, Zr–Cu–Al–Fe показали следующее:

– при всех использованных способах деформирования (кручение под высоким давлением, многократная прокатка, барическая обработка) в аморфных сплавах происходит образование полос сдвига, приводящих к образованию ступенек на поверхности образцов;

– образовавшиеся полосы сдвига являются зонами повышенного свободного объема (пониженной плотности), что характеризуется увеличением кратчайшего расстояния между атомами в этих областях и, как следствие, сдвигом диффузного гало на рентгенограммах в сторону меньших углов;

– величина сдвига диффузного гало (радиуса первой координационной сферы в аморфной структуре) зависит от условий получения материала, степени деформации и физических констант материала (модуля Юнга, модуля сдвига);

– количество полос сдвига и морфология поверхности деформированных аморфных сплавов определяются видом деформации и физическими свойствами материала.

Авторы благодарят В.И. Кулакова за проведение барических обработок.

Список литературы

  1. Perepezko J.H. Nucleation-controlled reactions and metastable structures // Prog. Mater.Sci. 2004. V. 49. P. 263–284. https://doi.org/10.1016/S0079-6425(03)00028-8

  2. Mu J., Fu H., Zhu Z., Wang A., Li H., Hu Z.Q., Zhang H. Synthesis and Properties of Al–Ni–La Bulk Metallic Glass // Adv. Eng. Mater. 2009. V. 11. P. 530–532. https://doi.org/10.1002/adem.200900100

  3. Yang B.J., Yao J.H., Chao Y.S., Wang J.Q., Ma E. Developing aluminum-based bulk metallic glasses // Phil. Mag. 2010. V. 90. P. 3215–3231. https://doi.org/10.1080/14786435.2010.484401

  4. Chunchu V.J., Markandeyulu G. Magnetoimpedance studies in as quenched Fe73.5Si13.5B8CuV3−xAlNbx nanocrystalline ribbons // Appl. Phys. 2013. V. 113. P. 17A321. https://doi.org/10.1063/1.4795800

  5. Maaß R., Samwer K., Arnold W., Volkert C.A. A single shear band in a metallic glass: Local core and wide soft zone // Appl. Phys. Lett. 2014. V. 105. P. 171902. https://doi.org/10.1063/1.4900791

  6. Ohta M., Yoshizawa Y. Magnetic properties of nanocrystalline Fe82.65Cu1.35Si푥B16−x alloys (x = 0–7) // Appl. Phys. Lett. 2007. V. 91. P. 062517. https://doi.org/10.1063/1.2769956

  7. Makino A., Men H., Kubota T., Yubuta K., Inoue A. New Fe-metalloids based nanocrystalline alloys with high Bs of 1.9T and excellent magnetic softness // J. Appl. Phys. 2009. V. 105. P. 07A308. https://doi.org/10.1063/1.3058624

  8. Abrosimova G., Matveev D., Pershina E., Aronin A. Effect of treatment conditions on parameters of nanocrystalline structure in Al-based alloys // Mat. Lett. 2016. V. 183. P. 131–134. https://doi.org/10.1016/j.matlet.2016.07.053

  9. Aronin A., Matveev D., Pershina E., Tkatch V., Abrosimova G. The effect of changes in Al-based amorphous phase structure on structure forming upon crystallization // J. Alloy. Compd. 2017. V. 715. P. 176–183. https://doi.org/10.1016/j.jallcom.2017.04.305

  10. Сверхбыстрая закалка жидких сплавов / Под ред. Г. Герман. М.: Металлургия, 1986. 374 с.

  11. Meng F., Tsuchiya K., Seiichiro I.I., Yokoyama Y. Reversible transition of deformation mode by structural rejuvenation and relaxation in bulk metallic glass // Appl. Phys. Lett. 2012. V. 101. P. 121914. https://doi.org/10.1063/1.4753998

  12. Boltynjuk E., Gunderov D., Ubyivovk E., Monclús M., Yang L., Molina-Aldareguia J., Tyurin A., Kilmametov A., Churakova A., Churyumov A. Enhanced strain rate sensitivity of Zr-based bulk metallic glasses subjected to high pressure torsion // J. Alloys Compd. 2018. V. 747. P. 595–602. https://doi.org/10.1016/j.jallcom.2018.03.018

  13. Gunderov D., Astanin V., Churakova A., Sitdikov V., Ubyivovk E., Islamov A., Jing Tao Wang. Influence of High-Pressure Torsion and Accumulative High-Pressure Torsion on Microstructure and Properties of Zr-Based Bulk Metallic Glass Vit105 // Metals. 2020. V. 10. P. 1433. https://doi.org/10.3390/met10111433

  14. Chen Y.M., Ohkubo T., Mukai T., Hono K. Structure of shear bands in Pd40Ni40P20 bulk metallic glass // J. Mater. Res. 2009. V. 24. P. 1–9. https://doi.org/10.1557/jmr.2009.0001

  15. Greer A.L., Cheng Y.Q., Ma E. Shear bands in metallic glasses // Mater.Sci. Eng. R Reports. 2013. V. 74. P. 71–132. https://doi.org/10.1016/j.mser.2013.04.001

  16. He J., Kaban I., Mattern N., Song K., Sun B., Zhao J., Kim D.H., Eckert J., Greer A.L. Local microstructure evolution at shear bands in metallic glasses with nanoscale phase separation // Sci. Reports. 2016. V. 6. P. 25 832. https://doi.org/10.1038/srep25832

  17. Rösner H., Peterlechner M., Kübel C., Schmidt V., Wilde G. Density changes in shear bands of a metallic glass determined by correlative analytical transmission electron microscopy // Ultramicroscopy. 2014. V. 142. P. 1–9. https://doi.org/10.1016/j.ultramic.2014.03.006

  18. Şopu D., Scudino S., Bian X.L., Gammer C., Eckert J. Atomic-scale origin of shear band multiplication in heterogeneous metallic glasses // Scripta Mater. 2020. V. 178. P. 57–61. https://doi.org/10.1016/j.scriptamat.2019.11.006

  19. Glezer A.M., Khriplivets I.A., Sundeev R.V., Louzguine-Luzgin D.V., Pogozhev Yu.S., Rogachev S.O., Bazlov A.I., Tomchuk A.A. Quantitative characteristics of shear bands formed upon deformation in bulk amorphous Zr-based alloy // Mater. Letters. 2020. V. 281. P. 128 659. https://doi.org/10.1016/j.matlet.2020.128659

  20. Liu C., Roddatis V., Kenesei P., Maaß R. Shear-band thickness and shear-band cavities in a Zr-based metallic glass // Acta Mater. 2017. V. 140. P. 206–216. https://doi.org/10.1016/j.actamat.2017.08.032

  21. Постнова Е.Ю., Абросимова Г.Е., Аронин А.С. Поверхность и структура аморфных сплавов после барической обработки // Поверхность. Рентгеновские, Синхротронныеи Нейтронные Исследования. 2021. Т. 21. № 11. С. 5–10. https://doi.org/10.31857/S1028096021110169

  22. Mironchuk B., Abrosimova G., Bozhko S., Pershina E., Aronin A. Correlation between phase transformation and surface morphology under severe plastic deformation of theAl87Ni8La5 amorphous alloy // J. Non-Crystal. Solids. 2022. V. 571. P. 121279. https://doi.org/10.1016/j.jnoncrysol.2021.121279

  23. Aronin A.S., Louzguine-Luzgin D.V. On nanovoids formation in shear bands of an amorphous Al-based alloy // Mechanics of Materials. 2017. V. 113. P. 19–23. https://doi.org/10.1016/j.mechmat.2017.07.007

  24. Lewandowski J.J., Greer A.L. Temperature rise at shear bands in metallic glasses // Nature Mater. 2006. V. 5. P. 15–18. https://doi.org/10.1038/nmat1536

  25. Csontos A.A., Shiflet G.J. Formation and chemistry of nanocrystalline phases formed during deformation in aluminum-rich metallic glasses // Nano Structured Mater. 1997. V. 9. P. 281–289. https://doi.org/10.1016/S0965-9773(97)90068-4

  26. Georgarakis K. Shear band melting and serrated flow in metallic glasses // App. Phys. Lett. 2008. V. 93. P. 031 907. https://doi.org/10.1063/1.2956666

  27. Hartley K.A., Duffy J., Hawley. R.H. Measurement of the temperature profile during shear band formation in steels deforming at high strain rates // J. Mech. Solids. 1987. V. 35. P. 283–301. https://doi.org/10.1016/0022-5096(87)90009-3

  28. Li J.G., Umemoto M., Todaka Y., Fujisaku K., Tsuchiya K. The dynamic phase transformation and formation of nanocrystalline structure in sus304 austenitic stainless steel subjected to high pressure torsion // Rev. Adv. Mater. Sci. 2008. V. 18. P. 577–582. https:// www.ipme.ru/e-journals/RAMS/no_71808/umemoto.pdf.

  29. Jiang W.H., Atzmon M. The effect of compression and tension on shear-band structure and nanocrystallization in amorphous Al90Fe5Gd5: a high-resolution transmission electron microscopy study // Acta Materialia. 2003. V. 51. P. 4095–4105. https://doi.org/10.1016/S1359-6454(03)00229-5

  30. Kim J.J., Choi Y., Suresh S., Argon A.S. Nanocrystallization during nanoindentation of a bulk amorphous metal alloy at room temperature // Science 2002. V. 295. P. 654–657. https://doi.org/10.1126/science.1067453

  31. Schmidt V., Rösner H., Peterlechler M., Wilde G. Quantitative Measurement of Density in a Shear Band of Metallic Glass MonitoredAlongits Propagation Direction // Phys. Rev. Lett. 2015. V. 115. P. 035501. https://doi.org/10.1103/PhysRevLett.115.035501

  32. Абросимова Г.Е., Матвеев Д.В., Аронин А.С. Формирование наноструктур в гомогенной и гетерогенной аморфной фазе // УФН. 2022. Т. 192. № 3. С. 247–266. https://doi.org/10.3367/UFNr.2021.04.038974

  33. Doolittle A.K. Studies in Newtonian flow. II. The dependence of the viscosity of liquids on free-space // J. Appl. Phys. 1951. V. 22. P. 1471–1475.

  34. Haruyama O., Inoue A. Free volume kinetics during sub-structural relaxation of a bulk Pd40Ni40P20 metallic glass // Appl. Phys. Lett. 2006. V. 88. P. 131 906. https://doi.org/10.1063/1.2189833

  35. Rätzke K., Hüppe P.W., Faupel F. Transition from Single-Jump Type to Highly Cooperative Diffusion during Structural Relaxation of a Metallic Glass // Phys. Rev. Lett. 1992. V. 68. P. 2347–2349.

  36. Dmowski W., Iwashita T., Chuang C.P., Almer J., Egami T. Elastic Heterogeneity in Metallic Glasses // Phys. Rev. Lett. 2010. V. 105. P. 205502. https://doi.org/10.1103/PhysRevLett.105.205502

  37. Yavari A.R., Moulec A.L., Inoue A., Nishiyama N., Lupu N., Matsubara E., Botta W.J., Vaughan G., Michiel M.D., Kvick Å. Excess free volume in metallic glasses measured by X-ray diffraction // Acta Mater. 2005. V. 53. P. 1611–1619. https://doi.org/10.1016/j.actamat.2004.12.011

  38. Cohen M.H., Grest G.S. Liquid-glass transition, a free-volume approach // Phys. Rev. B 1979. V. 20. P. 1077.

  39. Turnbull D., Cohen M.H. Free-Volume Model of the Amorphous Phase: Glass Transition // J. Chem. Phys. 1961. V. 34. P. 120–125. https://doi.org/10.1063/1.1731549

  40. Pan J., Chen Q., Liu L., Li Y. Softening and dilatation in a single shear band // Acta Mater. 2011. V. 59. P. 5146–5158. https://doi.org/10.1016/j.actamat.2011.04.047

  41. Greer A.L. Partially or fully devitrified alloys for mechanical properties // Mat. Sci. Eng. 2001. V. 304–306. P. 68–72. https://doi.org/10.1016/S0921-5093(00)01449-0

  42. Boucharat N., Hebert R., Rösner H., Valiev R., Wilde G. Synthesis routes for controlling the microstructure in nanostructured Al88Y7Fe5 alloys // J. All. Comp. 2007. V. 434–435. P. 252–254. https://doi.org/10.1016/j.jallcom.2006.08.128

  43. Wilde G., Rösner H. Nanocrystallization in a shear band: An in situ investigation // Appl. Phys. Lett. 2011. V. 98. P. 251904. https://doi.org/10.1063/1.3602315

  44. Gunderov D., Astanin V. Influence of HPT Deformation on the Structure and Properties of Amorphous Alloys // Metals. 2020. V. 10. P. 415. https://doi.org/10.3390/met10030415

  45. Gunderov D.V., Churakova A.A., Astanin V.V., Asfandiyarov R.N., Hahn H., Valiev R.Z. Accumulative HPT of Zr-based bulk metallic glasses // Mater. Lett. 2020. V. 261. P. 127000. https://doi.org/10.1016/j.matlet.2019.127000

  46. Masumoto T., Maddin R. Structural stability and mechanical properties of amorphous metals // Mater. Sci. Eng. 1975. V. 19. P. 1–24. https://doi.org/10.1016/0025-5416(75)90002-6

  47. Wang X.D., Bednarcik J., Saksi K., Franz H., Cao Q.P., Jiang A.Z. Tensile behavior of bulk metallic glasses by in situ x-ray diffraction // Appl. Phys. Lett. 2007. V. 91. P. 081913. https://doi.org/10.1063/1.2773945

  48. Stoica M., Das J., Bednarcik J., Franz H., Mattern N., Wang W.H., Eckert J. Strain distribution in Zr64.13Cu15.75Ni10.12Al10 bulk metallic glass investigated by in situ tensile tests under synchrotron radiation // J. Appl. Phys. 2008. V. 104. P. 013522. https://doi.org/10.1063/1.2952034

  49. Wang X.D., Bednarcik J., Franz H., Lou H.B., He Z.H., Cao Q.P., Jiang J.A. Local strain behavior of bulk metallic glasses under tension studied by in situ x-ray diffraction // Appl. Phys. Lett. 2009. V. 94. P. 011911. https://doi.org/10.1063/1.3064136

  50. Абросимова Г.Е., Аронин А.С., Афоникова Н.С., Кобелев Н.П. Влияние деформации на изменение структуры аморфной фазы Pd40Ni40P20 // ФТТ. 2010. Т. 52. № 9. С. 1763–1768. https://doi.org/10.1134/S1063783410090179

  51. Hebert R.J., Boucharat N., Perepezko J.H., Rösner H., Wilde G. Calorimetric and microstructural analysis of deformation induced crystallization reactions in amorphous Al88Y7Fe5 alloy // J. Alloys Compd. 2007. V. 434. P. 18–21. https://doi.org/10.1016/j.jallcom.2006.08.134

  52. Abrosimova G., Chirkova V., Pershina E., Volkov N., Sholin I. Aronin A. The Effect of Free Volume on the Crystallization of Al87Ni8Gd5 Amorphous Alloy // Metals. 2022. V. 12. P. 332. https://doi.org/10.3390/met12020332

  53. Valiev R.Z., Islamgaliev R.K., Alexandrov I.V. Bulk Nanostructured Materials from Severe Plastic Deformation // Prog. Mater. Sci. 2000. V. 45. P. 103–189. https://doi.org/10.1016/S0079-6425(99)00007-9

  54. Degtyarev M.V., Chashchukhina T.I., Voronova L.M., Patselov A.M., Pilyugin V.P. Influence of the relaxation processes on the structure formation in pure metals and alloys under high-pressure torsion // Acta Mater. 2007. V. 55. P. 6039–6050. https://doi.org/10.1016/j.actamat.2007.04.017

  55. Zhilyaev A.P., Langdon T.G. Using high-pressure torsion for metal processing: Fundamentals and applications // Progress in Materials Science. 2008. V. 53. P. 893–979. https://doi.org/10.1016/j.pmatsci.2008.03.002

  56. Chashchukhina T.I., Degtyarev M.V., Voronova L.M. Effect of pressure on the evolution of copper microstructure upon large plastic deformation // Physics of metals and metallography. 2010. V. 109. P. 201–209. https://doi.org/10.1134/S0031918X10020122

  57. Скрышевский А.Ф. Структурный анализ жидкостей и аморфных тел. М.: Высшая школа, 1980. 328 с.

  58. Gunderov D.V., Boltynjuk E.V., Sitdikov V.D., Abrosimova G.E., Churakova A.A., Kilmametov A.R., Valiev R.Z. Free volume measurement of severely deformed Zr62Cu22Al10Fe5Dy1 bulk metallic glass // IOP Conf. Series: Journal of Physics: Conf. Series. 2018. V. 1134. P. 012 010. https://doi.org/10.1088/1742-6596/1134/1/012010

  59. Абросимова Г. Эволюция структуры аморфных сплавов // УФН. 2011. Т. 181. № 12. С. 1265. https://doi.org/10.3367/UFNr.0181.201112b.1265

  60. Abrosimova G., Aronin A., Budchenko A. Amorphous phase decomposition in Al–Ni–RE system alloys // Mater. Letters. 2015. V. 139. P. 194–196. https://doi.org/10.1016/j.matlet.2014.10.076

  61. Abrosimova G., Aronin A. On decomposition of amorphous phasein metallic glasses // Rev. Adv. Mater. Sci. 2017. V. 50. № 1–2. P. 55–61. http://www.ipme.ru/e-journals/RAMS/no_15017/07_15017_abrosimova.pdf

  62. Abrosimova G., Gunderov D., Postnova E., Aronin A. Changes in the Structure of Amorphous Alloys under Deformation by High-Pressure Torsion and Multiple Rolling // Materials. 2023. V. 16. P. 1321. https://doi.org/10.3390/ma16031321

  63. Бойчишин Д., Ковбуз М., Герцик О., Носенко В., Котур Б. Влияние структурирования аморфных металлических сплавов Al87Y5–xGdxNi8–y (x = 0, 1, 5; y = 0, 4) на их механические свойства // ФТТ. 2013. Т. 55. № 2. С. 209–212.

  64. Microstructure and properties of Materials / Ed. J.C.M. Li. World Scientific. Singapore, 2000. 439 p.

  65. Lewandowski J.J., Wang W.H., Greer A.L. Intrinsic plasticity or brittleness of metallic glasses // Phil. Mag. Letters. 2005. V. 85. P. 77–87. https://doi.org/10.1080/09500830500080474

  66. Глезер А.М., Шурыгина Н.А. Аморфно-нанокристаллические сплавы. М., Физматлит, 2013. 452 с.

  67. Gu X.J., Poon S.J., Shiflet G.J., Widom M. Ductility improvement of amorphous steels: Roles of shear modulus and electronic structure // Acta Materialia. 2008. V. 56. P. 88–94. https://doi.org/10.1016/j.actamat.2007.09.011

  68. Судзуки К., Фудзимори Х., Хасимото Л. Аморфные металлы. М.: Металлургия, 1987. 328 с.

  69. Zhang Z., Keppens V., Liaw P.K., Yokoyama Y., Inoue A. Elastic properties of Zr-based bulk metallic glasses studied by resonant ultrasound spectroscopy // J. Mater. Res. 2007. V. 22. P. 364–367. https://doi.org/10.1557/jmr.2007.0040

  70. Kassner M.E., Smith K., Eliasson V. Creep in amorphous metals // J. Mater. Res. Tech. 2015. V. 4. P. 100–107. https://doi.org/10.1016/j.jmrt.2014.11.003

  71. Физические величины. Справочник / Под ред. Григорьева И.С., Мейлихова Е.З. М.: Энергоатомиздат, 1991. 1232 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал