1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 124, № 9, 2023

Физика металлов и металловедение, 2023, T. 124, № 9, стр. 861-872

Атомистическое моделирование самодиффузии и диффузии Со вдоль симметричных границ зерен наклона $\left[ {2\bar {1}\bar {1}0} \right]$ в α-Ti

М. Г. Уразалиев a, *, М. Е. Ступак a, В. В. Попов a

a Институт физики металлов им. М.Н. Михеева УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия

* E-mail: urazaliev@imp.uran.ru

Поступила в редакцию 05.07.2023
После доработки 01.08.2023
Принята к публикации 01.08.2023

Полный текст (PDF)

Аннотация

Методами компьютерного моделирования исследованы структура, точечные дефекты, самодиффузия и диффузия Со для четырех энергетически предпочтительных границ зерен (ГЗ) с осью наклона $\left[ {2\bar {1}\bar {1}0} \right]$ в гексагональном плотноупакованном (ГПУ) Ti. Методом молекулярно-статического моделирования рассчитаны структура и энергии рассматриваемых границ, а также энергии образования точечных дефектов в них. Продемонстрированы зависимости энергий образования точечных дефектов от расстояния от плоскости границы зерна. Методом молекулярной динамики рассчитаны коэффициенты зернограничной самодиффузии для рассматриваемых ГЗ. Результаты моделирования самодиффузии сравниваются с имеющимися экспериментальными данными. Также выполнено моделирование зернограничной диффузии Со в α-Ti. Показано, что структура ГЗ влияет на параметры зернограничной диффузии как в случае самодиффузии, так и в случае примесной диффузии, и коэффициенты зернограничной диффузии могут отличатся на несколько порядков, в зависимости от структуры.

Ключевые слова: границы зерен, молекулярная статика, молекулярная динамика, точечные дефекты, зернограничная диффузия

ВВЕДЕНИЕ

Титан имеет широкий спектр применений в медицине и является важным металлом в аэрокосмической технике. Атомная структура и энергия границ зерен (ГЗ), а также энергия образования в них точечных дефектов существенно влияют на многие свойства поликристаллических материалов [1]. Прямое экспериментальное определение этих параметров связано со значительными трудностями. Поэтому атомистическое моделирование структуры и свойств ГЗ получило широкое распространение. На сегодняшний день опубликован ряд работ и обзоров, посвященных изучению и моделированию структуры и энергии границ зерен, а также энергий образования точечных дефектов в них. Однако в большинстве публикаций изучали металлы с кубической структурой [2–9]. Гораздо меньше исследований посвящено ГПУ металлам, особенно титану. Существует лишь несколько работ, посвященных моделированию ГЗ в титане, например, [10–16]. Эти публикации в основном посвящены изучению деформации и зернограничных дислокаций, и только в трех публикациях были рассчитаны энергии образования вакансий в ГЗ титана [16–18] Практически нет исследований, которые бы определяли энергии собственных или примесных внедренных атомов в ГЗ α-Ti.

Имеется несколько публикаций по экспериментальному определению параметров зернограничной самодиффузии и примесной диффузии в титане [19–21]. Эти результаты касаются большеугловых ГЗ общего типа. В то же время важно знать параметры диффузии вдоль некоторых специальных ГЗ. Экспериментальное определение параметров диффузии вдоль специальных границ представляет значительные трудности, и на сегодняшний день такие результаты для титана отсутствуют в литературе. Больше возможностей предоставляет атомистическое моделирование зернограничной диффузии, но имеется только две публикации, в которых были рассчитаны параметры зернограничной диффузии в специальных ГЗ титана [17, 22]. Таким образом, очевидно, что в настоящее время имеется недостаточно информации об энергии образования точечных дефектов в границах зерен и зернограничной диффузии в титане.

Цель настоящей работы – моделирование диффузии в четырех симметричных границах наклона с осью наклона $\left[ {2\bar {1}\bar {1}0} \right]$ в α-Ti, расчет структуры и энергии исследуемых ГЗ, энергии образования точечных дефектов в них. Для исследования были выбраны двойниковые границы $\left( {01\bar {1}1} \right),$ $\left( {01\bar {1}2} \right),$ $\left( {01\bar {1}3} \right)$ и симметричная граница наклона $\left( {02\bar {2}1} \right).$ В наших недавних работах рассчитана структура и энергия ГЗ, энергия образования вакансий и зернограничная самодиффузия по вакансионному механизму для нескольких специальных ГЗ α-Ti [17, 18]. В настоящей работе поставлена задача выполнить моделирование зернограничной самодиффузии отдельно по междоузельному и по вакансионному механизмам, а также диффузии кобальта вдоль ГЗ α-Ti.

МЕТОДИКА АТОМИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Для проведения расчетов использовали потенциал межатомного взаимодействия 2NN MEAM для системы титан–кобальт, основанный на модифицированном методе погруженного атома [23]. Файл потенциала получен из репозитория NIST [24]. Период решетки, энергии связи, модули упругости, поверхностная энергия и энергии образования вакансий, рассчитанные с использованием этого потенциала для ГПУ-титана, хорошо согласуются с экспериментальными значениями этих параметров (табл. 1). Этот потенциал был разработан для двойной системы Co–Ti. Поэтому он может быть использован для моделирования диффузии кобальта в ГЗ ГПУ титана.

Таблица 1.

Сравнение экспериментальных значений характеристик α-титана со свойствами, рассчитанными на основе выбранного потенциала межатомного взаимодействия

Свойство a, нм c/a Ecoh, эВ/атом C11, ГПа C12, ГПа C44, ГПа C13, ГПа C33, ГПа C66, ГПа Объемный модуль упругости, ГПа Esurf, Дж/м2 Evac, эВ
Эксперимент 0.295 [25] 1.587 [25] 4.85 [26] 176.1 [26] 86.9 [26] 50.8 [26] 68.3 [26] 190.5 [26] 44.6 [26] 105.1 [25] 1.92 [28] 1.27 [27]
Расчет 0.295 1.633 4.87 174 82 41 73 185 46 109.75 2.1 1.78

Ecoh – энергия когезии, Esurf – поверхностная энергия, Evac – энергия образования вакансий.

Метод молекулярной статики (МС) был использован для расчета структуры и энергии границ зерен, а также энергий образования в них точечных дефектов. В этом методе, по умолчанию, отсутствует движение атомов, поэтому считается, что отсутствие температуры соответствует условному 0 К. Используя программу LAMMPS [29], расчеты выполнены для 4 специальных ГЗ наклона с осью $~\left[ {2\bar {1}\bar {1}0} \right],$ которые согласно [12] и [17] имеют минимальные энергии образования соответствующих ГЗ. Это три двойниковые ГЗ: $\left( {01\bar {1}3} \right),$ θ = 64.3°; $\left( {01\bar {1}2} \right),$ θ = 86.62°; $\left( {01\bar {1}1} \right),$ θ = = 124.12° и одна симметричная ГЗ $\left( {02\bar {2}1} \right),$ θ = 150.3°.

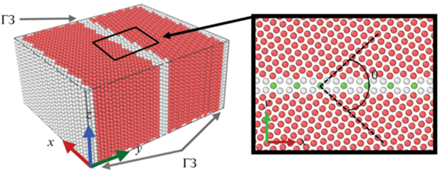
Блок МС-моделирования показан на рис. 1. Периодические граничные условия заданы во всех трех направлениях. Блок содержит 2 зерна (Зерно 1 и Зерно 2), которые повернуты относительно друг друга вокруг оси наклона z на угол Θ, соответствующий специальному углу разориентации. Полученный бикристалл содержит 2 одинаковые ГЗ: в центре и по краям блока. Для формирования геометрии моделируемого блока использована программа ATOMSK [30]. В качестве визуализатора для структурного анализа использована программа OVITO [31].

Рис. 1.

Пример блока моделирования, содержащего 2 зерна, повернутых относительно друг друга на угол Θ.

На этапе построения ГЗ атомы выстраивали до границы зерен, и соседние зерна могли содержать атомы, расположенные очень близко друг к другу. Удаление атомов, расположенных слишком близко друг к другу, осуществляли путем определения критического расстояния между ними. Структура ГЗ и энергия для каждой разориентации были получены для различных исходных конфигураций в результате поиска локального минимума энергии с использованием метода сопряженных градиентов.

Энергию ГЗ рассчитывали из выражения:

(1)
${{E}_{{{\text{ГЗ}}}}} = \frac{{{{E}_{{\text{P}}}} - N{{E}_{{{\text{coh}}}}}}}{{2S}},$
где Ep – полная потенциальная энергия релаксированного бикристалла, N – число атомов системы, Ecoh – энергия когезии (энергия связи на атом в идеальном кристалле), S – площадь ГЗ. Множитель 2, присутствующий в знаменателе, необходим, так как в системе две ГЗ.

В работе были рассчитаны энергии образования точечных дефектов в различных позициях в исследуемых ГЗ на разных расстояниях от плоскости границы. Энергия образования точечных дефектов рассчитана по формуле:

(2)
${{E}_{{{\text{pd}}}}} = {{E}_{f}} - \left( {{{N}_{0}} \pm 1} \right)\frac{{{{E}_{i}}}}{{{{N}_{0}}}}~{\kern 1pt} ~.$

Здесь ${{E}_{i}}$ – начальная энергия системы, перед удалением или добавлением атома, ${{N}_{0}}$ – общее число атомов, ${{E}_{f}}$ – энергия системы после удаления или добавления атома, Ei/N0 – энергия на атом. Энергия образования вакансии определена как энергия, необходимая для удаления атома в ГЗ и создания его в решетке бесконечно далеко от ГЗ, что соответствует знаку минус. Энергия образования собственного атома внедрения определена как энергия, необходимая для удаления атома в решетке бесконечно далеко от ГЗ и создания его в ГЗ, что соответствует знаку плюс.

Энергия образования атома кобальта в позиции внедрения в ГЗ рассчитана по формуле [32]:

(3)
${{E}_{{{\text{Co}}}}} = {{E}_{f}} - {{E}_{i}} - \,\,~E_{{{\text{coh}}}}^{{{\text{Co}}}},$
где ${{E}_{i}}$ – начальная энергия системы, ${{E}_{f}}$ – энергия системы после добавления атома кобальта, и $E_{{{\text{coh}}}}^{{{\text{Co}}}}$ – энергия связи атома кобальта.

В табл. 2 для исследуемых ГЗ приведены размеры блоков моделирования, количество атомов в них, энергии ГЗ, минимальные энергии образования собственных точечных дефектов и внедренных атомов кобальта в ГЗ.

Таблица 2.

Размеры блоков моделирования для каждой ГЗ, количество атомов в них, энергии ГЗ, минимальные энергии образования вакансий (Evac), собственных атомов внедрения (Eint) и внедренных атомов кобальта (ECo) в ГЗ

Угол разориентации Плоскость Размеры блока моделирования Количество атомов в блоке моделирования EГЗ, мДж/м2 Evac, эВ Eint, эВ ECo, эВ
ГЗ Lx, Å Ly, Å Lz, Å
64.3° $\left( {01\bar {1}3} \right)$ 107.5 124.6 29.2 22 080 114.5 1.562 2.019 –0.356
86.62° $\left( {01\bar {1}2} \right)$ 111.2 125.4 29.2 23 040 266.6 1.058 1.779 0.065
124.12° $\left( {01\bar {1}1} \right)$ 107.9 115.6 29.2 20 400 96.6 1.401 2.464 0.729
150.3° $\left( {02\bar {2}1} \right)$ 98.66 128.4 29.2 20 800 506.8 1.003 1.604 –0.007

Для проверки стабильности границы при конечной температуре и расчета коэффициента диффузии применяли метод прямой молекулярной динамики. Использовали изотермо-изобарический ансамбль (NPT). Изменение температуры контролировали при помощи термостата Нозе–Гувера [33].

В случае МД-моделирования при повышенных температурах может происходить миграция границы. Поэтому для предотвращения миграции ГЗ использовали фиксированные условия на краях блока моделирования. Фиксированные условия достигали путем выключения термостата в атомах, находящихся в этой области (ширина области порядка 0.5 нм). На рис. 2 показана схема блока МД-моделирования.

Рис. 2.

Схема блока молекулярно-динамического моделирования. Серым цветом указана зона с фиксированными атомами.

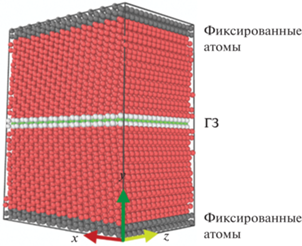
После молекулярно-статического моделирования структуры ГЗ был сформирован блок моделирования, содержащий около 20 000 атомов. Данный блок для каждой ГЗ использовали как начальное условие МД-моделирования для проверки стабильности структуры ГЗ и расчета коэффициента зернограничной диффузии.

Проверку стабильности структуры проводили следующим образом. Выполняли нагрев системы до заданной температуры в течение 2 нс, затем производили отжиг в течение 20 нс, после чего запускали процедуру минимизации энергии ГЗ.

В результате анализа полученных выходных данных проверяли структуру на стабильность при различных температурах с помощью программы OVITO [31] и встроенных в него модификаций для анализа структуры, таких как CNA [34]. Эта проверка показала, что структуры всех рассмотренных ГЗ стабильны вплоть до 1100 K.

В работе выполнено моделирование зернограничной самодиффузии как для вакансионного, так и для междоузельного механизмов. Это было сделано, поскольку в публикациях по атомистическому моделированию диффузии сообщали о возможности реализации различных механизмов массопереноса [35, 36]. В результате был установлен доминирующий механизм самодиффузии.

Перед расчетом в границе зерна создавали один точечный дефект в положении, соответствующем минимальной энергии образования точечного дефекта, и запускали моделирование. Временной шаг выбран порядка 1 фемтосекунды. Время моделирования составляло 10 наносекунд. При этом коллективное среднеквадратичное смещение атомов в границе зерна рассчитывали по формулам:

(4)
$\begin{gathered} \left\langle {x_{i}^{2}\left( t \right)} \right\rangle = \frac{{\sum\limits_{i = 1}^n {{{{\left( {{{x}_{i}} - {{x}_{{i0}}}} \right)}}^{2}}} }}{n}~, \\ \left\langle {z_{i}^{2}\left( t \right)} \right\rangle = \frac{{\sum\limits_{i = 1}^n {{{{\left( {{{z}_{i}} - {{z}_{{i0}}}} \right)}}^{2}}} }}{n}. \\ \end{gathered} $

Расчет зернограничной диффузии проводили в плоскости границы зерен в двух направлениях: в направлении оси наклона (направление z) и перпендикулярно ей (направление x). Здесь xi и zi координаты атомов в момент времени t; xi0 и zi0 – начальные координаты атомов, n число атомов в области ГЗ внутри блока. Ширину области ГЗ полагали ~1 нм.

Коэффициенты зернограничной самодиффузии рассчитывали по формулам:

(5)
${{D}_{x}} = \frac{{\left\langle {x_{i}^{2}\left( t \right)} \right\rangle }}{{2t}}\frac{n}{N}~,\,\,{{D}_{z}} = \frac{{\left\langle {z_{i}^{2}\left( t \right)} \right\rangle }}{{2t}}\frac{n}{N},$
где $\left\langle {x_{i}^{2}\left( t \right)} \right\rangle $ и $\left\langle {z_{i}^{2}\left( t \right)} \right\rangle $ – средние квадратичные смещения (СКС) атомов в зоне ГЗ за время t, в соответствующих направлениях, параллельных плоскости ГЗ; n – число атомов в области ГЗ внутри блока; N – число атомов на 1 точечный дефект. Множитель n/N добавлен, чтобы учесть, что количество атомов в ГЗ в блоке моделирования отличается от количества атомов, приходящихся на 1 точечный дефект.

Количество атомов, приходящихся на 1 точечный дефект, рассчитывали как величину, обратную равновесной концентрации точечных дефектов, ${{C}_{{{\text{pd}}}}}$:

(6)
$N = \frac{1}{{{{C}_{{{\text{pd}}}}}}}.$

При расчете равновесной концентрации точечных дефектов мы предполагали, что в реальном материале точечных дефектов с минимальной энергией образования подавляющее большинство. С учетом этого равновесную концентрацию точечных дефектов рассчитывали по формуле:

(7)
${{C}_{{{\text{pd}}}}} = \exp \left( { - {{E}_{{{\text{pdmin}}}}}{\text{/}}kT} \right)~{\kern 1pt} ,$
где ${{E}_{{{\text{pdmin}}}}}$ – минимальная энергия образования точечного дефекта в ГЗ, T – абсолютная температура.

При расчете зернограничной диффузии кобальта в титане предполагали, что она протекает по межузельному механизму. Это предположение основано на результатах мессбауэровских исследований, показавших, что реализуется междоузельный механизм зернограничной диффузии, если размер диффундирующего атома заметно меньше размера матричного атома [37]. Именно этот случай реализуется для зернограничной диффузии кобальта в титане, поскольку радиус атомов кобальта (0.125 нм) намного меньше радиуса атомов титана (0.146 нм) [38].

Зернограничная диффузия кобальта в титане рассчитана в диапазоне температур от 800 до 1100 К. Расчет проводили для 10 нс с шагом 1 фс. Примесные атомы кобальта в количестве 8 атомов создавали в позициях, соответствующих минимальной энергии образования атомов кобальта в ГЗ титана, после чего запускали моделирование. Коэффициенты зернограничной диффузии границ зерен в ГЗ титана рассчитывали по следующим формулам:

(8)
${{D}_{{x\_{\text{Сo}}}}} = \frac{{\left\langle {x_{i}^{2}\left( t \right)} \right\rangle }}{{2t}},\,\,{{D}_{{z\_{\text{Сo}}}}} = \frac{{\left\langle {z_{i}^{2}\left( t \right)} \right\rangle }}{{2t}},$
где $\left\langle {x_{i}^{2}\left( t \right)} \right\rangle $ и $\left\langle {z_{i}^{2}\left( t \right)} \right\rangle $ – СКС атомов кобальта в зоне ГЗ вдоль зернограничной плоскости, за период t.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

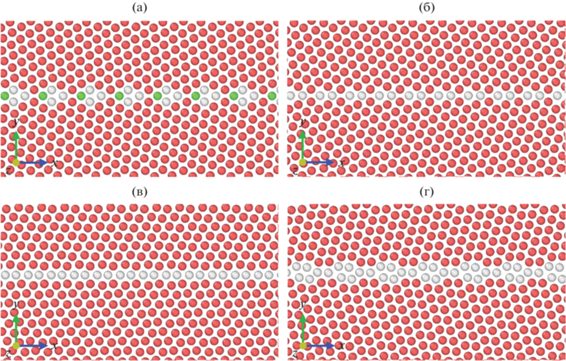
Расчетные энергии ГЗ приведены в табл. 2, а релаксированные структуры ГЗ показаны на рис. 3. Для демонстрации структур ГЗ использован анализ атомного окружения (CNA) [34], встроенный в OVITO [31], что позволяет определить тип решетки (ГПУ обозначен красным, ГЦК – зеленым, типы, не относящиеся к основным – белым). Как видно на рис. 3, структуры состоят из одинаковых повторяющихся структурных элементов, что характерно для симметричных границ наклона.

Рис. 3.

Структура ГЗ наклона в α-Ti: а – $\left( {01\bar {1}3} \right),$ θ = 64.3°, б – $\left( {01\bar {1}2} \right),$ θ = 86.62°, в – $\left( {01\bar {1}1} \right),$ θ = 124.12°, г – $\left( {02\bar {2}1} \right),$ θ = = 150.3°. В визуализации использован анализ CNA [34].

Экспериментальное определение энергий специальных ГЗ является сложной задачей, и в литературе отсутствуют достоверные данные об энергии специальных границ зерен в поликристаллическом титане. Поэтому мы сравнили результаты, полученные в данной работе, с результатами расчетов, представленными в литературе. Структура и энергии ГЗ в титане, полученные в данной работе, близки к результатам, приведенным в работах [13] и [18], в которых аналогичные расчеты проводили с другим потенциалом межатомного взаимодействия.

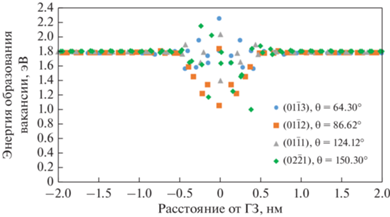
Результат расчетов энергии образования вакансий представлен как функция энергии от расстояния от ГЗ на рис. 4. Как видно из этого графика, ширина области ГЗ, в которой энергия образования вакансии значительно меньше, чем в объеме, составляет около 1 нм. Почти такая же ширина области ГЗ, в которой энергия образования вакансий заметно меньше, чем в объеме, была получена в работах [39–41]. Эта величина была принята за ширину ГЗ, которая использована при расчете зернограничной самодиффузии. Следует отметить, что положения вакансии в области ГЗ могут иметь более высокую энергию, чем в объеме. Аналогичную ситуацию наблюдали в [14].

Рис. 4.

Энергии образования вакансий в исследуемых ГЗ.

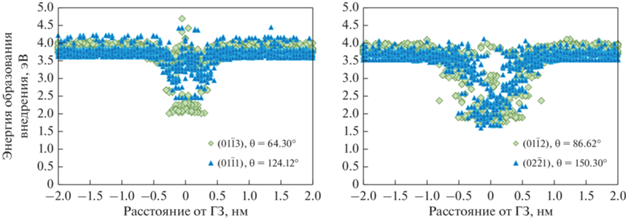
На рис. 5 представлены расчетные зависимости энергии образования собственных атомов внедрения в рассматриваемых границах зерен. Ширина приграничных областей, в которых энергия образования собственных атомов внедрения значительно меньше, чем в объеме, составляет 1.0–2.0 нм. Это заметно больше, чем в случае с вакансиями. Сравнение минимальных энергий образования собственных атомов внедрения и вакансий (табл. 2) показывает, что энергия образования вакансий в границах значительно ниже, чем у собственных атомов внедрения.

Рис. 5.

Энергии образования собственных атомов внедрения в исследуемых границах зерен.

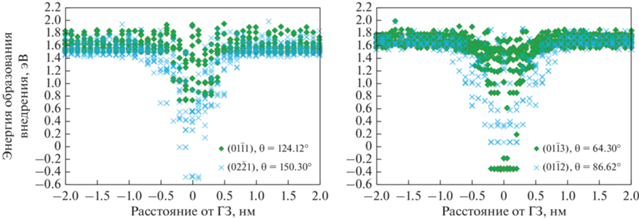
Процедура расчета энергии образования внедренных в ГЗ атомов кобальта аналогична расчету энергии образования собственных внедренных атомов; атомы кобальта создавали в аналогичных положениях, и энергия образования была рассчитана с использованием уравнения (3). На рис. 6 представлены результаты расчетов образования примесных атомов кобальта в исследуемых ГЗ α‑Ti. Ширина приграничной области, в которой энергия образования атомов кобальта значительно меньше, чем в объеме, примерно такая же, как и в случае образования собственных атомов внедрения. Примечательно, что минимальная энергия образования атомов кобальта значительно ниже, чем энергия образования собственных атомов внедрения, и ниже энергии образования вакансий в ГЗ (табл. 2). Более того, энергия образования атомов кобальта может быть даже отрицательной.

Рис. 6.

Энергия образования внедренного атома кобальта в ГЗ титана.

Позиции точечных дефектов с минимальной энергией в ГЗ показаны на рис. 7. Эти позиции были использованы в дальнейшем для моделирования диффузии по соответствующему механизму.

Рис. 7.

Исследуемые границы зерен с локализованными и указанными положениями минимума энергии образования точечных дефектов в ГЗ: a – $\left( {01\bar {1}3} \right),$ θ = 64.3°, б – $\left( {01\bar {1}2} \right),$ θ = 86.62°, в – $\left( {01\bar {1}1} \right),$ θ = 124.12°, г – $\left( {02\bar {2}1} \right),$ θ = 150.3°. Визуализация представлена с использованием анализатора структуры CNA. Символы ($\vartriangle $) и ($\square $) обозначают позиции, соответствующие минимуму энергии образования атомов кобальта и собственных атомов внедрения, а символ ($ \otimes $) обозначает минимальную энергию образования вакансии.

Поскольку точечные дефекты определяют диффузию в ГЗ, концентрация точечных дефектов (уравнение (7)) является важнейшим параметром, от которого зависит коэффициент диффузии. Доминирующий механизм диффузии зависит от типа точечных дефектов, концентрация которых в ГЗ больше, то есть от концентрации точечных дефектов определенного типа.

Концентрация соответствующих точечных дефектов сильно влияет на значения коэффициента самодиффузии. В случае самодиффузии по междоузельному механизму наблюдали непрямой механизм диффузии. В случае непрямого механизма внедренные атомы смещают соседние атомы в регулярной решетке в другие позиции внедрения и занимают их место. Этот механизм диффузии наблюдали в работах [35, 36] при моделировании самодиффузии в меди и железе.

Как указывали выше, все исследованные ГЗ сохраняют свою структуру до 1100 К, и в настоящей работе расчеты зернограничной самодиффузии в титане проводили в интервале температур 800–1100 К. Полученные результаты представлены на рис. 8. Для зернограничной самодиффузии в титане вакансионный механизм является доминирующим. Это следует из сравнения температурных зависимостей коэффициента самодиффузии в титане по вакансионному и междоузельному механизмам.

Рис. 8.

Температурные зависимости коэффициента зернограничной самодиффузии в титане для вакансионного (штриховая линия “-----”) и межузельного (сплошная линия “—”) механизмов массопереноса для направлений параллельно (а) и перпендикулярно (б) оси наклона. На рис. 8а и 8б также представлены экспериментальные данные (пунктирная линия из точек “······”).

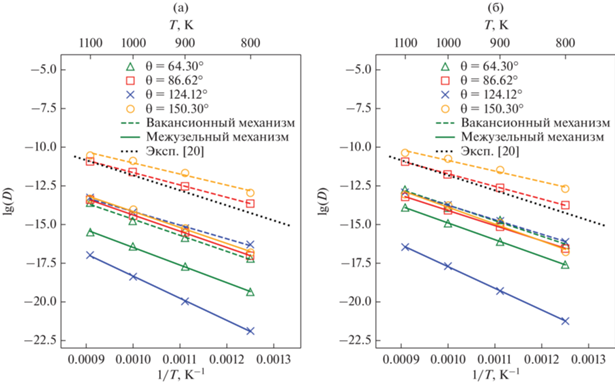
Значения коэффициента самодиффузии для разных ГЗ могут отличаться на несколько порядков. Аналогичную ситуацию наблюдали в работе [35], где моделировали зернограничную самодиффузию в меди. Для сравнения на рис. 8 представлена экспериментальная температурная зависимость коэффициента зернограничной диффузии в титане [20].

Видно, что коэффициенты для двух ГЗ $\left( {01\bar {1}2} \right),$ θ = 86.62° и $\left( {02\bar {2}1} \right),$ θ = 150.3° по вакансионному механизму весьма близки к экспериментальным, тогда как коэффициент диффузии в ГЗ $\left( {01\bar {1}3} \right),$ θ = 64.3° и $\left( {01\bar {1}1} \right),$ θ = 124.12° на несколько порядков ниже экспериментальных значений. Существенная разница между расчетными и экспериментальными значениями коэффициентов самодиффузии для некоторых специальных границ объясняется тем, что экспериментальные измерения коэффициента зернограничной самодиффузии проводились для обычных высокоугловых границ зерен общего типа.

При изучении примесной зернограничной диффузии кобальта нет необходимости делать поправку на концентрацию точечных дефектов, как в случае самодиффузии (уравнение (7)), когда концентрация точечных дефектов экспоненциально зависит от энергии их образования. Поэтому величина энергии образования атомов кобальта в позициях внедрения в ГЗ Ti не может влиять на коэффициент диффузии. В данной работе моделировали зернограничную диффузию Co, концентрация которого соответствовала разбавленному раствору.

Обнаружено, что примесные атомы кобальта, случайно расположенные в ГЗ титана, в результате диффузии стекают в определенные позиции в границах зерен, так называемые ловушки, что соответствует зернограничной сегрегации примесей. Положения ловушек определяются из молекулярной статики и представляют собой энергетически выгодные положения атомов кобальта (рис. 7). Таким образом, существует два процесса, потенциально влияющих на расчет коэффициента диффузии – преимущественная диффузия по ГЗ и перетекание атомов кобальта в энергетически выгодные позиции, включая перескоки между близкими энергетически выгодными позициями.

Если атомы кобальта поместить в энергетически выгодные позиции до начала моделирования диффузии, они редко покидают эти области. Чтобы исключить влияние потока кобальта в ловушки на расчет диффузии, моделирование проводили с начальными положениями атомов кобальта в ловушках.

Зернограничная диффузия кобальта в титане рассчитана в диапазоне температур от 800 до 1100 K. Полученные результаты представлены на рис. 9. Видно, что коэффициенты зернограничной диффузии кобальта в титане могут существенно различаться для разных границ, хотя и не так сильно, как для самодиффузии.

Рис. 9.

Температурные зависимости коэффициента зернограничной диффузии кобальта в титане для направлений параллельно (а) и перпендикулярно (б) оси наклона.

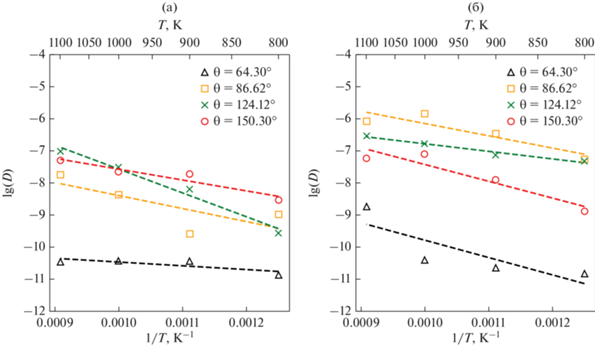
В случае зернограничной диффузии Co в α-Ti имеет место ее чередующийся характер, т.е. чередование быстрой и медленной диффузии. Следствием такого характера массопереноса является большая погрешность при определении коэффициента диффузии. Чередование быстрой и медленной диффузии объясняется периодичностью ловушек вдоль ГЗ.

Скорость диффузии различна для разных ГЗ и разных направлений. Данные, представленные на рис. 9, свидетельствуют о том, что диффузия в границах зерен по разным направлениям полностью определяется атомной структурой конкретной границы зерен, что предполагает и структуру ловушек в ГЗ.

Сравнение коэффициентов зернограничной самодиффузии и диффузии кобальта в титане показывает, что кобальт диффундирует по границам зерен титана значительно быстрее, чем происходит зернограничная самодиффузия.

На основании полученных температурных зависимостей коэффициентов самодиффузии и диффузии кобальта в ГЗ определены энтальпии активации зернограничной самодиффузии и диффузии Со в ГЗ титана. Полученные результаты представлены в табл. 3. Энтальпия активации самодиффузии находится в разумном согласии с экспериментом (1.94 эВ/атом [20] для самодиффузии и 0.73 эВ/атом для зернограничной диффузии Co в α-Ti [21]). Отметим, что энергия активации самодиффузии значительно выше энергии активации диффузии атомов кобальта по границам зерен титана.

Таблица 3.

Энергии активации самодиффузия и диффузия кобальта по ГЗ титана, перпендикулярно $\left( \bot \right)$ и параллельно $\left( \parallel \right)$ оси наклона в плоскости ГЗ наклона

Границы зерен Q, эВ/атом
зернограничная самодиффузия зернограничная диффузия Со
вакансии внедрения
$ \bot $ оси наклона $\parallel $ оси наклона $ \bot $ оси наклона $\parallel $ оси наклона $ \bot $ оси наклона $\parallel $ оси наклона
$\left( {01\bar {1}3} \right) = 64.3$ 2.01 2.07 2.15 2.27 1.08 0.23
$\left( {01\bar {1}2} \right) = 86.62$ 1.62 1.59 1.95 2.09 0.76 0.81
$\left( {01\bar {1}1} \right)~\,\, = 124.12$ 1.86 1.75 2.79 2.85 0.47 1.47
$\left( {02\bar {2}1} \right)\,\,~ = 150.3$ 1.37 1.43 2.17 2.06 1.04 0.67

Экспериментальное исследование также показало, что коэффициент самодиффузии значительно ниже, а энтальпия активации выше, чем в случае диффузии кобальта по границам зерен титана [19]. По-видимому, этот эффект объясняется двумя обстоятельствами. Во-первых, различием в механизмах зернограничной диффузии: диффузия кобальта протекает по межузельному механизму, а самодиффузия – по вакансионному [19]. Во-вторых, разница в энергиях образования вакансий и внедренных атомов кобальта в α-Ti: энергия образования внедренных атомов кобальта значительно меньше энергии образования вакансий.

ЗАКЛЮЧЕНИЕ

Специальные ГЗ наклона с осью $\left[ {2\bar {1}\bar {1}0} \right]$ в ГПУ титане были изучены с помощью атомистического моделирования с использованием межатомного потенциала на основе метода второго ближайшего соседа модифицированного встроенного атома (2NN MEAM) для двойной системы Co–Ti. Для исследования были выбраны четыре границы, соответствующие локальным минимумам энергии ГЗ.

Методом молекулярной статики рассчитаны структуры и энергии исследуемых ГЗ и энергии образования в них точечных дефектов (вакансий, собственных атомов внедрения, внедрений атомов кобальта).

Продемонстрированы зависимости энергий образования точечных дефектов от расстояния до плоскости ГЗ. Показано, что ширина приграничной области, в которой энергия образования точечных дефектов существенно меньше, чем в объеме, составляет около 1 нм для вакансий и 1.0–2.0 нм для собственных атомов внедрения.

Методом молекулярной динамики оценена термическая устойчивость исследуемых ГЗ, а также проведено моделирование зернограничной диффузии в температурном диапазоне стабильности структуры ГЗ.

Для определения доминирующего механизма самодиффузии в ГЗ был проведен сравнительный анализ параметров диффузии между системой, содержащей вакансии, и системой, содержащей собственные атомы внедрения. Для моделирования диффузии использован прямой метод МД. Проведено сравнение коэффициента диффузии и энергии активации.

Показано, что коэффициенты диффузии для разных специальных границ могут различаться на несколько порядков. Коэффициенты диффузии атомов кобальта по границам зерен α-Ti на несколько порядков выше коэффициентов зернограничной самодиффузии, что объясняется двумя причинами. Во-первых, самодиффузия протекает по вакансионному механизму, тогда как диффузия кобальта по границам зерен титана идет по межузельному механизму. Во-вторых, энергия образования вакансий в границах зерен намного выше, чем внедренных атомов кобальта.

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-13-00063, https://rscf.ru/project/21-13-00063/, ИФМ УрО РАН).

При проведении работ был использован суперкомпьютер “Уран” ИММ УрО РАН.

Авторы выражают признательность Ю.Н. Горностыреву за консультации и помощь в обсуждении результатов.

Список литературы

  1. Sutton A.P., Balluffi R.W. Interfaces in Crystalline Materials. Clarendon Press, New York: Oxford University Press, 1995. 819 p.

  2. Korneva M.A., Starikov S.V., Zhilyaev A.P., Akhatov I.S., Zhilyaev P.A. Atomistic Modeling of Grain Boundary Migration in Nickel // Adv. Eng. Mater. 2020. V. 22. P. 2000115. https://doi.org/10.1002/adem.202000115

  3. He H., Ma S., Wang S. Survey of Grain Boundary Energies in Tungsten and Beta-Titanium at High Temperature // Materials. 2022. V. 15. P. 156. https://doi.org/10.3390/ma15010156

  4. He H., Ma S., Wang S. Molecular dynamics investigation on tilt grain boundary energies of beta-titanium and tungsten at high temperature // Mater. Res. Express. 2021. V. 8. P. 116509. https://doi.org/10.1088/2053-1591/ac3606

  5. Tschopp M.A., McDowell D.L. Structures and energies of Σ3 asymmetric tilt grain boundaries in copper and aluminium // Phil. Mag. 2007. V. 87. № 22. P. 3147–3173. https://doi.org/10.1080/14786430701255895

  6. Frolov T., Olmsted D.L., Asta M., Mishin Y. Structural phase transformations in metallic grain boundaries // NATURE COMMUNICATIONS. 2013. V. 4. P. 1899. https://doi.org/10.1038/ncomms2919

  7. Zhang L., Lu C., Tieu. K. A review on atomistic simulation of grain boundary behaviors in face-centered cubic metals // Comp. Mater. Sci. 2016. V. 118. P. 180–191. https://doi.org/10.1016/j.commatsci.2016.03.021

  8. Liu Z.-H., Feng Y.-X., Shang J.-X Characterizing twist grain boundaries in BCC Nb by molecular simulation: Structure and shear deformation // Applied Surface Science. 2016. V. 370 P. 19–24. https://doi.org/10.1016/j.apsusc.2016.02.097

  9. Frolov T., Setyawan W., Kurtz R.J., Marian J., Oganov A.R., Rudd R.E., Zhu Q. Grain boundary phases in bcc metals // Nanoscale. 2018. V. 10(17). P. 8253–8268. https://doi.org/10.1039/C8NR00271A

  10. Wang J., Beyerlein I.J. Atomic Structures of [01$\bar {1}$0] Symmetric Tilt Grain Boundaries in Hexagonal Close-Packed (hcp) Crystals // Metall. Mater. Trans. A. 2012. V. 43. P. 3556–3569. https://doi.org/10.1007/s11661-012-1177-610.1007/s11661-012-1177-6

  11. Liu P., Xie J., Wang A., Ma D., Mao Z. Molecular dynamics simulation on the deformation mechanism of monocrystalline and nano-twinned TiN under nanoindentation // Mater. Chem. Phys. 2020. V. 252. P. 123263. https://doi.org/10.1016/j.matchemphys.2020.123263

  12. Barrett C., Martinez J., Nitol M. Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in titanium // Metals. 2022. V. 12. P. 895. https://doi.org/10.3390/met12060895

  13. Wang J., Beyerlein. I.J. Atomic structures of symmetric tilt grain boundaries in hexagonal close packed (hcp) crystals // Modelling Simul. Mater. Sci. Eng. 2012. V. 20. P. 024002. https://doi.org/10.1088/0965-0393/20/2/024002

  14. Bhatia M.A., Solanki K.N. Energetics of vacancy segregation to symmetric tilt grain boundaries in hexagonal closed pack materials // J. Appl. Phys. 2013. V. 114. P. 244309. https://doi.org/10.1063/1.4858401

  15. Wang J., Yadav S.K., Hirth J.P., Tomé C.N., Beyerlein I.J. Pure-Shuffle Nucleation of Deformation Twins in Hexagonal-Close-Packed Metals// Materials Research Letters. 2013. V. 1. № 3. P. 126–132. https://doi.org/10.1080/21663831.2013.792019

  16. Ma Shang-Yi, Wang Shao-Qing. The formation and anisotropic/isotropic diffusion behaviors of vacancy in typical twin boundaries of α-Ti: An ab initio study// Comp. Mater. Sci. 2019. V. 159. P. 257–264. https://doi.org/10.1016/j.commatsci.2018.12.030

  17. Уразалиев М.Г., Ступак М.Е., Попов В.В. Атомистическое моделирование специальных границ наклона в α-Ti: структура, энергия, точечные дефекты, зернограничная самодиффузия // ФММ. 2022. Т. 123. № 6. С. 614–620.

  18. Urazaliev M.G., Stupak M.E., Popov V.V. Energetically favorable configurations of symmetric tilt grain boundaries in HCP titanium // AIP Conference Proceedings. 2022. V. 2466. P. 030047.

  19. Herzig C., Willecke R., Vieregge K. Self-diffusion and fast cobalt impurity diffusion in the bulk and in grain boundaries of hexagonal titanium // Phil. Mag. A. 1991. V. 63. № 5. P. 949–958. https://doi.org/10.1080/01418619108213927

  20. Herzig C., Wilger T., Przeorski T., Hisker F., Divinski S. Titanium tracer diffusion in grain boundaries of α-Ti. α2-Ti3Al. and γ-TiAl and in α2/γ interphase boundaries // Intermetallics. 2001. V. 9. P. 431–442. https://doi.org/10.1016/S0966-9795(01)00022-X

  21. Fiebig J., Divinski S., Rösner H., Estrin Y., Wilde G. Diffusion of Ag and Co in ultrafine-grained α-Ti deformed by equal channel angular pressing // J. Appl. Phys. 2011. V. 110. P. 083514. https://doi.org/10.1063/1.3650230

  22. Fernández J.R., Monti A.M., Pasianott R.C., Vitek V. An atomistic study of formation and migration of vacancies in (1121) twin boundaries in Ti and Zr // Phil. Mag. A. 2000. V. 80. № 6. P. 1349–1364. https://doi.org/10.1080/01418610008212123

  23. Oh S.-H., Seol D., Lee B.-J. Second nearest-neighbor modified embedded-atom method interatomic potentials for the Co-M (M = Ti, V) binary systems // Calphad. 2020. V. 70. P. 101791. https://doi.org/10.1016/j.calphad.2020.101791

  24. NIST Interatomic Potentials Repository: https:// www.ctcms.nist.gov/potentials.

  25. Kittel C., McEuen P. Introduction to Solid State Physics. V. 8. Wiley. New York, 1996.

  26. Fisher E.S., Renken C.J. Single-Crystal Elastic Moduli and the hcp → bcc Transformation in Ti, Zr, and Hf // Phys. Rev. 1964. V. 135. I.2A. P. 482. https://doi.org/10.1103/PhysRev.135.A482

  27. Hashimoto E., Smirnov E.A., Kino T. Temperature dependence of the Doppler-broadened lineshape of positron annihilation in α-Ti // J. Phys. F: Met. Phys. 1984. V. 14. P L215. https://doi.org/10.1088/0305-4608/14/10/004

  28. Tyson W.R., Miller W.A. Surface free energies of solid metals. Estimation from liquid surface tension measurements // Surf. Sci. 1977. V. 62. I. 1. P. 267–276. https://doi.org/10.1016/0039-6028(77)90442-3

  29. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics // J. Comp. Phys. 1995. V. 117. № 1. P. 1–19.https://doi.org/10.1006/jcph.1995.1039

  30. Hirel P. Atomsk: A tool for manipulating and converting atomic data files // Comput. Phys. Comm. 2015. V. 197. P. 212–219. https://doi.org/10.1016/j.cpc.2015.07.012

  31. Stukowski. A. Visualization and analysis of atomistic simulation data with OVITO – the Open Visualization Tool // Modelling Simul. Mater. Sci. Eng. 2010. V. 18. P. 015012. https://doi.org/10.1088/0965-0393/18/1/015012

  32. Suzudo T., Yamaguchi M., Hasegawa A. Stability and mobility of rhenium and osmium in tungsten: first principles study // Modelling Simul. Mater. Sci. Eng. 2014. V. 22. P. 075006. https://doi.org/10.1088/0965-0393/22/7/075006

  33. Nosé S. A unified formulation of the constant temperature molecular dynamics methods // J. Chem. Phys. 1984. V. 81. P. 511. https://doi.org/10.1063/1.447334

  34. Faken D., Jónsson H. Systematic Analysis of Local Atomic Structure Combined with 3D Computer Graphics // Comput. Mater. Sci. 1994. V. 2. P. 279–286. https://doi.org/10.1016/0927-0256(94)90109-0

  35. Suzuki A., Mishin Y. Atomistic Modeling of Point Defects and Diffusion in Copper Grain Boundaries // Interface Sci. 2003. V. 11. P. 131–148. https://doi.org/10.1023/A:1021599310093

  36. Starikov S., Mrovec M., Drautz R. Study of grain boundary self-diffusion in iron with different atomistic models // Acta Mater. 2020. V. 188. P. 560–569. https://doi.org/10.1016/j.actamat.2020.02.027

  37. Popov V.V. Mossbauer spectroscopy of interfaces in metals // Phys. Met. Metal. 2012. V. 113. № 13. P. 1257–1289. https://doi.org/10.1134/S0031918X12130029

  38. Grigoriev I.S., Meilikhov E.Z. Handbook of Physical Values. Energoatomizdat, Moscow, 1991.

  39. Ступак М.Е., Уразалиев М.Г., Попов В.В. Структура и энергия симметричных границ наклона 〈110〉 в поликристаллическом W // ФММ. 2020. Т. 121. № 8. С. 877–883. https://doi.org/10.31857/S0015323020080112

  40. Уразалиев М.Г., Ступак М.Е, Попов В.В. Структура и энергия симметричных границ наклона с осью 〈110〉 в Ni и энергии образования вакансий в границах зерен // ФММ. 2021. Т. 122. № 7. С. 713–720. https://doi.org/10.1134/S0031918X21070139

  41. Hallil A., Metsu A., Bouhattate J., Feaugas X. Correlation between vacancy formation and Σ3 grain boundary structures in nickel from atomistic simulations // Phil. Mag. 2016. V. 96. № 20. P. 2088–2114. https://doi.org/10.1080/14786435.2016.1189616

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал