Физика плазмы, 2019, T. 45, № 12, стр. 1157-1164

О МГД-колебаниях плазменного шнура конечной проводимости при наличии скачка параметров в пристеночной области

В. В. Арсенин^*

Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

Поступила в редакцию 14.05.2019
После доработки 20.06.2019
Принята к публикации 25.06.2019

DOI: 10.1134/S0367292119120011

Аннотация

В модели прямого цилиндра в сильном продольном магнитном поле рассматриваются МГД-колебания плазмы конечной проводимости в ситуации, когда в плазме отсутствует резонансная поверхность, на которой компонента волнового вектора возмущения вдоль поля обращается в нуль. При высокой проводимости имеются крупномасштабные, с радиальной длиной волны порядка радиуса шнура колебания, во всем объеме мало отличающиеся от тех, что описываются идеальной МГД. Показано, что при наличии скачка плотности и электронной температуры на некоторой магнитной поверхности около стенки, наряду с такими колебаниями, благодаря конечности проводимости возможно существование другой МГД-моды. В этой моде возмущения крупномасштабны и почти идеальны в большей части объема плазмы, но мелкомасштабны по радиальной координате и не идеальны в пристеночной области.

Ключевые слова: МГД, конечная проводимость, пристеночная плазма, крупномасштабная и мелкомасштабная составляющие колебаний

1. ВВЕДЕНИЕ

При высокой, но конечной проводимости плазмы вдоль магнитного поля радиальная собственная функция МГД-колебаний плазменного шнура включает две составляющие: крупномасштабную, которая при ${{\sigma }_{{||}}} \to \infty $ переходит в движение, описываемое идеальной МГД, и мелкомасштабную, характерный радиальный масштаб которой определяется величиной проводимости. Мелкомасштабная часть возмущения может быть локализована: около резонансной магнитной поверхности ${{k}_{{||}}} = {\mathbf{k}} \cdot {\mathbf{B}}{\text{/}}B = 0$, если таковая находится в плазме; около поверхностей резкого изменения параметров плазмы по радиусу; около стенки. Первый случай реализуется, в частности, в тиринг-неустойчивости. Вычисления мелкомасштабной составляющей в тиринг-неустойчивости при ограничении проводимости столкновениями проделаны в [1, 2], этой неустойчивости посвящена обширная литература. Подход [1, 2] применим и при другом механизме ограничения проводимости – из-за инерции электронов [3]. Локализация возле стенки имеет место при плавных радиальных профилях невозмущенных величин в отсутствие в плазме резонансной поверхности, причем в этом случае амплитуда мелкомасштабной составляющей мала по сравнению с крупномасштабной, и возмущение в целом мало отличается от идеальной МГД-моды [4]. В настоящей работе изучается роль конечности проводимости в колебаниях шнура в ситуации, когда резонанс ${{k}_{{||}}} = 0$ в плазме отсутствует, но есть резкое изменение проводимости на некоторой поверхности r = const вблизи стенки. В таком случае в МГД, помимо решения, всюду близкого к идеальной МГД-моде, при определенного вида дисперсии продольной проводимости может быть и другое крупномасштабное решение. Оно почти во всем объеме плазмы мало отличается от решения в идеальной МГД, однако содержит значительную мелкомасштабную неидеальную составляющую, локализованную в пристеночном слое.

2. УРАВНЕНИЯ КОЛЕБАНИЙ

Рассматриваем МГД-колебания длинного тонкого шнура плазмы конечной проводимости. Используем модель прямого цилиндра плазмы низкого давления, $\beta = 8\pi p{\text{/}}{{B}^{2}} \ll 1$, в сильном аксиальном магнитном поле, ${{B}_{z}} \gg {{B}_{\vartheta }}$. В предположении, что тензор проводимости диагональный и ${{\sigma }_{{||}}} \gg {{\sigma }_{ \bot }}$(значок $ \bot $ относится к направлениям поперек B), длинноволновые по z возмущения $ \propto {\kern 1pt} {\kern 1pt} \exp (im\vartheta - i{{k}_{z}}z - i\omega t)$ (при моделировании тонкого тороидального шнура ${{k}_{z}} = n{\text{/}}R$, R – большой радиус тора, n – тороидальное волновое число) электрического потенциала и вектор-потенциала магнитного поля описываются системой уравнений (см. [5, 6]) из z-компоненты уравнения Максвелла

(1)

${{\Delta }_{ \bot }}{{\tilde {A}}_{z}} - \frac{{4\pi }}{c}i{{\sigma }_{{||}}}\left( {{{k}_{{||}}}\tilde {\varphi } - \frac{\omega }{c}{{{\tilde {A}}}_{z}}} \right) = 0$

и уравнения квазинейтральности ($\nabla \cdot {\mathbf{\tilde {j}}} = 0$)

(2)

$ - {{\nabla }_{ \bot }} \cdot ({{\sigma }_{ \bot }}{{\nabla }_{ \bot }}\tilde {\varphi }) + \frac{{im}}{{r{{B}_{z}}}}\frac{{d{{j}_{z}}}}{{dr}}{{\tilde {A}}_{z}} + {{k}_{{||}}}{{\sigma }_{{||}}}\left( {{{k}_{{||}}}\tilde {\varphi } - \frac{\omega }{c}{{{\tilde {A}}}_{z}}} \right) = 0.$

Здесь ${{k}_{{||}}} = {\mathbf{k}} \cdot {\mathbf{B}}{\text{/}}B$ = ${{B}_{\vartheta }}(m - nq){\text{/}}r{{B}_{z}}$– проекция волнового вектора на направление B, $q(r)$ – запас устойчивости, ${{j}_{z}}$ – невозмущенная плотность тока, c – скорость света, ${{\nabla }_{ \bot }} = \nabla - \frac{{\mathbf{B}}}{B}\left( {\frac{{\mathbf{B}}}{B} \cdot \nabla } \right)$, ${{\Delta }_{ \bot }} = $ $ = \frac{d}{{rdr}}r\frac{d}{{dr}} - \frac{{{{m}^{2}}}}{{{{r}^{2}}}}$. Принято во внимание, что с точностью $\sim {\kern 1pt} {{({{k}_{z}}a)}^{2}}$, где a – радиус шнура, z – компонента плотности тока возмущения равна ${{\tilde {j}}_{{||}}}$, а лапласиан $\Delta {{\tilde {A}}_{z}}$ сводится к ${{\Delta }_{ \bot }}{{\tilde {A}}_{z}}$. Сделаем еще несколько пояснений. Величины ${{\tilde {j}}_{{r,\,\vartheta }}}$ малы по сравнению с ${{\tilde {j}}_{z}}$, поэтому компонентами ${{\tilde {A}}_{{r,\,\vartheta }}}$ в возмущении вектор-потенциала и с ними возмущением z-компоненты магнитного поля, ${{\tilde {B}}_{z}}$, пренебрежено – происходит только изгибание силовых линий с появлением ${{\tilde {B}}_{r}}$, ${{\tilde {B}}_{\vartheta }}$, без сгущения/разрежения. Влияние малой кривизны невозмущенного магнитного поля на колебания игнорируется. Поперечная проводимость ${{\sigma }_{ \bot }} = - (i\omega {\text{/}}4\pi )\omega _{{pi}}^{2}{\text{/}}\omega _{{ci}}^{2}$, где ${{\omega }_{{pi}}}$ и ${{\omega }_{{ci}}}$– ионные плазменная и циклотронная частоты, связана с инерцией ионов (поляризационным током); частоты колебаний много меньше ${{\omega }_{{ci}}}$, длины волн в направлении перпендикулярном ${\mathbf{B}}$ много больше ионного ларморовского радиуса ${{\rho }_{i}}$, конечностью ${{\rho }_{i}}$ пренебрегается, так что движение поперек B гидродинамическое ${{{\mathbf{\tilde {v}}}}_{ \bot }} = c{{{\mathbf{\tilde {E}}}}_{ \bot }} \times {\mathbf{B}}{\text{/}}{{B}^{2}}$, дрейфовые эффекты не учитываются. Если рассматривается ситуация (как в разд. 4), когда имеется слой с резким радиальным изменением этих величин, в котором дрейфовые эффекты могли бы быть важны, мы, чтобы остаться в рамках принятой модели, можем ограничиться случаем $m = 0$. У ${{\sigma }_{{||}}}$ есть, вообще говоря, не только временная, но и связанная с тепловым движением пространственная дисперсия, ${{\sigma }_{{||}}} = $ $ = {{\sigma }_{{||}}}(r,\omega ,{{k}_{{||}}})$.

Исключением

(3)

$\tilde {\varphi } = \frac{\omega }{{{{k}_{{||}}}c}}{{\tilde {A}}_{z}} + \frac{c}{{4\pi i{{k}_{{||}}}{{\sigma }_{{||}}}}}{{\Delta }_{ \bot }}{{\tilde {A}}_{z}}$

система (1), (2) приводится к одному уравнению четвертого порядка для ${{\tilde {A}}_{z}}$

(4)

$\begin{gathered} {{\nabla }_{ \bot }} \cdot \left[ {\varepsilon {{\nabla }_{ \bot }}\left( {\frac{\omega }{{{{k}_{{||}}}c}}{{{\tilde {A}}}_{z}} + \frac{c}{{{{k}_{{||}}}\omega \eta }}{{\Delta }_{ \bot }}{{{\tilde {A}}}_{z}}} \right)} \right] + \\ \, + \frac{{4\pi }}{\omega }\frac{m}{{r{{B}_{z}}}}\frac{{d{{j}_{z}}}}{{dr}}{{{\tilde {A}}}_{z}} = \frac{{{{k}_{{||}}}c}}{\omega }{{\Delta }_{ \bot }}{{{\tilde {A}}}_{z}}, \\ \end{gathered} $

где введены компоненты диагонального тензора диэлектрической проницаемости $\varepsilon = 4\pi i{{\sigma }_{ \bot }}{\text{/}}\omega $ и $\eta = 4\pi i{{\sigma }_{{||}}}{\text{/}}\omega $. Считается

(5)

$4\pi \left| {{{\sigma }_{{ \bot ,\,||}}}{\text{/}}\omega } \right| \gg 1,$

и вакуумное слагаемое в диэлектрическом тензоре в расчет не принимается. Неравенства (5) предполагаем выполненными вплоть до стенки, окружающей плазму. Саму стенку $r = a$ для простоты полагаем идеально проводящей.

Граничные условия на оси – ограниченность возмущения

(6)

${{\left. {{{{\tilde {A}}}_{z}}} \right|}_{{r = 0}}} < \infty ,$

(7)

${{\left. {\tilde {\varphi }} \right|}_{{r = 0}}} < \infty .$

На стенке

(8)

${{\left. {{{{\tilde {A}}}_{z}}} \right|}_{{r = a}}} = 0,$

(9)

${{\left. {\tilde {\varphi }} \right|}_{{r = a}}} = 0,$

что обеспечивает обращение в нуль тангенциальной компоненты электрического поля, которая в стенке равна нулю и должна быть непрерывной (иначе ${\mathbf{\tilde {B}}} = (c{\text{/}}i\omega )\nabla \times {\mathbf{\tilde {E}}}$ не будет ограничено). Имея в виду соотношение (3) и выполнение (8), условие (9) можно записать как

(9')

${{({{\Delta }_{ \bot }}{{\tilde {A}}_{z}})}_{{r = a}}} = 0.$

3. ДВА ТИПА РЕШЕНИЙ

При бесконечной продольной проводимости, $\eta = \infty $, уравнение (4) переходит в уравнение второго порядка

(10)

${{\nabla }_{ \bot }} \cdot \left[ {\varepsilon {{\nabla }_{ \bot }}\left( {\frac{\omega }{{{{k}_{{||}}}c}}{{{\tilde {A}}}_{z}}} \right)} \right] + \frac{{4\pi }}{\omega }\frac{m}{{r{{B}_{z}}}}\frac{{d{{j}_{z}}}}{{dr}}{{\tilde {A}}_{z}} = \frac{{{{k}_{{||}}}c}}{\omega }{{\Delta }_{ \bot }}{{\tilde {A}}_{z}}.$

Дополненное граничными условиями (6), (8), оно дает спектр возмущений в идеальной ($\tilde {\varphi } = (\omega {\text{/}}{{k}_{{||}}}c){{\tilde {A}}_{z}}$) МГД, зависящий от профиля тока и положения стенки [7]. Если невозмущенные величины изменяются по r на длинах $ \gtrsim {\kern 1pt} a$, где a – радиус шнура, то характерная частота (или при неустойчивости, инкремент) порядка альфвеновской. В рассматриваемом случае, когда в плазме отсутствует поверхность ${{k}_{{||}}} = 0$, характерная длина волны по r порядка a.

При высокой, но конечной продольной проводимости, ${{({{k}_{{||}}}a)}^{{ - 2}}} \ll \left| {\eta {\text{/}}\varepsilon } \right| < \infty $, уравнение (4) представляет собой уравнение с малым параметром при старших производных. Из четырех частных решений для двух – крупномасштабных по радиусу – слагаемое с ${{\eta }^{{ - 1}}}$ в (4) мало. Эти решения близки к решениям уравнения (10).

Два другие частные решения мелкомасштабные, сильно изменяющиеся по радиусу на расстоянии $\lambda \ll a$; для этих решений главными в уравнении (4) являются члены с радиальными производными. Если на длине λ вариации невозмущенных величин, включая $d\ln {{k}_{{||}}}{\text{/}}dr$, малы, то мелкомасштабные решения можно искать в квазиклассическом приближении${{\tilde {A}}_{z}} \propto g\exp \left( {\int {\kappa dr} } \right)$, где

(11)

$\kappa = \left| {{{k}_{{||}}}} \right|{{\left[ {\frac{\eta }{\varepsilon }{{{\left( {1 - \frac{{{{\omega }^{2}}}}{{\omega _{A}^{2}}}} \right)}}^{{ - 1}}}} \right]}^{{1/2}}},$

${{\omega }_{A}} = \left| {{{k}_{{||}}}} \right|c{\text{/}}{{\varepsilon }^{{1/2}}}$ – альфвеновская частота, $\left| {{{\kappa }^{{ - 1}}}d\ln g{\text{/}}dr} \right| \ll 1$. Формула (11) получается, когда в (4) оставлены только упомянутые главные члены. Два различающиеся решения соответствуют двум значениям квадратного корня. Величина λ имеет порядок $\left| {{{\kappa }^{{ - 1}}}} \right|$. Если $\left| \kappa \right|{{\rho }_{i}} \ll 1$, то и при наличии мелкомасштабной составляющей движение поперек ${\mathbf{B}}$ описывается МГД. Однако присутствие значительной мелкомасштабной составляющей делает неприменимой идеальную МГД, поскольку в (3) становится существенно слагаемое с лапласианом, так что $\tilde {\varphi } \ne (\omega {\text{/}}{{k}_{{||}}}c){{\tilde {A}}_{z}}$.

В радиальную собственную функцию, удовлетворяющую условиям (6)–(9), входят, вообще говоря, все четыре частные решения, причем их комбинация в разных областях по $r$ (например, разделенных поверхностью с разрывом параметров) может быть разной. При плавных, без резких изменений на расстояниях $ \lesssim {\kern 1pt} \lambda $, профилях компонент диэлектрического тензора ε, η собственная функция, помимо крупномасштабной составляющей, содержит только одно, привязанное к стенке и спадающее от нее внутрь плазмы, мелкомасштабное решение. Его амплитуда мала по сравнению с характерным значением крупномасштабной составляющей в объеме плазмы (что следует из необходимости соблюдения условия (9')), так что в целом собственная функция близка к идеальной моде [4]. Наша задача – рассмотреть ситуацию, когда величины ε, η не плавные, а со скачкообразным поведением в слое толщиной $ \lesssim {\kern 1pt} \lambda $. Нет ли в этом случае собственных МГД-колебаний, сильно отличающихся от идеальной моды, в которых мелкомасштабная составляющая ${{\tilde {A}}_{z}}$ сравнима по величине с крупномасштабной?

4. МОДЕЛЬ СО СКАЧКОМ ПРОВОДИМОСТЕЙ ОКОЛО СТЕНКИ

Пусть η и ε как функции радиальной координаты испытывают внутри плазмы, в окрестности $r = b$, скачки – перепады на расстоянии $ \lesssim {\kern 1pt} \lambda $. Считаем, что вне этой окрестности параметры плазмы, и с ними η, ε меняются плавно – на длинах $ \gtrsim {\kern 1pt} a$. Поскольку $\varepsilon = {{({{\omega }_{{pi}}}{\text{/}}{{\omega }_{{ci}}})}^{2}}$, то разрыв ε, если он есть, обязан разрыву плотности плазмы. В поведении $\eta (r)$ может играть роль и радиальная зависимость температуры. Пусть $D = a - b \ll a$. Примем для простоты, что на радиальной периферии шнура, которой принадлежит поверхность $r = b$ и в которой локализована мелкомасштабная составляющая ${{\tilde {A}}_{z}}$, плотность невозмущенного тока ${{j}_{z}}$ равна нулю.

Предполагаем, что для данных m и k_z величина ${{k}_{{||}}}$ в плазме не обращается в нуль и что для рассматриваемой частоты нет альфвеновского резонанса $\omega = {{\omega }_{A}}$.

При $r = b$ в возмущениях должны соблюдаться:

– непрерывность ${{\tilde {A}}_{z}}$

(12)

${{\left. {{{{\tilde {A}}}_{z}}} \right|}_{{r = b + 0}}} = {{\left. {{{{\tilde {A}}}_{z}}} \right|}_{{r = b - 0}}},$

так как скачок $[{{\tilde {A}}_{z}}]$ величины ${{\tilde {A}}_{z}}$ означал бы существование в тонком переходном слое δr большого поля ${{\tilde {B}}_{\vartheta }}\sim [{{\tilde {A}}_{z}}]{\text{/}}\delta r$, энергия которого $ \propto {\kern 1pt} {{[{{\tilde {A}}_{z}}]}^{2}}{\text{/}}\delta r$ при $\delta r \to 0$ стремится к бесконечности;

– следующая из непрерывности тангенциальной составляющей ${\mathbf{\tilde {E}}}$ непрерывность $\tilde {\varphi }$

(13)

${{\left. {\tilde {\varphi }} \right|}_{{r = b + 0}}} = {{\left. {\tilde {\varphi }} \right|}_{{r = b - 0}}},$

что можно записать в другой форме (напоминаем (3))

(13')

${{({{\eta }^{{ - 1}}}{{\Delta }_{ \bot }}{{\tilde {A}}_{z}})}_{{r = b + 0}}} = {{({{\eta }^{{ - 1}}}{{\Delta }_{ \bot }}{{\tilde {A}}_{z}})}_{{r = b - 0}}};$

– непрерывность $\partial {{\tilde {A}}_{z}}{\text{/}}\partial r$ (означающая непрерывность ${{\tilde {B}}_{\vartheta }}$)

(14)

${{\left. {\frac{{\partial {{{\tilde {A}}}_{z}}}}{{\partial r}}} \right|}_{{r = b + 0}}} = {{\left. {\frac{{\partial {{{\tilde {A}}}_{z}}}}{{\partial r}}} \right|}_{{r = b - 0}}},$

вытекающая из (1) благодаря ограниченности правой части;

– непрерывность радиальной компоненты электрической индукции

(15)

$\left[ {\varepsilon \frac{\partial }{{\partial r}}\left( {\frac{\omega }{{{{k}_{{||}}}c}}{{{\tilde {A}}}_{z}} + \frac{c}{{\omega {{k}_{{||}}}\eta }}{{\Delta }_{ \bot }}{{{\tilde {A}}}_{z}}} \right)} \right]_{{b - 0}}^{{b + 0}} = 0$

получается интегрированием (4).

4.1. Решения в пристеночной области

Величины, относящиеся к крупномасштабной составляющей возмущения, помечаем индексом L, к мелкомасштабной – индексом S. Чтобы не загромождать запись, индекс z у ${{\tilde {A}}_{z}}$ в дальнейшем опускаем.

Будем интересоваться возмущениями, в которых мелкомасштабная составляющая локализована около стенки и поверхности $r = b$. Длина ее экспоненциального спада от этих поверхностей привязки составляет $\Lambda = {{\left| {\operatorname{Re} \kappa } \right|}^{{ - 1}}}$. Пусть на каждом из двух участков по r: в примыкающем к поверхности $r = b$ промежутке толщиной $\sim {\kern 1pt} \Lambda $ при $r < b$ и в слое $b < r < a$ – относительные изменения невозмущенных величин и ${{k}_{{||}}}$ малы (в частности, ввиду тонкости пристеночного слоя, $D \ll a$, можно считать величины η и ε в нем равными соответственно ${{\left. \eta \right|}_{{r = a}}}$ и ${{\left. \varepsilon \right|}_{{r = a}}}$, каковые значения, напоминаем, полагаются отличными от нуля). В пренебрежении этими изменениями мелкомасштабная составляющая $\tilde {A}$ выглядит так:

при $r < b$

(16)

${{\tilde {A}}_{S}} = \tilde {A}_{S}^{{( - )}}\exp \left[ {{{\kappa }^{{( - )}}}(r - b)} \right],$

где $\tilde {A}_{S}^{{( - )}}$ – постоянная, ${{\kappa }^{{( - )}}}\;\; = \;\;\left| {{{k}_{{||}}}} \right|\;\; \times $ $ \times \;[{{\eta }^{{( - )}}}{\text{/}}{{\varepsilon }^{{( - )}}}{{(1 - {{\omega }^{2}}{\text{/}}\omega _{A}^{{( - )2}}]}^{{1/2}}}$, ${{\eta }^{{( - )}}} = {{\left. \eta \right|}_{{r = b - 0}}}$, ${{\varepsilon }^{{( - )}}} = {{\left. \varepsilon \right|}_{{r = b - 0}}}$, причем берется значение квадратного корня (11) с $\operatorname{Re} {{\kappa }^{{( - )}}} > 0$, с тем чтобы с удалением от $r = b$ в сумме $\tilde {A} = {{\tilde {A}}_{L}} + {{\tilde {A}}_{S}}$ осталось (при $a\operatorname{Re} {{\kappa }^{{( - )}}} \gg 1$) только ${{\tilde {A}}_{L}}$ и тем самым при ${{\left. {{{{\tilde {A}}}_{L}}} \right|}_{{axis}}} < \infty $ обеспечивалось выполнение граничных условий на оси;

при $b < r < a$

(17)

${{\tilde {A}}_{S}} = \tilde {A}_{S}^{{( + )}}\frac{{\operatorname{sh} \left( {{{\kappa }^{{( + )}}}(a - r)} \right)}}{{\operatorname{sh} \left( {{{\kappa }^{{( + )}}}(a - b)} \right)}},$

где $\tilde {A}_{S}^{{( + )}}$ – постоянная, ${{\kappa }^{{( + )}}}\;\; = \;\;\left| {{{k}_{{||}}}} \right|\;\; \times $ $ \times \;[{{\eta }^{{( + )}}}{\text{/}}{{\varepsilon }^{{( + )}}}{{(1 - {{\omega }^{2}}{\text{/}}\omega _{A}^{{( + )2}}]}^{{1/2}}}$, ${{\eta }^{{( + )}}} = {{\left. \eta \right|}_{{r = b + 0}}}$, ${{\varepsilon }^{{( + )}}} = {{\left. \varepsilon \right|}_{{r = b + 0}}}$, и взята такая линейная комбинация решений $\exp ( \pm {{\kappa }^{{( + )}}}r)$, чтобы выполнялось условие ${{\left. {{{{\tilde {A}}}_{S}}} \right|}_{{r = a}}} = 0$.

Что касается крупномасштабных частей, ${{\tilde {A}}_{L}}$, то в области $r < b$ берется крупномасштабное решение (4), ограниченное на оси, а в промежутке $b < r < a$ –решение, принимающее нулевое значение при $r = a$. Вообще говоря, эти функции – их вид мы уточним ниже – не составляют единого по всему радиусу крупномасштабного, без присутствия ${{\tilde {A}}_{S}}$, решения, удовлетворяющего условиям (6), (8) одновременно. Как упомянуто в разд. 3, при $\gamma \equiv {{({{k}_{{||}}}a)}^{2}}\left| {\eta {\text{/}}\varepsilon } \right| \gg 1$ и плавных профилях η, ε уравнение (4) имеет решения, в которых величина ${{\tilde {A}}_{S}}$ мала по сравнению с характерным (например, среднеквадратичным) значением ${{\tilde {A}}_{L}}(r)$ в сечении плазмы. Они мало отличаются от собственных функций ${{\tilde {A}}_{{ideal}}}$ задачи (10), (6), (8). По крайней мере в случае, когда на описываемой радиальной периферии плотность плазмы значительно меньше, чем в основном объеме, так что локальная альфвеновская частота на периферии сильно превышает собственную частоту,

(18)

${{\left. {{{\omega }_{A}}} \right|}_{{{\text{periph}}}}} \gg \left| \omega \right|,$

колебания, близкие к идеальной МГД-моде, имеются и при наличии скачка. В самом деле, при $\gamma \gg 1$, пренебрежении членом с ${{\eta }^{{ - 1}}}$ и соблюдении (18) уравнение (4) на бестоковой периферии имеет одинаковый вид (${{\Delta }_{ \bot }}\tilde {A} = 0$) независимо от радиального хода параметров. В этом приближении, если профили невозмущенных величин различаются только на разреженной периферии, то для них собственная функция возмущения почти одинакова и $ \approx {\kern 1pt} {{\tilde {A}}_{{ideal}}}$. Мы сейчас ищем решение, отличающееся от такого почти идеального: не предполагаем малости ${{\tilde {A}}_{S}}$ по сравнению с характерной величиной ${{\tilde {A}}_{L}}$ в плотной области, $\tilde {A}_{L}^{{(0)}}$, и малости ${{\tilde {A}}_{L}}$ при $r \geqslant b$ по сравнению с $\tilde {A}_{L}^{{(0)}}$. По одну сторону от разрыва параметров крупномасштабная составляющая

(19)

${{\tilde {A}}_{L}} = \tilde {A}_{L}^{{( - )}}F\left( {\frac{r}{a}} \right),\quad r < b,$

где $\tilde {A}_{L}^{{( - )}}$ – постоянная, а F – плавная функция, равная единице при $r = b$ и ограниченная на оси. Она близка к решению уравнения второго порядка (10) с теми же граничными условиями. (Конкретный вид этого решения задачи идеальной МГД для нас несуществен. Важно лишь, что оно мало изменяется на длине Λ. В дальнейшем будет фигурировать только амплитуда $\tilde {A}_{L}^{{( - )}}$ – значение ${{\tilde {A}}_{L}}$ при $r = b - 0$.) По другую сторону разрыва, в тонком, $D \ll a$, слое $b < r < a$ функцию ${{\tilde {A}}_{L}}$ с нулем на стенке можно представить разложением

(20)

${{\tilde {A}}_{L}} = \tilde {A}_{L}^{{( + )}}\frac{{a - r}}{D}\left( {1 + O\left( {\frac{{a - r}}{a}} \right)} \right),\quad r > b,$

$\tilde {A}_{L}^{{( + )}}$ – постоянная.

Будем полагать амплитуды $\tilde {A}_{L}^{{( - )}},$ $\tilde {A}_{L}^{{( + )}},$ $\tilde {A}_{S}^{{( - )}},$ $\tilde {A}_{S}^{{( + )}}$ одного порядка по параметру $\lambda {\text{/}}a$. При этом, поскольку в области локализации ${{\tilde {A}}_{S}}$ главный вклад в ${{\Delta }_{ \bot }}\tilde {A}$ вносит слагаемое ${{\partial }^{2}}{{\tilde {A}}_{S}}{\text{/}}\partial {{r}^{2}}$, а согласно (17) величина ${{({{\partial }^{2}}{{\tilde {A}}_{S}}{\text{/}}\partial {{r}^{2}})}_{{r = a}}} = 0$, то на стенке выполняются не только условие (8), но в главном порядке и требование (9'). Условия (6), (7) тоже удовлетворяются, так как величина мелкомасштабной составляющей колебаний ${{\tilde {A}}_{S}}$ (16) становится пренебрежимо малой вблизи оси плазменного цилиндра.

4.2. Сшивка решений при $r = b$

Запишем условия сшивки, используя малость λ по сравнению с длинами изменения крупномасштабной составляющей $\tilde {A}$ и невозмущенных величин вне переходного слоя.

Около поверхности $r = b$, в областях 0 < $ < \left| {(r - b)\kappa } \right| \lesssim 1$, лапласиан ${{\Delta }_{ \bot }}{{\tilde {A}}_{L}}$, фигурирующий в (13), (15), много меньше ${{\Delta }_{ \bot }}{{\tilde {A}}_{S}}$, а в равенстве (14) можно опустить, как малое $\sim {\kern 1pt} D{\text{/}}a$, слагаемое ${{\left. {\partial {{{\tilde {A}}}_{L}}{\text{/}}\partial r} \right|}_{{r = b - 0}}}$. Пусть выполняется неравенство (18), тогда в (15) существенны только члены с ${{\Delta }_{ \bot }}{{\tilde {A}}_{S}}$. В результате соотношения (12)–(15) сводятся к

(21)

$\tilde {A}_{L}^{{( - )}} + \tilde {A}_{S}^{{( - )}} = \tilde {A}_{L}^{{( + )}} + \tilde {A}_{S}^{{( + )}},$

(22)

$\frac{{{{\kappa }^{{( - )2}}}}}{{{{\eta }^{{( - )}}}}}\tilde {A}_{S}^{{( - )}} = \frac{{{{\kappa }^{{( + )2}}}}}{{{{\eta }^{{( + )}}}}}\tilde {A}_{S}^{{( + )}},$

(23)

${{\kappa }^{{( - )}}}\tilde {A}_{S}^{{( - )}} = - {{D}^{{ - 1}}}\tilde {A}_{L}^{{( + )}} - [{{\kappa }^{{( + )}}}\operatorname{cth} ({{\kappa }^{{( + )}}}D)]\tilde {A}_{S}^{{( + )}},$

(24)

$\frac{{{{\varepsilon }^{{( - )}}}}}{{{{\eta }^{{( - )}}}}}{{\kappa }^{{( - )2}}}{{\kappa }^{{( - )}}}\tilde {A}_{S}^{{( - )}} = - \frac{{{{\varepsilon }^{{( + )}}}}}{{{{\eta }^{{( + )}}}}}{{\kappa }^{{( + )2}}}[{{\kappa }^{{( + )}}}\operatorname{cth} ({{\kappa }^{{( + )}}}D)]\tilde {A}_{S}^{{( + )}},$

причем в ${{\kappa }^{{( - )}}}$ и ${{\kappa }^{{( + )}}}$ нужно множитель ${{(1 - {{\omega }^{2}}{\text{/}}\omega _{A}^{2})}^{{ - 1}}}$ положить, раз предполагается (18), равным единице.

Равенства (22), (24) совместимы, если

(25)

${{\varepsilon }^{{( - )}}}{{\kappa }^{{( - )}}} = - {{\varepsilon }^{{( + )}}}{{\kappa }^{{( + )}}}\operatorname{cth} ({{\kappa }^{{( + )}}}D).$

Входящие в ${{\kappa }^{{( - )}}}$, ${{\kappa }^{{( + )}}}$ величины ${{\eta }^{{( - )}}}$, ${{\eta }^{{( + )}}}$ зависят от частоты, и в случае разрешимости относительно $\omega $ (это возможно не при всяких ${{\eta }^{{( - )}}}$, ${{\eta }^{{( + )}}}$; решения нет, в частности, если ${{\eta }^{{( - )}}}$, ${{\eta }^{{( + )}}}$ вещественны и положительны) уравнение (25) дает собственную частоту, примеры будут приведены ниже. При этом отношение амплитуд $\tilde {A}_{S}^{{( + )}}$ и $\tilde {A}_{S}^{{( - )}}$ есть

(26)

$\frac{{\tilde {A}_{S}^{{( + )}}}}{{\tilde {A}_{S}^{{( - )}}}} = \frac{{{{\varepsilon }^{{( + )}}}}}{{{{\varepsilon }^{{( - )}}}}},$

а из (21)–(23) получаем связь $\tilde {A}_{S}^{{( - )}}$, $\tilde {A}_{S}^{{( + )}}$ и $\tilde {A}_{L}^{{( + )}}$ с $\tilde {A}_{L}^{{( - )}}$:

(27)

$\tilde {A}_{S}^{{( - )}} = \frac{{{{\varepsilon }^{{( - )}}}}}{{{{\varepsilon }^{{( + )}}} - {{\varepsilon }^{{( - )}}}}}\tilde {A}_{L}^{{( - )}},$

(28)

$\tilde {A}_{S}^{{( + )}} = \frac{{{{\varepsilon }^{{( + )}}}}}{{{{\varepsilon }^{{( + )}}} - {{\varepsilon }^{{( - )}}}}}\tilde {A}_{L}^{{( - )}},$

(29)

$\tilde {A}_{L}^{{( + )}} = 0.$

Подчеркнем, что хотя практически во всем объеме плазмы, $r < b - \xi \Lambda $, где ξ – несколько единиц, движение крупномасштабное ($\tilde {A} \approx {{\tilde {A}}_{L}}$) и почти идеальное, частота, находимая из (25), отлична от собственной частоты ${{\omega }_{{ideal}}}$ идеальной моды (10), (6), (8), так что радиальный ход $\tilde {A}$ существенно отличается от ${{\tilde {A}}_{{ideal}}}$. При приближении к стенке не происходит, как у функции ${{\tilde {A}}_{{ideal}}}$, падения $\tilde {A}$ до малых значений еще при $r < b - \xi \Lambda $. (Заметим в связи с этим, что для моды, близкой к ${{\tilde {A}}_{{ideal}}}$, мы не могли бы перейти от (14) к (23), так как порядок слагаемого ${{(\partial {{\tilde {A}}_{L}}{\text{/}}\partial r)}_{{r = b - 0}}}$ в (14) был бы ${{\left. {{{{\tilde {A}}}_{L}}} \right|}_{{r = b - 0}}}{\text{/}}D$.)

4.3. Примеры разрешимости (25)

Разрешимость уравнения (25) и тем самым существование решения, в котором амплитуды $\tilde {A}_{L}^{{( + )}}$, $\tilde {A}_{S}^{{( - )}}$, $\tilde {A}_{S}^{{( + )}}$ того же порядка по $\lambda {\text{/}}a$, что $\tilde {A}_{L}^{{( - )}}$, зависит от вида функций ${{\eta }^{{( - )}}}(\omega )$ и ${{\eta }^{{( + )}}}(\omega )$. Ниже даны два примера, когда разрешимость имеет место¹ ¹.

4.3.1. Пусть температура электронов в пристеночном промежутке $b < r < a$ много меньше, чем при $r < b$. Рассмотрим область частот

(30)

$\left| {{{k}_{{||}}}v_{{Te}}^{{( - )}}} \right| \gg \left| \omega \right| \gg \left| {{{k}_{{||}}}v_{{Te}}^{{( - )}}{{{({{m}_{e}}{\text{/}}{{m}_{i}})}}^{{1/2}}}} \right|,\quad \left| {{{k}_{{||}}}v_{{Te}}^{{( + )}}} \right|,$

${{v}_{T}}_{e}$ – тепловая скорость. В бесстолкновительном приближении продольная компонента диэлектрического тензора в окрестности поверхности $r = b$ при $\left| {\operatorname{Im} \omega {\text{/}}\operatorname{Re} \omega } \right| \ll 1$ выглядит как

(31а)

$\begin{gathered} {{\eta }^{{( - )}}} = \eta {\kern 1pt} {{'}^{{( - )}}} + i\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}},\quad \eta {\kern 1pt} {{'}^{{( - )}}} = \frac{{2\omega _{{pe}}^{{( - )2}}}}{{k_{{||}}^{2}v_{{Te}}^{{( - )2}}}}, \\ \left| {\frac{{\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}}}}{{\eta {\kern 1pt} {{'}^{{\left( - \right)}}}}}} \right| \ll 1,\quad \omega \eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}} > 0,\quad r = b - 0, \\ \end{gathered} $

(31б)

$\begin{gathered} {{\eta }^{{( + )}}} = \eta {\kern 1pt} {{'}^{{( + )}}} + i\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}},\quad \eta {\kern 1pt} {{'}^{{( + )}}} = - \frac{{\omega _{{pe}}^{{( + )2}}}}{{{{\omega }^{2}}}}, \\ \left| {\frac{{\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}}}}{{\eta {\kern 1pt} '{{{\kern 1pt} }^{{\left( + \right)}}}}}} \right| \ll 1,\quad \omega \eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}} > 0,\quad r = b + 0, \\ \end{gathered} $

см., например, [8]. В пренебрежении малой антиэрмитовой частью $\eta $ имеем

(32)

${{\kappa }^{{( - )}}} = {{K}^{{( - )}}},\quad {{K}^{{( - )}}} = \frac{1}{{\rho _{i}^{{( - )}}}}\sqrt {\frac{{T_{i}^{{( - )}}}}{{T_{e}^{{( - )}}}}} ,$

(33)

${{\kappa }^{{( + )}}} = i{{K}^{{( + )}}},\quad {{K}^{{( + )}}} = \sqrt {\frac{{{{m}_{i}}}}{{{{m}_{e}}}}} \left| {{{k}_{{||}}}} \right|\frac{{{{\omega }_{{ci}}}}}{{\left| \omega \right|}},$

и уравнение (25) принимает вид

(34)

${{\varepsilon }^{{( - )}}}{{K}^{{( - )}}} = - {{\varepsilon }^{{( + )}}}{{K}^{{( + )}}}\operatorname{ctg} ({{K}^{{( + )}}}D).$

При этом условие гидродинамичности $\left| {{{\kappa }^{{( - )}}}} \right|\rho _{i}^{{( - )}} \ll 1$ требует, чтобы было $T_{i}^{{( - )}} \ll T_{e}^{{( - )}}$. Для малости $\left| {{{\kappa }^{{( + )}}}} \right|\rho _{i}^{{( + )}}$ достаточно (поскольку $\left| {\omega {\text{/}}{{k}_{{||}}}v_{{Te}}^{{( + )}}} \right| \gg 1$), чтобы $T_{i}^{{( + )}}\tilde { < }T_{e}^{{( + )}}$. Отметим также, что для ${{\kappa }^{{( - )}}}$ (32) величина Λ того же порядка, что λ.

Из (34) получаем связь частоты с толщиной пристеночного слоя D

(35)

${{\omega }^{2}} = \frac{{{{m}_{i}}}}{{{{m}_{e}}}}{{\left( {{{\omega }_{{ci}}}\frac{{{{k}_{{||}}}D}}{\alpha }} \right)}^{2}},$

где α – один из корней уравнения

(36)

$\alpha \operatorname{ctg} \alpha = - \frac{{{{\varepsilon }^{{( - )}}}}}{{{{\varepsilon }^{{( + )}}}}}{{K}^{{( - )}}}D.$

В функции $\omega (D)$ допустимые D – такие, чтобы значение $\omega $ принадлежало интервалу $\left| \omega \right| < \min {{\omega }_{A}}$, так что альфвеновский резонанс невозможен² ².

Поясним роль связи (34). В области 0 < $ < r < b - \xi \lambda $ функция $\tilde {A}$, сводящаяся там к ${{\tilde {A}}_{L}}$, подчиняется фактически (ввиду того, что в крупномасштабных колебаниях член с ${{\eta }^{{ - 1}}}$ в (4) мал) уравнению второго порядка (10), при соблюдении (6) ход $\tilde {A}(r)$ в этой области предопределен частотой ω. Если последняя не близка к собственной частоте ${{\omega }_{{ideal}}}$ в задаче (10), (6), (8), то продолжение этого решения в область $r > b - \xi \lambda $ не будет удовлетворять условию (8) на стенке. При выполнении (34) функция ${{\left. {{{{\tilde {A}}}_{L}}} \right|}_{{r < b - \xi \lambda }}}$ может быть сшита с решением ${{\left. {\tilde {A}} \right|}_{{r > b - \xi \lambda }}}$ полного уравнения четвертого порядка (4), удовлетворяющим требованиям (8), (9'). Эти требования выполняются благодаря тому, что в периферийной области в колебаниях участвует неидеальная мелкомасштабная составляющая. Отметим, что для небольших $\alpha \sim \pi $ расстояние D, при котором существует наше решение, порядка длины λ. Если интересоваться колебаниями выявленного типа с частотой, равной некоторой доле $\varsigma $ от альфвеновской частоты, рассчитанной по плотности ${{n}_{0}}$ в центральной области плазменного цилиндра, то они возможны при $D\sim \varsigma {{({{r}_{0}}{{n}_{0}})}^{{ - 1/2}}}$, где ${{r}_{0}} = $ $ = {{e}^{2}}{\text{/}}{{m}_{e}}{{c}^{2}}$ – классический радиус электрона.

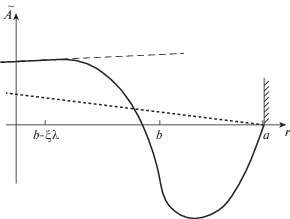
Радиальная зависимость возмущения около стенки показана на рис. 1.

Рис. 1.

Радиальная зависимость вектор-потенциала возмущения в пристеночной области при ${{\eta }^{{( - )}}}$ (31а) и ${{\eta }^{{( + )}}}$ (31б) в случае ${{\varepsilon }^{{( + )}}} < {{\varepsilon }^{{( - )}}}$. Сплошная линия –$\tilde {A}$ при $\omega \ne {{\omega }_{{ideal}}}$. В области $r < b - \xi \lambda $ изменение $\tilde {A}$ на длине λ слабое, $\lambda \left| {d\ln \tilde {A}{\text{/}}dr} \right| \ll 1$. Штриховая линия – продолжение $\tilde {A}_{L}^{{( - )}}$ в область $r > b - \xi \lambda $. Пунктир – ход крупномасштабной моды, близкой к идеальной ($\omega \approx {{\omega }_{{ideal}}}$).

При учете $\eta {\kern 1pt} '{{'}^{{( + )}}}$, $\eta {\kern 1pt} '{{'}^{{( - )}}}$, из-за которых появляются $\operatorname{Im} {{\kappa }^{{( - )}}}$ и $\operatorname{Re} {{\kappa }^{{( + )}}}$, собственная частота приобретает мнимую добавку, соответствующую затуханию. Из (25) несложно найти декремент

(37)

$\begin{gathered} \Gamma = \\ = \frac{{{{\varepsilon }^{{( + )}}}}}{{{{\varepsilon }^{{( - )}}}}}{{\left[ {(1 + {{{\operatorname{tg} }}^{2}}\alpha ){{K}^{{( - )}}}D + \frac{{{{\varepsilon }^{{( + )}}}}}{{{{\varepsilon }^{{( - )}}}}}} \right]}^{{ - 1}}}\frac{{\omega \eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}}}}{{2\eta {\kern 1pt} {{'}^{{( - )}}}}} + \frac{{\omega \eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}}}}{{2\left| {\eta {\kern 1pt} {{'}^{{( + )}}}} \right|}}. \\ \end{gathered} $

4.3.2. Другой пример разрешимости (25). Пусть, как и в предыдущем пункте, температура $T_{e}^{{( - )}}$ существенно больше $T_{e}^{{( + )}}$, но рассматривается область частот $\left| {\omega {\text{/}}{{k}_{{||}}}{{v}_{{Te}}}} \right| \gg 1$. При этом по обе стороны от поверхности $r = b$ имеем $\eta \approx \eta {\kern 1pt} ' = $ $ = - \omega _{{pe}}^{2}{\text{/}}{{\omega }^{2}}$. Вклад же в η черенковского взаимодействия волны с частицами $\eta {\kern 1pt} '{\kern 1pt} ' \propto \exp ( - {{(\omega {\text{/}}{{k}_{{||}}}{{v}_{{Te}}})}^{2}})$, и, поскольку $v_{{Te}}^{{( - )}} > v_{{Te}}^{{( + )}}$, то $\left| {\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}}{\text{/}}\eta {\kern 1pt} {{'}^{{( - )}}}} \right| \gg \left| {\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}}{\text{/}}\eta {\kern 1pt} {{'}^{{( + )}}}} \right|$. Имея в виду последнее неравенство, слагаемым $\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( + )}}}$ в ${{\eta }^{{( + )}}}$ пренебрежем, а $\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}}$ в ${{\eta }^{{( - )}}}$ оставим. Будем предполагать, что $\left| {\operatorname{Im} \omega {\text{/}}\operatorname{Re} \omega } \right| \ll 1$ и

(38)

$\eta {\kern 1pt} '{{'}^{{( - )}}}\operatorname{Re} \omega \gg 2[\omega _{{pe}}^{{2( - )}}{\text{/}}{{(\operatorname{Re} \omega )}^{2}}]\left| {\operatorname{Im} \omega } \right|,$

так что и при $\operatorname{Im} \omega \ne 0$ мнимая часть ${{\eta }^{{( - )}}}$ определяется именно величиной $\eta {\kern 1pt} '{{'}^{{( - )}}}$. Тогда при $r < b$ требование спада мелкомасштабной составляющей вглубь шнура, $\operatorname{Re} {{\kappa }^{{( - )}}} > 0$, оставляет из двух значений $\kappa = \left| {{{k}_{{||}}}} \right|{{(\eta {\text{/}}\varepsilon )}^{{1/2}}}$ одно:

(39)

${{\kappa }^{{( - )}}} \approx i\bar {K}\left( {1 - \frac{{i\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - )}}}}}{{2\left| {\eta {\kern 1pt} {{'}^{{( - )}}}} \right|}}} \right)\operatorname{sign} \operatorname{Re} \omega ,$

где $\bar {K} = \left| {{{k}_{{||}}}} \right|\sqrt {\left| {\eta {\kern 1pt} {{'}^{{( - )}}}} \right|{\text{/}}{{\varepsilon }^{{( - )}}}} $, $\eta {\kern 1pt} {{'}^{{( - )}}} = - \omega _{{pe}}^{{( - )2}}{\text{/}}{{(\operatorname{Re} \omega )}^{2}}$ и второе слагаемое в скобках по абсолютной величине $ \ll {\kern 1pt} 1$. В пренебрежении этим слагаемым соотношение (25) сведется к

(40)

$i{{\varepsilon }^{{( - )}}}\bar {K}\operatorname{sign} \operatorname{Re} \omega = - {{\varepsilon }^{{( + )}}}{{\kappa }^{{( + )}}}\operatorname{cth} ({{\kappa }^{{( + )}}}D),$

здесь

(41)

${{\kappa }^{{( + )}}} = {{\left( { - \frac{{k_{{||}}^{2}\omega _{{pe}}^{{( + )2}}}}{{{{\varepsilon }^{{( + )}}}{{\omega }^{2}}}}} \right)}^{{1/2}}} \approx i\sqrt {\frac{{k_{{||}}^{2}\omega _{{pe}}^{{( + )2}}}}{{{{\varepsilon }^{{( + )}}}{{{(\operatorname{Re} \omega )}}^{2}}}}} \left( {1 - \frac{{i\operatorname{Im} \omega }}{{\operatorname{Re} \omega }}} \right).$

Пусть ${{\varepsilon }^{{( + )}}} \ll {{\varepsilon }^{{( - )}}}$. Интересуемся решением (40) с $\left| {{{\kappa }^{{( + )}}}} \right|D \gtrsim 1$. Учитывая, что $\bar {K}{\text{/}}\left| {{{\kappa }^{{( + )}}}} \right| \approx 1$ (входящее в $\kappa $ отношение $\eta {\kern 1pt} '{\text{/}}\varepsilon $ не зависит от плотности), в первом приближении по ${{\varepsilon }^{{( + )}}}{\text{/}}{{\varepsilon }^{{( - )}}}$имеем

(42)

$\begin{gathered} \sqrt {\frac{{{{m}_{i}}}}{{{{m}_{e}}}}} \frac{{{{\omega }_{{ci}}}}}{{|\operatorname{Re} \omega |}}\left| {{{k}_{{||}}}} \right|D\left( {1 - i\frac{{\operatorname{Im} \omega }}{{\operatorname{Re} \omega }}} \right) = \\ \, = \pi + i\frac{{{{\varepsilon }^{{( + )}}}}}{{{{\varepsilon }^{{( - )}}}}}\operatorname{sign} \operatorname{Re} \omega ; \\ \end{gathered} $

взят наименьший отличный от нуля корень $\alpha = \pi $ уравнения $\operatorname{tg} \alpha = 0$ (для простоты и в согласии с примечанием 2 мы ограничились самым длинноволновым по r решением в области $b < r < a$). Отсюда

(43)

${{(\operatorname{Re} \omega )}^{2}} = \frac{{{{m}_{i}}}}{{{{m}_{e}}}}{{\left( {{{\omega }_{{ci}}}\frac{{{{k}_{{||}}}D}}{\pi }} \right)}^{2}},$

(44)

$\operatorname{Im} \omega = - \frac{{{{\varepsilon }^{{( + )}}}}}{{\pi {{\varepsilon }^{{( - )}}}}}\left| {\operatorname{Re} \omega } \right|.$

При малых ${{\varepsilon }^{{( + )}}}{\text{/}}{{\varepsilon }^{{( - )}}}$ исходное предположение $\left| {\operatorname{Im} \omega {\text{/}}\operatorname{Re} \omega } \right| \ll 1$ и условие (38) выполняются.

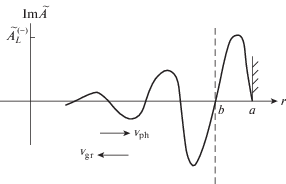
Обратим внимание на то, что в мнимую добавку (44) величины $\eta {\kern 1pt} '{\kern 1pt} {{'}^{{( - , + )}}}$ не входят. Наличие у η антиэрмитовой компоненты проявилось, однако, в отборе (39), в результате которого мелкомасштабная составляющая $\tilde {A}$ в области $b - \xi \Lambda < r < b$ представляет собой в первом приближении по $\eta {\kern 1pt} '{\kern 1pt} '{\text{/}}\eta {\kern 1pt} '$ волну, бегущую по r: мнимая часть величины ${{\kappa }^{{( - )}}}$ (39) отлична от нуля (она даже много больше действительной части). Радиальная фазовая скорость волны направлена к поверхности $r = b$, а групповая скорость и вместе с нею поток энергии – от этой поверхности. Именно бегущий характер мелкомасштабной составляющей при $r < b$, в конечном счете обязанный резистивности, обуславливает затухание колебаний (43), имеющих положительную энергию. Радиальная структура возмущения иллюстрируется рис. 2, на котором для случая вещественного и положительного $\tilde {A}_{L}^{{( - )}}$ показано поведение $\operatorname{Im} \tilde {A}(r)$. Что касается $\operatorname{Re} \tilde {A}$, то при $r < b - \xi \Lambda $ она близка к $\tilde {A}_{L}^{{( - )}}$ (которая в свою очередь близка к $\tilde {A}_{{L\;ideal}}^{{( - )}}$), в промежутке $b - \xi \Lambda < r < b$ по мере приближения к $r = b$ уменьшается, испытывая осцилляциии по r, а при $b < r < a$ мала, как $({{\varepsilon }^{{( + )}}}{\text{/}}{{\varepsilon }^{{( - )}}})A_{L}^{{( - )}}$.

Рис. 2.

$\operatorname{Im} \tilde {A}$как функция радиальной координаты при вещественном $\tilde {A}_{L}^{{( - )}} > 0$ в случае $\eta {\kern 1pt} {{'}^{{( - , + )}}} = $ $ = - \omega _{{pe}}^{{( - , + )\,2}}{\text{/}}{{\omega }^{2}}$.

4.4 Дополнительные замечания

1. В предположении (18) соотношение $\nabla \cdot {\mathbf{\tilde {j}}} = 0$ (4) для мелкомасштабной составляющей в области $b - \xi \Lambda < r < a$ есть уравнение почти потенциальных (${\mathbf{\tilde {E}}} \approx - \nabla \tilde {\varphi }$) колебаний

(45)

$\begin{gathered} 0 = {{\nabla }_{ \bot }} \cdot \left[ {\varepsilon {{\nabla }_{ \bot }}\left( {\frac{c}{{{{k}_{{||}}}\omega \eta }}{{\Delta }_{ \bot }}\tilde {A}} \right)} \right] - \frac{{{{k}_{{||}}}c}}{\omega }{{\Delta }_{ \bot }}\tilde {A} \approx \\ \, \approx \frac{\partial }{{\partial r}}\left[ {\varepsilon \frac{\partial }{{\partial r}}\left( {\frac{c}{{{{k}_{{||}}}\omega \eta }}\left( {\frac{{{{\partial }^{2}}\tilde {A}}}{{\partial {{r}^{2}}}}} \right)} \right)} \right] - \frac{{{{k}_{{||}}}c}}{\omega }\frac{{{{\partial }^{2}}\tilde {A}}}{{\partial {{r}^{2}}}} = \\ \, = \frac{c}{{{{k}_{{||}}}\omega \eta }}\left\{ {\frac{\partial }{{\partial r}}\left[ {\varepsilon \frac{\partial }{{\partial r}}\left( {\left( {\frac{{{{\partial }^{2}}\tilde {A}}}{{\partial {{r}^{2}}}}} \right)} \right)} \right] - \eta k_{\parallel }^{2}\frac{{{{\partial }^{2}}\tilde {A}}}{{\partial {{r}^{2}}}}} \right\} = \\ \, = \frac{\partial }{{\partial r}}\left( {\varepsilon \frac{{\partial{ \tilde {\varphi }}}}{{\partial r}}} \right) - \eta k_{{||}}^{2}\tilde {\varphi }, \\ \end{gathered} $

где выражение для возмущения потенциала, $\tilde {\varphi } = (c{\text{/}}{{k}_{{||}}}\omega \eta ){{\partial }^{2}}\tilde {A}{\text{/}}\partial {{r}^{2}}$, согласуется с (3), так как ${{\Delta }_{ \bot }}\tilde {A} \approx {{\partial }^{2}}\tilde {A}{\text{/}}\partial {{r}^{2}} = {{\kappa }^{2}}\tilde {A}$ и первое слагаемое в правой части (3) мало. При этом, однако, присутствие почти идеальной крупномасштабной составляющей $\tilde {A}_{L}^{{( - )}}$ в колебаниях обязательно: без нее невозможна непрерывность $\tilde {A}$ при $r = b$.

2. Для рассмотренной мелкомасштабной составляющей, поперечные волновые числа в которой имеют порядок $\left| \kappa \right|\sim \left| {{{k}_{{||}}}{{{({{\sigma }_{{||}}}{\text{/}}{{\sigma }_{ \bot }})}}^{{1/2}}}} \right|$, заложенное в относительно простую модель колебаний (1), (2) представление о важности лишь диагональных компонент диэлектрического тензора (так что z-компонента плотности тока возмущения ${{\tilde {j}}_{z}} \approx {{\sigma }_{{||}}}{{\tilde {E}}_{{||}}}$, а вклады ${{\sigma }_{{zr}}}{{\tilde {E}}_{r}}$, ${{\sigma }_{{z\vartheta }}}{{\tilde {E}}_{\vartheta }}$ в нее, связанные с недиагональными компонентами тензора проводимости, малы), является оправданным, поскольку выполняется неравенство ${{\left| {{{\sigma }_{{zr}}}} \right|}^{2}} \ll \left| {{{\sigma }_{ \bot }}{{\sigma }_{\parallel }}} \right|$.

3. В описанной моде энергия магнитного поля возмущения, сосредоточенная около стенки, оказывается, благодаря большому вкладу компоненты ${{\tilde {B}}_{\vartheta }}$, пропорциональному ${{(\partial{ \tilde {A}}{\text{/}}\partial r)}^{2}}$, много больше, чем во всем остальном объеме плазмы. В отличие от идеальной МГД-моды, где при $\left| {\omega {\text{/}}{{k}_{{||}}}c} \right| \ll 1$ плотность магнитной энергии ${{\tilde {B}}^{2}}{\text{/}}8\pi $ много больше ${{\tilde {E}}^{2}}{\text{/}}8\pi $, в решении с неидеальной мелкомасштабной составляющей, локализованной на радиальной периферии, в этой области величина ${{\tilde {E}}^{2}}{\text{/}}8\pi $ может быть больше ${{\tilde {B}}^{2}}{\text{/}}8\pi $.

4. В разобранных примерах конечность продольной проводимости (ограниченность η), которая обеспечивает существование мелкомасштабной составляющей у возмущения, не связана с резистивностью плазмы: диэлектрической проницаемости (31а) отвечает емкостный характер импеданса, а (31б) – индуктивный.

5. ЗАКЛЮЧЕНИЕ

Итак, в плазме высокой, но конечной проводимости, кроме колебаний, мало отличающихся во всем объеме шнура от идеальной МГД-моды $\omega = \omega (m,{{k}_{z}})$, возможно (по крайней мере при $m = 0$, когда дрейфовые эффекты не важны) – при наличии скачка плотности и электронной температуры в окрестности некоторой магнитной поверхности, находящейся на малом, порядка длины изменения мелкомасштабной составляющей возмущения, расстоянии D от стенки, – существование другой МГД-моды, почти идеальной в большей части объема и неидеальной (почти потенциальной) в пристеночной области. Ее частота связана с этим расстоянием: $\omega = \omega ({{k}_{z}},D)$.

Автор благодарен А.М. Какурину, А.С. Кукушкину и А.В. Тимофееву за обсуждения.

Список литературы

Furth H.P., Killeen J., Rosenbluth M.N. // Phys. Fluids. 1963. V. 6. P. 459.
Johnson J.L., Green J.M., Coppi B. // Phys. Fluids. 1963. V. 6. P. 1169.
Погуце О.П., Юрченко Э.И. // Физика плазмы. 1977. Т. 3. С. 504. [O.P. Pogutse, E.I. Yurchenko // Sov. J. Plasma Phys. 3, 283 (1977)]
Арсенин В.В. // Физика плазмы. 2018. Т. 44. С. 855. [V.V. Arsenin // Plasma Phys. Rep. 44, 967 (2018)]
Кадомцев Б.Б., Погуце О.П. Вопросы теории плазмы. Вып. 5 / Под ред. М.А. Леонтовича. М.: Атомиздат, 1967. С. 209. [B.B. Kadomtsev, O.P. Pogutse. Reviews of Plasma Physics. Vol. 5 / Leontovich M.A., Ed. Consultants Bureau, New York, London, 1970]
Rutherford P.H., Furth H.P., Rosenbluth M.N. // Plasma Phys. Controlled Nuclear Fusion Res. (Proc. IV IAEA Conf., Madison, 1971. CN 28/F-16). Vienna: IAEA, 1971. V. II. P. 553.
Шафранов В.Д. // ЖТФ. 1970. Т. 40. С. 241. [V.D. Shafranov // Sov. Phys. Tech. Phys. 15, 175 (1970)]
Шафранов В.Д. Вопросы теории плазмы. Вып. 3 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963. С. 3. [V.D. Shafranov. Reviews of Plasma Physics. Vol. 3 / Leontovich M.A., Ed. Consultants Bureau, New York, 1967]

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал