Физика плазмы, 2019, T. 45, № 3, стр. 258-267
Влияние магнитного поля на спектральные характеристики теплового движения заряженных частиц в изотропной ловушке
О. С. Ваулина a, *, Э. А. Саметов b
a Объединенный институт высоких температур РАН
Москва, Россия
b Московский физико-технический институт
Московская обл., Долгопрудный, Россия
* E-mail: olga.vaulina@bk.ru
Поступила в редакцию 26.07.2018
После доработки 16.08.2018
Принята к публикации 20.09.2018
Аннотация
Представлены результаты аналитического и численного исследований влияния постоянного магнитного поля на спектральные характеристики теплового движения заряженных частиц в изотропной электростатической ловушке. Предложено аналитическое соотношение для спектральной плотности смещений центра масс исследуемых систем. Полученное соотношение проверено путем численного моделирования для ансамблей с различным количеством частиц, взаимодействующих с кулоновским потенциалом в широком диапазоне параметров.
1. ВВЕДЕНИЕ
Броуновское движение в системах взаимодействующих частиц широко распространено в природе и наблюдается, например, в биологических и полимерных коллоидных растворах, в плазме продуктов сгорания, в атмосфере Земли и т.д. [1–6]. Особый интерес вызывает влияние теплового движения заряженных частиц на их динамику во внешних магнитных и электрических полях [7–12].
Экспериментальный, теоретический и численный анализ теплового движения взаимодействующих пылевых частиц в протяженных и ограниченных ансамблях, формирующихся в газоразрядной плазме без магнитного поля, представлен в работах [13–19]. Зависимости траекторий и среднеквадратичных смещений одиночной броуновской частицы (N = 1) в электростатической ловушке под воздействием магнитного поля исследовались в теоретических работах [8–10]. Влияние теплового движения ограниченного облака заряженных частиц (N ≤ 500) на их динамику в постоянных электрических и магнитных полях недавно исследовалось численно в [11, 12]. Экспериментальные исследования динамики пылевых частиц в магнитном поле представлены в работах [20–23] для газоразрядной плазмы.
Значительный рост интереса к исследованиям динамики заряженных частиц во внешних электромагнитных полях, наблюдаемый в настоящее время, по большей части связан с проблемами эффективности энергетических установок для управляемого термоядерного синтеза [24–26], а также с развитием плазменных методов переработки отработанного ядерного топлива (ОЯТ) и радиоактивных отходов (РАО) [27–31].
В настоящей работе представлены аналитические и численные исследования спектральной плотности для тепловых смещений центра масс ансамблей заряженных частиц в потенциальном поле электростатической ловушки под воздействием постоянного магнитного поля. В обычных тлеющих разрядах (как переменного, так и постоянного токов) в отсутствие магнитного поля, В = 0, в центре газоразрядных камер наблюдается некоторое превышение концентрации ионов над электронной концентрацией [32]. Данное обстоятельство приводит к формированию эффективных ловушек для отрицательно заряженных частиц (например, для частиц пыли [5, 6]). В плазме с магнитным полем, В ≠ 0, в центре газоразрядной камеры ситуация может быть обратной (за счет “замагничивания” электронов плазмы), т.е. могут существовать условия для удержания положительно заряженных частиц и/или ионов. Так, например, наличие электростатических ловушек для положительно заряженных ионов в установках по разделению компонентов ОЯТ может возникать за счет “замагничивания” электронов на осях камер разрядов зеркального (отражательного) типа, которые обычно используются для данных целей [27–31].
Следует отметить, что в отличие от других характеристик системы (параметра неидельности, коэффициентов тепло- и массопереноса, среднеквадратичных смещений частиц и т.д.), информация о спектральной плотности тепловых смещений частиц позволяет анализировать спектр частот собственных колебаний в исследуемых системах. Это, в свою очередь, дает возможность оценить реакцию системы на кратковременные или периодические внешние возмущения [33].
2. ОСНОВНЫЕ УРАВНЕНИЯ
Запишем уравнения движения (уравнения Ланжевена) для одной заряженной частицы с массой M и зарядом Q в постоянном электрическом поле ловушки ${\mathbf{E}} = [{{E}_{x}},{{E}_{y}},{{E}_{z}}]$ и в магнитном поле В = Вy (направленном по оси y) под воздействием случайной силы ${{{\mathbf{F}}}_{b}} = [{{F}_{{bx}}},{{F}_{{by}}},{{F}_{{bz}}}]$, которая является источником стохастической (тепловой) энергии частиц
(2)
$\frac{{d{{V}_{x}}}}{{dt}} = - \nu {{V}_{x}} - \omega _{t}^{2}x + {{\omega }_{В }}{{V}_{z}} + \frac{{{{F}_{{bx}}}}}{M},$(3)
$\frac{{d{{V}_{z}}}}{{dt}} = - \nu {{V}_{z}} - \omega _{t}^{2}z - {{\omega }_{В }}{{V}_{x}} + \frac{{{{F}_{{bz}}}}}{M}.$Здесь y, x, z – смещения частицы от ее равновесного положения, ${{V}_{y}} = dy{\text{/}}dt$, ${{V}_{x}} = dx{\text{/}}dt$, ${{V}_{z}} = dz{\text{/}}dt$, ν – коэффициент трения заряженных частиц за счет их столкновений с нейтралами окружающего газа, ωt =(Qα/M)1/2 – характерная частота ловушки, ωВ = QВ/M – циклотронная частота вращения в магнитном поле В, α – величина градиента внешнего электрического поля E, а В – величина индукции магнитного поля.
Корни характеристического уравнения (ωВ = 0) для (1) имеют хорошо известный вид
(4)
$\lambda _{{1,2}}^{*} = - \frac{\nu }{2} \pm i{{\left( {\omega _{t}^{2}--\frac{{{{\nu }^{2}}}}{4}} \right)}^{{1/2}}}.$Корни характеристического уравнения для системы (2), (3) можно записать в виде
где ${{\Psi }_{1}} = \nu (1 + {{D}_{1}}{\text{/}}\sqrt 2 ){\text{/}}2$, ${{\Psi }_{2}} = \nu (1 - {{D}_{1}}{\text{/}}\sqrt 2 ){\text{/}}2$, ${{\Omega }_{1}} = $ $ = ({{\omega }_{B}} + \nu {{D}_{2}}{\text{/}}\sqrt 2 ){\text{/}}2$, ${{\Omega }_{2}} = ({{\omega }_{B}} - \nu {{D}_{2}}{\text{/}}\sqrt 2 ){\text{/}}2$,(6а)
$\begin{gathered} {{D}_{1}} = \left[ {{{{\left( {{{{\left[ {1 - {{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}} - 4{{{\left( {\frac{{{{\omega }_{t}}}}{\nu }} \right)}}^{2}}} \right]}}^{2}} + 4{{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}}} \right)}}^{{1/2}}} + } \right. \\ {{\left. {\mathop + \limits_{_{{_{{_{{_{{_{{}}}}}}}}}}}^{^{{^{{}}}}} \;1 - {{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}} - 4{{{\left( {\frac{{{{\omega }_{t}}}}{\nu }} \right)}}^{2}}} \right]}^{{1/2}}}, \\ \end{gathered} $(6б)
$\begin{gathered} {{D}_{2}} = \left[ {{{{\left( {{{{\left[ {1 - {{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}} - 4{{{\left( {\frac{{{{\omega }_{t}}}}{\nu }} \right)}}^{2}}} \right]}}^{2}} + 4{{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}}} \right)}}^{{1/2}}} - } \right. \\ {{\left. {\mathop - \limits_{_{{_{{_{{}}}}}}}^{^{{^{{}}}}} \;1 + {{{\left( {\frac{{{{\omega }_{В }}}}{\nu }} \right)}}^{2}} + 4{{{\left( {\frac{{{{\omega }_{t}}}}{\nu }} \right)}}^{2}}} \right]}^{{1/2}}}. \\ \end{gathered} $Средний квадрат отклонений $\left\langle {y{{{(t)}}^{2}}} \right\rangle $ частицы в направлении y от ее начального положения и автокорреляционная функция $\left\langle {y(t*)y({{t}^{*}} + t)} \right\rangle $ могут быть представлены в форме [14, 15, 34, 35]
(7)
$\begin{gathered} \left\langle {y{{{(t)}}^{2}}} \right\rangle = \frac{{2T}}{{M\omega _{t}^{2}}} \times \\ \times \;\left[ {1 - \exp \left( { - \frac{{\nu t}}{2}} \right)\left( {\cos (\nu t\psi ) + \frac{{\sin (\nu t\psi )}}{{2\psi }}} \right)} \right], \\ \end{gathered} $(8)
$\begin{gathered} \left\langle {y({{t}^{*}})y({{t}^{*}} + t)} \right\rangle = \\ = \;\frac{{2T}}{{M\omega _{t}^{2}}}\left[ {\exp \left( { - \frac{{\nu t}}{2}} \right)\left( {\cos (\nu t\psi ) + \frac{{\sin (\nu t\psi )}}{{2\psi }}} \right)} \right]. \\ \end{gathered} $Здесь и далее T – температура частиц в энергетических единицах, $\psi = {{(4{{\xi }^{2}} - 1)}^{{1/2}}}{\text{/}}2$, $\xi = {{\omega }_{t}}{\text{/}}\nu $, а угловые скобки, $\left\langle {} \right\rangle $, обозначают усреднение по всем отрезкам времени, равным t [1–4, 14, 15, 34, 35]. При этом при t → 0: $\left\langle {y{{{({{t}^{*}})}}^{2}}} \right\rangle = 2T{\text{/}}(М \omega _{t}^{2})$, $\left\langle {y{{{(t)}}^{2}}} \right\rangle = 0$, а при t → ∞: $\left\langle {y{{{({{t}^{*}})}}^{2}}} \right\rangle = 0$ и $\left\langle {y{{{(t)}}^{2}}} \right\rangle = 2T{\text{/}}(М \omega _{t}^{2})$.
Спектральная плотность случайного процесса задается косинусом – преобразованием Фурье для соответствующей автокорреляционной функции [36]. Таким образом, спектральная плотность, Ge(ω), для случайных смещений частицы в ловушке в направлении y (при ωВ = 0), т.е. спектральная плотность классического затухающего осциллятора, может быть записана как [35, 37]
(9)
$G{{(\omega )}_{e}} = \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\nu \omega _{t}^{2}}}{{{{\omega }^{4}} + ({{\nu }^{2}} - \omega _{t}^{{}}){{\omega }^{2}} + \omega _{t}^{4}}}$Рассмотрим решения задачи для системы уравнений (2), (3) (при ωВ ≠ 0). Средний квадрат отклонений, $\left\langle {x{{{(t)}}^{2}}} \right\rangle \equiv \left\langle {z{{{(t)}}^{2}}} \right\rangle $, частицы для этой системы в направлениях x и z от ее положения равновесия и автокорреляционная функция, $\left\langle {x({{t}^{*}})x({{t}^{*}}\, + \,t)} \right\rangle \, \equiv \,\left\langle {z({{t}^{*}})z({{t}^{*}}\, + \,t)} \right\rangle $, при условии ${{({{\Psi }_{{1,2}}})}^{2}}\, \ll $ $ \ll {{{\text{(}}{{\Omega }_{{1,2}}})}^{2}}$ (см. Приложение) могут быть представлены как
(10)
$\begin{gathered} \left\langle {x{{{(t)}}^{2}}} \right\rangle = \frac{{2T}}{{M\omega _{t}^{2}}} \times \\ \times \;\left( {{{B}_{1}}\left[ {1 - \exp \left( { - \frac{{{{\nu }_{1}}t}}{2}} \right)\left( {\cos ({{\nu }_{1}}t{{\psi }_{1}}) + \frac{{\sin ({{\nu }_{1}}t{{\psi }_{1}})}}{{2{{\psi }_{1}}}}} \right)} \right] + } \right. \\ + \;\left. {{{B}_{2}}\left[ {1 - \exp \left( { - \frac{{{{\nu }_{2}}t}}{2}} \right)\left( {\cos ({{\nu }_{2}}t{{\psi }_{2}}) + \frac{{\sin ({{\nu }_{2}}t{{\psi }_{2}})}}{{2{{\psi }_{2}}}}} \right)} \right]} \right), \\ \end{gathered} $(11)
$\begin{gathered} \left\langle {x({{t}^{*}})x({{t}^{*}} + t)} \right\rangle = \frac{{2T}}{{M\omega _{t}^{2}}} \times \\ \times \;\left( {{{B}_{1}}\left[ {\exp \left( { - \frac{{{{\nu }_{1}}t}}{2}} \right)\left( {\cos ({{\nu }_{1}}t{{\psi }_{1}}) + \frac{{\sin ({{\nu }_{1}}t{{\psi }_{1}})}}{{2{{\psi }_{1}}}}} \right)} \right] + } \right. \\ + \;\left. {{{B}_{2}}\left[ {\exp \left( { - \frac{{{{\nu }_{2}}t}}{2}} \right)\left( {\cos ({{\nu }_{2}}t{{\psi }_{2}}) + \frac{{\sin ({{\nu }_{2}}t{{\psi }_{2}})}}{{2{{\psi }_{2}}}}} \right)} \right]} \right), \\ \end{gathered} $При этом спектральная плотность, Gem(ω), для случайных смещений частицы в направлениях x и/или z в постоянном магнитном поле имеет вид
(12)
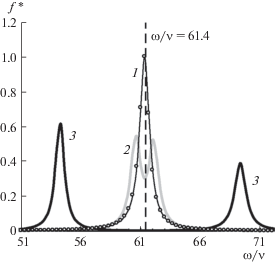
$\begin{gathered} {{G}_{{em}}}(\omega ) = \frac{{2T}}{{M\omega _{t}^{2}}}\left[ {\frac{{В _{1}^{{}}{{\nu }_{1}}{{\omega }_{1}}^{2}}}{{{{\omega }^{4}} + ({{\nu }_{1}}^{2} - 2{{\omega }_{1}}^{2}){{\omega }^{2}} + {{\omega }_{1}}^{4}}} + } \right. \\ \left. { + \;\frac{{{{B}_{2}}{{\nu }_{2}}{{\omega }_{2}}^{2}}}{{{{\omega }^{4}} + ({{\nu }_{2}}^{2} - 2{{\omega }_{2}}^{2}){{\omega }^{2}} + {{\omega }_{2}}^{4}}}} \right], \\ \end{gathered} $При ωВ → 0 уравнения (10)–(12) переходят в соотношения (7)–(9) соответственно. Иллюстрация зависимости спектральной плотности G(ω) ≡ ≡ Gem(ω) от ω/ν для различных ωВ/ν представлена на рис. 1.
Рис. 1.
Нормированные спектральные плотности ${{f}^{*}}(\omega ) = G(\omega ){\text{/}}(2T{\text{/}}M\omega _{t}^{2}\nu )$(12) при ωt/ν ≅ 61.4 для различных соотношений ωВ/ν: 1 – 0.015; 2 – 1.5; 3 – 15. Символами показаны функции ${{f}^{*}}(\omega )$ для ωt/ν ≅ 61.4 при ωВ = 0 (9).
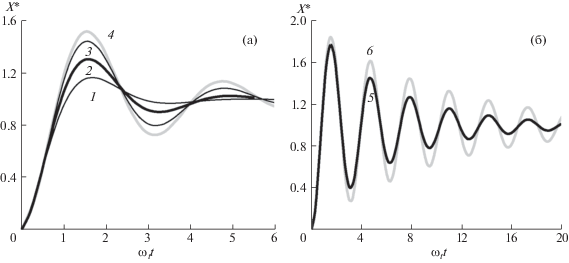
Следует отметить, что для диагностики параметров ограниченных и протяженных систем в лабораторных экспериментах зачастую используется анализ поведения среднего квадрата отклонений частиц от их начального положения (например, функции $\langle x{{(t)}^{2}}\rangle $ в отсутствие магнитного поля, ωВ = 0) [14, 17]. Иллюстрация зависимостей $\langle x{{(t)}^{2}}\rangle $ при различных ξ = ωt/ν для ωВ = 0 показана на рис. 2. В случае ограниченных систем такие измерения позволяют найти величину среднеквадратичного отклонения $2T{\text{/}}(М \omega _{t}^{2})$ при t → ∞. Откуда при наличии информации о среднем квадрате скорости анализируемых частиц, T/М, легко определить значение характерной частоты ловушки ωt. Данные о коэффициенте трения частиц ν в этом случае могут быть получены путем анализа максимума функции $\langle x{{(t)}^{2}}\rangle $ (для ξ < 3), см. рис. 2а, или путем “подгонки” численных и экспериментальных данных [14, 17, 19, 20]. Так, например, при $\xi = {{\omega }_{t}}{\text{/}}\nu > 5$ спадание пиков кривых $\langle x{{(t)}^{2}}\rangle $ определяется функцией exp(–νt) и, соответственно, отражает величину ν (см. рис. 2б). Тем не менее тепловые флуктуации в реальных системах могут сильно исказить величину восстанавливаемого коэффициента ν.
Рис. 2.
Нормированное среднеквадратичное смещение частицы $X* = \langle x{{(t)}^{2}}\rangle {\text{/}}(2T{\text{/}}M\omega _{t}^{2})$ в зависимости от ωtt для ωВ = 0 при ξ2= (ωt/ν)2: 1 – 1; 2 – 2; 3 – 4; 4 – 6; 5 – 36; 6 – 100.
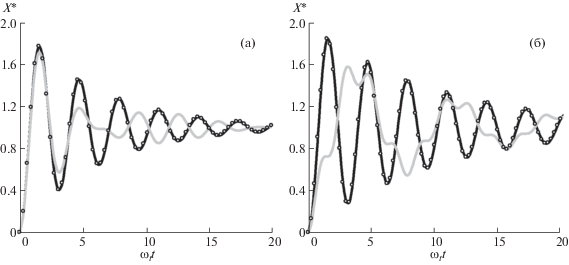
Добавим также, что такая процедура хороша только для систем, имеющих одну характерную частоту ωt. При наличии двух, или более гармоник (характерных частот) в исследуемой системе простой анализ функций $\langle x{{(t)}^{2}}\rangle $ становится затруднительным, см. рис. 3. Тем не менее исследование спектральных характеристик анализируемой системы позволяют легко решить данную задачу (см. рис. 1, а также рисунки ниже для систем с параметрами, аналогичным представленным на рис. 3).
Рис. 3.
Нормированное среднеквадратичное смещение частицы ${{X}^{*}} = \left\langle {x{{{(t)}}^{2}}} \right\rangle {\text{/}}(2T{\text{/}}M\omega _{t}^{2})$ в зависимости от ωtt (серые линии) для ωt/ν ≅ 6.14, ωВ/ν ≅ 1.5 (а); ωt/ν ≅ 10, ωВ/ν ≅ 15 (б). Символами на черных линиях показаны функции X*(ωtt) при ω = 0.
Следует отметить, что уравнения типа (1)–(3) могут использоваться для анализа движения центра масс любого ограниченного ансамбля частиц с попарным взаимодействием, а также для отдельной частицы в системе, состоящей из N частиц, в случае, когда влиянием межчастичного взаимодействия можно пренебречь. Подчеркнем, что для попарных (взаимных) сил межчастичного взаимодействия (Fij = Fji, где Fij – величина силы, действующая со стороны j-й частицы на частицу i; j ≠ i) их сумма в ансамбле, состоящем из N частиц, равна 0. И, соответственно, для движения центра масс системы таких частиц имеют место уравнения типа (1)–(3) [38].
Для анализа физических свойств однородных структур заряженных частиц (которые можно характеризовать постоянной концентрацией n) обычно используется параметр неидеальности $\Gamma = {{Q}^{2}}{{n}^{{1/3}}}{\text{/}}T$, отражающий отношение энергии взаимодействия между частицами системы к их температуре. При этом в линейном электрическом поле величина концентрации частиц, n, может быть получена из уравнения Пуассона $n \cong 3\alpha {\text{/}}(4\pi Q)$, и, соответственно, для среднего межчастичного расстояния имеет место соотношение ${{l}_{p}} \cong {{(4\pi Q{\text{/}}3\alpha )}^{{1/3}}}$ [35]. Для оценки радиуса ограниченной структуры в первом приближении можно использовать соотношение $R \cong $ $ \cong {{(3N{\text{/}}4\pi n)}^{{1/3}}}$, где N – число частиц. По своей сути, величина R является минимальным радиусом такой структуры. Реальный (эффективный) радиус ансамбля будет расти с ростом температуры частиц [35].
3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И ИХ ОБСУЖДЕНИЕ
Численное моделирование динамики систем заряженных частиц в линейной и изотропной электростатической ловушке выполнялось методом молекулярной динамики Ланжевена. Расчеты проводились для одной частицы (N = 1) и для ансамблей, состоящих из N = 50, 250 и 500 частиц. Техника моделирования подробно описана в работах [5, 6]. Шаг интегрирования составлял от $\Delta t \cong {{(40\max [{{\omega }_{t}};\nu ])}^{{ - 1}}}$ до $\Delta t \cong {{(100\max [{{\omega }_{t}};\nu ])}^{{ - 1}}}$ в зависимости от начальных условий задачи. Время расчетов tc после установления равновесия в моделируемых системах варьировалось от $\sim {\kern 1pt} {{10}^{3}}{\text{/}}\min [{{\omega }_{t}};\quad\nu ]$ до $\sim {{10}^{4}}{\text{/}}\min [{{\omega }_{t}};\quad\nu ]$.
Расчеты проводились для систем частиц с кулоновским взаимодействием в широком диапазоне их параметров неидеальности: от Γ ~ 0.1 до Γ ~ 100. Величина индукции магнитного поля В изменялась в пределах от 300 до $3 \times {{10}^{4}}$ Гс. Значение параметра ξ = ωt/ν варьировалось от ~1 до ~70, отношение ωВ/ν – от ~0.15 до ~15.
Во всех рассмотренных случаях моделируемые системы являлись устойчивыми. Температура частиц не отличалась от заданной, а их функции распределения по скоростям соответствовали распределению Максвелла. При этом при t → ∞, значения среднеквадратичного смещения центра масс системы от его начального положения составляли $\left\langle {{{x}^{2}}} \right\rangle \cong \left\langle {{{y}^{2}}} \right\rangle \cong \left\langle {{{z}^{2}}} \right\rangle \cong 2T{\text{/}}(NМ \omega _{t}^{2})$.
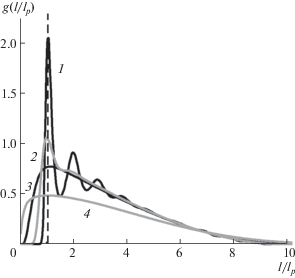
Парные корреляционные функции g(l) для ансамблей из N = 500 частиц с различными параметрами Г показаны на рис. 4. В качестве нормировки величины g(l), представленной на этих рисунках, использовалось предположение однородной концентрации частиц равной n ≅ ≅ 3α/(4πQ). Легко увидеть, что первый пик функций g(l) для Г ≥ 0.1 хорошо соответствует величине ${{l}_{p}} \cong {{(4\pi Q{\text{/}}3\alpha )}^{{1/3}}}$, полученной в приближении однородной системы, а для оценки радиуса неидеальных систем может быть использовано соотношениеR ≅ (3N/4πn)1/3.
Рис. 4.
Парная корреляционная функция g(l/lp) для ансамблей из N = 500 частиц с различными параметрами Г: 1 – 90; 2 – 9; 3 – 0.9; 4 – 0.09. Здесь lp ≅ ≅ (4πQ/3α)1/3.
Следует подчеркнуть, что перечисленные выше характеристики ($\left\langle {{{{(\Delta x)}}^{2}}} \right\rangle $, g(l), lp, R) не зависели от величины индукции магнитного поля В.
Численные исследования показали, что вне зависимости от параметра неидеальности Г и числа частиц N в моделируемых ансамблях спектральные плотности смещений их центра масс хорошо соответствуют предлагаемым аналитическим соотношениям (9), (12).
Нормированные спектральные плотности ${{f}^{*}}(\omega ) = NG(\omega ){\text{/}}(2T{\text{/}}M\omega _{t}^{2}\nu )$, полученные для различных параметров задачи (ωt/ν, ωВ/ν, Г, N), а также аналитические решения (9), (12) показаны на рис. 5–7. (Вычисления спектральной плотности проводились на основе численных расчетов смещений x(t), y(t) и z(t) при помощи процедуры “N-D fast Fourier transform” в пакете прикладных программ MATLAB.)
Рис. 5.
Нормированные спектральные плотности $f{\text{*}}(\omega ) = NG(\omega ){\text{/}}(2T{\text{/}}M\omega _{t}^{2}\nu )$ для центра масс системы частиц при их смещениях вдоль магнитного поля (ωВ = 0), полученные путем численного моделирования (серые линии), и из аналитического решения задачи (9) (черные линии), для ωt/ν ≅ 6.14, N = 50, Г = 90 (а) и ωt/ν ≅ 1, N = 500, Г = 45(б).
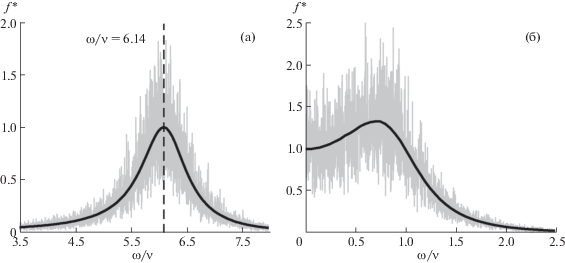
Рис. 6.
Нормированные спектральные плотности для центра масс системы $f{\text{*}}(\omega )$ для центра масс системы частиц при их смещениях в плоскости ортогональной магнитному полю (ωВ/ν ≅ 1.5), полученные путем численного моделирования (серые линии), и из аналитического решения задачи (12) (черные линии) для ωt/ν ≅ 6.14, N = 50, Г = 90 (а) и ωt/ν ≅ 1, N = 500, Г = 45(б).
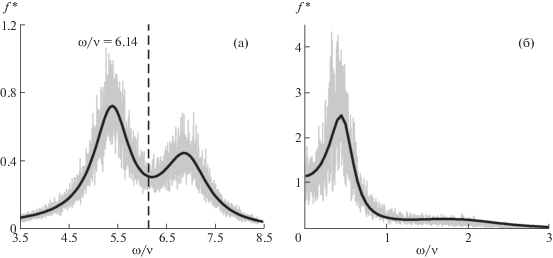
Рис. 7.
Нормированные спектральные плотности для центра масс системы $f{\text{*}}$ при ωB = 0 (кривая 1) и ωB/ν ≅ 15 (кривая 2), полученные путем численного моделирования (серые линии), и из аналитического решения задачи (черные линии), для ωt/ν ≅ 61.4, N = = 500, Г = 20 (а) и ωt/ν ≅ 10, N = 50, Г = 10 (б).
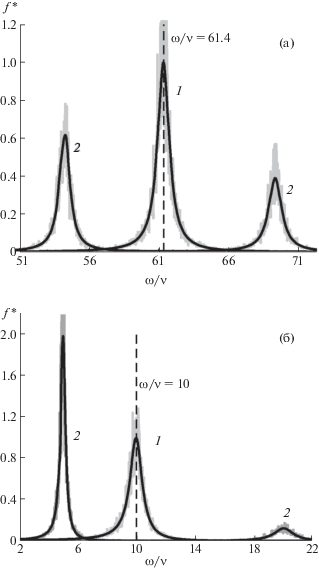
Следует отметить, что для всех представленных случаев величина ${{({{\Psi }_{{1,2}}})}^{2}} \ll {{({{\Omega }_{{1,2}}})}^{2}}$, за исключением случая ωВ/ν ≅ 1.5, ωt/ν ≅ 1 (см. рис. 6б), когда ${{({{\Psi }_{{1,2}}})}^{2}} \cong 0.25{{({{\Omega }_{{1,2}}})}^{2}}$. Тем не менее и для этого случая получены хорошие совпадения между численными и аналитическими результатами.
Численные исследования также показали, что отклонения формы спектральных распределений для отдельных частиц ансамбля от аппроксимирующих функций (9), (12) наблюдаются при Γ > < 0.1. С ростом величины Γ характерная частота спектра смещается в сторону меньших частот относительно частоты колебаний центра масс системы как для смещений частиц вдоль магнитного поля (ωВ = 0), так и для смещений в плоскости ортогональной магнитному полю (ωВ/ν ≠ 0). Иллюстрация поведения нормированных спектральных плотностей $f{\text{*}}(\omega {\text{/}}\nu )$ для отдельных частиц ансамбля с ростом Γ для случая ωВ = 0 представлена на рис. 8. Следует отметить, что простая подгонка численных данных, полученных для отдельных частиц таких систем (при Γ > 0.1), аналитическими соотношениями (9), (12) не позволяет получить физически обоснованных результатов. Тем не менее можно предположить, что данное обстоятельство связано с уменьшением коэффициента диффузии частиц с ростом параметра Γ, которое, в свою очередь, происходит за счет роста эффективной диссипации в сильно коррелируемых системах [14, 15, 35].
Рис. 8.
Нормированные спектральные плотности f*(ω/ν) для отдельных частиц ансамбля (серые линии), состоящего из N = 50 частиц, при ωВ = 0, ωt/ν ≅ 6.1 и различных параметрах Γ: 0.2 (а); 0.45 (б); 2 (в). Черными линиями показаны аналитические функции для центра масс-системы.
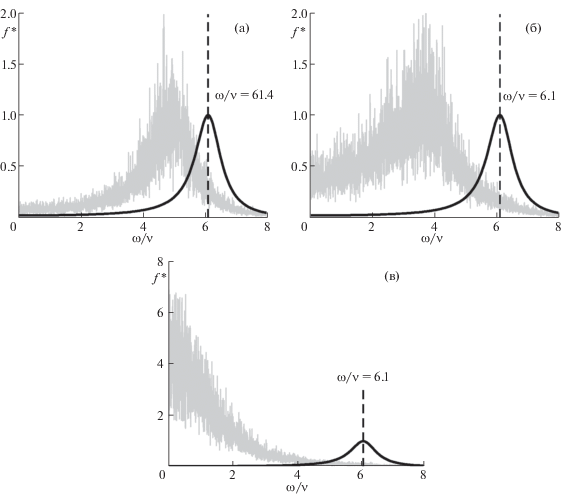
В заключение данного раздела следует отметить, что измерения спектральных плотностей смещений для центра масс ограниченной системы частиц позволяет восстанавливать характерные параметры исследуемых ансамблей (ν, ωt, ωВ) даже при наличии значительных тепловых флуктуаций в анализируемой системе.
4. ЗАКЛЮЧЕНИЕ
Выполнено аналитическое и численное исследование динамики ансамблей заряженных частиц в электростатической ловушке под воздействием постоянного магнитного поля. Представлены корни характеристического уравнения, позволяющие анализировать спектр частот колебаний в исследуемых системах частиц. Предложено аналитическое соотношение для спектральной плотности смещений центра масс исследуемых систем. Полученное соотношение проверено путем численного моделирования для кластеров с различным количеством частиц, взаимодействующих с кулоновским потенциалом, в широком диапазоне параметров.
Численные исследования показали, что вне зависимости от параметра неидеальности Г и числа частиц N в моделируемых ансамблях спектральные плотности смещений их центра масс хорошо соответствуют предлагаемым аналитическим соотношениям, а характерные частоты для центра масс могут быть получены путем аналитического решения системы уравнений для одной заряженной частицы.
Кроме того, решение уравнений движения (1)–(3) при заданной частоте трения ν зависит только от относительных значений параметров ωB/ν, ωt/ν. Таким образом, полученные результаты справедливы для частиц любой массы и зарядов (например, для случая пылевой плазмы, для ионов сепарируемого вещества ОЯТ и т.д.).
Результаты настоящей работы применимы для ограниченных систем при любом типе попарных взаимодействий и могут быть полезны для разработки новых методов диагностики физических характеристик таких систем, а также для анализа условий формирования различных кластеров, которые представляют интерес в физике плазмы, медицине, биологии, физике полимеров и коллоидных систем.
Данная работа была поддержана Российским научным фондом (грант № 14-29-00231).
ПРИЛОЖЕНИЕ
Любое решение F(t) для задачи (2), (3) можно представить в виде суперпозиции
При этом, для функции $\left\langle {x{{{(t)}}^{2}}} \right\rangle $ величина ${{С }_{0}} = {\text{ }}2T{\text{/}}(М \omega _{t}^{2})$, для $\left\langle {x({{t}^{*}})x({{t}^{*}} + t)} \right\rangle --{{С }_{0}} = 0$. Для поиска коэффициентов Сi ($i = 1,2,3,4$) указанных функций используются начальные условия задачи: $F\left( 0 \right) = {{Т }_{0}}$, $dF\left( 0 \right){\text{/}}dt = 0$, ${{d}^{2}}F\left( 0 \right){\text{/}}d{{t}^{2}} = {{Т }_{2}}$, ${{d}^{3}}F\left( 0 \right){\text{/}}d{{t}^{3}} = 0$, где Т0 = 0 для $\left\langle {x{{{(t)}}^{2}}} \right\rangle $, ${{T}_{0}} = $ $ = {\text{ }}2T{\text{/}}(М \omega _{t}^{2})$ для $\left\langle {x({{t}^{*}})x({{t}^{*}} + t)} \right\rangle $, Т2 = 2T/М для $\left\langle {x{{{(t)}}^{2}}} \right\rangle $ и Т2 = –2T/М для $\left\langle {x({{t}^{*}})x({{t}^{*}} + t)} \right\rangle $. Тогда для коэффициентов Сi можно записать следующую систему уравнений:
Здесь и далее знак “–” для функции $\left\langle {x{{{(t)}}^{2}}} \right\rangle $, знак “+” для $\left\langle {x({{t}^{*}})x({{t}^{*}} + t)} \right\rangle $,
(А6)
${{С }_{1}} = \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{t}^{2}({{\lambda }_{2}} + {{\lambda }_{3}} + {{\lambda }_{4}}) - {{\lambda }_{2}}{{\lambda }_{3}}{{\lambda }_{4}}}}{{({{\lambda }_{1}} - {{\lambda }_{2}})({{\lambda }_{1}} - {{\lambda }_{3}})({{\lambda }_{1}} - {{\lambda }_{4}})}},$(А7)
${{С }_{2}} = \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{ - \omega _{t}^{2}({{\lambda }_{1}} + {{\lambda }_{3}} + {{\lambda }_{4}}) + {{\lambda }_{1}}{{\lambda }_{3}}{{\lambda }_{4}}}}{{({{\lambda }_{1}} - {{\lambda }_{2}})({{\lambda }_{2}} - {{\lambda }_{3}})({{\lambda }_{2}} - {{\lambda }_{4}})}},$(А8)
${{С }_{3}} = \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{t}^{2}({{\lambda }_{1}} + {{\lambda }_{2}} + {{\lambda }_{4}}) - {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{4}}}}{{({{\lambda }_{1}} - {{\lambda }_{3}})({{\lambda }_{2}} - {{\lambda }_{3}})({{\lambda }_{3}} - {{\lambda }_{4}})}},$(А9)
${{С }_{4}} = \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{ - \omega _{t}^{2}({{\lambda }_{1}} + {{\lambda }_{2}} + {{\lambda }_{3}}) + {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}}}{{({{\lambda }_{1}} - {{\lambda }_{4}})({{\lambda }_{2}} - {{\lambda }_{4}})({{\lambda }_{3}} - {{\lambda }_{4}})}}.$Используя значения λi (5а), (5б), в предположении ${{D}_{1}}^{2} \ll {{D}_{2}}{{\omega }_{В }}{\text{/}}(\nu \sqrt 2 )$ и ${{\nu }^{2}} - {{D}_{1}}^{2}{\text{/}}2 \ll 2{{\omega }_{{1,2}}}$ (где ${{\omega }_{1}} = {{(\Psi _{1}^{2} + \Omega _{1}^{2})}^{{1/2}}}$, а ${{\omega }_{2}} = {{(\Psi _{2}^{2} + \Omega _{2}^{2})}^{{1/2}}}$) формулы (6)–(9) можно представить в виде
(А10)
$\begin{gathered} {{С }_{1}} \cong \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{t}^{2} - \omega _{2}^{2}}}{{{{\omega }_{В }}\nu {{D}_{2}}{\text{/}}\sqrt 2 }}\frac{{{{\lambda }_{2}}}}{{({{\lambda }_{1}} - {{\lambda }_{2}})}} \equiv \\ \equiv \pm \;{{B}_{1}}\frac{{2T}}{{M\omega _{t}^{2}}}\frac{{{{\lambda }_{2}}}}{{({{\lambda }_{1}} - {{\lambda }_{2}})}}, \\ \end{gathered} $(А11)
$\begin{gathered} {{С }_{2}} \cong \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{t}^{2} - \omega _{2}^{2}}}{{{{\omega }_{В }}\nu {{D}_{2}}{\text{/}}\sqrt 2 }}\frac{{{{\lambda }_{2}}}}{{({{\lambda }_{2}} - {{\lambda }_{1}})}} \equiv \\ \equiv \; \pm {{B}_{1}}\frac{{2Т }}{{M\omega _{t}^{2}}}\,\frac{{{{\lambda }_{1}}}}{{({{\lambda }_{2}} - {{\lambda }_{1}})}}, \\ \end{gathered} $(А12)
$\begin{gathered} {{С }_{3}} \cong \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{1}^{2} - \omega _{t}^{2}}}{{{{\omega }_{В }}\nu {{D}_{2}}{\text{/}}\sqrt 2 }}\frac{{{{\lambda }_{2}}}}{{({{\lambda }_{2}} - {{\lambda }_{1}})}} \equiv \\ \equiv \; \pm {{B}_{2}}\frac{{2T}}{{M\omega _{t}^{2}}}\frac{{{{\lambda }_{4}}}}{{({{\lambda }_{3}} - {{\lambda }_{4}})}}, \\ \end{gathered} $(А13)
$\begin{gathered} {{С }_{4}} \cong \pm \frac{{2T}}{{M\omega _{t}^{2}}}\frac{{\omega _{1}^{2} - \omega _{t}^{2}}}{{{{\omega }_{В }}\nu {{D}_{2}}{\text{/}}\sqrt 2 }}\frac{{{{\lambda }_{2}}}}{{({{\lambda }_{2}} - {{\lambda }_{1}})}} \equiv \\ \equiv \pm {{B}_{2}}\frac{{2T}}{{M\omega _{t}^{2}}}\frac{{{{\lambda }_{3}}}}{{({{\lambda }_{4}} - {{\lambda }_{3}})}}. \\ \end{gathered} $Здесь ${{B}_{1}} = \sqrt 2 (\omega _{t}^{2} - \omega _{2}^{2}){\text{/}}({{D}_{2}}{{\omega }_{В }}\nu )$, ${{B}_{2}} = \sqrt 2 (\omega _{1}^{2} - \omega _{t}^{2}){\text{/}}$ ${\text{/}}({{D}_{2}}{{\omega }_{В }}\nu )$.
Отметим, что упомянутые выше условия ($D_{1}^{2} \ll {{D}_{2}}{{\omega }_{В }}{\text{/}}(\nu \sqrt 2 )$ и ${{\nu }^{2}} - D_{1}^{2}{\text{/}}2 \ll 2{{\omega }_{{1,2}}}$) выполняются, когда ${{({{\Psi }_{{1,2}}})}^{2}} \ll {{({{\Omega }_{{1,2}}})}^{2}}$.
Список литературы
Photon Correlation and Light Beating Spectroscopy / Eds. H.Z. Cummins, E.R. Pike.N.Y.: Plenum, 1974.
Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975.
Balescu R. Equilibrium and Nonequilibrium Statistical Mechanics. Chichester: Wiley Interscience, 1975.
Овчинников А.А., Тимашев С.Ф., Белый А.А. Кинетика диффузионно-контролируемых химических процессов. М.: Химия, 1986.
Ваулина О.С., Петров О.Ф., Фортов В.Е., Храпак А.Г., Храпак С.А. Пылевая плазма (эксперимент и теория). М.: Физматлит, 2009.
Complex and Dusty Plasmas / Eds. Fortov V.E., Morfill G.E. CRC Press, 2010.
Raizer Y.P., Kisin V.I., Allen J.E. Gas Discharge Physics. Berlin, Heidelberg: Springer, 2011.
Jiménez-Aquino J.I., Velasco R.M., Uribe F.J. // Phys. Rev. E. 2008. V. 77. P. 051105.
Hou L.J., Mišković Z.L., Piel A., Shukla P.K. // Phys. Plasmas. 2009. V. 16. P. 053705.
Farokhi B., Shahmansouri M., Shukla P.K. // Phys. Plasmas. 2009. V. 16. P. 063703.
Ваулина О.С., Лисин Е.А., Саметов Э.А. // ЖЭТФ. 2017. Т. 152. С. 1144.
Sametov E.A., Timirkhanov R.A.,Vaulina O.S. // Phys. Plasmas. 2017. V. 24. P. 123504.
Ваулина О.С., Адамович К.Г. // ЖЭТФ. 2008. Т. 133. С. 1091.
Ваулина О.С., Адамович К.Г., Петров О.Ф., Фортов В.Е. // ЖЭТФ. 2008. Т. 134. С. 367.
Ваулина О.С., Лисин Е.А., Гавриков А.В., Петров О.Ф., Фортов В.Е. // ЖЭТФ. 2010. Т. 137. С. 751.
Vaulina O.S., Lisin E.A. // Phys. Plasmas. 2009. V. 16. P. 113702.
Фортов В.Е., Петров О.Ф., Ваулина О.С., Косс К.Г. // Письма ЖЭТФ. 2013. Т. 97. С. 366.
Hebner G.A., Riley M.E., Greenberg K.E. // Phys. Rev. E. 2002. V. 66. P. 046407.
Vaulina O.S., Drangevski I.E. //Phys. Scripta. 2006. V. 73. P. 577.
Васильев M.М., Дьячков Л.Г., Антипов С.Н., Пет-ров О.Ф., Фортов В.E. // Письма ЖЭТФ. 2007. Т. 86. С. 414.
D'yachkov L.G., Petrov O.F., Fortov V.E. // Contributions Plasma Phys. 2009. V. 49. P. 134.
Karasev V.Yu., Dzlieva E.S., Ivanov A.Yu., Eikhval’d A.I. // Phys. Rev. E. 2006. V. 74. P. 066403.
Sato N., Uchida G., Kaneko T. // Phys. Plasmas. 2001. V. 8. P. 1786.
Post R.F. // Rev. Mod. Phys. 1956. V. 28. P. 338.
Artsimovich L.A. Controlled thermonuclear reactions. N.Y.: Gordon and Breach, 1964.
Aymar R., Barabaschi P., Shimomura Y. // Plasma Phys. Control. Fusion. 2002. V. 44. P. 519.
Тимофеев А.В.// Физика плазмы 2007. Т. 33. С. 971.
Cluggish B.P., Anderegg F.A., Freeman R.L., Gilleland J., Hilsabeck T.J., Isler R.C. // Plasma Phys. 2005. V. 12. P. 057101.
Ворона Н.А., Гавриков А.В., Самохин А.А., Смирнов В.П., Хомяков Ю.С. // Ядерная физика и инжиниринг. 2014. Т. 5. С. 944.
Смирнов В.П., Самохин А.А., Ворона Н.А., Гаври-ков А.В. // Физика плазмы. 2013. Т. 39. С. 523.
Юферов В.Б., Егоров А.М., Ильичева В.О., Шарый С.В., Живанков К.И. // Вопросы атомной науки и техники. Сер.: Физика радиационных повреждений и радиационное материаловедение 2013. Т. 101. С. 148.
Райзер Ю.П. Физика газового разряда. М.: Наука, 1987.
Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2012. Т. 142. С. 1077.
Chandrasekhar S. // Rev. Mod. Phys. 1943. V. 15. P. 1.
Ваулина О.С., Саметов Э.А. // ЖЭТФ. 2018. Т. 154. С. 407.
Воронов А.А. Теория автоматического управления. Часть 2. Москва: Высш. шк., 1986.
Щегольков А.А. // Молодежный научно-технический вестн. 2013. Т. 8. С. 24.
Ваулина О.С., Лисина И.И., Лисин Е.А. // Физика плазмы. 2018. Т. 44. С. 229.
Дополнительные материалы отсутствуют.


