Физика плазмы, 2020, T. 46, № 2, стр. 121-138
Четыре тензора, определяющие тепло- и электропроводность невырожденных электронов в замагниченной плазме
М. В. Глушихина *
Институт космических исследований РАН
Москва, Россия
* E-mail: m.glushikhina@iki.rssi.ru
Поступила в редакцию 03.07.2019
После доработки 05.09.2019
Принята к публикации 20.09.2019
Аннотация
Получено решение уравнения Больцмана для плазмы в магнитном поле с невырожденными электронами и ионами методом Чепмена–Энскога. Для получения приближенного решения использованы полиномы Сонина до третьего порядка. Рассмотрена полностью ионизованная плазма. Получены более точные значения компонент тензоров диффузии, термодиффузии и диффузионного термоэффекта по сравнению с предыдущими работами по данной тематике.
1. ВВЕДЕНИЕ
Перенос тепла и заряда в замагниченной невырожденной плазме играет важную роль в описании ее поведения как в лабораторных условиях, так и в строении и эволюции звезд. Кинетические коэффициенты, такие как теплопроводность, диффузия, термодиффузия и диффузионный термоэффект определяют потоки тепла и плотности токов. Зная распределение тепла и тока, можно рассчитать магнитотепловую эволюцию, распределение магнитного поля и температуры по поверхности звезд или описать поведение плазмы, получаемой и ускоряемой в лабораторных условиях.
Классические методы кинетической теории газов были разработаны Максвеллом, Больцманом, Гильбертом, Энскогом и Чепменом. Эти методы представлены в монографии Чепмена и Каулинга [1]. Они основаны на решении уравнения Больцманна методом последовательных приближений. В качестве нулевого приближения берется термодинамически равновесная функция распределения: для невырожденного газа – распределение Максвелла, если вырождение важно – распределение Ферми–Дирака. Равновесная функция распределения не дает точного решения уравнения Больцмана при наличии неоднородности. Следуя [1], мы ищем решение уравнения Больцманна в первом приближении как разложение по полиномам Сонина (Лагерра). Для учета вырождения, используется система ортогональных функций, которые являются обобщением полиномов Сонина, предложенная в [2–4], см. также [5]. Обычно для вычисления теплопроводности берутся первые два члена разложения. В [6] было показано, что такое приближение дает существенные погрешности для коэффициента теплопроводности, которые становятся намного меньше, когда используется разложение до третьей степени полинома.
Первое применение уравнения Больцмана к газу из заряженных частиц было сделано Чепменом [1]. Из-за расходимости интеграла столкновений при больших прицельных параметрах для частиц с кулоновским взаимодействием в качестве верхнего предела интегрирования по прицельному параметру было взято среднее расстояние между частицами. Таким образом, были получены коэффициенты вязкости, теплопроводности и диффузии для газов, состоящих из заряженных частиц. Расхождение интеграла столкновений для кулоновского взаимодействия при больших прицельных параметрах показывает, что рассеяние частиц с большим прицельным параметром и малым изменением импульса при единичном столкновении играет более важную роль, чем столкновения с большим изменением импульса. Ландау использовал этот факт для упрощения интеграла столкновений Больцмана [7]. Он выполнил разложение функции распределения после столкновения при малых изменениях импульса и оставил первые два члена разложения.
Кинетические коэффициенты для невырожденной плазмы при наличии и отсутствии магнитного поля были вычислены в [8–11] с использованием метода разложения Чепмена–Энскога. Брагинский [12, 13] вычислил кинетические коэффициенты для невырожденной плазмы в магнитном поле, состоящей из электронов и одного сорта положительно заряженных ионов, используя кинетические уравнения, нормированные на средние скорости, различные для ионов и электронов. Был использован интеграл столкновений Ландау и учитывались два полинома в разложении. Такой же подход использовался в [14], где представлены вычисления кинетических коэффициентов для полностью ионизированной плазмы со сложным составом. Кинетические коэффициенты для полностью ионизированной плазмы в магнитном поле были получены прямым численным расчетом уравнения Фоккера–Планка в [15].
Компоненты тензора теплопроводности для вырожденных звездных ядер были вычислены в приближении Лоренца для водородной плазмы в [16] и [17]. В [18] представлены нерелятивистские вычисления на основе квантового уравнения переноса Ленарда–Балеску для теплопроводности и электрической проводимости плазмы с сильно вырожденными, слабо связанными электронами и невырожденными, слабо связанными ионами. В [19] были вычислены коэффициенты диффузии, термодиффузии и диффузионного термоэффекта для плазмы в магнитном поле с сильно вырожденными электронами и невырожденными ядрами в приближении Лоренца. В работе [20] вычисляется тензор теплопроводности для произвольно вырожденных электронов и невырожденных ядер в магнитном поле.
Данная работа посвящена решению уравнения Больцмана методом Чепмена–Энскога для электронов в невырожденной плазме. Найдены тензоры термодиффузии, диффузии и диффузионного термоэффекта с использованием разложения из трех полиномов, и на примере лоренцевского газа показано, что метод обладает хорошей сходимостью к точному решению. Получено аналитическое выражение для компонент этих тензоров в трехполиномиальном приближении с учетом электрон-электронных столкновений для случая невырожденных электронов в присутствии магнитного поля. Учет третьей степени полинома существенно улучшил точность результатов. В приближении двух полиномов полученное решение совпадает с опубликованными результатами.
2. УРАВНЕНИЕ БОЛЬЦМАНА И УРАВНЕНИЕ ПЕРЕНОСА
Мы используем уравнение Больцмана для невырожденных электронов в магнитном поле, с учетом взаимодействия электронов с ионами и друг с другом. Уравнение Больцмана, описывающее изменение функции распределения электронов f с течением времени в присутствии электрического и магнитного полей, записывается как [10, 11]
(1)
$\frac{{\partial f}}{{\partial t}} + {{c}_{i}}\frac{{\partial f}}{{\partial {{r}_{i}}}} - \frac{e}{{{{m}_{e}}}}\left( {{{E}_{i}} + \frac{1}{c}{{\varepsilon }_{{ikl}}}{{c}_{k}}{{B}_{l}}} \right)\frac{{\partial f}}{{\partial {{c}_{i}}}} + J = 0.$Здесь $( - e),\;{{m}_{e}}$ – заряд (отрицательный) и масса электрона, ${{E}_{i}},{{B}_{i}}$ – напряженность электрического поля и магнитная индукция, ${{\varepsilon }_{{ikl}}}$ – полностью антисимметричный тензор Леви–Чивиты, c – скорость света. Интеграл столкновений J для невырожденых электронов и однозарядных ионов, согласно [1–4], записывается в форме
(2)
$\begin{gathered} J = {{J}_{{ee}}} + {{J}_{{eI}}} = \int {[f{{f}_{1}} - f{\text{'}}f_{1}^{'}]{{g}_{{ee}}}bdbd\varepsilon d{{c}_{{1i}}}} + \\ \, + \int {[f{{f}_{I}} - f{\text{'}}f_{{\text{I}}}^{'}]{{g}_{{eI}}}bdbd\varepsilon d{{c}_{{Ii}}}} . \\ \end{gathered} $Здесь прицельный параметр b и ε – геометрические параметры столкновения частиц с относительными скоростями ${{g}_{{ee}}}$, ${{g}_{{eI}}}$.
Интегрирование в электронной части интеграла столкновений в (2) производится по фазовому пространству налетающих частиц ($d{{c}_{{1i}}}$) и их физическому пространству ($bdbd\varepsilon $) [1]. Функции со скоростями после столкновения отмечены штрихами.
Уравнение Больцмана для электронов с интегралом парных столкновений (2) может применяться, когда электронный газ считается почти идеальным, т. е. кинетическая энергия электронов много больше, чем энергия электростатических взаимодействий. Это справедливо для плазмы достаточно малой плотности. Детальное обсуждение применимости интеграла парных столкновений (2) и его модификаций для невырожденных газов высокой плотности можно найти в [1].
Введем тепловую скорость электронов ${{v}_{i}} = $ $ = {{c}_{i}} - {{c}_{{0i}}}$, где ${{c}_{{0i}}}$ является средней массовой скоростью. Таким образом, мы можем написать уравнение Больцманна относительно тепловой скорости в форме [11]
(3)
$\begin{gathered} \frac{{df}}{{dt}} + {{{v}}_{i}}\frac{{\partial f}}{{\partial {{r}_{i}}}} - \left[ {\frac{e}{{{{m}_{e}}}}\left( {{{E}_{i}} + \frac{1}{c}{{\varepsilon }_{{ikl}}}{{{v}}_{k}}{{B}_{l}}} \right) + \frac{{d{{c}_{{0i}}}}}{{dt}}} \right]\frac{{\partial f}}{{\partial {{{v}}_{i}}}} - \\ \, - \frac{e}{{{{m}_{e}}c}}{{\varepsilon }_{{ikl}}}{{{v}}_{k}}{{B}_{l}}\frac{{\partial f}}{{\partial {{{v}}_{i}}}} - \frac{{\partial f}}{{\partial {{{v}}_{i}}}}{{{v}}_{k}}\frac{{\partial {{c}_{{0i}}}}}{{\partial {{r}_{k}}}} + J = 0, \\ \end{gathered} $Уравнения переноса для концентрации электронов, полного импульса и энергии электронов в двухкомпонентной смеси из электронов и ядер могут быть получены обычным способом из уравнения Больцмана в квазинейтральной плазме [1, 9–11] как
(4)
$\frac{{d{{n}_{e}}}}{{dt}} + {{n}_{e}}\frac{{\partial {{c}_{{0i}}}}}{{\partial {{r}_{i}}}} + \frac{\partial }{{\partial {{r}_{i}}}}({{n}_{e}}\left\langle {{{{v}}_{i}}} \right\rangle ) = 0,$(6)
$\begin{gathered} \frac{3}{2}k{{n}_{e}}\frac{{dT}}{{dt}} - \frac{3}{2}kT\frac{\partial }{{\partial {{r}_{i}}}}({{n}_{e}}\left\langle {{{{v}}_{i}}} \right\rangle ) + \frac{{\partial {{q}_{{ei}}}}}{{\partial {{r}_{i}}}} = \\ \, = {{j}_{i}}\left( {{{E}_{i}} + \frac{1}{c}{{\varepsilon }_{{ikl}}}{{c}_{{0k}}}{{B}_{l}}} \right) - {{\rho }_{e}}\left\langle {{{{v}}_{i}}} \right\rangle \frac{{d{{c}_{{0i}}}}}{{dt}}, \\ \end{gathered} $(7)
$\left\langle {{{{v}}_{{\alpha i}}}} \right\rangle = \frac{1}{{{{n}_{\alpha }}}}\int {{{f}_{\alpha }}{{{v}}_{{\alpha i}}}d{{c}_{{\alpha i}}}} ,\quad {{n}_{e}} = \int {fd{{c}_{{ei}}}} ,$(8)
${{c}_{{0i}}} = \frac{1}{\rho }\sum\limits_\alpha \,{{\rho }_{\alpha }}\left\langle {{{c}_{{ai}}}} \right\rangle ,\quad {{j}_{i}} = - {{n}_{e}}e\left\langle {{{{v}}_{i}}} \right\rangle ,$(9)
${{q}_{{\alpha i}}} = \frac{1}{2}{{n}_{\alpha }}{{m}_{\alpha }}\left\langle {{v}_{\alpha }^{2}{{{v}}_{{\alpha i}}}} \right\rangle ,\quad \rho = \sum\limits_\alpha \,{{m}_{\alpha }}{{n}_{\alpha }}$Здесь суммирование производится по электронам и ионам, ${{P}_{e}} = {{n}_{e}}{{m}_{e}}\left\langle {{{{v}}^{2}}} \right\rangle {\text{/}}3$, когда мы пренебрегаем электронной вязкостью, ${{P}_{e}}$ является электронным давлением; $\left\langle {{{{v}}_{i}}} \right\rangle $ – средняя скорость электронов в сопутствующей системе, ${{q}_{i}}$ – тепловой поток электронов и ${{j}_{i}}$ – электрический ток электронов. Здесь и в дальнейшем рассмотрении мы полагаем среднюю массовую скорость равной средней скорости ионов ${{c}_{{0i}}} = \left\langle {{{c}_{{Ii}}}} \right\rangle $, также мы рассматриваем электрический ток и тепловой поток только от электронов.
3. ВЫВОД ОБЩИХ УРАВНЕНИЙ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОНОВ В ПЕРВОМ ПРИБЛИЖЕНИИ
Уравнение Больцмана может быть решено методом последовательных приближений Чепмена–Энскога [1]. Данный метод используется, когда функции распределения близки к своим термодинамически равновесным значениям, а отклонения считаются линейными. Уравнение для второго порядка отклонений от функции равновесного распределения было получено в [22] для простого газа, см. также [1]. Применение данного подхода сильно ограничено сложностью уравнения и узкой областью, где играют роль корреляции второго порядка.
Нулевое приближение для функции распределения электронов – это распределение Максвелла, которое найдено путем приравнивания к нулю интеграла столкновений ${{J}_{{ee}}}$ из (2)
(10)
${{f}_{0}} = {{n}_{e}}\mathop {\left( {\frac{{{{m}_{e}}}}{{2\pi kT}}} \right)}\nolimits^{3/2} ex{{p}^{{\left( { - {{m}_{e}}{{{v}}^{2}}/2kT} \right)}}},\quad \int {{{f}_{0}}d{{{v}}_{i}}} = {{n}_{e}}.$Здесь k – постоянная Больцмана, T – температура. Функция распределения для ионов в нулевом приближении ${{f}_{{I0}}}$ предполагается аналогичной функции распределения электронов.
Пользуясь (10) в (4)–(9), мы получаем нулевое приближение для уравнения переноса, в этом приближении $\left\langle {{{{v}}_{i}}} \right\rangle = 0$, ${{q}_{i}} = 0$.
В первом приближении мы ищем функцию f в виде
Функция χ позволяет записать решение в виде
(13)
${{d}_{i}} = \frac{{{{\rho }_{N}}}}{\rho }\frac{{\partial ln{{P}_{e}}}}{{\partial {{r}_{i}}}} - \frac{{{{\rho }_{e}}}}{{{{P}_{e}}}}\frac{1}{\rho }\frac{{\partial {{P}_{N}}}}{{\partial {{r}_{i}}}} + \frac{e}{{kT}}\left( {{{E}_{i}} + \frac{1}{c}{{\varepsilon }_{{ikl}}}{{c}_{{0k}}}{{B}_{l}}} \right).$Плазма предполагается квазинейтральной. Функции ${{A}_{i}}$ и ${{D}_{i}}$ определяют тепловой поток и диффузию соответственно. Подставляя (12) в уравнение для χ, получаем уравнения для ${{A}_{i}}$, ${{D}_{i}}$ [1]. В работах [10, 11] было показано, что в присутствии магнитного поля с аксиальным вектором ${{B}_{i}}$, полярные вектора ${{A}_{i}}$ и ${{D}_{i}}$ можно искать в виде
(14)
$\begin{gathered} {{A}_{i}} = {{A}^{{(1)}}}{{{v}}_{i}} + {{A}^{{(2)}}}{{\varepsilon }_{{ijk}}}{{{v}}_{j}}{{B}_{k}} + {{A}^{{(3)}}}{{B}_{i}}({{{v}}_{j}}{{B}_{j}}), \\ {{D}_{i}} = {{D}^{{(1)}}}{{{v}}_{i}} + {{D}^{{(2)}}}{{\varepsilon }_{{ijk}}}{{{v}}_{j}}{{B}_{k}} + {{D}^{{(3)}}}{{B}_{i}}({{{v}}_{j}}{{B}_{j}}), \\ \end{gathered} $(15)
${{\xi }_{A}} = {{A}^{{(1)}}} + iB{{A}^{{(2)}}},\quad {{\xi }_{D}} = {{D}^{{(1)}}} + iB{{D}^{{(2)}}},$(16)
$\begin{gathered} {{f}_{0}}\left( {{{u}^{2}} - \frac{5}{2}} \right){{u}_{i}} = \\ = - iB{{f}_{0}}\frac{{e{{\xi }_{A}}}}{{{{m}_{e}}c}}{{u}_{i}} + {{I}_{{ee}}}({{\xi }_{A}}{{u}_{i}}) + {{I}_{{eI}}}({{\xi }_{{AIi}}}{{u}_{{Ii}}}), \\ \end{gathered} $(17)
${{f}_{0}}{{u}_{i}} = - iB{{f}_{0}}\frac{{e{{\xi }_{D}}}}{{{{m}_{e}}c}}{{u}_{i}} + {{I}_{{ee}}}({{\xi }_{D}}{{u}_{i}}) + {{I}_{{eI}}}({{\xi }_{{DIi}}}{{u}_{{Ii}}}),$(18)
$\begin{gathered} {{I}_{{ee}}}({{\xi }_{k}}{{u}_{i}}) = \int {{{f}_{0}}{{f}_{{01}}}} ({{\xi }_{k}}{{u}_{i}} + {{\xi }_{{k1}}}{{u}_{{1i}}} - \\ \, - \xi _{k}^{'}u_{i}^{'} - \xi _{{k1}}^{'}u_{{1i}}^{'}){{g}_{{ee}}}bdbd\varepsilon d{{c}_{{1i}}}, \\ \end{gathered} $(19)
$\begin{gathered} {{I}_{{eI}}}({{\xi }_{k}}{{u}_{{Ii}}}) = \int {{{f}_{0}}{{f}_{{I0}}}} ({{\xi }_{k}}{{u}_{i}} - \xi _{k}^{'}u_{i}^{'}){{g}_{{eI}}}bdbd\varepsilon d{{c}_{{Ii}}}, \\ k = A,D. \\ \end{gathered} $Согласно [1], решение для функций ${{\xi }_{A}}$ и ${{\xi }_{D}}$ ищется в форме ряда ортогональных полиномов. Полиномы Сонина являются коэффициентами разложения функции ${{(1 - s)}^{{ - \tfrac{3}{2} - 1}}}exp[xs{\text{/}}(1 - s)]$ по степеням s
(20)
${{(1 - s)}^{{ - \tfrac{3}{2} - 1}}}exp\left( {\frac{{xs}}{{1 - s}}} \right) = \Sigma S_{{3/2}}^{{(p)}}(x){{s}^{p}}.$Они ортогональны,
(21)
$\int\limits_0^\infty {{{e}^{{ - x}}}S_{{3/2}}^{{(p)}}(x)S_{{3/2}}^{{(q)}}(x){{x}^{{3/2}}}dx} = \frac{{\Gamma (p + 5{\text{/}}2)}}{{p!}}{{\delta }_{{pq}}},$(22)
$\begin{gathered} S_{{3/2}}^{{(0)}}(x) = 1,\quad S_{{3/2}}^{{(1)}}(x) = \frac{5}{2} - x, \\ S_{{3/2}}^{{(2)}}(x) = \frac{{35}}{8} - \frac{7}{2}x + \frac{1}{2}{{x}^{2}}. \\ \end{gathered} $Мы ищем ${{\xi }_{A}}$, ${{\xi }_{D}}$, ${{D}^{{(3)}}}$ и ${{A}^{{(3)}}}$ в виде
(23)
$\begin{gathered} {{\xi }_{A}} = {{a}_{0}}S_{{3/2}}^{{(0)}} + {{a}_{1}}S_{{3/2}}^{{(1)}} + {{a}_{2}}S_{{3/2}}^{{(2)}}, \\ {{A}^{{(3)}}} = {{c}_{0}}S_{{3/2}}^{{(0)}} + {{c}_{1}}S_{{3/2}}^{{(1)}} + {{c}_{2}}S_{{3/2}}^{{(2)}}, \\ {{\xi }_{D}} = {{d}_{0}}S_{{3/2}}^{{(0)}} + {{d}_{1}}S_{{3/2}}^{{(1)}} + {{d}_{2}}S_{{3/2}}^{{(2)}}, \\ {{D}^{{(3)}}} = {{z}_{0}}S_{{3/2}}^{{(0)}} + {{z}_{1}}S_{{3/2}}^{{(1)}} + {{z}_{2}}S_{{3/2}}^{{(2)}}. \\ \end{gathered} $Умножая (16) и (17) на $S_{{3/2}}^{{(0)}}({{u}^{2}}){{u}_{i}}$, $S_{{3/2}}^{{(1)}}({{u}^{2}}){{u}_{i}}$ и $S_{{3/2}}^{{(2)}}({{u}^{2}}){{u}_{i}}$ и интегрируя относительно $d{{c}_{i}}$, мы получаем системы уравнений в общем виде для коэффициентов теплопроводности и термодиффузии
(24)
$\left\{ \begin{gathered} 0 = - \frac{3}{2}i\omega {{n}_{e}}{{a}_{0}} + {{a}_{0}}({{a}_{{00}}} + {{b}_{{00}}}) + \hfill \\ \, + {{a}_{1}}({{a}_{{01}}} + {{b}_{{01}}}) + {{a}_{2}}({{a}_{{02}}} + {{b}_{{02}}}), \hfill \\ - \frac{{15}}{4}{{n}_{e}} = - \frac{{15}}{4}i\omega {{n}_{e}}{{a}_{1}} + {{a}_{0}}({{a}_{{10}}} + {{b}_{{10}}}) + \hfill \\ \, + {{a}_{1}}({{a}_{{11}}} + {{b}_{{11}}}) + {{a}_{2}}({{a}_{{12}}} + {{b}_{{12}}}), \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{n}_{e}}{{a}_{2}} + {{a}_{0}}({{a}_{{20}}} + {{b}_{{20}}}) + \hfill \\ \, + {{a}_{1}}({{a}_{{21}}} + {{b}_{{21}}}) + {{a}_{2}}({{a}_{{22}}} + {{b}_{{22}}}), \hfill \\ \end{gathered} \right.$(25)
$\left\{ \begin{gathered} - \frac{3}{2} = - \frac{3}{2}i\omega {{n}_{e}}{{d}_{0}} + {{d}_{0}}({{a}_{{00}}} + {{b}_{{00}}}) + \hfill \\ \, + {{d}_{1}}({{a}_{{01}}} + {{b}_{{01}}}) + {{d}_{2}}({{a}_{{02}}} + {{b}_{{02}}}), \hfill \\ 0 = - \frac{{15}}{4}i\omega {{n}_{e}}{{d}_{1}} + {{d}_{0}}({{a}_{{10}}} + {{b}_{{10}}}) + \hfill \\ \, + {{d}_{1}}({{a}_{{11}}} + {{b}_{{11}}}) + {{d}_{2}}({{a}_{{12}}} + {{b}_{{12}}}), \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{n}_{e}}{{d}_{2}} + {{d}_{0}}({{a}_{{20}}} + {{b}_{{20}}}) + \hfill \\ \, + {{d}_{1}}({{a}_{{21}}} + {{b}_{{21}}}) + {{d}_{2}}({{a}_{{22}}} + {{b}_{{22}}}). \hfill \\ \end{gathered} \right.$Здесь ${{a}_{{jk}}}$, ${{b}_{{jk}}}$ матричные элементы для интегралов столкновений, $\omega = eB{\text{/}}({{m}_{e}}c)$ – циклотронная частота.
4. МАТРИЧНЫЕ ЭЛЕМЕНТЫ ${{a}_{{jk}}}$ И ${{b}_{{jk}}}$
Для расчета матричных элементов ${{a}_{{jk}}}$, введем следующие переменные [1]:
(26)
${{g}_{{ee}}} = {\text{|}}{{g}_{{ee,i}}}{\text{|}} = {\text{|}}g_{{ei,i}}^{'}{\text{|}} = g_{{ee}}^{'},\quad {{G}_{{0i}}} = {{G}_{{li}}} - {{c}_{{0i}}},$Здесь ${{G}_{{li}}}$ скорость центра масс двух сталкивающихся электронов в лабораторной системе отсчета, ${{G}_{{0i}}}$ – та же величина в сопутствующей системе отсчета, ${{g}_{{ee,i}}}$ – относительная скорость сталкивающихся электронов перед столкновением, $g_{{ee,i}}^{'}$ – та же величина после столкновения; ${{{v}}_{i}}$ и ${{{v}}_{{1i}}}$ – скорости сталкивающихся частиц в сопутствующей системе отсчета, определенной выше. Введем безразмерные переменные
(27)
$d{{c}_{i}}d{{c}_{{1i}}} = \mathop {\left( {\frac{{2kT}}{{{{m}_{e}}}}} \right)}\nolimits^3 d{{G}_{i}}d{{g}_{i}},\quad {{g}_{i}} * g_{i}^{'} = {{g}^{2}}cos(\theta )$Элементы
(28)
$\begin{gathered} {{a}_{{j0}}} = \int {{{f}_{0}}{{f}_{{01}}}S_{{3/2}}^{{(j)}}({{u}^{2}}){{u}_{i}}} \text{[}{{u}_{i}} + {{u}_{{1i}}} - \\ \, - u_{i}^{'} - u_{{1i}}^{'}]gbdbd\varepsilon d{{g}_{i}}d{{G}_{i}} = 0 \\ \end{gathered} $(29)
$\begin{gathered} {{a}_{{jk}}} = \int {{{f}_{0}}{{f}_{{01}}}} \text{[}S_{{3/2}}^{{(j)}}({{u}^{2}}){{u}_{i}} + S_{{3/2}}^{{(j)}}(u_{1}^{2}){{u}_{{1i}}} - \\ \, - S_{{3/2}}^{{(j)}}(\mathop {u'}\nolimits^2 )u_{i}^{'} - S_{{3/2}}^{{(j)}}(u_{1}^{{'2}})u_{{1i}}^{'}]S_{{3/2}}^{{(k)}}({{u}^{2}}){{u}_{i}}gbdbd\varepsilon d{{g}_{i}}d{{G}_{i}}. \\ \end{gathered} $Для того чтобы вычислить матричные элементы ${{b}_{{jk}}}$ и ${{a}_{{jk}}}$ нужно, согласно [1], вычислить следующий типичный интеграл:
(30)
$\begin{gathered} \frac{1}{{{{n}_{\alpha }}{{n}_{\beta }}}}\int {{{f}_{\alpha }}{{f}_{\beta }}} \text{[}S_{{3/2}}^{{(j)}}({{u}^{2}}){{u}_{i}} - \\ \, - S_{{3/2}}^{{(j)}}({{u}^{{'2}}})u_{i}^{'}]S_{{3/2}}^{{(k)}}({{u}^{2}}){{u}_{i}}{{g}_{{\alpha \beta }}}bdbd\varepsilon d{{c}_{{\alpha i}}}d{{c}_{{\beta i}}}, \\ \end{gathered} $Проинтегрировав как показано в [1], можем записать
(31)
$\begin{gathered} {{[S_{{3/2}}^{{(j)}}({{u}^{2}}){{u}_{i}},S_{{3/2}}^{{(k)}}({{u}^{2}}){{u}_{i}}]}_{e}} = \\ \, = {{\pi }^{{ - 3/2}}}\int {{{e}^{{ - {{g}^{2}}}}}} \sum {{{A}_{{jkrl}}}{{g}^{{2r}}}} (1 - co{{s}^{l}}(\theta ))gbdbd\epsilon dg, \\ \end{gathered} $Введем функции $\Omega _{{ee}}^{{(l)}}(r)$ как
(32)
$\Omega _{{ee}}^{{(l)}}(r) = \sqrt \pi \int\limits_0^\infty {{{e}^{{ - {{g}^{2}}}}}{{g}^{{2r + 1}}}{{\phi }_{{ee}}}(l)dg} ,$Таким образом (31) можно выразить через (32)
(34)
${{[S_{{3/2}}^{{(j)}}({{u}^{2}}){{u}_{i}},S_{{3/2}}^{{(k)}}({{u}^{2}}){{u}_{i}}]}_{e}} = 8\sum {{{A}_{{jkrl}}}\Omega _{{ee}}^{{(l)}}(r)} $Матричные коэффициенты ${{a}_{{jk}}}$ в общем виде выглядят так
(35)
$\begin{gathered} {{a}_{{11}}} = 4n_{e}^{2}\Omega _{{ee}}^{{(2)}}(2), \\ {{a}_{{12}}} = 7n_{e}^{2}\Omega _{{ee}}^{{(2)}}(2) - 2n_{e}^{2}\Omega _{{ee}}^{{(2)}}(3), \\ {{a}_{{22}}} = \frac{{77}}{4}n_{e}^{2}\Omega _{{ee}}^{{(2)}}(2) - 7n_{e}^{2}\Omega _{{ee}}^{{(2)}}(3) + n_{e}^{2}\Omega _{{ee}}^{{(2)}}(4). \\ \end{gathered} $Расчет матричных элементов ${{b}_{{jk}}}$, выполняется аналогично, см. [1].
Введем функции $\Omega _{{ei}}^{{(l)}}(r)$, аналогично (32):
(36)
$\Omega _{{ei}}^{{(l)}}(r) = \sqrt \pi \int\limits_0^\infty {{{e}^{{ - {{g}^{2}}}}}{{g}^{{2r + 2}}}\phi _{{ei}}^{{(l)}}dg} ,$Интегрируя в (37) по прицельному параметру db, видим, что интеграл логарифмически стремится к бесконечности. Он сходится при более точном рассмотрении кулоновских столкновений в плазме с учетом корреляционных функций [23], при этом возникает верхний предел интегрирования ${{b}_{{max}}}$.
Для электрон-ионных столкновений с ${{g}_{{ei}}} \sim {{{v}}_{e}}$ приближенное выражение для кулоновского логарифма записывается в виде [24]
(38)
$\Lambda = ln\left( {\frac{{{{b}_{{max}}}\bar {v}_{e}^{2}{{m}_{e}}}}{{Z{{e}^{2}}}}} \right),\quad \Lambda \gg 1,$Выражение для электрон-электронного кулоновского логарифма получается из (38) при $Z = 1$. Величина ${{b}_{{max}}}$ – общий радиус дебаевского экранирования для электронов ${{r}_{{\mathcal{D}e}}}$ и ионов ${{r}_{{\mathcal{D}i}}}$, которую можно выразить как
(40)
$\frac{1}{{b_{{\max }}^{2}}} = \frac{1}{{r_{{\mathcal{D}i}}^{2}}} + \frac{1}{{r_{{\mathcal{D}e}}^{2}}} = \frac{{4\pi {{{\text{e}}}^{2}}}}{{kT}}\left( {{{n}_{N}}{{Z}^{2}} + {{n}_{e}}} \right).$Средняя частота электрон-ионных столкновений ${{\nu }_{{ei}}}$ в [25] в предельном случае невырожденных электронов записывается как
(41)
${{\nu }_{{ei}}}\frac{4}{3}\sqrt {\frac{{2\pi }}{{{{m}_{e}}}}} \frac{{{{Z}^{2}}{{e}^{4}}{{n}_{N}}\Lambda }}{{{{{(kT)}}^{{3/2}}}}},\quad {{\tau }_{{nd}}} = 1{\text{/}}{{\nu }_{{nd}}}.$С учетом (36), элементы симметричной матрицы ${{b}_{{ij}}}$ имеют вид
(43)
${{b}_{{01}}} = 8{{n}_{e}}{{n}_{i}}\left( {\frac{5}{2}\Omega _{{ei}}^{{(1)}}(1) - \Omega _{{ei}}^{{(1)}}(2)} \right),$(44)
${{b}_{{11}}} = 8{{n}_{e}}{{n}_{i}}\left( {\frac{{25}}{4}\Omega _{{ei}}^{{(1)}}(1) - 5\Omega _{{ei}}^{{(1)}}(2) + \Omega _{{ei}}^{{(1)}}(3)} \right),$(45)
${{b}_{{02}}} = 8{{n}_{e}}{{n}_{i}}\left[ {\frac{{35}}{8}\Omega _{{eN}}^{{(1)}}(1) - \frac{7}{2}\Omega _{{eN}}^{{(1)}}(2) + \frac{1}{2}\Omega _{{eN}}^{{(1)}}(3)} \right],$(46)
$\begin{gathered} {{b}_{{12}}} = 8{{n}_{e}}{{n}_{N}}\left[ {\frac{{175}}{{16}}\Omega _{{ei}}^{{(1)}}(1) - \frac{{105}}{8}\Omega _{{ei}}^{{(1)}}(2) + } \right. \\ \, + \left. {\frac{{19}}{4}\Omega _{{ei}}^{{(1)}}(3) - \frac{1}{2}\Omega _{{ei}}^{{(1)}}(4)} \right], \\ \end{gathered} $(47)
$\begin{gathered} {{b}_{{22}}} = 8{{n}_{e}}{{n}_{i}}\left[ {\frac{{{{{35}}^{2}}}}{{{{8}^{2}}}}\Omega _{{ei}}^{{(1)}}(1) - \frac{{245}}{8}\Omega _{{ei}}^{{(1)}}(2) + } \right. \\ \left. {\, + \frac{{133}}{8}\Omega _{{ei}}^{{(1)}}(3) - \frac{7}{2}\Omega _{{ei}}^{{(1)}}(4) + \frac{1}{4}\Omega _{{ei}}^{{(1)}}(5)} \right]. \\ \end{gathered} $Согласно [1] находим выражения для $\Omega _{{eN}}^{{(1)}}(r)$ в виде
(48)
$\begin{gathered} \Omega _{{ei}}^{{(1)}}(r) = \sqrt \pi \frac{{{{e}^{4}}\Lambda {{Z}^{2}}}}{{{{{(2kT)}}^{2}}}}\Gamma (r),\quad \Gamma (1) = 1; \\ \Gamma (2) = 1;\quad \Gamma (3) = 2;\quad \Gamma (4) = 6;\quad \Gamma (5) = 24. \\ \end{gathered} $Используя (41), можно записать ${{b}_{{jk}}}$
(49)
${{b}_{{00}}} = 8\sqrt \pi \frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{3{{n}_{e}}}}{{2{{\tau }_{{nd}}}}},$(50)
${{b}_{{01}}} = 12\sqrt \pi \frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{9{{n}_{e}}}}{{4{{\tau }_{{nd}}}}},$(51)
${{b}_{{11}}} = 26\sqrt \pi \frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{39{{n}_{e}}}}{{8{{\tau }_{{nd}}}}},$(52)
${{b}_{{02}}} = 15\sqrt \pi \frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{45{{n}_{e}}}}{{16{{\tau }_{{nd}}}}},$(53)
${{b}_{{12}}} = \frac{{69\sqrt \pi }}{2}\frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{207{{n}_{e}}}}{{32{{\tau }_{{nd}}}}},$(54)
${{b}_{{22}}} = \frac{{433\sqrt \pi }}{8}\frac{{{{n}_{e}}{{n}_{N}}{{e}^{4}}{{Z}^{2}}\Lambda }}{{{{{(2kT)}}^{{3/2}}}\sqrt {{{m}_{e}}} }} = \frac{{1299{{n}_{e}}}}{{128{{\tau }_{{nd}}}}}.$Для плазмы с $\Lambda \gg 1$ из (38) имеем
(55)
${{\phi }_{{ee}}}(2) \approx \frac{{16{{e}^{4}}}}{{m_{e}^{2}g_{{ee}}^{3}}},\quad \Omega _{{ee}}^{{(2)}}(r) = \sqrt \pi \frac{{{{e}^{4}}\Lambda }}{{\sqrt {{{m}_{e}}} {{{(kT)}}^{{3/2}}}}}\Gamma (r).$Пользуясь (55), имеем из (35) c ${{n}_{e}} = Z{{n}_{i}}$
(56)
${{a}_{{11}}} = 4n_{e}^{2}\frac{{\sqrt \pi {{\Lambda }_{{ei}}}{{e}^{4}}}}{{\sqrt {{{m}_{e}}} {{{(kT)}}^{{3/2}}}}} = \frac{3}{{\sqrt 2 }}\frac{{{{n}_{e}}}}{{Z{{\tau }_{{nd}}}}},$5. ВЫРАЖЕНИЯ ДЛЯ ТЕНЗОРОВ КОЭФФИЦИЕНТОВ ПЕРЕНОСА В МАГНИТНОМ ПОЛЕ
Общее соотношение для потока тепла ${{q}_{i}}$, и средней направленной (диффузионной) скорости электронов $\left\langle {{{{v}}_{i}}} \right\rangle $, записываются в виде
(59)
${{q}_{i}} = - {{\lambda }_{{ij}}}\frac{{\partial T}}{{\partial {{x}_{j}}}} - {{n}_{e}}{{\nu }_{{ij}}}{{d}_{j}} = q_{i}^{{(A)}} + q_{i}^{{(D)}},$(60)
$\left\langle {{{{v}}_{i}}} \right\rangle = - {{\mu }_{{ij}}}\frac{{\partial T}}{{\partial {{x}_{j}}}} - {{n}_{e}}{{\eta }_{{ij}}}{{d}_{j}} = \left\langle {{v}_{i}^{{(A)}}} \right\rangle + \left\langle {{v}_{i}^{{(D)}}} \right\rangle ,$(61)
$\begin{gathered} {{\lambda }_{{ik}}} = \frac{5}{2}\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}\left\{ {\left[ {a_{0}^{1} - a_{1}^{1}} \right]{{\delta }_{{ik}}} - } \right. \\ \left. {\, - {{\varepsilon }_{{ikn}}}{{B}_{n}}\left[ {b_{0}^{1} - b_{1}^{1}} \right] + {{B}_{i}}{{B}_{k}}\left[ {c_{0}^{1} - c_{1}^{1}} \right]} \right\}, \\ \end{gathered} $(62)
$\begin{gathered} {{\nu }_{{ik}}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\left\{ {\left[ {d_{0}^{1} - d_{1}^{1}} \right]{{\delta }_{{ik}}} - } \right. \\ \, - \left. {{{\varepsilon }_{{ikn}}}{{B}_{n}}\left[ {e_{0}^{1} - e_{1}^{1}} \right] + {{B}_{i}}{{B}_{k}}\left[ {z_{0}^{1} - z_{1}^{1}} \right]} \right\}, \\ \end{gathered} $(63)
${{\mu }_{{ik}}} = \frac{k}{{{{m}_{e}}}}\left\{ {a_{0}^{1}{{\delta }_{{ik}}} - {{\varepsilon }_{{ikn}}}{{B}_{n}}b_{0}^{1} + {{B}_{i}}{{B}_{k}}c_{0}^{1}} \right\},$(64)
${{\eta }_{{ik}}} = \frac{{kT}}{{{{m}_{e}}}}\left\{ {d_{0}^{1}{{\delta }_{{ik}}} - {{\varepsilon }_{{ikn}}}{{B}_{n}}e_{0}^{1} + {{B}_{i}}{{B}_{k}}z_{0}^{1}} \right\}.$Здесь $a_{0}^{1}$, $b_{0}^{1}$ есть действительные и мнимые части коэффициента ${{a}_{0}}$
(65)
$\begin{gathered} {{a}_{0}} = a_{0}^{1} + iBb_{0}^{1},\quad {{a}_{1}} = a_{1}^{1} + iBb_{1}^{1}, \\ {{B}^{2}}c_{0}^{1} = {{(a_{0}^{1})}_{{B = 0}}} - a_{0}^{1},\quad {{B}^{2}}c_{1}^{1} = {{(a_{1}^{1})}_{{B = 0}}} - a_{1}^{1}, \\ \end{gathered} $(66)
$\begin{gathered} {{d}_{0}} = d_{0}^{1} + iBe_{0}^{1},\quad {{d}_{1}} = d_{1}^{1} + iBe_{1}^{1}, \\ {{B}^{2}}z_{0}^{1} = {{(d_{0}^{1})}_{{B = 0}}} - d_{0}^{1},\quad {{B}^{2}}z_{1}^{1} = {{(d_{1}^{1})}_{{B = 0}}} - d_{1}^{1}. \\ \end{gathered} $Метод нахождения коэффициентов тензора теплопроводности ${{\lambda }_{{ij}}}$ для произвольного вырождения подробно изложен в работе [20], где найдены для них аналитические выражения. Для сильно вырожденных электронов, коэффициенты термодиффузии, диффузии и диффузионного термоэффекта в приближении Лоренца найдены в работе [19].
5.1. Тензор термодиффузии для невырожденных электронов
Чтобы найти коэффициент ${{a}_{0}}$, необходимо решить систему уравнений (24) с матричными элементами ${{b}_{{jk}}}$ из (49)–(54) и матричными элементами ${{a}_{{jk}}}$ из (56)–(58). Система для трехполиномиального решения для электронов в присутствии магнитного поля, согласно (24), с учетом (49)–(54),(56)–(58), записывается как
(67)
$\left\{ \begin{gathered} 0 = - \frac{3}{2}i\omega {{\tau }_{{nd}}}{{a}_{0}} + \frac{3}{2}{{a}_{0}} + \frac{9}{4}{{a}_{1}} + \frac{{45}}{{16}}{{a}_{2}}, \hfill \\ - \frac{{15}}{4}{{\tau }_{{nd}}} = - \frac{{15}}{4}i\omega {{\tau }_{{nd}}}{{a}_{1}} + \frac{9}{4}{{a}_{0}} + \hfill \\ \, + \frac{3}{2}\left( {\frac{{13}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{a}_{1}} + \frac{9}{8}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{a}_{2}}, \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{\tau }_{{nd}}}{{a}_{2}} + \frac{{45}}{{16}}{{a}_{0}} + \hfill \\ \, + \frac{9}{8}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{a}_{1}} + \frac{3}{{32}}\left( {\frac{{433}}{4} + \frac{{45\sqrt 2 }}{Z}} \right){{a}_{2}}. \hfill \\ \end{gathered} \right.$Два первых уравнения при ${{a}_{2}} = 0$ определяют двухполиномиальное приближение, давая с учетом (63) следующие результаты для случая $B = 0$:
(69)
$\mu _{{nd}}^{{(2)}} = \frac{{15}}{4}\frac{k}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{1 + \sqrt 2 {\text{/}}Z}} = 3.75\frac{k}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{1 + \sqrt 2 {\text{/}}Z}}.$Результаты выше совпадают с результатами, полученными в [9, 10].
В трехполиномиальном приближении и при $B = 0$ мы получаем решение (67) для ${{a}_{0}}$ в виде
(70)
${{a}_{0}} = \frac{{165}}{{32}}\frac{{1 + 15\sqrt 2 {\text{/}}(11Z)}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{\tau }_{{nd}}},$(71)
$\mu _{{nd}}^{{(3)}} = 5.1563\frac{k}{{{{m}_{e}}}}\frac{{1 + 15\sqrt 2 {\text{/}}(11Z)}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{\tau }_{{nd}}}.$Величина
(72)
$Q = \frac{{32{{m}_{e}}\mu _{{nd}}^{{(3)}}}}{{165k{{\tau }_{{nd}}}}} = \frac{{1 + 15\sqrt 2 {\text{/}}(11Z)}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}},$Таблица 1.
Значения Q для различных химических элементов: водород ($Z = 1$); гелий ($Z = 2$); углерод ($Z = 6$); кислород ($Z = 8$); железо (Z = 26), ожидаемые для наружных слоев белых карликов и нейтронных звезд
| Z | 1 | 2 | 6 | 8 | 26 | ∞ |
| Q | 0.268 | 0.407 | 0.653 | 0.712 | 0.885 | 1 |
В двухполиномиальном приближении с учетом магнитного поля, принимая ${{a}_{2}} = 0$, мы получаем решение системы (67) в виде
(73)
${{a}_{0}} = \frac{{15}}{4}{{\tau }_{{nd}}}\mathop {\left[ {1 + \frac{{\sqrt 2 }}{Z} - \frac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2} - \left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right)i\omega {{\tau }_{{nd}}}} \right]}\nolimits^{ - 1} ,$(74)
$a_{0}^{1} = \frac{{15}}{4}{{\tau }_{{nd}}}\left( {1 + \frac{{\sqrt 2 }}{Z} - \frac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2}} \right)\zeta ,$(75)
$b_{0}^{1} = \frac{{15}}{4}\frac{{\omega \tau _{{nd}}^{2}}}{B}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right)\zeta ,$(76)
$\begin{gathered} \zeta = \left[ {\mathop {\left( {1 + \frac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + } \right. \\ \mathop {\, + \left. {{{{\left( {\frac{{449}}{{16}} + \frac{{13}}{2}\frac{{\sqrt 2 }}{Z} + \frac{2}{{{{Z}^{2}}}}} \right)}}^{{}}}{\kern 1pt} {{\omega }^{2}}\tau _{{nd}}^{2} + \frac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}} \right]}\nolimits^{ - 1} . \\ \end{gathered} $В трехполиномиальном приближении решение системы (67) имеет вид
(77)
${{a}_{0}} = \frac{{165}}{{32}}{{\tau }_{{nd}}}\left( {1 + \frac{{15\sqrt 2 }}{{11Z}} - \frac{{35}}{{11}}i\omega {{\tau }_{{nd}}}} \right)\frac{1}{{{{\zeta }_{1}} - i\omega {{\tau }_{{nd}}}{{\zeta }_{2}}}},$(78)
$\begin{gathered} a_{0}^{1} = \frac{{165}}{{32}}{{\tau }_{{nd}}}\left[ {\left( {1 + \frac{{15\sqrt 2 }}{{11Z}}} \right){{\zeta }_{1}} + \frac{{35}}{{11}}{{\omega }^{2}}\tau _{{nd}}^{2}{{\zeta }_{2}}} \right] \times \\ \, \times \frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}, \\ \end{gathered} $(79)
$\begin{gathered} b_{0}^{1} = \frac{{165}}{{32}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\left[ { - \frac{{35}}{{11}}{{\zeta }_{1}} + \left( {1 + \frac{{15\sqrt 2 }}{{11Z}}} \right){{\zeta }_{2}}} \right] \times \\ \, \times \frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}, \\ \end{gathered} $(80)
${{\zeta }_{1}} = 1 + \frac{{61\sqrt 2 }}{{16Z}} + \frac{9}{{2{{Z}^{2}}}} - \left( {\frac{{5385}}{{128}} + \frac{{365\sqrt 2 }}{{32Z}}} \right){{\omega }^{2}}\tau _{{nd}}^{2},$(81)
${{\zeta }_{2}} = \frac{{1017}}{{64}} + \frac{{667\sqrt 2 }}{{32Z}} + \frac{9}{{2{{Z}^{2}}}} - \frac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}.$Значения $c_{0}^{1}$ в двух и трехполиномиальном приближении определяются с использованием (65).
Диффузионная скорость $\left\langle {{v}_{i}^{A}} \right\rangle $ из (60), (63) может быть записана в виде
(82)
$\begin{gathered} \left\langle {{v}_{i}^{A}} \right\rangle = - \frac{k}{{{{m}_{e}}}}\left[ {a_{0}^{1}{{\delta }_{{ik}}} - {{\varepsilon }_{{ikn}}}{{B}_{n}}b_{0}^{1} + {{B}_{i}}{{B}_{k}}c_{0}^{1}} \right]\frac{{\partial T}}{{\partial {{r}_{k}}}} = \\ \, = {{\left\langle {{v}_{i}^{A}} \right\rangle }^{{(1)}}} + {{\left\langle {{v}_{i}^{A}} \right\rangle }^{{(2)}}} + {{\left\langle {{v}_{i}^{A}e} \right\rangle }^{{(3)}}}, \\ \end{gathered} $(83)
${{\left\langle {{v}_{i}^{A}} \right\rangle }^{{(1)}}} = - \frac{k}{{{{m}_{e}}}}a_{0}^{1}\frac{{\partial T}}{{\partial {{r}_{i}}}} = - \mu _{{nd}}^{{(1)}}\frac{{\partial T}}{{\partial {{r}_{i}}}},$(84)
${{\left\langle {v_{i}^{A}} \right\rangle }^{{(2)}}} = \frac{k}{{{{m}_{e}}}}{{\varepsilon }_{{ikn}}}{{B}_{n}}b_{0}^{1}\frac{{\partial T}}{{\partial {{r}_{k}}}} = {{\varepsilon }_{{ikn}}}{{B}_{n}}\mu _{{nd}}^{{(2)}}\frac{{\partial T}}{{\partial {{r}_{k}}}},$(85)
${{\left\langle {v_{i}^{A}} \right\rangle }^{{(3)}}} = - \frac{k}{{{{m}_{e}}}}{{B}_{i}}{{B}_{k}}c_{0}^{1}\frac{{\partial T}}{{\partial {{r}_{k}}}} = - {{B}_{i}}{{B}_{k}}\mu _{{nd}}^{{(3)}}\frac{{\partial T}}{{\partial {{r}_{k}}}}.$Для двухполиномиального приближения получаем
(86)
$\begin{gathered} \mu _{{nd}}^{{(12)}} = \frac{k}{{{{m}_{e}}}}a_{0}^{1} = \frac{{15}}{4}\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}} \times \\ \, \times \frac{{1 + \tfrac{{\sqrt 2 }}{Z} - \tfrac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $(87)
$\begin{gathered} \mu _{{nd}}^{{(22)}} = - \frac{k}{{{{m}_{e}}}}b_{0}^{1} = - \frac{{15}}{4}\frac{k}{{{{m}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B} \times \\ \, \times \frac{{\tfrac{{23}}{4} + \tfrac{{\sqrt 2 }}{Z}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $Выражения для коэффициентов термодиффузии в трехполиномиальном приближении могут быть записаны явно, с использованием (78)–(85)
(89)
$\begin{gathered} \mu _{{nd}}^{{(13)}} = \frac{k}{{{{m}_{e}}}}a_{0}^{1} = \\ \, = \frac{{165}}{{32}}\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}}\frac{{\left( {1 + \tfrac{{15\sqrt 2 }}{{11Z}}} \right){{\zeta }_{1}} + \tfrac{{35}}{{11}}{{\omega }^{2}}\tau _{{nd}}^{2}{{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}}, \\ \end{gathered} $(90)
$\begin{gathered} \mu _{{nd}}^{{(23)}} = - \frac{k}{{{{m}_{e}}}}b_{0}^{1} = \\ \, = - \frac{{165}}{{32}}\frac{k}{{{{m}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\frac{{ - \tfrac{{35}}{{11}}{{\zeta }_{1}} + \left( {1 + \tfrac{{15\sqrt 2 }}{{11Z}}} \right){{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}}, \\ \end{gathered} $Пользуясь (63), можно получить другую форму записи компонентов тензора термодиффузии в магнитном поле. Три компоненты теплового потока: параллельная ${{\left\langle {v_{i}^{A}} \right\rangle }_{{||}}}$, перпендикулярная ${{\left\langle {v_{i}^{A}} \right\rangle }_{ \bot }}$ к магнитному полю B, и компонента Холла ${{\left\langle {v_{i}^{A}} \right\rangle }_{{{\text{hall}}}}}$, перпендикулярная к обоим векторам $\nabla T$ и B, с учетом (69) или (71) определяются соотношениями
(93)
${{\left\langle {{v}_{i}^{A}} \right\rangle }_{ \bot }} = - {{\mu }_{ \bot }}\nabla {{T}_{ \bot }},\quad {{\mu }_{ \bot }} = \frac{k}{{{{m}_{e}}}}a_{0}^{1},$(94)
${{\left\langle {{v}_{i}^{A}} \right\rangle }_{{{\text{hall}}}}} = - {{\mu }_{{{\text{hall}}}}}\frac{{\nabla T \times {\mathbf{B}}}}{B},\quad {{\mu }_{{{\text{hall}}}}} = - \frac{k}{{{{m}_{e}}}}Bb_{0}^{1}.$Различие между двух- и трехполиномиальным приближением можно охарактеризовать сравнением величин $Q_{ \bot }^{{(2)}}$ и $Q_{ \bot }^{{(3)}}$
(95)
$Q_{ \bot }^{{(2)}} = \frac{{\mu _{{nd}}^{{(12)}}}}{{\mu _{{nd}}^{{(3)}}}},\quad Q_{ \bot }^{{(3)}} = \frac{{\mu _{{nd}}^{{(13)}}}}{{\mu _{{nd}}^{{(3)}}}},$5.2. Точное решение в приближении Лоренца
Приближение Лоренца для решения кинетического уравнения используется, когда масса легких частиц намного меньше, чем масса тяжелых частиц, и, кроме того, можно пренебречь электрон-электронными столкновениями. В этом приближении линеаризованное уравнение Больцмана имеет точное решение. Данное приближение хорошо работает для переноса в металле, где сильное электронное вырождение позволяет пренебречь электрон-электронными столкновениями. Приближение Лоренца можно использовать для проверки приближенного полиномиального решения, так как оно дает возможность проследить за сходимостью приближенного решения к точному с увеличением степени полиномов. Решение в приближении Лоренца рассматривалось в разных подходах [1, 16, 17, 27], см. также [24]. Для теплопроводности сходимость полиномиального решения к точному была рассмотрена в [20]. Точное решение в явном виде для приближения Лоренца получено для случая $B = 0$:
(96)
$\left\langle {{v}_{i}^{A}} \right\rangle = - \frac{{128k}}{\Lambda }\frac{{{{m}_{e}}{{{(kT)}}^{3}}}}{{{{n}_{N}}{{n}_{e}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\left( {{{G}_{4}} - \frac{5}{8}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{3}}} \right)\frac{{\partial T}}{{\partial {{r}_{{\text{i}}}}}}.$Здесь ${{G}_{i}}$ – интеграл Ферми, см. [24]. В предельных случаях коэффициент в (96) сводится к
(97)
$\begin{gathered} \mu _{e}^{l} = \frac{{12k}}{{{{\pi }^{{3/2}}}\Lambda {{n}_{N}}}}\frac{{{{{(kT)}}^{{3/2}}}}}{{{{{\text{e}}}^{4}}{{Z}^{2}}\sqrt {2{{m}_{e}}} }} = \frac{{16k}}{{{{m}_{e}}\pi }}{{\tau }_{{nd}}}(ND) \hfill \\ \,\;\;\, = \frac{2}{{3\Lambda }}\frac{{{{k}^{2}}T\pi h}}{{{{n}_{e}}{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{m}_{e}}}}\mathop {\left( {\frac{{3{{n}_{e}}}}{{8\pi }}} \right)}\nolimits^{4/3} = \frac{{4{{\pi }^{3}}}}{3}\frac{{{{k}^{2}}T}}{{{{n}_{e}}{{h}^{2}}}}\mathop {\left( {\frac{{3{{n}_{e}}}}{\pi }} \right)}\nolimits^{1/3} {{\tau }_{d}}(D). \hfill \\ \end{gathered} $Точные формулы в модели Лоренца используются [1] для оценки точности полиномиального приближения. Вклад электрон-электронных столкновений в коэффициент термодиффузии для различных Z можно оценить из графика нормированных трехполиномиальных коэффициентов термодиффузии в направлении, перпендикулярном к магнитному полю, введя величину $Q_{ \bot }^{{(3l)}}$, определяемую как
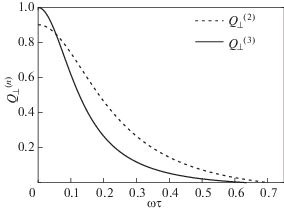
Здесь $\mu _{{e,nd}}^{l}$ взято из верхней строчки в (97). Кривые для различных Z, включая $Z = \infty $, относящиеся к приближению Лоренца, изображены на рис. 2. Пересечение графиков с осью y на рис. 2 происходит в точках, данных в табл. 1, умноженных на $\mu _{{nd}}^{{(3)}}{\text{/}}\mu _{{e,nd}}^{l} = 1.0124$. При $\omega \tau = 0.25$ имеем $Q_{ \bot }^{{(3l)}} = 0.0824,$ 0.0908, 0.1159, 0.0025 для $Z = \infty $, $26,\;6,\;2$ соответственно.
Рис. 2.
Графики значений $Q_{ \bot }^{{(3l)}}$ как функции $\omega \tau $ в трехполиномиальном приближении для невырожденной плазмы гелия ($Z = 2$), углерода ($Z = 6$), железа (Z = 26) в сравнении с лоренцевской плазмой, формально отвечающей $Z = \infty $. Отклонение от лоренцевской плазмы связано с вкладом электрон-электронных столкновений. Пересечение лоренцевской трехполиномиальной кривой ($Z = \infty $) с осью Y при 1.0124 связано с отклонением от точного решения в приближении Лоренца.

5.3. Вычисления полиномов без учета столкновений между электронами, термодиффузия
Чтобы проверить точность полиномиального приближения для коэффициентов термодиффузии, мы сравниваем их с коэффициентами, полученными как точное решение в приближении Лоренца. В отсутствии магнитного поля в приближении Лоренца с ${{a}_{{jk}}} = 0$ система (24) сводится к
(99)
$\left\{ \begin{gathered} 0 = {{a}_{0}}{{b}_{{00}}} + {{a}_{1}}{{b}_{{01}}} + {{a}_{2}}{{b}_{{02}}}, \hfill \\ - \frac{{15}}{4}{{n}_{e}} = {{a}_{0}}{{b}_{{10}}} + {{a}_{1}}{{b}_{{11}}} + {{a}_{2}}{{b}_{{12}}}, \hfill \\ 0 = {{a}_{0}}{{b}_{{20}}} + {{a}_{1}}{{b}_{{21}}} + {{a}_{2}}{{b}_{{22}}}. \hfill \\ \end{gathered} \right.$С учетом (49)–(54) запишем данную систему как
(100)
$\left\{ \begin{gathered} 0 = \frac{3}{2}{{a}_{0}} + \frac{9}{4}{{a}_{1}} + \frac{{45}}{{16}}{{a}_{2}}, \hfill \\ - \frac{{15}}{4}{{\tau }_{{nd}}} = \frac{9}{4}{{a}_{0}} + \frac{{39}}{8}{{a}_{1}} + \frac{{207}}{{32}}{{a}_{2}}, \hfill \\ 0 = \frac{{45}}{{16}}{{a}_{0}} + \frac{{207}}{{32}}{{a}_{1}} + \frac{{1299}}{{128}}{{a}_{2}}. \hfill \\ \end{gathered} \right.$Эта система записывается для трехполиномиального приближения. Два первых уравнения при ${{a}_{2}} = 0$ задают двухполиномиальное приближение, давая, с учетом (63), следующие результаты:
(101)
${{a}_{0}} = \frac{{15}}{4}{{\tau }_{{nd}}},\quad \mu _{{ndl}}^{{(2)}} = \frac{{15}}{4}\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}} = 3.75\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}}.$В трехполиномиальном приближении мы получаем решение (100) для ${{a}_{0}}$ и, с учетом (63), коэффициент термодиффузии в виде:
(102)
${{a}_{0}} = \frac{{165}}{{32}}{{\tau }_{{nd}}},\quad \mu _{{ndl}}^{{(3)}} = \frac{{165}}{{32}}\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}} = 5.1563\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}}.$Термодиффузию, полученную методом последовательных приближений полиномов, следует сравнить с точным решением $\lambda _{{nd}}^{l}$, полученным методом Лоренца (97) для невырожденных электронов
(103)
$\mu _{{nd}}^{{(l)}} = \frac{{16}}{\pi }\frac{k}{{{{m}_{e}}}}{{\tau }_{{nd}}} = 5.0931\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}}.$Ясно, что двухполиномиальное решение недооценивает коэффициент термодиффузии на 26%, а трехполиномиальное решение переоценивает приблизительно на 1.3%. Уравнения в случае трехполиномиального приближения в присутствии магнитного поля получены из (24) с учетом (49)–(54), (100) в виде
(104)
$\left\{ \begin{gathered} 0 = - \frac{3}{2}i\omega {{\tau }_{{nd}}}{{a}_{0}} + \frac{3}{2}{{a}_{0}} + \frac{9}{4}{{a}_{1}} + \frac{{45}}{{16}}{{a}_{2}}, \hfill \\ - \frac{{15}}{4}{{\tau }_{{nd}}} = - \frac{{15}}{4}i\omega {{\tau }_{{nd}}}{{a}_{1}} + \frac{9}{4}{{a}_{0}} + \frac{{39}}{8}{{a}_{1}} + \frac{{207}}{{32}}{{a}_{2}}, \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{\tau }_{{nd}}}{{a}_{2}} + \frac{{45}}{{16}}{{a}_{0}} + \frac{{207}}{{32}}{{a}_{1}} + \frac{{1299}}{{128}}{{a}_{2}}. \hfill \\ \end{gathered} \right.$Явное решение уравнений (104) для двух- и трехполиномиальных приближений определяется формулами (73)–(79) при формально бесконечном значении Z.
5.4. Частично вырожденные электроны
Для частично вырожденных электронов, для которых матричные коэффициенты ${{b}_{{jk}}}$ были посчитаны в работе [20], при ${{x}_{0}} = 0$ с уровнем вырождения $DL = {{\varepsilon }_{{fe}}}{\text{/}}kT = 1.011$, система (24) записывается в виде
(105)
$\left\{ \begin{gathered} 0 = - 1.5i\omega {{n}_{e}}{{a}_{0}} + {{a}_{0}}{{b}_{{00}}} + {{a}_{1}}{{b}_{{01}}} + {{a}_{2}}{{b}_{{02}}}, \hfill \\ - 3.88{{n}_{e}} = - 3.88i\omega {{n}_{e}}{{a}_{1}} + {{a}_{0}}{{b}_{{10}}} + {{a}_{1}}{{b}_{{11}}} + {{a}_{2}}{{b}_{{12}}}, \hfill \\ 0 = - 7.138i\omega {{n}_{e}}{{a}_{2}} + {{a}_{0}}{{b}_{{20}}} + {{a}_{1}}{{b}_{{21}}} + {{a}_{2}}{{b}_{{22}}}. \hfill \\ \end{gathered} \right.$В отсутствие магнитного поля эта система сводится к
(106)
$\left\{ \begin{gathered} 0 = 1.5{{a}_{0}} + 2.16{{a}_{1}} + 2.588{{a}_{2}}, \hfill \\ - 3.88{{\tau }_{{d0}}} = 2.16{{a}_{0}} + 5.162{{a}_{1}} + 6.671{{a}_{2}}, \hfill \\ 0 = 2.588{{a}_{0}} + 6.671{{a}_{1}} + 11.038{{a}_{2}}. \hfill \\ \end{gathered} \right.$Первые два уравнения при ${{a}_{2}} = 0$ определяют двухполиномиальное приближение, которое с учетом (63), дает следующий результат:
(107)
${{a}_{0}} = 2.723{{\tau }_{{d0}}},\quad \mu _{{d0l}}^{{(2)}} = 2.723\frac{k}{{{{m}_{e}}}}{{\tau }_{{d0}}}.$В трехполиномиальном приближении, с учетом (63), мы получаем решение (106) для ${{a}_{0}}$, ${{a}_{1}}$, а также коэффициент теплопроводности в виде
(108)
${{a}_{0}} = 3.533{{\tau }_{{d0}}},\quad \mu _{{d0l}}^{{(3)}} = 3.533\frac{k}{{{{m}_{e}}}}{{\tau }_{{d0}}}.$Сравним коэффициент термодиффузии, полученный методом последовательных приближений полиномами с точным решением $\mu _{{nd}}^{l}$, полученным методом Лоренца (96) для невырожденных электронов
(109)
$\mu _{{d0}}^{{(l)}} = 0.744\frac{{16}}{\pi }\frac{k}{{{{m}_{e}}}}{{\tau }_{{d0}}} = 3.789\frac{k}{{{{m}_{e}}}}{{\tau }_{{d0}}}.$Видно, что двухполиномиальное решение недооценивает коэффициент термодиффузии более, чем на 28%, а трехполиномиальное решение отличается от точного решения приблизительно на 7%.
6. ТЕНЗОРЫ ДИФФУЗИИ И ДИФФУЗИОННОГО ТЕРМОЭФФЕКТА ДЛЯ НЕВЫРОЖДЕННЫХ ЭЛЕКТРОНОВ
Для невырожденных электронов тензоры (64) и (62) записываются в виде
(110)
${{\eta }_{{ik}}} = \frac{{kT}}{{{{m}_{e}}}}\left[ {d_{0}^{1}{{\delta }_{{ik}}} - {{\epsilon }_{{ijk}}}{{B}_{n}}e_{0}^{1} + {{B}_{i}}{{B}_{k}}z_{0}^{1}} \right],$(111)
$\begin{gathered} {{\nu }_{{ik}}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{n}_{e}}\left[ {(d_{0}^{1} - d_{1}^{1}){{\delta }_{{ik}}} - } \right. \\ \, - \left. {{{\epsilon }_{{ijk}}}{{B}_{n}}(e_{0}^{1} - e_{1}^{1}) + {{B}_{i}}{{B}_{k}}(z_{0}^{1} - z_{1}^{1})} \right]. \\ \end{gathered} $Чтобы найти коэффициенты ${{d}_{0}}$, ${{d}_{1}}$ для произвольного вырождения электронов, аналогично поиску коэффициентов термодиффузии, необходимо решить систему уравнений (25) с матричными элементами ${{b}_{{jk}}}$ из (42)–(47) и матричными элементами ${{a}_{{jk}}}$.
Для невырожденных электронов с учетом трехполиномиального разложения, система (25) должна быть записана как
(112)
$\left\{ \begin{gathered} - \frac{3}{2}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = - \frac{3}{2}i\omega {{\tau }_{{nd}}}{{d}_{0}} + \frac{3}{2}{{d}_{0}} + \frac{9}{4}{{d}_{1}} + \frac{{45}}{{16}}{{d}_{2}}, \hfill \\ 0 = - \frac{{15}}{4}i\omega {{\tau }_{{nd}}}{{d}_{1}} + \frac{9}{4}{{d}_{0}} + \frac{3}{2}\left( {\frac{{13}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{d}_{1}} + \hfill \\ \, + \frac{9}{8}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{d}_{2}}, \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{\tau }_{{nd}}}{{d}_{2}} + \frac{{45}}{{16}}{{d}_{0}} + \frac{9}{8}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right){{d}_{1}} + \hfill \\ \, + \frac{3}{{32}}\left( {\frac{{433}}{4} + \frac{{45\sqrt 2 }}{Z}} \right){{d}_{2}}. \hfill \\ \end{gathered} \right.$Два первых уравнения при ${{d}_{2}} = 0$ определяют двухполиномиальное приближение, давая с учетом (64), (62) следующие результаты для случая $B = 0$:
(113)
${{d}_{0}} = - \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{13{\text{/}}4 + \sqrt 2 {\text{/}}Z}}{{1 + \sqrt 2 {\text{/}}Z}},\quad {{d}_{1}} = \frac{3}{2}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{1}{{1 + \sqrt 2 {\text{/}}Z}},$(114)
$\begin{gathered} \eta _{{nd}}^{{(2)}} = - \frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{13{\text{/}}4 + \sqrt 2 {\text{/}}Z}}{{1 + \sqrt 2 {\text{/}}Z}}, \\ \nu _{{nd}}^{{(2)}} = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}}\frac{{19{\text{/}}4 + \sqrt 2 {\text{/}}Z}}{{1 + \sqrt 2 {\text{/}}Z}}. \\ \end{gathered} $Результаты выше совпадают с результатами, полученными в [9, 10].
В трехполиномиальном приближении и при $B = 0$ мы получаем решение (112) для ${{d}_{0}}$ и ${{d}_{1}}$, в виде
(115)
${{d}_{0}} = - \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{217{\text{/}}64 + 151\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}},$(116)
${{d}_{1}} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{33{\text{/}}16 + 45\sqrt 2 {\text{/}}(16Z)}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}},$(117)
$\begin{gathered} \eta _{{nd}}^{{(3)}} = \\ = - \frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{217{\text{/}}64 + 151\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}, \\ \end{gathered} $(118)
$\begin{gathered} \nu _{{nd}}^{{(3)}} = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}} \times \\ \times \;\frac{{349{\text{/}}64 + 196\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}{{\tau }_{{nd}}}. \\ \end{gathered} $Значения величины
(119)
$\begin{gathered} U = \frac{{64{{m}_{e}}{{n}_{e}}\eta _{{nd}}^{{(3)}}}}{{217kT{{\tau }_{{nd}}}}} = \\ \, = - \frac{{1 + 302\sqrt 2 {\text{/}}(17Z) + 288(217{{Z}^{2}})}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}, \\ \end{gathered} $(120)
$\begin{gathered} W = \frac{{128{{m}_{e}}\nu _{{nd}}^{{(3)}}}}{{1745{{k}^{2}}{{T}^{2}}{{\tau }_{{nd}}}}} = \\ \, = - \frac{{1 + 784\sqrt 2 {\text{/}}(349Z) + 288{\text{/}}(349{{Z}^{2}})}}{{1 + 61\sqrt 2 {\text{/}}(16Z) + 9{\text{/}}(2{{Z}^{2}})}}, \\ \end{gathered} $Таблица 2.
Значения U для различных химических элементов: водород ($Z = 1$); гелий ($Z = 2$); углерод (Z = = 6); кислород ($Z = 8$); железо (Z = 26), ожидаемые для наружных слоев белых карликов и нейтронных звезд
| Z | 1 | 2 | 6 | 8 | 26 | ∞ |
| U | 0.575 | 0.684 | 0.836 | 0.868 | 0.949 | 1 |
Таблица 3.
Значения W для различных химических элементов: водород ($Z = 1$); гелий ($Z = 2$); углерод ($Z = 6$); кислород ($Z = 8$); железо (Z = 26), ожидаемые для наружных слоев белых карликов и нейтронных звезд
| Z | 1 | 2 | 6 | 8 | 26 | ∞ |
| W | 0.459 | 0.579 | 0.767 | 0.809 | 0.925 | 1 |
В двухполиномиальном приближении с учетом магнитного поля, принимая ${{d}_{2}} = 0$, мы получаем решение системы (112) в виде
(121)
$\begin{gathered} {{d}_{0}} = \left( { - \frac{{13}}{4} - \frac{{\sqrt 2 }}{Z} + \frac{5}{2}i\omega {{\tau }_{{nd}}}} \right)\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} \times \\ \, \times \mathop {\left[ {1 + \frac{{\sqrt 2 }}{Z} - \frac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2} - \left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right)i\omega {{\tau }_{{nd}}}} \right]}\nolimits^{ - 1} , \\ \end{gathered} $(122)
$d_{0}^{1} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\left( { - \frac{{13}}{4} - \frac{{17\sqrt 2 }}{{4Z}} - \frac{{25}}{4}{{\omega }^{2}}\tau _{{nd}}^{2} - \frac{2}{{{{Z}^{2}}}}} \right)\zeta ,$(123)
$e_{0}^{1} = - \frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\left( {\frac{{259}}{{16}} + \frac{{13\sqrt 2 }}{{2Z}} + \frac{2}{{{{Z}^{2}}}} + \frac{{25}}{4}{{\omega }^{2}}\tau _{{nd}}^{2}} \right)\zeta ,$(124)
${{d}_{1}} = \frac{{13}}{4}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\mathop {\left[ {1 + \frac{{\sqrt 2 }}{Z} - \frac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2} - \left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right)i\omega {{\tau }_{{nd}}}} \right]}\nolimits^{ - 1} ,$(125)
$d_{1}^{1} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{3}{2}\left( {1 + \frac{{\sqrt 2 }}{Z} - \frac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2}} \right)\zeta ,$(126)
$e_{1}^{1} = \frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\frac{3}{2}\left( {\frac{{23}}{4} + \frac{{\sqrt 2 }}{Z}} \right)\zeta ,$В трехполиномиальном приближении решение системы (112) имеет вид
(127)
$\begin{gathered} {{d}_{0}} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\left( { - \frac{{217}}{{64}} - \frac{{151\sqrt 2 }}{{16Z}} - \frac{9}{{2{{Z}^{2}}}} + \frac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2} + } \right. \\ \, + \left. {i\omega {{\tau }_{{nd}}}\left( {\frac{{3985}}{{128}} + \frac{{365\sqrt 2 }}{{32Z}}} \right)} \right)\frac{1}{{{{\zeta }_{1}} - i\omega {{\tau }_{{nd}}}{{\zeta }_{2}}}}, \\ \end{gathered} $(128)
$\begin{gathered} d_{0}^{1} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\left[ {\left( { - \frac{{217}}{{64}} - \frac{{151\sqrt 2 }}{{16Z}} - \frac{9}{{2{{Z}^{2}}}} + \frac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right){{\zeta }_{1}}} \right. - \\ \left. { - \;{{\omega }^{2}}\tau _{{nd}}^{2}\left( {\frac{{3985}}{{128}} + \frac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{2}}} \right]\frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}, \\ \end{gathered} $(129)
$\begin{gathered} e_{0}^{1} = \frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\left[ {\left( {\frac{{3985}}{{128}} + \frac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{1}} - } \right. \\ - \left. {\left( {\frac{{217}}{{64}} + \frac{{151\sqrt 2 }}{{16Z}} + \frac{9}{{2{{Z}^{2}}}} - \frac{{175}}{{16}}{{\omega }^{2}}{{\tau }^{2}}} \right){{\zeta }_{2}}} \right]\frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}, \\ \end{gathered} $(130)
${{d}_{1}} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\left( {\frac{{33}}{{16}} + \frac{{45\sqrt 2 }}{{16Z}} - \frac{{105}}{{16}}i\omega {{\tau }_{{nd}}}} \right)\frac{1}{{{{\zeta }_{1}} - i\omega {{\tau }_{{nd}}}{{\zeta }_{2}}}},$(131)
$\begin{gathered} d_{1}^{1} = \frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\left[ {\left( {\frac{{33}}{{16}} + \frac{{45\sqrt 2 }}{{16Z}}} \right){{\zeta }_{1}} + \frac{{105}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}{{\zeta }_{2}}} \right] \times \\ \, \times \frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}, \\ \end{gathered} $(132)
$\begin{gathered} e_{1}^{1} = \frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\left[ { - \frac{{105}}{{16}}{{\zeta }_{1}} + \left( {\frac{{33}}{{16}} + \frac{{45\sqrt 2 }}{{16Z}}} \right){{\zeta }_{2}}} \right] \times \\ \, \times \frac{1}{{\zeta _{1}^{2} + {{\omega }^{2}}\tau _{{nd}}^{2}\zeta _{2}^{2}}}. \\ \end{gathered} $Значения $z_{0}^{1}$ в двух- и трехполиномиальном приближении определяются с использованием (66).
Скорость $\left\langle {{v}_{i}^{D}} \right\rangle $ может быть записана в виде
(133)
$\begin{gathered} \left\langle {{v}_{i}^{D}} \right\rangle = - {{n}_{e}}\frac{{kT}}{{{{m}_{e}}}}\left[ {d_{0}^{1}{{\delta }_{{ik}}} - {{\varepsilon }_{{ikn}}}{{B}_{n}}e_{0}^{1} + {{B}_{i}}{{B}_{k}}z_{0}^{1}} \right]{{d}_{k}} = \\ \, = {{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(1)}}} + {{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(2)}}} + {{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(3)}}}. \\ \end{gathered} $Поток тепла $q_{i}^{{(D)}}$ может быть записан как
(134)
$\begin{gathered} q_{i}^{D} = - {{n}_{e}}\frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\left[ {(d_{0}^{1} - d_{1}^{1}){{\delta }_{{ik}}} - } \right. \\ \, - \left. {{{\varepsilon }_{{ikn}}}{{B}_{n}}(e_{0}^{1} - e_{1}^{1}) + {{B}_{i}}{{B}_{k}}(z_{0}^{1} - z_{1}^{1})} \right]{{d}_{k}} = \\ \, = q_{i}^{{D(1)}} + q_{i}^{{D(2)}} + q_{i}^{{D(3)}}, \\ \end{gathered} $Откуда:
(135)
${{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(1)}}} = - {{n}_{e}}\frac{{kT}}{{{{m}_{e}}}}d_{0}^{1}{{d}_{k}} = - {{n}_{e}}\eta _{{nd}}^{{(1)}}{{d}_{k}},$(136)
${{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(2)}}} = {{n}_{e}}\frac{{kT}}{{{{m}_{e}}}}{{\varepsilon }_{{ikn}}}{{B}_{n}}e_{0}^{1}{{d}_{k}} = {{n}_{e}}{{\varepsilon }_{{ikn}}}{{B}_{n}}\eta _{{nd}}^{{(2)}}{{d}_{k}},$(137)
${{\left\langle {{v}_{i}^{D}} \right\rangle }^{{(3)}}} = - {{n}_{e}}\frac{{kT}}{{{{m}_{e}}}}{{B}_{i}}{{B}_{k}}z_{0}^{1}{{d}_{k}} = - {{n}_{e}}{{B}_{i}}{{B}_{k}}\eta _{{nd}}^{{(3)}}{{d}_{k}},$(138)
$q_{i}^{{D(1)}} = - {{n}_{e}}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(d_{0}^{1} - d_{1}^{1}){{\delta }_{{ik}}}{{d}_{k}} = - {{n}_{e}}\nu _{{nd}}^{{(1)}}{{d}_{k}},$(139)
$\begin{gathered} q_{i}^{{D(2)}} = {{n}_{e}}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}{{\varepsilon }_{{ikn}}}{{B}_{n}}(e_{0}^{1} - e_{1}^{1}){{d}_{k}} = \\ = {{n}_{e}}{{\varepsilon }_{{ikn}}}{{B}_{n}}\nu _{{nd}}^{{(2)}}{{d}_{k}}, \\ \end{gathered} $(140)
$\begin{gathered} q_{i}^{{D(3)}} = - {{n}_{e}}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}{{B}_{i}}{{B}_{k}}(z_{0}^{1} - z_{1}^{1}){{d}_{k}} = \\ = - {{n}_{e}}{{B}_{i}}{{B}_{k}}\nu _{{nd}}^{{(3)}}{{d}_{k}}. \\ \end{gathered} $Для двухполиномиального приближения получаем
(141)
$\begin{gathered} \eta _{{nd}}^{{(12)}} = \frac{{kT}}{{{{m}_{e}}}}d_{0}^{1} = \frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} \times \\ \, \times \frac{{ - \tfrac{{13}}{4} - \tfrac{{17\sqrt 2 }}{{4Z}} - \tfrac{2}{{{{Z}^{2}}}} - \tfrac{{25}}{4}{{\omega }^{2}}\tau _{{nd}}^{2}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $(142)
$\begin{gathered} \eta _{{nd}}^{{(22)}} = - \frac{{kT}}{{{{m}_{e}}}}e_{0}^{1} = - \frac{{kT}}{{{{m}_{e}}}}\frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B} \times \\ \, \times \frac{{ - \tfrac{{259}}{{16}} - \tfrac{{13\sqrt 2 }}{{2Z}} - \tfrac{2}{{{{Z}^{2}}}} - \tfrac{{25}}{4}{{\omega }^{2}}\tau _{{nd}}^{2}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $(144)
$\begin{gathered} \nu _{{nd}}^{{(12)}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(d_{0}^{1} - d_{1}^{1}) = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} \times \\ \, \times \frac{{ - \tfrac{{19}}{4} - \tfrac{{23\sqrt 2 }}{{4Z}} - \tfrac{2}{{{{Z}^{2}}}} - \tfrac{5}{2}{{\omega }^{2}}\tau _{{nd}}^{2}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $(145)
$\begin{gathered} \nu _{{nd}}^{{(22)}} = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(e_{0}^{1} - e_{1}^{1}) = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\frac{1}{{{{n}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B} \times \\ \, \times \frac{{ - \tfrac{{397}}{{16}} - \tfrac{{8\sqrt 2 }}{Z} - \tfrac{2}{{{{Z}^{2}}}} - \tfrac{{25}}{4}{{\omega }^{2}}\tau _{{nd}}^{2}}}{{\mathop {\left( {1 + \tfrac{{\sqrt 2 }}{Z}} \right)}\nolimits^2 + \left( {\tfrac{{449}}{{16}} + \tfrac{{13}}{2}\tfrac{{\sqrt 2 }}{Z} + \tfrac{2}{{{{Z}^{2}}}}} \right){{\omega }^{2}}\tau _{{nd}}^{2} + \tfrac{{25}}{4}{{\omega }^{4}}\tau _{{nd}}^{4}}}, \\ \end{gathered} $Выражения для коэффициентов диффузии в трехполиномиальном приближении могут быть записаны явно, с использованием (128)–(132):
(147)
$\eta _{{nd}}^{{(13)}} = \frac{{kT}}{{{{m}_{e}}}}d_{0}^{1} = \frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{\left( { - \tfrac{{217}}{{64}} - \tfrac{{151\sqrt 2 }}{{16Z}} - \tfrac{9}{{2{{Z}^{2}}}} + \tfrac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right){{\zeta }_{1}} - {{\omega }^{2}}{{\tau }^{2}}\left( {\tfrac{{3985}}{{128}} + \tfrac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}},$(148)
$\eta _{{nd}}^{{(23)}} = - \frac{{kT}}{{{{m}_{e}}}}e_{0}^{1} = - \frac{{kT}}{{{{m}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{{B{{n}_{e}}}}\frac{{\left( {\tfrac{{3985}}{{128}} + \tfrac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{1}} - \left( {\tfrac{{217}}{{64}} + \tfrac{{151\sqrt 2 }}{{16Z}} + \tfrac{9}{{2{{Z}^{2}}}} - \tfrac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right){{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}},$Аналогично для диффузионного термоэфффекта
(150)
$\nu _{{nd}}^{{(13)}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(d_{0}^{1} - d_{1}^{1}) = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{\tau }_{{nd}}}}}{{{{m}_{e}}}}\frac{{\left( { - \tfrac{{349}}{{64}} - \tfrac{{49\sqrt 2 }}{{4Z}} - \tfrac{9}{{2{{Z}^{2}}}} + \tfrac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right){{\zeta }_{1}} - {{\omega }^{2}}{{\tau }^{2}}\left( {\tfrac{{4825}}{{128}} + \frac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}},$(151)
$\nu _{{nd}}^{{(23)}} = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(e_{0}^{1} - e_{1}^{1}) = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B}\frac{{\left( {\tfrac{{4825}}{{128}} + \tfrac{{365\sqrt 2 }}{{32Z}}} \right){{\zeta }_{1}} - {{\zeta }_{2}}\left( {\tfrac{{349}}{{64}} + \tfrac{{196\sqrt 2 }}{{16Z}} + \tfrac{9}{{2{{Z}^{2}}}} - \frac{{175}}{{16}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right)}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}},$Получим другую форму записи компонентов тензоров диффузии и диффузионного термоэффекта в магнитном поле аналогично термодиффузии. Три компоненты теплового потока и диффузионной скорости: параллельные ${{\left\langle {{v}_{i}^{D}} \right\rangle }_{{||}}}$, $q_{{||}}^{D}$, перпендикулярные ${{\left\langle {{v}_{i}^{D}} \right\rangle }_{ \bot }}$, $q_{ \bot }^{D}$ к магнитному полю B, и компоненты Холла ${{\left\langle {{v}_{i}^{D}} \right\rangle }_{{{\text{hall}}}}}$, $q_{{{\text{hall}}}}^{D}$, перпендикулярные к обоим векторам $\nabla T$ и B, определяются соотношениями
(153)
${{\left\langle {{v}_{i}^{D}} \right\rangle }_{{||}}} = - {{n}_{e}}{{\eta }_{{||}}}{{d}_{{||}}},\quad q_{{||}}^{D} = - {{n}_{e}}{{\nu }_{{||}}}{{d}_{{||}}},$(154)
${{\eta }_{{||}}} = \frac{{kT}}{{{{m}_{e}}}}[d_{0}^{1} + {{B}^{2}}(z_{0}^{1})] = {{\eta }_{{nd}}},$(155)
${{\nu }_{{||}}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}[(d_{0}^{1} - d_{1}^{1}) + {{B}^{2}}(z_{0}^{1} - z_{1}^{1})] = {{\nu }_{{nd}}},$(156)
${{\left\langle {{v}_{i}^{D}} \right\rangle }_{ \bot }} = - {{n}_{e}}{{\eta }_{ \bot }}{{d}_{ \bot }},\quad {{\eta }_{ \bot }} = \frac{{kT}}{{{{m}_{e}}}}(d_{0}^{1}),$(157)
$q_{ \bot }^{D} = - {{n}_{e}}{{\nu }_{ \bot }}{{d}_{ \bot }},\quad {{\nu }_{ \bot }} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}(d_{0}^{1} - d_{1}^{1}),$(158)
${{\left\langle {{v}_{i}^{D}} \right\rangle }_{{{\text{hall}}}}} = - {{n}_{e}}{{\eta }_{{{\text{hall}}}}}\frac{{{\mathbf{d}} \times {\mathbf{B}}}}{B},\quad {{\eta }_{{{\text{hall}}}}} = \frac{{kT}}{{{{m}_{e}}}}Be_{0}^{1}.$(159)
$\begin{gathered} q_{{{\text{hall}}}}^{D} = - {{n}_{e}}{{\nu }_{{{\text{hall}}}}}\frac{{\nabla T \times {\mathbf{B}}}}{B}, \\ {{\nu }_{{{\text{hall}}}}} = \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}B(e_{0}^{1} - e_{0}^{1}). \\ \end{gathered} $Результаты для двух полиномов совпадают с соответствующими результатами, полученными в [9, 10].
Различие между двух и трехполиномиальным приближением можно охарактеризовать сравнением величин $U_{ \bot }^{{(2)}}$, $W_{ \bot }^{{(2)}}$ и $U_{ \bot }^{{(3)}}$, $W_{ \bot }^{{(3)}}$:
(160)
$\begin{gathered} U_{ \bot }^{{(2)}} = \frac{{\eta _{{nd}}^{{(12)}}}}{{\eta _{{nd}}^{{(3)}}}},\quad U_{ \bot }^{{(3)}} = \frac{{\eta _{{nd}}^{{(13)}}}}{{\eta _{{nd}}^{{(3)}}}}, \\ W_{ \bot }^{{(2)}} = \frac{{\nu _{{nd}}^{{(12)}}}}{{\nu _{{nd}}^{{(3)}}}},\quad W_{ \bot }^{{(3)}} = \frac{{\nu _{{nd}}^{{(13)}}}}{{\nu _{{nd}}^{{(3)}}}}, \\ \end{gathered} $Рис. 3.
Диффузионный термоэффект. Сравнение двух- и трехполиномиального приближения для невырожденной углеродной плазмы при $Z = 6$ для различных $\omega \tau $.
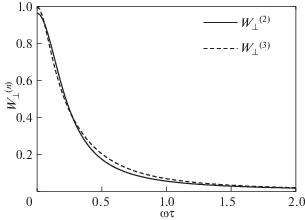
Рис. 4.
Диффузия. Сравнение двух- и трехполиномиального приближения для невырожденной углеродной плазмы при $Z = 6$ для различных $\omega \tau $.
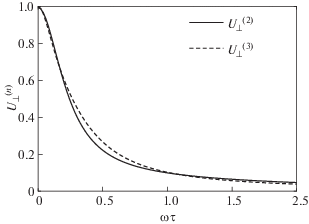
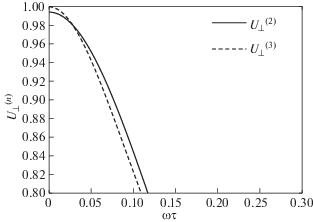
Рис. 5.
Увеличенный сегмент графика сравнения двух- и трехполиномиального приближения для диффузии при $\omega \tau < 0.15$.
Система уравнений (4)–(6) может быть дополнена уравнениями Максвелла
Для скалярной проводимости σ, когда
(161)
${\mathbf{j}} = \sigma \left( {{\mathbf{E}} + \frac{1}{c}{\mathbf{v}} \times {\mathbf{B}}} \right),$(162)
$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = \nabla \times ({\mathbf{v}} \times {\mathbf{B}}) + \frac{{{{c}^{2}}}}{{4\pi \sigma }}\Delta {\mathbf{B}}.$При строгом учете кинетических коэффициентов выражение для вектора электрического тока ${{j}_{i}}$ выглядит сложнее:
(163)
$\begin{gathered} {{j}_{i}} = - e{{n}_{e}}\left\langle {{{{v}}_{i}}} \right\rangle = - e{{n}_{e}}\left[ {\left\langle {{v}_{i}^{{(A)}}} \right\rangle + \left\langle {{v}_{i}^{{(D)}}} \right\rangle } \right] = \\ \, = - e{{n}_{e}}\left[ { - {{\mu }_{{ij}}}\frac{{\partial T}}{{\partial {{x}_{j}}}} - {{n}_{e}}{{\eta }_{{ij}}}{{d}_{j}}} \right]. \\ \end{gathered} $Записывая компоненты ${{j}_{i}}$ относительно направления магнитного поля $\vec {B}$ электрический ток электронов в плазме записывается в виде
(164)
$\begin{gathered} {{j}_{{||}}} = e{{n}_{e}}\left( {{{n}_{e}}{{\eta }_{{||}}}{{d}_{{||}}} + {{\mu }_{{||}}}\nabla {{T}_{{||}}}} \right), \\ {{j}_{ \bot }} = e{{n}_{e}}\left( {{{n}_{e}}{{\eta }_{ \bot }}{{d}_{ \bot }} + {{\mu }_{ \bot }}\nabla {{T}_{ \bot }}} \right), \\ {{j}_{{{\text{hall}}}}} = e{{n}_{e}}\left( {{{n}_{e}}{{\eta }_{{{\text{hall}}}}}\frac{{{\mathbf{d}} \times {\mathbf{B}}}}{B} + {{\mu }_{{{\text{hall}}}}}\frac{{\nabla T \times {\mathbf{B}}}}{B}} \right). \\ \end{gathered} $Для полноты можно выписать выражения для тензора теплопроводности, полученные для трехполиномиального приближения, в [20]:
(165)
$\begin{gathered} \lambda _{{nd}}^{{(13)}} = \frac{5}{2}\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}(a_{0}^{1} - a_{1}^{1}) = \frac{{2125}}{{64}}\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}} \times \\ \, \times \frac{{\left( {1 + \tfrac{{18\sqrt 2 }}{{17Z}} - \tfrac{{14}}{{17}}{{\omega }^{2}}\tau _{{nd}}^{2}} \right){{\zeta }_{1}} + \left( {\tfrac{{1133}}{{340}} + \tfrac{{9\sqrt 2 }}{{17Z}}} \right){{\omega }^{2}}\tau _{{nd}}^{2}{{\zeta }_{2}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}}, \\ \end{gathered} $(166)
$\begin{gathered} \lambda _{{nd}}^{{(23)}} = - \frac{5}{2}\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}(b_{0}^{1} - b_{1}^{1}) = - \frac{{2125}}{{64}}\frac{{{{k}^{2}}T{{n}_{e}}}}{{{{m}_{e}}}}\frac{{\omega \tau _{{nd}}^{2}}}{B} \times \\ \, \times \frac{{\left( {1 + \tfrac{{18\sqrt 2 }}{{17Z}} - \tfrac{{14}}{{17}}{{\omega }^{2}}{{\tau }^{2}}} \right){{\zeta }_{2}} - \left( {\tfrac{{1133}}{{340}} + \tfrac{{9\sqrt 2 }}{{17Z}}} \right){{\zeta }_{1}}}}{{\zeta _{1}^{2} + {{\omega }^{2}}{{\tau }^{2}}\zeta _{2}^{2}}}, \\ \end{gathered} $(167)
${{B}^{2}}\lambda _{{nd}}^{{(33)}} = \lambda _{{nd}}^{{(13)}}(B = 0) - \lambda _{{nd}}^{{(13)}}.$6.1. Точное решение в приближении Лоренца для диффузии и диффузионного термоэфффекта
Аналогично главе 5.2 получим точное решение для приближения Лоренца при $B = 0$:
(168)
$\left\langle {{v}_{i}^{D}} \right\rangle = - {{n}_{e}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{\eta }_{{ij}}}{{d}_{j}} = \frac{{32}}{\Lambda }\frac{{{{m}_{e}}{{{(kT)}}^{4}}}}{{{{n}_{e}}{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{3}}{{d}_{i}},$(169)
$q_{i}^{D} = - {{n}_{e}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{\nu }_{{ij}}}{{d}_{j}} = \frac{{128}}{\Lambda }\frac{{{{m}_{e}}{{{(kT)}}^{5}}}}{{{{n}_{N}}{{Z}^{2}}{{e}^{4}}{{h}^{3}}}}\frac{{{{G}_{{5/2}}}}}{{{{G}_{{3/2}}}}}{{G}_{4}}\frac{{\partial T}}{{\partial {{r}_{{\text{i}}}}}}.$В предельных случаях коэффициенты в (168), (169) сводятся к
Вклад электрон-электронных столкновений в коэффициенты диффузии и диффузионного термоэффекта для различных Z можно оценить из графиков нормированных трехполиномиальных коэффициентов в направлении, перпендикулярном к магнитному полю, введя величины $U_{ \bot }^{{(3l)}}$ и $W_{ \bot }^{{(3l)}}$, определяемые как
(172)
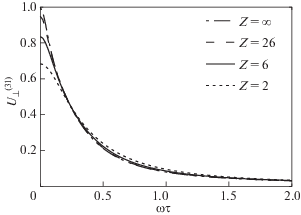
$U_{ \bot }^{{(3l)}} = \frac{{\eta _{{nd}}^{{(13)}}}}{{\eta _{e}^{l}}},\quad W_{ \bot }^{{(3l)}} = \frac{{\nu _{{nd}}^{{(13)}}}}{{\nu _{e}^{l}}}.$Кривые для различных Z, включая $Z = \infty $, относящиеся к приближению Лоренца, изображены на рис. 6, 7. Пересечение графиков с осью y на рисунках происходит в точках, данных в табл. 2 и 3, умноженных на $\eta _{{nd}}^{{(3)}}{\text{/}}\eta _{e}^{l} = 0.9985$, $\nu _{{nd}}^{{(3)}}{\text{/}}\nu _{e}^{l} = 1.0038$. При $\omega \tau = 1$ имеем $U_{ \bot }^{{(3l)}} = 0.0079,$ 0.081, 0.0086, 0.095 для $Z = \infty ,\;26,\;6,\;2$ соответственно и $W_{ \bot }^{{(3l)}}$ = = 0.0443, 0.0455, 0.0488, 0.0563 для $Z = \infty ,\;26,\;6,\;2$.
Рис. 6.
Графики значений диффузионного термоэффекта $W_{ \bot }^{{(3l)}}$ как функции $\omega \tau $ в трехполиномиальном приближении для невырожденной плазмы гелия ($Z = 2$), углерода ($Z = 6$), железа (Z = 26) в сравнении с лоренцевской плазмой, формально отвечающей $Z = \infty $. Пересечение лоренцевской трехполиномиальной кривой ($Z = \infty $) с осью Y при 1.0038 связано с отклонением от точного решения в приближении Лоренца.
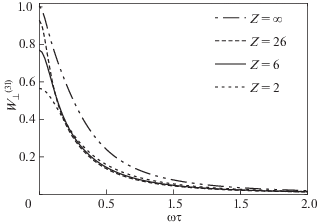
Рис. 7.
Графики значений диффузии $U_{ \bot }^{{(3l)}}$ как функции $\omega \tau $ в трехполиномиальном приближении для невырожденной плазмы гелия ($Z = 2$), углерода ($Z = 6$), железа (Z = 26) в сравнении с лоренцевской плазмой, формально отвечающей $Z = \infty $. Пересечение лоренцевской трехполиномиальной кривой ($Z = \infty $) с осью Y при 0.9985 связано с отклонением от точного решения в приближении Лоренца.
6.2. Вычисления полиномов без учета столкновений между электронами
Чтобы проверить точность полиномиального приближения для коэффициентов диффузии и диффузионного термоэффекта, мы сравниваем их с коэффициентами, полученными как точное решение в приближении Лоренца. В отсутствии магнитного поля, с ${{a}_{{jk}}} = 0$, система (112) сводится к
(173)
$\left\{ \begin{gathered} - \frac{3}{2} = {{d}_{0}}{{b}_{{00}}} + {{d}_{1}}{{b}_{{01}}} + {{d}_{2}}{{b}_{{02}}}, \hfill \\ 0 = {{d}_{0}}{{b}_{{10}}} + {{d}_{1}}{{b}_{{11}}} + {{d}_{2}}{{b}_{{12}}}, \hfill \\ 0 = {{d}_{0}}{{b}_{{20}}} + {{d}_{1}}{{b}_{{21}}} + {{d}_{2}}{{b}_{{22}}}. \hfill \\ \end{gathered} \right.$С учетом (49)–(54) запишем данную систему как
(174)
$\left\{ \begin{gathered} - \frac{3}{2}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = \frac{3}{2}{{d}_{0}} + \frac{9}{4}{{d}_{1}} + \frac{{45}}{{16}}{{d}_{2}}, \hfill \\ 0 = \frac{9}{4}{{d}_{0}} + \frac{{39}}{8}{{d}_{1}} + \frac{{207}}{{32}}{{d}_{2}}, \hfill \\ 0 = \frac{{45}}{{16}}{{d}_{0}} + \frac{{207}}{{32}}{{d}_{1}} + \frac{{1299}}{{128}}{{d}_{2}}. \hfill \\ \end{gathered} \right.$Эта система записывается для трехполиномиального приближения. Два первых уравнения при ${{d}_{2}} = 0$ задают двухполиномиальное приближение, давая следующие результаты:
(175)
$\begin{gathered} {{d}_{0}} = \frac{{ - 13}}{4}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\quad {{d}_{1}} = \frac{3}{2}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}, \\ \eta _{{ndl}}^{{(2)}} = - \frac{{13}}{4}\frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = - 3.25\frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}, \\ \nu _{{ndl}}^{{(2)}} = - \frac{5}{2}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}\frac{{19}}{4} = - 11.875\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}}. \\ \end{gathered} $В трехполиномиальном приближении мы получаем решение (174) для ${{d}_{0}}$, ${{d}_{1}}$ и коэффициенты в виде
(176)
$\begin{gathered} {{d}_{0}} = - \frac{{217}}{{64}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}},\quad {{d}_{1}} = \frac{{33}}{{16}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}, \\ \eta _{{ndl}}^{{(3)}} = - \frac{{217}}{{64}}\frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = - 3.3906\frac{{kT}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}}, \\ \nu _{{ndl}}^{{(3)}} = - \frac{5}{2}\frac{{349}}{{64}}\frac{{{{k}^{2}}{{T}^{2}}{{n}_{e}}}}{{{{m}_{e}}}}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = \\ \, = - \frac{{1745}}{{128}}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}} = - 13.6328\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}}. \\ \end{gathered} $Абсолютные значения диффузии и диффузионного термоэффекта, полученные методом последовательных приближений полиномов, следует сравнить с точным решением $\nu _{{nd}}^{l}$, $\eta _{{nd}}^{l}$ полученным методом Лоренца (168), (169) для невырожденных электронов
(177)
$\eta _{{nd}}^{{(l)}} = - \frac{{32}}{{3\pi }}\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{nd}}} = - 3.3954\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{nd}}},$(178)
$\nu _{{nd}}^{{(l)}} = - \frac{{128}}{{3\pi }}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}} = - 13.5816\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{nd}}}.$Ясно, что двухполиномиальное решение недооценивает значение коэффициента диффузии на 4.28%, диффузионного термоэффекта на 12.53%, а трехполиномиальное решение отличается от точного приблизительно на 0.14% для диффузии и на 0.38% для диффузионного термоэффекта. Уравнения в случае трехполиномиального приближения в присутствии магнитного поля получены из (112) с учетом (49)–(54), (174) в виде
(179)
$\left\{ \begin{gathered} - \frac{3}{2}\frac{{{{\tau }_{{nd}}}}}{{{{n}_{e}}}} = - \frac{3}{2}i\omega {{\tau }_{{nd}}}{{d}_{0}} + \frac{3}{2}{{d}_{0}} + \frac{9}{4}{{d}_{1}} + \frac{{45}}{{16}}{{d}_{2}}, \hfill \\ 0 = - \frac{{15}}{4}i\omega {{\tau }_{{nd}}}{{d}_{1}} + \frac{9}{4}{{d}_{0}} + \frac{{39}}{8}{{d}_{1}} + \frac{{207}}{{32}}{{d}_{2}}, \hfill \\ 0 = - \frac{{105}}{{16}}i\omega {{\tau }_{{nd}}}{{d}_{2}} + \frac{{45}}{{16}}{{d}_{0}} + \frac{{207}}{{32}}{{d}_{1}} + \frac{{1299}}{{128}}{{d}_{2}}. \hfill \\ \end{gathered} \right.$Явное решение уравнений (179) для двух и трехполиномиальных приближений определяется формулами (122)–(132) при формально бесконечном значении Z.
6.3. Частично вырожденные электроны
Для плазмы с произвольно вырожденными электронами в магнитном поле система (173) будет выглядеть, по аналогии с [20], следующим образом:
(180)
$\left\{ \begin{gathered} - \frac{3}{2} = - \frac{3}{2}i\omega {{n}_{e}}{{d}_{0}} + {{d}_{0}}{{b}_{{00}}} + {{d}_{1}}{{b}_{{01}}} + {{d}_{2}}{{b}_{{02}}}, \hfill \\ 0 = - \frac{{15}}{4}\left( {\frac{{7{{G}_{{7/2}}}}}{{2{{G}_{{3/2}}}}} - \frac{{5G_{{5/2}}^{2}}}{{2G_{{3/2}}^{2}}}} \right)i\omega {{n}_{e}}{{d}_{1}} + \hfill \\ \, + {{d}_{0}}{{b}_{{10}}} + {{d}_{1}}{{b}_{{11}}} + {{d}_{2}}{{b}_{{12}}}, \hfill \\ 0 = - \frac{{105}}{{16}}\left( { - \frac{{35}}{8}\frac{{G_{{7/2}}^{2}}}{{G_{{3/2}}^{2}}} + \frac{{49}}{2}\frac{{G_{{7/2}}^{2}}}{{G_{{5/2}}^{2}}}\frac{{{{G}_{{7/2}}}}}{{{{G}_{{3/2}}}}} - } \right. \hfill \\ \, - \left. {\frac{{63}}{2}\frac{{{{G}_{{9/2}}}}}{{{{G}_{{5/2}}}}}\frac{{{{G}_{{7/2}}}}}{{{{G}_{{3/2}}}}} + \frac{{99}}{8}\frac{{{{G}_{{11/2}}}}}{{{{G}_{{3/2}}}}}} \right)i\omega {{n}_{e}}{{d}_{2}} + {{d}_{0}}{{b}_{{20}}} \hfill \\ \, + {{d}_{1}}{{b}_{{21}}} + {{d}_{2}}{{b}_{{22}}}. \hfill \\ \end{gathered} \right.$Для частично вырожденных электронов с уровнем вырождения $DL = {{\varepsilon }_{{fe}}}{\text{/}}kT = 1.011$ и при отсутствии магнитного поля, система (180) записывается в виде
(181)
$\left\{ \begin{gathered} - 1.5 = {{d}_{0}}{{b}_{{00}}} + {{d}_{1}}{{b}_{{01}}} + {{d}_{2}}{{b}_{{02}}}, \hfill \\ 0 = {{d}_{0}}{{b}_{{10}}} + {{d}_{1}}{{b}_{{11}}} + {{d}_{2}}{{b}_{{12}}}, \hfill \\ 0 = {{d}_{0}}{{b}_{{20}}} + {{d}_{1}}{{b}_{{21}}} + {{d}_{2}}{{b}_{{22}}}. \hfill \\ \end{gathered} \right.$С учетом значений коэффициентов ${{b}_{{jk}}}$, полученных в [20], эту систему можно переписать в виде:
(182)
$\left\{ \begin{gathered} - 1.5\frac{{{{\tau }_{{d0}}}}}{{{{n}_{e}}}} = 1.5{{d}_{0}} + 2.16{{d}_{1}} + 2.588{{d}_{2}}, \hfill \\ 0 = 2.16{{d}_{0}} + 5.162{{d}_{1}} + 6.671{{d}_{2}}, \hfill \\ 0 = 2.588{{d}_{0}} + 6.671{{d}_{1}} + 11.038{{d}_{2}}. \hfill \\ \end{gathered} \right.$Первые два уравнения при ${{d}_{2}} = 0$ определяют двухполиномиальное приближение, которое с учетом (64) и (62), дает следующий результат:
(183)
$\begin{gathered} {{d}_{0}} = - 2.5161\frac{{{{\tau }_{{d0}}}}}{{{{n}_{e}}}},\quad {{d}_{1}} = 1.0528\frac{{{{\tau }_{{d0}}}}}{{{{n}_{e}}}}, \\ \eta _{{d0l}}^{{(2)}} = - 2.516\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{d0}}},\quad \nu _{{d0l}}^{{(2)}} = - 9.853\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{d0}}}. \\ \end{gathered} $В трехполиномиальном приближении, мы получаем решение (182) для ${{d}_{0}}$, ${{d}_{1}}$, а также коэффициенты диффузии и диффузионного термоэффекта в виде
(184)
$\begin{gathered} {{d}_{0}} = - 2.591{{\tau }_{{d0}}},\quad {{d}_{1}} = 1.3658{{\tau }_{{d0}}}, \\ \eta _{{d0l}}^{{(3)}} = - 2.591\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{d0}}},\quad \nu _{{d0l}}^{{(3)}} = - 10.873\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{d0}}}. \\ \end{gathered} $Коэффициенты, полученные методом последовательных приближений полиномами, следует сравнить с точным решением $\eta _{{nd}}^{l}$, $\nu _{{nd}}^{l}$, полученным методом Лоренца (170), (171) для невырожденных электронов
(185)
$\eta _{{d0}}^{{(l)}} = - 0.744\frac{{32}}{{3\pi }}\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{d0}}} = - 2.526\frac{{kT}}{{{{m}_{e}}{{n}_{e}}}}{{\tau }_{{d0}}},$(186)
$\nu _{{d0}}^{{(l)}} = - 0.744\frac{{128}}{{3\pi }}\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{d0}}} = - 10.105\frac{{{{k}^{2}}{{T}^{2}}}}{{{{m}_{e}}}}{{\tau }_{{d0}}}.$Видно, что двухполиномиальное решение для диффузии отличается от точного на 0.4%, а трехполиномиальное решение – на 2.6%. Для диффузионного термоэффекта: двухполиномиальное на 2.5%, а трехполиномиальное приблизительно на 8% отличаются от точного.
7. ЗАКЛЮЧЕНИЕ
В данной работе найдены тензоры кинетических коэффициентов диффузии, термодиффузии и дифузионного термоэффекта для невырожденных электронов в неквантующем магнитном поле. Тензоры получены из решения кинетического уравнения Больцмана классическим методом Чепмена–Энскога с использованием разложения на полиномы Сонина и учетом двух и трех членов разложения. Учитываются электрон-ионные и электрон-электронные столкновения. Тензоры записаны для произвольного локального направления магнитного поля и градиента температуры в декартовой системе координат согласно [11]. Наши результаты в двухполиномиальном случае точно согласуются с результатами предыдущих работ [8–10, 12, 13]. Аналитическое решение в трехполиномиальном приближении прежде не было получено.
Значения коэффициентов теплопроводности, полученные в статьях Брагинского [12, 13] в двухполиномиальном приближении, в два раза меньше, чем соответствующие значения для теплопроводности, полученной в статье [20]. Это связано с подходом, используемом в работе [12], который отличается от классического метода Чепмена–Энскога [1]. В [12] считалось, что половина теплового потока скрыта в так называемой “тепловой силе” таким образом, что результирующий тепловой поток в сопутствующей системе отсчета одинаков в обоих рассмотрениях. Далее представлены значения коэффициентов теплопроводности и электропроводности вдоль линий магнитного поля ($B = 0$), при $Z = 1$:
(187)
$\begin{gathered} \lambda _{\parallel }^{{{\text{Braginski}}}} = 3.1616\frac{{{{n}_{e}}{{k}^{2}}T{{\tau }_{{nd}}}}}{{{{m}_{e}}}}, \\ \lambda _{\parallel }^{{2{\text{ - pol}}}} = 6.45\frac{{{{n}_{e}}{{k}^{2}}T{{\tau }_{{nd}}}}}{{{{m}_{e}}}}, \\ \lambda _{\parallel }^{{3{\text{ - pol}}}} = 7.6133\frac{{{{n}_{e}}{{k}^{2}}T{{\tau }_{{nd}}}}}{{{{m}_{e}}}}. \\ \end{gathered} $В [15] коэффициенты, полученные численно, сравнивались с работой Брагинского:
(188)
$\lambda _{\parallel }^{{{\text{E}} - {\text{H}}}} = 3.203\frac{{{{n}_{e}}T{{k}^{2}}{{\tau }_{{nd}}}}}{{{{m}_{e}}}}.$Если учесть, что половина теплового потока скрыта в “тепловой силе”, то $\lambda _{\parallel }^{{2 - {\text{pol}}}}$ и $\lambda _{\parallel }^{{3 - {\text{pol}}}}$ из (187) получим:
(189)
$\begin{gathered} \lambda _{\parallel }^{{'2{\text{ - pol}}}} = 3.225\frac{{{{n}_{e}}{{k}^{2}}T{{\tau }_{{nd}}}}}{{{{m}_{e}}}}, \\ \lambda _{\parallel }^{{'3{\text{ - pol}}}} = 3.8066\frac{{{{n}_{e}}{{k}^{2}}T{{\tau }_{{nd}}}}}{{{{m}_{e}}}}. \\ \end{gathered} $Значения коэффициентов электропроводности из работы [15] и из данной статьи, полученные в двух- и трехполиномиальном приближении, совпадают до десятых:
(190)
$\begin{gathered} \sigma _{\parallel }^{{{\text{E}} - {\text{H}}}} = 1.9763\frac{{n_{e}^{2}{{\tau }_{{nd}}}}}{{{{m}_{e}}}},\quad \sigma _{\parallel }^{{2{\text{ - pol}}}} = 1.9319\frac{{n_{e}^{2}{{\tau }_{{nd}}}}}{{{{m}_{e}}}}, \\ \sigma _{\parallel }^{{3{\text{ - pol}}}} = 1.9497\frac{{n_{e}^{2}{{\tau }_{{nd}}}}}{{{{m}_{e}}}}. \\ \end{gathered} $На примере приближения Лоренца было показано, что точность приближения рядом ортогональных функций, аналогичных полиномам Сонина, уменьшается с увеличением степени вырождения. Для невырожденных электронов, без учета электрон-электронных столкновений, значение коэффициента термодиффузии в двухполиномиальном приближении недооценивает точное решение, полученное в приближении Лоренца при $B = 0$, на 26%, а в трехполиномиальном приближении переоценивает приблизительно на 1%. Для частично вырожденных электронов, при ${{x}_{0}} = 0$, двухполиномиальное решение недооценивает точное на 28%, а трехполиномиальное недооценивает точное на 7%. Следует отметить, что электрон-электронные столкновения еще больше уменьшают значения коэффициента.
Значение коэффициента диффузии, полученное из двухполиномиального приближения недооценивают точное решение приблизительно на 4%, а трехполиномиальное решение недооценивает точное на 0.14% для невырожденных электронов. В случае частичного вырождения диффузия, полученная из двухполиномиального решения, на 0.4% недооценивает точное, а полученная из трехполиномиального – на 3% переоценивает точное.
Коэффициент диффузионного термоэффекта для невырожденных электронов в двухполиномиальном приближении на 12% недооценивает, а в трехполиномиальном на 0.4% переоценивает точное решение. При частичном вырождении электронов, двухполиномиальное решение на 2.5% недооценивает, а трехполиномиальное на 8% переоценивает точное решение.
Метод Чепмена–Энскога можно использовать для достаточно плотного газа (плазмы), где время между столкновениями частиц есть наименьшая величина среди других характерных времен. В присутствии магнитного поля в дополнение ко времени жизни системы и характерному времени изменений параметров в плазме добавляется время вращения по ларморовскому кругу ${{\tau }_{L}} = 2\pi {\text{/}}\omega $. Это время должно быть намного меньше, чем τ, порядка ${{\tau }_{{nd}}}$ или ${{\tau }_{d}}$, что приводит к условию, при котором можно пользоваться методом Чепмена–Энскога, в виде
Поэтому данную работу можно успешно применять при $\omega \tau \lesssim 1$, а для больших $\omega \tau $ могут быть получены только качественные оценки.
Автор искренне благодарна Г.С. Бисноватому-Когану за обсуждения и помощь.
Работа была поддержана грантом Российского научного фонда № 18-12-00378.
Список литературы
Чепмен С., Каулинг Т. Математическая теория неоднородных газов. М.: Иностр. лит., 1960.
Uehling E., Uhlenbeck G. // Phys. Rev. 1933. V. 43. P. 552.
Uehling E. // Phys. Rev. 1934. V. 46. P. 917.
Tomonaga S.Z. // Z. Phys. 1938. V. 110. P. 573.
Бисноватый-Коган Г.С., Романова М.М. // ЖЭТФ. 1982. Т. 83. С. 449.
Имшенник В.С. // Астрономич. ж. 1961. Т. 38. С. 652.
Ландау Л.Д. // ЖЭТФ. 1937. Т. 7. С. 203.
Landshoff R. // Phys. Rev. 1951. V. 82. P. 442.
Marshall W. // At. Energy Res Estable. 1960. № T/R. P. 2419.
Бисноватый-Коган Г.С. Транспортные свойства частично ионизированной двухтемпературной плазмы и изотропные поправки к максвелловской функции распределения. Тезисы диплома, Московский физико-технический институт, 1964.
Бисноватый-Коган Г.С. // Прикладная механика и техническая физика. 1964. № 3. С. 43.
Брагинский С.И. // ЖЭТФ. 1958. Т. 33. С. 459.
Брагинский С.И. // Вопросы теории плазмы. Вып. 1 / Под ред. М.А. Леонтовича. М.: Госатомиздат, 1963.
Боброва Н.А., Сасоров П.В. // Физика плазмы. 1993. Т. 19. С. 789.
Epperlein E.M., Haines M.G. // Phys. Fluids. 1986. V. 29. P. 1029.
Wyller A.A. // Astrophisica Norvegica. 1964. V. 9. P. 79.
Wyller A.A. // Astrophys. J. 1973. V. 184. P. 517.
Lampe M. // Phys. Rev. 1968. V. 170. P. 306.
Бисноватый-Коган Г.С., Глушихина М.В. // Физика Плазмы. 2018. Т. 44. С. 971.
Бисноватый-Коган Г.С., Глушихина М.В. //Физика Плазмы. 2018. Т. 44. С. 355.
Tamm I.E. // Basics of the theory of electricity, 9th ed. Nauka, 1976.
Burnett D. // Proc. London Mathemat. Soc. 1936. V. 40. P. 382.
Балеску Р. Равновесная и неравновесная статистическая механика. М.: Мир, 1978.
Bisnovatyi-Kogan G.S. Stellar Physics I: Fundamental Concepts and Stellar Equilibrium. Springer, 2001.
Гинзбург В.Л., Рухадзе А.А. Волны в магнитоактивной плазме. М.: Наука, 2013.
Калихман Л.Е. Элементы магнитной газодинамики. М.: Атомиздат, 1964.
Schatzman E. White dwarfs. Amsterdam: North Holland, 1958.
Landau L.D., Lifshitz E.M. Electrodynamics of Continuous Media. V. 8. Pergamon Press, Oxford, 1984.
Дополнительные материалы отсутствуют.