Физика плазмы, 2020, T. 46, № 3, стр. 227-236

1. ВВЕДЕНИЕ

Исследования плазменных флуктуаций являются важными как для описания фундаментальных процессов в плазме, так и для диагностики плазмы методом рассеяния электромагнитных волн на флуктуациях плотности электронов. Такие исследования постоянно расширяются в связи с совершенствованием методов диагностики и более детальным изучением плазменных систем в лаборатории и в космосе. При этом во многих реальных плазменных системах свойства флуктуаций существенным образом зависят от неоднородности электронной концентрации. Здесь могут играть роль как регулярная неоднородность [1–7], так и случайные неоднородности [8–17].

Как следует из работ [9, 10], случайные неоднородности могут приводить к существенному изменению флуктуационных спектров, особенно в окрестности плазменных резонансов. Поэтому диагностика плазмы, основанная на наблюдении характеристик спектров плазменных флуктуаций, должна учитывать роль случайных неоднородностей концентрации, если последние имеют достаточно высокую интенсивность.

В работах [9, 10, 12] влияние случайных неоднородностей на спектры флуктуаций рассматривалось в условиях теплового равновесия плазмы. При этих условиях для расчета спектра достаточно найти эффективную диэлектрическую проницаемость плазмы, учитывающую случайные неоднородности, а затем получить выражение для спектра с помощью флуктуационно-диссипативного соотношения. Таким образом, в данном случае спектр полностью определяется действительной и мнимой частью эффективной диэлектрической проницаемости.

Однако приближение теплового равновесия часто оказывается неприменимым в реальных плазменных системах как в лаборатории, так и в космических условиях. При этом функции распределения частиц по импульсам могут существенно отличаться от максвелловских, а если распределения Максвелла для частиц плазмы имеют место, то температуры электронов и ионов могут сильно отличаться. Кроме того, в работе [10] показано, что использованное в [9, 10] приближение холодной плазмы приводит к расходимости выражения для флуктуационного спектра в области плазменных резонансов. Отметим, что область резонансов является наиболее информативной при наблюдении рассеяния электромагнитных волн флуктуациями плотности электронов.

В настоящей работе рассчитан спектр ленгмюровских флуктуаций в случайно-неоднородной плазме с учетом теплового движения электронов. Полученные выражения применимы для произвольных неравновесных функций распределения частиц при условии, что такие распределения не приводят к неустойчивости плазмы. Как следует из результатов работы, даже относительно слабые случайные неоднородности могут приводить к значительному уширению спектральной линии, превышающему естественное уширение, которое обусловлено как бесстолкновительными эффектами, так и столкновениями электронов с ионами. Результаты работы показывают, что учет влияния случайных неоднородностей может оказаться необходимым при интерпретации экспериментов по рассеянию электромагнитных волн плазменными флуктуациями.

2. ЭЛЕКТРОННЫЕ ФЛУКТУАЦИИ В ПЛАЗМЕ, СОДЕРЖАЩЕЙ СЛУЧАЙНЫЕ НЕОДНОРОДНОСТИ ЭЛЕКТРОННОЙ КОНЦЕНТРАЦИИ

При расчете ленгмюровских флуктуаций воспользуемся уравнением для фазовой плотности заряженных частиц плазмы ${{N}_{a}}$ в отсутствие внешних полей [18]

где ${\mathbf{v}} = p{\text{/}}{{m}_{a}}$ – скорость; ${{e}_{a}}$ и ${{m}_{a}}$ – заряд и масса частицы сорта a соответственно. Фазовая плотность ${{N}_{a}}$ – микроскопическая (случайная) величина, которая определяется координатами и импульсами частиц в данный момент времени, а суммирование выполняется по всем частицам в системе. Электрическое поле E связано с фазовой плотностью уравнением Пуассона

В уравнении (1) мы пренебрегли магнитным полем, что соответствует соотношению

В дальнейшем будем считать плазму статистически стационарной. Рассмотрим далее практически важный случай, когда пространственный масштаб ленгмюровских флуктуаций ${{D}_{L}}$ значительно меньше, чем масштаб случайных неоднородностей ${{D}_{i}}$. Соотношение ${{D}_{L}} \ll {{D}_{i}}$ имеет место, например, в экспериментах по некогерентному рассеянию радиоволн в ионосфере. В этих экспериментах интересующий нас масштаб ленгмюровских флуктуаций ${{D}_{L}}$ определяется длиной пробной волны и имеет порядок одного метра или менее. Наиболее же интенсивные неоднородности естественного происхождения имеют масштаб от сотен метров до километров и выше [8]. Более того, интенсивность неоднородностей возрастает с увеличением масштаба. Аналогичное соотношение имеет место и для временных масштабов ленгмюровских флуктуаций и случайных неоднородностей.

Микроскопическая фазовая плотность электронов, усредненная по масштабу, характерному для ленгмюровских флуктуаций, пропорциональна функции распределения частиц по импульсам ${{f}_{e}}\left( {\mathbf{p}} \right)$

где $n\left( {\mathbf{r}} \right)$ – зависящая от координат концентрация электронов. Индекс L в символе усреднения обозначает усреднение на характерном масштабе ленгмюровских флуктуаций. Фактически $n\left( {\mathbf{r}} \right)$ является случайной величиной и описывает возмущения концентрации в случайных неоднородностях с пространственными масштабами, значительно превышающими масштаб ленгмюровских флуктуаций.

При расчете спектров флуктуаций в рассматриваемой нами задаче процедура усреднения разбивается на два этапа: вначале выполняется усреднение по масштабу ленгмюровских флуктуаций, а затем по ансамблю случайных неоднородностей (см. ниже).

Мы будем рассматривать случай статистически однородной плазмы, когда электронная концентрация, усредненная по ансамблю случайных неоднородностей, равна постоянной величине ${{n}_{0}}$. При этом среднее электрическое поле равно нулю и случайное электрическое поле E можно заменить флуктуациями $\delta {\mathbf{E}}$.

Для расчета спектров флуктуаций удобно использовать уравнение для флуктуаций электрического поля, полученное в работах [19, 20]

где ${{\hat {Q}}_{{t,r}}}$ – интегральный оператор, представляющий собой преобразование Фурье по координатам и преобразование Лапласа по времени

Как показано в [19], уравнение (5) есть точное следствие (1)–(3). В выражении (5) выполняется суммирование по всем сортам частиц a; $E\left( {t,{\mathbf{r}}} \right) = {{E}_{{\mathbf{k}}}}\left( {t,{\mathbf{r}}} \right)$ – проекция электрического поля на вектор k. Правая часть уравнения (5), зависящая от фазовой плотности в момент времени $t = 0$, играет роль источника флуктуаций в бесстолкновительном приближении (см. [21]).

Функция ${{\epsilon }^{M}}\left( {t,{\mathbf{r}},\omega ,{\mathbf{k}}} \right)$ – микроскопическая (случайная) диэлектрическая проницаемость, введенная в [19, 20]. Усреднение ${{\epsilon }^{M}}$ на масштабе ленгмюровских флуктуаций дает обычную продольную диэлектрическую проницаемость плазмы

где удержан только парциальный вклад электронов в продольную диэлектрическую проницаемость и $n = {{n}_{e}}$ – концентрация электронов. Из выражения (7) видно, что продольная диэлектрическая проницаемость ε является случайной величиной, определяемой случайной концентрацией электронов $n\left( {\mathbf{r}} \right)$.

В уравнении (5) и далее $\Delta > 0$, и в конечных результатах необходимо совершить предельный переход $\Delta \to 0$. Преобразование Лапласа по времени в (6) обеспечивает более строгий подход, чем преобразование Фурье, так как в стационарном случае подынтегральная функция $\delta E\left( {t,x} \right)$ остается конечной при $t \to \infty $, и возможны такие реализации $\delta E\left( {t,{\mathbf{r}}} \right)$, при которых интеграл Фурье сходиться не будет. Знак Δ фактически определяет правило обхода полюса в ряде важных интегралов, как например, в формуле для продольной диэлектрической проницаемости (7). В случае обычного преобразования Фурье необходимо дополнительно задавать правило интегрирования с учетом особенности $\mathop {\left( {\omega - {\mathbf{kv}}} \right)}\nolimits^{ - 1} $. Использование преобразования Лапласа оказывается также очень удобным для расчета спектров флуктуационных величин, если найдены сами эти величины (см. ниже).

В работе [22] показано, что в неоднородной среде уравнение (5) можно привести к виду

где σ – вклад в линейную проводимость неравновесной плазмы, обусловленный столкновениями электронов с ионами [23], а ${{S}_{{coll}}}(\omega ,{\mathbf{k}})$ – дополнительный вклад в источник флуктуаций, связанный со столкновениями. Величины σ и ${{S}_{{coll}}}$ учитывают не только электрон-ионные столкновения, но и влияние коллективных эффектов на процесс столкновений. Конкретный вид величин σ и ${{S}_{{coll}}}$, а также их влияние на спектры флуктуаций достаточно подробно изучались в работе [19]. Поэтому мы не будем приводить здесь эти результаты, а ограничимся лишь некоторыми частными случаями для σ и ${{S}_{{coll}}}$, чтобы проиллюстрировать роль столкновений в спектре плазмы со случайными неоднородностями и сделать оценки для реальной плазмы (см. ниже).

Подставим в (8) оператор ${{\hat {Q}}_{{t,r}}}\left( {\omega ,{\mathbf{k}}} \right)$ (6)

В левую часть уравнения (9) входит фурье-преобразование двух величин, зависящих от r. Причем, вектор k, входящий в функцию $\varepsilon \left( {{\mathbf{r}},\omega ,{\mathbf{k}}} \right)$, при выполнении преобразования Фурье необходимо рассматривать как постоянный параметр. Преобразование Фурье для произведения $\varepsilon \left( {{\mathbf{r}},\omega ,{\mathbf{k}}} \right)E\left( {\omega ,{\mathbf{r}}} \right)$ в уравнении (9) можно выразить через свертку фурье-образов диэлектрической проницаемости и электрического поля

Соотношение (10) представляет собой интегральное уравнение для случайной величины $\delta E\left( {\omega ,{\mathbf{q}}} \right)$. При этом влияние случайных неоднородностей учитывается в диэлектрической проницаемости ε, а также в источнике флуктуаций ${{S}_{f}} + {{S}_{{coll}}}$. Учитывая свойства фурье-преобразования, получим, что фурье-образ продольной диэлектрической проницаемости $\varepsilon \left( {{\mathbf{k}} - {\mathbf{q}},\omega ,{\mathbf{k}}} \right)$ существенно отличен от нуля в области волновых векторов $\left| {{\mathbf{k}} - {\mathbf{q}}} \right| \lesssim D_{i}^{{ - 1}}$ (напомним, что волновой вектор k здесь играет роль постоянного параметра, а ${{D}_{i}}$ – характерный масштаб случайных неоднородностей). Характерный масштаб изменений фурье-образа $\delta E\left( {\omega ,{\mathbf{q}}} \right)$ имеет порядок $D_{L}^{{ - 1}} \gg D_{i}^{{ - 1}}$ (${{D}_{L}}$ – характерный масштаб ленгмюровских флуктуаций). Поэтому подынтегральное выражение в (10) отлично от нуля в относительно узкой области волновых векторов ${\mathbf{q}} \approx $ ${\mathbf{k}}$, где мало меняется величина $\delta E\left( {\omega ,{\mathbf{q}}} \right)$. В соответствии с этим величину $\delta E\left( {\omega ,{\mathbf{q}}} \right)$ можно разложить в ряд Тейлора в окрестности вектора ${\mathbf{q}} = {\mathbf{k}}$

Далее ограничимся нулевым членом разложения в формуле (11). Такое приближение позволяет учесть уширение спектральной линии, вызванное случайными неоднородностями.

Для определения точности этого приближения, оценим отбрасываемый нами последний член в правой части (11). Как уже отмечено выше, модуль разности волновых векторов $\left| {{\mathbf{k}} - {\mathbf{q}}} \right|$, которая дает существенный вклад в левую часть (10), не превосходит обратный характерный размер случайных неоднородностей $D_{i}^{{ - 1}}$. Поскольку характерный масштаб изменения Фурье-образа $\delta E\left( {\omega ,{\mathbf{k}}} \right)$ составляет $D_{L}^{{ - 1}}$, производную $\partial \delta E\left( {\omega ,{\mathbf{k}}} \right){\text{/}}\partial {\mathbf{k}}$ можно оценить как $\delta E{\text{/}}\left( {D_{L}^{{ - 1}}} \right) = \delta E{{D}_{L}}$. Поэтому отбрасываемый последний член в разложении (11) имеет порядок $\delta E\left( {\omega ,{\mathbf{k}}} \right){{D}_{L}}{\text{/}}{{D}_{i}}$, и в случае крупномасштабных случайных неоднородностей $\left( {{{D}_{i}} \gg {{D}_{L}}} \right)$ этот член существенно меньше основного члена $\delta E\left( {\omega ,{\mathbf{k}}} \right)$. При этом относительная ошибка расчета ленгмюровских флуктуаций имеет порядок ${{D}_{L}}{\text{/}}{{D}_{i}}$.

Учитывая сказанное, подставим в уравнение (10) $\delta E\left( {\omega ,{\mathbf{k}}} \right)$ вместо $\delta E\left( {\omega ,{\mathbf{q}}} \right)$. Тогда интегрирование по q в левой части уравнения (10) сводится к интегралу

Выполняя соответствующие замены переменных и учитывая конкретный вид преобразования Фурье (6), получим

Таким образом, интеграл (12) выражается через диэлектрическую проницаемость ε в точке ${\mathbf{r}} = 0$.

Учитывая (7), введем обозначения

где символ ~ означает, что $\tilde {\varepsilon }\left( {\omega ,{\mathbf{k}}} \right)$ и $\tilde {n}$ – случайные функции, определяемые случайным значением электронной концентрации в точке ${\mathbf{r}} = 0$. Выполнив все описанные преобразования, вместо уравнения (10) получим явное выражение для флуктуаций электрического поля в правую часть которого входят источники флуктуаций ${{S}_{f}}$ и ${{S}_{{coll}}}$, а также зависящая от случайных неоднородностей диэлектрическая проницаемость $\tilde {\varepsilon }$.

3. СПЕКТР ЛЕНГМЮРОВСКИХ ФЛУКТУАЦИЙ В СЛУЧАЙНО-НЕОДНОРОДНОЙ ПЛАЗМЕ

Чтобы найти спектр флуктуаций, вначале рассмотрим статистический момент для Фурье-образа флуктуаций электрического поля, используя формулу (15)

где величина представляет собой вклад в статистический момент, обусловленный бесстолкновительным источником ${{S}_{f}}\left( {\omega ,{\mathbf{k}}} \right)$, Второе слагаемое в правой части (16) описывает дополнительный вклад в статистический момент, вызванный столкновениями. При выводе соотношения (16) учтено, что перекрестные средние источников $\left\langle {{{S}_{f}}S_{{coll}}^{*}} \right\rangle $ и $\left\langle {S_{f}^{*}{{S}_{{coll}}}} \right\rangle $ обращаются в нуль (см. [19]).

При получении правой части (17) удержан только вклад электронов в источник флуктуаций. При этом фазовую плотность ${{N}_{e}}$ в источнике можно заменить флуктуациями $\delta {{N}_{e}}$.

Для нахождения среднего, входящего в правую часть (17), воспользуемся формулой [21], которая в случае статистически стационарной плазмы имеет вид

Формула (18) непосредственно следует из представления фазовой плотности (1), если при вычислении среднего значения отбросить парную корреляционную функцию частиц. δ-функции в правой части (18) появляются в процессе усреднения произведений соответствующих δ-функций в фазовой плотности по ансамблю частиц. Таким образом, δ-функции в (18) есть представление некоррелированных частиц в источнике флуктуаций. Как показано в [21], отбрасывание корреляций в источнике флуктуаций соответствует так называемому поляризационному приближению, когда считается, что парные корреляции существенно меньше произведения одночастичных функций распределения. Данное приближение обычно хорошо выполняется в газовой плазме. Подчеркнем, что приближение (18) применимо только для источника флуктуаций, но не для самих флуктуаций.

Выполним преобразования Фурье (6) в (18)

Подставим это выражение в правую часть (17) и проинтегрируем обе части полученного выражения по ${{{\mathbf{k}}}_{2}}$

Так же, как и при интегрировании по q в уравнении (10), учтем, что концентрация электронов $n\left( {\mathbf{r}} \right)$ медленно меняется на характерном масштабе ленгмюровских флуктуаций. Это означает, что Фурье-образ концентрации $n\left( {{\mathbf{k}} - {{{\mathbf{k}}}_{2}}} \right)$ отличен от нуля лишь в относительно узкой области волновых чисел $\left| {{{{\mathbf{k}}}_{2}} - {\mathbf{k}}} \right| \ll k$. Напомним, что k − волновое число ленгмюровских флуктуаций, определяющее их масштаб. Поэтому в интеграле по ${{{\mathbf{k}}}_{2}}$ в правой части уравнения (20) мы можем заменить ${{{\mathbf{k}}}_{2}}$ на k везде, кроме сомножителя $n\left( {{\mathbf{k}} - {{{\mathbf{k}}}_{2}}} \right)$. Далее, при интегрировании по ${{{\mathbf{k}}}_{2}}$ проделаем такие же преобразования, как в (13). В результате получим

Подставим последнее соотношение в правую часть (20). Затем применим к обеим частям полученного выражения оператор $\mathop {lim}\limits_{\Delta \to 0} 2\Delta $ и выполним усреднение обеих частей выражения по статистическому ансамблю неоднородностей электронной концентрации. При этом в левой части полученной формулы уже будет стоять полное среднее ${{\left\langle {\delta E\left( {\omega ,{\mathbf{k}}} \right)\delta E{\text{*}}\left( {\omega ,{{{\mathbf{k}}}_{2}}} \right)} \right\rangle }^{f}}$ по всем масштабам флуктуационных возмущений:

а в правую часть входит среднее от величины, определяемой случайной электронной концентрацией в точке ${\mathbf{r}} = 0$ (см. (14)).

Предел в правой части (22) выражается через $\delta $-функцию

Предельное значение подынтегрального выражения в левой части (22) в случае статистически стационарной плазмы содержит искомый спектр флуктуаций электрического поля $\mathop {\left( {\delta E\delta E} \right)}\nolimits_{\omega ,{\mathbf{k}}} $, обусловленный бесстолкновительным источником ${{S}^{f}}$ [18]

При этом спектр определяется как Фурье-образ автокорреляционной функции флуктуаций электрического поля

где

В формулах (25), (26) учтено, что плазма является статистически однородной и стационарной. Поэтому корреляционная функция (26) зависит от разности моментов времени и координат.

Подставим выражения (23), (24) в формулу (22). После этого интеграл по ${{{\mathbf{k}}}_{2}}$ в левой части (22) легко вычисляется благодаря наличию δ-функции в выражении (24). В результате вместо выражения (22) окончательно получим

где $\tilde {\varepsilon }\left( {\omega ,{\mathbf{k}}} \right)$ и $\tilde {n}$ – величины, определяемые случайным значением электронной концентрации в точке ${\mathbf{r}} = 0$, а усреднение выполняется по ансамблю случайных неоднородностей. Зависимость результата (27) от статистического среднего случайной величины $\tilde {n}{\text{/}}\mathop {\left| {\tilde {\varepsilon }} \right|}\nolimits^2 $ только в одной точке есть следствие статистической однородности задачи.

Применим теперь оператор $\int {d{{{\mathbf{k}}}_{2}}\mathop {lim}\limits_{\Delta \to 0} 2\Delta } $ ко второму слагаемому правой части (16). В соответствии с [19] имеем аналогично (24)

где $\mathop {\left( {{{S}_{{coll}}}{{S}_{{coll}}}} \right)}\nolimits_{\omega ,{\mathbf{k}}} $ – спектральная функция столкновительного источника, рассчитанная в [19]. В случае, когда влияние коллективных эффектов на процесс столкновений является несущественным, эта функция имеет вид

Далее, проведя процедуру, аналогичную той, что использована выше для случая бесстолкновительного источника, получим вклад в спектр флуктуаций электрического поля, обусловленный столкновительным источником. Суммируя полученный результат с (27), найдем окончательное выражение для спектра ленгмюровских флуктуаций электрического поля в случайно-неоднородной плазме с учетом электрон-ионных столкновений.

где ${{e}_{i}}$ и ${{n}_{i}}$ – соответственно заряд и концентрация ионов.

Также представляет интерес расчет спектра флуктуаций электронной плотности $\mathop {\left( {\delta {{n}_{e}}\delta {{n}_{e}}} \right)}\nolimits_{\omega ,{\mathbf{k}}} $, поскольку именно на этих флуктуациях происходит рассеяние электромагнитных волн, используемое в экспериментах по диагностике плазмы. В случае ленгмюровских флуктуаций достаточно легко рассчитать величину $\mathop {\left( {\delta {{n}_{e}}\delta {{n}_{e}}} \right)}\nolimits_{\omega ,{\mathbf{k}}} $ с помощью соотношения (27) и уравнения Пуассона (2). Переходя в этом уравнении к Фурье-образам флуктуаций, получим

где учтено, что ${\mathbf{k}}\left\| {{\kern 1pt} \delta {\mathbf{E}}\left( {\omega ,{\mathbf{k}}} \right)} \right.$. Подставив второе из уравнений (31) в (24), найдем связь между спектрами флуктуаций электрического поля и плотности электронов

Подставляя спектр флуктуаций электрического поля в формулу (32), найдем явное выражение для спектра флуктуаций плотности электронов

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Формулы (30), (33) справедливы для спектров флуктуаций в неравновесной плазме, когда функция распределения электронов по импульсам ${{f}_{e}}\left( {\mathbf{p}} \right)$ может отличаться от распределения Максвелла.

Следует подчеркнуть, что в настоящей работе мы не рассматриваем неустойчивости плазмы, которые могут возникать при определенных условиях, например, при взаимодействии плазмы с пучком электронов [24]. Также, как и в случае устойчивой плазмы, случайные неоднородности электронной концентрации могут оказывать влияние на спектры флуктуаций в неустойчивой плазме, однако исследование такого влияния выходит за рамки настоящей статьи. Поэтому полученные в работе результаты применимы для таких распределений, для которых не достигаются пороговые условия возбуждения неустойчивостей.

При выводе формул (30), (33) не использовалось предположение о малости возмущений концентрации в случайных неоднородностях, поэтому среднеквадратичное отклонение концентрации в неоднородностях $\mathop {\left\langle {\mathop {\left( {\Delta n} \right)}\nolimits^2 } \right\rangle }\nolimits^{1/2} $ может быть сравнимо со средней электронной концентрацией ${{n}_{0}}$.

В пределе $\mathop {\left\langle {\mathop {\left( {\Delta n} \right)}\nolimits^2 } \right\rangle }\nolimits^{1/2} \to 0$ выражения (30), (33) сводятся к формулам для спектров флуктуаций в регулярной плазме. При этом, среднюю величину $\left\langle {\tilde {n}{\text{/}}\mathop {\left| {\tilde {\varepsilon }\left( {\omega ,{\mathbf{k}}} \right)} \right|}\nolimits^2 } \right\rangle $ следует заменить на ${{n}_{0}}{\text{/}}\mathop {\left| {{{\varepsilon }_{0}}\left( {\omega ,{\mathbf{k}}} \right)} \right|}\nolimits^2 $ где ${{\varepsilon }_{0}}\left( {\omega ,{\mathbf{k}}} \right)$ – усредненная по случайным неоднородностям продольная диэлектрическая проницаемость плазмы, которая получается из (14) путем замены $n\left( {\mathbf{r}} \right) = {{n}_{0}}$. В частности, в отсутствие столкновений при $\mathop {\langle {{{(\Delta n)}}^{2}}\rangle }\nolimits^{1/2} \to 0$ получим

где в выражении для ${{\varepsilon }_{0}}\left( {\omega ,{\mathbf{k}}} \right)$ следует устремить к нулю проводимость σ, что соответствует пренебрежению столкновениями. Соотношение (34) совпадает с известным результатом (см., например, [21]).

В условиях теплового равновесия, когда функция ${{f}_{e}}\left( {\mathbf{p}} \right)$ является распределением Максвелла с температурой электронов ${{T}_{e}}$

интеграл по импульсам в формулах для спектров (30), (33), (34) можно выразить через мнимую часть продольной диэлектрической проницаемости ${{\varepsilon }_{0}}$ при помощи соотношения и спектр электрического поля (30) при ${{\langle \mathop {(\Delta n)}\nolimits^2 \rangle }^{{1/2}}} \to $ $ \to 0$ сводится к выражению (см. [19])

Отсюда видим, что спектр флуктуаций электрического поля в равновесном случае в отсутствие случайных неоднородностей полностью выражается через диэлектрическую проницаемость ${{\varepsilon }_{0}}$ и температуру системы ${{T}_{e}}$. При этом интенсивность спектра пропорциональна мнимой части ${{\varepsilon }_{0}}$ и температуре ${{T}_{e}}$, в соответствии с флуктуационно-диссипативной теоремой (см., например, [24]). Согласно (14), мнимая часть усредненной диэлектрической проницаемости $\varepsilon _{0}^{{''}}$ зависит от проводимости σ, которая, в свою очередь, связана с частотой электрон-ионных соударений.

В равновесном случае проводимость σ выражается через частоту столкновений электронов с ионами ${{\nu }_{{ei}}}$ следующим образом

где ${{\omega }_{{Le}}} = \mathop {\left( {4\pi e_{e}^{2}{{n}_{0}}{\text{/}}{{m}_{e}}} \right)}\nolimits^{1/2} $ – электронная ленгмюровская частота, а частота электрон-ионных столкновений определяется выражениями (см., например, [26]) – кулоновский логарифм.

Выражения для спектров (30), (33) пропорциональны усредненному значению функции, зависящей от возмущений электронной плотности в неоднородностях $\tilde {n}$ (напомним, что $\tilde {\varepsilon }$ также зависит от $\tilde {n}$). Представим флуктуации $\tilde {n}$ в виде

где $\Delta n$ – отклонение концентрации от среднего значения ${{n}_{0}}$ в случайных неоднородностях, а X – относительное отклонение концентрации. Чтобы выполнить усреднение в (30), (33), необходимо знать функцию распределения плотности вероятности $F\left( X \right)$ для случайной величины X. Конкретный вид функции F зависит от типа турбулентности. Тем не менее с различной степенью точности функцию F во многих случаях можно аппроксимировать Гауссовым распределением [11, 13, 15, 16]

При этом, как показывают численные расчеты, основные выводы настоящей работы остаются неизменными даже при значительном отличии функции распределения $F\left( X \right)$ от распределения Гаусса.

Относительный уровень возмущений концентрации в неоднородностях можно определить как ${{(\langle {{X}^{2}}\rangle )}^{{1/2}}}$. Для распределения (41) эта величина совпадает с коэффициентом σ: ${{(\langle {{X}^{2}}\rangle )}^{{1/2}}} = \sigma $. Использование функции распределения (41) имеет смысл, когда относительный уровень возмущений электронной концентрации в случайных неоднородностях $\sigma \ll 1$. В противном случае имеется существенная вероятность реализаций, при которых выражение (40) для концентрации $\widetilde n$ окажется отрицательным. При $\sigma \ll 1$ такие реализации вносят незначительный вклад в полученные ниже результаты. Таким образом, в дальнейшем ограничимся рассмотрением относительно слабых возмущений электронной плотности в случайных неоднородностях $\sigma \ll 1$.

Подставляя выражения (40), (41) в спектральную функцию (33), получим

где $\varepsilon _{e}^{0}\left( {\omega ,{\mathbf{k}}} \right)$ – усредненный по ансамблю неоднородностей вклад электронов в продольную диэлектрическую проницаемость плазмы, который получается при замене $n \to {{n}_{0}}$ в выражении (14).

Для иллюстрации формулы (42) предположим, что распределение электронов по импульсам является максвелловским с температурой ${{T}_{e}}$ (см. (35)). Тогда в окрестности электронной ленгмюровской частоты величины ${{\varepsilon }^{0}}$ и $\varepsilon _{e}^{0}$, входящие в (42), приближенно можно представить в виде

где ${{r}_{{De}}} = \mathop {\left[ {{{T}_{e}}{\text{/}}\left( {4\pi e_{e}^{2}{{n}_{0}}} \right)} \right]}\nolimits^{1/2} $ – дебаевский радиус электронов, а также предполагается, что ${\text{(}}\omega \;\; - $ $ - \;{{\omega }_{{Le}}}){\text{/}}{{\omega }_{{Le}}} \ll 1$ и $k{{r}_{{De}}} \ll 1$. Мнимая часть диэлектрической проницаемости (43) содержит два слагаемых, первое из которых соответствует затуханию Ландау, а второе обусловлено электрон-ионными столкновениями.

Согласно выражениям (43) реальная часть продольной диэлектрической проницаемости приближенно равна

Величина ${\text{Re}}{{\varepsilon }^{0}}\left( {\omega ,{\mathbf{k}}} \right)$ обращается в нуль на частоте ленгмюровских колебаний ${{\omega }_{0}}\, = \,{{\omega }_{{Le}}}\, + \,(3{\text{/}}2){{\omega }_{{Le}}}{{k}^{2}}r_{{De}}^{2}$.

Отметим, что учет теплового движения и столкновений электронов приводит к появлению мнимой части в продольной диэлектрической проницаемости и обеспечивает сходимость выражений для спектров флуктуаций. При этом мнимая часть диэлектрической проницаемости определяет уширение спектра в окрестности плазменной линии в регулярной плазме, т.е. в отсутствие неоднородностей.

Учитывая выражение (44), получим, что реальная часть диэлектрической проницаемости ${\text{Re}}{{\varepsilon }^{0}}(\omega ,{\mathbf{k}})$ сравнивается с мнимой частью ${\text{Im}}{{\varepsilon }^{0}}(\omega ,{\mathbf{k}})$, когда относительное отклонение частоты от плазменного резонанса $\delta \omega = \left( {\omega - {{\omega }_{0}}} \right){\text{/}}{{\omega }_{0}}$ примерно равно ${\text{Im}}{{\varepsilon }^{0}}\left( {\omega ,{\mathbf{k}}} \right){\text{/}}2$. Отсюда найдем величину уширения спектра плазменной линии в регулярной плазме $\delta {{\omega }_{{\text{B}}}}$ в единицах относительной частоты

Спектральная функция ленгмюровских флуктуаций плотности (42) рассчитывалась нами численно с учетом соотношений (43), (44). Результаты расчета представлены на рис. 1. При этом произведение $k{{r}_{{De}}}$ предполагалось равным 0.2, а отношение ${{\nu }_{{ei}}}{\text{/}}{{\omega }_{{Le}}} = {{10}^{{ - 4}}}$. Эти значения соответствуют величинам, характерным для ионосферных экспериментов.

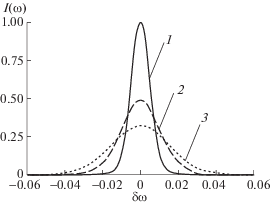
Так, например, если частота зондирования при некогерентном рассеянии составляет ${{f}_{s}}$ = = 500 МГц, то волновое число флуктуаций k, на которых происходит обратное рассеяние, равно $k = 2 \times 2\pi {{f}_{s}}{\text{/}}c = 0.2$ см⁻¹. При ${{r}_{{De}}} = $ 1 см получаем $k{{r}_{{De}}} = 0.2$. В F-слое ионосферы частота столкновений ${{\nu }_{{ei}}}$ имеет порядок 10³ с^–1, а электронная ленгмюровская частота ${{\omega }_{{Le}}}$ – величина порядка 10⁷ с^–1, что дает отношение ${{\nu }_{{ei}}}{\text{/}}{{\omega }_{{Le}}} \sim {{10}^{{ - 4}}}$. Подставляя приведенные параметры в формулу (43), для мнимой части диэлектрической проницаемости имеем $\left| {{\text{Im}}{{\varepsilon }^{0}}\left( {\omega ,{\mathbf{k}}} \right)} \right| = \left| {{\text{Im}}\varepsilon _{e}^{0}\left( {\omega ,{\mathbf{k}}} \right)} \right|$ ≈ 7 × 10^–4. В единицах относительной частоты $\delta \omega = \left( {\omega - {{\omega }_{0}}} \right){\text{/}}{{\omega }_{0}}$ полученная оценка приблизительно равна уширению спектральной линии, которое имело бы место в отсутствие случайных неоднородностей. Для большинства некогерентных радаров частота ${{f}_{s}}$ меньше 500 МГц, и уширение, связанное с затуханием Ландау оказывается еще меньше.

Как видно из рис. 1, даже слабые неоднородности с относительным возмущением концентрации σ ~ (1–3) × 10^–2 приводят к уширению плазменной линии δω ~ (1–3) × 10^–2, значительно превышающему нашу оценку для уширения вследствие затухания Ландау и электрон-ионных столкновений. Из рисунка также следует, что спектр плазменной линии расширяется с увеличением интенсивности случайных неоднородностей, т.е. с ростом параметра σ.

Подчеркнем, что относительные возмущения электронной концентрации в неоднородностях σ ~ (1–3) × 10^–2, использованные нами при расчете этих графиков, характерны для естественных ионосферных условий [8]. Еще большие значения σ могут достигаться в экспериментах по искусственному возмущению ионосферы радиоволнами высокой интенсивности [14]. Таким образом, в ионосфере уширение спектра флуктуаций в области ленгмюровской частоты, обусловленное случайными неоднородностями, как правило, должно значительно превосходить столкновительное уширение и уширение, обусловленное затуханием Ландау.

Приведенные оценки не учитывают геомагнитное поле в ионосфере. Фактически, эти оценки соответствуют случаю, когда направление распространения ленгмюровских волн и магнитного поля близки друг к другу. В этом случае магнитное поле слабо влияет на ленгмюровские волны. Такая ситуация реализуется в экспериментах по наблюдению обратного рассеяния теми радарами, которые расположены в средних и высоких широтах (радары в России, Северной Европе, Аляске). Основной массив экспериментальных данных в настоящее время поступает от этих радаров. Вместе с тем, развитый в данной работе метод может быть расширен и на случай, когда волновой вектор ленгмюровских волн составляет произвольный угол с магнитным полем.

В реальных экспериментах по некогерентному рассеянию радиоволн ширина плазменной линии зависит также от градиента электронной концентрации в плазме. При этом, с увеличением длины зондирующего импульса возрастает измеряемая ширина плазменной линии. Существует, однако, способ получить “истинный” спектр плазменной линии, не связанный с регулярной неоднородностью плазмы, даже при наличии градиента концентрации. Это достигается за счет линейной частотной модуляции зондирующего сигнала [25, 27].

Можно подобрать скорость модуляции таким образом, что влияние регулярной неоднородности будет устранено. Тогда экспериментально полученная ширина плазменной линии будет определяться одним из механизмов, рассмотренных выше. Следовательно, приведенные нами расчеты уширения спектра из-за случайных неоднородностей могут определять минимально достижимую ширину плазменной линии в подобных экспериментах.

С другой стороны, экспериментальные данные об “истинной” ширине плазменной линии могут дать возможность оценить интенсивность случайных неоднородностей электронной концентрации на основе результатов настоящей работы. Если оценки для уширения плазменной линии из-за электрон-ионных столкновений и затухания Ландау оказываются существенно меньше экспериментальных значений, то необходимо принимать во внимание возможность уширения спектра флуктуаций за счет случайных неоднородностей. Подбирая в этом случае величину σ таким образом, чтобы она давала необходимую ширину спектра (см. рис. 1), можно получить относительную величину возмущений электронной концентрации в случайных неоднородностях.

5. ЗАКЛЮЧЕНИЕ

В настоящей работе развит метод расчета флуктуаций в неравновесной плазме, содержащей случайные неоднородности электронной концентрации. Метод позволяет рассчитать спектры плазменных флуктуаций для произвольных функций распределения частиц по импульсам, если такие распределения не приводят к неустойчивости плазмы. С помощью данного метода получены спектры флуктуаций электрического поля и плотности электронов в окрестности ленгмюровской частоты, когда в плазме присутствуют случайные неоднородности электронной концентрации. При этом предполагается, что неоднородности являются крупномасштабными, т.е. их размеры существенно превышают характерный масштаб плазменных флуктуаций.

В работе показано, что влияние случайных неоднородностей приводит к уширению спектральной линии для ленгмюровских флуктуаций. При этом величина уширения в реальных плазменных системах (например, в ионосфере) даже в случае слабых неоднородностей может значительно превосходить уширение, обусловленное известными механизмами, такими как затухание Ландау и электрон-ионные столкновения.

Результаты настоящей работы позволяют оценить величину относительных возмущений электронной концентрации в неоднородностях из экспериментов по рассеянию электромагнитных волн на флуктуациях плотности электронов. Такие эксперименты дают возможность определить ширину спектра ленгмюровских флуктуаций. Далее, используя спектральные функции флуктуаций, полученные в данной работе, можно определить, какой уровень возмущений электронной концентрации в неоднородностях соответствует экспериментальным данным для ширины спектра.

Развитый в данной работе метод может быть распространен на флуктуации в других спектральных областях (в частности, на область ионного звука), а также на случайные неоднородности электронной температуры. Такие неоднородности с достаточно высокими возмущениями температуры формируются, например, в экспериментах по модификации ионосферы мощным радиоизлучением [28].