Физика плазмы, 2020, T. 46, № 3, стр. 251-256
Учет влияния различных термоядерных реакций на условия термоядерного зажигания дейтерий-тритиевого топлива
M. Nazirzadeh a, *, S. T. Mohammadi a, H. Nanakar a
a Department of Physics, Center of Basic Science, Khatam olAnbia-PBU-University
Tehran, Iran
* E-mail: mehdinaziry@yahoo.com
Поступила в редакцию 29.05.2019
После доработки 14.07.2019
Принята к публикации 22.08.2019
Аннотация
Изучено влияние различных термоядерных реакций на условия термоядерного горения эквимолярной смеси дейтерия и трития. Условия зажигания определяются тремя параметрами: начальная плотность топлива, начальная температура и размер горячей точки. Для расчета критического параметра зажигания (произведения начальной плотности и минимального радиуса горячей точки) использовалась четырехтемпературная модель. Показано, что учет совместного влияния всех термоядерных реакций приводит к более быстрому достижению условий зажигания термоядерного топлива, чем в случае, когда влияние отдельных реакций не учтено.
1. ВВЕДЕНИЕ
В исследованиях по инерциальному термоядерному синтезу (ИТС) дейтерий-тритиевое (ДТ) топливо считается наиболее перспективным с точки зрения получения термоядерного зажигания. При ИТС лазеры используются для сжатия термоядерного топлива с целью создания горячей точки, в которой происходит зажигание термоядерной реакции, и затем термоядерное горение распространяется от горячей точки к более холодным внешним слоям топлива, создавая условия успешного зажигания во всем объеме [1, 2].
В неравновесных условиях плазма обычно описывается в рамках простой трехтемпературной (3Т) модели, в которой электроны, ионы и поле излучения характеризуются тремя различными температурами ${{T}_{e}}$, ${{T}_{i}}$ и ${{T}_{r}}$, соответственно. При этом считается, что в течение всего процесса зажигания поле излучения с температурой ${{T}_{r}}$ описывается законом Планка. Однако при описании динамики зажигания в оптически толстой плазме [3] это предположение приводит к значительной ошибке. Температуры ионов, рассчитанные в рамках 3Т теории и в корректной мульти-групповой модели [4], отличаются весьма существенно.
Для адекватного описания процессов, происходящих при термоядерном зажигании топлива, предложена четырехтемпературная (4Т) модель, в которой радиационная температура, используемая в обычных 3Т-моделях, дополнена радиационной температурой фотонов, характеризующей распределение фотонов по энергии. В рамках 4Т-модели при превышении определенной пороговой энергии происходит переход: плазма из оптически толстой превращается в оптически тонкую. При этом распределение фотонов по энергии меняется от распределения, характерного для абсолютно черного тела, до распределения Бозе–Эйнштейна с конечным химическим потенциалом [4].
Высокая чувствительность термоядерного зажигания к температуре и плотности ионов делает исследование термоядерных реакций важным инструментом в изучении плазмы [1]. В настоящей работе будет рассмотрено влияние различных реакций, протекающих в ДТ плазме, на результаты расчета температуры плазмы и критического параметра зажигания (минимальной поверхностной плотности). Ионы топлива участвуют в следующих реакциях термоядерного синтеза:
(2)
$D + D \to T\left( {1.01\;{\text{МэВ}}} \right) + p\left( {3.02\;{\text{МэВ}}} \right)\left( {50\% } \right),$(3)
$D + D \to {\text{H}}{{{\text{e}}}^{3}}\left( {0.82\;{\text{МэВ}}} \right) + n\left( {2.45\;{\text{МэВ}}} \right)\left( {50\% } \right),$(4)
$D + {\text{H}}{{{\text{e}}}^{3}} \to p\left( {14.7\;{\text{МэВ}}} \right) + \alpha \left( {3.6\;{\text{МэВ}}} \right).$Реакция (1) является первичной. Реакции (2), (3) и (4) называют вторичными, поскольку в них участвуют энергичные реагенты T и He3, которые, в свою очередь, сами являются реагентами термоядерных реакций и могут оперативно вступать в реакции с тепловыми дейтронами по мере того, как они перемещаются внутри топлива и покидают его [1]. Для определения минимальных условий, необходимых для генерации горячей точки, в которой инициируется реакция термоядерного синтеза, и дальнейшего распространения волны термоядерного горения, то есть, для инициации самоподдерживающейся термоядерной реакции, необходим точный расчет влияния всех реакций, происходящих в плазме с участием ионов топлива. В представляемой работе изучается влияние различных реакций на величину критического параметра зажигания дейтерий-тритиевого топлива. Ниже дано краткое описание 4Т-модели.
2. ОСНОВНЫЕ УРАВНЕНИЯ ЧЕТЫРЕХТЕМПЕРАТУРНОЙ МОДЕЛИ
Мы интересуемся условием термоядерного горения эквимолярной смеси дейтерия и трития в неравновесной плазме. В 4Т-модели поле излучения характеризуется двумя температурами. Одна – это температура ${{T}_{R}}$, которая является стандартной радиационной температурой, используемой в 3Т модели. Она пропорциональна корню четвертой степени из плотности энергии излучения. Вторая температура ${{T}_{P}}$ представляет собой истинную термодинамическую температуру распределения фотонов по энергии. В отличие от 3Т-модели, в которой плазма считается оптически толстой на протяжении всего времени зажигания, в 4Т-модели плазма из оптически толстой превращается в оптически тонкую, как только энергия фотонов превышает некоторое критическое пороговое значение [4]. Другими словами, при низких энергиях распределение фотонов по энергии определяется законом Планка. Но с увеличением температуры фотонов распределение фотонов по энергии меняется и становится распределением Бозе–Эйнштейна. Согласно [5, 6] эволюция ансамбля фотонов может быть описана с помощью кинетического уравнения
(5)
${{\rho }_{\varepsilon }}\frac{{\partial {{n}_{E}}}}{{\partial t}} = {{C}_{B}}\left( {{{T}_{e}},{{n}_{E}}} \right) + {{C}_{C}}\left( {{{T}_{e}},{{n}_{E}}} \right),$(6)
$n_{E}^{0} = \frac{1}{{{{e}^{{{{\left( {\mu + E} \right)} \mathord{\left/ {\vphantom {{\left( {\mu + E} \right)} {{{T}_{P}}}}} \right. \kern-0em} {{{T}_{P}}}}}}} - 1}} = \frac{1}{{{{e}^{{\alpha + {E \mathord{\left/ {\vphantom {E {{{T}_{P}}}}} \right. \kern-0em} {{{T}_{P}}}}}}} - 1}} = \frac{1}{{{{e}^{{\alpha + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \gamma }} \right. \kern-0em} \gamma }}}} - 1}},$Плотности энергии фотонов, ${{E}_{P}}$, и самих фотонов, ${{N}_{\gamma }}$, соответственно, могут быть записаны в виде [4]
(7)
${{E}_{P}} = \frac{{8\pi T_{P}^{4}}}{{{{h}^{3}}{{c}^{3}}}}\int\limits_9^\infty {dy{{y}^{3}}} \frac{1}{{{{e}^{{\alpha + y}}} - 1}} = \frac{{8\pi T_{P}^{4}}}{{{{h}^{3}}{{c}^{3}}}}F\left( \alpha \right),$(8)
$F\left( \alpha \right) = \int\limits_0^\infty {dy{{y}^{3}}\frac{1}{{{{e}^{{\alpha + y}}} - 1}}} ,$(9)
${{N}_{\gamma }} = \frac{{8\pi T_{P}^{3}}}{{{{h}^{3}}{{c}^{3}}}}\int\limits_0^\infty {dy{{y}^{2}}\frac{1}{{{{e}^{{\alpha + y}}} - 1}}} \equiv {{N}_{{\gamma 0}}}\left( {{{T}_{P}}} \right)D\left( \alpha \right),$В уравнении (5) ${{C}_{B}}$ и ${{C}_{C}}$ – операторы, описывающие тормозное излучение и комптоновское рассеяние, а ${{\rho }_{\varepsilon }} = 8\pi T_{e}^{3}{{\varepsilon }^{2}}{\text{/}}{{h}^{3}}{{c}^{3}}$ – безразмерная плотность состояний фотонов. В нерелятивистском приближении оператор комптоновского рассеяния дается выражением [4]
(10)
$\begin{gathered} {{C}_{C}}\left( {{{T}_{e}},{{n}_{E}}} \right) \equiv \\ \, \equiv {{v}_{C}}{{N}_{{\gamma 0}}}\left( {{{T}_{e}}} \right)\frac{{{{T}_{e}}}}{{{{m}_{e}}{{c}^{2}}}}\frac{\partial }{{\partial \varepsilon }}\left[ {{{\varepsilon }^{4}}\left( {{{n}_{\varepsilon }}\left( {1 + {{n}_{\varepsilon }}} \right) + \frac{\partial }{{\partial \varepsilon }}{{n}_{\varepsilon }}} \right)} \right], \\ \end{gathered} $(11)
${{C}_{B}}\left( {{{T}_{e}},{{n}_{E}}} \right) = {{v}_{B}}{{n}_{e}}\sqrt {\frac{{{{m}_{e}}{{c}^{2}}}}{{2{{T}_{e}}}}} \frac{{{{e}^{{ - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}}{{K}_{0}}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}} \right)}}{\varepsilon } - c{{k}_{E}}{{\rho }_{\varepsilon }}{{n}_{E}},$(12)
${{k}_{E}} = \frac{{{{v}_{B}}}}{c}\frac{{{{n}_{e}}}}{{{{N}_{{\gamma 0}}}\left( {{{T}_{e}}} \right)}}\sqrt {\frac{{{{m}_{e}}{{c}^{2}}}}{{2{{T}_{e}}}}} \frac{{{{e}^{{ - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}}K{}_{0}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}} \right)\left( {{{e}^{\varepsilon }} - 1} \right)}}{{{{\varepsilon }^{3}}}},$(13)
$\begin{gathered} {{v}_{B}} = \frac{{32}}{{3\sqrt \pi }}{{Z}^{2}}\frac{{{{e}^{2}}}}{{\hbar c}}{{r}_{e}}^{2}c{{n}_{e}} = \\ \, = \frac{4}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{Z}^{2}}\frac{{{{e}^{2}}}}{{\hbar c}}c{{\sigma }_{T}}{{n}_{e}} = \frac{4}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{Z}_{{{\text{eff}}}}}\frac{{{{e}^{2}}}}{{\hbar c}}{{v}_{C}}. \\ \end{gathered} $В начале термоядерного горения тормозное излучение является основным механизмом потерь. С увеличением температуры фотонов до пороговой энергии ${{\varepsilon }_{0}}$ потери за счет комптоновского рассеяния сравниваются с потерями на тормозное излучение, а при энергиях выше критической энергии ${{\varepsilon }_{0}}$ комптоновское рассеяние становится доминирующим механизмом потерь. Приравнивая скорости потерь за счет тормозного излучения и комптоновского рассеяния, получаем следующее уравнение для определения пороговой энергии [4]:
(14)
$\frac{{\sqrt {2{{\pi }^{3}}} }}{{{{Z}_{{eff}}}}}\frac{{\hbar c}}{{{{e}^{2}}}}\frac{{{{N}_{{\gamma 0}}}\left( {{{T}_{e}}} \right)}}{{{{n}_{e}}}}{{\left( {\frac{{{{T}_{e}}}}{{{{m}_{e}}{{c}^{2}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = \frac{{\left( {0.81 - \ln {{\varepsilon }_{0}}} \right)}}{{\varepsilon _{0}^{3}}},$Решая уравнение (14), можно определить энергетическую границу, разделяющую фазы термоядерного горения оптически толстой и оптически тонкой ДТ плазмы.
3. УРАВНЕНИЯ ГОРЕНИЯ
Чтобы установить минимальные условия термоядерного зажигания, были произведены расчеты зависимости различных параметров плазмы от поверхностной плотности среды. В расчетах учтены потери на тормозное излучение и комптоновское рассеяние, обмен энергией между электронами и ионами, электронная теплопроводность и скорость распространения волны горения в бесконечной однородной среде. Мы предположили, что внутри бесконечной среды, состоящей из термоядерного топлива с плотностью ${{\rho }_{0}}$, часть топлива, занимающая некоторый объем, мгновенно нагревается до высокой температуры. Если выделение энергии в результате протекающих в нагретом объеме реакций термоядерного синтеза превышает все возможные потери, может начаться распространение горения на остальную часть топлива.
Согласно [8], уравнения для температуры ионов и электронов как функций поверхностной плотности среды $x = {{\rho }_{0}}r$ могут быть записаны как
(15)
$\frac{{d{{T}_{i}}}}{{dx}} = - \frac{3}{x}{{T}_{i}} + \frac{{{{q}_{i}}\left( {x,{{T}_{i}},{{T}_{e}}} \right)}}{{{{C}_{{Vi}}}{{U}_{{\max }}}}},$(16)
$\frac{{d{{T}_{e}}}}{{dx}} = - \frac{3}{x}{{T}_{e}} + \frac{{{{q}_{e}}\left( {x,{{T}_{i}},{{T}_{e}},{{T}_{R}}} \right)}}{{{{C}_{{Ve}}}{{U}_{{\max }}}}},$Если предполагается, что распределение энергии фотонов в течение всего процесса зажигания планковское, то уравнение для радиационной температуры как функции поверхностной плотности среды будет [8]
(17)
$\frac{{d{{T}_{R}}}}{{dx}} = - \frac{3}{{4x}}{{T}_{R}} + \frac{{{{q}_{R}}\left( {x,{{T}_{e}},{{T}_{R}}} \right)}}{{{{C}_{{Vr}}}{{U}_{{\max }}}}},$Как сказано выше, в 4Т-модели, при определенной пороговой энергии, при которой скорость потерь за счет комптоновского рассеяния равна скорости потерь за счет тормозного излучения, распределение фотонов по энергии меняется от распределения, характерного для абсолютно черного тела, к распределению типа распределения Бозе–Эйнштейна, при этом поле излучения может быть охарактеризовано двумя температурами. Такими температурами являются: стандартная радиационная температура ${{T}_{R}}$ (как в 3T‑модели) и истинная температура ${{T}_{P}}$ энергетического распределения фотонов. Уравнение для фотонной температуры как функции параметра зажигания также может быть получено с использованием подхода Фролова [12, 13]
(19)
$\frac{{\partial {{T}_{P}}}}{{\partial x}} = - \frac{3}{{4x}}{{T}_{P}} - \frac{{{{T}_{P}}}}{4}\frac{{\partial F}}{{\partial \alpha }}\frac{{\partial \alpha }}{{\partial x}} + \frac{{{{q}_{p}}\left( {x,{{T}_{e}},{{T}_{P}}} \right)}}{{\frac{{32\pi }}{{{{h}^{3}}{{c}^{3}}}}T_{P}^{3}F\left( \alpha \right){{\rho }_{0}}{{U}_{{\max }}}}}.$Здесь $\partial \alpha {\text{/}}\partial x$ – изменение коэффициента ослабления, фигурирующее в уравнении переноса [4, 13]
(20)
$\frac{{\partial \alpha }}{{\partial x}} = \frac{1}{{{{\rho }_{0}}{{V}_{{\max }}}{{N}_{{\gamma 0}}}}}\frac{{\left( { - {{{\dot {N}}}_{B}} + \frac{{{{I}_{1}}(\alpha )}}{{4F(\alpha )}}\frac{{{{P}_{{{\text{rad}}}}}}}{{{{T}_{P}}}}} \right)}}{{\left( {{{I}_{0}}(\alpha ) - \frac{{I_{1}^{2}(\alpha )}}{{4F(\alpha )}}} \right)}},$(21)
$\begin{gathered} {{{\dot {N}}}_{B}} = {{v}_{C}}{{n}_{e}}\frac{4}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{Z}_{{{\text{eff}}}}}\frac{{{{e}^{2}}}}{{\hbar c}}\sqrt {\frac{{{{m}_{e}}{{c}^{2}}}}{{2{{T}_{e}}}}} \times \\ \, \times \int\limits_{{{\varepsilon }_{0}}}^\infty {d\varepsilon } \frac{{{{e}^{{ - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}}{{K}_{0}}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}} \right)}}{\varepsilon }\frac{{\left( {{{e}^{{\alpha + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \gamma }} \right. \kern-0em} \gamma }}}} - {{e}^{\varepsilon }}} \right)}}{{{{e}^{{\alpha + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \gamma }} \right. \kern-0em} \gamma }}}} - 1}}, \\ \end{gathered} $(23)
$\begin{gathered} {{P}_{C}} = {{v}_{C}}{{n}_{e}}\frac{4}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{Z}_{{{\text{eff}}}}}\frac{{{{e}^{2}}}}{{\hbar c}}\sqrt {\frac{{{{T}_{e}}{{m}_{e}}{{c}^{2}}}}{2}} \times \hfill \\ \, \times \int\limits_0^\infty {d\varepsilon {{e}^{{ - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}}}}} {{K}_{0}}\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon 2}} \right. \kern-0em} 2}} \right)\frac{{\left( {{{e}^{{\alpha + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \gamma }} \right. \kern-0em} \gamma }}}} - {{e}^{\varepsilon }}} \right)}}{{{{e}^{{\alpha + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \gamma }} \right. \kern-0em} \gamma }}}} - 1}}, \hfill \\ \end{gathered} $(24)
${{I}_{0}}\left( \alpha \right) = \int\limits_0^\infty {\frac{{{{\varepsilon }^{2}}{{e}^{{\alpha + \varepsilon }}}}}{{{{{\left( {{{e}^{{\alpha + \varepsilon }}} - 1} \right)}}^{2}}}}} \,d\varepsilon ,$(25)
${{I}_{1}}\left( \alpha \right) = \int\limits_0^\infty {\frac{{{{\varepsilon }^{3}}{{e}^{{\alpha + \varepsilon }}}}}{{{{{\left( {{{e}^{{\alpha + \varepsilon }}} - 1} \right)}}^{2}}}}} \,d\varepsilon = - \frac{{dF\left( \alpha \right)}}{{d\alpha }}.$Решая совместно уравнения для производных по поверхностной плотности от коэффициента ослабления, температур ионов, электронов, фотонов и радиационной температуры, можно получить информацию не только о динамике плотности ионов, но и об эволюции самого процесса горения.
Одна из основных целей данной работы состоит в нахождении критического параметра зажигания ${{x}_{c}}$, представляющего собой произведение начальной плотности ${{\rho }_{0}}$ и минимального радиуса горячей точки ${{r}_{0}}$ (${{x}_{c}} = {{\rho }_{0}}{{r}_{0}}$). Для значений x больших, чем критический параметр зажигания ($x > {{x}_{c}}$), зажигание термоядерных реакций будет успешным, а для $x < {{x}_{c}}$ начавшееся горение будет прервано.
4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Для совместного решения восьми уравнений, в которые входят температуры ионов и электронов, радиационная температура и температура фотонов (${{T}_{i}}$, ${{T}_{e}}$, ${{T}_{R}}$, ${{T}_{P}}$), коэффициент ослабления α, плотности трития, дейтерия и ионов He3, являющиеся функциями поверхностной плотности $x = {{\rho }_{0}}r$, и рассмотрения зажигания ДТ топлива в рамках 4Т-модели, были написаны программы на языке Fortran. Эти восемь уравнений описывают баланс энергий ионов, электронов, фотонов, излучения, изменение плотности ионов и изменение коэффициента ослабления. Совместное решение этих уравнений возможно только при определенных начальных значениях параметров. В полностью ионизованной плазме начальная плотность топлива ${{\rho }_{0}}\;[{\text{г/с}}{{{\text{м}}}^{{\text{3}}}}]$ коррелирует с начальной плотностью электронов. Задавая начальную плотность электронов, можно получить начальные плотности ионов $\left( {{{n}_{{{\text{D}}0}}},{{n}_{{{\text{T}}0}}},{{n}_{{{\text{H}}{{{\text{e}}}^{3}}}}}} \right)$. На рис. 1 показаны зависимости температур компонентов плазмы от поверхностной плотности для ${{\rho }_{0}} = $ = 120 г/см3 (иначе, для ${{n}_{{\text{D}}}} = {{n}_{{\text{T}}}} = 1.4 \times {{10}^{{25}}}$ см–3) и начальных температур ${{T}_{{i0}}} = {{T}_{{e0}}} = {{T}_{{R0}}} = {{T}_{{P0}}} = $ = 5 кэВ. В этих условиях рассчитанный критический параметр зажигания ${{x}_{c}}$ оказался равным 1.3 г/см3.
Рис. 1.
Зависимости ионной, электронной, фотонной и радиационной температур от поверхностной плотности для ДТ-топлива при ${{x}_{c}} = 1.3$ г/см3.
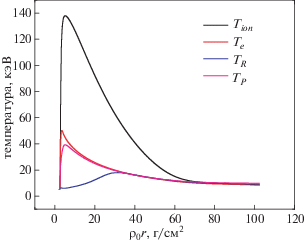
На рис. 2 и 3 для различных термоядерных реакций приведены зависимости ионной и электронной температур от поверхностной плотности. Количество энергии, выделяемое в результате реакции, влияет на температуры ионов и электронов. Очевидно, что если учесть все реакции синтеза, происходящие в горячей точке, то количество энергии, идущей на нагрев ионов и электронов, увеличивается.
Рис. 2.
Зависимость ионной температуры от поверхностной плотности при начальных плотностях ионов nD= nT = 1.4 × 1025 см–3 и температурах Ti0 = Te0 = = TR0 = TP0 = 5 кэВ.
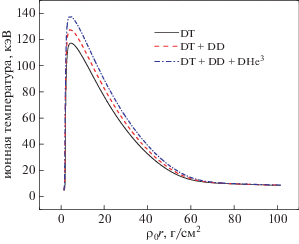
Рис. 3.
Зависимость электронной температуры от поверхностной плотности при тех же начальных параметрах, что на рис. 2.
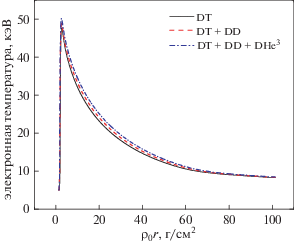
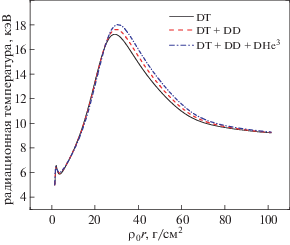
В 4Т-модели начальное распределение фотонов по энергии соответствует распределению излучения абсолютно черного тела с коэффициентом ослабления $\alpha = 0$. Затем при некоторой пороговой энергии распределение фотонов по энергии превращается в распределение Бозе–Эйнштейна, а плазма из оптически толстой превращается в оптически тонкую. Двумя основными каналами потерь в горячей плазме являются потери на тормозное излучение и потери за счет комптоновского рассеяния. Фотоны, которые рождаются в процессе тормозного излучения, могут участвовать также и в другом процессе, приводящем к потерям, – в комптоновском рассеянии. В режиме тонкой плазмы комптоновское рассеяние, являющееся преобладающим механизмом потерь, нагревает фотоны, не увеличивая при этом их число. Это меняет распределение фотонов по энергии и приводит к возрастанию энергии фотонов за счет увеличения коэффициента ослабления α, что видно из уравнения (9). При увеличении коэффициента ослабления распределение фотонов трансформируется, превращаясь в распределение типа распределения Бозе–Эйнштейна, и поскольку число фотонов сохраняется, температура фотонов возрастает. Как видно из рис. 4 и 5, чем выше температура электронов, тем большая энергия передается фотонам при тормозном излучении и комптоновском рассеянии.
Рис. 4.
Зависимость фотонной температуры от поверхностной плотности при тех же начальных параметрах, что на рис. 2.
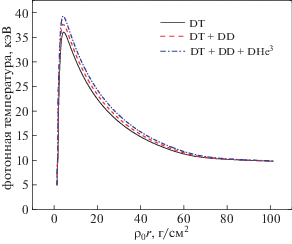
Рис. 5.
Зависимость радиационной температуры от поверхностной плотности при тех же начальных параметрах, что на рис. 2.
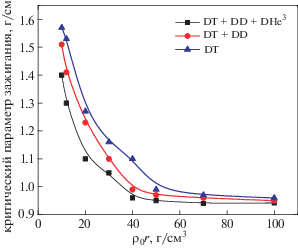
Критический параметр зажигания различных термоядерых реакций как функция объемной плотности в диапазоне ${{10}^{2}} \leqslant {{\rho }_{0}}\;[{\text{г/с}}{{{\text{м}}}^{{\text{3}}}}] \leqslant {{10}^{3}}$ показан на рис. 6. Очевидно, что при учете всех реакций критический параметр зажигания меньше, чем в случае, когда учитываются не все реакции.
Рис. 6.
Зависимости критического параметра зажигания ДТ-топлива ${{x}_{c}} = {{\rho }_{0}}{{r}_{0}}$ от начальной плотности топлива ${{\rho }_{0}}$, рассчитанные в диапазоне изменения плотности ${{10}^{2}} \leqslant {{\rho }_{0}}\;[{\text{г/с}}{{{\text{м}}}^{{\text{3}}}}] \leqslant {{10}^{3}}$, для различных термоядерных реакций.
5. ВЫВОДЫ
В этой статье восемь связанных дифференциальных уравнений решены совместно относительно поверхностной плотности с использованием метода Рунге–Кутта четвертого порядка, и рассчитан критический параметр зажигания для различных реакций в рамках 4Т-модели.
В соответствии с 4Т-моделью, вид функции распределения фотонов по энергии влияет на характер термодинамического горения топлива. Показано, что рассчитанный критический параметр зажигания и температуры компонентов плазмы различный для каждой термоядерной реакции. Если учесть все протекающие в плазме термоядерные реакции, то в расчетах условия зажигания ДТ-топлива достигаются быстрее, чем в случаях, когда некоторые из этих реакций не учтены.
Список литературы
Rinderknecht H.G., Rosenberg M.J., Zylstra A.B., Lahman B., Seguin F.H., Frenje J.A., Li C.K., Gatu John-son M., Petrasso R.D., Berzak L.F. // Phys. Plasmas. 2015. V. 22. 082709.
Lindl J. // Phys. Plasmas. 1995. V. 2. P. 3933.
Atzeni S., Meyer T.V. The Physics of Inertial Fusion. Oxford Univ Press, 2007.
Molvig K., Alme M., Webster R., Galloway C. // Phys. Plasmas. 2009. V. 16. 023301.
Cooper G. // Phys. Rev. D. 1971. V. 3. P. 2312.
Компанеец А.С. // ЖЭТФ. 1957. Т. 31. С. 876. [A.S. Kompaneets // Sov. Phys. JETP 4, 730 (1957)]
Patria R.K. Statistical Mechanics, 2nd Edition. Oxford: Butterworth and Heinemann, 1996.
Nayak B., Menon S.V.G. // Laser Part. Beams. 2012. V. 30. P. 517.
Fraley G.S., Linnebur E.J., Mason R., Morse R.L. // Phys. Fluids. 1974. V. 17. P. 474.
Basko M.M. // Nucl. Fusion . 1990. V. 30. P. 2443.
Аврорин Е.Н., Феоктистов Л.П., Шибаршов Л.И. // Физика плазмы. 1980. Т. 6. С. 965. [E.N. Avrorin, L.P. Feoktistov, L.I. Shibarshov // Sov. J. Plasma Phys. 6, 527 (1980)]
Frolov A.M., Smith V.H., Smith G.T. // Can. J. Phys. 2002. V. 80. P. 43.
Ghasemizad A., Nazirzadeh M., Khanbabaie B. // Phys. Plasmas. 2016. V. 23. 082707.
Дополнительные материалы отсутствуют.


