Физика плазмы, 2020, T. 46, № 9, стр. 847-853

1. ВВЕДЕНИЕ

Пылевые частицы, левитирующие над горизонтальным электродом в газоразрядной плазме, часто образуют различные структуры. Результаты исследования подобных образований изложены во многих обзорах и монографиях (например, [1–4]). В частности, при определенных условиях могут формироваться линейные цепочки частиц, расположенные в равновесном положении вдоль одной прямой [5].

При анализе динамики линейных или более сложных пылевых структур существенно, что, в отличие от классической механики, благодаря направленному потоку ионов, для межчастичных сил не выполняется третий закон Ньютона. Аналитическая форма подобных невзаимных сил неизвестна, поэтому для теоретического исследования колебаний и устойчивости используются какие-либо модельные потенциалы. В частности, при помощи модели ионного фокуса было показано, что невзаимность сил приводит к связи вертикальных и горизонтальных колебаний линейной цепочки частиц и развитию неустойчивости связанных волн [6–8].

В работе [9] при анализе устойчивости линейной цепочки частиц межчастичное взаимодействие рассчитывалось численными методами, исходя из модели плазмы с холодным потоком ионов и максвелловскими электронами. Было показано, что наряду с неустойчивостью связанных волн в определенной области параметров плазмы может реализоваться еще один канал апериодической неустойчивости. Цель настоящей работы заключается в выводе укороченных уравнений, описывающих нелинейную динамику цепочки частиц вблизи порога неустойчивостей. Используется стандартный метод медленно меняющихся амплитуд (например, [10, 11]).

В разделе 2 описана используемая модель плазмы и введены безразмерные переменные. Далее (раздел 3) выписаны общие уравнения движения, в разделе 4 выводятся укороченные уравнения для неустойчивости связанных волн, а в разделе 5 обсуждается нелинейная стадия апериодической неустойчивости. Все громоздкие формулы перенесены в три приложения.

2. МОДЕЛЬ И ОБОЗНАЧЕНИЯ

Рассматривается бесконечная линейная цепочка пылевых частиц в приэлектродном слое плазмы. Предполагается, что в вертикальном (ось z) направлении частицы удерживаются внешней силой с потенциалом ${{U}_{{ext}}}(z) = \Omega _{0}^{2}{{z}^{2}}{\text{/}}2$, и движение происходит в плоскости $xz$. В равновесном состоянии частицы расположены на одинаковом расстоянии a друг от друга с координатами $x_{n}^{{(0)}} = na$, $z_{n}^{{(0)}} = {{z}^{{(0)}}}$ ($n = 0, \pm 1, \pm 2 \ldots $). Межчастичные силы считаются потенциальными, т.е. сила, действующая на частицу 1 со стороны частицы 2, равна ${\mathbf{F}}({{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}) = - \nabla U({{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}})$ (${\mathbf{r}} = (x,z)$), и невзаимными, т.е. $U(x,z) = U( - x,z) \ne U(x, - z)$.

Пылевые частицы имеют одинаковые постоянные заряды Q и расположены в плазме, состоящей из направленного потока холодных ионов и максвелловских электронов. Соответствующий потенциал взаимодействия имеет вид

Удобный способ численного расчета силовых констант (2) описан в приложении 1. Заметим, что в случае взаимных сил, подчиняющихся третьему закону Ньютона, все выражения (2) с нечетным индексом j обращаются в нуль.

Используются безразмерные переменные с масштабом длины $\lambda = u{\text{/}}{{\omega }_{{pi}}}$, межчастичные силы нормализованы на ${{Q}^{2}}{\text{/}}{{\lambda }^{2}}$, а масштаб времени для частиц с массой ${{M}_{0}}$ равен $M_{0}^{{1/2}}{{\lambda }^{{3/2}}}{\text{/|}}Q{\text{|}}$. В этих переменных коэффициенты (2) помимо межчастичного расстояния зависят от единственного характеризующего плазму параметра $M = ({{n}_{e}}{\text{/}}{{n}_{i}})u\sqrt {{{m}_{i}}{\text{/}}{{T}_{e}}} $, где ${{n}_{{e,i}}}$ – равновесные плотности электронов и ионов, а ${{m}_{i}}$ – масса ионов. В общем случае плазма в пристеночном слое не является нейтральной, т.е. ${{n}_{e}} \ne {{n}_{i}}$, однако при этом неоднородностью плазмы пренебрегается. Представляет интерес случай чисто ионного потока с $M = 0$, когда влиянием электронов можно пренебречь. Для квазинейтральной плазмы с ${{n}_{e}} = {{n}_{i}}$ параметр M совпадает с числом Маха потока, т.е. отношением скорости u к скорости ионного звука.

Величины ${{\Omega }_{0}}$, a и M считаются независимыми управляющими параметрами, при этом все силовые константы (2) зависят от a и M. Заметим, что в сверхзвуковом потоке ($M > 1$) потенциал (1) всегда положителен, и пылевые частицы отталкиваются друг от друга. В дозвуковом или чисто ионном потоке ($M < 1$) существует область параметров $(a,M)$, для которых возникает притяжение между частицами [9].

При наличии притяжения между частицами используемую математическую модель необходимо уточнить. Мы считаем цепочку частиц бесконечной, однако любая реальная система конечна. Если границы цепочки свободны, т.е. крайние частицы ничем не удерживаются, то притяжение должно приводить к формированию структуры с некоторым равновесным размером и межчастичным расстоянием, которые определяются параметрами потенциала. Иными словами, величина a при этом не является независимым управляющим параметром, а зависит от величины M.

С другой стороны, можно представить себе ситуацию, когда крайние частицы как-то удерживаются или вся цепочка представляет собой кольцевую структуру с большим, но конечным радиусом. В этом случае среднее межчастичное расстояние определяется полным числом частиц и может считаться управляющим параметром. В настоящей статье мы ставим задачу именно таким образом.

3. УРАВНЕНИЯ ДВИЖЕНИЯ

Если межчастичное взаимодействие достаточно мало, то при анализе динамики цепочки частиц можно ограничиться учетом взаимодействия с ближайшими соседями. Для используемой здесь модели плазмы это приближение имеет разумную точность при $a > 2$ [9]. Общее уравнение движения для частицы с номером n имеет вид

Обозначая конечные разности как $\Delta {{f}_{n}} = {{f}_{{n + 1}}} - $ $ - \;{{f}_{{n - 1}}}$ и ${{\Delta }^{2}}{{f}_{n}} = {{f}_{{n + 1}}} - 2{{f}_{n}} + {{f}_{{n - 1}}}$ ($f = x,z$), запишем линейные члены разложения силы в виде

Следующие члены разложения силы имеют более громоздкий вид и выписаны в приложении 2.

В линейном приближении по ${{x}_{n}}$, ${{z}_{n}}$ уравне-ния (4) описывают две моды колебаний цепочки c пространственно-временной зависимостью вида ${{{\mathbf{r}}}_{n}} \sim exp( - i{{\omega }_{{1,2}}}(k)t + ikn)$, которые при определенных значениях управляющих параметров могут стать неустойчивыми. Для потенциала вида (1) существуют два канала неустойчивости [9]. При ${{u}_{{2,0}}} > 0$ и для достаточно большой частоты ${{\Omega }_{0}} > $ $ > {{\Omega }_{{cr}}}(a,M)$ обе ветви колебаний устойчивы. По мере уменьшения частоты внешнего потенциала при ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ развивается неустойчивость связанных волн. В точке бифуркации ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$ две ветви колебаний сливаются при $k = {{k}_{0}}$ ($0 < {{k}_{0}} < \pi $), при этом ${{\omega }_{1}}({{k}_{0}}) = {{\omega }_{2}}({{k}_{0}}) = {{\omega }_{0}}$ и выполняются соотношения

Как показано в [9], при ${{u}_{{2,0}}} < 0$ и ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ возникает дополнительный канал апериодической неустойчивости. Эта неустойчивость развивается при $k = \pi $, и в горизонтальном направлении смещения частиц пропорциональны ${{x}_{n}} \sim {{( - 1)}^{n}}$, а в линейном приближении ${{z}_{n}} = 0$.

Цель дальнейшего исследования заключается в выводе укороченных уравнений, описывающих влияние нелинейных членов разложения силы в (4) на развитие неустойчивостей пылевой цепочки. При этом предполагается, что управляющие параметры лежат вблизи границы одной из областей неустойчивости. Обычно в нелинейной физике выводятся укороченные уравнения для бегущих волн. Однако в данном случае больший интерес представляет нелинейная динамика стоячей волны или, что то же самое, двух бегущих волн с одинаковыми амплитудами, распространяющихся во встречных направлениях. Можно заранее предугадать, что влияние нелинейных членов приведет либо к ускорению развития неустойчивости, либо к ее насыщению при достижении амплитуды возмущения некоторого конечного значения. Поэтому основное внимание уделяется определению областей в пространстве управляющих параметров, в которых реализуется тот или иной сценарий развития неустойчивости.

4. НЕУСТОЙЧИВОСТЬ СВЯЗАННЫХ ВОЛН

4.1. Многомасштабное разложение

Неустойчивость связанных волн развивается при ${{\Omega }_{0}} < {{\Omega }_{{cr}}}(a,M)$ (6), а инкремент вблизи границы неустойчивости пропорционален $\sqrt {{{\Omega }_{{cr}}} - {{\Omega }_{0}}} $. Введем формальный малый параметр $\epsilon \ll 1$, по которому будет проводиться разложение, и положим ${{\Omega }_{0}} = {{\Omega }_{{cr}}} + {{\epsilon }^{2}}\delta $. Величина δ заменяет управляющий параметр ${{\Omega }_{0}}$: при $\delta > 0$ система устойчива, при $\delta < 0$ – неустойчива. Для получения укороченных уравнений представим возмущения в виде разложения по гармоникам

(7)

$\begin{gathered} {{x}_{n}}(t) = \epsilon X(\tau )cos({{k}_{0}}n)cos({{\omega }_{0}}t) + \\ \, + \sum\limits_{j \geqslant 2} \,{{\epsilon }^{j}}\sum\limits_{l,m} \,x_{{l,m}}^{{(j)}}(\tau ){{e}^{{i({{k}_{0}}nl + {{\omega }_{0}}tm)}}}, \\ {{z}_{n}}(t) = \epsilon Z(\tau )sin({{k}_{0}}n)cos({{\omega }_{0}}t) + \\ \, + \sum\limits_{j \geqslant 2} \,{{\epsilon }^{j}}\sum\limits_{l,m} \,z_{{l,m}}^{{(j)}}(\tau ){{e}^{{i({{k}_{0}}nl + {{\omega }_{0}}tm)}}}, \\ \end{gathered} $

где введено медленное время $\tau = \epsilon t$, а частота ${{\omega }_{0}}$ и волновой вектор ${{k}_{0}}$ в точке бифуркации определяются соотношениями (6). Дальнейшие расчеты стандартны, но весьма громоздки. Поэтому ниже приводится лишь общая схема вычислений.

Подставим разложение (7) в уравнения движения (4) c силами в правой части (5), (19), (20) и запишем результат в виде ${{{\mathbf{A}}}_{n}}(t,\tau ) = 0$. Далее, разложим функцию ${{{\mathbf{A}}}_{n}}(t,\tau )$ по степеням $\epsilon $, а также по пространственным и временным гармоникам ${{{\mathbf{A}}}_{n}}(t,\tau )$ = $\sum\nolimits_{j,l,m} {{{\epsilon }^{j}}exp[i({{k}_{0}}nl + {{\omega }_{0}}tm)]{\mathbf{A}}_{{l,m}}^{{(j)}}(\tau )} $ и приравняем каждый член разложения нулю. В первом порядке по $\epsilon $ получаем

(8)

$Z(\tau ) = \sigma X(\tau ),$

где $\sigma = {\text{sign}}({{u}_{{1,1}}}) = \pm 1$. Таким образом, в первом порядке по малому параметру $\epsilon $ частицы совершают колебания с частотой ${{\omega }_{0}}$ вдоль прямых линий, расположенных под углом ${{k}_{0}}n$ к оси x (рис. 1).

Рис. 1.

Смещение частиц линейной цепочки в случае неустойчивости связанных волн: $a = 4$, $M = 1.5$, ${{k}_{0}} \approx 2.16$.

Во втором порядке разложения по $\epsilon $ из условий ${\mathbf{A}}_{{ \pm 1, \pm 1}}^{{(2)}} = 0$ возникают небольшие поправки к линейной поляризации (8) $x_{{ \pm 1,1}}^{{(2)}} = - i\alpha {{X}_{{,\tau }}}(\tau )$, $z_{{ \pm 1,1}}^{{(2)}} = $ $ = \pm \sigma \alpha {{X}_{{,\tau }}}(\tau )$, где $\alpha = {{\omega }_{0}}{\text{/}}(co{{s}^{2}}({{k}_{0}}{\text{/}}2)\Omega _{{cr}}^{2})$.

Возмущения на второй пространственной гармонике получаются из соотношений ${\mathbf{A}}_{{2,0}}^{{(2)}}(\tau ) = 0$, ${\mathbf{A}}_{{2,2}}^{{(2)}}(\tau ) = 0$ и пропорциональны квадрату амплитуды возмущений на основной гармонике ${{x}_{{2,s}}}(\tau ) = $ $ = {{\alpha }_{{x,s}}}X{{(\tau )}^{2}}$, ${{z}_{{2,s}}}(\tau ) = {{\alpha }_{{z,s}}}X{{(\tau )}^{2}}$ ($s = 0,2$). Коэффициенты пропорциональности оказываются довольно громоздкими и выписаны в Приложении 3.

Возмущения на нулевой пространственной гармонике можно получить из соотношений ${\mathbf{A}}_{{0,0}}^{{(2)}}(\tau ) = 0$, ${\mathbf{A}}_{{0,2}}^{{(2)}}(\tau ) = 0$:

(9)

$\begin{gathered} {{z}_{{0,0}}}(\tau ) = - \frac{{\left( {{{u}_{{0,3}}} + {{u}_{{2,1}}}} \right)si{{n}^{2}}({{k}_{0}}{\text{/}}2)X{{{(\tau )}}^{2}}}}{{\Omega _{{cr}}^{2}}}, \\ {{z}_{{0,2}}}(\tau ) = \frac{{\left( {{{u}_{{0,3}}} + {{u}_{{2,1}}}} \right)si{{n}^{2}}({{k}_{0}}{\text{/}}2)X{{{(\tau )}}^{2}}}}{{8\omega _{0}^{2} - 2\Omega _{{cr}}^{2}}} \\ \end{gathered} $

и ${{x}_{{0,0}}}(\tau ) = {{x}_{{0,2}}}(\tau ) = 0$.

Для основной гармоники члены порядка ${{\epsilon }^{3}}$ в (7) можно получить из соотношений ${\mathbf{A}}_{{ \pm 1, \pm 1}}^{{(3)}} = 0$, которые представляют собой вырожденную систему линейных уравнений относительно $x_{{ \pm 1, \pm 1}}^{{(3)}}$, $z_{{ \pm 1, \pm 1}}^{{(3)}}$. Условие существования решения обеспечивает отсутствие секулярного роста и записывается как $iA_{{x,1,1}}^{{(3)}} + \sigma A_{{z,1,1}}^{{(3)}} = 0$, что приводит к соотношению

(10)

$\begin{gathered} \alpha \frac{{{{d}^{2}}X(\tau )}}{{d{{\tau }^{2}}}} + \delta {{\gamma }_{1}}X(\tau ) + {{\gamma }_{3}}X{{(\tau )}^{3}} + {{\beta }_{x}}X(\tau )({{x}_{{2,0}}}(\tau ) + \\ \, + {{x}_{{2,2}}}(\tau )) + {{\beta }_{z}}X(\tau )({{z}_{{2,0}}}(\tau ) + {{z}_{{2,2}}}(\tau )) = 0. \\ \end{gathered} $

Явные выражения для входящих сюда коэффициентов выписаны в Приложении 3 (21). Коэффициенты ${{\beta }_{{x,z}}}$ ведут свое происхождение от квадратичного члена разложения силы ${\mathbf{F}}_{n}^{{(2)}}$ (19), а ${{\gamma }_{3}}$ – от кубического ${\mathbf{F}}_{n}^{{(3)}}$ (20). Заметим, что уравнение (10) не содержит членов, соответствующих возмущениям на нулевой пространственной гармонике (9), и в этом проявляется специфика нелинейных членов разложения силы (19), (20), зависящих только от конечно-разностных производных.

Таким образом, в процессе развития неустойчивости связанных волн цепочка как целое медленно смещается вдоль оси z на величину ${{z}_{{0,0}}}(\tau )$ и совершает колебания на частоте $2{{\omega }_{0}}$ с амплитудой ${{z}_{{0,2}}}(\tau )$. Однако обратного влияния эти движения на динамику основной гармоники не оказывают. Аналогичное поведение наблюдается также для двух частиц, взаимодействующих посредством невзаимных сил [12], и характерно для невзаимной механики.

Собирая коэффициенты при степенях $X(\tau )$ в уравнении (10), перепишем его в виде

(11)

$\alpha \frac{{{{d}^{2}}X(\tau )}}{{d{{\tau }^{2}}}} = - \frac{{\partial V(X(\tau ))}}{{\partial X(\tau )}},$

где

(12)

$V(X) = \frac{1}{2}\delta {{\gamma }_{1}}{{X}^{2}} + \frac{1}{4}\gamma {{X}^{4}},$

а коэффициент $\gamma = {{\gamma }_{3}} + {{\beta }_{x}}({{\alpha }_{{x,0}}} + {{\alpha }_{{x,2}}}) + {{\beta }_{z}}({{\alpha }_{{z,0}}} + $ $ + \;{{\alpha }_{{z,2}}})$.

Из уравнения (11) видно, что характерный временной масштаб изменения амплитуды определяется как $\sqrt {{\text{|}}\delta {{\gamma }_{1}}{\text{|/}}\alpha } $, а характерный масштаб нелинейности – $\sqrt {{\text{|}}\delta {{\gamma }_{1}}{\text{/}}\gamma {\text{|}}} $. Поскольку величины $\alpha > 0$ и ${{\gamma }_{1}} > 0$ (21) всегда положительны, на качественном уровне динамика цепочки определяется знаком коэффициента γ. Если $\gamma > 0$, то в области неустойчивости ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ ($\delta < 0$) эффективный потенциал (12) имеет два дополнительных минимума при $X = \pm {\text{|}}\delta {\text{|}}{{\gamma }_{1}}{\text{/}}\gamma $, и неустойчивость связанных волн насыщается при конечных амплитудах возмущения. Если же $\gamma < 0$, то влияние нелинейности приводит к ускорению развития неустойчивости, которая приобретает взрывной характер, т.е. $X(t) \sim 1{\text{/}}({{t}_{0}} - t)$, где время сингулярности ${{t}_{0}}$ определяется начальными условиями.

4.2. Численный анализ

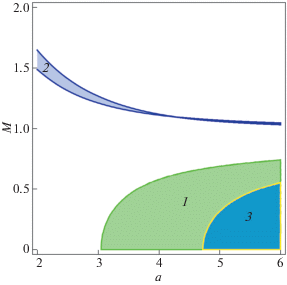
Значения параметров a и M, для которых $\gamma > 0$, показаны в области 2 на рис. 2. Границы этой области получены численно при помощи потенциала (1) и коэффициентов, выписанных в Приложении 3. Область представляет собой узкую полосу, лежащую при $M > 1$. Вне областей 1 и 2 на рис. 2 неустойчивость связанных волн имеет взрывной характер.

Рис. 2.

Область 1 – ${{u}_{{2,0}}} < 0$, 2 – $\gamma > 0$, 3 – ${{u}_{{4,0}}} < 0$.

Одна из границ области 2 на рис. 2 совпадает с линией уровня коэффициента ${{u}_{{1,1}}}(a,M) = 0$, поэтому более обозримые выражения можно получить, разлагая все коэффициенты по степеням ${{u}_{{1,1}}}$. Заметим, прежде всего, что при ${{u}_{{1,1}}} = 0$ неустойчивость связанных волн отсутствует. При малых значениях этого коэффициента ${{u}_{{1,1}}} \to 0$ в соответствии с (6) волновой вектор ${{k}_{0}}$ стремится к границе зоны Бриллюэна ${{k}_{0}} \to \pi - 2{\text{|}}{{u}_{{1,1}}}{\text{|/}}({{u}_{{2,0}}} - {{u}_{{0,2}}})$. Ведущие члены разложения коэффициентов ${{\gamma }_{1}}$, γ равны

$\begin{gathered} {{\gamma }_{1}} \approx \frac{{u_{{1,1}}^{2}}}{{4{{u}_{{2,0}}}({{u}_{{2,0}}} - {{u}_{{0,2}}})}}, \\ \gamma \approx - \frac{{{{u}_{{1,1}}}{{u}_{{2,1}}}\left( {{{u}_{{1,2}}} + {{u}_{{3,0}}}} \right)}}{{4u_{{2,0}}^{2}}}. \\ \end{gathered} $

В пределе ${{u}_{{1,1}}} \to 0$ основной вклад в величину γ дает член ${{\alpha }_{{x,0}}}$ в (11), определяемый уравнениями (22). Иными словами, вблизи границы области 2 на рис. 2 характерная амплитуда смещения $\sqrt {{{\gamma }_{1}}{\text{/}}\gamma } $ определяется виртуальными смещениями на второй пространственный и нулевой временной гармонике.

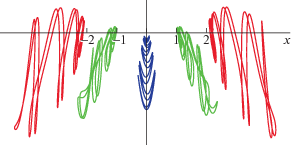
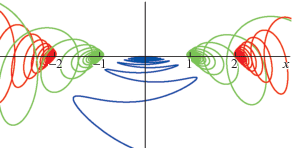
Движение отдельных пылевых частиц представляет собой суперпозицию быстрых колебаний на частоте ${{\omega }_{0}}$ и медленных движений, описываемых уравнениями (9) и (11). В увеличенном масштабе примеры траекторий частиц показаны на рис. 3, 4. В случае параметров, лежащих в области 2 на рис. 2, частицы движутся по сложным незамкнутым траекториям, расположенным вблизи исходного положения равновесия (рис. 3). При развитии взрывной неустойчивости (рис. 4) частицы после нескольких колебаний быстро покидают положение равновесия.

Рис. 3.

Пример траекторий частиц при насыщении неустойчивости связанных волн: $a = 2.5$, $M = 1.35$.

Рис. 4.

Пример траекторий частиц при развитии взрывной неустойчивости: $a = 2.5$, $M = 1.5$.

5. АПЕРИОДИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ

Другой канал неустойчивости [9] обусловлен притяжением между частицами в горизонтальном направлении в дозвуковом потоке ионов ($0 \leqslant M < 1$). Эта неустойчивость цепочки частиц возникает при ${{\Omega }_{0}} > {{\Omega }_{{cr}}}$ (6) и смене знака коэффициента ${{u}_{{2,0}}}$ (область 1 на рис. 2). При этом неустойчивость носит апериодический характер и развивается при $k = \pi $, т.е. в линейном приближении смещения частиц имеют вид ${{x}_{n}} \sim {{( - 1)}^{n}}$, ${{z}_{n}} = 0$.

Для нелинейного описания апериодической неустойчивости положим ${{u}_{{2,0}}} = {{\epsilon }^{2}}\delta $ ($\epsilon \ll 1$). Заметим, что если волновой вектор возмущения лежит на границе зоны Бриллюэна $k = \pi $, то пространственная конфигурация, соответствующая второй гармонике с $k = 2\pi $, совпадает с однородной конфигурацией $k = 0$. По этой причине нелинейные члены разложения силы (19), (20) либо не зависят от номера частицы n, либо пропорциональны ${{( - 1)}^{n}}$, и разложение, аналогичное (7), можно записать в виде

В силу симметрии задачи нелинейные процессы не могут приводить к однородному смещению цепочки частиц вдоль оси x, поэтому можно сразу же положить ${{\xi }_{0}}(\tau ) = 0$. После подстановки (13) в (4) во втором порядке по $\epsilon $ получаем ${{\zeta }_{0}}(\tau ) = - 4{{u}_{{2,1}}}X{{(\tau )}^{2}}{\text{/}}\Omega _{0}^{2}$ и ${{\zeta }_{1}}(\tau ) = 0$. Члены, пропорциональные ${{\epsilon }^{3}}$, дают ${{\xi }_{1}}(\tau ) = 0$ и

Динамика частиц при развитии апериодической неустойчивости определяется уравнением нелинейного осциллятора, аналогичным (11). Заметим, что нелинейность в (14) обусловлена кубическим членом разложения силы (20), а влияние квадратичных членов (19) приводит к смещению цепочки частиц в вертикальном направлении.

На качественном уровне в области неустойчивости $\delta < 0$ вся динамика определяется знаком коэффициента ${{u}_{{4,0}}}$. При ${{u}_{{4,0}}} > 0$ нелинейные колебания ограничены и по амплитуде имеют порядок $X(\tau ) \sim \sqrt {{\text{|}}\delta {\text{|/}}{{u}_{{2,0}}}} $, а при ${{u}_{{4,0}}} < 0$ неустойчивость носит взрывной характер. Параметры a и M, для которых в используемой модели плазмы ${{u}_{{4,0}}} < 0$, показаны на рис. 2 областью 3. Эта область лежит достаточно далеко от границы области 1. Таким образом, при развитии апериодической неустойчивости частицы разбиваются на пары, совершающие противофазные нелинейные колебания. При наличии диссипации должна формироваться структура, в которой в каждой элементарной ячейке содержатся две частицы.

6. ЗАКЛЮЧЕНИЕ

В настоящей работе были получены укороченные уравнения, описывающие нелинейную динамику цепочки пылевых частиц вблизи порогов двух неустойчивостей. Показано, что нелинейное насыщение неустойчивости связанных волн возможно лишь в узкой области чисел Маха сверхзвукового ионного потока. Для большинства значений чисел Маха и межчастичных расстояний неустойчивость связанных волн носит взрывной характер. Для апериодической неустойчивости, развивающейся в дозвуковом потоке, насыщение всегда происходит на слабонелинейном уровне.

Следует отметить, что полученные уравнения (11), (14) совпадают с уравнением нелинейного осциллятора и имеют интеграл движения, аналогичный энергии. В то же время, для исходных уравнений (3), (4) интегралы движения неизвестны и, возможно, их не существует. Причина появления интеграла движения укороченных уравнений заключается в следующем.

В работе [9] было показано, что линеаризованные уравнения (4) при помощи некоторой замены переменных могут быть записаны в виде уравнений Гамильтона. Это означает, что при достаточно малых возмущениях решение полных уравнений (4) близко к решению некоторой гамильтоновой системы. Построенное здесь асимптотическое разложение представляет собой аппроксимацию решения (4), имеющую соответствующий интеграл движения.