Физика плазмы, 2020, T. 46, № 9, стр. 854-862
Трехмерные изотермические ионно-звуковые ударные волны в ультрарелятивистской вырожденной электрон-позитрон-ионной магнитоплазме
E. F. El-Shamy a, b, M. M. Selim b, *, A. El-Depsy b
a Department of Physics, College of Science, King Khalid University
P.O. 9004 Abha, Saudi Arabia
b Department of Physics, Faculty of Science, Damietta University
P.O. 34517 New, Damietta, Egypt
* E-mail: mselim2000@yahoo.com
Поступила в редакцию 03.05.2019
После доработки 01.09.2019
Принята к публикации 22.10.2019
Аннотация
Рассмотрены свойства трехмерных изотермических ионно-звуковых ударных волн (ИИЗУВ), распространяющихся в замагниченной электрон-позитрон-ионной плазме. Свойства волн меняются при взаимодействии с ультрарелятивистскими вырожденными электронами и позитронами, а также из-за наличия химических потенциалов. Считается, что холодные ионы замагничены и инерционны, а электроны и позитроны подчиняются статистике Ферми–Дирака. Для получения нелинейного уравнения Захарова–Кузнецова–Бюргерса (НУЗКБ) использована хорошо известная редуцированная теория возмущений. Аналитическое выражение для решения в виде ударной волны получено с использованием метода гиперболического тангенса. Кроме того, обсуждаются асимптотика и устойчивость решений в виде ударных волн. В рамках рассматриваемой модели, возбуждаемые нелинейные изотермические ионно-звуковые волны существуют только в виде неосциллирующих ИИЗУВ. Численно исследовано влияние химического потенциала, наличия ультрарелятивистских вырожденных электронов и протонов и магнитного поля на основные свойства трехмерных ИИЗУВ. Численные исследования позволили получить важную информацию о распространении и динамике ИИЗУВ. Установлено, что амплитуды неосциллирующих ИИЗУВ уменьшаются при увеличении химических потенциалов ультрарелятивистских вырожденных электронов и позитронов.
1. ВВЕДЕНИЕ
В последние годы при исследовании квантовой плазмы были получены необычайно важные результаты. Стимулом быстрого развития исследований в данной области является то, что полученные результаты могут быть востребованы в различных областях науки [1–4]. Например, значительный интерес представляют исследования возбуждения нелинейных волн в квантовой плазме, поскольку они способствуют более глубокому изучению основных свойств таких компактных астрофизических объектов, как белые карлики и нейтронные звезды [5–8]. Исследования квантовой вырожденной плазмы также важны для понимания таких процессов, как коллапс и рождение звезд. В работах [9–11] был получен математический критерий того, какая звезда является белым карликом. При этом белый карлик считался вырожденной и высокоплотной звездой, и к электронам была применена статистика Ферми–Дирака. Недавно полученные данные наблюдений за белыми карликами показали, что помимо электронов и позитронов в их плазме также присутствуют ионы. Очевидно, что плотная электрон-позитрон-ионная (ЭПИ) плазма является одним из наиболее важных и привлекательных для исследователей видов квантовой плазмы. Поэтому нелинейное распространение ионно-звуковых электростатических (уединенных/ударных) волн в квантовой ЭПИ плазме исследовалось в целом ряде работ [12–19]. Во всех этих работах предполагалось, что электроны и позитроны являются Ферми-газами с нулевой температурой (т.е. полностью вырожденными и абсолютно холодными, T = 0). Поэтому в используемых моделях квантовой плазмы температура считалась нулевой, что позволило значительно упростить математические уравнения, использованные для анализа волновых процессов в такой плазме. Например, в работе [17] было показано, что фазовый сдвиг квантовых ионно-звуковых солитонов сильно зависит от квантовой поправки для дифракции. В работе [19] было показано, что по мере уменьшения релятивистского эффекта возрастает инкремент модуляционной неустойчивости, изменяющей форму ионно-звуковых солитонов. Однако использование численного анализа в предположении нулевой температуры в реальной квантовой плазме может не дать адекватного описания распространения нелинейных электростатических волн в различных средах [20–25]. Поэтому в этих работах предприняты разнообразные попытки улучшить качество теоретического анализа. Для анализа и решения нелинейных уравнений был применен новый метод (так называемый метод псевдопотенциала Бернулли). Кроме того, была получена точная оценка интегралов Ферми–Дирака [26]. На протяжении последних нескольких лет авторы этих работ изучали распространение нелинейных волн в вырожденной плазме при ненулевых температурах ($T \ne 0$). Впоследствии были проведены и другие теоретические исследования распространения нелинейных солитонов в плотной вырожденной плазме с ненулевой температурой [2, 27]. В работе [24] исследовано распространение изотермических ионно-звуковых волн в вырожденной плазме в рамках как линейной, так и нелинейной теорий. Было установлено, что увеличение химического потенциала приводит к возникновению положительного электрического потенциала. В работе [25] было установлено, что скорость звука должна превышать скорость распространения солитона. В работе [28] было обнаружено, что фазовая скорость, амплитуда и ширина позитронных акустических уединенных волн возрастают при наличии ненулевых распределений Томаса–Ферми. Однако свойства трехмерных изотермических ионно-звуковых ударных волн (ИИЗУВ), распространяющихся в плотной вырожденной магнитоплазме, не изучены до сих пор. В настоящей работе для вывода нелинейного уравнения Захарова–Кузнецова–Бюргерса (НУЗКБ), которое допускает существование решений в виде ИИЗУВ, используется хорошо известная редуцированная теория возмущений. Структуры типа ударной волны обычно формируются в результате установления равновесия между нелинейностью плазменной среды, являющейся причиной увеличения крутизны фронта волны, и ее диссипацией, возникающей вследствие вязкости, наличия столкновений и взаимодействия волны с частицами плазменной среды. Поэтому диссипация является одним из факторов, играющих важную роль в нелинейном распространении структур, подобных ударной волне [29]. Кроме того, при решении уравнения НУЗКБ учитывается кинематическая вязкость, возникающая при взаимодействии между релятивистскими вырожденными компонентами магнитоплазмы (эффект Бюргерса). Хорошо известно, что преобладание диссипации приводит к распространению ударных волн с неосциллирующим профилем. С другой стороны, когда при описании нелинейной дисперсной среды дисперсный член преобладает над диссипативным, то возникают осцилляции профиля ударной волны [30, 31].
Исследуем численно природу трехмерных ИИЗУВ, распространяющихся в астрофизических объектах высокой плотности, таких как нейтронные звезды и белые карлики [20, 22, 32]. Возбуждение трехмерной ударной волны в вырожденной ЭПИ магнитоплазме более вероятно, чем возбуждение одномерной волны. Поэтому целью настоящей работы является изучение нелинейного возбуждения ИИЗУВ в трехмерной плазме, представляющей собой холодную ионную жидкость, в которой также присутствуют ультрарелятивистские вырожденные безынерционные электроны и позитроны. Кроме того, в рамках данной модели обсуждаются условия формирования осциллирующих/неосциллирующих профилей ИИЗУВ. В этой связи мы рассмотрим влияние химических потенциалов, наличия ультрарелятивистских вырожденных электронов и позитронов, а также магнитного поля на интенсивность и крутизну профиля ИИЗУВ, формирующихся в релятивистской вырожденной магнитоплазме.
Статья построена следующим образом. В разд. 2 представлено уравнение состояния вырожденного электрон-позитронного Ферми-газа. Основные уравнения, используемые в расчетах, приведены в разд. 3. Уравнение НУЗКБ получено с использованием хорошо известной редуцированной теории возмущений. В разд. 4 исследованы асимптотическое поведение и устойчивость по отношению к малому возмущению аналитического решения, а также условия формирования осциллирующих/неосциллирующих профилей ИИЗУВ. В разд. 5 обсуждаются некоторые численные иллюстрации полученных результатов.
2. УРАВНЕНИЕ СОСТОЯНИЯ ВЫРОЖДЕННОГО ЭЛЕКТРОН-ПОЗИТРОННОГО ФЕРМИ-ГАЗА
Хорошо известно, что плотность состояний релятивистского Ферми-газа с кинетической энергией E, движущегося в объеме V, определяется выражением [34]
(1)
$G\left( E \right) = \frac{{{{g}_{s}}VE}}{{2{{\pi }^{2}}{{h}^{3}}{{c}^{3}}}}\sqrt {{{E}^{2}} - {{m}^{2}}{{c}^{4}}} ,$(2)
$G\left( E \right) \approx \frac{{V~}}{{{{\pi }^{2}}{{h}^{3}}{{c}^{3}}}}\left( {{{E}^{2}} - \frac{1}{2}{{m}^{2}}{{c}^{4}}} \right).$В этом случае число частиц Ферми-газа может быть записано в виде [34]
(3)
$N\left( {\mu ,T} \right) = \mathop \smallint \limits_0^\infty \frac{{G\left( E \right)dE}}{{{{e}^{{\sigma \left( {E - \mu } \right)}}} + 1}},$(4)
$n\left( {\mu ,T} \right) = \frac{{N\left( {\mu ,T} \right)}}{V} = \frac{1}{{{{\pi }^{2}}{{h}^{3}}{{c}^{3}}}}\mathop \smallint \limits_0^\infty \frac{{\left( {{{E}^{2}} - {{m}^{2}}{{c}^{4}}{\text{/}}2} \right)dE}}{{{{e}^{{\sigma \left( {E - \mu } \right)}}} + 1}}.$Используя разложение Зоммерфельда, после некоторых математических преобразований можно получить следующее выражение:
(5)
$n\left( {\mu ,T} \right) \approx \frac{{8~\pi }}{{{{{\left( {hc} \right)}}^{3}}}}\left( {\frac{{{{\mu }^{3}}}}{3} + \left( {\frac{{{{\pi }^{2}}}}{{3{{\sigma }^{2}}}} - \frac{1}{2}{{m}^{2}}{{c}^{4}}} \right)\mu } \right).$Принимая во внимание это уравнение, можно получить следующие выражения для распределений ультрарелятивистских вырожденных электронов и позитронов соответственно [20, 24, 33]
(6)
${{n}_{e}}\left( {{{\mu }_{e}},{{T}_{{Fe}}}} \right) = \frac{{8\pi }}{{{{{\left( {hc} \right)}}^{3}}}}\left[ {\frac{{\mu _{e}^{3}}}{3} + \left( {\frac{{{{\pi }^{2}}}}{{3\sigma _{e}^{3}}} - \frac{1}{2}m_{e}^{2}{{c}^{4}}} \right){{\mu }_{e}}} \right],$(7)
${{n}_{p}}\left( {{{\mu }_{p}},{{T}_{{Fp}}}} \right) = \frac{{8\pi }}{{{{{\left( {hc} \right)}}^{3}}}}\left[ {\frac{{\mu _{p}^{3}}}{3} + \left( {\frac{{{{\pi }^{2}}}}{{3\sigma _{p}^{3}}} - \frac{1}{2}m_{p}^{2}{{c}^{4}}} \right){{\mu }_{p}}} \right].$В настоящей работе мы предполагаем, что волновой процесс сжатия-разрежения является изотермическим (т.е. TFs = const, s = e, p для электронов и позитронов соответственно). Вырожденная плазма считается бесстолкновительной и идеальной. В такой плазме термодинамическое равновесие может устанавливаться в результате некоррелированного кулоновского взаимодействия между частицами [23, 24]. Устремляя к нулю массу электронов и позитронов (ms → 0) в уравнениях для импульса, после некоторых алгебраических преобразований можно получить соотношение между химическим потенциалом электронов/позитронов и потенциалом электростатической волны ϕ в виде
Подставляя (8) в уравнения (6) и (7) и полагая $\phi = 0,$ получаем выражение для невозмущенной плотности электронов и позитронов
(9)
${\text{\;}}n_{s}^{{\left( 0 \right)}}~ = \frac{{8\pi }}{{{{{\left( {hc} \right)}}^{3}}}}\left( {\frac{{\mu _{{0s}}^{3}}}{3} + {{\mu }_{{0s}}}\left( {\frac{{{{\pi }^{2}}}}{{3\sigma _{s}^{2}}} - \frac{1}{2}m_{s}^{2}{{c}^{4}}} \right)} \right),$3. ОСНОВНЫЕ УРАВНЕНИЯ
Рассмотрим трехмерную замагниченную плазму, состоящую из невырожденных инерционных холодных ионов и ультрарелятивистских вырожденных безынерционных электронов и позитронов. Плазма находится во внешнем однородном магнитном поле ${\mathbf{B}} = {{{\text{B}}}_{0}}{{{\mathbf{e}}}_{z}},$ где ${{{\mathbf{e}}}_{z}}$ – единичный вектор, направленный вдоль оси z. Динамика нелинейных трехмерных ИИЗУВ, распространяющихся в такой плазме, определяется следующим уравнением непрерывности
(10)
$\frac{{\partial {{n}_{i}}}}{{\partial t}} + \nabla \cdot \left( {{{n}_{i}}{{{\mathbf{u}}}_{i}}} \right) = 0,$(11)
$\begin{gathered} \left( {\frac{{\partial {{{\mathbf{u}}}_{i}}}}{{\partial t}} + \left( {{{{\mathbf{u}}}_{i}} \cdot \nabla } \right){{{\mathbf{u}}}_{i}}} \right) = \\ \, = - \nabla \phi + \Omega \left( {{{{\mathbf{u}}}_{i}} \times {{{\mathbf{e}}}_{z}}} \right) + {{\eta }_{i}}{{\nabla }^{2}}{{{\mathbf{u}}}_{i}}. \\ \end{gathered} $Плотности инерционных холодных ионов, электронов и позитронов связаны уравнением Пуассона
где $\beta = n_{e}^{{\left( 0 \right)}}{\text{/}}n_{i}^{{\left( 0 \right)}}$ и $\alpha = n_{p}^{{\left( 0 \right)}}{\text{/}}n_{i}^{{\left( 0 \right)}}$. Из уравнений (6), (7) и (9) получаем нормализованные распределения, соответственно, для релятивистских вырожденных электронов и позитронов(13)
${{n}_{e}} = \frac{1}{{{{C}_{{1e}}}}}\left( {{{C}_{{1e}}} + {{C}_{{2e}}}\phi + {{\mu }_{{0e}}}{{\phi }^{2}} + \frac{{{{\phi }^{3}}}}{3}} \right),$(14)
${{n}_{p}} = \frac{1}{{{{C}_{{1p}}}}}\left( {{{C}_{{1p}}} - {{C}_{{2p}}}{{\sigma }_{F}}\phi + {{\mu }_{{0p}}}\sigma _{F}^{2}{{\phi }^{2}} - \sigma _{F}^{3}\frac{{{{\phi }^{3}}}}{3}} \right),$Чтобы исследовать нелинейное распространение ИИЗУВ, используем редуцированную теорию возмущений [35], согласно которой независимые переменные в уравнениях (10)–(14) в движущейся системе координат можно записать следующим образом:
(15)
$\begin{gathered} X = {{\varepsilon }^{{1/2}}}x,\quad Y = {{\varepsilon }^{{1/2}}}y,\quad Z = {{\varepsilon }^{{1/2}}}\left( {z - \lambda t} \right), \\ T = {{\varepsilon }^{{3/2}}}t,\quad {{\eta }_{i}} = {{\varepsilon }^{{1/2}}}{{\eta }_{0}}, \\ \end{gathered} $(16)
$\begin{gathered} \psi = {{\psi }^{{\left( 0 \right)}}} + \mathop \sum \limits_{n = 1}^\infty ~{{\varepsilon }^{n}}{{\psi }^{{\left( n \right)}}}, \\ {\text{и\;}}\quad {{u}_{{i\left( {X,Y} \right)}}} = {{\varepsilon }^{{3/2}}}u_{{i\left( {X,Y} \right)}}^{{\left( 1 \right)}} + {{\varepsilon }^{2}}u_{{i\left( {X,Y} \right)}}^{{\left( 2 \right)}} + \ldots , \\ \end{gathered} $(17)
${\psi } = \left[ {{{n}_{i}},{{u}_{{iZ}}},\phi } \right]\quad {\text{и}}\quad {{{\psi }}^{{\left( 0 \right)}}}\left[ {1,0,0} \right].$Подставляя разложения в (15) и (16) в уравне-ния (10)–(14) и оставив в выражении для ${\varepsilon }$ только члены низшего порядка, получаем следующие соотношения:
(19)
$u_{{iX}}^{{\left( 1 \right)}} = - \frac{1}{\Omega }\frac{{\partial {{\phi }^{{\left( 1 \right)}}}}}{{\partial Y}},$(20)
$u_{{iY}}^{{\left( 1 \right)}} = \frac{1}{\Omega }\frac{{\partial {{\phi }^{{\left( 1 \right)}}}}}{{\partial X}},$Из этих уравнений следует выражение для фазовой скорости ИИЗУВ λ
(22)
$\lambda = \frac{1}{{\sqrt {\beta \frac{{{{C}_{{2e}}}}}{{{{C}_{{1e}}}}} + \alpha {{\sigma }_{F}}\frac{{{{C}_{{2p}}}}}{{{{C}_{{1p}}}}}} }}.$Рассматривая члены следующего порядка в разложении для ε, используя уравнения (18)–(22), получаем окончательное эволюционное уравнение (уравнение НУЗКБ) в виде
(23)
$\begin{gathered} \frac{{\partial \phi }}{{\partial T}} + A\phi \frac{{\partial \phi }}{{\partial Z}} + B\frac{{{{\partial }^{3}}\phi }}{{\partial {{Z}^{3}}}} + C\frac{\partial }{{\partial Z}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{Y}^{2}}}}} \right)\phi - \\ \, - D\left( {\frac{{{{\partial }^{2}}}}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{Y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{Z}^{2}}}}} \right)\phi = 0. \\ \end{gathered} $Здесь, коэффициент нелинейности равен $A = $ $ = B\left( {\frac{3}{{{{\lambda }^{4}}}} - 2\left( {\beta \frac{{{{\mu }_{{0e}}}}}{{{{C}_{{1e}}}}} - \alpha \sigma _{F}^{2}\frac{{{{\mu }_{{0p}}}}}{{{{C}_{{1p}}}}}} \right)} \right)$, коэффициенты дисперсии равны $B = {{\lambda }^{3}}{\text{/}}2$ и $C = B\left( {1 + {{\Omega }^{{ - 2}}}} \right)$, а коэффициент диссипации составляет ${\text{D}} = {{{\eta }}_{0}}{\text{/}}2$. Уравнение НУЗКБ описывает нелинейные свойства ИИЗУВ. Для простоты, в уравнении (23) мы предположили, что ${\text{\;}}\phi = {{\phi }^{{\left( 1 \right)}}}$.
4. МЕТОД ГИПЕРБОЛИЧЕСКОГО ТАНГЕНСА И УСЛОВИЯ РАСПРОСТРАНЕНИЯ ИИЗУВ С ОСЦИЛЛИРУЮЩИМИ И НЕОСЦИЛЛИРУЮЩИМИ ПРОФИЛЯМИ
Преобразуем потенциал к виду $\phi \left( {X,Y,Z,~T} \right) = $ $ = \varphi (\xi )$, используя следующую замену переменных:
(24)
$\xi = \frac{1}{\delta }\left( {{{\ell }_{x}}X + {{\ell }_{y}}Y + {{\ell }_{z}}Z - {{u}_{0}}T} \right).$Тогда уравнение (23) примет вид
(25)
$\begin{gathered} - {{u}_{0}}\frac{{d\varphi }}{{d\xi }} + A{{\ell }_{z}}\varphi \frac{{d\varphi }}{{d\xi }} + \\ \, + \frac{{{{\ell }_{z}}}}{{{{\delta }^{2}}}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)\frac{{{{d}^{3}}\varphi }}{{d{{\xi }^{3}}}} - \frac{D}{\delta }\frac{{{{d}^{2}}\varphi }}{{d{{\xi }^{2}}}} = 0. \\ \end{gathered} $(26)
$\begin{gathered} \frac{{{{d}^{2}}\varphi }}{{d{{\xi }^{2}}}} = \frac{{{{u}_{0}}{{\delta }^{2}}}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\varphi - \\ \, - \frac{{A{{\delta }^{2}}}}{{2\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}{{\varphi }^{2}} + \\ \, + \frac{{\delta D}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\frac{{d\varphi }}{{d\xi }}. \\ \end{gathered} $Уравнение (26) можно рассматривать как уравнение движения частицы единичной массы в силовом поле, а φ и ξ играют роли обобщенной координаты и времени [27]. В общем случае, профили ИИЗУВ существенно зависят от всех физических параметров, входящих в коэффициент диссипации. Чтобы найти условие, определяющее коэффициент диссипации, соответствующий формированию осциллирующих/неосциллирующих профилей ИИЗУВ, исследуем асимптотику аналитического решения уравнения (26). Предположив, что $\varphi = {{\varphi }_{0}} + \tilde {\varphi }$, и линеаризовав уравнение (26), считая ${{\varphi }_{0}} = 2{{u}_{0}}{\text{/}}A{{\ell }_{z}}$ и ${{\varphi }_{0}} \gg \tilde {\varphi },$ получаем [36]
(27)
$\begin{gathered} \frac{{{{d}^{2}}\tilde {\varphi }}}{{d{{\xi }^{2}}}} - \frac{{\delta D}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\frac{{d\tilde {\varphi }}}{{d\xi }} + \\ \, + \frac{{{{u}_{0}}{{\delta }^{2}}}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\tilde {\varphi } = 0. \\ \end{gathered} $Решение уравнения (27) прямо пропорционально величине $~{{e}^{{p\xi }}}$, где
Поэтому при $D > {{\left[ {4{{u}_{0}}{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)} \right]}^{{1/2}}}$ будут формироваться неосциллирующие профили ИИЗУВ, тогда как при $D < $ $ < {{\left[ {4{{u}_{0}}{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)} \right]}^{{1/2}}}$ будет происходить распространение ИИЗУВ с осциллирующими профилями.
Теперь для получения аналитического решения НУЗКБ воспользуемся методом гиперболического тангенса [37]
(28)
$\varphi \left( \xi \right) = {{f}_{0}} + {{f}_{1}}{\text{tanh}}\,\xi + {{f}_{2}}{{\left( {{\text{tanh}}\,\xi } \right)}^{2}}.$Оценка констант ${{f}_{0}}$, ${{f}_{1}}$ и ${{f}_{2}}$ может быть получена путем подстановки выражения (28) в уравне-ние (25). Получаем полиномиальное уравнение относительно $\tanh \xi $. Приравнивая нулю коэффициенты при ${{\left( {\tanh \xi } \right)}^{i}}$, $i = 0,1,2,...$ и решая полученную систему алгебраических уравнений относительно неизвестных ${{u}_{0}}$, δ, ${{f}_{0}}$, ${{f}_{1}}$ и${{f}_{2}}$, получаем
Ширина ИИЗУВ равна ${{\delta }^{{ - 1}}} = D{\text{/}}$ ${\text{/}}\left[ {10{{\ell }_{{\text{z}}}}(({\text{B}} - {\text{C}})\ell _{{\text{z}}}^{2} + {\text{C}})} \right]$, и постоянная скорость системы координат равна ${{u}_{0}} = 6{{D}^{2}}{\text{/}}$ ${\text{/}}\left[ {25{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)} \right]$. Следовательно, уравнение (28) может быть записано в виде
(29)
$\varphi \left( \xi \right) = {{\varphi }_{{\max }}}\left( {1 + {{{\operatorname{sech} }}^{2}}\xi {\text{/}}2 - \tanh \xi } \right).$В уравнении (29) амплитуда ИИЗУВ равна ${{\varphi }_{{\max }}} = 6{{D}^{2}}{\text{/}}\left[ {25A\ell _{z}^{2}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)} \right]$. Подчеркнем, что условие $D > \left[ {4{{u}_{0}}{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)} \right]$ выполняется независимо от численных значений величин B, C и ${{\ell }_{{\text{z}}}}$. Таким образом, в рассматриваемой системе могут распространяться только ИИЗУВ с неосциллирующим профилем.
Теперь изучим, является ли полученное решение уравнения (29) в виде $\Psi = \varphi \left( \xi \right) + \varepsilon {{\tilde {\varphi }}_{1}}$ ($\varepsilon \ll 1$) устойчивым по отношению к малому возмущению (${{\tilde {\varphi }}_{1}}$). Подставляя Ψ в уравнение (26) и линеаризуя его относительно ${{{\tilde {\varphi }}}_{1}}$, получаем дифференциальное уравнение относительно возмущения ${{{\tilde {\varphi }}}_{1}}$ [38]
(30)
$\begin{gathered} \frac{{{{d}^{2}}{{{\tilde {\varphi }}}_{1}}}}{{d{{\xi }^{2}}}} = \frac{{\delta D}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\frac{{d{{{\tilde {\varphi }}}_{1}}}}{{d\xi }} + \\ \, + \frac{{{{u}_{0}}{{\delta }^{2}}}}{{{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}{{{\tilde {\varphi }}}_{1}} - \frac{{A{{\delta }^{2}}}}{{\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}}\varphi {{{\tilde {\phi }}}_{1}}. \\ \end{gathered} $Уравнение (30) имеет решение, пропорциональное ${{e}^{{\rho \xi }}}$. Кроме того, параметр ρ удовлетворяет характеристическому полиному [38]
(31)
$\begin{gathered} {{\rho }_{{1,2}}} = \frac{\delta }{{2{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)}} \times \\ \, \times \left( {D \pm \sqrt {{{D}^{2}} - 4{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)\left( {{{\ell }_{z}}A\varphi - {{u}_{0}}} \right)} } \right). \\ \end{gathered} $Следовательно, возможны три разных случая. Очевидно, что небольшое возмущение аналитического решения экспоненциально нарастает (затухает), если параметр ρ является действительным положительным (отрицательным) числом. Наконец, если параметр ρ – мнимое число, то ИИЗУВ имеет осциллирующий профиль. Следовательно, мы получаем следующее математическое выражение:
(32)
${{D}^{2}} - 4{{\ell }_{z}}\left( {\left( {B - C} \right)\ell _{z}^{2} + C} \right)\left( {{{\ell }_{z}}A\varphi - {{u}_{0}}} \right) < 0.$Поэтому, подставляя (29) в (32), получаем следующее условие:
Очевидно, что условие (33) никогда не выполняется, независимо от численного значения ξ. Другими словами, это означает, что распространение ИИЗУВ с осциллирующими профилями недопустимо, независимо от параметров используемой модели. Итак, уравнение имеет два действительных корня, и его общее решение может быть записано в виде
(34)
${{\tilde {\varphi }}_{1}} = {{g}_{1}}{{e}^{{{{\rho }_{1}}\xi }}} + {{g}_{2}}{{e}^{{{{\rho }_{2}}\xi }}},$5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
В настоящем разделе мы рассмотрим трехмерные ИИЗУВ с неосциллирующими профилями, распространяющиеся в астрофизической плазме белых карликов [20, 22, 32, 33]. На рис. 1–8 представлены численные зависимости потенциала ИИЗУВ с неосциллирующим профилем от таких физических параметров, как ${{\mu }_{{0e}}}$, ${{\mu }_{{0p}}}$, ${{\sigma }_{e}}$, ${{\sigma }_{p}}$, α, Ω, ${{{\eta }}_{0}}$ и ${{\ell }_{z}}$. Рисунки 1 и 2 иллюстрируют эволюцию профилей неосциллирующих ИИЗУВ при изменении химических потенциалов, соответственно, ультрарелятивистских вырожденных электронов и позитронов ${{{\mu }}_{{0{\text{e}}}}}\left( {{{{\mu }}_{{0{\text{p}}}}}} \right)$. Видно, что амплитуды неосциллирующих ИИЗУВ уменьшаются с ростом ${{\mu }_{{0e}}}$ и ${{\mu }_{{0p}}}$, поскольку при увеличении ${{\mu }_{{0e}}}$ и ${{\mu }_{{0p}}}$ плотности электронов и позитронов в трехмерных нелинейных неосциллирующих ИИЗУВ также возрастают, что приводит к увеличению нелинейного коэффициента A, поэтому амплитуды неосциллирующих ИИЗУВ уменьшаются. То есть величина химического потенциала ультрарелятивистских вырожденных электронов и позитронов значительно влияет на форму неосциллирующих ИИЗУВ. На рис. 3 и 4 показана эволюция профилей нелинейных неосциллирующих ИИЗУВ при изменении отношений температуры Ферми к температуре электронов σe и позитронов σp соответственно. Амплитуда и крутизна профиля трехмерных неосциллирующих ИИЗУВ немного возрастают с увеличением σe и σp. Рисунок 5 показывает изменение профиля неосциллирующей ИИЗУВ при изменении отношения плотностей позитронов и ионов α. Видно, что как интенсивность, так и крутизна профиля нелинейных ИИЗУВ уменьшаются с уменьшением α. Влияние ионной циклотронной частоты Ω на профили трехмерных неосциллирующих ИИЗУВ показано на рис. 6. Обнаружено, что при увеличении Ω амплитуда неосциллирующих ИИЗУВ возрастает, а их ширина уменьшается. Влияние кинематической вязкости ионов ${{{\eta }}_{0}}$ на профили трехмерных неосциллирующих ИИЗУВ показано на рис. 7. Очевидно, что амплитуда и крутизна профиля нелинейных неосциллирующих ИИЗУВ возрастают при увеличении ${{{\eta }}_{0}}$. Хорошо известно, что если компоненты вырожденной магнитоплазмы обладают вязкостью, то это приводит к появлению члена Бюргерса D в уравнении НУЗКБ. Соответственно, интенсивность и крутизна профиля нелинейных неосциллирующих ИИЗУВ увеличиваются. На рис. 8 показано, как меняются профили нелинейных неосциллирующих ИИЗУВ с ростом величины направляющих косинусов ${{\ell }_{z}}$. Видно, что амплитуды ИИЗУВ возрастают, а ширины профилей уменьшаются. Очевидно, что параметры ${{\mu }_{{0e}}}$, ${{\mu }_{{0p}}}$, α, Ω, ${{{\eta }}_{0}}$ и ${{\ell }_{z}}$ оказывают сильное влияние на форму профилей нелинейных неосциллирующих ИИЗУВ. С физической точки зрения, подобное изменение профиля нелинейной неосциллирующей ИИЗУВ означает, что падение напряжения в направлении, поперечном направлению распространения этой волны, возрастает. Таким образом, все больше и больше частиц будут ускоряться.
Рис. 1.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений ${{\mu }_{{0e}}}$ при следующих значениях остальных параметров: ${{\mu }_{{0p}}} = 0.3$, σe = 20, σp = 30, α = 1.7, Ω = 0.05, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.

Рис. 2.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений ${{\mu }_{{0p}}}$ при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, σe = 20, σp = 30, α = 1.7, Ω = 0.05, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.

Рис. 3.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений σe при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σp = 30, α =1.7, Ω = 0.05, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.

Рис. 4.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений σp при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σe = 20, α = 1.7, Ω = 0.05, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.
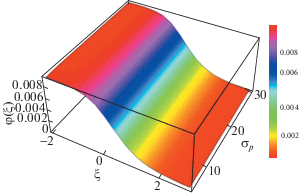
Рис. 5.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений α при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σe = 20, σp =30, Ω = 0.05, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.
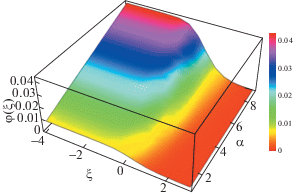
Рис. 6.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений Ω при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σe = 20, σp = 30, α=1.7, η0 = 0.5 и ${{\ell }_{z}}$ = 0.5.

Рис. 7.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений η0 при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σe = 20, σp = 30, α = 1.7, Ω = 0.05 и ${{\ell }_{z}}$ = 0.5.

Рис. 8.
Трехмерные профили потенциала φ изотермической ударной волны для различных значений ${{\ell }_{z}}$ при следующих значениях остальных параметров: ${{\mu }_{{0e}}} = 0.2$, ${{\mu }_{{0p}}} = 0.3$, σe = 20, σp = 30, α = 1.7, Ω = 0.05 и η0 = 0.5.

В данной работе были изучены особенности распространения трехмерных ИИЗУВ в ультрарелятивистской вырожденной ЭПИ магнитоплазме, состоящей из невырожденных инерционных холодных ионов и релятивистских вырожденных безынерционных электронов и позитронов. Уравнение НУЗКБ было выведено с использованием редуцированной теории возмущений. С использованием метода гиперболического тангенса было получено общее решение этого уравнения и проанализированы необходимые условия, обеспечивающие распространение нелинейных ИИЗУВ с осциллирующим/неосциллирующим профилем. В рамках данной модели плазмы аналитически и численно получено, что в плазме могут распространяться только нелинейные неосциллирующие ИИЗУВ. При этом амплитуды нелинейных ИИЗУВ являются конечными, а их основные характеристики (интенсивность, крутизна профиля и т.д.) определяются параметрами инерционных холодных ионов и релятивистских вырожденных безынерционных электронов и позитронов. Показано, что исследование зависимостей профилей ИИЗУВ от таких параметров, как химические потенциалы ${\text{\;}}{{{\mu }}_{{0{\text{e}}}}}$ и ${{{\mu }}_{{0{\text{p}}}}}$, отношение плотностей позитронов и ионов α, ионная циклотронная частота Ω, кинематическая вязкость ионов ${{{\eta }}_{0}}$ и величина направляющих косинусов ${{\ell }_{z}}$, вносит существенный вклад в понимание природы трехмерных неосциллирующих ИИЗУВ. Мы надеемся, что данное исследование будет полезным для ученых, исследующих природу трехмерных ИИЗУВ, распространяющихся в плотных астрофизических объектах, таких как белые карлики.
Авторы выражают благодарность Деканату отделения научных исследований Университета им. короля Халида за финансовую поддержку этой работы в рамках программы финансирования исследовательских групп (проект № KKU–R.G.P.1/52/39). Авторы также благодарят редактора и его сотрудников за любезную помощь в издании данной статьи.
Список литературы
Markowich P.A., Ringhofer C.A., Schmeiser C. Semiconductor Equations. Springer-Verlag, New York, 1990.
Ang L.K., Kwan T.J.T., Lau Y.Y. Phys. Rev. Lett. 2003. V. 91. P. 208303.
Killian T.C. Nature (London). 2006. V. 441. P. 298.
Glenzer S.H., Landen O.L., Neumayer P. Phys. Rev. Lett. 2007. V. 98. P. 065002.
Michel F.C. Theory of Neutron Star Magnetosphere. Chicago University Press, Chicago, 1991.
Rahman A., Ali S., Mirza A.M., Qamar A. Phys. Plasmas. 2013. V. 20. P. 042305.
El-Shamy E.F. Phys. Rev. E. 2015. V. 91. P. 033105.
El-Shamy E.F., Al-Chouikh R.C., El-Depsy A., Al-Wadie N.S. Phys. Plasmas. 2016. V. 23. P. 122122.
Chandrasekhar S. Astrophys. J. 1931. V. 74. P. 81.
Chandrasekhar S. Philos. Mag. 1931. V. 11. P. 592.
Chandrasekhar S. Mon. Not. R. Astron. Soc. 1935. V. 170. P. 405.
Haas F., Garcia L.G., Goedert J., Manfredi G. Phys. Plasmas. 2003. V. 10. P. 3858.
Khanand S.A., Masood W. Phys. Plasmas. 2008. V. 15. P. 062301.
Mahmood S., Mushtaq A. Phys. Lett. A. 2008. V. 372. P. 3467.
El-Shamy E.F., Moslem W.M., Shukla P.K. Phys. Lett. A. 2009. V. 374. P. 290.
Masood W., Mirza A.M., Nargis Sh., Ayub M. Phys. Plasmas. 2009. V. 16. P. 042308.
El-Labany S.K., El-Shamy E.F., El-Taibany W.F. and Shukla P.K. Phys. Lett. A. 2010. V. 374. P. 960.
Haas F. J. Plasma Phys. 2016. V. 82. P. 705820602.
Islam S., Sultana S., Mamun A.A. Phys. Plasmas. 2017. V. 24. P. 092115.
Dubinov A.E. Plasma Phys. Rep. 2007. V. 33. P. 210.
Dubinov A.E., Dubinova A.A. Plasma Phys. Rep. 2008. V. 34. P. 403.
Dubinov A.E., Sazonkin M.A. Plasma Phys. Rep. 2009. V. 35. P. 14.
Dubinov A.E., Dubinova A.A., Sazonkin M.A. J. Commun. Technol. Electron. 2010. V. 55. P. 907.
Dubinov A.E., Sazonkin M.A. JETP. 2010. V. 111. P. 865.
Dubinov A.E., Kitaev I.N. Phys. Plasmas. 2014. V. 21. P. 102105.
Mladek B.M., Kahl G., Neumann M. J. Chem. Phys. 2006. V. 124. P. 064503.
El-Depsy A., Selim M.M. IEEE Trans. Plasma Sci. 2016. V. 44. P. 2901.
Haas F., Mahmood S. Phys. Rev. E. 2018. V. 97. P. 063206.
Rahman M.M., Alam M.S., Mamun A.A. J. Korean Phys. Soc. 2014. V. 64. P. 1828.
Sahu B., Roychoudhury R. Phys. Plasmas. 2007. V. 14. P. 072310.
Hussain S., Akhtar N. Phys. Plasmas. 2013. V. 20. P. 012305.
El-Shamy E.F., Al-Asbali A.M. Phys. Plasmas. 2014. V. 21. P. 093701.
Rahman A., Masood W., Eliasson B., Qamar A. Phys. Plasmas. 2013. V. 20. P. 092305.
Tong D. Statistical Physics, University of Cambridge Part II Mathematical Tripos. Cambridge, 2012, http: //www.damtp.cam.ac.uk/user/tong/statphys.html.
Washimi H., Taniuti T. Phys. Rev. Lett. 1966. V. 17. P. 996.
Masood W., Siddiq M., Nargis S., Mirza A.M. Phys. Plasmas. 2009. V. 16. P. 013705.
Malfliet W. J. Comput. Appl. Math. 2004. V. 164. P. 529.
Sultana S., Sarri G., Kourakis I. Phys. Plasmas. 2012. V. 19. P. 012310.
Дополнительные материалы отсутствуют.


