Физика плазмы, 2021, T. 47, № 2, стр. 117-125
Плазменный кристалл как временной кристалл
А. М. Игнатов *
Институт общей физики им. А.М. Прохорова РАН
Москва, Россия
* E-mail: aign@fpl.gpi.ru
Поступила в редакцию 04.07.2020
После доработки 17.08.2020
Принята к публикации 20.08.2020
Аннотация
Исследуется нелинейная стадия развития неустойчивости связанных волн планарного плазменного кристалла во внешнем удерживающем силовом поле. Предполагается, что частицы расположены в плазме с максвелловскими электронами и с направленным потоком холодных ионов. Показано, что влияние нелинейности приводит либо к ускорению неустойчивости, либо к формированию временного кристалла, состоящего из одной или трех устойчивых волн. В пространстве внешних параметров построены области существования различных фаз.
1. ВВЕДЕНИЕ
Пылевые частицы в слабоионизованной плазме газового разряда приобретают значительный отрицательный заряд, благодаря чему оказываются сильно взаимодействующими между собой. Изучению динамики ансамблей сильно взаимодействующих частиц посвящена значительная часть физики пылевой плазмы (например, [1–4]). В частности, в наземных лабораторных условиях частицы группируются в приэлектродной части разряда, где могут формировать упорядоченную структуру в виде двумерной гексагональной решетки, называемую плазменным кристаллом.
В достаточно грубом приближении можно считать, что плазма в приэлектродной области состоит из электронов, распределенных по Больцману, и направленного потока холодных ионов, причем скорость потока сравнима со скоростью ионного звука. Сильная анизотропия плазмы приводит к тому, что распределение потенциала электрического поля, создаваемого точечным зарядом, не является четной функцией координат. Как следствие, силы, действующие между отдельными заряженными частицами, являются невзаимными, т.е. для них нарушается третий закон Ньютона. Невзаимность межчастичных сил приводит к связи вертикальных и горизонтальных смещений частиц плазменного кристалла и, при определенных условиях, возникновению так называемой неустойчивости связанных волн. Теория этой неустойчивости развивалась при помощи различных модельных потенциалов взаимодействия. Подробный обзор как экспериментов, так и теории можно найти в [4].
Концепция временнóго кристалла (time crystal) появилась в работах [5, 6], где было высказано предположение, что как в классических, так и в квантовых системах состояние с минимальной энергией может периодически изменяться во времени. Эта идея инициировала многочисленные дискуссии, и было предложено несколько физических реализаций временнóго кристалла. Обзор современного состояния вопроса можно найти, например, в работах [7, 8].
В процессе развития неустойчивости связанных волн плазменного кристалла возникает некоторая осциллирующая во времени структура, поэтому плазменный кристалл может быть хорошим кандидатом на роль временнóго кристалла. Основной вопрос заключается в том, что происходит с неустойчивостью связанных волн на нелинейной стадии. Возможны два варианта: либо нелинейные процессы приводят к ускорению развития неустойчивости и полному разрушению кристалла, либо нелинейность приводит к насыщению неустойчивости. Поскольку неустойчивость носит осцилляционный характер, в последнем случае может формироваться временной кристалл.
Настоящая статья является продолжением серии работ [9–12], в которых динамика линейного или планарного плазменного кристалла исследовалась при помощи потенциала взаимодействия, рассчитываемого численными методами. Основной целью работы является исследование влияния нелинейного взаимодействия колебаний на развитие неустойчивости связанных волн планарного плазменного кристалла.
Статья организована следующим образом. В разд. 2 вкратце описана используемая модель, а в разд. 3 приведены необходимые для дальнейшего соотношения линейной теории из работы [11]. Далее (разд. 4) описана общая схема вывода нелинейных уравнений для комплексных амплитуд неустойчивых волн, обсуждаются общие свойства полученных уравнений (разд. 5) и некоторые стационарные решения (разд. 6). Вычисления проводятся для произвольного невзаимного потенциала межчастичного взаимодействия. Явный вид потенциала используется в разделе 7, где приведены результаты численных расчетов.
Аналитические выкладки оказываются весьма громоздкими, поэтому значительная часть аналитических и все численные расчеты были проведены при помощи пакета Mathematica. Многие формулы являются практически необозримыми и поэтому их обсуждение носит повествовательный характер.
2. МОДЕЛЬ
Частицы, образующие плазменный кристалл, нумеруются двумя целыми индексами m, n. В равновесии все частицы расположены на одной высоте ${{z}_{{m,n}}} = {{z}_{0}}$ и в горизонтальной плоскости образуют правильную гексагональную решетку, т.е. горизонтальные координаты $\rho = (x,y)$ частиц равны ${{\rho }_{{m,n}}} = a(m{{{\mathbf{a}}}_{1}} + n{{{\mathbf{a}}}_{2}})$, где a – межчастичное расстояние. В качестве базисных выбираются единичные векторы ${{{\mathbf{a}}}_{1}} = (1,0)$, ${{{\mathbf{a}}}_{2}} = (1,\sqrt 3 ){\text{/}}2$.
Считается, что частицы имеют одинаковые постоянные заряды $Q$ и расположены в плазме, состоящей из направленного потока холодных ионов и максвелловских электронов. Соответствующий потенциал взаимодействия имеет вид
(1)
$U({\mathbf{r}}) = \frac{{4\pi {{Q}^{2}}}}{{{{{(2\pi )}}^{3}}}}\int {d{\mathbf{k}}\frac{{exp(i{\mathbf{kr}})}}{{{{{\mathbf{k}}}^{2}}\epsilon ( - {\mathbf{ku}},{\mathbf{k}})}}} ,$(2)
${{u}_{{i,j}}} = \mathop {\left. {\frac{{{{\partial }^{{i + j}}}U(a,z)}}{{\partial {{a}^{i}}\partial {{z}^{j}}}}} \right|}\nolimits_{z = 0} .$Заметим, что потенциал (1) получен в рамках линейной теории отклика плазмы и, поэтому, применим для описания взаимодействия частиц лишь для достаточно больших межчастичных расстояний. При этом каких-либо ограничений на характер динамики пылевых частиц не возникает.
Используются безразмерные переменные с масштабом длины $\lambda = u{\text{/}}{{\omega }_{{pi}}}$, межчастичные силы нормализованы на ${{Q}^{2}}{\text{/}}{{\lambda }^{2}}$, а масштаб времени для частиц с массой ${{M}_{0}}$ равен $M_{0}^{{1/2}}{{\lambda }^{{3/2}}}{\text{/}}\left| Q \right|$. В этих переменных величины (2) помимо межчастичного расстояния зависят от единственного характеризующего плазму параметра, который пропорционален числу Маха ионного потока, $M = ({{n}_{e}}{\text{/}}{{n}_{i}})u\sqrt {{{m}_{i}}{\text{/}}{{T}_{e}}} $, где ${{n}_{{e,i}}}$ – равновесные плотности электронов и ионов, а ${{m}_{i}}$ – масса ионов.
В безразмерных переменных общие уравнения движения для частицы с индексом m, n записываются в виде
(3)
${{{\mathbf{\ddot {r}}}}_{{m,n}}} = - \Omega _{0}^{2}{{{\mathbf{e}}}_{z}}{{z}_{{m,n}}} + \sum\limits_{m{\kern 1pt} ',n{\kern 1pt} ' \ne 0} \,{\mathbf{F}}({{{\mathbf{r}}}_{{m,n}}} - {{{\mathbf{r}}}_{{m + m{\kern 1pt} ',n + n{\kern 1pt} '}}}) - \mu {{{\mathbf{\dot {r}}}}_{{m,n}}},$3. ЛИНЕЙНЫЕ СООТНОШЕНИЯ
В случае волны с волновым вектором k = = $({{k}_{x}},{{k}_{y}})$ смещения частиц имеют вид ${{{\mathbf{r}}}_{{m,n}}} = $ $ = {\mathbf{r}}exp(i{{{\mathbf{a}}}_{{m,n}}} \cdot {\mathbf{k}})$, где ${{{\mathbf{a}}}_{{m,n}}} = m{{{\mathbf{a}}}_{1}} + n{{{\mathbf{a}}}_{2}}$. Линеаризованные уравнения движения (3) имеют вид ${\mathbf{\ddot {r}}} = {\mathbf{M}}({\mathbf{k}}) \cdot {\mathbf{r}}$, а силовая матрица в приближении ближайших соседей равна [11]
(4)
$\begin{gathered} \, + 3{{u}_{{2,0}}}\left[ {cos\left( {{{\theta }_{1}}} \right)cos\left( {{{\theta }_{2}}} \right) - 1} \right], \\ {{M}_{{zz}}} = - \Omega _{0}^{2} + \\ \, + 2{{u}_{{0,2}}}\left[ {cos\left( {2{{\theta }_{1}}} \right) + 2cos\left( {{{\theta }_{1}}} \right)cos\left( {{{\theta }_{2}}} \right) - 3} \right], \\ \end{gathered} $Дисперсионное уравнение задается полиномом $P(\omega ,{{k}_{x}},{{k}_{y}},{{\Omega }_{0}})$ = $det[{{\omega }^{2}}{\mathbf{I}} + {\mathbf{M}}({{k}_{x}},{{k}_{y}})]$ = 0, где I – единичная матрица. Неустойчивость связанных волн развивается при слиянии двух корней дисперсионного уравнения, когда дискриминант $D({{k}_{x}},{{k}_{y}},{{\Omega }_{0}})$ полинома $P(\omega ,{{k}_{x}},{{k}_{y}},{{\Omega }_{0}})$ обращается в нуль.
Как показано в [11], для коэффициентов (2) с потенциалом взаимодействия (1) существуют два случая. Если $M < 1$, то при уменьшении ${{\Omega }_{0}}$ первыми теряют устойчивость колебания с волновыми векторами ${{{\mathbf{k}}}_{i}}$ ($i = 1 \ldots 6$), где ${{{\mathbf{k}}}_{1}} = ({{k}_{0}},0)$, а остальные ${{{\mathbf{k}}}_{{2 \ldots 6}}}$ получаются последовательными поворотами на угол $\pi {\text{/}}3$. Критические значения частоты ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$ и волнового вектора ${{k}_{0}}$ получаются из двух соотношений
(5)
$D({{k}_{0}},0,{{\Omega }_{{cr}}}) = 0,\quad \frac{{\partial D({{k}_{0}},0,{{\Omega }_{{cr}}})}}{{\partial {{k}_{0}}}} = 0.$Векторы поляризации шести двукратно вырожденных колебаний с волновыми векторами ${{{\mathbf{k}}}_{i}}$ при ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$ равны ${{{\mathbf{p}}}_{i}} = (i{\text{sign}}({{u}_{{1,1}}}){{{\mathbf{k}}}_{i}}{\text{/}}{{k}_{0}},1)$. Частоты этих колебаний совпадают и определяются из дисперсионного уравнения $P({{\omega }_{0}},{{k}_{0}},0,{{\Omega }_{{cr}}}) = 0$.
Характерный пример дисперсионной зависимости при ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$ и $M < 1$ изображен на рис. 1, где белыми пятнами обозначены области неустойчивости и показаны попадающие в них векторы ${{{\mathbf{k}}}_{i}}$. На рисунке также изображены все возможные (за исключением нулевого вектора) суммы двух векторов из набора ${{{\mathbf{k}}}_{i}}$.
Рис. 1.
Контурный график высокочастотной ветви колебаний $max{{\omega }^{2}}$ при ${{\Omega }_{0}} < {{\Omega }_{{cr}}}$. Граница первой зоны Бриллюэна показана пунктирным шестиугольником ($a = 3$, $M = 0.5$, ${{k}_{0}} \approx 2.35$, ${{\Omega }_{0}} = 0.602$, ${{\Omega }_{{cr}}} \approx 0.604$).
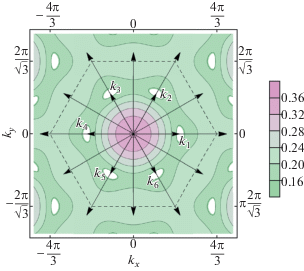
Аналогичным образом, при $M > 1$ потеря устойчивости происходит для 6 векторов, один из которых направлен вдоль оси y, а остальные получаются последовательными поворотами на угол $\pi {\text{/}}3$. В ходе дальнейшего анализа мы, для определенности, обсуждаем случай $M < 1$ и используем набор векторов, определяемых соотношениями (5).
Для потенциала межчастичного взаимодействия вида (1) наряду с неустойчивостью связанных волн в определенных областях параметров a, M возникают апериодические неустойчивости, не зависящие от управляющего параметра ${{\Omega }_{0}}$ и связанные с теми или иными структурными изменениями плазменного кристалла [11]. Мы избегаем этих областей, где требуется другое нелинейное описание.
4. ВЫВОД НЕЛИНЕЙНЫХ УРАВНЕНИЙ
При достижении частоты ${{\Omega }_{0}}$ критического значения одновременно теряют устойчивость шесть колебаний с волновыми векторами ${{{\mathbf{k}}}_{i}}$ (рис. 1). По этой причине для описания нелинейной стадии развития неустойчивости необходимо учитывать все шесть волн. Полагая, что частота ${{\Omega }_{0}}$ близка к критической, запишем ${{\Omega }_{0}} = {{\Omega }_{{cr}}} + {{\varepsilon }^{2}}\delta $, где ε – малый параметр. При $\delta > 0$ система устойчива, а при $\delta < 0$ развивается неустойчивость связанных волн с инкрементом порядка ε.
Представим смещение частицы с индексами $m,n$ в виде
(6)
$\begin{gathered} {{{\mathbf{r}}}_{{m,n}}}(t) = 2{\text{Re}}\left\{ {\sum\limits_{i = 1}^6 \,{{e}^{{i{{\theta }_{{i,mn}}}}}}\left[ {\varepsilon {{A}_{i}}(\tau ){{{\mathbf{p}}}_{i}} + {{\varepsilon }^{2}}{{{\mathbf{P}}}_{i}}(\tau ) + } \right.} \right. \\ \, + \left. {{{\varepsilon }^{3}}{{{\mathbf{Q}}}_{i}}(\tau )} \right] + \left. {{{\varepsilon }^{2}}\sum\limits_{i = 0}^{18} \,\sum\limits_{s = 0,2} \,{{e}^{{i\theta _{{i,mn}}^{s}}}}{\mathbf{B}}_{i}^{s}(\tau )} \right\}, \\ \end{gathered} $Величины ${\mathbf{B}}_{i}^{s}(\tau )$ соответствуют возмущениям на различных комбинационных гармониках колебаний с волновыми векторами ${{{\mathbf{k}}}_{i}}$. Фазы комбинационных гармоник равны $\theta _{{i,mn}}^{s} = {\mathbf{k}}_{i}^{{(2)}} \cdot {{{\mathbf{a}}}_{{m,n}}} - s{{\omega }_{0}}t$, где $s = 0,2$ и волновые векторы ${\mathbf{k}}_{i}^{{(2)}}$ представляют собой различные суммы пар векторов ${{{\mathbf{k}}}_{i}} + {{{\mathbf{k}}}_{j}}$. Всего существует 19 таких векторов: нулевой вектор ${\mathbf{k}}_{0}^{{(2)}} = (0,0)$, 6 векторов ${{{\mathbf{k}}}_{i}}$, 6 векторов $2{{{\mathbf{k}}}_{i}}$ и 6 векторов $\sqrt 3 {{{\mathbf{k}}}_{i}}$, повернутых на угол $\pi {\text{/}}6$ (рис. 1). Эти комбинационные гармоники могут быть медленными с нулевой частотой ($s = 0$) или быстрыми с частотой $2{{\omega }_{0}}$ ($s = 2$).
Учитывая соотношение ${{\Omega }_{0}} = {{\Omega }_{{cr}}} + {{\varepsilon }^{2}}\delta $, подставим (6) в (3) и разложим уравнения движения по степеням ε. Первый порядок разложения по ε в силу (5) тождественно обращается в нуль.
Во втором порядке разложения по ε выделим сначала члены, пропорциональные ${{e}^{{ - i{{\omega }_{0}}t}}}$, и решим получившиеся уравнения относительно поправок ${{{\mathbf{P}}}_{i}}$. С учетом (5) получаем ${{P}_{{z,i}}} = 0$, а горизонтальные компоненты параллельны горизонтальным компонентам векторов поляризации ${{{\mathbf{p}}}_{i}}$
(7)
$\begin{gathered} {{P}_{{\alpha ,i}}} = {\text{sign}}({{u}_{{1,1}}})\beta \frac{{d{{A}_{i}}(\tau )}}{{d\tau }}{{p}_{{a,i}}}, \\ (\alpha = x,y,\quad i = 1 \ldots 6), \\ \end{gathered} $Уравнения для величин ${\mathbf{B}}_{i}^{s}(\tau )$ записываются в виде $[{{s}^{2}}\omega _{0}^{2}{\mathbf{I}} + {\mathbf{M}}({\mathbf{k}}_{i}^{{(2)}})] \cdot {\mathbf{B}}_{i}^{s}(\tau ) = {\mathbf{G}}_{i}^{s}$ (s = 0, 2, i = = 0...18), где ${\mathbf{M}}({\mathbf{k}})$ – матрица (4) при ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$, а правые части ${\mathbf{G}}_{i}^{s}$ представляют собой различные квадратичные комбинации амплитуд вида ${{A}_{i}}(\tau ){{A}_{j}}(\tau )$ для $s = 2$ и ${{A}_{i}}(\tau ){{A}_{j}}(\tau ){\kern 1pt} *$ для $s = 0$. Матрицы ${{s}^{2}}\omega _{0}^{2}{\mathbf{I}} + {\mathbf{M}}({\mathbf{k}}_{i}^{{(2)}})$ не вырождены, т.е. спектр колебаний кристалла является нераспадным и резонансные трехволновые процессы запрещены. Это обстоятельство позволяет получить явные выражения для величин ${\mathbf{B}}_{i}^{s}(\tau )$.
Для комбинационных возмущений с нулевым волновым вектором ${\mathbf{k}}_{0}^{{(2)}} = (0,0)$ горизонтальные компоненты векторов ${\mathbf{B}}_{0}^{s}(\tau )$ равны нулю, а вертикальные пропорциональны $B_{{z,0}}^{0}(\tau ) \sim {{\sum {\left| {{{A}_{i}}(\tau )} \right|} }^{2}}$, $B_{{z,0}}^{2}(\tau ) \sim {{A}_{1}}{{A}_{4}} + {{A}_{2}}{{A}_{5}} + {{A}_{3}}{{A}_{6}}$. При $i > 0$ горизонтальные компоненты смещений на второй пространственной гармонике ${\mathbf{B}}_{i}^{s}(\tau )$ параллельны векторам ${\mathbf{k}}_{i}^{{(2)}}$, а все вертикальные отличны от нуля.
В следующем порядке разложения по ε уравнения для поправок ${{{\mathbf{Q}}}_{i}}(\tau )$ имеют вид $[\omega _{0}^{2}{\mathbf{I}} + {\mathbf{M}}({{{\mathbf{k}}}_{i}})] \cdot $ $ \cdot \;{\mathbf{Q}}_{i}^{s}(\tau ) = {{{\mathbf{G}}}_{i}}$, где правые части ${{{\mathbf{G}}}_{i}}$ с учетом вычисленных возмущений ${{P}_{i}}(\tau )$ (7) и ${\mathbf{B}}_{i}^{s}(\tau )$ представляют собой различные комбинации ${{A}_{i}}{{A}_{j}}A_{k}^{*}$ и ${{d}^{2}}{{A}_{i}}{\text{/}}d{{\tau }^{2}}$. Поскольку матрицы $\omega _{0}^{2}{\mathbf{I}} + {\mathbf{M}}({{{\mathbf{k}}}_{i}})$ при ${{\Omega }_{0}} = {{\Omega }_{{cr}}}$ в силу соотношений (5) вырождены, решение для поправок третьего порядка ${{{\mathbf{Q}}}_{i}}(\tau )$ существует лишь при условии ${{{\mathbf{p}}}_{i}} \cdot {{{\mathbf{G}}}_{i}} = 0$, где ${{{\mathbf{p}}}_{i}}$ – векторы поляризации основных гармоник. Наложение этого условия позволяет исключить секулярные члены разложения и получить уравнения для комплексных амплитуд ${{A}_{i}}(\tau )$. Сами по себе поправки ${{{\mathbf{Q}}}_{i}}(\tau )$ при выбранной точности описания нас не интересуют.
Для волны 1 уравнение, описывающее нелинейную динамику вблизи критической точки, имеет вид
(8)
$\begin{gathered} \, - {{A}_{1}}(\tau )\left[ {{{\delta }_{1}}{{{\left| {{{A}_{1}}(\tau )} \right|}}^{2}} + {{\delta }_{2}}({{{\left| {{{A}_{2}}(\tau )} \right|}}^{2}} + {{{\left| {{{A}_{6}}(\tau )} \right|}}^{2}}) + } \right. \\ \, + {{\delta }_{3}}({{\left| {{{A}_{3}}(\tau )} \right|}^{2}} + {{\left| {{{A}_{5}}(\tau )} \right|}^{2}}) + \left. {{{\delta }_{4}}{{{\left| {{{A}_{4}}(\tau )} \right|}}^{2}}} \right] - \\ \end{gathered} $Коэффициент γ в уравнениях (8) равен $\gamma = \delta {{\Omega }_{{cr}}}{\text{/}}(\beta {{\omega }_{0}})$ и его знак совпадает со знаком δ, т.е. в области устойчивости кристалла (${{\Omega }_{0}} > {{\Omega }_{{cr}}}$) $\gamma > 0$, а при развитии неустойчивости связанных волн $\gamma < 0$. Заметим, что простой перенормировкой масштабов этот коэффициент можно обратить в +1 или –1, поэтому на качественном уровне характер развития неустойчивости определяется соотношениями между пятью коэффициентами ${{\delta }_{i}}$. Явные аналитические выражения для этих коэффициентов слишком громоздки для того, чтобы быть опубликованными в каком-либо общепринятом формате. Однако величины ${{\delta }_{i}}$ в конечном итоге выражаются через производные потенциала взаимодействия (2) с $i + j \leqslant 4$ и могут быть рассчитаны численными методами.
Физический смысл уравнений (8) достаточно прозрачен. Во-первых, поскольку неустойчивость возникает в результате гибридизации двух волн, эти уравнения имеют второй порядок по времени. Линейный член в правой части, пропорциональный γ, описывает либо медленные биения двух волн при $\gamma > 0$, либо экспоненциальный рост амплитуды при $\gamma < 0$.
Нелинейные члены в уравнении (8) описывают все возможные резонансные четырехволновые процессы для набора из шести волн. Например, член, пропорциональный ${{\delta }_{1}}$, отвечает за самовоздействие (или нелинейный сдвиг частоты) возмущения с волновым вектором ${{{\mathbf{k}}}_{1}}$. Член, пропорциональный ${{\delta }_{2}}$, описывает параметрическое воздействие волн 2 и 6 на волну 1 и так далее. Последний член в (8) отвечает возбуждению волны 1 при слиянии волн 2, 4, 5 или 3, 4, 6. При этом выполняются соответствующие резонансные условия, например, ${{{\mathbf{k}}}_{2}} + {{{\mathbf{k}}}_{5}} - {{{\mathbf{k}}}_{4}} = {{{\mathbf{k}}}_{1}}$, ${{\omega }_{0}} + {{\omega }_{0}} - {{\omega }_{0}} = {{\omega }_{0}}$.
Как уже отмечалось, при $M > 1$ потеря устойчивости происходит для другого набора из шести волн, который отличается от изображенного на рис. 1 поворотом на угол $\pi {\text{/}}6$. Для этого случая были проведены аналогичные вычисления. Окончательные укороченные уравнения, разумеется, также имеют вид (8), однако явные выражения для коэффициентов ${{\delta }_{i}}$ отличаются от случая $M < 1$.
Заметим, что комбинационные возмущения $B_{{z,0}}^{0}(\tau )$ и $B_{{z,0}}^{2}(\tau )$ описывают медленное и быстрое (на частоте $2{{\omega }_{0}}$) вертикальные смещения кристалла как целого. Однако, так же как и в случае линейной цепочки пылевых частиц [12], обратного влияния на динамику основных гармоник эти движения не оказывают.
5. ЭФФЕКТИВНЫЙ ПОТЕНЦИАЛ
Для дальнейшего анализа удобно переписать (8) в виде уравнений движения частицы единичной массы в комплексном шестимерном пространстве
(9)
$\frac{{{{d}^{2}}{{A}_{i}}(\tau )}}{{d{{\tau }^{2}}}} = - \frac{{\partial U({{A}_{i}})}}{{\partial A_{i}^{*}(\tau )}} - \mu {\kern 1pt} '\frac{{d{{A}_{1}}(\tau )}}{{d\tau }},\quad (i = 1 \ldots 6),$(11)
$\begin{gathered} {{U}_{4}}({{A}_{i}}) = \sum\limits_{i = 1}^6 \,\left[ {\frac{{{{\delta }_{1}}}}{2}{{{\left| {{{A}_{i}}} \right|}}^{4}} + {{\delta }_{2}}{{{\left| {{{A}_{i}}} \right|}}^{2}}{{{\left| {{{A}_{{i + 1}}}} \right|}}^{2}} + } \right. \\ \, + \left. {{{\delta }_{3}}{{{\left| {{{A}_{i}}} \right|}}^{2}}{{{\left| {{{A}_{{i + 2}}}} \right|}}^{2}} + \frac{{{{\delta }_{4}}}}{2}{{{\left| {{{A}_{i}}} \right|}}^{2}}{{{\left| {{{A}_{{i + 3}}}} \right|}}^{2}}} \right] + \\ \, + 2{{\delta }_{5}}{\text{Re}}\left[ {{{A}_{1}}{{A}_{4}}A_{3}^{*}A_{6}^{*} + {{A}_{1}}{{A}_{4}}A_{2}^{*}A_{5}^{*} + {{A}_{2}}{{A}_{5}}A_{3}^{*}A_{6}^{*}} \right], \\ \end{gathered} $Бесконечно малый член $ - \mu {\kern 1pt} 'd{{A}_{i}}(\tau ){\text{/}}d\tau $ в правой части укороченных уравнений (9) указывает, что в процессе эволюции амплитуды параметрически связанных волн стремятся к стационарным решениям (9), соответствующим минимумам эффективной потенциальной энергии $U({{A}_{i}})$.
Заметим, что система (9) обладает очевидным свойством симметрии, унаследованным от симметрии исходной решетки. Если существует какое-то стационарное решение $A_{i}^{0}$, то стационарными будут также решения, получающиеся циклической перестановкой амплитуд $A_{i}^{0}$. В дальнейшем все подобные решения мы будем считать эквивалентными.
Поскольку нас интересует развитие неустойчивости, коэффициент $\gamma < 0$ в (8), (10). В точке ${{A}_{i}} = 0$ расположен локальный максимум потенциала $U({{A}_{i}})$. Если коэффициенты ${{\delta }_{i}}$ таковы, что член четвертого порядка (11) положителен для любых амплитуд ${{A}_{i}}$, то обязательно должны существовать глобальные минимумы потенциала $U({{A}_{i}})$. В этом случае неустойчивость связанных волн насыщается на слабонелинейной стадии и по порядку величины ${{A}_{i}} \sim \sqrt {\left| \gamma \right|} $.
Если же функция ${{U}_{4}}$ может менять знак, то существует путь, по которому решение уравнений (9) может уходить на бесконечность за конечное время, и в этом случае мы имеем дело со взрывным характером развития неустойчивости. В этом случае решение быстро выходит за пределы применимости использованного здесь приближения. Это, в частности, происходит, если в (11) коэффициент ${{\delta }_{1}} < 0$. (Например, ${{U}_{4}} < 0$ если ${{A}_{1}} \ne 0$, ${{A}_{{2 \ldots 6}}} = 0$.) Иными словами, неравенство ${{\delta }_{1}} > 0$ представляет собой необходимое, но, вообще говоря, не достаточное условие насыщения неустойчивости на слабонелинейной стадии. Однако отсутствие знакоопределенности ${{U}_{4}}$ не исключает возможности существования локальных минимумов $U({{A}_{i}})$, которые соответствуют метастабильным стационарным решениям (9).
Таким образом, возникают две проблемы. Во-первых, нужно найти критерий положительной определенности величины (11). Это позволит определить ограничения на коэффициенты ${{\delta }_{i}}$ и в конечном итоге очертить в пространстве внешних параметров a, M область, в которой неустойчивость насыщается на слабонелинейной стадии. Во-вторых, нужно найти стационарные решения уравнений (9) и исследовать их устойчивость, т.е. выяснить характер критических точек потенциала $U({{A}_{i}})$.
Решение поставленных проблем немного облегчается введением модулей и фаз комплексных амплитуд ${{A}_{i}} = {{R}_{i}}{{e}^{{i{{\phi }_{i}}}}}$. От фаз зависит только последний член в (11), пропорциональный ${{\delta }_{5}}$, причем они входят только в двух комбинациях. Например, можно положить ${{\chi }_{1}} = {{\phi }_{1}} + {{\phi }_{4}} - {{\phi }_{2}} - {{\phi }_{5}}$, ${{\chi }_{2}} = {{\phi }_{1}} + {{\phi }_{4}} - {{\phi }_{3}} - {{\phi }_{6}}$, тогда (11) переписывается как
(12)
$\begin{gathered} {{U}_{4}} = \sum\limits_{i = 1}^6 \,\left[ {\frac{{{{\delta }_{1}}}}{2}R_{i}^{4} + {{\delta }_{2}}R_{i}^{2}R_{{i + 1}}^{2} + {{\delta }_{3}}R_{i}^{2}R_{{i + 2}}^{2} + \frac{{{{\delta }_{4}}}}{2}R_{i}^{2}R_{{i + 3}}^{2}} \right] + \\ \, + 2{{\delta }_{5}}[{{R}_{1}}{{R}_{2}}{{R}_{4}}{{R}_{5}}cos{{\chi }_{1}} + {{R}_{1}}{{R}_{3}}{{R}_{4}}{{R}_{6}}cos{{\chi }_{2}} + \\ \, + {{R}_{2}}{{R}_{3}}{{R}_{5}}{{R}_{6}}cos({{\chi }_{1}} - {{\chi }_{2}})]. \\ \end{gathered} $Таким образом, в (10), (11) четыре фазы можно выбрать произвольно, т.е. в общем случае каждому стационарному решению соответствует четырехмерное многообразие.
В заключение этого раздела следует обсудить вопрос об интегралах движения уравнений (9). Очевидно, что при $\mu {\kern 1pt} ' = 0$ величина $E = $ $ = \sum\nolimits_i \,{{\left| {{{{\dot {A}}}_{i}}} \right|}^{2}} + U({{A}_{i}})$ является интегралом движения и играет роль энергии, а система (9) может быть записана в виде уравнений Гамильтона. Однако для общих исходных уравнений (3) при $\mu = 0$ с невзаимными силами интегралы движения, аналогичные энергии, не известны.
Также, как и в случае линейной цепочки пылевых частиц [12], причина кажущегося противоречия заключается в том, что линеаризованные уравнения движения могут быть записаны в форме уравнений Гамильтона. Это делается при помощи простой замены переменных, приведенной в [10], однако для случая планарного кристалла получающиеся выражения слишком громоздки. При малых отклонениях от равновесия уравнения (3) близки к гамильтоновым, и использованное здесь асимптотическое разложение по степеням амплитуд сохраняет соответствующую структуру.
6. СТАЦИОНАРНЫЕ РЕШЕНИЯ
Для иллюстрации того, что может происходить при изменении коэффициентов нелинейности, рассмотрим несколько простых стационарных решений уравнений (9).
6.1. Одна волна
Предположим, что только одна из амплитуд отлична от нуля. Пусть, например, ${{A}_{1}} \ne 0$ и ${{A}_{{2 \ldots 6}}} = 0$, тогда единственное стационарное решение (9) существует при ${{\delta }_{1}} > 0$ и равно $A_{1}^{0} = \sqrt {\left| \gamma \right|{\text{/}}{{\delta }_{1}}} $. Соответствующее значение полного потенциала при этом равно $min(U) = {{U}_{{min,1}}} = - {{\gamma }^{2}}{\text{/}}(2{{\delta }_{1}})$.
Положим ${{A}_{1}} = A_{1}^{0} + \delta {{A}_{1}}$, ${{A}_{i}} = \delta {{A}_{i}}$ ($i = 2 \ldots 6$) и линеаризуем уравнения (9) по малым отклонениям $\delta {{A}_{i}}$. В результате получаем набор собственных частот ν, позволяющих определить устойчивость решения в виде одной волны.
В спектре колебаний присутствует одна мода с нулевой частотой $\nu = 0$, соответствующая умножению амплитуды $A_{1}^{0}$ на произвольный фазовый множитель. В силу отмеченного выше произвола в выборе некоторых фаз колебаний, подобные нейтрально устойчивые моды всегда существуют. Другая устойчивая мода имеет частоту ${{\nu }^{2}} = 2\left| \gamma \right|$ и соответствует колебаниям амплитуды волны, т.е. $\delta {{A}_{1}} \ne 0$ и $\delta {{A}_{{2 \ldots 6}}} = 0$. Остальные частоты и поляризации колебаний имеют вид
(13)
$\begin{gathered} {{\nu }^{2}} = \left| \gamma \right|\frac{{{{\delta }_{2}} - {{\delta }_{1}}}}{{{{\delta }_{1}}}},\quad \delta {{A}_{2}} \ne 0\;\; \vee \;\;\delta {{A}_{6}} \ne 0, \\ {{\nu }^{2}} = \left| \gamma \right|\frac{{{{\delta }_{3}} - {{\delta }_{1}}}}{{{{\delta }_{1}}}},\quad \delta {{A}_{3}} \ne 0\;\; \vee \;\;\delta {{A}_{5}} \ne 0, \\ {{\nu }^{2}} = \left| \gamma \right|\frac{{{{\delta }_{4}} - {{\delta }_{1}}}}{{{{\delta }_{1}}}},\quad \delta {{A}_{4}} \ne 0. \\ \end{gathered} $Таким образом, условия существования и устойчивости одной нелинейной волны следуют из положительности квадратов частот (13) и записываются как
При нарушении одного из неравенств (14) волна неустойчива относительно возбуждения некоторых других волн. Например, если ${{\delta }_{3}} < {{\delta }_{1}}$, то происходит параметрическое возбуждение волн 3 и 5, если ${{\delta }_{4}} < {{\delta }_{1}}$, то возбуждается волна 4, распространяющаяся в противоположном направлении (см. рис. 1).
6.2. Две встречные волны
Если ${{A}_{1}} = {{A}_{4}} \ne 0$, а остальные амплитуды равны нулю ${{A}_{{2,3,5,6}}} = 0$, то стационарное решение уравнений (9) существует при ${{\delta }_{1}} + {{\delta }_{4}} > 0$ и равно ${{\left| {A_{1}^{0}} \right|}^{2}} = {{\left| {A_{4}^{0}} \right|}^{2}} = \left| \gamma \right|{\text{/}}({{\delta }_{1}} + {{\delta }_{4}})$. Линеаризуя уравнения (9) в окрестности стационарного решения, можно получить полный спектр колебаний, аналогичный (13).
Представляет интерес одно из колебаний с частотой ${{\nu }^{2}} = 2\left| \gamma \right|({{\delta }_{1}} - {{\delta }_{4}}){\text{/}}({{\delta }_{1}} + {{\delta }_{4}})$, при этом $\delta {{A}_{1}} = $ $ = - \delta {{A}_{4}}$. Если ${{\delta }_{4}} > {{\delta }_{1}}$, то в соответствии с критерием (14) одна волна устойчива, а в комбинации со встречной волной – нет. При этом эффективный потенциал равен
6.3. Три волны
Еще одно симметричное решение возникает, когда отличны от нуля амплитуды трех волн, распространяющихся под углом $2\pi {\text{/}}3$ друг к другу. Для существования подобного решения необходимо, чтобы ${{\delta }_{1}} + 2{{\delta }_{3}} > 0$, при этом, например, ${{\left| {A_{1}^{0}} \right|}^{2}} = {{\left| {A_{3}^{0}} \right|}^{2}} = {{\left| {A_{5}^{0}} \right|}^{2}} = \left| \gamma \right|{\text{/}}({{\delta }_{1}} + 2{{\delta }_{3}})$, ${{A}_{{2,5,6}}} = 0$, а фазы волн произвольны. Минимум эффективного потенциала для суперпозиции трех волн равен $min(U) = {{U}_{{min,3}}} = - 3{{\gamma }^{2}}{\text{/}}(2{{\delta }_{1}} + 4{{\delta }_{3}})$.
При линеаризации уравнений (9) в окрестности подобного стационарного решения возникает, в частности, колебание с частотой ${{\nu }^{2}} = 2\left| \gamma \right|({{\delta }_{1}} - {{\delta }_{3}}){\text{/}}({{\delta }_{1}} + 2{{\delta }_{3}})$ ($\delta {{A}_{1}} = - \delta {{A}_{3}}$ или $\delta {{A}_{1}} = $ $ = - \delta {{A}_{5}}$). При $0 < {{\delta }_{1}} < {{\delta }_{3}}$ минимум потенциала приходится на одну волну с $min(U) = {{U}_{{min,1}}}$, а при $0 < {{\delta }_{3}} < {{\delta }_{1}}$ (13) она теряет устойчивость и становится выгодной конфигурация из трех волн с $min(U) = {{U}_{{min,3}}}$.
7. ЧИСЛЕННЫЙ АНАЛИЗ
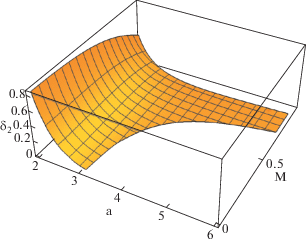
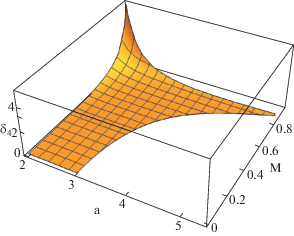
Коэффициенты нелинейности, входящие в уравнения (9), рассчитывались в области параметров $2 \leqslant a \leqslant 6$, $0 \leqslant M \leqslant 2$ на сетке с шагом $\Delta a = 0.01$ $\Delta M = 0.01$. Метод вычисления производных потенциала (1), (2) описан в работе [12]. Зависимости коэффициентов ${{\delta }_{i}}$ от a и M показаны на рис. 2–6, где вырезаны области параметров, соответствующие апериодическим неустойчивостям. Заметим, что только один коэффициент ${{\delta }_{1}}$ меняет знак при $M < 1$, а остальные коэффициенты всегда положительны. Для сверхзвукового потока ($M > 1$) коэффициент ${{\delta }_{1}} < 0$ всегда отрицателен, то есть в этом случае неустойчивость связанных волн носит взрывной характер.
Рис. 2.
Зависимость коэффициента ${{\delta }_{1}}$ от a и M. Сплошной кривой показана линия уровня ${{\delta }_{1}} = 0$.

7.1. Критерий глобальной устойчивости
Как уже отмечалось, условие положительности величины ${{U}_{4}} > 0$ (11), (12) для любых значений амплитуд гарантирует существование глобального минимума эффективной потенциальной энергии и насыщения неустойчивости связанных волн на слабонелинейной стадии.
В численных расчетах вопрос о положительности ${{U}_{4}}$ выяснялся следующим образом. Для глобальной устойчивости нужно, чтобы ${{U}_{4}} > 0$ для любых ${{R}_{i}}$, ${{\chi }_{i}}$. Поскольку ${{U}_{4}}$ (12) – однородная функция амплитуд ${{R}_{i}}$, достаточно вычислить ее минимум при условии $\sum R_{i}^{2} = 1$. Если полученная величина положительна, то ${{U}_{4}} > 0$ для любых ${{R}_{i}}$.
В явном виде это удобно сделать, вводя гиперсферические координаты $R,{{\alpha }_{i}}$ ($i = 1 \ldots 5$) в пространстве ${{R}_{1}} \ldots {{R}_{6}}$. Функция (12) тогда записывается в виде ${{U}_{4}} = {{R}^{4}}\tilde {U}({{\alpha }_{i}},{{\chi }_{i}})$. Если $min\tilde {U} > 0$, то неустойчивость связанных волн насыщается на слабонелинейной стадии, в противном случае неустойчивость носит взрывной характер. Заметим, что, поскольку могут существовать локальные минимумы эффективного потенциала, определение знака $min\tilde {U}$ не освобождает нас от необходимости поиска всех стационарных решений (9).
7.2. Стационарные состояния
Стационарные решения уравнений (9) искались численно в каждой точке сетки в пространстве параметров a, M. При этом учитывался отмеченный произвол в выборе фаз колебаний, то есть произвольные четыре амплитуды ${{A}_{i}}$ считались действительными, а остальные две – комплексными. Полное число полученных стационарных решений для каждой точки a, M оказывается довольно большим и в некоторых случаях достигает нескольких сотен. Далее выбирались неэквивалентные решения и вычислялись собственные частоты уравнений, линеаризованных в окрестности стационарной точки. Это позволяло определить устойчивость полученного решения.
Результаты расчетов приведены на рис. 7, где на плоскости параметров a, M изображены области с различным характером поведения неустойчивости на нелинейной стадии. Через ${{A}_{{1,2}}}$ на рисунке обозначены области, в которых развиваются различные апериодические неустойчивости [11], и где исследовать неустойчивость связанных волн не имеет смысла.
Рис. 7.
Области с различным поведением неустойчивости связанных волн. В области 1 устойчива одна нелинейная волна, в области 2 – три нелинейных волны. В областях ${{A}_{{1,2}}}$ развиваются различные апериодические неустойчивости. Штриховая линия задается условием ${{\delta }_{1}} = 0$.
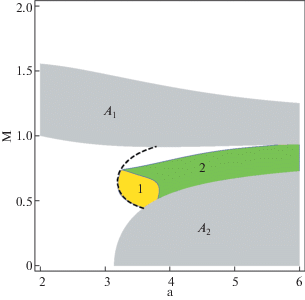
В области 1 реализуется конфигурация, описанная в разделе 6.1, в которой устойчива лишь одна волна, распространяющаяся вдоль одного из векторов ${{{\mathbf{k}}}_{i}}$ (рис. 1). Границы области 1 определяются кривыми ${{\delta }_{1}} = 0$ и ${{\delta }_{1}} = {{\delta }_{3}}$.
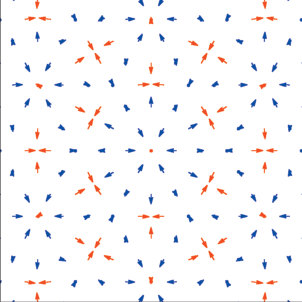
В области 2 на рис. 7 устойчивы три волны с одинаковыми амплитудами, распространяющиеся под углом $2\pi {\text{/}}3$ друг к другу (разд. 6.3). Фазы волн ${{\phi }_{i}}$ при этом произвольны. Характерный пример горизонтальных смещений частиц кристалла при ${{\phi }_{i}} = 0$ показан на рис. 8. Поскольку направления смещений зависят от фаз волн, они в достаточной степени произвольны. Однако для любого выбора фаз получающийся узор симметричен относительно поворота на угол $2\pi {\text{/}}3$.
Рис. 8.
(Цветной онлайн) Горизонтальные смещения частиц для суперпозиции трех нелинейных волн (область 2 на рис. 7). Синими стрелками показаны смещения с ${{z}_{{m,n}}} < 0$, красными – с ${{z}_{{m,n}}} > 0$ ($a = 5$, $M = 0.8$).
Вне областей 1, 2 на рис. 7 функция ${{U}_{4}}$ (11), (12) не является знакоопределенной, и неустойчивость связанных волн носит взрывной характер. Локальных минимумов эффективного потенциала в исследованной области параметров обнаружено не было. Все найденные критические точки эффективного потенциала являются либо максимумами, либо седловыми точками.
8. ЗАКЛЮЧЕНИЕ
Общая картина развития неустойчивости связанных волн двумерного плазменного кристалла выглядит следующим образом. При достижении жесткости внешнего удерживающего потенциала ${{\Omega }_{0}}$ определенного критического значения ${{\Omega }_{{cr}}}$ теряют устойчивость одновременно шесть волн, распространяющихся под углом $\pi {\text{/}}3$ друг к другу. Нелинейное взаимодействие этих волн между собой приводит к одному из трех вариантов развития неустойчивости. В большинстве случаев нелинейность приводит к ускорению неустойчивости, которая приобретает взрывной характер.
Однако в пространстве внешних параметров a и M есть две области, в которых неустойчивость насыщается на слабонелинейной стадии. При наличии малой диссипации в области 1 на рис. 7 параметрическое взаимодействие приводит к тому, что выживает лишь одна из шести волн. Исходная пространственная симметрия кристалла при этом понижается с ${{C}_{6}}$ до ${{C}_{1}}$. В области 2 на рис. 7 устойчивой оказывается комбинация из трех волн, распространяющихся под углом $2\pi {\text{/}}3$ друг к другу. Пространственная симметрия при этом понижается с ${{C}_{6}}$ до ${{C}_{3}}$. В обоих случаях частицы кристалла осциллируют с определенной частотой и амплитудой, пропорциональной $\sqrt {{{\Omega }_{{cr}}} - {{\Omega }_{0}}} $.
Формирующиеся при этом структуры обладают всеми чертами временнóго кристалла. При достижении частоты ${{\Omega }_{0}}$ критического значения происходит спонтанное нарушение трансляционной симметрии времени, при этом одновременно нарушается дискретная пространственная симметрия. Заметим, что, в отличие от других известных примеров [7, 8], переход плазменного кристалла в состояние временнóго кристалла происходит в результате постоянной во времени внешней накачки энергией.
Список литературы
Комплексная и пылевая плазма / Ред. Фортов В.Е., Морфилл Г.Е. М.: Физматлит, 2012.
Tsytovich V.N., Morfill G.E., Vladimirov S.V., Tho-mas H.M. Elementary Physics of Complex Plasmas. Lect. Notes Phys. 731. Belin, Heidelberg: Springer, 2008.
Vladimirov S.V., Ostrikov K., Samarian A.A. Physics and Applications of Complex Plasmas. Imperial College Press, 2005.
Кедель Л., Носенко В., Жданов С., Ивлев А.В., Лаут И., Яковлев Е.В., Крючков Н.П., Овчаров П.В., Липаев А.М., Юрченко С.О. // УФН. 2019. Т. 189. С. 1070.
Wilczek F. // Phys. Rev. Lett. 2012. V. 109. P.160401.
Shapere A., Wilczek F. // Phys. Rev. Lett. 2012. V. 109. P.160402.
Sacha K., Zakrzewski J.// Rep. Prog. Phys. 2018. V. 81. P. 016401.
Yao N.Y., Nayak C., Balents L., Zaletel M.P. // Nat. Phys. 2020. V. 16. P. 438.
Игнатов А.М. // Физика плазмы. 2019. Т. 45. С. 825.
Игнатов А.М. // Физика плазмы. 2020. Т. 46. С. 213.
Игнатов А.М. // Физика плазмы. 2020. Т. 46. С. 358.
Игнатов А.М. // Физика плазмы. 2020. Т. 46. С. 847.
Дополнительные материалы отсутствуют.