Физика плазмы, 2021, T. 47, № 3, стр. 195-219

1. ПРЕДСТАВЛЕНИЕ ПОЛЯ В ВИДЕ СОБСТВЕННЫХ ФУНКЦИЙ ВНУТРИ И ВНЕ ПЛАЗМЫ

Известно, что в плазме малого размера возможны два типа резонанса – уже упоминавшийся ранее резонанс напряжений – геометрический плазма–слой пространственного заряда [32, 33] и резонанс токов, наблюдающийся, если действительная часть диэлектрической проницаемости обращается в ноль. В разряде большой площади, когда основная доля энергии передается поверхностной волне, расчеты предполагают, что высшие моды не оказывают существенного влияния на импеданс разряда в целом. Тем не менее в феноменологической модели, предложенной в [31], показано, что для корректного расчета импеданса существенны как поверхностные волны, так и высшие моды.

В данном разделе на примере разряда, сосредоточенного в конечной области пространства r < R, мы продемонстрируем расчет распределения поля и импеданса разряда. Геометрия разрядной камеры, для которой проводится расчет приведена на рис. 1. Мы покажем, что импеданс разряда определяется взаимодействием токов, вызванных тремя типами полей: полем поверхностной волны, полем нераспространяющихся мод в плазме и полем нераспространяющихся мод, сосредоточенным вне плазмы. В общем случае резонанс обусловливается компенсацией напряжений и токов, вносимых всеми типами полей. Однако в некоторых случаях отдельные типы полей могут не оказывать никакого влияния при определенных параметрах плазмы. Например, геометрический резонанс и резонанс токов, аналогичные наблюдаемым в разряде малого размера, вызваны взаимодействием поля поверхностной волны и поля высших мод плазменного столба (в первую очередь полем первой высшей моды). Компенсация импедансов высших мод плазменного столба и высших волноводных мод реально представляет собой резонанс поля поверхностной волны, распространяющейся вдоль внешней границы плазмы, легко наблюдаемый в СВЧ-плазме в волноводе [34, 35]. Конечно, резонансные частоты будут сдвинуты за счет наличия слоев пространственного заряда у электродов. Разумеется, на наблюдаемые резонансы будут оказывать влияние и параметры внешней цепи [36]. В данной работе мы ограничимся рассмотрением разряда с одинаковыми слоями пространственного заряда. Рассмотрен случай, когда размер плазмы меньше размера электродов. В этом случае возбуждение высших типов волн обусловлено осевой неоднородностью плазмы, но не связано с электродинамическими эффектами у границ электрода.

Рис. 1.

Типичная схема экспериментальной установки 1, 2 – электроды, 3 – плазма, 4 – слои пространственного заряда между плазмой и стенкой (электродами), 5 – разрядная камера, 6 – граница расчетной области, через которую идет возбуждение электромагнитного поля; 2L – межэлектродное расстояние, d₁, d₂ – толщины слоев пространственного заряда.

Поле внутри плазмы может быть представлено в виде суммы собственных волн трехслойной структуры (ТС) металл–слой пространственного заряда–плазма–слой пространственного заряда–металл $\left\{ {{{{\mathbf{e}}}_{{n{\mathbf{ + }}}}}\left( z \right),{{{\mathbf{h}}}_{{n{\mathbf{ + }}}}}\left( z \right)} \right\}$ [8, 19, 37–39]. При записи (1), (2) и ниже под обозначениями ${{{\mathbf{h}}}_{{{\mathbf{0\varphi + }}}}}(z) = $ $ = \;\;{{{\mathbf{\varphi }}}_{{\mathbf{0}}}}{{h}_{{0\varphi + }}}(z)$ и ${{{\mathbf{e}}}_{{0z{\mathbf{ + }}}}}(z)\;\; = \;\;{{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{h}_{{0{\mathbf{\varphi + }}}}}(z){{{{{{h}_{{0 + }}}} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}} k}} \right. \kern-0em} k}} \mathord{\left/ {\vphantom {{{{{{h}_{{0 + }}}} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}} k}} \right. \kern-0em} k}} {\varepsilon (z)}}} \right. \kern-0em} {\varepsilon (z)}}$, ${{{\mathbf{e}}}_{{nz{\mathbf{ + }}}}}(z) = {{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{h}_{{n{\mathbf{\varphi + }}}}}(z){{{{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}} \mathord{\left/ {\vphantom {{{{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}} {\varepsilon (z)}}} \right. \kern-0em} {\varepsilon (z)}}$ мы понимаем зависящие только от z сомножители в представлении поля, приведенном в приложениях к работам [31, 40], $\rho = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} $ – волновое сопротивление вакуума, $k = {\omega \mathord{\left/ {\vphantom {\omega с}} \right. \kern-0em} с}$, ω – круговая частота электромагнитного поля, с – скорость света, r₀, φ₀, z₀ – единичные орты в направлениях r, φ, z. В плазме (|z|  <  L и r < R) $\varepsilon \left( z \right) = {{\varepsilon }_{P}} = 1 - {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {\left( {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)} \right)}}} \right. \kern-0em} {\left( {{{n}_{C}}\left( {1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} \right)} \right)}}$, ${{n}_{C}} = {{m{{\omega }^{2}}{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{m{{\omega }^{2}}{{\varepsilon }_{0}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}$ – критическая концентрация электронов, e, m – заряд и масса электрона, n_e и ν – плотность и эффективная частота столкновений электронов, вне плазмы $\varepsilon \left( z \right) = {{\varepsilon }_{1}} = 1$. Используя эти выражения, при r < R получим для z компоненты электрического поля E_z и азимутальной компоненты магнитного поля H_φ

Первое слагаемое в (2) описывает волну ТЕМ, приходящую из периферийной области (R₁ < r < < R₃) благодаря полю, генерируемому источником в области возбуждения (R₁ < r < R₂), второе – рассеянную трехслойной структурой TEM-волну, распространяющуюся в сторону периферийной области. Для этих волн ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}_{{0{\mathbf{ + }}z}}}\left( z \right) = \rho {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}_{{0{\mathbf{ + }}\varphi }}}\left( z \right)$. Сумма в уравнении (2) представляет собой сумму возбуждаемых высших мод поля, для которых ${{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}_{{nz{\mathbf{ + }}}}}(z) = {{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{n{\mathbf{\varphi + }}}}}(z){{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}} k}} \right. \kern-0em} k}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{n + }}} = \sqrt {{{{\left( {{{n\pi } \mathord{\left/ {\vphantom {{n\pi } L}} \right. \kern-0em} L}} \right)}}^{2}} - {{k}^{2}}} $. При этом мы предположили, что эти волны затухают в радиальном направлении достаточно быстро, поэтому их отражение от границ электродов и боковой стенки разрядной камеры пренебрежимо мало. Мы пока не учитываем высшие моды поля в области без плазмы, возбуждаемые на границе электрода. В соответствии с формулами для токов и напряжений, приведенными в [31], получим на внешней границе электродов r = R₁

При этом импеданс разряда при r = R₁ определяется формулой

Здесь и далее везде под напряжением электрода U мы понимаем напряжение между электродом и вакуумной камерой, поэтому разность потенциалов между электродами равна 2U. Соотношения (3) позволяют рассчитать электрическое и магнитное поле ТЕМ волн на границе плазмы (в точке r = R)

В дальнейшем удобнее использовать в расчетах именно параметры ${{H}^{{ext}}}\left( R \right)$ и ${{E}^{{ext}}}\left( R \right)$, вместо амплитуд цилиндрических волн ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{0}}$ и ${{A}^{{ext}}}$. Равенство тангенциальных компонент электромагнитного поля на боковой поверхности плазмы приводит к уравнению

При его решении можно считать заданной амплитуду магнитного поля ТЕМ-волн H^ext(kR), тогда амплитуда электрического поля E^ext(kR) должна быть определена из (6). Затем соотношения (5) дают возможность рассчитать коэффициенты A_TEM и A^ext, а соотношения (3), (4) – рассчитать импеданс разряда. Ограничиваясь в данной работе четными волнами, получим при r < R

На боковой границе плазмы (r = R) в силу (6) полученные значения совпадают. На большом расстоянии от границы поля высших волн затухают, поэтому в последнем выражении можно оставить только первое слагаемое. Резонанс токов соответствует обращению в нуль знаменателя данного выражения, а резонанс напряжений – числителя.

Необходимость расчета полей высших мод диктуется их участием в развитии локальных возмущений плотности электронов в областях резкого изменения формы металлических элементов установки – границ электродов, углов вакуумной камеры и т. п. Амплитуда этих возмущений плотности может быть сравнима и даже превышать среднюю плотность электронов в разряде. Поэтому мы должны по возможности точно описывать поля в этой области разряда, не ограничиваясь одной пространственной модой (например, поверхностной волной). Поэтому важно найти коэффициенты разложения поля в плазме по собственным функциям трехслойного волновода. Следует отметить, что как собственные функции в области, заполненной плазмой $\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}$, так и в области, свободной от плазмы $\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}$, представляют полную систему функций. И те, и другие могут быть использованы для представления поля границе плазмы. Для общности и удобства записи введем также системы собственных функций сопряженного к оператору Максвелла уравнения $\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}$ и $\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{n}^{ + },{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{n}^{ + }} \right\}$ [37].

Систему уравнений для коэффициентов A_n+, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{{n + }}}$ можно получить двояким образом: используя либо биортогональность систем собственных функций $\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}$ и $\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{n}^{ + },{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{n}^{ + }} \right\}$, либо собственных функций $\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}$ и $\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}$. Таким образом, уравнение (6) приводится к бесконечной системе матричных уравнений. Ее решение может быть проведено после оставления конечного числа слагаемых в разложениях поля (число оставленных собственных функций внутри и вне плазмы должно быть равным). Число уравнений в результате будет в два раза превышать число собственных функций.

При выборе большого числа собственных мод оба метода должны дать одинаковые результаты. Однако при этом могут сыграть свою роль ошибки округления при вычислении отдельных членов ряда, плохая обусловленность получаемой матрицы, а также громоздкость получаемой задачи.

2. РАЗЛОЖЕНИЕ ПОЛЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ПО СОБСТВЕННЫМ ВОЛНАМ ПУСТОГО ВОЛНОВОДА

Выберем функции из семейства $\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}$. Отметим, что осевые зависимости для этих функций полностью совпадают. Умножим каждое из уравнений для электрического поля на $\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{j + z}}^{ + }} \right\}$ и каждое из уравнений для магнитного поля на $\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + \varphi }}^{ + }} \right\}$ и проинтегрируем от 0 до L. Полученная система уравнений будет иметь вид

В данном случае ε_P – диэлектрическая проницаемость в центре плазменного столба (z = 0). Уравнения (7) записаны таким образом, чтобы при d → 0 третье и последующие уравнения переходили в уравнения для поверхностной волны, распространяющейся вдоль боковой поверхности. Выражения для коэффициентов ${{C}_{{Bnj + }}}$, ${{C}_{{Enj + }}}$ с учетом аналитических формул для полей [40] ввиду их громоздкости приведены в Приложении 1; квадраты норм волн в пустом волноводе рассчитываются по стандартным выражениям $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{2} = L$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{j + }}^{2} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$. Иногда нам также понадобится норма для собственной функции электрического поля $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{E} = \rho \sqrt L $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{j + }}^{E} = \rho {{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}\sqrt {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} $. Следует отметить, что коэффициенты ${{C}_{{E00 + }}}$ ${{C}_{{Ej0 + }}}$, ${{C}_{{E0n + }}}$ и ${{C}_{{Enj + }}}$ определены разными формулами. В системе (7) можно выделить первых два уравнения, которые позволяют рассчитать амплитуду поверхностной волны и электрическое поле ТЕМ-волн на границе разряда, как функцию магнитного поля. Остальные уравнения позволяют рассчитать амплитуды высших волн как функции амплитуды поверхностной волны. Из этих уравнений можно записать общие соотношения

Последнее выражение свидетельствует о том, что наличие высших мод может существенно повлиять на положение резонансов. Усредненное по высоте электрическое поле на границе плазмы в пустой части разрядной камеры приводит к выражению для импеданса

Таким образом в соответствии с общими соотношениями возбуждение высших мод поля приводит к изменению положения как резонансов тока (нули знаменателя), так и резонансов напряжения (нули числителя). В соответствии с общими формулами (2) мы видим, что амплитуды высших волн зависят как от напряжения основной моды (слагаемое содержащее ${{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)$), так и от ее тока (${{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)$). На первый взгляд, из (8) следует, что при изменении характеристик линии в среднем ее импеданс будет равен нулю, т.е. участки с емкостным и с индуктивным импедансом на оси плотностей электронов будут занимать примерно одинаковые области, так как все слагаемые тем или иным образом зависят от функций Бесселя. Поэтому интересно записать соотношение (8) таким образом, чтобы выделить отдельно составляющие, относительно слабо и сильно зависящие от соотношения между длиной радиальной поверхностной волны и радиусом плазмы (т.е. в конечном счете от плотности электронов):

Можно получить аналогичное выражение для проводимости разряда

Из (10) следует, что при возбуждении поверхностной волны в выражении для импеданса можно выделить два слагаемых. При фиксированной фазе тока первое слагаемое описывает импеданс, вносимый радиальными поверхностными волнами и высшими модами поля, возбуждение которых связано с напряжением на линии, т.е. фаза которых изменяется в соответствии с фазой напряжения. Второе слагаемое описывает возбуждение высших волн током, протекающим по линии, их фаза связана с фазой тока и это слагаемое вносит индуктивный импеданс. Аналогичный анализ может быть проведен для проводимости (10) с той разницей, что привязку по фазе лучше привести к напряжению.

3. РАЗЛОЖЕНИЕ ПОЛЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ПО СОБСТВЕННЫМ ФУНКЦИЯМ ТРЕХСЛОЙНОЙ ПЛАЗМЕННОЙ СТРУКТУРЫ

Теперь выберем функции из семейства $\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}$ и $\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}$. Условия ортогональности для этих функций рассмотрены в работе [40]. Там же рассчитаны квадраты нормы $N_{{j + }}^{2}$ для всех волн. Аналог системы уравнений (7) имеет вид

Выражения для коэффициентов $D_{{jn}}^{B}$, $D_{{jn}}^{E}$ также приведены в Приложении 1. При сравнении матриц уравнений (7) и (11) мы видим, что их элементы для электрического и магнитного полей меняются местами. Можно получить общие формулы амплитуд соответствующих мод и импедансов, повторяя действия предыдущего раздела статьи. Импеданс разряда и амплитуды различных мод определяются выражениями

Для амплитуды поверхностной волны, возбуждаемой в плазме, получим ${{A}_{{0 + }}}{{J}_{1}}\left( {{{h}_{ + }}R} \right)N_{{0 + }}^{2} = $ $ = {{H}^{{ext}}}\left( {kR} \right)D_{{00 + }}^{B} - \sum\limits_{n = 1}^K {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}_{{n + }}}} {{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)D_{{0n + }}^{B}$. Отметим, что при учете только одной моды обе формулы дают одинаковый результат для импеданса. Как мы уже говорили ранее, в общем случае система уравнений содержит бесконечное число уравнений. С учетом возможных ошибок при вычислении коэффициентов, численное решение этой системы уравнений, может оказаться более трудоемким, чем непосредственное решение уравнений Максвелла с помощью метода конечных элементов или разностных методов. Тем не менее указанная система оказывается очень удобной для классификации резонансных состояний, поскольку вблизи резонанса при качественном анализе число коэффициентов можно существенно сократить. Рассмотрим классификацию возможных резонансов.

4. УПРОЩЕННОЕ УРАВНЕНИЕ ДЛЯ ИМПЕДАНСА РАЗРЯДА

Формула (8) (или (12)) дает общее выражение для импеданса разряда. Однако для понимания результатов их необходимо упростить. Предположим, что влияние слоев пространственного заряда в уравнениях для высших мод в уравнениях (7) мало, поэтому осевые постоянные распространения для высших волн в плазме и вне плазмы близки. Тогда в (8) и (12) можно оставить только одно диагональное слагаемое. Матрицы S_ij и P_ij становятся диагональными, и решения, полученные в предыдущем параграфе, существенно упрощаются. Из (7) для элементов матрицы следует

Следует отметить, что справедливость данного приближения нуждается в дополнительном исследовании, которое оказывается очень громоздким и может быть темой отдельной статьи. В пользу этого приближения может сыграть тот факт, что вклады возмущений с меньшим волновым числом и с большим волновым числом будут иметь разные знаки и частично компенсировать друг друга. Тем не менее переход от общих формул разд. 3 к формулам данного раздела означает переход от количественного исследования к качественному. Используя выражения для различных компонент поля [31, 40], мы можем получить следующее выражение для импеданса разряда

Детали расчета и выражения для амплитуд волн см. в Приложениях 2 и 3. Аналогичное выражение для малых плотностей, когда поверхностная волна отсутствует, имеет вид

Проанализируем теперь различные типы резонансов, которые могут наблюдаться в разряде.

4.2. Резонансы радиальных поверхностных волн и геометрический резонанс плазма–слой пространственного заряда

Кроме резонансов связанных с возбуждением поверхностных волн у боковой поверхности, в разряде могут быть еще два типа резонансов. Все эти резонансы описываются нулями числителя (резонанс напряжений) или знаменателя (резонанс токов) в выражениях (8), (12), (13) или (14).

Во-первых, это резонансы, связанные с возбуждением радиальных поверхностных волн, математически описываются функциями Бесселя и связаны с их нулями.

Во-вторых, физически также это резонансы, связанные с глобальным распределением токов и напряжения в разряде, среди которых можно выделить резонанс токов, наблюдающийся при выполнении условия

$\operatorname{Re} {{\varepsilon }_{P}} = 0$

и резонанс напряжений, получивший в квазистатическом разряде название “геометрический резонанс плазмы и слоя” [32, 33]. В этом случае индуктивный импеданс, вносимый высшими модами, компенсируется импедансом короткой разомкнутой линии, который имеет емкостной характер. Этот резонанс наблюдается при высоких плотностях плазмы, когда ее радиус меньше длины поверхностной волны. Условие резонанса, при учете индуктивного импеданса, вносимого высшими типами мод (при плотностях электронов выше резонансной для боковой поверхностной волны), описывается соотношением

$\begin{gathered} \operatorname{Re} \frac{{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)}}{{R{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}\left( {\mathop {\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E00 + }}} - }\limits_{} } \right. \\ \, - \left. {\sum\limits_{j = 1}^K {\sum\limits_{i = 1}^K {{{S}_{{ji}}}{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}R} \right)\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E0i + }}}} } {{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)\frac{{{{{\tilde {h}}}_{{j + }}}}}{k}{{C}_{{Ej0 + }}}} \right) - \\ \, - \frac{1}{R}\sum\limits_{j = 1}^K {\sum\limits_{i = 1}^K {{{S}_{{ji}}}\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}}}{k}{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}R} \right){{C}_{{B0i + }}}} } {{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right)\frac{{{{{\tilde {h}}}_{{j + }}}}}{k}{{C}_{{Ej0 + }}} = 0. \\ \end{gathered} $

Используя приближенное выражение (13) получим

$\begin{gathered} \operatorname{Re} \left( {\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E00 + }}} - \sum\limits_{n = 1}^K {C_{{Bnn + }}^{{ - 1}}} \left( {\frac{{{{h}_{{0 + }}}}}{k}{{C}_{{E0n + }}}\frac{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}}{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)}} + } \right.} \right. \\ \,\left. {\left. { + \frac{{{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}{{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)}}{{C}_{{B0n + }}}\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}}}{k}} \right)\frac{{{{I}_{0}}\left( {{{{\tilde {h}}}_{{n + }}}R} \right)}}{{{{I}_{1}}\left( {{{{\tilde {h}}}_{{n + }}}R} \right)}}} \right) = 0. \\ \end{gathered} $

Для разряда малого размера ${{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} \mathord{\left/ {\vphantom {{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}} \right. \kern-0em} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}} = $ $ = {{\left( {{{{{h}_{{0 + }}}R} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}R} 2}} \right. \kern-0em} 2}} \right)}^{{ - 1}}}$. При уменьшении плотности электронов в точке геометрического резонанса происходит смена емкостного импеданса разряда на индуктивный. При дальнейшем уменьшении плотности электронов растет глубина проникновения высших волн в плазму и индуктивный импеданс, вносимый вторым слагаемым, увеличивается. Осцилляции первого слагаемого в последнем выражении приводят к всплескам амплитуды поглощения, связанным с возбуждением поверхностных волн, либо к появлению новых резонансов тока и напряжения, если поглощение поверхностных волн невелико и амплитуда отраженной от центра разряда волны мала. В противном случае, если реактивная часть импеданса, вносимая поверхностными волнами, будет превышать индуктивный импеданс основной моды, возможно не только появление дополнительных всплесков, но и новых резонансов тока и напряжения.

Результаты расчета импеданса по формуле (13) приведены на рис. 2 для различных радиусов плазмы 2, 5 10, 15 и 20 см при длине плазменного столба 8 см. Отношение эффективной частоты столкновений к частоте поля равно 0.1. Толщина слоев – 3 мм. При расчетах учитывалось возбуждение поверхностной волны и двух высших мод. Расчеты показывают, что в области возбуждения поверхностных волн разряд в целом имеет индуктивный импеданс, поскольку в силу большого поглощения поверхностных волн, вносимый ими импеданс почти везде чисто активный. При более высоких плотностях электронов сказывается отражение поверхностной волны от центра разряда, приводящее к всплескам поглощения на кривой импеданса. На рис. 2 эти всплески заметны при радиусах разряда 5 см и выше и отмечены тонкими вертикальными линиями и звездочкой. Заметность этих всплесков увеличивается с ростом плотности электронов, так как с одной стороны при этом уменьшается затухание поверхностной волны, а с другой стороны уменьшается индуктивный импеданс высших мод, на фоне которого он наблюдается.

Рис. 2.

Импеданс разряда (1 – Re Z, 2 – Im Z, Ом) (результаты аналитического расчета) для симметричного разряда при синфазном возбуждении; радиус плазмы R = 2 (a), 5 (б), 10 (в), 15 (г) и 20 (д) см; частота поля 135.6 МГц; толщина слоев d₁ = d₂ = 3 мм. Частота столкновений – 0.1 от частоты поля. В области, где отсутствует распространение поверхностных волн масштаб уменьшен в 20 раз (3 – Re Z/20, 4 – Im Z/20, Ом). Звездочкой и вертикальной линией обозначено положение резонансов, связанных с возбуждением поверхностных волн.

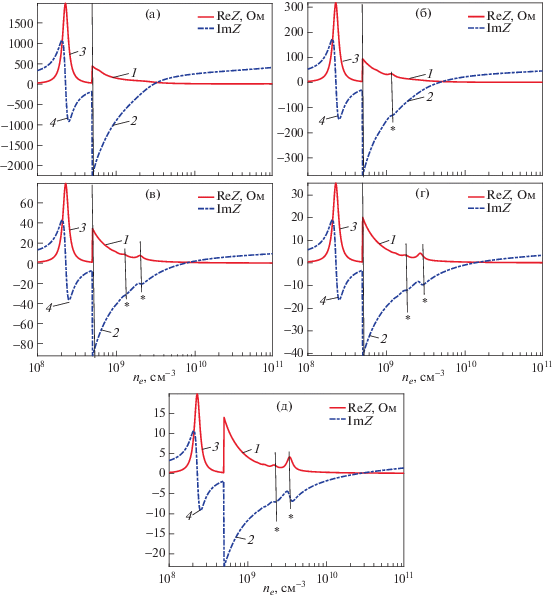
На всех графиках наблюдаются резонансы тока при плотности, равной критической, и геометрический резонанс, который при увеличении радиуса смещается в область больших плотностей электронов, что связано с уменьшением отношения ${{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} \mathord{\left/ {\vphantom {{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}} \right. \kern-0em} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}$.

5. ВЛИЯНИЕ ВНЕШНЕЙ ЧАСТИ РАЗРЯДНОЙ КАМЕРЫ НА ИМПЕДАНС РАЗРЯДА

Прежде чем перейти к сравнению результатов аналитических расчетов с численным решением уравнений Максвелла, исследуем влияние внешней части камеры на импеданс разряда в целом. В рассматриваемой геометрии разряда следует учесть влияние внешней части электродов, области возбуждения, периферийной части рабочей камеры и линии, соединяющей камеру с источником поля. Рассмотрим эти процессы последовательно.

5.2. Влияние импеданса внешней части рабочей камеры и высших мод поля, возбуждаемых вблизи точки подвода мощности

В предыдущем пункте изучена задача о влиянии дополнительной площади электродов вблизи разряда. Теперь мы исследуем влияние внешней части камеры (рис. 1). Расчет может быть проведен точно также, как и для разрядной камеры, полностью заполненной плазмой [40], с точностью до замены собственных волн трехслойной структуры собственными волнами внешнего волновода (Приложение 5)

(16)

$\begin{gathered} {{Z}_{{D2}}} = \left[ {{{{\left( {{{Z}_{{D1}}} - i\frac{L}{{2\pi {{R}_{1}}}}\rho \frac{{{{Q}_{0}}\left( {k{{R}_{1}}} \right)}}{{{{Q}_{1}}\left( {k{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}} - } \right. \\ {{\left. {\, - \frac{{2i}}{\rho }\sum\limits_{n = 1}^\infty {\frac{k}{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}}}{{{\left( {\frac{{{{I}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{I}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}} + \frac{{{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}{{{{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}{{R}_{1}}} \right)}}} \right)}}^{{ - 1}}}} } \right]}^{{ - 1}}}. \\ \end{gathered} $

Здесь ${{Z}_{{D1}}}$ определяется формулами разд. 5.1 или Приложения 4, $z = {{\rho L} \mathord{\left/ {\vphantom {{\rho L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}$. Эквивалентная схема для разряда в этих условиях геометрии приведена на рис. 3. Здесь Z₀ – импеданс плазмы (рассчитываемый по формулам разд. 2 с учетом высших мод), Line 1 – линия передачи энергии от плоскости возбуждения до границы разряда, образуемая внешней частью электродов. Обычно размер этой области мал по сравнению с длиной ВЧ-волны в вакууме, поэтому этот импеданс представляет собой емкость, подсоединенную параллельно разряду. Последовательно с этой линией включена замкнутая линия Line 3, образованная внешней пустой частью вакуумной камеры. Параллельно этой линии подключены сосредоточенные элементы, представляющие собой вклад полей высших волн пустого волновода, порождаемых в области возбуждения. Следует отметить, что в отличие от случая камеры, полностью заполненной плазмой, возбуждение высших мод в пустом волноводе вносит дополнительный емкостной импеданс, причем импедансы, вносимые высшими модами при r < R и r > R также в согласии с предыдущей формулой соединены последовательно. На схеме так же обозначены: Z_S – внутреннее сопротивление источника питания, U_S – его эдс, $Z_{e}^{j}$, $Z_{i}^{j}$ – импедансы, вносимые высшими модами, возбуждаемыми внутри и вне плазмы.

Рис. 3.

Эквивалентная схема разряда. Line 1 – разомкнутая длинная линия, описывающая поверхностную волну в области r < R₁, Line 3 – замкнутая линия в периферийной области, описывающая распространение волны TEM в области r > R₂, Z_ji, Z_je – сосредоточенные последовательно включенные импедансы, описывающие возбуждение высших мод поля во внутренней r < R и внешней r > R областях. Line 2 – линия, подводящая энергию от генератора, Z_S – внутреннее сопротивление генератора.

Из полученных формул следуют два очевидных вывода.

1. Возбуждение высших мод поля приводит к появлению дополнительных токов, сдвигающих положение резонансов тока.

2. Поле волны ТЕМ во внешней части камеры тоже может существенно повлиять на возбуждение поля в разряде. При этом импеданс внешней части камеры оказывается соединенным с импедансом внутренней части последовательно (для каждой волны). Это означает, что он не будет влиять на положение резонансов токов, но может существенно изменить значение плотностей электронов, на которых наблюдается резонанс напряжений. При малых размерах вносимый этой частью камеры импеданс будет индуктивным. При его большой величине геометрический резонанс плазма–слой может исчезнуть. С другой стороны, компенсация реактивной части импеданса центральной части может обеспечить резкое увеличение поля в центре разряда. А если в точке подвода энергии импеданс внешней части оказывается очень большим $H_{0}^{{ext}}\left( {{{R}_{3}}} \right) \to 0$ (четвертьволновый поршень), то амплитуда поля в области плазмы оказывается очень малой, и поддержание разряда в этих условиях может стать невозможным.

Результаты расчета импеданса с помощью аналитических формул приведены на рис. 4. Отношение емкости, подключенной параллельно разряду, к емкости разряда при малых токах уменьшается при увеличении радиуса разряда, поэтому смещение положения резонанса токов в сторону больших концентраций электронов максимально для разряда диаметром 2 см и монотонно уменьшается с увеличением его радиуса. В силу малости вносимой внешними частями индуктивности положение геометрического резонанса практически не меняется (см. рис. 2 и 4). Поэтому для разряда малого размера, плотности электронов, при которых наблюдается резонанс токов и при которых наблюдается резонанс напряжений достаточно близки. В остальных случаях эти плотности различаются в 3–10 раз.

Рис. 4.

Влияние импеданса, вносимого периферийной частью рабочей камеры на импеданс разряда (1 – Re Z, 2 – Im Z, Ом) (результаты аналитического расчета) для симметричного разряда при синфазном возбуждении. Радиус плазмы R = 2 (a), 5 (б), 10 (в), 15 (г) и 20 (д) см; частота поля 135.6 МГц; толщина слоев d₁ = d₂ = 3 мм. Частота столкновений – 0.1 от частоты поля.

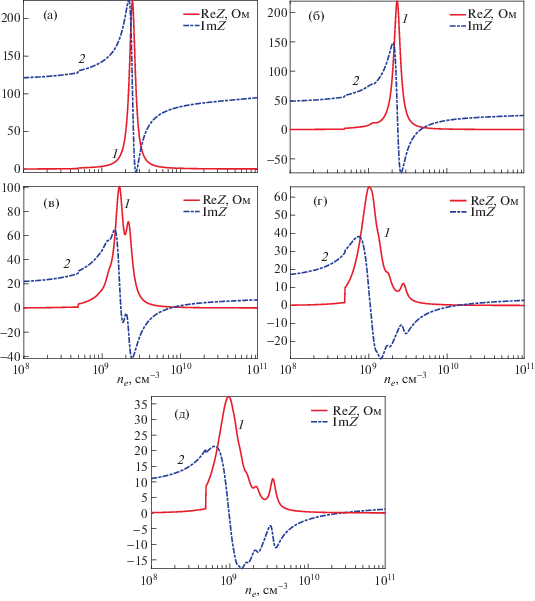
Резонанс токов, как и в случае разрядной камеры, полностью заполненной плазмой наблюдается при компенсации индуктивного тока через плазму и емкостного тока, протекающего через область, не заполненную плазмой. При плотностях ниже, чем плотность геометрического резонанса и выше резонанса токов, в среднем разряд имеет индуктивный импеданс. На фоне относительно слабо изменяющегося индуктивного импеданса заметны слабо выраженные резонансы, связанные с отражением поверхностной волны от центра разряда. Малое влияние этих резонансов обусловлено сильным поглощением поверхностной волны. При учете дополнительной емкости эти резонансы проявляются более ярко, чем на рис. 2, так как часть индуктивного импеданса, вносимого высшими модами, компенсируется емкостью внешней части камеры.

6. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАЗРЯДА С СИММЕТРИЧНЫМ ВОЗБУЖДЕНИЕМ

Аналитические результаты, полученные в предыдущих пунктах, сопоставлялись с численными расчетами, проводимыми с помощью математического пакета COMSOL Multiphysics^®. Также как в [40] уравнения Максвелла решались в области пространства, включающей центральную часть камеры (0 < r < R₃, –L < z < L) и межэлектродное пространство, (R₁ < r < R₂, –L < |z| < L + + L₂), рис. 1. На электродах и стенке вакуумной камеры ставились нулевые граничные условия для тангенциальной компоненты электрического поля. Рассматривался разряд с симметричным возбуждением, для которого ток I, втекающий через нижний электрод, равен току, вытекающему через верхний. На внешней границе 6 (R₁ < r < R₂, –|z| = L + L₂) азимутальное магнитное поле считалось заданным ${{H}_{\varphi }}\left( {r, \pm \left( {L + {{L}_{2}}} \right)} \right) = {I \mathord{\left/ {\vphantom {I {2\pi r}}} \right. \kern-0em} {2\pi r}}$.

Импеданс рассчитывался в нескольких точках. Во-первых, на границе разряда (r = R), в этом случае в соответствии с общими формулами статьи [31]

При этом предполагалось, что ток определяется усредненным по высоте значением магнитного поля (обсуждение различных вариантов связи тока электродов, с помощью которого рассчитывается импеданс, и пространственного распределения поля приведено в [31]).

Во-вторых, на границе 6 расчетной области, формулы для импеданса в данном случае совпадают с приведенными в [40]:

Распределение плотности электронов в плазме при расчетах было однородно, а диэлектрическая проницаемость была задана в модели холодной плазмы. Со стороны внешней стенки разряд ограничен диэлектриком с ε = 1.

Рис. 5.

Импеданс разряда (1 – Re Z, 2 – Im Z, Ом) (результаты численного моделирования) для симметричного разряда при синфазном возбуждении. Рисунок справа представляет собой те же кривые, что и на рисунках выше, но в большем масштабе. Параметры такие же, как и на рис. 4. Импеданс рассчитывался на внешней границе плазмы.

Рис. 6.

То же, что и на рис. 5. Исключено влияние внешней части камеры, так как R₃ = R₂, однако учитывается емкость подводящей линии.

Расчеты импеданса на границе разряда приведены на рис. 5 (1, r = R). Поскольку значения импеданса существенно падают при изменении плотности электронов на три порядка, кривые построены в двух масштабах (рисунки слева и справа), позволяющих показать поведение импеданса и при низких и при высоких плотностях плазмы. Сравнение с аналитическими расчетами (рис. 2) показывает их качественное согласие. При малых плотностях (менее 5–6 критических) результаты согласуются и количественно, однако с ростом плотности электронов рассогласование численной и аналитической кривых нарастает. Геометрический резонанс плазма–слой пространственного заряда в численных расчетах лежит при более низких значениях плотности электронов. Это рассогласование может быть связано с теми приближениями, которые делались при аналитическом расчете – использованием диагонального приближения в получаемой матрице и учетом только двух высших мод. Однако наличие всплесков импеданса (причем как в аналитических, так и в численных расчетах) свидетельствует о существенном изменении соотношения между амплитудами поля поверхностной волны и нераспространяющихся мод.

Расчеты импеданса на границе расчетной области проводились на расстоянии L₂ = 1 см (2, рис. 6) и L₂ = 10 см (3, в статье не приводятся) от границы разрядной камеры. Влияние периферийной части рабочей камеры при разности радиусов R₃–R₂ менее 5 см и частоте 135.6 МГц, как показали оценки и численные расчеты в COMSOL Multiphysics^® несущественно, так как индуктивность, вносимая внешней частью камеры, менее 0.01 мкГн. Емкости периферийной части электродов и внешней подводящей линии, напротив, существенно изменяют положение резонанса токов в сторону больших плотностей, положение геометрических резонансов плазма–слой практически не меняется (рис. 6). Резонансы, связанные с возбуждением поверхностных волн, при компенсации части индуктивного импеданса высших мод емкостью подводящей линии проявляются более ярко.

Поскольку в численном счете влияние резонансов, связанные с возбуждением стоячих поверхностных волн, на расчетных вольт-амперных кривых при отношении частоты столкновений электронов к частоте поля ν/ω = 0.1 проявлены слабо, были также проведены расчеты при ν/ω = = 0.01 (рис. 7), хотя для типичных ВЧ-разрядов данное значение частоты столкновений слишком мало. На рис. 7 явно выделен скачок импеданса (A), связанный с появлением бегущих радиальных поверхностных волн. Этот скачок наблюдается при плотности электронов немного меньше удвоенной критической, что может быть обусловлено влиянием слоя пространственного заряда. Однако для точного определения причины этого сдвига необходимо проведение дополнительных расчетов, в том числе прямого расчета дисперсии собственных волн трехслойной структуры с учетом столкновений, но без использования теории возмущений. Дальнейший рост плотности электронов приводит к появлению всплесков поглощения и осцилляций на кривой мнимой части импеданса, соответствующих возбуждению стоячих поверхностных волн. Значения плотностей электронов, при которых возбуждаются стоячие поверхностные волны у боковой поверхности, не изменяются при изменении радиуса разряда (B). В то же время резонансы, связанные с возбуждением радиальных стоячих поверхностных волн, при увеличении радиуса плазмы перемещаются в область более высоких плотностей электронов (C). Отдельно обозначен геометрический резонанс плазма–слой (D).

Рис. 7.

Импеданс разряда (1 – Re Z, 2 – Im Z, Ом) (результаты численного моделирования) для симметричного разряда при синфазном возбуждении. Все расчеты такие же, как на рис. 5, только частота столкновений – 0.01 от частоты поля.

Отметим, что изменение параметров внешней цепи очень сильно влияет на положение на оси концентраций электронов резонансов тока, которые можно назвать глобальными, так как компенсация напряжений и токов происходит в разряде в целом, и изменение этих токов и напряжений с изменением параметров плазмы происходит плавно. В то же время положение (но не амплитуда) внутренних резонансов (возбуждение поверхностных волн) определяется внутренними свойствами системы и слабо зависит от параметров внешней цепи. Амплитуда их может резко возрастать, если положение этого резонанса близко к положению глобального резонанса.

Следует отметить, что при расчете характеристик разряда в данной работе мы предполагали, что радиус электродов, превышает радиус плазмы, поэтому поверхностные волны и высшие типы мод возбуждались не полем источника непосредственно, а только после преобразования последнего в волну ТЕМ. Мы рассмотрим второй случай в одной из следующих работ, одновременно с аналитическими расчетами.

На рис. 8–10 приведены рассчитанные пространственные распределения напряженности магнитного поля в плазме. Поскольку в отличие от случая полностью заполненной разрядной камеры [40] зависимости импеданса от плотности электронов при всех радиусах плазмы (2, 5, 10, 15 и 20 см) качественно меняются слабо, в данной работе мы проведем сравнение распределений азимутального магнитного поля в разрядах разного радиуса с плотностями плазмы, соответствующим одинаковым характерным точкам на зависимости импеданса от плотности электронов. Поскольку во всех случаях внешняя часть разрядной кафедры имеет одинаковую конфигурацию, сравнение пространственного распределения полей позволит оценить влияние изменения размера плазмы на пространственное распределение поля. На рис. 8a, б, 9a, б, 10a, б, приведены распределения поля для разряда радиусом 2 см, 8в, г, 9в, г, 10в, г – 5 см, 8д, е, 9д, е, 10д, е – 10 см, 8ж, з, 9ж, з, 10ж, з – 15 см, 8и, к, 9и, к, 10и, к – 20 см. При повышении плотности электронов свыше двух критических в разряде малого радиуса наблюдаются резонансы, связанные с возбуждением стоячей поверхностной волны на боковой диэлектрической стенке разряда. При увеличении радиуса большую роль начинает играть возбуждение поверхностной волны, распространяющейся вдоль электрода. В силу того, что коэффициент поглощения этой волны существенно выше, чем у волны, распространяющейся вдоль боковой поверхности, ее наличие приводит к перераспределению протекающего тока в эту волну и поверхностная волна у боковой поверхности становится менее заметной.

Рис. 8.

Пространственное распределение магнитного поля при возбуждении поверхностной волны у боковой поверхности разряда при различных радиусах плазмы и рабочей камеры. Условия соответствуют рис. 2. Слева – действительная составляющая магнитного поля, справа – мнимая, А/м. Радиус плазмы 2 см (a, б), 5 см (в, г), 10 см (д, е), 15 см (ж, и), 20 см (и, к).

Рис. 9.

Распределение магнитного поля в плазме при плотности электронов, соответствующей резонансу токов разряда при различных радиусах плазмы и рабочей камеры. Условия соответствуют рис. 4, а распределение параметров рис. 8.

Рис. 10.

Распределение магнитного поля в плазме при плотности электронов, соответствующей резонансу напряжений при различных радиусах плазмы и рабочей камеры. Условия соответствуют рис. 3, а распределение параметров рис. 8.

Рисунок 9 соответствует резонансу токов. В этом случае ток по области вне плазмы компенсируется током по плазменному столбу. С увеличением радиуса плазмы плотность тока, протекающая через плазму, должна уменьшаться. В силу этого плотность электронов, соответствующая резонансу, падает. В основном в силу малой плотности плазмы и большой глубине проникновения поля высшей моды ток переносится высшими модами поля. Поскольку одновременно растет радиус разряда, то улучшаются условия возбуждения радиальной поверхностной волны, которую можно обнаружить на рис. 9д–е, однако амплитуда этой волны существенно меньше амплитуды поля высшей моды.

Наконец, рис. 10 содержит распределение поля, соответствующее геометрическому резонансу, плазма–слой пространственного заряда. В резонансной точке энергия, перекачиваемая в поверхностною волну и высшие моды поля примерно равны. Длина поверхностной волны при высоких плотностях электронов оказывается больше размеров системы, поэтому ее ток распределен по площади электрода равномерно. В то же время ток высших мод сосредоточен вблизи границы плазмы, т.е. протекает по меньшей площади. Поэтому амплитуда магнитного поля высших мод оказывается выше, хотя и не намного, амплитуды поля поверхностной волны. Таким образом, анализ пространственной структуры высокочастотного поля с помощью численных расчетов подтверждает качественную картину, полученную в аналитических расчетах.

Сравним полученные кривые импеданса с теми, которые были получены в предыдущей работе цикла ([40], рис. 2) для расчетов, выполненных при одинаковых радиусах плазмы. Во-первых, глобальный резонанс токов, вызванный резонансом тока через плазму и тока через дополнительную емкость внешней области камеры и емкость подводящей линии, в рассматриваемой в данной статье линии сдвинут в область больших плотностей электронов. Это отличие вполне согласуется с формулой (15) и связано с дополнительной емкостью, которую вносит не закрытая плазмой часть электродов.

Во-вторых, резонансы, связанные с возбуждением поверхностных волн, выражены слабее, чем для камеры, полностью заполненной плазмой. По-видимому, это отличие связано с конфигурацией поля источника, возбуждающего плазму. В работе [40] это поле сосредоточено в области вблизи электрода (в модели используется δ-образный источник). В этой области поле поверхностной волны максимально, а поле высших мод, наоборот имеет минимум. В данной работе и поверхностные волны и высшие типы волн возбуждаются волной ТЕМ, распределение поля которой по оси равномерно, что должно дать преимущество возбуждению высших мод поля, имеющих максимум в центре (z = 0).

В-третьих, в рассматриваемой в данной работе геометрии возможен резонанс, связанный с компенсацией токов высших мод полей вне и внутри плазмы – резонансное возбуждение поверхностных волн у боковой поверхности.

Отметим, что в целом в данной геометрии есть возможность влиять на поле двух компонент: поле поверхностной волны и поле высших мод. В то же время в полностью заполненной камере есть три компоненты: поверхностная волна в центральной области, поверхностная волна в периферийной области и высшие моды в окрестности области возбуждения, что дает преимущества в возможностях управления пространственным распределением плотности электронов, но, с другой стороны, может привести и к дополнительным сложностям.

При противофазном возбуждении разряда в области без плазмы в рассматриваемой конструкции разрядной камеры распространяющихся волн нет, по крайней мере, если расстояние между пластинами меньше длины волны в вакууме. Поэтому ток на боковую стенку при противофазном возбуждении должен протекать через очень малую емкость между плазмой и стенкой. Таким образом, в симметричном разряде в рассматриваемой геометрии возбуждение антисимметричных волн затруднено. Однако возбуждение этих волн возможно при нарушении симметрии (размера слоев, плотности электронов), в особенности если учесть, что такое нарушение может происходить спонтанно [34, 35, 41]. Как следует из расчета дисперсионных кривых [31] длина антисимметричных волн с широкой области плотностей электронов существенно меньше, чем симметричных. Поэтому резонансы, связанные с возбуждением этих волн, наблюдаются при более высоких плотностях электронов, что подтверждается расчетами, выполненными для разрядной камеры, полностью заполненной плазмой [40]. Несимметрия разряда в не полностью разрядной вакуумной камере может привести к возбуждению антисимметричных волн и появлению дополнительных резонансов. Этот вопрос нуждается в дополнительном исследовании в будущих работах.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

Основные результаты работы могут быть сформулированы следующим образом.

1. Аналитические расчеты поля в емкостном высокочастотном разряде низкого давления показали, что поле в плазме с достаточной точностью может быть представлено в виде суммы поверхностных и нераспространяющихся собственных мод Е-волн в трехслойной структуре слой пространственного заряда–плазма–слой пространственного заряда, окруженной металлическими электродами. Для корректного расчета импеданса разряда и пространственного распределения поля необходимо учитывать как поверхностные волны, так и высшие не распространяющиеся моды поля.

2. Основной наблюдаемый в разряде резонанс тока, который мы будем называть “глобальным”, связан с компенсацией емкостного импеданса внешней части камеры и индуктивного импеданса разряда. Поскольку этот резонанс для рассматриваемой геометрии наблюдается в условиях, когда длина поверхностной волны кратна размерам плазмы, резонансы, соответствующие этим волнам, в массе своей маскируются данным резонансом.

3. Основной резонанс напряжений, наблюдаемый в системе, – геометрический резонанс плазмы и слоя. В области параметров, характерных для плазменных реакторов, и частоты поля, рассматриваемой в задаче, он наблюдается при размерах плазмы меньше 15 см. При больших размерах длинная линия, вдоль которой распространяются поверхностные волны, имеет индуктивный импеданс, или ее емкостной импеданс недостаточен для компенсации индуктивного импеданса, вносимого высшими модами.

4. Высшие моды поля имеют большую амплитуду и играют большую роль в поддержании разряда в сравнении с разрядом, полностью заполняющим разрядную камеру [36].

5. Для корректного аналитического описания свойств разряда с плотностями от критической до удвоенной критической теория возмущений по параметру ν/ω недостаточна. Поэтому характеристики поверхностных и не распространяющихся волн должны быть дополнительно исследованы без использования теории возмущений.

6. Влияние емкости цепи, соединяющей плазму с генератором и индуктивности, вносимой пустой частью камеры, могут оказывать существенное влияние на характеристики разряда и даже на возможность его поддержания. Роль этих эффектов растет с увеличением частоты поля, поддерживающего разряд.

7. Сопоставление в целом результатов аналитических расчетов и численного моделирования свойств разряда с помощью пакета COMSOL Multiphysics^® показало их удовлетворительное качественное согласие.

Проведенные в данном цикле работ (включая [31, 40]) исследования показали, что импеданс высокочастотного емкостного разряда низкого давления в целом, а также пространственное распределение поля определяется высшими, нераспространяющимися модами поля не в меньшей степени, чем поверхностными волнами, распространяющимися вдоль интерфейсов, плазма–слой пространственного заряда–металл. Высшие типы мод возбуждаются у всех резких неоднородностей рабочей камеры – границ (и ребер) электродов, углов вакуумной камеры, в области подвода энергии. При этом соотношение амплитуд различных типов волн может очень сильно изменяться в зависимости от плотности плазмы и выбранной геометрии рабочей камеры. Поэтому получение единых рекомендаций для всех возможных режимов разряда, которые требуются для реализации существующих (и возможно новых) технологических процессов маловероятно. Тем не менее расчеты дают возможность оценить эффективность передачи энергии в данную моду поля, в каких условиях какой вид полей оказывает какое влияние на импеданс, и как он может влиять на пространственное распределение плотности плазмы. Наше исследование наглядно демонстрирует возможность выбирать и исследовать широкий класс установок не только на основании экспериментального опыта на предыдущих установках, но на основе теоретического анализа электродинамических свойств системы.