Физика плазмы, 2021, T. 47, № 8, стр. 728-740
МГД-моделирование турбулентного развития “сосисочной” неустойчивости Z-пинча
С. Ф. Гаранин a, *, В. Ю. Долинский a
a Российский федеральный ядерный центр – Всероссийский научно-исследовательский институт
экспериментальной физики
Саров, Нижегородская обл., Россия
* E-mail: sfgaranin@vniief.ru
Поступила в редакцию 17.03.2021
После доработки 02.04.2021
Принята к публикации 06.04.2021
Аннотация
C помощью двумерных осесимметричных МГД-расчетов изучалось развитие перетяжки Z-пинча с учетом коротковолновых малых возмущений, т.е. с учетом развития двумерной турбулентности. Влияние магнитной диффузии и теплопроводности предполагалось малым, и существенным лишь в зонах, где их необходимо учитывать (на границах плазма/вакуум и вблизи оси). Рассматривалась эволюция цилиндрического плазменного столба с синусоидальным возмущением границы и малыми случайными возмущениями плотности под действием постоянного тока. Расчеты показали, что развитие турбулентности препятствует формированию перетяжки с неограниченно уменьшающимся радиусом и вытеканием плазмы из зоны сжатия. Некоторое влияние на максимальные параметры сжатия оказывает амплитуда начального возмущения, поскольку при ее увеличении перетяжка формируется быстрее, коротковолновые возмущения успевают развиться до меньшего уровня, и образующаяся турбулентная плазма слабее экранирует зону сжатия. При сжатии перетяжки не происходит и генерации высоких напряжений вблизи оси, что могло бы способствовать формированию ионных пучков и генерации нейтронов за счет ускорительного механизма. В расчетах довольно быстро устанавливается МГД-равновесное состояние на границе перестановочной неустойчивости. Из-за отсутствия неограниченного сжатия в перетяжке Z-пинча зажечь плазму в перетяжке, по-видимому, затруднительно даже при мультимегаамперных токах источника.
1. ВВЕДЕНИЕ
В настоящее время Z-пинчами традиционно называют динамические системы, в которых магнитное поле имеет только азимутальную компоненту, а все величины, в основном, осесимметричны и зависят от двух цилиндрических координат, r и z. К Z-пинчам относят разряды типа плазменного фокуса, осесимметричные системы с импульсным напуском газа, разряды по проволочкам, а также так называемые Z-пинч-лайнерные системы с цилиндрической имплозией относительно тонких оболочек-лайнеров, включая даже не вполне осесимметричные многопроволочные лайнеры.
Для описания течений плазмы в Z-пинчах широко применяется магнитогидродинамический (МГД) подход, в котором плазма рассматривается как сплошная среда, характеризующаяся макроскопическими параметрами – плотностью, скоростью, давлением и температурой. Как правило, критерии применимости МГД-подхода к описанию течений плазмы в Z-пинчах при невысоких температурах и до финальной стадии сжатия плазмы вблизи оси удовлетворяются.
МГД-подход показал, что при отклонении конфигурации Z-пинча от идеальной цилиндрической формы, которая определяется условием Беннетта [1], развиваются МГД-неустойчивости. Особенно важную роль среди этих неустойчивостей играет “сосисочная” неустойчивость, в которой сохраняется осевая симметрия (мода m = 0), а магнитное поле вне пинча тогда зависит от радиуса как $B\sim 1{\text{/}}r$, и, следовательно, магнитное давление на плазму пинча будет пропорционально ${{p}_{B}}\sim 1{\text{/}}{{r}^{2}}$. В этом случае провалившиеся по радиусу области плазмы под действием возросшего магнитного давления будут проваливаться еще сильнее, и возмущения будут нарастать.
Линейная стадия развития неустойчивости Z‑пинча впервые исследовалась в [2–4]. Инкременты развития неустойчивости λ азимутально симметричной моды m = 0 для скинированного пинча (радиус которого R больше скин-слоя) равны:
для коротковолновых возмущений $kR \gg 1$ развитие “сосисочной” неустойчивости сводится [5] к рэлей-тейлоровской (РТ) неустойчивости и имеет инкремент,
где– эффективное ускорение силы тяжести, ${{c}_{{\text{A}}}} = $ $ = B{\text{/}}\sqrt {4\pi \rho } $, B – магнитное поле на радиусе пинча, ρ – плотность вещества пинча;
для длинноволновых возмущений $kR \ll 1$,
γ – показатель адиабаты.Если пинч не является скинированным, а все величины в нем распределены по радиусу, то для коротких длин волн $kR \gg 1$ для каждого значения радиуса можно определить инкремент развития сосисочной неустойчивости. Эти инкременты должны при $kR \gg 1$ стремиться к постоянному пределу, зависящему от градиентов логарифма величины $\Phi = {{p}^{{1/\gamma }}}r{\text{/}}B$ [5]
(4)
${{\lambda }^{2}} = - \frac{{2c_{{\text{A}}}^{2}}}{{{{r}^{2}}}}\frac{{\partial \ln \Phi }}{{\partial \ln r}},$Таким образом, линейная теория показывает, что сосисочная неустойчивость может развиваться по мере уменьшения радиуса пинча все более быстро, и имеются основания считать, что на финальной стадии при развитии неустойчивости (в перетяжке) будут реализовываться большие магнитные поля и высокие плотности энергии. Изучение нелинейного развития сосисочной неустойчивости является непростой задачей, поскольку инкременты растут с уменьшением разрешаемых масштабов. Для изучения этого вопроса использовались разные методы (см., например, обзоры [6, 7] и ссылки там), в том числе модельные задачи, частные идеальные (не учитывающих рост целого спектра возмущений) аналитические [8] или автомодельные [5, 9] решения. Выдвигались различные гипотезы о том, что на финальной стадии сжатия перетяжки ее динамика будет следовать некоторым автомодельным решениям. Так, например, если считать сжатие адиабатическим, длину перетяжки l пропорциональной ее радиусу R, а, следовательно, время вытекания плазмы из области перетяжки $t\sim l{\text{/}}{{v}_{T}}\sim R{\text{/}}{{v}_{T}}$ (${{v}_{T}}$ – скорость звука в перетяжке), получаем [7] зависимости радиуса, плотности ρ и температуры T плазмы от времени (t считаем отрицательным, $t \to 0$, так что радиус зануляется при t = 0)
(5)
$\begin{gathered} R\sim {{( - t)}^{{\gamma /(2\gamma - 1)}}}, \\ \rho \sim {{( - t)}^{{ - 2/(2\gamma - 1)}}}, \\ T\sim {{( - t)}^{{ - 2(\gamma - 1)/(2\gamma - 1)}}} \\ \end{gathered} $Если считать сжатие адиабатическим, а длину перетяжки фиксированной, то характерные величины будут меняться следующим образом:
В [9] были проведены численные расчеты развития скинированной перетяжки в идеальных предположениях (без учета магнитной диффузии и при полном отсутствии мелкомасштабных возмущений). Получено, что в этом случае реализуется режим (6), в котором длина перетяжки l не уменьшается с уменьшением радиуса. Однако достижение больших сжатий в численном расчете оказалось невозможным из-за развивающихся неустойчивостей. Максимальное сжатие по радиусу, полученное в этих расчетах, составило 5.2 раза.
Высокие плотности энергии, которые потенциально могли бы реализовываться в перетяжке Z-пинчей (частным случаем которых можно считать плазменный фокус), давали надежду на осуществление зажигания термоядерных реакций (см., например, [10, 11], где для режима (5) считалось возможным получение сжатия по радиусу 104, достижение критерия Лоусона, а затем термоядерная детонация) или, по крайней мере, на получение высокого нейтронного выхода.
Кроме того, уже в самых первых экспериментах с Z-пинчами было выяснено, что получаемые в них нейтроны не являются термоядерными, а генерируются за счет столкновений ионов, ускоренных до энергий, намного превышающих тепловые, с ионами плазмы пинча. Этот механизм генерации нейтронов получил название ускорительного или пучково-мишенного (beam-target). Но и этот механизм мог бы быть следствием больших напряжений, развивающихся, когда значительный магнитный поток уходит на ось за короткие времена, соответствующие максимальному сжатию перетяжки. В последние годы продолжается активное изучение механизмов нейтронной генерации в Z-пинчах и плазменном фокусе. В работах [12–14], где в Z-пинче зарегистрированы ионы, ускоренные до десятков МэВ, обсуждаются возможные механизмы генерации столь энергичных ионов и их влияние на нейтронный выход, и среди возможных механизмов этой генерации есть и развитие, и разрыв перетяжки. Надо сказать, что в этих работах, а также в работах, цитируемых в [15], где тоже возможно образование и развитие перетяжек, энергии зарегистрированных на разных установках ионов превышают в десятки (и даже сотню) раз те энергии, которые могут обеспечивать начальные напряжения на генераторах тока, используемых в экспериментах.
Далее, существует подход к расчету нейтронного выхода в плазменном фокусе, предложенный в [16], в котором на фоне МГД-расчета учитывается движение ионных пучков, ускоряемых напряжением, вызванным в области фокусировки аномальным сопротивлением. Столкновение ускоренных ионов с плотной плазмой в области фокусировки приводит к генерации нейтронов, и в [16, 17] показано, что такой подход хорошо описывает экспериментальные результаты по генерации нейтронов для ряда геометрий плазменного фокуса. Этот подход может быть также основан на механизме развития перетяжки и нейтронный выход здесь может также зависеть от того, возможно ли проникновение тока на малый радиус и уход значительного магнитного потока на ось за короткие времена.
Таким образом, для всех этих задач и явлений общим является вопрос, может ли развитие перетяжки довести ток до малых радиусов и создать область с высокой плотностью энергии или же создать условия для генерации вблизи оси высоких напряжений. Этот вопрос можно исследовать с помощью осесимметричных МГД-расчетов, по возможности, предполагая малосущественными магнитную диффузию и теплопроводность, однако учитывая максимально возможным образом весь спектр малых возмущений, которые могут влиять на развитие перетяжки. Из-за сложного турбулентного характера возникающего течения заранее трудно предсказать результаты и дать ответ на этот вопрос. В настоящей работе будет сделана попытка провести такого рода расчеты.
Предположение несущественности магнитной диффузии и теплопроводности представляется разумным для экспериментов с большой энергетикой и высокой плотностью плазмы. Однако заранее следует оговориться, что для конкретных условий тех или иных экспериментов эти явления переноса могут быть важны, как впрочем, и другие, не учитываемые нами, процессы. И, конечно, трехмерность экспериментов и развитие азимутально несимметричных мод неустойчивости (не только сосисочной $m = 0$ моды, которая только и учитывается нами), может повлиять на результаты, хотя многие результаты экспериментов с плазменным фокусом и с камерой МАГО неплохо описываются осесимметричными расчетами.
Одним из явлений, которые могут препятствовать глубокому сжатию перетяжки, является возможное наличие плазменной короны, окружающей пинч, которая, несмотря на относительную малую плотность, может при глубоких сжатиях шунтировать ток, протекающий через пинч, и препятствовать проникновению тока на малые радиусы, а, следовательно, получению высоких плотностей энергии и генерации высоких напряжений на оси. Эти явления изучались в ряде работ теоретически и экспериментально (см., например, [5, 18–20]), и там показано, что при не очень малой плотности короны ее влияние может быть важным. В настоящей работе мы предполагаем, что плотность короны очень мала и ее влияние на сжатие пинча пренебрежимо. Таким образом, мы не учитываем этот отрицательный фактор для сжатия пинча. Поэтому можно ожидать, что при его учете результаты по сжатию перетяжки и получению в пинче высоких плотностей энергии и напряжений будут только хуже.
2. ПОСТАНОВКА ЗАДАЧИ. ФИЗИЧЕСКАЯ МОДЕЛЬ
Рассмотрим плазменный столб радиусом R0, заполненный идеальным газом с плотностью ρ0 и давлением p0 c показателем адиабаты γ = 5/3, давление плазмы которого вначале уравновешено силами текущего вдоль цилиндра тока. В начальный момент времени имеется малое периодическое по длине цилиндра аксиально-симметричное возмущение
(a – амплитуда возмущения), так что, строго говоря, равновесие пинча в начальный момент времени несколько нарушено, и это должно послужить затравкой к развитию перетяжки. Мы рассматривали два варианта такого возмущения с разной длиной волны l/R0 = 2 и l/R0 = 4; результаты получились качественно похожими, и ниже будут представлены только для l/R0 = 4. Кроме этого возмущения мы предполагали, что в каждой счетной ячейке имеется случайное малое возмущение плотности на уровне 10–3. Таким образом, имелся целый спектр возмущений, создающий затравку для развития турбулентности. При этом по мере уточнения расчетов (уменьшения размеров счетных ячеек) эффективный масштаб малых возмущений должен уменьшаться и зависимость от их величины также, а масштабы и спектры возмущений должны были определяться развившейся турбулентностью.На рис. 1 представлена геометрия, для которой проводились наши расчеты.
В качестве единиц измерения в расчетах мы взяли:
для расстояний – удвоенный начальный радиус плазменного столба 2R0,
для плотности плазмы – начальную плотность плазмы в столбе ρ0,
для магнитного поля – начальное магнитное поле на радиусе столба B0,
единица измерения времени определялась из соотношения $[t] = {{R}_{0}}{\text{/}}{{c}_{{\text{A}}}}$, где ${{c}_{{\text{A}}}}$ определяется по B0 и ρ0, тогда в принятых единицах альфвеновская скорость будет равна ${{c}_{{\text{A}}}} = 0.5$,
для магнитного потока – $[\Phi ] = 2Il{\text{/}}c$, где I – ток, текущий по плазменному столбу,
для напряжения – $[U] = [\Phi ]{{c}_{A}}{\text{/}}{{R}_{0}}$,
начальная температура плазмы определялась из условия равновесия давления плазмы и давления магнитного поля, создаваемого током I, текущим по плазменному столбу.
Область над плазменным столбом считается вакуумом. В начальный момент времени вакуум заполнен веществом с плотностью 10–5ρ0, температура вещества в вакууме такая же, как у плазменного столба. Вакуум заполнен магнитным потоком таким образом, что произведение $B(r) \cdot r = {\text{const}}$ определяется током, протекающим по плазменному столбу.
В нашем модельном расчете мы хотели обеспечить как можно более идеальное МГД-описание (большие числа магнитного Рейнольдса, к тому же растущие по мере уточнения расчетов). При этом в расчетах все же хотелось при сжатии перетяжки до малых радиусов обеспечить возможность вытекания магнитного потока на ось и получение при этом высоких напряжений на оси, чтобы исследовать возможности получения пучков ионов с высокими энергиями [12–15] и получения высоких нейтронных выходов по мишенному механизму [16, 17]. Для этой цели мы предположили, что коэффициент магнитной диффузии имеет вид
где ${{c}_{{\text{A}}}}$ – альфвеновская скорость, Δ – размер счетной ячейки. Таким образом, в вакууме, плотность равна нулю и ${{c}_{{\text{A}}}} = \infty $, ${{\kappa }_{B}}$ будет также бесконечен и обеспечит постоянство тока в вакуумной области. По мере уточнения задачи (уменьшения Δ) магнитное число Рейнольдса будет возрастать и задача для большей части масштабов будет в этом смысле стремиться к идеальной. В области же малых радиусов r ~ Δ, если магнитное поле дойдет до них, магнитная диффузия с коэффициентом (8) может обеспечить вытекание магнитного потока и формирование больших напряжений на оси.Как известно [5], диффузия из вакуума в плазму вызывает перегрев граничащего с вакуумом вещества, который для спитцеровской плазменной проводимости [21], не зависящей от плотности, в расчетах может приводить к бесконечно быстрому полному скинированию магнитного поля. В случае нашей магнитной диффузии с коэффициентом (8) этого не будет происходить, однако граничная с вакуумом зона тем не менее может перегреваться до бесконечных температур, что все же неудобно в расчетах. Чтобы этого не происходило, необходим учет теплопроводности. Мы предполагали, что наша модельная теплопроводность также как (8) должна уменьшаться по мере уточнения расчетов. Поэтому мы выбрали для нее коэффициент температуропроводности ${{\kappa }_{T}}$, по порядку величины совпадающим с (8), а конкретно, пользуясь тем, что для плазменного скин-слоя отношение теплового давления к магнитному должно быть порядка единицы $\beta \equiv p{\text{/}}({{B}^{2}}{\text{/}}8\pi )\sim 1$, мы выбрали его равным
и, таким образом, не зависящим от магнитного поля, а для идеальной плазмы, для которой $p\sim \rho T$, пропорциональным только корню из температуры, ${{\kappa }_{T}}\sim \sqrt T $.Граничные условия в расчете учитывались следующим образом. Границы по z считались жесткими идеально проводящими теплоизолированными стенками. Внешняя граница по радиусу r = Rmax считалась жесткой теплоизолированной стенкой. За внешней границей по r была введена строка фиктивных ячеек, в которых задавалось граничное значение магнитного поля, соответствующее току I. При этом магнитное поле имело возможность диффундировать как из области фиктивных ячеек в расчетный объем, так и наоборот, из расчетного объема в область фиктивных ячеек, приводя тем самым к уменьшению магнитного потока в объеме. Граница r = 0 соответствовала оси плазменного столба в осесимметричном расчете. На границе r = 0 радиальная компонента скорости и радиальная составляющая потока тепла считались нулевыми. Магнитное поле через ось имело возможность диффундировать, и тем самым приводить к выходу магнитного потока и росту z-компоненты напряженности электрического поля на оси. Для того чтобы избавиться от трудностей расчета диффузии магнитного поля для нулевого радиуса, мы отступали от оси на шаг равный Δ/4.
При вычислении давления и внутренней энергии плазмы использовалось уравнение состояния идеального одноатомного газа.
3. СХЕМА РАСЧЕТА И ОСОБЕННОСТИ ЧИСЛЕННОЙ МОДЕЛИ
Расчеты проводились для прямоугольной области, на которой была введена регулярная однородная прямоугольная сетка с равными ребрами Δr = Δz ≡ Δ (Δr, Δz – шаг сетки по r и z координате соответственно). Скалярные величины определялись в центрах ячеек, векторные величины определялись на ребрах ячеек сетки.
МГД-расчет включал в себя следующие основные этапы:
– газодинамический этап счета, на котором определяются скорость, плотность, и удельная внутренняя энергия;
– расчет проводимости, распределение магнитного и электрического полей;
– расчет теплопроводности и джоулева нагрева плазмы;
– расчет температуры и давления плазмы.
Газодинамический этап расчета проводился по явной схеме. Для аппроксимации дифференциальных уравнений использовалась схема с разностями “против потока” [22]. Аппроксимация потоковых слагаемых проводилась по методу Лелевьера [23]. Для расчета скоростей и импульсов, определенных на ребрах ячеек основной сетки, была введена дополнительная смещенная сетка. Пересчет скоростей на ребра смещенной сетки выполнялся путем усреднения скоростей со смежных ребер основной (несмещенной) сетки. Такой подход с использованием разнесенных сеток позволяет получить второй порядок аппроксимации градиентов давления в уравнениях для импульса, несмотря на использование лишь четырех точек [24], а также избежать нефизических осцилляций в решении [23, 24].
Для обеспечения консервативности по полной энергии, внутренняя энергия на газодинамическом этапе расчета вычислялась как разность между полной и кинетической энергией плазмы. Для сквозного расчета ударных волн в плазме была введена искусственная вязкость [25].
Расчет магнитного и электрического полей проводился с использованием неявной схемы прогонок по строкам и столбцам с итерациями [26]. При этом расчет компонент магнитного поля, связанных с альфвеновской скоростью, был совмещен с расчетом электрических полей (см. работы [16, 17]). Такой подход позволяет избавиться от ограничения Куранта на величину счетного шага по времени, возникающего при расчете по явным схемам из-за наличия областей с низкой плотностью:
где Δt – шаг по времени, Δ – линейный размер ячейки, q = 0.25 – 0.75, ${{c}_{{ms}}} = \sqrt {c_{s}^{2} + c_{A}^{2}} $, cs – скорость звука в веществе, ${{c}_{{\text{A}}}}$ – альфвеновская скорость, $\left| {\vec {v}} \right|$ – модуль скорости плазмы.Расчет теплопроводности выполнялся по явной схеме. Для обеспечения устойчивости расчета в этом случае вводилось искусственное ограничение на величину коэффициента температуропроводности, таким образом, чтобы для текущего временного шага условие устойчивости Куранта $\Delta t < \frac{{{{{{\Delta }}}^{2}}}}{{2{{\kappa }_{T}}}}$ не нарушалось. При вычислении коэффициента теплопроводности ${{\lambda }_{T}} = {{C}_{p}} \cdot \rho \cdot {{\kappa }_{T}}$ (${{C}_{p}}$ – удельная теплоемкость при постоянном давлении) плотность на ребра пересчитывалась с использованием гармонического усреднения значений в смежных с ребром ячейках. Такой поход помог избавиться от нефизического вытекания энергии из разогретого вакуума в плазму.
В представленных расчетах было введено ограничение на температуру $T < 60$ для вакуумных областей с плотностью ≤10–3 ρ0. Такой же подход использовался в работе [17], с тем отличием, что в работе [17] ограничение вводилось для областей с плотностью ≤10–1 ρ0. Данное ограничение позволяло избежать в наших расчетах перегрева вакуума (по-видимому, из-за нефизических счетных эффектов) и уменьшить экранировку области пинча от тока, протекающего по малоплотной плазме. Для расчетов на сетках 0.0025 × 0.0025 и 0.00125 × 0.00125 дисбаланс по полной энергии, возникающий из-за искусственного уменьшения температуры, не превышал 15% и 7%, соответственно, на момент времени t = 5, соответствующий концу расчета.
Расчеты были выполнены на сетках с различными размерами ячеек 0.01 × 0.01, 0.005 × 0.005, 0.0025 × 0.0025 и 0.00125 × 0.00125. При этом для самой подробной сетки число ячеек расчетной области достигало 6.4 млн. Провести расчеты с таким числом ячеек за разумное время позволило распараллеливание кода с использованием программного интерфейса OpenMP. Расчет на сетке 6.4 млн. ячеек потребовал примерно 100 часов машинного времени на 6-и ядерном процессоре Intel Core i7-990X с тактовой частотой 3.46 ГГц.
4. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Для того, чтобы определить основные закономерности развития сосисочной неустойчивости и выяснить адекватность нашей численной модели нами были проведены численные расчеты с разными сетками (начиная со сравнительно грубых и до достаточно тонких) и разными амплитудами возмущений.
Что касается разрешений сеток, выяснилось, что основные закономерности развития неустойчивости проявляются уже при разрешении сетки 0.01, хотя максимальные достигаемые в расчетах значения физических величин несколько увеличиваются при дроблении сетки, выходя примерно на предельные значения при разрешении сетки 0.0025.
На рис. 2 представлены распределения плотности, давления и величины Br, полученные в расчете с разрешением сетки 0.0025 и амплитудой начального возмущения a = 0.05 для разных моментов времени. Эволюция развития возмущений показывает, что из-за развития турбулентности формирования перетяжки с малым радиусом и вытеканием плазмы из зоны сжатия не происходит. Происходит перемешивание и экранирование струями плазмы зоны сжатия. В итоге, максимальные давления, плотности и магнитные поля в зоне сжатия (см. табл. 1) не растут неограниченно по мере сжатия, как можно было ожидать согласно сценариям (5, 6), а увеличившись до некоторого уровня, далее стабилизируются и остаются примерно на постоянном уровне. При этом из-за того, что магнитное поле практически не доходит до оси, напряжение на оси остается очень малым (табл. 1, рис. 3, кривая a = 0.05), однако спадает оно медленно, по-видимому, с характерным временем турбулентности, т.е. порядка единицы.
Рис. 2.
Распределения а) плотности (ρ); б) давления (p); и в) произведения магнитного поля на радиус (Br) на различные моменты времени для расчета на сетке 0.0025 × 0.025, a = 0.05.

Таблица 1.
Максимальные величины, достигаемые в задаче с a = 0.05
| Величина | Увеличение | Время tmax | z | r | Максимальное напряжение на оси |
|---|---|---|---|---|---|
| сетка 0.01 × 0.01 | |||||
| ρ | 1.96 | 2.3 | 1.225 | 0.045 | 0.038 |
| T | 2.54 | 2.3 | 1.225 | 0.045 | |
| p | 4.98 | 2.3 | 1.225 | 0.045 | |
| B | 1.27 | 2.1 | 1.215 | 0.255 | |
| сетка 0.005 × 0.005 | |||||
| ρ | 3.18 | 2.2 | 0.932 | 0.0025 | 0.038 |
| T | 5.31 | 2.2 | 0.932 | 0.0025 | |
| p | 16.9 | 2.2 | 0.932 | 0.0025 | |
| B | 1.64 | 2.0 | 1.192 | 0.182 | |
| сетка 0.0025 × 0.0025 | |||||
| ρ | 2.63 | 2.4 | 0.651 | 0.0013 | 0.018 |
| T | 5.07 | 2.4 | 0.651 | 0.0013 | |
| p | 13.3 | 2.4 | 0.651 | 0.0013 | |
| B | 1.76 | 2.3 | 0.869 | 0.166 | |
Примечание к таблице 1 – tmax – момент времени, в который в задаче достигается максимальное давление p или максимальное магнитное поле B; z, r – координаты соответствующей точки; ρ и T – значения плотности и температуры в точке с максимальным давлением
Рис. 3.
Напряжения на оси для расчетов с амплитудами начального возмущения a = 0.05; a = 0.2; a = 0.3 (сетка 0.0025 × × 0.0025).

Дробление сетки, при котором одновременно уменьшается роль магнитной диффузии и теплопроводности и начальных хаотических возмущений, показало (см. табл. 1), что по мере утоньшения сетки происходит некоторый рост достигаемых максимальных давлений, плотностей и магнитных полей, который затем стабилизируется. Напряжение на оси имеет тенденцию к уменьшению по мере дробления сетки, что говорит о том, что развитие сосисочной неустойчивости с учетом двумерной турбулентности само по себе не приводит к большим напряжениям на оси и не может вызывать разгон ионов до высоких энергий, наблюдаемый в ряде экспериментов на Z‑пинчах и плазменном фокусе [12–14]. Для объяснения этих результатов, по-видимому, необходимо привлекать модели, выходящие за рамки двумерной МГД, учитывать кинетику и/или трехмерные эффекты.
Итак, расчеты показывают, что со временем происходит стабилизация развития сосисочных возмущений. К какому же состоянию будет приходить плазма в этих двумерных МГД-расчетах? Разумно предположить, что это будет МГД равновесное состояние на границе перестановочной неустойчивости по Кадомцеву [27]. На рис. 4 приведено сравнение профилей давления, полученных из МГД-расчета и кадомцевских профилей, параметры которых подбирались из наилучшего согласования с профилями из МГД-расчета. Средние профили давления по радиусу в МГД-расчетах, были получены путем усреднения 2D‑распределений по z. Момент времени, для которого средний профиль имеет максимальное значение вблизи оси, соответствует моменту времени 2.4, который и представлен на рис. 4а. Для представленных на рис. 4 средних МГД-профилей давления был осуществлен подбор параметров b и p0 для кадомцевского профиля:
(11)
$p = {{p}_{0}}{{\left( {\frac{\beta }{{0.8 + \beta }}} \right)}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}};\quad r = b\frac{{{{{(0.8 + \beta )}}^{{1/4}}}}}{{{{\beta }^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}}$(12)
$\delta = \frac{1}{n}{{\sum\limits_{i = 1}^n {\left( {p_{i}^{{{\text{МГД}}}} - p_{i}^{{{\text{Кад}}}}} \right)} }^{2}}$Рис. 4.
Сравнение МГД и кадомцевского профилей для сетки 0.0025 см на моменты времени: а) – t = 2.4; б) – t = 4 . В легендах к рисункам приведены значения параметров b и p0 для кадомцевского профиля.

Нами было обнаружено, что увеличение амплитуды начального возмущения приводит к увеличению достигаемых в ходе сжатия перетяжки, давлений, плотностей и магнитных полей в зоне сжатия, а также к возрастанию напряжений на оси пинча. В качестве примера расчета с увеличенной амплитудой на рис. 5 представлены распределения плотности, давления и величины $Br$, полученные в расчете с разрешением сетки 0.00125 и амплитудой начального возмущения a = 0.3 для разных моментов времени. Сравнение рис. 5 и рис. 2 показывает, что хотя общая тенденция перемешивания и закрытия струями плазмы зоны перетяжки сохраняется (и в итоге в перетяжке не происходит неограниченного пинчевания и выхода магнитного поля на сколь угодно малые радиусы), можно отметить, что для задачи с большим a мелкомасштабные неустойчивости не успевают так развиться, как в задаче с a = 0.05, и перетяжка для задачи с a = 0.3 сжимается сильнее. В итоге, в задаче с a = 0.3 достигаются большие давления, плотности и магнитные поля в зоне сжатия (см. табл. 2). Благодаря возрастанию магнитного поля в зоне сжатия при увеличении a возрастают и напряжения на оси, хотя и остаются относительно небольшими (табл. 2, рис. 3, кривая a = 0.3), но спадают они по-прежнему медленно, с характерным временем порядка единицы.
Рис. 5.
Распределения а) плотности (ρ); б) давления (p); и в) произведения магнитного поля на радиус (Br) на различные моменты времени для расчета на сетке 0.00125 × 0.0125, a = 0.3.
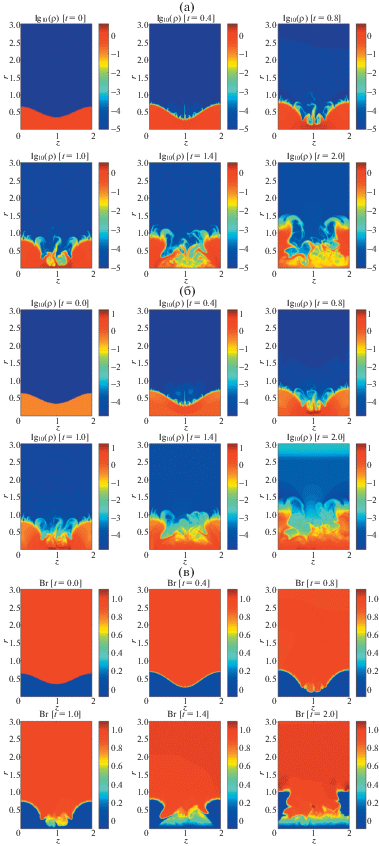
Таблица 2.
Максимальные величины, достигаемые в задаче с a = 0.3
| Величина | Увеличение | Время tmax | z | r | Максимальное напряжение на оси |
|---|---|---|---|---|---|
| сетка 0.01 × 0.01 | |||||
| ρ | 3.38 | 1.7 | 0.005 | 0.005 | 0.308 |
| T | 5.58 | 1.7 | 0.005 | 0.005 | |
| p | 18.8 | 1.7 | 0.005 | 0.005 | |
| B | 2.40 | 1.2 | 1.265 | 0.125 | |
| сетка 0.005 × 0.005 | |||||
| ρ | 1.42 | 1.1 | 0.902 | 0.008 | 0.262 |
| T | 17.6 | 1.1 | 0.902 | 0.008 | |
| p | 25.0 | 1.1 | 0.902 | 0.008 | |
| B | 3.64 | 1.0 | 0.892 | 0.072 | |
| сетка 0.0025 × 0.0025 | |||||
| ρ | 5.35 | 1.5 | 1.999 | 0.001 | 0.278 |
| T | 13.7 | 1.5 | 1.999 | 0.001 | |
| p | 73.2 | 1.5 | 1.999 | 0.001 | |
| B | 4.12 | 1.4 | 1.531 | 0.054 | |
| сетка 0.00125×0.00125 | |||||
| ρ | 5.47 | 1.1 | 1.096 | 0.001 | 0.102 |
| T | 11.9 | 1.1 | 1.096 | 0.001 | |
| p | 65.3 | 1.1 | 1.096 | 0.001 | |
| B | 4.12 | 1.1 | 1.098 | 0.031 | |
Примечание к таблице 2 – tmax – момент времени, в который в задаче достигается максимальное давление p или максимальное магнитное поле B, z, r – координаты соответствующей точки, ρ и T – значения плотности и температуры в точке с максимальным давлением
5. РАЗМЕРНЫЕ ОЦЕНКИ ДЛЯ I = 10 МА
Оценим характерные величины, фигурирующие в наших расчетах, если для рассматриваемой нами задачи о перетяжке ориентироваться на ток I = 10 МА и характерное время 10–7 с, которые рассматривались в работах [10, 11], где обсуждалась возможность зажигания термоядерной реакции в перетяжках Z-пинча. Если при этом принять за единицу измерения времени характерное время 10–7 с, а за единицу измерения расстояния – начальный диаметр пинча, рассматриваемый в [10], $2{{R}_{0}}$ = 1 см, то согласно разделу 2 остальными единицами измерений будут:
| скорость | 107 см/с, |
| магнитное поле | B0 = 4 МГс, |
| начальная плотность плазмы | ρ0 ≈ 0.051 г/см3, |
| начальное давление плазмы в столбе | p0 ≈ 0.64 Мбар, |
| напряжение | U = 400 кВ, |
| начальная температура для D-T плазмы | T0 ≈ 0.016 кэВ. |
В этом случае согласно табл. 1 максимальными величинами, достигаемыми в задаче с a = 0.3, будут:
| плотность плазмы | ρ ≈ 0.28 г/см3, |
| температура | T ≈ 0.19 кэВ, |
| давление плазмы | p ≈ 42 Мбар, |
| магнитное поле | B = 16 МГс, |
| напряжение | U = 41 кВ. |
Характерный размер сжатой плазмы согласно рис. 5 для t = 1 можно оценить как 0.1 см по радиусу r и 0.3 см по z. Полученные значения температуры и ρr далеки от необходимых для зажигания термоядерной реакции. К сожалению, даже увеличение тока до 100 МА может на этом пути не привести к зажиганию.
6. РОЛЬ СОСИСОЧНОЙ НЕУСТОЙЧИВОСТИ В ПЛАЗМЕННОМ ФОКУСЕ
Наше рассмотрение автомодельного двумерного МГД-развития перетяжки показывает, что собственно турбулентная (т.е. реальная) сосисочная неустойчивость не приводит к генерации высоких (и неограниченно растущих в МГД-приближении при дроблении сетки) напряжений на оси пинча. Тем не менее, в двухтемпературной МГД-модели расчета плазменного фокуса [16, 17] при наличии аномального сопротивления плазмы происходит генерация высоких напряжений на оси пинча (превышающих в 20 раз напряжение на конденсаторной батарее), которые приводят к формированию ионных пучков и генерации нейтронного излучения за счет ускорительного механизма. Модель описывает экспериментальный нейтронный выход, получаемый на многих установках плазменного фокуса. Чем это объясняется? Часть аргументов для объяснения этого приводится в [17].
Первое, это то, что граница токово-плазменной оболочки (ТПО) остается в расчетах гладкой, хотя априори могла бы быть искажена из-за развития РТ-неустойчивости. Это свойство является общим для многих течений в условиях нелинейного развития РТ-неустойчивости: известно, что “пузыри” (bubbles) в РТ-неустойчивости имеют гладкую форму. Аналогичная гладкость границы плазмы имеется и в расчетах камеры МАГО [5]. Можно предположить, что на больших масштабах, сравнимых с полным масштабом задачи, двумерные эффекты (растягивание масштабов в пузыре и шир (shear) скорости) подавляют развитие неустойчивости, что и наблюдается в экспериментах и расчетах.
Второе, это то, что к оси ТПО подходит с большой амплитудой основной гармоники возмущения, и, согласно нашим результатам, развитие мелкомасштабной сосисочной неустойчивости будет ослаблено. К тому же, вероятно, наличие заметной скорости ТПО также будет способствовать ослаблению развития мелкомасштабной сосисочной неустойчивости.
Третье: по-видимому, включение аномального сопротивления плазмы, имеющее кинетическую, а не МГД, природу, происходит довольно рано, когда магнитный поток, находящийся за ТПО, еще не заэкранирован развитой сосисочной неустойчивостью.
Возможно, влиянием перечисленных факторов и их разной ролью в разных геометриях камер плазменного фокуса объясняется то, что не во всех случаях модель [16, 17] удовлетворительно объясняет нейтронный выход из этих камер.
7. ЗАКЛЮЧЕНИЕ
C помощью двумерных осесимметричных МГД-расчетов изучалось развитие перетяжки Z‑пинча с учетом коротковолновых малых возмущений, т.е. с учетом развития двумерной турбулентности. Влияние магнитной диффузии и теплопроводности предполагалось малым, и существенным лишь в зонах, где их необходимо учитывать (на границах плазма/вакуум и вблизи оси, куда должен вытекать магнитный поток, поступающий к оси из-за развития перестановочной сосисочной неустойчивости).
Расчеты показали, что из-за развития турбулентности формирования перетяжки с малым радиусом и вытеканием плазмы из зоны сжатия не происходит. Происходит перемешивание и экранирование струями плазмы зоны сжатия. В итоге, максимальные давления, плотности и магнитные поля в зоне сжатия не растут неограниченно по мере сжатия, а увеличившись до некоторого уровня, далее стабилизируются и остаются примерно на постоянном уровне. Улучшение разрешения сетки, и, таким образом, улучшение точности расчетов качественно не меняет характер течения, несколько меняются только сами достигаемые максимальные параметры сжатия из-за случайного характера развития турбулентности. Заметное влияние на максимальные параметры сжатия оказывает амплитуда начального возмущения, поскольку при ее увеличении перетяжка формируется быстрее, коротковолновые возмущения успевают развиться до меньшего уровня, и образующаяся турбулентная плазма слабее экранирует зону сжатия. Для амплитуды начального возмущения a, составляющей 5% начального радиуса пинча, максимальное давление внутри пинча, полученное в расчете при развитии перетяжки, увеличилось в 13 раз по сравнению с начальным, а максимальное магнитное поле увеличилось в 1.8 раза по сравнению с начальным на поверхности пинча. Для амплитуды же a = 0.3 увеличение давления составило 65 раз, а увеличение магнитного поля 4 раза.
Расчеты показали также, что в двумерной осесимметричной МГД-модели при сжатии перетяжки не происходит и генерации высоких напряжений вблизи оси, что могло бы способствовать формированию ионных пучков и генерации нейтронов за счет ускорительного механизма. Так в расчетах с a = 0.05 максимальные развивающиеся напряжения составляют примерно 0.02 [U], где $[U](МВ) = 0.02I(МА)\frac{l}{{{{R}_{0}}}} \cdot {{c}_{A}}$ (107 см/с), а в расчетах с a = 0.3 максимальные напряжения примерно равны 0.1 [U]. Со временем напряжение на оси медленно спадает, с характерным гидродинамическим временем турбулентности, т.е. порядка единицы.
В двумерных расчетах довольно быстро устанавливается МГД равновесное состояние на границе перестановочной неустойчивости по Кадомцеву [27].
Из-за того, что максимальные давления, плотности и магнитные поля в зоне сжатия не растут неограниченно по мере сжатия, предположение, на котором основывалась концепция [10, 11] по получению зажигания термоядерных реакций, не выполняется, и зажечь плазму в перетяжке Z‑пинча из-за развития сосисочной неустойчивости при токе I ~ 10 МА вряд ли удастся. Есть сомнения, что на этом пути возможно получение зажигания даже при токе I ~ 100 МА.
Несмотря на отрицательную роль мелкомасштабной сосисочной неустойчивости, нейтронный выход для ряда геометрий плазменного фокуса успешно описывается с помощью ускорительного механизма. Это можно объяснить тем, что благодаря большой кривизне и высокой скорости токово-плазменной оболочки развитие мелкомасштабных рэлей-тейлоровской и сосисочной неустойчивости оказывается подавленным, а включение кинетического аномального сопротивления происходит при не слишком больших сжатиях перетяжки.
Авторы выражают благодарность В.В. Янькову, предложившему проведение исследований возможности получения зажигания с помощью МГД-расчетов. Это предложение в значительной степени способствовало проведению настоящей работы. Авторы благодарят также Д. Клира за полезные обсуждения экспериментов по генерации высокоэнергичных ионов в Z-пинчах.
Список литературы
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982.
Трубников Б.А. // Физика плазмы и проблема управляемых термоядерных реакций. М.: Изд-во АН СССР, 1958. Т. 1. С. 289.
Kruskal M., Schwarzschild M. // Proc. Roy. Soc. A. 1954. V. 223. P. 348.
Шафранов В.Д. // Атом. энергия. 1956. № 5. С. 38.
Гаранин С.Ф. Физические процессы в системах МАГО-MTF. Саров: РФЯЦ-ВНИИЭФ, 2012.
Дьяченко В.Ф., Имшенник В.С. // Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Атомиздат, 1974. Вып. 8. С. 164.
Вихрев В.В., Брагинский С.И. // Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Атомиздат, 1980. Вып. 10. С. 243.
Трубников Б.А., Жданов С.К. // Письма в ЖЭТФ. 1985. Т. 41. № 7. С 292.
Гаранин С.Ф., Чернышев Ю.Д. // Физика плазмы. 1987. Т. 13. № 8. С. 974.
Яньков В.В. Препринт ИАЭ-4218/7. Москва. 1985.
Яньков В.В. // Физика плазмы. 1991. Т. 17. № 5. С. 521.
Klir D., Kravarik J., Kubes P., Rezac K., Anan’ev S.S., Bakshaev Yu.L., Blinov P.I., Chernenko A.S., Kaza-kov E.D., Korolev V.D., Meshcherov B.R., Ustroev G.I., Juha L., Krasa J., Velyhan A. // Phys. Plasmas. 2008. V. 15. P. 032701. https://doi.org/10.1063/1.2839352
Klir D., Shishlov A.V., Kokshenev V.A., Kubes P., Re-zac K., Cherdizov R.K., Cikhardt J., Cikhardtova B., Dudkin G.N., Fursov F.I., Hyhlik T., Kaufman J., Kovalchuk B.M., Krasa J., Kravarik J., Kurmaev N.E., Labetsky A.Yu., Munzar V., Orcikova H., Padalko V.N., Ratakhin N.A., Sila O., Stodulka J., Turek K., Varla-chev V.A., Wagner R. // New J. Phys. 2018. V. 20. P. 053064.
Klir D., Jackson S.L., Shishlov A.V., Kokshenev V.A., Rezac K., Beresnyak A.R., Cherdizov R.K., Cikhardt J., Cikhardtova B., Dudkin G.N., Engelbrecht J.T., Fur-sov F.I., Krasa J., Kravarik J., Kubes P., Kurmaev N.E., Munzar V., Ratakhin N.A., Turek K., Varlachev V.A. // Matter and Radiation at Extremes. 2020. V. 5. P. 026401. https://doi.org/10.1063/1.5132845
Lebedev S.V., Frank A., Ryutov D.D. // Rev. Mod. Phys. 2019. V. 91. № 2. P. 025002.
Гаранин С.Ф., Мамышев В.И. // Физика плазмы. 2008. Т. 34. № 8. С. 695.
Гаранин С.Ф., Долинский В.Ю., Мамышев В.И., Макеев Н.Г., Маслов В.В. // Физика плазмы. 2020. Т. 46. № 10. С. 695.
Гаранин С.Ф., Мамышев В.И. // Вопросы атомной науки и техники. Сер. Теоретическая и прикладная физика. 1989. № 1. С. 23.
Сасоров П.В. // Физика плазмы. 1991. Т. 17. Вып. 12. С. 1507.
Бакшаев Ю.Л., Бартов А.В., Блинов П.И., Черненко А.С., Данько С.А., Калинин Ю.Г., Кингсеп А.С., Королев В.Д., Мижирицкий В.И., Смирнов В.П., Шашков А.Ю., Сасоров П.В., Ткаченко С.И. // Физика плазмы. 2007. Т. 33. № 4. С. 291.
Брагинский С.И. // Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Атомиздат, 1963. Вып. 1. С. 183.
Флетчер К. Вычислительные методы в динамике жидкостей. Т. 1: Основные положения и общие методы. М.: Мир, 1991.
Робертс К., Поттер Д. Вычислительные методы в физике плазмы / Под ред.: Б. Олдер, С. Фернбах, М. Ротенберг, М.: Мир, 1974. С. 335.
Флетчер К. Вычислительные методы в динамике жидкостей. Т. 2: Методы расчета различных течений. М.: Мир, 1991.
Нох В.Ф. Вычислительные методы в гидродинамике / Под ред: Б. Олдер, С. Фернбах, М. Ротенберг. М.: Мир, 1967. С. 128.
Самарский А.А., Попов Ю.П. Разностные схемы газовой динамики. М.: Наука, 1975.
Кадомцев Б.Б. Вопросы теории плазмы / Под ред. М.А. Леонтовича. М.: Атомиздат, 1963. Вып. 2. С. 132.
Дополнительные материалы отсутствуют.



