Физика плазмы, 2022, T. 48, № 10, стр. 962-966

1. ВВЕДЕНИЕ

Особенностью Z-пинчей является генерация значительного количества высокоэнергетичных (быстрых) ионов при сжатии перетяжки, образующейся как результат развития неустойчивости. Реакциями синтеза с участием быстрых ионов дейтерия (или трития) объясняется сравнительно высокий наблюдаемый выход нейтронов [1]. С одной стороны, с учетом эффективной передачи энергии от магнитного поля быстрым ионам это вызывает определенный оптимизм в отношении перспектив мощных источников нейтронов, а, возможно, и термоядерных реакторов на основе Z-пинчей. С другой стороны, считается, что быстрые ионы рождаются в момент разрыва перетяжки, и, поэтому, их доля незначительна.

Быстрые ионы наблюдаются в экспериментах с различными типами нагрузки [1–5]. Детали механизма генерации быстрых ионов на данный момент не получили объяснения на уровне количественных оценок. Сложилась терминология, по которой выделяют “ускорительный” механизм и “тепловой”. В первом случае приходится предполагать, что на стадии разрыва перетяжки возникают экстремально высокие электрические поля. Тепловой механизм подразумевает нагрев при сжатии перетяжки, и, в принципе, на его основе можно удовлетворительно объяснить наблюдаемый спектр ионов [6]. Но тепловой механизм не учитывает особенностей роста энергии ионов в зависимости от их энергии, и, соответственно, от частоты столкновений. Не исключено также, что указанные два механизма могут дополнять друг друга. Поэтому необходимо моделирование кинетики всех ионов без искусственного разделения их на “быстрые” и “тепловые”.

Для оценки выхода нейтронов в [7] рассматривалось модельное распределение ионов по энергиям с определенным условием “сшивки” низкоэнергетичной максвелловской части с высокоэнергетичным “хвостом”, имеющим степенную зависимость от энергии. Оценки выхода нейтронов D–D-реакции в сжимающейся перетяжке для степенного и максвелловского распределений [8] показали значительное превышение отношения выхода нейтронов к средней энергии ионов в первом случае по сравнению со вторым. Оценки в [9] показывают, что можно выделить бесстолкновительную фракцию ионов высоких энергий. На конечной стадии сжатия протекает два параллельных процесса – максвеллизация низкоэнергетичной фракции и ускорение бесстолкновительной высокоэнергетичной фракции. Набор энергии бесстолкновительными ионами при сжатии можно описать как их отражение от сжимающих “стенок” магнитного поля [10]. На основе такой модели в [9] даны оценки выхода нейтронов и его анизотропии. В той или иной мере упомянутые выше оценки подразумевают отдельное рассмотрение ионов с высокими энергиями.

В работе [11] рассматривалось увеличение энергии ионов при “отражении” от магнитных “стенок” и кинетическое моделирование их распределения на основе уравнения Фоккера–Планка в высокоэнергетичном приближении. Несмотря на довольно грубые допущения, в [11] продемонстрирован механизм формирования немаксвелловского распределения ионов при высоких энергиях как результат баланса двух конкурирующих процессов – ускорения при взаимодействии с увеличивающимся магнитным полем и торможения при столкновениях с электронами.

Таким образом, интерпретация спектра ионов, испускаемых Z-пинчем, требует знания их функции распределения по энергиям во все моменты времени сжатия перетяжки, что возможно при использовании кинетического уравнения для всего диапазона энергий (скоростей) с учетом как кулоновских столкновений ионов с ионами и, главным образом, с электронами, а также воздействия нарастающего во времени магнитного поля. В настоящей работе исследование в такой постановке выполнено на основе уравнения Фоккера–Планка.

2. РАСПРЕДЕЛЕНИЕ И СПЕКТР ИОНОВ

Нестационарное уравнение Фоккера–Планка для ионов в перетяжке рассмотрим в рамках следующих приближений. Функцию распределения $f({v},t)$ по скоростям считаем однородной в пространстве и изотропной по направлениям скорости. Используем дивергентную форму, в которой силовое воздействие переменного магнитного поля учитывается в выражении потока в фазовом пространстве скоростей.

При указанных приближениях уравнение Фоккера–Планка имеет вид

где D – коэффициент кулоновской диффузии, A – коэффициент кулоновского трения, b – коэффициент ускорения при взаимодействии с переменным магнитным полем, ${{\tau }_{{v}}}$ – характерное время потерь.

Высокоэнергетичные ионы взаимодействуют прежде всего с электронами, а также с ионами сравнительно низких энергий. Электроны можно считать максвелловскими. Поэтому для коэффициентов диффузии D и трения A будем использовать выражения, соответствующие потенциалам Розенблюта–Трубникова [12, 13] для максвелловского фона [14]. При этом, в частности, выполняется соотношение $D = - \frac{{kT}}{{mv}}A$.

Коэффициент ускорения при взаимодействии с нарастающим во времени магнитным полем $b = \frac{{\delta v}}{{\delta t}}$, где $\delta {v}$ – изменение скорости за время δt. По модели магнитного поршня как движущихся стенок $\delta v \approx - \frac{{da}}{{dt}}$, где a – текущий радиус перетяжки. Время пролета между стенками составляет $\delta t \approx a{\text{/}}v$. В результате

Отметим, что ускорение в переменном магнитном поле B связано с индуцируемым вихревым электрическим полем E, величину которого оценим из соотношения $\frac{{\Delta B}}{{\Delta t}} \approx \frac{E}{r}$, где r = a, a – текущий радиус перетяжки. На участке траектории частицы при ее “отражении” от области переменного магнитного поля $\frac{{\Delta B}}{{\Delta t}} \approx \frac{{\partial B}}{{\partial r}}\frac{{da}}{{dt}} \approx - \frac{B}{r}\frac{{da}}{{dt}}$, где $\Delta t \approx \frac{m}{{eB}}$. Изменение импульса частицы соответствует силе, действующей со стороны электрического поля, т.е. $m\delta v \approx eE\Delta t \approx er\Delta B \approx - er\frac{B}{r}\frac{{da}}{{dt}} \times $ $ \times \;\frac{m}{{eB}} = - m\frac{{da}}{{dt}}$ . На основе этих оценок приходим к тому же результату, что выражен соотношением (2).

Для решения необходимо задать ряд параметров фоновой плазмы. В рамках самосогласованной постановки они должны зависеть от искомой функции распределения ионов. Однако в этом случае необходимо решать также задачу описания динамики перетяжки, что не входит в цели данного этапа анализа. Поэтому используем простые соотношения, соответствующие автомодельному решению [6], качественно описывающие изменение параметров во времени

где N – число частиц на единицу длины; T – температура; a – радиус перетяжки; n – плотность (концентрация частиц); τ – характерное время потерь частиц; те же величины с индексом “0” – начальные значения, соответствующие началу процесса сжатия перетяжки; α ~ 10 – параметр, характеризующий траектории ионов с учетом магнитного поля, k – постоянная Больцмана, m – масса иона.

Изменение магнитного поля в автомодельном решении учтено с помощью условия Беннета. Автомодельное решение имеет свойство $n \propto {{T}^{{3{\text{/}}2}}}$, что важно с точки зрения эволюции функции распределения максвелловских компонентов – электронов, в частности. При t → t₁ автомодельное решение приводит к особенности. Поэтому в качестве окончания процесса (разрыва перетяжки) принимаем, например, t = 0.95t₁.

Характерное время потерь $\tau {v}$, входящее в (1), по аналогии с (7), (8) примем в виде зависимости

где ${{\alpha }_{v}}$ – постоянная.

В выражении (8) в рамках гидродинамического описания время потерь зависит от текущего значения радиуса перетяжки и характерной тепловой скорости частиц, связанной с текущей температурой. Так как при кинетическом моделировании автомодельное решение используется нами для задания свойств “фоновой плазмы”, то для выражения (9) описывает потери частиц подобным образом с той разницей, что время потерь различно для частиц различных энергий и зависит от скорости “пробной” частицы.

В приосевой области пинча поле практически нулевое, на границе сверхсильное поле соответствует величине тока, протекающего через поперечное сечение пинча. Траектории частиц в таком неоднородном поле имеют сложный вид [4], что затрудняет строгий учет структуры поля и траекторий частиц. Поэтому используется изотропное приближение для функции распределения, а особенности сложных траекторий при этом упрощенно учитываются с помощью коэффициента α (или ${{\alpha }_{v}}$).

Полезно проанализировать уравнение (1) при высоких энергиях. Можно пренебречь кулоновской диффузией. В коэффициенте кулоновского трения можно ограничиться учетом только столкновений ионов с электронами, тогда $A \approx - v{\text{/}}{{\tau }_{s}}$, где τ_s – время замедления быстрых ионов на электронах. Так как мы предполагаем $n \propto {{T}^{{3{\text{/}}2}}}$, то τ_s = = const. С учетом зависимости параметров от времени запишем (1) для области высоких энергий

где ${{v}_{0}} = \sqrt {\tfrac{{k{{T}_{0}}}}{m}} $ – характерная тепловая скорость ионов по начальной температуре.

Как можно видеть из (10), в качестве масштаба времени следует принять t₁, а масштаба скорости – ${{v}_{0}}$. Тогда отношение t₁/τ_s можно рассматривать как безразмерный параметр задачи. Торможение на электронах описывается первым слагаемым в квадратных скобках, ускорение переменным магнитным полем – вторым слагаемым, потери частиц описываются последним членом в правой части. При t → t₁ основными процессами становятся нагрев и потери частиц. Учитывая их зависимость от скорости можно утверждать, что именно эти процессы формируют немаксвелловское распределение ионов высоких энергий на завершающей стадии сжатия перетяжки. Параметр t₁/τ_s определяет начало этой стадии как переход быстрых ионов в бесстолкновительный режим.

При численном моделировании рассматривалось уравнение Фоккера–Планка в виде (1). В качестве начальных условий использовалось максвелловское распределение с температурой T₀ = = 3 кэВ. Начальная плотность n₀ = 2 × 10²⁶ м^–3; высота перетяжки h = 2.5 мм, начальный радиус a₀ = 2.5 мм (равен радиусу невозмущенного пинча); высота всего пинча H = 12.5 мм (необходима для иллюстрации полного количества частиц различных энергий). Значениях указанных параметров были выбраны так, чтобы характерные времена сжатия перетяжки и торможения быстрых ионов были одного порядка. В частности, при указанных условиях t₁/τ_s ≈ 0.5. Для таких условий величина тока должна быть I = 8.7 МА, энергия, вложенная в плазму, – W₀ ≈ 70 кДж (энергия генератора порядка нескольких МДж), что соответствует уровню существующих экспериментальных установок.

В расчетах принято значение параметра, входящего в формулу (9), ${{\alpha }_{v}} = 10$. Первое граничное условие учитывало особенности баланса частиц в фазовом пространстве при $v \to 0$, а именно, в первой ячейке по скорости отдельно рассматривался баланс плотности частиц и их поток. Второе граничное условие – равенство нулю искомой функции при $v \to \infty $ обеспечивалось при достаточно большом, но конечном значении скорости, так, чтобы это значение не влияло на результат.

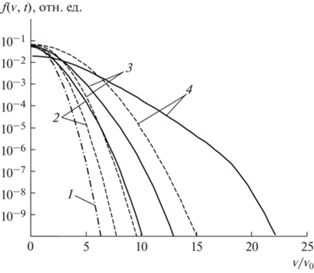
Результаты расчета представлены на рис. 1, где показана функция распределения, нормированная на плотность частиц (на их число в единице объема). Отметим, что уравнение (1) соответствует нормировке функции распределения на полное число частиц. Момент времени t = 0.95t₁ принят за окончание процесса сжатия перетяжки, т.е. условный ее разрыв. Для рассматриваемых условий t₁/τ_s ≈ 0.5. Как можно видеть, в области высоких энергий функция распределения ионов по скоростям сильно отличается от максвелловской, в особенности на завершающей стадии сжатия.

Отметим, что рассчитанные интегральные характеристики (число частиц, полная энергия), а также средняя энергия, в пределах 10–15% отличаются от соответствующих величин, заданных по автомодельному решению. При этом качественное изменение во времени полностью подобно.

Функция распределения – мгновенная характеристика системы в каждый момент времени t. В рассматриваемом случае приближенно принимаем, что параметры плазмы существенно изменяются в объеме перетяжки, а в остальной “невозмущенной” части пинча параметры остаются практически постоянными. Энергетический спектр ионов – интегральная величина, включающая информацию о функции распределения за время процесса сжатия от начального момента (t = 0) до конечного (или некоторого текущего) момента времени t. Говоря о спектре ионов, мы должны ориентироваться на величину, соответствующую той, что детектируется в экспериментах. Поэтому спектр ионов складывается из потока ионов за время от начального момента до конечного, а также включает те ионы, которые остались в перетяжке и в невозмущенной части пинча на момент условного разрыва перетяжки.

Спектр ионов, покидающих перетяжку

где $E = \frac{{m{{v}^{2}}}}{2}$ – энергия иона, ${{f}_{E}}(E,t)$ – функция распределения по энергиям.

Вклад “невозмущенной” части пинча в спектр представляет из себя фактически максвелловскую функцию распределения по энергиям, соответствующую начальной температуре T₀ и начальной концентрации ионов n₀. Распределение ионов в пинче на момент условного разрыва перетяжки также включается в суммарный спектр.

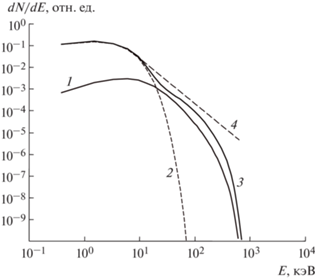
Результаты расчета спектра приведены на рис. 2, где также показана вспомогательная зависимость dN/dE ∝ E^–2. Для рассмотренных условий можно говорить, что при энергиях E ~ ~ 100 кэВ спектр сравнительно близок к степенной зависимости. Отметим, что эта зависимость проявляется в более явном виде при увеличении конечного времени, т.е. при t → t₁.

3. ЗАКЛЮЧЕНИЕ

Кинетический подход позволяет количественно определить распределение ионов по скоростям (и по энергиям), формируемое при сжатии перетяжки Z-пинча с учетом их ускорения при воздействии нарастающего во времени магнитного поля. Отношение t₁/τ_s характерного времени сжатия и времени замедления быстрых ионов на электронах показывает, что максимальная передача энергии быстрым ионам реализуется при больших временах замедления, т.е. при сравнительно низких плотностях.

В рамках приближения, предполагающего заданные законы изменения параметров во времени, кинетическое моделирование продемонстрировало картину генерации спектра ионов, в целом соответствующую экспериментальным представлениям. Для построения более точной самосогласованной модели необходимо использование кинетического описания совместно с уравнениями макроскопической динамики перетяжки.