Физика плазмы, 2022, T. 48, № 11, стр. 1066-1074

1. ВВЕДЕНИЕ

Известно, что большая часть космической плазмы представляет собой плазму с конденсированной дисперсной фазой. Такую плазму часто называют пылевой плазмой [1]. В межзвездном пространстве пыль везде встречается вместе с газом. На ее долю приходится примерно один процент от массы газа. Интерес к изучению непосредственно космических пылевых частиц растет. Межпланетная пыль регулярно собирается бортовыми коллекторами в стратосфере Земли [2]. В 2006 г. была организована миссия НАСАStardust (“Звездная пыль”), осуществившая сбор и доставку капсулы с образцами частиц из окрестностей ядра кометы 81P/Wild 2 на Землю [3]. Примером повышенного интереса к пылевой плазме в космосе может также служить история исследования лунной пыли. В недавней американской миссии LADEE (Lunar Atmosphere and Dust Environment Explorer – “исследователь лунной атмосферы и пылевой среды”) [4] проводились наблюдения за лунной пылью с орбиты космического модуля. Следует также упомянуть, что на протяжении уже почти двадцати лет международной группой исследователей, в которую входят и казахстанские ученые, проводятся эксперименты с пылевой плазмой в условиях микрогравитации на борту Международной космической станции (МКС) [5].

Измерения, выполненные космическими аппаратами, показали, что отклонение от равновесного распределения частиц часто обнаруживается в солнечном ветре, в плазме планетарных магнитосфер и некоторых других астрофизических объектах из-за присутствия частиц с высокими энергиями [6, 7]. В большинстве случаев распределение частиц имеет степенной “хвост” в области высоких энергий, и по имеющимся эмпирическим данным лучше всего такое распределение соответствует так называемому семейству каппа- распределений (κ-распределений) [8]. В настоящее время оно уже нашло интересные применения в пылевой космической плазме. Например, в работе [9] были исследованы пыле-акустические солитоны в пылевой плазме с κ-распределенными ионами.

Одной из важных задач в области космической пылевой плазмы является исследование зарядки пылевых частиц. Размеры пылевых частиц, входящих в состав космической плазмы, составляют от десятых и сотых долей микрометра до нескольких микрометров, благодаря чему частицы могут приобретать очень большие статические электрические заряды за счет потоков ионов и электронов на их поверхность. В случае учета вторично-электронных ионн-электронных эмиссионных процессов пылинки могут заряжатся положительно. Целью данной работы является исследование процесса зарядки пылевых частиц в космической неравновесной плазме с учетом различных механизмов зарядки. Для описания процесса зарядки пылинок широко применяется метод ограниченного орбитального движения, так называемое приближение OML (orbit motion limited). В уравнениях, полученных на основе этого метода, было использовано равновесное распределение Максвелла. Мы использовали приближение OML с учетом каппа-распределения. Получены выражения для потоков электронов и ионов на основе каппа-распределения, получена зависимость приведенного заряда пылевой частицы от параметров системы.

2. ТЕОРИЯ И РЕЗУЛЬТАТЫ

Модель приближения OML [10] позволяет из законов сохранения энергии и момента импульса определить сечения поглощения электронов и ионов пылевой частицей. Применимость метода обычно выражается следующим условием:

где ${{\lambda }_{D}}$ – длина экранирования плазмы (радиус Дебая), ${{l}_{{e(i)}}}$ – длина свободного пробега электронов (ионов), a – радиус пылевой частицы. Также подразумевается, что другие пылевые частицы не оказывают влияния на движение электронов и ионов в ее окрестности.

В приближении OML считается, что электроны и ионы поглощаются в том случае, если их траектории пересекают поверхность пылевой частицы или касаются ее. Тогда сечения поглощения, зависящие от их скоростей, имеют следующий вид:

где ${{m}_{{e(i)}}}$ – масса электронов (ионов), а $v$ – скорости электронов и ионов относительно пылевой частицы, ${{\varphi }_{s}}$ – связанный с зарядом стационарный потенциал поверхности пылевой частицы. В рамках приближения ограниченного орбитального движения ${{\sigma }_{e}}(v)$ и ${{\sigma }_{i}}(v)$ не зависят от конкретной формы распределения электрического потенциала в окрестности пылевой частицы. Потоки электронов и ионов на поверхность частицы определяются интегрированием соответствующего сечения с функциями распределения частиц по скоростям ${{f}_{{e(i)}}}(v)$где ${{n}_{{e(i)}}}$ – концентрация электронов (ионов). Выражение для максвелловского распределения плазменных частиц по скоростям

Каппа-распределение плазменных частиц по скоростям записывается следующим образом:

где ${{v}_{{Te(i)}}} = \sqrt {{{k}_{B}}{{T}_{{e(i)}}}{\text{/}}{{m}_{{e(i)}}}} $ обозначает тепловую скорость электронов (ионов), κ – спектральный индекс, ${{k}_{B}}$ – постоянная Больцман, ${{T}_{{e(i)}}}$ – температура электронов (ионов).

Стоит отметить, что при $\kappa \to \infty $ каппа-распределение стремится к распределению Максвелла, что и можно наблюдать из рис. 1. Распределения скоростей представлены в безразмерном виде $f\left[ {\nu {\kern 1pt} *} \right] = {{f}_{e}}\left( {\nu {\kern 1pt} * = \frac{v}{{{{v}_{{Te}}}}}} \right)v_{{Te}}^{3}$.

Интегрирование (3) с учетом (2) и (4) дает следующие выражения для потоков ионов и электронов

В настоящей работе получены выражения для потоков электронов и ионов на основе κ-распределения, которые записываются следующим образом:

Стационарный потенциал поверхности и заряд пылевой частицы определяется равенством потоков ионов и электронов, поглощаемых частицей

Вводим следующие безразмерные параметры, которые широко используются в разных работах [11, 12]

здесь z – абсолютная величина заряда частицы в единицах $a{{k}_{B}}{{T}_{e}}{\text{/}}e$ (в дальнейшем просто приведенный заряд), ${{Z}_{d}}$ – зарядовое число пылевой частицы (заряд, выраженный в единицах элементарного заряда $e$), τ и μ – отношения температур и масс электронов и ионов, соответственно. Надо отметить, что в обычной газоразрядной плазме отношение температур $\tau \gg 1$$(\tau \sim 10{\kern 1pt} - {\kern 1pt} 100)$, абсолютная величина заряда $z \geqslant 1$ и конечно, $\mu \ll 1$. В табл. 1 представлены параметры реальных плазм в космосе и в экспериментальных установках, приведенные в работе [13].

Выражения (6), (7) для потоков электронов и ионов распределения Максвелла в безразмерном виде записываются как

для каппа-распределения где $a{\kern 1pt} * = \frac{a}{{{{a}_{0}}}}$ – отношение радиуса пылевых частиц к среднему расстоянию между частицами ${{a}_{0}} = {{\left( {\frac{3}{{4\pi {{n}_{e}}}}} \right)}^{{1/3}}}$. Для частицы с радиусом $a = 1\,\,мкм$ и ${{n}_{е}} \approx {{10}^{9}}$ см^–3, $a{\kern 1pt} * \approx {{10}^{{ - 1}}}$, а параметр $n{\kern 1pt} * = \frac{{{{n}_{e}}}}{{{{n}_{i}}}}$ является отношением концентраций электронов и ионов. На рис. 2 представлена зависимость потоков электронов и ионов от параметра z. Результаты показывают схожее поведение с результатами, полученными на основе максвелловского распределения при $\kappa \to \infty $.

С учетом безразмерных переменных и выражений для потоков ионов и электронов уравнение (10) для распределения Максвелла может быть переписано в виде

Если перезаписать уравнение (10) для потоков электронов и ионов с учетом каппа-распределения, получим следующее выражение:

Для уединенной частицы условие квазинейтральности имеет вид ${{n}_{i}} = {{n}_{e}}$. Тем самым величину приведенного параметра $z$ определяют фактически отношения температур электронов и ионов плазмы, а также род газа (отношение масс электронов и ионов).

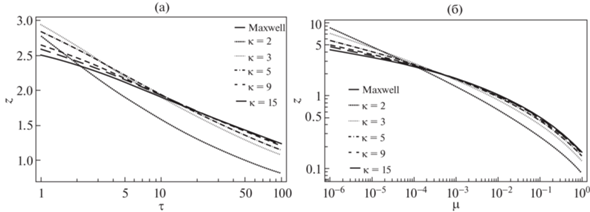
Абсолютная величина безразмерного заряда уединенной сферической пылевой частицы как функция отношения температур электронов и ионов τ и как функция отношения масс электронов и ионов μ представлена на рис. 3. Данные результаты получены с помощью выражений (16) и (17), на основе распределения Максвелла и каппа-распределения, соответственно. Приведенный заряд частицы z уменьшается с увеличением как отношения температур τ, так и отношения масс электронов и ионов $\mu $.

Выражения (16) и (17) получены для уединенных частиц в плазме. Однако концентрация пылевых частиц может сильно влиять на их заряд. За счет ухода заметной части свободных электронов на соседние пылевые частицы, уменьшается их потенциал и заряд по абсолютной величине. Для учета данного обстоятельства и считая условие (1) выполненным, используя выражения для потоков электронов и ионов (12)–(15), принимая во внимание вклад пылевой компоненты в зарядовый состав плазмы, условие квазинейтральности записывается

И вместо уравнений (16) и (17) выражения для определения равновесного потенциала записываются для максвелловского и каппа-распределения следующим образом:

где параметр $P = \left| {{{Z}_{d}}} \right|\frac{{{{n}_{d}}}}{{{{n}_{e}}}}$ – определяет отношение плотностей заряда пылевой и электронной компонент и называется параметром Хавнеса [14]. Вычисленный при $P \ll 1$ заряд соответствует заряду уединенной частицы, а при $P > 1$ он существенно уменьшается по абсолютной величине, что и можно наблюдать из рис. 4, построенного на основе уравнений (19) и (20) для параметра каппа $\kappa = 5$. Более подробно данную зависимость для разных значений параметра каппа можно видеть на рис. 5.

Для получения зависимости заряда z от времени используется уравнение [12]

где суммирование производится по всем потокам заряженных частиц ${{I}_{J}}$, поглощаемых либо эмитируемых пылевой частицей, взятым с соответствующим знаком. Стационарный заряд пылевых частиц определяется выражением

При рассмотрении зарядки пылевых частиц в отсутствие эмиссионных процессов за счет потоков ионов и электронов для максвелловского распределения скоростей частиц используем выражения для потоков электронов (6) и ионов (7) на поверхность заряженной уединенной сферической частицы в приближении OML. Введем безразмерное время: $t{\kern 1pt} * \to \frac{{{{\omega }_{{pi}}}}}{{\sqrt {2\pi } }}\left( {\frac{a}{{{{\lambda }_{{Di}}}}}} \right)t$, ${{\lambda }_{{Di}}} = \sqrt {{{k}_{B}}{{T}_{i}}{\text{/}}4\pi {{e}^{2}}{{n}_{i}}} $ – ионный дебаевский радиус, ${{\omega }_{{pi}}} = \frac{{{{v}_{{Ti}}}}}{{{{\lambda }_{{Di}}}}}$ – ионная плазменная частота, и перепишем уравнение (21) для максвелловского распределения скоростей частиц

для каппа-распределения скоростей частиц

Вместе с начальным условием $z(t{\kern 1pt} * = 0) = 0$ уравнение позволяет определить стационарный приведенный заряд $z = z\left( {\tau ,\mu } \right)$ при $t{\kern 1pt} * \to \infty $ и характерное время $t_{{ch}}^{*}\left( {\tau ,\mu } \right)$ зарядки пылевой частицы от незаряженного состояния. В работе [11] характерное время зарядки определено как ${{t}_{{ch}}} = \frac{{\left| {{{Z}_{d}}} \right|}}{{{{I}_{0}}}}$, где ${{I}_{0}} = {{I}_{{e0}}} = {{I}_{{i0}}}$ – потоки электронов и ионов в стационарном состоянии. А частота зарядки ${{\Omega }_{{\,ch}}}$ как частота релаксации малых возмущений заряда к стационарному значению, ${{\Omega }_{{\,ch}}} = {{\left. {\frac{{d{{I}_{0}}}}{{d{{Z}_{d}}}}} \right|}_{{{{Z}_{{d0}}}}}},$ где значение производной вычисляется для стационарного заряда.

На рис. 6 представлены результаты вычисления зарядки пылевых частиц в отсутствие эмиссионных процессов за счет потоков ионов и электронов при соотношении температур электронов и ионов $\tau = 50$ для плазмы с ионами аргона. Также, на рисунке безразмерные величины $\Omega _{{\,ch}}^{{ - 1}}$ и ${{t}_{{ch}}}$ указаны вертикальными штриховыми линиями. Вертикальные линии (первые две слева) соответствуют значениям величины $\Omega _{{\,ch}}^{{ - 1}}$ для макселловского и каппа-распределения (слева направо), а две другие вертикальные линии соответсвуют значениям величины ${{t}_{{ch}}}$. То есть результаты показывают, что для немаксвелловского распределения скоростей частиц характерное время зарядки пылевых частиц увеличивается почти в два раза по сравнению с характерным временем зарядки частиц для макселловского распределения частиц. Отметим, что горизонтальная линия показывает стационарный приведенный заряд пылевых частиц. Результаты показывают хорошее согласие с результатами работы для максвелловского распределения [11]. Для плазмы с ионами гелия, которая более широко распространена в космосе чем плазма аргона, результаты ведут себя аналогично.

При вторичной электронной эмиссии поток вторичных эмитированных электронов ${{I}_{{se}}}$ связан с потоком первичных электронов ${{I}_{e}}$ через коэффициент вторичной электронной эмиссии δ, определяющего отношение потока выбитых вторичных электронов ${{I}_{{se}}}$ с поверхности пылевой частицы к потоку ${{I}_{e}}$ падающих электронов ${{I}_{{se}}} = \delta {{I}_{e}}$. Коэффициент δ зависит как от энергии первичных электронов Е, так и от материала пылевой частицы. Зависимость $\delta (Е)$ оказывается почти универсальной для различных материалов, если нормировать δ на величину максимального значения коэффициента вторичной электронной эмиссии ${{\delta }_{m}}$, а текущую энергию падающих электронов E на энергию ${{E}_{m}}$, при которой этот максимум ${{\delta }_{m}}$ достигается. Для некоторых материалов, из которых состоит пылевая частица величины параметров ${{\delta }_{m}}$, и ${{E}_{m}}$ составляют ${{\delta }_{m}} \sim \left( {1{\kern 1pt} - {\kern 1pt} 4} \right)$, ${{E}_{m}} \sim \left( {0.2{\kern 1pt} - {\kern 1pt} 0.4} \right)$ кэВ. Таким образом для вычисления зарядки пылевых частиц за счет вторичной электронной эмиссии выражение (21) перезаписывается следующим образом:

где ${{I}_{e}},\,\,{{I}_{i}}$ – потоки электронов и ионов соответствующей функции распределения скоростей частиц, тогда как поток вторичной электронной эмиссии определяется выражением здесь функция ${{F}_{{5,B}}} = {{F}_{{5,B}}}\left( x \right)$ задана в интегральном виде и нижний предел определяется положительным квадратом ${{B}^{2}} = 4e{{\varphi }_{s}}{\text{/}}{{E}_{m}}$. Надо отметить, что так как обьектом исследования является космическая пылевая плазма, мы рассматриваем случай, когда ${{\varphi }_{s}} < 0$.

Таким образом выражение (25) для макселловского распределения имеет вид

для каппа-распределения здесь $\beta = 3.7{{\delta }_{m}}{{F}_{{5,B}}}\left( {\frac{{{{E}_{m}}}}{{4{{k}_{B}}{{T}_{e}}}}} \right)$. В работах [15], где исследуется зарядка пылевых частиц в результате вторичной электронной эмиссии, значение коэффициента вторичной эмиссии берется ${{\delta }_{m}} = 15$, а отношение $\frac{{{{E}_{m}}}}{{{{k}_{B}}{{T}_{e}}}} \simeq 180$, данные значения были использованы и в данной статье.

Результаты учета вторичной электронной эмиссии показывают (рис. 7), что время зарядки не меняется с увеличением параметра каппа, а величина приведенного заряда уменьшается с увеличением параметра каппа.

За счет эффекта фотоэмиссии при облучении пылевых частиц в плазме потоком фотонов с энергией, превосходящей работу выхода фотоэлектрона с их поверхности, пылевые частицы могут приобретать положительный заряд [16, 17]. Так как характерная величина работы выхода фотоэлектрона для большинства веществ не превышает 6 эВ, фотоны с энергией меньше 12 эВ могут зарядить частицы, не ионизируя при этом буферный газ (как правило водород). От свойств источника излучения, материала частиц, а также знака их заряда зависит величина потока эмитированных электронов, которая выражается следующим образом [17]:

здесь J_p – плотность потока фотонов, Y_p – квантовый выход материала пылевых частиц. А выражение (21) с учетом потока фотонов для максвелловского распределения записывается следующим образом: для каппа-распределения где $\alpha = \sqrt {2\pi } \frac{{{{Y}_{p}}{{J}_{p}}}}{{{{n}_{e}}{{v}_{{Te}}}}}$, здесь безразмерное время уже другое, связанное с электронной плазменной частотой $t{\kern 1pt} ' \to \frac{{{{\omega }_{{pe}}}}}{{\sqrt {2\pi } }}\left( {\frac{a}{{{{\lambda }_{{De}}}}}} \right)t$, ${{\lambda }_{{De}}} = \sqrt {{{k}_{B}}{{T}_{e}}{\text{/}}4\pi {{e}^{2}}{{n}_{e}}} $ – электронный дебаевский радиус, ${{\omega }_{{pe}}} = \frac{{{{v}_{{Te}}}}}{{{{\lambda }_{{De}}}}}$ – электронная плазменная частота.

На рис. 8 представлены результаты исследования зарядки пылевых частиц за счет фотоэлектронной эмиссии частиц для плазмы с ионами аргона. Параметр квантового выхода материала брался как Y_p = 0.5, а концентрация электронов ${{n}_{e}} \approx {{10}^{9}}$ см^–3. Безразмерное время зарядки увеличивается с увеличением параметра каппа, и, наоборот, с увеличением параметра каппа уменьшается абсолютная величина безразмерного приведенного заряда z.

3. ВЫВОДЫ

В работе исследован процесс зарядки пылевой частицы в космической плазме. Для исследования был использован метод орбитального ограниченного движения. Уравнения данного метода решались на основе каппа-распределения, определяемое параметром $\kappa $, значение которого в расчетах может изменятся от 2 до 100. В результате исследования получена зависимость приведенного заряда пылевой частицы от параметров системы. Получены выражения для потоков электронов и ионов на основе каппа-распределения. Показано, что при параметре $\kappa \to \infty $ эти формулы переходят в выражения, полученные на основе максвелловского распределения. Иследование процесса зарядки пылевых частиц с учетом различных механизмов было проведено для широкого диапазона значений параметров системы: соотношения масс электронов и ионов, соотношения температуры электронов и ионов. Зависимость приведенного заряда от времени зарядки без учета эмисионных процессов показала, что характерное время зарядки для каппа-распределения увеличивается по сравнению с характерным временем зарядки частиц для максвелловского распределения частиц. Результаты учета вторичной электронной эмиссии показывают, что время зарядки не меняется с увеличением параметра каппа, а величина приведенного заряда уменьшается с увеличением этого параметра. В то же время при учете фотоэлектронной эмиссии безразмерное время зарядки увеличивается с увеличением параметра каппа, и, наоборот, с увеличением параметра каппа уменьшается абсолютная величина приведенного заряда. В дальнейшем результаты исследований планируем применить для исследования зарядки пылевых части в реальных астрофизических объектах.

Настоящая работа была выполнена при поддержке гранта АР09058005 МОН РК.