Физика плазмы, 2022, T. 48, № 2, стр. 168-183

1. ВВЕДЕНИЕ

Ускорение заряженных частиц из плазмы под действием мощных лазерных импульсов продолжает оставаться одной из актуальных тематик современной физики высоких плотностей энергии. Энергия ионов, генерируемых при таком взаимодействии, до сих пор не превысила порог 100 МэВ [1, 2]. Сильно проигрывающие классическим ускорителям как по энергии, так и по числу частиц такие пучки ускоренных ионов могут представлять практический интерес благодаря своей ультракороткой длительности, малым пространственным размерам, а также компактности современных лазерных установок. Потенциальные области применения включают в себя: инициирование ядерных реакций [3], генерацию узконаправленных пучков нейтронов [4], радиографию полей в плотной плазме [5, 6], ядерную фармакологию и создание короткоживущих изотопов [7, 8], “быстрый поджиг” термоядерных мишеней [9–11] и многие другие.

Развитие лазерных систем высокой мощности позволяет уже сейчас достигать интенсивностей лазерного излучения порядка 10²² Вт/см² [12, 13]. При столь высоких световых потоках и небольших размерах мишени становится возможна ситуация практически полного удаления электронов из плазмы. Реализуется режим кулоновского взрыва. При этом ускоряющее поле является максимально возможным для данной конфигурации плазмы. Поэтому анализ характеристик ионов из взрывающихся мишеней очень важен для понимания предельно достижимых возможностей лазерного ускорения [14]. Важную роль в подобном анализе, безусловно, играет построение теоретических моделей.

Экспериментально наблюдался пока только взрыв сферических кластеров [15–18], из которых, благодаря быстрому трехмерному падению электростатического поля, возможно полное удаление электронов уже при умеренных интенсивностях лазерного излучения. По этой же причине исследования кулоновского взрыва в основном посвящены сферическим мишеням [19–28]. Для плоских мишеней рассматривается модель направленного кулоновского взрыва [29–31].

В данной работе мы сконцентрируемся на изучении плоских мишеней, как обеспечивающих направленный поток ускоренных частиц большей плотности, чем достигается в газе атомных кластеров. Несмотря на свою простоту, связанную с отсутствием необходимости самосогласованно учитывать поведение электронной компоненты плазмы, кулоновский взрыв все еще недостаточно изучен теоретически.

Повышение эффективности ускорения связано с использованием мишеней с двумя сортами ионов [27, 29, 32]. “Подталкивая” более легкие частицы своим кулоновским полем, тяжелые ионы остова играют роль “кулоновского поршня”, что положительно сказывается на спектрально-энергетических характеристиках ускоренных частиц [33, 34]. Собственное поле легких ионов увеличивает как их энергию, так и спектральную ширину [34]. Таким образом, модель, пригодная для проведения оптимизационных исследований в широком диапазоне параметров, должна учитывать и движение “поршня”, и поле легких ионов.

Имеющиеся теоретические работы не удовлетворяют этому критерию в полной мере. Например, в [35] рассмотрена плоская двухкомпонентная мишень без учета движения тяжелых ионов, поле легких ионов считается пренебрежимо малым (они являются примесью). В работе [36] для сферической мишени учтено движение “поршня”, но без поля примеси. Учет движения “поршня” для плоских мишеней в пренебрежении полем примеси был сделан для ее слоистого [37] и однородного распределения [38]. Наконец, в работе [34] описано и движение тяжелых ионов, и самодействие легких ионов. Последнее было сделано только в рамках теории возмущений, что опять же ограничивает применение модели.

В настоящей работе мы ликвидируем оставшийся пробел и предлагаем теоретическую модель, являющуюся обобщением работы [34] на произвольное количество (полный заряд) легких ионов в мишени. Оптимальные параметры слоистых мишеней [34], существенно улучшающие характеристики ионов, находятся в диапазоне малых значений заряда легких ионов, где хорошо работает теория возмущений. По этой причине в данной работе слоистые мишени не рассматриваются.

Предлагаемая аналитическая модель построена в рамках пренебрежения действием поля легких ионов на разлет ионов остова. Для определения точности получаемых результатов они сравниваются с численным решением. Таким же образом определяются границы применимости рассматриваемой модели. Аналогично оригинальной работе [34], спектрально-энергетические характеристики ускоренных легких ионов анализируются на “детекторе”, расположенном на фиксированном расстоянии от мишени. Исследована зависимость от основных управляющих параметров относительного заряда (числа частиц) легких ионов с энергиями вблизи максимальной. Найдено оптимальное значение доли легких ионов в мишени, при которой генерируются пучки наилучшего качества. Также проведено сравнение с результатами теории возмущений из работы [34]. Рассмотрен предельный переход к бесконечно тяжелым ионам остова, аналогично работе [35].

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим плазму мишени, содержащую ионы двух сортов: тяжелые составляют ее основу, остов, и легкие. В рамках механизма кулоновского взрыва электроны считаются удаленными из объема мишени под действием лазерного импульса. Это выполняется при достаточно высоких, ультрарелятивистских интенсивностях падающего излучения. Условием для удаления электрона из мишени является превышение лазерного поля над электростатическим полем притяжения со стороны ионов. Первое можно выразить через безразмерную амплитуду, ${{a}_{L}}$, следующим образом: ${{E}_{L}} = {{a}_{L}}{{m}_{e}}\omega c{\text{/}}e$ (e – элементарный заряд, c – скорость света, ${{m}_{e}}$ – масса электрона). Напряженность поля плоского заряженного ионного слоя есть ${{E}_{C}} = 2\pi \sigma $, где поверхностная плотность заряда, σ, выражается через объемную плотность ионов мишени, n, с зарядом Z и ее толщину L: $\sigma = ZneL$. C учетом электронейтральности мишени, ${{n}_{e}} = Zn$, где ${{n}_{e}}$ – плотность электронов в мишени (до их удаления), условие ${{E}_{L}} > {{E}_{C}}$ принимает вид

где ${{n}_{{cr}}}$ – критическая плотность для данной частоты лазерного излучения ω (длины волны λ). Условие (1) обсуждается, например, в [31, 39–41] и, очевидно, отличается от ограничений, накладываемых на лазерное поле для реализации кулоновского взрыва сферического кластера [20, 27]. Также выражение (1) совпадает с полученным аналитически критерием релятивистской прозрачности плазменного слоя конечной толщины [42]. Подставляя выражения для безразмерной амплитуды лазерного поля ${{a}_{L}} = 0.85\lambda \;[{\text{мкм}}]\sqrt {I[xt\;{\text{Вт/с}}{{{\text{м}}}^{2}}] \times {{{10}}^{{ - 18}}}} $ и критической плотности ${{n}_{{cr}}} = {{m}_{e}}{{\omega }^{2}}{\text{/}}4\pi {{e}^{2}}$, окончательно получаем условие на интенсивность которое, как видно, не зависит от длины волны падающего излучения. Оценка (2) для полностью ионизованной мишени из алюминия толщиной $L = 50$ нм дает $I > 1.7 \times {{10}^{{22}}}$ Вт/см². Для взрыва углеродной мишени толщиной 10 нм и плотностью 1 г/см³ достаточно интенсивности 10²⁰ Вт/см². Таким образом, варьируя параметры мишени, можно добиться реализации кулоновского взрыва при интенсивностях 10²⁰–10²² Вт/см². Естественно, если речь идет об облучении мишеней с толщинами в несколько нанометров [43], необходимы лазерные импульсы с высокими контрастами.

Для максимизации выхода ускоренных частиц целесообразно рассматривать твердотельные, закритические мишени: ${{n}_{e}} > {{n}_{{cr}}}$. Эффективное удаление электронов требует хорошего, объемного проникновения лазерного поля внутрь мишени. Это означает, что ее толщина не должна превышать глубины скин-слоя излучения (релятивистского для рассматриваемых интенсивностей)

Здесь $\gamma = \sqrt {1 + a_{L}^{2}} $ – Лоренц-фактор электронов в лазерном поле. Для мишени из алюминия при интенсивности 10²² Вт/см² имеем условие $L \leqslant {{\lambda }_{{sk}}} \approx 60$ нм. В общем случае толщина мишени должна находиться в диапазоне от нескольких до сотен нм. Отметим согласие данных оценок с ограничениями на толщину мишени для реализации кулоновского взрыва, полученными выше (формула (2) при заданной интенсивности). Для рассматриваемых диапазонов параметров толщина мишени, требуемая для реализации кулоновского взрыва (2), оказывается практически всегда меньше толщины скин-слоя.

На расстояниях разлета плазмы, меньших, чем размер пятна фокусировки лазерного импульса, можно пренебречь трехмерными эффектами и рассматривать одномерную постановку [14, 31, 44]. Пусть мишень изначально занимает область пространства $ - L{\text{/}}2 \leqslant x \leqslant L{\text{/}}2$. Для системы, состоящей из двух сортов ионов, легких (индекс “l”) и тяжелых (индекс “h”), уравнения Власова для ионных функций распределения имеют вид

Находя характеристики и используя симметрию относительно $x = 0$, получаем следующую систему уравнений движения ионов в самосогласованном электростатическом поле

где ${{m}_{l}}$ и ${{m}_{h}}$, ${{Z}_{l}}$ и ${{Z}_{h}}$, ${{x}_{l}}$ и ${{x}_{h}}$, ${{x}_{{l0}}}$ и ${{x}_{{h0}}}$ – соответствующие массы, заряды, текущие и начальные координаты легких и тяжелых ионов. Для напряженности электрического поля имеем где ${{n}_{h}}$, ${{n}_{l}}$ – плотности тяжелых ионов и легких ионов соответственно. Стоит отметить, что из-за симметрии граничное условие для электрического поля имеет вид

Плотности частиц в (6) выражаются через производные по лагранжевым координатам

где ${{n}_{{h0}}}$ и ${{n}_{{l0}}}$ – начальные плотности тяжелых и легких ионов соответственно.

Проведем обезразмеривание: координаты ионов будут измеряться в величинах $L{\text{/}}2$, плотности тяжелых и легких ионов в плотностях ${{n}_{{h0}}}$ и ${{n}_{{l0}}}$ соответственно, время – в единицах обратной плазменной частоты тяжелых ионов ${{\omega }_{{ph}}} = \sqrt {4\pi {{n}_{{h0}}}Z_{h}^{2}{{e}^{2}}{\text{/}}{{m}_{h}}} $, электрическое поле – в единицах $2\pi {{Z}_{h}}e{{n}_{{h0}}}L$, энергия тяжелых частиц – в $\pi {{({{Z}_{h}}eL)}^{2}}{{n}_{{h0}}}$, легких – в $\pi {{({{Z}_{h}}eL)}^{2}}{{n}_{{h0}}}{{m}_{l}}{\text{/}}{{m}_{h}}$. Так как будут рассмотрены только однородные мишени, в начальный момент времени все ионы распределены однородно на отрезке от 0 до 1. При интегрировании (6) слагаемые, отвечающие за самодействие, можно упростить. Поскольку плотности являются изначально неубывающими, то и электрическое поле является неубывающей функцией, следовательно, движение частиц будет однопотоковым. Тогда можно перейти от интегрирования текущей плотности к начальной, а поскольку ионы распределены однородно, получаем

Подставляя поле в систему (5), приходим к следующей системе уравнений:

где первые слагаемые в каждом уравнении отвечают за ускорение под действием поля ионов того же сорта (самодействие), а вторые − противоположного. При обезразмеривании возник параметр который мы, следуя работам [34, 38], будем называть кинематическим. Он определяет, насколько эффективнее ускоряются легкие ионы в общем поле по сравнению с тяжелыми. Формально этот параметр находится в диапазоне $1 \leqslant \mu < \infty $, в реальных же экспериментах он не превышает 10, а с учетом рассмотренного ограничения на интенсивность его характерный диапазон $2 \leqslant \mu \leqslant 7$. К примеру, для мишени из гидрированного алюминия он примерно равен 2, а для гидрированного свинца при интенсивности 10¹⁹ Вт/см² достигает 6 (толщина мишени (2) для реализации кулоновского взрыва при такой интенсивности и концентрации свинца 3 × 10²² см^–3 равна ≈1 нм). Значение μ = 2 встречается достаточно часто, поскольку при полной ионизации у тяжелых элементов $Z \approx A{\text{/}}2$, а в качестве легких ионов обычно выступает водород. В отдельных случаях возможно даже значение $\mu < 1$. К примеру, при интенсивности 10¹⁹ Вт/см² для мишени из алюминия и кислорода он равен примерно 0.9 (толщина мишени из (2) составляет ≈1.5 нм). В таком случае тяжелые ионы будут двигаться быстрее легких и удобнее проводить обезразмеривание на величины, отвечающие легким ионам.

Параметр

является отношением полного заряда легких ионов к полному заряду мишени. Последний, строго говоря, зависит от энергии лазерного импульса, которая расходуется, в том числе, на ионизацию. При проведении оптимизационных исследований величину Q будем считать фиксированной. Возможные значения параметра ρ лежат в диапазоне $0 \leqslant \rho \leqslant 1$, причем $\rho = 0$ соответствует полному отсутствию легких ионов, а $\rho = 1$ – тяжелых.

Плотности частиц каждого сорта в (10)–(11) после обезразмеривания имеют вид

Совокупность уравнений (10), (11), (14) составляет общую систему уравнений движения частиц в самосогласованном поле. Получение аналитического решения будет рассмотрено в следующем разделе.

3. АНАЛИТИЧЕСКАЯ МОДЕЛЬ

Аналитическое решение общей системы уравнений будем искать, пренебрегая влиянием поля легкой ионной компоненты на движение тяжелой. То есть мы не будем учитывать второй член в правой части уравнения (11). Данное приближение оправдано, так как в силу наличия множителя $\mu > 1$ в (10) легкие ионы эффективнее реагируют на ускоряющее поле, а значит движутся быстрее, чем тяжелые. Это приводит к тому, что большая их часть быстро пересечет фронт тяжелых ионов, а значит подынтегральное выражение в (11) должно достаточно быстро убывать со временем в области интегрирования. Также из уравнения (11) видно, что чем меньше значение ρ, тем лучше работает используемое приближение. Точное условие применимости будет найдено далее на основе полученного решения.

В рамках описанного приближения уравнение (11) легко интегрируется и приводит к равноускоренному движению тяжелых ионов, очевидно совпадающему с решением для взрыва плоской мишени с одним сортом ионов [44]

откуда, используя (14), получаем

Опуская здесь и далее индекс “l”, можем записать уравнение для легких ионов в следующем виде:

Здесь, аналогично работе [34], введено время $t{\kern 1pt} * = t{\kern 1pt} *({{x}_{0}})$, соответствующее тому моменту, когда частица с данной начальной координатой ${{x}_{0}}$ догоняет фронт тяжелых ионов, двигающийся по закону (15): ${{x}_{{hf}}} = (1 + {{t}^{2}}{\text{/}}2)$.

В отличие от работы [34] ищем аналитическое решение уравнения (15) без предположений о малости $\rho $ и использования теории возмущений. Решение первого из уравнений (17) можно представить как сумму общего решения однородного уравнения (левая часть) и частного решения неоднородного. Это возможно, поскольку в нашем случае, как можно убедиться, частное решение удается подобрать как равноускоренное движение

где константа a найдена из подстановки в уравнение. Для однородного уравнения имеем

Решение этого уравнения уже было рассмотрено в работе [34]. При переходе к переменной $z = - {{t}^{2}}{\text{/}}2$ оно сводится к дифференциальному уравнению Эйлера для гипергеометрической функции, откуда общее решение принимает вид

Подставляя сумму ${{x}_{{gn}}} = {{x}_{{gh}}} + {{x}_{{pn}}}$ в общее уравнение и используя начальные условия, находим константы

Решением второго из уравнений (17), как видно, является движение под действием максимального ускорения от вклада всех ионов остова. Таким образом, полное решение (17) имеет следующий вид:

Использовано обозначение $F(t)$ для гипергеометрической функции

Введенные коэффициенты $A({{x}_{0}})$ и $B({{x}_{0}})$ находятся из сшивки в момент времени $t = t{\kern 1pt} *({{x}_{0}})$. Неявным образом он определяется следующим выражением:

Сами коэффициенты выражаются как

Здесь использовано следующее обозначение:

для гипергеометрической функции, возникшей при дифференцировании $F(t)$: $\dot {F}(t) = \mu t{{F}_{1}}(t)$.

Следуя работе [34], будем рассматривать характеристики ускоренных ионов при пересечении ими некоторой плоскости, а не в определенный момент времени. Это соответствует экспериментальной постановке регистрации частиц, прилетающих на детектор. Исходя из одномерности постановки, координата модельного “детектора” должна быть ограничена. В качестве характерной границы одномерного движения приближенно выбирается диаметр пятна фокусировки лазерного импульса [14, 31, 44]. Такой выбор позволяет с хорошей точностью оценить энергию, так как в ходе одномерной стадии ускорения ионы набирают основную часть своей полной энергии: 75% [44] или около 80% [14]. При субмикронной толщине мишени и фокусировке в пятно в несколько микрометров координата “детектора”, ${{x}_{d}}$, будет иметь значение в несколько десятков.

Зарегистрированная энергия частиц выражается следующим образом:

В данном случае ${{t}_{d}} = {{t}_{d}}({{x}_{0}})$ – это время, за которое частица долетает до “детектора”, по аналогии с $t{\kern 1pt} *({{x}_{0}})$ выражаемое неявным образом:

Координата иона с начальным положением $x_{0}^{*}$ в момент его регистрации “детектором” совпадает с фронтом тяжелых ионов. Соответственно, легкие ионы с ${{x}_{0}} < x_{0}^{*}$ не успевают пересечь этот фронт до регистрации “детектором”, а с ${{x}_{0}} > x_{0}^{*}$, наоборот, успевают. Граница между решениями, $x_{0}^{*}$, выражается следующим образом:

Из (27) можно найти спектр ионов, зафиксированный “детектором”, по следующей формуле:

Конечные выражения для спектральных распределений мы не приводим по причине их громоздкости.

В случае, когда масса тяжелых ионов значительно больше массы легких, то есть при $\mu \to \infty $ (12), вышеперечисленные результаты упрощаются. При таком условии, рассмотренном также в работах [34, 35], можно считать тяжелые ионы неподвижными. Тогда, аналогичным образом решая уравнения (17), но уже с отсутствующим слагаемым ${{t}^{2}}{\text{/}}2$ в знаменателе первого члена в правой части, получаем

Введенные коэффициенты $A({{x}_{0}})$, $B({{x}_{0}})$, а также $t{\text{*}}({{x}_{0}})$ выражаются тогда следующим образом:

Это решение может быть также получено из общего (22) предельным переходом $\mu \to \infty $ и с учетом соответствующей малости $t{\kern 1pt} * \ll 1$ (24).

Поскольку тяжелые ионы неподвижны, то введение $x_{0}^{*}$ не имеет смысла, так как все легкие ионы пересекут фронт тяжелых прежде, чем достигнут “детектора”. Тогда для энергии имеем простое выражение

Как видно, при $\mu \to \infty $ энергия становится линейной по μ, что приводит к одинаковому виду спектров, а также $\varepsilon ({{x}_{0}})$ квадратично по ${{x}_{0}}$, т.е. при некоторых значениях параметров возможна немонотонность зависимости энергии от ${{x}_{0}}$.

С использованием определения плотности (14), найденного решения (22) и уравнения движения тяжелых ионов (15), можно получить условие применимости рассматриваемой модели. Оно находится из условия малости второго члена уравнения (11) по сравнению с первым, т.е. малости воздействия легких ионов на тяжелые по сравнению с самодействием:

Так как левая часть неравенства зависит только от времени, можно ввести критическое время ${{t}_{{cr}}}$, соответствующее моменту, после которого влияние легких ионов на тяжелые становится незначительным. Такое время всегда существует при $\mu > 1$, поскольку из уравнений движения именно этот коэффициент обеспечивает более сильное ускорение легких ионов в общем самосогласованном поле ионов мишени. При этом берется первая часть решения (22), поскольку вторая часть соответствует тем легким ионам, которые уже покинули область влияния на тяжелые. Требуя справедливости сделанного приближения для как можно более ранних моментов времени, ${{t}_{{cr}}} \ll 1$, получаем

Отсюда находим границы значений управляющих параметров μ и ρ, в которых применима предлагаемая модель

где τ – некоторый момент времени, такой, что ${{t}_{{cr}}} < \tau \ll 1$, т.е. чем меньше это значение, тем более строгое условие применимости. Для определенности можно взять $\tau = 0.3$. Зависимость правой части (36) $ \propto {\kern 1pt} \mu $ связана с тем, что чем быстрее движутся легкие ионы, тем большим зарядом (ρ) они могут обладать, чтобы их влияние на тяжелые было несущественным.

Требование (34) получается из сравнения мгновенных значений сил, действующих на тяжелый ион. Можно провести сравнение по их интегральному действию, т.е. по вкладу в набираемую энергию. Подобный подход приводит к менее строгому ограничению.

Как видно, полученное условие применимости хорошо согласуется с нашими предположениями, представленными в начале этого раздела: малость параметра ρ или же, напротив, большое значение $\mu $. Однако стоит обратить внимание и на еще одно условие, позволяющее использовать построенную модель. Условие (36) получено из пренебрежения воздействием легких ионов на тяжелые. Однако поскольку мы интересуемся движением легких ионов, в случае, когда воздействием тяжелых ионов на легкие можно пренебречь, мы также можем использовать нашу модель, ведь в этом случае не имеет значения движение тяжелых ионов. Это условие выглядит следующим образом:

Оно должно выполняться для как можно большего времени и для большей части частиц. Поскольку $x({{x}_{0}},t)$ является возрастающей функцией, то может существовать момент времени, после которого это условие перестает выполняться. Для определенности в качестве предельного момента времени можно взять ${{t}_{d}}(0.1)$ – время достижения “детектора” частицы с начальной координатой ${{x}_{0}} = 0.1$, поскольку ${{t}_{d}}$ для частиц с бóльшей начальной координатой будет меньше. Так как выражение для ${{t}_{d}}$ (28) является неявным, то аналитическая оценка такого условия применимости представляет довольно сложную задачу, поэтому в дальнейшем оно будет рассчитано численным образом. По общему виду условия (37) можно заметить, что при ρ, достаточно близких к единице, наша модель будет применима. Это логично, поскольку переход $\rho \to 1$ соответствует случаю однокомпонентной мишени, когда влияние тяжелых ионов на движение легких отсутствует.

4. СРАВНЕНИЕ С ЧИСЛЕННЫМ РЕШЕНИЕМ

Для общего случая системы (10)–(11) без пренебрежения воздействием легких ионов на тяжелые было найдено численное решение, результаты которого в этом разделе будут сравниваться с результатами аналитической модели. С учетом ограничения на одномерность использовано значение координаты “детектора”, не превышающее толщину мишени больше, чем на порядок, т.е. ${{x}_{d}} = 20$. Например, это соответствует $L = $ 50 нм и ${{D}_{f}}$ =   = 0.5 мкм, что для лазера с энергией 1 Дж и длительностью лазерного импульса 50 фс дает значение интенсивности порядка 10²² Вт/см².

Зависимость энергии $\varepsilon ({{x}_{0}})$, зафиксированной “детектором”, находящимся в плоскости с координатой ${{x}_{d}}$, для $\mu = 2$ и различных значений ρ в диапазоне от 0.1 до 0.9 представлена на рис. 1.

Наличие пологого участка на графике $\varepsilon ({{x}_{0}})$ при $\rho = 0.1$ говорит о большом количестве частиц с близкими энергиями, т.е. формируется квазимоноэнергетический спектр. С увеличением ρ эта особенность пропадает, и при $\rho = 0.9$ зависимость почти линейна. Как видно из сравнения аналитической (сплошные кривые) и численной (штриховые кривые) зависимостей, условие либо малого, либо, наоборот, большого ρ действительно соответствует условию применимости нашей модели. Зависимость $x({{x}_{0}})$ при фиксированном t демонстрирует схожее поведение.

Отметим, что графики энергетических зависимостей на рис. 1 выпуклы вверх. Это связано с тем, что мы вычисляем энергию, зарегистрированную в определенной координате, а не в определенный момент времени. К примеру, для однокомпонентной мишени ($\rho \to 1$) зависимость энергии от координаты в заданный момент времени будет иметь вид $\varepsilon ({{x}_{0}}) \propto x_{0}^{2}$, в то время как в нашем случае (рис. 1) она практически линейна. Это делает возможной ситуацию, при которой зависимость $\varepsilon ({{x}_{0}})$ не будет монотонно возрастающей, как было видно по формуле (33). Для $\mu \to \infty $ из (33) можно получить границу $\rho {\kern 1pt} * = 1{\text{/}}({{x}_{d}} - 1)$, где при $\rho < \rho {\kern 1pt} *$ функция $\varepsilon ({{x}_{0}})$ является немонотонной и имеет максимум в координате ${{x}_{0}} = $ $ = \rho {{x}_{d}}{\text{/}}(1 + \rho )$. Для конечных $\mu $ немонотонность также наблюдается при довольно малых ρ, но их нахождение является достаточно сложной задачей.

Как видно на рис. 1, наибольшие отклонения модели от численного расчета наблюдаются у частиц с $x_{0}^{*} < {{x}_{0}} < x_{0}^{'}$ (границы показаны на рис. 1 вертикальными линиями). Начальная координата $x_{0}^{'}$ соответствует частице, которая половину времени движения до “детектора” находится позади фронта тяжелых ионов, а половину – перед. То есть эта величина является решением уравнения

Наибольшее отклонение от численных результатов для таких частиц имеет следующее объяснение. Проводя достаточно большое время в области, занятой тяжелыми ионами, эти частицы оказывают значительное влияние на движение тяжелых ионов. Построенная модель данного эффекта не учитывает. Поэтому появляется расхождение при вычислении самосогласованного поля ионов остова, а значит и в набираемой легкими ионами энергии. Значения энергии, получаемые по аналитической модели, оказываются завышенными. При отсутствии влияния со стороны легких ионов тяжелые ионы двигаются медленнее, поэтому момент пересечения их фронта, $t{\kern 1pt} *$ (24), достигается раньше. Это приводит к более быстрому переходу легких ионов в область максимального ускорения и набору больших значений энергии.

Также можно заметить, что при стремлении $\rho \to 1$ безразмерные значения энергии значительно увеличиваются. Это связано с проведенным обезразмериванием на величины, связанные с тяжелыми ионами. Концентрации тяжелых и легких ионов связаны через параметр ρ (13), а полный заряд мишени остается постоянным. Поэтому при увеличении ρ происходит рост ${{n}_{{l0}}}$ и уменьшение ${{n}_{{h0}}}$ (см. формулу (13)), а так как последняя величина входит в единицу энергии, мы наблюдаем рост ее безразмерных значений.

Численная оценка максимального значения энергии для $\rho = 0.1$ для полностью ионизованной мишени из гидрированного алюминия толщиной 50 нм при начальной плотности ионов Al ${{n}_{{h0}}} = 6 \times {{10}^{{22}}}$ см^–3 дает значение порядка 180 МэВ, для $\rho = 0.9$ с учетом неизменности полного заряда ионов мишени она также составляет около 180 МэВ.

Количественный анализ расхождений численного, ${{\varepsilon }_{{num}}}$, и аналитического, ${{\varepsilon }_{{mod}}}$, решения был проведен путем вычисления среднеквадратичного отклонения

Результаты сравнения для всего диапазона значений μ и ρ вместе с границами применимости представлены на рис. 2, где в случае (a) – ${{x}_{m}} = 0$, в случае (b) – $\varepsilon ({{x}_{m}}) = 0.7{{\varepsilon }_{{{\text{max}}}}}$.

Граница применимости для малых ρ найдена из условия (36) подстановкой $\tau = 0.3$, для больших ρ – интегрированием (37) по ${{x}_{0}}$ в момент времени ${{t}_{d}}(0.1)$ с условием превышения левой части правой в 5 раз. Как можно заметить из рис. 1 и 2, для высокоэнергетичных ионов с энергиями отклонения от численной модели существенно меньше. В целом, для основного диапазона значений кинематического параметра, $\mu > 2$, отклонения модели от численного результата не превышают 8% при любых значениях ρ. Если речь идет только о высокоэнергетичной части спектра, то там отклонения меньше 3%. Стоит отметить также высокую точность построенной модели за рамками формальных границ применимости.

Сравнение ионных спектров на “детекторе”, вычисленных по формуле (30), показано на рис. 3.

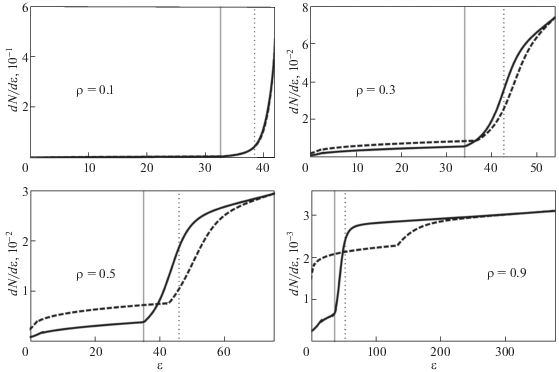
Как и было видно при анализе графиков на рис. 1, при малых $\rho $ спектр является квазимоноэнергетичным. Более сильное самодействие легких ионов при увеличении их полного числа приводит к росту максимальной энергии и увеличению спектральной ширины. При $\rho \to 1$ спектральное распределение становится практически однородным, что согласуется с рассмотренными выше энергетическими зависимостями. Действительно, на рис. 1 для $\rho = 0.9$ имеем $\varepsilon ({{x}_{0}}) \propto {{x}_{0}}$. Соответственно, при вычислении спектра и взятии производной (30) получаем $dN{\text{/}}d\varepsilon (\varepsilon ) \approx {\text{const}}$. Такой однородный спектр для однокомпонентной мишени ($\rho \to 1$) отличается от привычного экспоненциально спадающего теплового [14]. Как было показано выше при анализе рис. 1, это напрямую следует из вычисления нами энергии, зарегистрированной в определенной координате, а не в определенный момент времени.

Аналитические спектры хорошо согласуются с численными при малых ρ, как это было и в случае зависимости $\varepsilon ({{x}_{0}})$. При больших значениях параметра ρ расхождения в спектрах становится больше, чем для энергетических зависимостей. Это можно объяснить тем, что поскольку спектр находится взятием производной зависимости $\varepsilon ({{x}_{0}})$, которая, к тому же, находится в знаменателе (30), и при этом он сам зависит от $\varepsilon ({{x}_{0}})$, то он является более чувствительным к точности вычисления $\varepsilon ({{x}_{0}})$. Поэтому малые расхождения в энергетической зависимости могут приводить к большим искажениям спектральной, что и видно на рис. 3. Сравнение расхождений аналитических и численных спектров на основе среднеквадратичного отклонения

изображенное на рис. 4, это хорошо показывает (${{\varepsilon }_{m}}$ для (a) равен 0, для (б) – $0.7{{\varepsilon }_{{{\text{max}}}}}$).

Видно, что расхождения спектральных зависимостей являются более значительными по сравнению с энергетическими в области больших ρ. Максимальные значения отклонений также больше и достигают 30%. В высокоэнергетичной части спектра максимальное отклонение еще больше. Однако, аналогично энергии, это наблюдается лишь в небольшой области вблизи $\mu = 1$. При $\mu > 2$ отклонения не превышают 20%, в высокоэнергетической области этот показатель не больше 12%. В целом, зависимости $dN{\text{/}}d\varepsilon (\varepsilon )$ согласуются хуже, чем $\varepsilon ({{x}_{0}})$, по упомянутой выше причине – большей чувствительности производной к изменению функции $\varepsilon ({{x}_{0}})$.

Для количественного анализа качества генерируемых пучков ускоренных ионов введем величину ${{q}_{{n{\text{\% }}}}}$, соответствующую суммарному заряду легких ионов, попадающих в диапазон по энергиям от $(1 - 0.01n){{\varepsilon }_{{{\text{max}}}}}$ до ${{\varepsilon }_{{{\text{max}}}}}$:

Зависимость отношения этой величины ко всему заряду от параметров мишени при $n = 1{\text{\% }}$ показана на рис. 5.

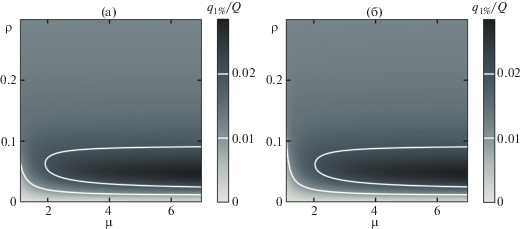
В первую очередь отметим хорошее согласие результатов, полученных аналитически и численно: при $\mu > 1.5$ зависимости практически совпадают. Из графиков также видно, что при фиксированном μ больше некоторого значения, существует оптимальное значение ρ, при котором достигается максимум величины ${{q}_{{1{\text{\% }}}}}{\text{/}}Q$, причем после преодоления этого максимума зависимость выходит на константу. Для более подробного анализа построим срезы графиков на рис. 5 при фиксированных μ. Для сравнения возьмем границы интервала кинематического параметра: $\mu = 2$ и $\mu = 7$, а также расширим спектральный диапазон пучка, рассмотрев дополнительно $n = 5{\text{\% }}$ и 10%. Для сравнения также построим зависимости, полученные по теории возмущений из работы [34]. Результаты приведены на рис. 6.

По данным графикам хорошо видно влияние доли легких ионов в мишени на качество их пучка. В начале, на этапе роста их количества увеличивается и число частиц, попадающих в узкий спектральный диапазон. После определенного момента дальнейшее увеличение их числа приводит к доминирующему действию собственного кулоновского расталкивания, и в узкой части спектра вблизи максимальной энергии концентрируется все меньше частиц, пока не перестает меняться совсем. При этом правильный подбор первоначального числа ускоряемых ионов позволяет в два раза увеличить их число в 1% спектральном диапазоне при $\mu = 2$ и в 3 раза – при $\mu = 7$. Естественно, важную роль в этом процессе играет формирование квазимоноэнергетической части в спектральном распределении (см. рис. 3).

При увеличении анализируемой спектральной ширины пучка, $n{\text{\% }}$, максимум функции ${{q}_{{n{\text{\% }}}}}{\text{/}}Q(\rho )$ становится менее выраженным. Это связано с уменьшением эффекта от формирования квазимоноэнергетического пучка на фоне большего числа анализируемых частиц. При $n \to 100{\text{\% }}$, к примеру, зависимость переходит в прямую пропорциональность, поскольку в этом случае ${{q}_{{100{\text{\% }}}}}{\text{/}}Q = \rho $. На графиках рис. 6 также видно, что теория возмущений хорошо работает только внутри своей области применимости при малых $\rho \lesssim 0.1$. Построенная модель совпадает с численным решением практически на всем диапазоне при $\mu > 2$, несмотря на то, что условие применимости (показано вертикальными линиями на рис. 6) является значительно более жестким, – вывод, согласующийся с графиками на рис. 2 и 4. Максимальное отклонение наблюдается вблизи максимума, причем при $n = 1{\text{\% }}$ для $\mu = 2$ отклонение положения максимума и его значения составляют всего 1% и 3%, а для $\mu = 7$ – 0.1% и 0.5% соответственно.

Также стоит отметить, что величину (41) можно рассчитать для кулоновского взрыва однокомпонентной фольги [44]

В данном случае $p = n{\text{/}}100$. Согласно определению (13), случай однокомпонентной фольги соответствует $\rho \to 1$, поэтому графики на рис. 6 стремятся к значению (42). Поскольку мы рассматриваем ${{x}_{d}} \gg 1$, то выражение в правой части (42) упрощается до величины p, а значит приближенно ${{q}_{{n{\text{\% }}}}}{\text{/}}Q \to p = n{\text{/}}100$ при $\rho \to 1$, в чем и можно убедиться на рис. 6.

Также представляет интерес поведение функции ${{\rho }_{{opt}}}(\mu )$, где ${{\rho }_{{opt}}}$ соответствует доле заряда легких ионов, при котором величина ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$ имеет максимальное значение. Такая зависимость представлена на рис. 7, где также изображено ${{\rho }_{{opt}}}(\mu \to \infty )$ из формул (31)–(33).

Видно, что зависимости в области, находящейся ниже изображенной границы применимости, согласуются достаточно хорошо, а выше, напротив, расходятся существенным образом. В частности, для численного решения при $\mu \to 1$ оптимум по параметру ρ пропадает, и максимальное значение функции наблюдается при $\rho = 1$. Это связано с тем, что при $\mu = 1$ ионы ничем не отличаются друг от друга, а поэтому зависимость ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$ является линейной. При этом параметр ρ показывает некоторую долю, взятую произвольно из общего количества одинаковых ионов. При увеличении μ, напротив, и численная, и аналитическая модель имеют асимптоту, что непосредственно следует из (33), ведь пропорциональность $\varepsilon \propto \mu $ означает, что вид спектра у всех $\mu $ одинаков с точностью до множителя, при интегрировании по энергии этот множитель сокращается, поэтому зависимость ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$ совпадает и для произвольных p и ${{x}_{d}}$ выглядит следующим образом:

В данном случае из-за немонотонности энергии, а также из-за того, что $\varepsilon ({{x}_{0}} = 0) \ne 0$ из (33), возникают границы по ρ которые могут быть выражены как

Находя максимум этого выражения, получаем

Использованы обозначения $\rho _{{opt}}^{*}(p)$ и $p{\kern 1pt} *$, которые не могут быть выражены точно аналитически, однако могут быть приближенно оценены следующими выражениями, исходя из малости ρ и p в этих пределах

Как можно заметить, после некоторого значения p максимум пропадает, что связано с тем, что зависимость ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$ при $p \to 1$ становится линейной.

С помощью формул (43), (45) можно оценивать асимптотические значения оптимальных параметров при больших $\mu $. Можно заметить, что значение ${{\rho }_{{opt}}}$ в данном случае непосредственно связано с максимумом параболической зависимости (33). Действительно, для ${{x}_{d}}$ и $n = 1{\text{\% }}$ ${{\rho }_{{opt}}} \approx 0.04$, в то время как максимум функции $\varepsilon ({{x}_{0}})$ появляется при $\rho * \approx 0.05$. Это связано с тем, что именно при ρ, близких к ρ*, будет наблюдаться квазимоноэнергетичность.

Интересна также оценка значений максимумов в точках ${{\rho }_{{opt}}}$, изображенная на рис. 8 в виде отношения ${{q}_{{1{\text{\% }}}}}({{\rho }_{{opt}}})$ к значению ${{q}_{{1{\text{\% }}}}}$ для однокомпонентной мишени. Видно, что максимум растет при увеличении μ и постепенно выходит на асимптоту, соответствующую значению этого максимума при $\mu \to \infty $. Таким образом, для получения пучков наибольшего качества необходимо как можно большее значение параметра μ, параметр ρ же, напротив, не должен быть слишком большим и близким к $\rho {\kern 1pt} *$.

5. ЗАКЛЮЧЕНИЕ

В работе построена обобщенная одномерная теоретическая модель лазерно-инициированного ускорения ионов тонкой мишени, содержащей ионы двух сортов, для произвольного относительного заряда легких ионов, ρ. Не претендуя на описание случая произвольной температуры электронов плазмы, мы рассмотрели случай кулоновского взрыва, реализуемый при ультрарелятивистских интенсивностях лазера. С учетом ограничения на одномерность модели, энергетические зависимости рассматривались на расстояниях, не превышающих толщину мишени больше, чем на порядок. Для повышения выхода ускоренных частиц рассмотрены закритические мишени с ${{n}_{e}} > {{n}_{{cr}}}$, поэтому учитывалось требование полного, объемного нагрева мишени лазерным излучением. Для используемых диапазонов параметров глубина скин-слоя практически всегда оказывается больше толщины, требуемой для реализации кулоновского взрыва. Единственным использованным приближением модели являлось пренебрежение воздействием легких ионов на движение тяжелых. На основе полученного решения были найдены пределы применимости такого допущения.

Сравнение энергетических зависимостей на “детекторе” для построенной модели с численным расчетом дает согласие в пределах 8% среднеквадратичного отклонения для практически реализуемых значений $\mu \geqslant 2$, отклонение спектральной зависимости находится впределах 20%. Для частиц, обладающих энергиями вблизи максимальной (0.7${{\varepsilon }_{{{\text{max}}}}}$–${{\varepsilon }_{{{\text{max}}}}}$), это отклонение еще меньше и составляет 3% и 12% для отклонений в энергии и спектральных распределений соответственно. Самое большое отклонение наблюдалось лишь в небольшой области вблизи $\mu \sim 1$, которая соответствует идентичным тяжелым и легким ионам, т.е. случаю одной компоненты, решение для которого является более простым.

Зависимость введенной величины ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$, соответствующей числу ионов в $n{\text{\% }}$-диапазоне вблизи максимальной энергии, показывает, что уже при $\mu = 2$ модель очень хорошо согласуется с численным решением на всем диапазоне ρ, в отличие от теории возмущений из [34], работающей лишь при малых $\rho \lesssim 0.1$. Зависимость оптимального значения доли легких ионов ${{\rho }_{{opt}}}(\mu )$, соответствующего квазимоноэнергетическому пучку ионов с наибольшим числом частиц, также хорошо это демонстрирует.

Для нахождения ${{\rho }_{{opt}}}(\mu \to \infty )$, являющейся постоянной величиной, рассмотрена упрощенная модель с неподвижными тяжелыми ионами, для которой найдена точная аналитическая зависимость ${{q}_{{n{\text{\% }}}}}(\rho ){\text{/}}Q$ для произвольных n и ${{x}_{d}}$, из которой рассчитана приближенная зависимость ${{\rho }_{{opt}}}(p)$. Построенная функция позволяет приближенно оценить оптимальное значение относительного заряда примесных ионов для максимального количества требуемой доли высокоэнергетических ионов для любой координаты “детектора” при условии достаточно большого $\mu $.

Из этих оценок следует, что при больших значениях кинематического параметра μ и, напротив, при довольно малых $\rho \sim \rho {\kern 1pt} * = 1{\text{/}}({{x}_{d}} - 1)$ количество ионов, обладающих энергиями, близкими к максимальной, является наибольшим, что дает соответствующие рекомендации по используемым мишеням. Такие параметры наблюдаются при использовании в качестве легких ионов водорода, а в качестве тяжелых – не полностью ионизованного тяжелого элемента, при этом с учетом большого заряда концентрация тяжелых ионов должна быть сопоставима или даже несколько меньше концентрации легких.