Физика Земли, 2020, № 3, стр. 98-111
Разделение потенциальных полей, создаваемых различными источниками с помощью модифицированных S-аппроксимаций
И. Э. Степанова 1, *, Д. Н. Раевский 1, А. В. Щепетилов 2
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
2 МГУ им. М.В. Ломоносова
г. Москва, Россия
* E-mail: tet@ifz.ru
Поступила в редакцию 04.03.2019
После доработки 20.05.2019
Принята к публикации 22.06.2019
Аннотация
Рассматриваются вопросы построения аналитических аппроксимаций геопотенциальных полей на основе модифицированного метода S-аппроксимаций, суть которого состоит в аппроксимации исходного поля суммой потенциалов простого и двойного слоев, распределенных на совокупности носителей, залегающих ниже заданного рельефа. Особое внимание уделяется применению новых, высокоэффективных методов решений систем линейных алгебраических уравнений (СЛАУ) больших и сверхбольших размерностей, к которым редуцируются обратные геофизические и геодезические задачи. Для их решения предложен усовершенствованный блочный метод контрастирования, заключающийся в разбиении исходной области на наиболее контрастные по характеру подобласти и дальнейшую деформацию блоков. Приведены результаты математических экспериментов по построению аналитических аппроксимаций аномальных гравитационного и магнитного полей и разделению полей, создаваемых различными группами источников.
ВВЕДЕНИЕ
При интерпретации гравиметрических и магнитометрических данных, вычислении поправок за рельеф, построении карт уклонений отвесной линии и т.п. возникает необходимость нахождения аналитических аппроксимаций функций, заданных приближенно на нерегулярной сети точек. В настоящее время предлагаются разнообразные методики решения проблемы выбора аппроксимационных конструкций (см., например, [Костицын и др., 2013; 2017; Мартышко и др., 2003; Кризский, 2011]. Для построения аналитических аппроксимаций рельефа местности и геопотециальных полей можно применить описанный в работах [Страхов, Степанова, 2002а; 2002б] метод S-аппроксимаций, а также улучшенный вариант этого метода – модифицированные S-аппроксимации [Степанова и др., 2017; 2018]. Методика построения S-аппроксимаций основана на применении фундаментальной формулы теории гармонических функций (третьей формулы Грина) [Кошляков и др., 1962]. В настоящей статье будет рассматриваться локальный вариант с декартовой системой координат и вертикальной осью, направленной вверх.
Если известны компоненты магнитного или гравитационного поля (например, первая производная потенциала по x3 на некотором рельефе), то можно представить потенциал поля в виде суммы потенциалов простого и двойного слоев, распределенных на нескольких горизонтальных плоскостях, которые залегают ниже заданного рельефа. Если систему координат выбрать так, чтобы одна из плоскостей простого и двойного слоев задавалась уравнением х3 = 0 (однако данное условие не является обязательным), то потенциал представляется в виде:
(1)
$\begin{gathered} V(M) = \\ = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{{{{\rho }_{{1,r}}}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}d{{\xi }_{2}}}}{{\sqrt {{{{({{x}_{1}} - {{\xi }_{1}})}}^{2}} + {{{({{x}_{2}} - {{\xi }_{2}})}}^{2}} + {{{\left( {{{x}_{3}} - {{H}_{r}}} \right)}}^{2}}} }} + } } } \\ + \,\,\sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{{{{\rho }_{{2,r}}}({{\xi }_{1}},{{\xi }_{2}})\left( {{{x}_{3}} - {{H}_{r}}} \right)d{{\xi }_{1}}d{{\xi }_{2}}}}{{{{{\left[ {\sqrt {{{{({{x}_{1}} - {{\xi }_{1}})}}^{2}} + {{{({{x}_{2}} - {{\xi }_{2}})}}^{2}} + {{{\left( {{{x}_{3}} - {{H}_{r}}} \right)}}^{2}}} } \right]}}^{3}}}}} } } , \\ M = ({{x}_{1}},{{x}_{2}},{{x}_{3}}). \\ \end{gathered} $В формуле (1) и далее использованы следующие обозначения: $M = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – точка измерений; $\,{{\xi }_{1}},\;{{\xi }_{2}}$ – точки на соответствующих поверхностях; ${{H}_{r}}$ – глубина залегания r-ой горизонтальной плоскости (расстояние от точки на плоскости до дневной поверхности) в рамках метода S-аппроксимаций; ${{\rho }_{{1,r}}}\left( {\hat {\xi }} \right),$ ${{\rho }_{{2,r}}}\left( {\hat {\xi }} \right) \in {{L}_{2}}\left( { - \infty , + \infty } \right)$ – неизвестные функции, подлежащие определению, $\hat {\xi } = ({{\xi }_{1}},{{\xi }_{2}}).$ Тогда производная по х3 потенциала V, взятая с обратным знаком, будет иметь вид:
(2)
$\begin{gathered} - \frac{{\partial V}}{{\partial {{x}_{3}}}}(M) = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{{{{\rho }_{{1,r}}}\left( {\hat {\xi }} \right)\left( {{{x}_{3}} - {{H}_{r}}} \right)d\hat {\xi }}}{{{{{\left[ {\sqrt {{{{({{x}_{1}} - {{\xi }_{1}})}}^{2}} + {{{({{x}_{2}} - {{\xi }_{2}})}}^{2}} + {{{\left( {{{x}_{3}} - {{H}_{r}}} \right)}}^{2}}} } \right]}}^{3}}}} + } } } \\ + \,\,\sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\frac{{{{\rho }_{{2,r}}}\left( {\hat {\xi }} \right){{{\left( {2{{{\left( {{{x}_{3}} - {{H}_{r}}} \right)}}^{2}} - {{{({{x}_{1}} - {{\xi }_{1}})}}^{2}} - {{{({{x}_{2}} - {{\xi }_{2}})}}^{2}}} \right)}}^{2}}d\hat {\xi }}}{{{{{\left[ {\sqrt {{{{({{x}_{1}} - {{\xi }_{1}})}}^{2}} + {{{({{x}_{2}} - {{\xi }_{2}})}}^{2}} + {{{\left( {{{x}_{3}} - {{H}_{r}}} \right)}}^{2}}} } \right]}}^{5}}}}} } } ,\,\,\,\,\hat {\xi } = ({{\xi }_{1}},{{\xi }_{2}}). \\ \end{gathered} $Пусть компоненты поля заданы в конечном множестве точек Мi, Mi = $({{x}_{{1,i}}},{{x}_{{2,i}}},{{x}_{{3,i}}})$, i = 1, 2, …, N; обозначим известную часть подынтегральной функции в первом слагаемом для r-го слоя в (2) в точке Мi через $Q_{{1,r}}^{{(i)}}$, а во втором слагаемом – через $Q_{{2,r}}^{{(i)}}$. Тогда получим:
(3)
$\begin{gathered} - \frac{{\partial V({{M}_{i}})}}{{\partial {{x}_{3}}}} \equiv {{f}_{i}} = \\ = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {{{\rho }_{{1,r}}}\left( {\hat {\xi }} \right)Q_{{1,r}}^{{(i)}}\left( {\hat {\xi }} \right) + {{\rho }_{{2,r}}}\left( {\hat {\xi }} \right)Q_{{2,r}}^{{(i)}}\left( {\hat {\xi }} \right)} \right)d\hat {\xi }} } } , \\ i = 1,2, \ldots ,N. \\ \end{gathered} $На практике компоненты поля бывают заданы с некоторой погрешностью δ, поэтому входной информацией являются значения fi,δ. С помощью решения вариационной задачи:
(4)
$\Omega (\rho ) = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {\rho _{{1,r}}^{2}\left( {\hat {\xi }} \right) + \rho _{{2,r}}^{2}\left( {\hat {\xi }} \right)} \right)d\hat {\xi }} } } = \mathop {{\text{min}}}\limits_\rho ,$(5)
$\begin{gathered} {{f}_{{i,{\delta }}}} - \\ - \,\,\sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {{{\rho }_{{1,r}}}\left( {\hat {\xi }} \right)Q_{{1,r}}^{{(i)}}\left( {\hat {\xi }} \right) + {{\rho }_{{2,r}}}\left( {\hat {\xi }} \right)Q_{{2,r}}^{{(i)}}\left( {\hat {\xi }} \right)} \right)d\hat {\xi }} } } = 0, \\ i = 1,2, \ldots ,N \\ \end{gathered} $(6)
$\begin{gathered} {{\rho }_{{1,r}}}^{{(a)}}\left( {\hat {\xi }} \right) = {{{\tilde {\rho }}}_{{1,r}}}\left( {\hat {\xi },\lambda } \right),\,\,\,\,{{\rho }_{{2,r}}}^{{(a)}}\left( {\hat {\xi }} \right) = {{{\tilde {\rho }}}_{{2,r}}}\left( {\hat {\xi },\lambda } \right), \\ {{{\tilde {\rho }}}_{{1,r}}}\left( {\hat {\xi },\lambda } \right) = \sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{{1,r}}^{{(i)}}\left( {\hat {\xi }} \right)} , \\ {{{\tilde {\rho }}}_{{2,r}}}\left( {\hat {\xi },\lambda } \right) = \sum\limits_{i = 1}^N {{{\lambda }_{i}}Q_{{2,r}}^{{(i)}}\left( {\hat {\xi }} \right)} ,\,\,\,\,r = 1,2,...,R. \\ \end{gathered} $Таким образом, приходим к следующей системе линейных алгебраических уравнений (СЛАУ):
элементы матрицы которой в нашем случае имеют вид:(8)
$\begin{gathered} {{a}_{{ij}}} = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {Q_{{1,r}}^{{(i)}}\left( {\hat {\xi }} \right)Q_{{1,r}}^{{(j)}}\left( {\hat {\xi }} \right) + Q_{{2,r}}^{{(i)}}\left( {\hat {\xi }} \right)Q_{{2,r}}^{{(j)}}\left( {\hat {\xi }} \right)} \right)d\hat {\xi }} ,} } {\text{ }} \\ 1 \leqslant i \leqslant N,\,\,\,\,1 \leqslant j \leqslant N. \\ \end{gathered} $Коэффициенты аij матрицы А могут быть вычислены явно с помощью интеграла Пуассона:
(9)
$\begin{gathered} {{a}_{{ij}}} = 2\pi \sum\limits_{r = 1}^R {\left\{ {\frac{{{{x}_{{3,i}}} + {{x}_{{3,j}}} - 2{{H}_{r}}}}{{{{{\left( {\sqrt {{{{({{x}_{{3,i}}} + {{x}_{{3,j}}} - 2{{H}_{r}})}}^{2}} + {{{({{x}_{{1,i}}} - {{x}_{{1,j}}})}}^{2}} + {{{({{x}_{{2,i}}} - {{x}_{{2,j}}})}}^{2}}} } \right)}}^{3}}}}} \right.} - \\ - \,\,\left. {\frac{{({{x}_{{3,i}}} + {{x}_{{3,j}}} - 2{{H}_{r}})\left( {9\left[ {{{{({{x}_{{1,i}}} - {{x}_{{1,j}}})}}^{2}} + {{{({{x}_{{2,i}}} - {{x}_{{2,j}}})}}^{2}}} \right] - 6{{{({{x}_{{3,i}}} + {{x}_{{3,j}}} - 2{{H}_{r}})}}^{2}}} \right)}}{{{{{\left( {\sqrt {{{{({{x}_{{3,i}}} + {{x}_{{3,j}}} - 2{{H}_{r}})}}^{2}} + {{{({{x}_{{1,i}}} - {{x}_{{1,j}}})}}^{2}} + {{{({{x}_{{2,i}}} - {{x}_{{2,j}}})}}^{2}}} } \right)}}^{7}}}}} \right\}, \\ 1 \leqslant i \leqslant N,\,\,\,\,1 \leqslant j \leqslant N. \\ \end{gathered} $В формулах (6)–(9) элементы матрицы системы представляют собой сумму выражений, зависящих от R-носителей – либо горизонтальных плоскостей, либо горизонтальных слоев, если в формуле (8) слагаемые проинтегрировать по вертикальной координате (в последнем случае, формула (9), разумеется, несколько изменится, но принцип построения аналитических аппроксимаций останется прежним). На практике требуется разделять поля, создаваемые различными носителями как гравитационных, так и магнитных масс. Это необходимо, в первую очередь, для выявления глубоко расположенных геологических структур. Поля, генерируемые приповерхностными, зачастую хаотически рассеянными источниками быстро затухают при аналитическом продолжении вверх. Однако, если имеются сравнимые по мощности массы, залегающие на разных горизонтах, то вычисление линейных трансформант от всего поля не позволит, в общем случае, идентифицировать источники. Модифицированные S-аппроксимации вместе с усовершенствованной методикой решения СЛАУ являются весьма эффективным инструментом решения описанной проблемы изучения глубинного строения земной коры. Следует отметить, что в упомянутых выше работах авторов речь шла исключительно о нахождении решения системы линейных алгебраических уравнений, общего для всех носителей. В настоящей работе подчеркивается роль структурно-параметрического подхода к решению вариационных задач [Страхов, Степанова, 2002а]: для каждого из носителей задается свой вектор решений; при этом элементы матрицы выглядят совершенно аналогично (9), только без знака суммы по R-носителям. Такой способ решения аппроксимационной задачи позволяет свободнее “маневрировать” при деформации блоков матрицы системы, что приводит к повышению качества решения.
ОПИСАНИЕ МОДИФИЦИРОВАННОГО МЕТОДА S-АППРОКСИМАЦИЙ
При применении “классического” метода S-аппроксимаций теряется существенная часть информации о геометрии носителя масс: о его гладкости, симметрии, приблизительной локализации. Постановка обратной задачи по поиску распределения плотности в классе равномерно непрерывных или равномерно дифференцируемых функций значительно усложнит алгоритм, что приведет к неизбежным ошибкам при его использовании. Поэтому одной из проблем является выбор такой постановки обратной задачи в рамках S-аппроксимации, в которой сочетались бы простота и наиболее полный учет априорной информации об исследуемой области. При построении аппроксимационной конструкции поля, заданного в узлах неравномерной сети точек с резкими перепадами высот, обусловленность матрицы СЛАУ (7) сильно возрастает. При решении системы с плохо обусловленной матрицей S-аппроксимации становятся физически неадекватны и приводят к бессмысленным с геофизической точки зрения результатам.
Одним из способов устранения указанных проблем является введение особого функционала, позволяющего уточнять некоторые пробные решения СЛАУ (7) в зависимости от имеющейся априорной информации. Основная конструкция S-аппроксимации на начальном этапе сохраняется, поэтому назовем такой метод модифицированным методом S-аппроксимаций [Степанова и др., 2018].
Не ограничивая общности, рассмотрим локальный вариант S-аппроксимации, когда сферичностью Земли можно пренебречь. Пусть задано N точек наблюдения ${{M}_{i}} = \left( {{{x}_{{1,i}}},{{x}_{{2,i}}},{{x}_{{3,i}}}} \right)$, i = 1, 2, …, N, в которых известны значения некоторого элемента поля ${{f}_{{i,\delta }}} = {{f}_{i}} + \delta {{f}_{i}}$, i = 1, 2, …, N. Если рассматривается вертикальная производная поля, то аппроксимация поля суммой простого и двойного слоев, расположенных на R-уровнях, задается соотношением (2). Далее ставится следующая вариационная задача:
(10)
$\begin{gathered} \Omega \left( \rho \right) + \mu \Xi \left( \rho \right) = \\ = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {\rho _{{1,r}}^{2}\left( {\hat {\xi }} \right) + \rho _{{2,r}}^{2}\left( {\hat {\xi }} \right)} \right)d\hat {\xi }} } } + \\ + \,\,\mu \Xi \left( \rho \right) = \mathop {\min }\limits_\rho , \\ {{f}_{{i,\delta }}} - \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left( {{{\rho }_{{1,r}}}\left( {\hat {\xi }} \right)Q_{{1,r}}^{{(i)}}\left( {\hat {\xi }} \right)} \right.} } } + \\ + \,\,\left. {{{\rho }_{{2,r}}}\left( {\hat {\xi }} \right)Q_{{2,r}}^{{(i)}}\left( {\hat {\xi }} \right)} \right)d\hat {\xi } = 0,\,\,\,\,{\text{ }}i = 1,2,..., \\ \end{gathered} $(11)
${{\hat {x}}^{\mu }}:{{\left( {\delta _{{\min }}^{\mu }} \right)}^{2}} \leqslant \left\| {A{{{\hat {x}}}^{\mu }} - {{f}_{\delta }}} \right\|_{E}^{2} \leqslant {{\left( {\delta _{{\max }}^{\mu }} \right)}^{2}},\,\,\,\,\mu \in \left[ {0,1} \right].$Для каждого значения параметра μ находится свое приближенное решение СЛАУ ${{\hat {x}}^{\mu }}$ (10), для которого выполняется условие (11). Нижнее и верхнее значения квадрата нормы невязки ${{\left( {\delta _{{\min }}^{\mu }} \right)}^{2}}$ и ${{\left( {\delta _{{\max }}^{\mu }} \right)}^{2}}$ корректируются для различных значений параметра μ. Делается это с той целью, что постановка обратной задачи (10) накладывает определенные ограничения на выбор решения системы. Из теории катастроф известно, что даже незначительное изменение функции ведет к изменению ее особенностей [Постон и др., 1980; Арнольд, 1990]. С физической точки зрения это приводит к тому, что меняется поведение всей системы. Поэтому для каждого последующего значения μ постоянные ${{\left( {\delta _{{\min }}^{\mu }} \right)}^{2}}$ и ${{\left( {\delta _{{\max }}^{\mu }} \right)}^{2}}$ необходимо корректировать.
На начальном этапе решения полагаем параметр μ = 0. В этом случае мы приходим к классическому варианту метода S-аппроксимаций, в котором система описывается соотношениями (6)–(9). Таким образом, находится решение $\hat {x}$, при котором плотности простого и двойного слоев описываются следующими соотношениями:
(12)
$\begin{gathered} {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi },{{{\hat {x}}}^{0}}} \right) = \sum\limits_{i = 1}^N {\hat {x}_{i}^{0}Q_{{k,r}}^{{(i)}}\left( {\hat {\xi }} \right) = \left( {{{{\hat {x}}}^{0}},{{Q}_{{k,r}}}\left( {\hat {\xi }} \right)} \right)} , \\ k = 1,2,\,\,\,\,r = 1,2,...,R. \\ \end{gathered} $Из формулы (12) следует, что аппроксимации функций ${{\rho }_{{k,r}}}\left( {\hat {\xi }} \right)$ зависят от найденного решения системы. Для наиболее быстрого решения системы с приемлемой точностью, следует выбрать константы ${{\left( {\delta _{{\min }}^{0}} \right)}^{2}}$ и ${{\left( {\delta _{{\max }}^{0}} \right)}^{2}}$ из следующих соображений:
(13)
$\begin{gathered} \varepsilon = \frac{{\left\| {A{{{\hat {x}}}^{0}} - {{f}_{\delta }}} \right\|_{E}^{2}}}{{\left\| {{{f}_{\delta }}} \right\|_{E}^{2}}},\,\,\,\,{{\left( {\delta _{{\max }}^{0}} \right)}^{2}} = c\varepsilon , \\ \frac{{{{{\left( {\delta _{{\max }}^{0}} \right)}}^{2}}}}{{{{{\left( {\delta _{{\min }}^{0}} \right)}}^{2}}}} = 10{\kern 1pt} - {\kern 1pt} 100. \\ \end{gathered} $То есть задавая точность аппроксимации ε, определяем значение констант ${{\left( {\delta _{{\min }}^{0}} \right)}^{2}}$ и ${{\left( {\delta _{{\max }}^{0}} \right)}^{2}}$. Константы c и $\varepsilon $ задаются из условий поставленной задачи и зависят от уровня помех.
Так как выбор функционала качества решения Ξ(ρ) зависит от имеющейся априорной информации, то выписать аналитические выражения для безусловной вариационной задачи (10) не представляется возможным. Однако, если известно решение системы (12) при μ = 0, то, увеличивая параметр регуляризации μ постепенно от 0 до 1, можно определенным образом варьировать вектор решения ${{\hat {x}}^{0}}$ СЛАУ, чтобы аппроксимации искомых функций удовлетворяли поставленным условиям. Не ограничивая общности, будем считать, что значения параметра регуляризации μ меняются по линейному закону:
где s соответствует определенному решению. Так, при s = 0 решением задачи (10) являются выражения (12). Аппроксимации искомых функций $\rho _{{k,r}}^{{({{a}^{\mu }})}}\left( {\hat {\xi }} \right)$ соответствующих разным значениям μ, можно представить в виде однопараметрического семейства функций:(15)
$\begin{gathered} \rho _{{k,r}}^{{({{a}^{\mu }})}}\left( {\hat {\xi }} \right) = {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{{{{\mu }_{s}}}}},{{\mu }_{s}}} \right),\,\,\,\,k = 1,2; \\ r = 1,2,...,R,\,\,\,\,{{\mu }_{s}} \in [0,1]. \\ \end{gathered} $Как было отмечено, функции ${{\tilde {\rho }}_{{k,r}}}\left( {\hat {\xi },{{{\hat {x}}}^{{{{\mu }_{s}}}}},{{\mu }_{s}}} \right)$ при различных значениях μ могут по-разному отображать физико-геологические параметры среды. Запишем выражение для s-й деформации аппроксимированной функции:
(16)
$\begin{gathered} {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{{{{\mu }_{s}}}}},{{\mu }_{s}}} \right) = {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{{{{\mu }_{{s - 1}}}}}},{{\mu }_{{s - 1}}}} \right) + {{\varepsilon }_{\mu }}{{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{s}}} \right), \\ k = 1,2;\,\,\,\,r = 1,2,...,R, \\ \end{gathered} $(17)
$\begin{gathered} \left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{{{{\mu }_{s}}}}},{{\mu }_{s}}} \right) = {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi },{{{\hat {x}}}^{{{{\mu }_{{s - 1}}}}}},{{\mu }_{{s - 1}}}} \right) + {{\varepsilon }_{\mu }}{{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{s}}} \right) = \\ = {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{{{{\mu }_{{s - 2}}}}}},{{\mu }_{{s - 2}}}} \right) + {{\varepsilon }_{\mu }}{{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{s}}} \right) + \\ + \,\,{{\varepsilon }_{\mu }}{{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{{s - 1}}}} \right) = ... = {{{\tilde {\rho }}}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{0}},0} \right) + \\ + \,\,{{\varepsilon }_{\mu }}\left( {{{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{s}}} \right) + {{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{{s - 1}}}} \right) + ... + {{f}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{\mu }_{1}}} \right)} \right), \\ k = 1,2;\,\,\,\,r = 1,2,...,R. \\ \end{gathered} $При таком представлении функция ${{\tilde {\rho }}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{0}},0} \right)$ играет роль нулевого приближения для однопараметрического семейства (15), в котором каждая функция является решением безусловной вариационной задачи (10). Поэтому под s-й деформацией функции подразумевается деформация именно нулевого приближения ${{\tilde {\rho }}_{{k,r}}}\left( {\hat {\xi }{\kern 1pt} ,{{{\hat {x}}}^{0}},0} \right)$, $k = 1,2$; r = 1, 2, …, R.
Целесообразным представляется выбор такого функционала качества решения, который давал бы наиболее содержательные результаты для поставленной задачи. Например, если требуется построить аналитическое продолжение поля вверх для выделения регионального фона [Мартышко и др., 2003] вместе с вычислением высших производных поля, то функционал качества решения для каждой из поставленных задач следует выбирать отдельно.
Локальный вариант. Если требуется найти высшие производные поля, в качестве функционала качества решения, дающего наиболее адекватные результаты, можно выбрать квадрат нормы горизонтальных производных плотностей простого и двойного слоев:
(18)
$\Xi \left( \rho \right) = \sum\limits_{r = 1}^R {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\sum\limits_{k = 1}^2 {\left( {{{{\left( {\frac{{\partial {{\rho }_{{k,r}}}\left( {\hat {\xi }} \right)}}{{\partial {{\xi }_{1}}}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{\rho }_{{k,r}}}\left( {\hat {\xi }} \right)}}{{\partial {{\xi }_{2}}}}} \right)}}^{2}}} \right)} } } } d\hat {\xi }{\kern 1pt} .$Выбор такого функционала обусловлен тем, что полученные аппроксимации дают картину наиболее общего поведения аномального потенциального поля, а горизонтальные и вертикальные производные находятся с приемлемой для геофизики точностью и будут представлять из себя более гладкие функции, чем при решении обычным методом S-аппроксимаций.
Можно дополнить функционал качества (18) еще и лапласианом от полученного решения с тем, чтобы случайная компонента сигнала отфильтровывалась на этапе аппроксимации (поскольку случайная помеха не является, в общем случае, гармонической функцией).
Кроме того, можно ввести дополнительную переменную ${{\xi }_{4}}$ и перейти в пространство двух комплексных переменных: ${{z}_{1}} = {{\xi }_{1}} + i{{\xi }_{2}},$ ${{z}_{2}} = {{\xi }_{3}} + i{{\xi }_{4}}$. Тогда требование плюригармоничности функции (т.е. решение должно удовлетворять условию $\frac{{{{\partial }^{2}}u}}{{\partial {{z}_{i}}\partial {{{\bar {z}}}_{j}}}} = 0,$ $i = 1,2;$ $j = 1,2.$), представляющей собой значения магнитного поля в заданной области, позволяет ограничить класс возможных решений обратной задачи.
Таким образом, мы приходим к большей устойчивости приближенного решения. Наш опыт показывает, что в случае равнинного и холмистого рельефа местности такой подход позволяет получить приблизительно на 10% более точное решение, чем без задания дополнительного функционала качества.
Если требуется найти аналитическое продолжение поля в нижнее или верхнее полупространство, то дополнительно целесообразным представляется выделение области $\tilde {D}$, в которой наблюдается наименьшая интенсивность поля. После такого качественного анализа, функционал качества решения можно выбрать следующим образом:
(19)
$\Xi \left( \rho \right) = \sum\limits_{r = 1}^R {\iint\limits_{\tilde {D}} {\left( {\rho _{{1,r}}^{2}\left( {\hat {\xi }} \right) + \rho _{{2,r}}^{2}\left( {\hat {\xi }} \right)} \right)}} d\hat {\xi }{\kern 1pt} .$Региональный вариант. Для аналитического продолжения полей вверх или вниз функционал Ξ(ρ), определяемый выражением (20), остается без изменений. В том случае, когда находятся высшие производные поля, выражение (19) принимает следующий вид:
(20)
$\begin{gathered} \Xi \left( \rho \right) = \\ = \sum\limits_{r = 1}^R {\iint\limits_{{{D}_{r}}} {\sum\limits_{k = 1}^2 {\left( {\frac{{{{{\left( {\frac{{\partial {{\rho }_{{k,r}}}\left( {\tilde {\varphi },\tilde {\vartheta }} \right)}}{{\partial{ \tilde {\vartheta }}}}} \right)}}^{2}}}}{{{{r}^{2}}{{{\sin }}^{2}}\tilde {\vartheta }}} + \frac{{{{{\left( {\frac{{\partial {{\rho }_{{k,r}}}\left( {\tilde {\varphi },\tilde {\vartheta }} \right)}}{{\partial{ \tilde {\varphi }}}}} \right)}}^{2}}}}{{{{r}^{2}}}}} \right)} }} d\tilde {\varphi }d\tilde {\vartheta }, \\ \end{gathered} $АНАЛИТИЧЕСКАЯ АППРОКСИМАЦИЯ МАГНИТНОГО ПОЛЯ ПО ДАННЫМ ДЕТАЛЬНОЙ ГИДРОМАГНИТНОЙ СЪЕМКИ
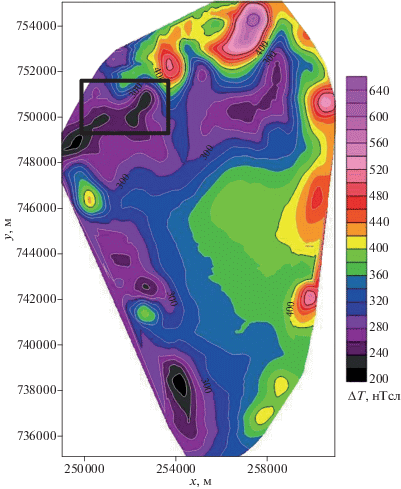
Данные гидромагнитной съемки озера Кинерет (рис. 1) были проинтерпретированы нами с помощью усовершенствованного метода блочного контрастирования. Модифицированные S-аппроксимации были построены с использованием структурно-параметрического подхода, как это было описано выше. Шаг сетки $h = 25$ м, общее количество валидных измерений равняется 264 442. В предыдущих работах авторов уже исследовался описываемый регион [Степанова и др., 2018]. Однако ранее размеры блоков в возникающей системе уравнений и глубины залегания плоскостей, на которых залегали носители магнитных масс, не варьировались. В настоящей статье предлагается алгоритм деформации блока, позволяющий выявлять наиболее “значимые” для формирования локальных аномалий геологические структуры.
Исходя из графического анализа аномального магнитного поля можно видеть, что исходная область характеризуется как крупными региональными, так и локальными аномалиями. Исходные данные были получены в результате многопрофильной гидромагнитной съемки, затем были интерполированы на равномерную сетку с шагом $h = 25$ м. Интерполирование данных эксперимента привело к появлению весьма специфических “дефектов” аномального магнитного поля, которые заглушают локальные аномалии исходного поля. Для демонстрации подобного рода “дефектов” на рис. 2 приведена северная часть аномального магнитного поля озера Кинерет.
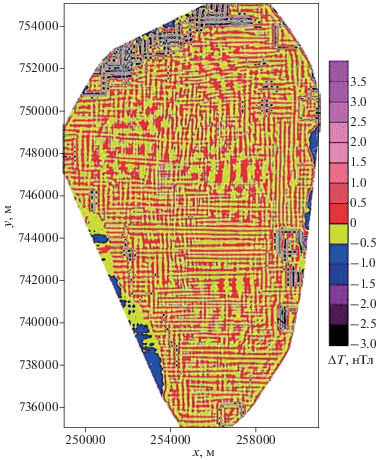
Рис. 2.
Северная часть озера Кинерет: (а) – теневая карта аномального магнитного поля; (б) – карта изолиний аномального магнитного поля. Пунктирными кривыми выделены дефектные зоны.
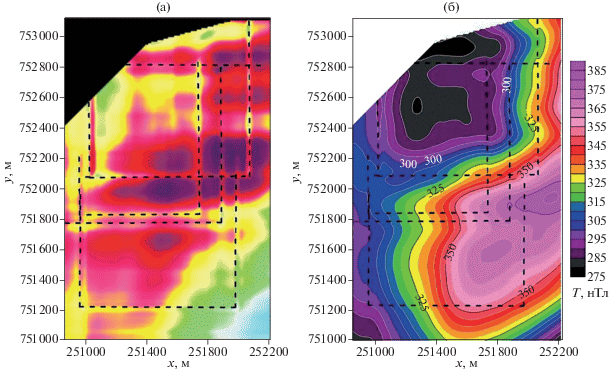
Исходя из графического анализа теневой карты (рис. 2а) можно видеть, что в поле наблюдаются резкие градиенты, которые проходят вдоль прямых линий. Такого рода помехи почти не влияют на региональные компоненты, но существенно искажают влияние приповерхностных источников.
В рамках модифицированной S-аппроксимации поле аппроксимировалось суммой простого и двойного слоев, распределенных на 4 семействах плоскостей, залегающих на глубинах 250 + 5t, 600 + 10t, 1100 + 15t и 2000 + 20t м соответственно ниже высотной отметки, на которой была проведена съемка (для данной гидромагнитной съемки она равняется –220 м); t – параметр, $t \in \left[ {0;5} \right],\;\Delta t = 0.1$ – шаг изменения параметра. Константы, являющиеся границами квадрата нормы невязки снизу и сверху, выбраны следующим образом: $\delta _{{\min }}^{2} = 6000$ нТл2, $\delta _{{\max }}^{2} = 30\,000$ нТл2. Размеры блоков деформировались по формуле
(21)
$\begin{gathered} M_{q}^{{(i + 1)}} = \sqrt {{{{\left( {M_{q}^{{(i)}}} \right)}}^{2}} - 4(M_{q}^{{(i)}} - 1)} ,\,\,\,\,q = 1,{\text{ }}2,{\text{ }}...,Q, \\ i = 1,...,{{N}_{i}},\,\,\,\,1 \leqslant {{N}_{i}} \leqslant N. \\ \end{gathered} $Такая деформация позволяет связать с каждым блоком матрицу, подобную целочисленной спиральной. Спиральные матрицы, в свою очередь, обладают рядом замечательных свойств и легко размещаются в оперативной памяти.
В формуле (21) дискретный индекс i связан с непрерывным параметром t линейной зависимостью:
При построении аналитических аппроксимаций применяется способ трехступенчатого контроля, предложенный В.Н. Страховым, который заключается в следующем. На первом шаге из исходных пунктов исключается около 20% пунктов, имеющих минимальные по модулю значения аномального поля, которые включаются в число контрольных, а оставшиеся 80% пунктов используются для построения аппроксимационной конструкции. На втором шаге из контрольных пунктов выделяется половина, имеющая максимальные по модулю отклонения от исходного поля, и они добавляются к числу пунктов, используемых для построения аппроксимации. Контроль точности производится по оставшимся контрольным пунктам (10%). На третьем шаге для построения аппроксимации используются все исходные пункты.
В табл. 1 приводятся результаты S-аппроксимации. Система линейных алгебраических уравнений (СЛАУ) решалась регуляризованным трехслойным итерационным методом Чебышева с использованием блочного метода контрастирования. Все вычисления проводились на суперкомпьютере “Ломоносов” НИВЦ МГУ. При вычислениях число процессоров выбрано равным 1024.
Таблица 1.
Озеро Кинерет. Результаты S-аппроксимации
| N N1 N2 |
${{\sigma }_{{\min }}}$, нТл | ${{\sigma }_{{\max }}}$, нТл | $\sigma $0, нТл | $\sigma $1, ${{\sigma }_{{{\text{конт}}\,1}}}$, нТл | $\sigma $2, ${{\sigma }_{{{\text{конт}}\,2}}}$, нТл | $\frac{\Delta }{T}$ |
|---|---|---|---|---|---|---|
| 264 442 | 0.1506 | 0.3368 | 0.22 | 0.6914 | 0.6571 | $\frac{{6.2986 \times {{{10}}^{{ - 4}}}}}{{0:22:09}}$ |
| 210 943 | 0.8012 | 0.748 | ||||
| 236 853 | ||||||
| 160 000 | 0.136 | 0.227 | 0.17 | 0.556 | 0.521 | $\frac{{4.1729 \times {{{10}}^{{ - 4}}}}}{{0:17:16}}$ |
| 129 000 | 0.663 | 0.559 | ||||
| 134 000 |
Приняты следующие обозначения: N – число исходных точек, N1 – число точек без контрольных точек I типа; N2 – число точек без контрольных точек II типа; ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} ;$ ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} $ – границы среднеквадратического отклонения, ${{\sigma }_{0}} = \frac{{\left\| {Ax - {{f}_{\delta }}} \right\|_{E}^{{}}}}{{\sqrt N }}$ – среднеквадратическое отклонение; ${{\sigma }_{1}}$ – среднеквадратичное отклонение, полученное с помощью аппроксимации аномального магнитного поля без контрольных точек I типа; ${{\sigma }_{{{\text{конт}}\,1}}}$ – среднеквадратичное отклонение, полученное в контрольных точках I типа; ${{\sigma }_{2}}$ – среднеквадратичное отклонение, полученное с помощью аппроксимации аномального магнитного поля без контрольных точек II типа; ${{\sigma }_{{{\text{конт}}\,2}}}$ – среднеквадратичное отклонение, полученное в контрольных точках II типа; ${\Delta } = \frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$ – показатель качества решения; T – время решения СЛАУ (ч : мин : с); роль контрольных точек второго типа играли дефектные зоны. Таким образом, с помощью предлагаемой методики можно выделить поля, создаваемые различными по своему вкладу в результирующее магнитное поле структурами. Основной вклад в поле дефектных зон (68% приблизительно) вносили массы, распределенные на самой верхней плоскости, как показали наши расчеты.
Время решения СЛАУ для данной модели составило всего 5 мин на персональном компьютере. Значение ${{\sigma }_{{\min }}} < {{\sigma }_{0}} < {{\sigma }_{{\max }}}$ и среднеквадратические отклонения ${{\sigma }_{{{\text{конт}}\,1}}}$ и ${{\sigma }_{{{\text{конт}}\,2}}}$, полученные в контрольных точка I и II типа, превышают ${{\sigma }_{0}}$ почти в 3 раза, что связано с наличием вышеуказанных “дефектов” в исходных интерполированных данных. На карте разностного магнитного поля (рис. 3) также выделяются аналогичные кривые, в которых разность между аппроксимацией и реальным полем максимальна. Во второй строке таблицы приводятся значения среднеквадратических отклонений, времени счета и т.д. для деформированного блока, т.е. число элементов исходной матрицы системы было уменьшено в соответствии с формулами (21)–(22). Было выполнено 10 серий расчетов с различными значениями параметра t в формуле (22). При уменьшении размерности блока на 25–35% существенных изменений в погрешности метода не происходит (при редукции блока на 50% среднеквадратическое отклонение ${{\sigma }_{0}}$ возросло на 15–18%), что позволяет сделать вывод об эффективности усовершенствованного метода блочного контрастирования при решении такого рода задач.
РАЗДЕЛЕНИЕ МАГНИТНЫХ ПОЛЕЙ В МОДЕЛЬНОМ ПРИМЕРЕ
В соответствии с изложенным во Введении к настоящей работе для нахождения производных геопотенциального поля в некоторой совокупности точек ${{M}_{\nu }}$ с координатами ${{x}^{{(\nu )}}} = ({{\hat {x}}^{{(\nu )}}},{{x}_{3}}^{{(\nu )}})$, из внешней области СD объема D в рамках метода линейных интегральных представлений необходимо действовать следующим образом.
По заданным плотностям ${{\rho }_{1}}({{\xi }_{1}},{{\xi }_{2}}) \in {{L}_{2}}(D)$ и ${{\rho }_{2}}({{\xi }_{1}},{{\xi }_{2}}) \in {{L}_{2}}(D)$ простого и двойного слоев (обозначим плоскость, на которой распределены простой и двойной слои через D) мы должны найти совокупность ограниченных линейных функционалов вида
(23)
$\begin{gathered} {{p}_{s}} = \int\limits_D {{{\rho }_{1}}({{\xi }_{1}},{{\xi }_{2}})P_{1}^{{(s)}}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}} d{{\xi }_{2}} + \\ + \,\,\int\limits_D {{{\rho }_{2}}({{\xi }_{1}},{{\xi }_{2}})P_{2}^{{(s)}}} ({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}d{{\xi }_{2}},\,\,\,\,s = 1,2, \ldots ,S,~ \\ \end{gathered} $(24)
$\begin{gathered} {{\left\| {P_{1}^{{(s)}}} \right\|}^{2}} = \int\limits_D {{{{(P_{1}^{{(s)}})}}^{2}}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}} d{{\xi }_{2}} < + \infty . \\ {{\left\| {P_{2}^{{(s)}}} \right\|}^{2}} = \int\limits_D {{{{(P_{2}^{{(s)}})}}^{2}}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}} d{{\xi }_{2}} < + \infty . \\ \end{gathered} $Действительно, значения аномалий силы тяжести $g({{M}_{\nu }};\rho )$ выражаются соотношением (23) при s = ν:
(25)
$\begin{gathered} P_{1}^{{(\nu )}}({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}) = \gamma \frac{{({{\xi }_{3}} - {{x}_{3}}^{{(\nu )}})}}{{{{R}^{3}}(\xi - {{x}^{{(\nu )}}})}}, \\ P_{2}^{{(\nu )}}({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}) = \\ = \gamma \frac{{({{{({{\xi }_{1}} - \hat {x}_{1}^{{(\nu )}})}}^{2}} + {{{({{\xi }_{2}} - \hat {x}_{2}^{{(\nu )}})}}^{2}} - 2{{{({{\xi }_{3}} - x_{3}^{{(\nu )}})}}^{2}})}}{{{{R}^{5}}(\xi - {{x}^{{(\nu )}}})}}, \\ \end{gathered} $(26)
$u({{M}_{\nu }};\rho ) = {{\left. {D_{x}^{\alpha }g(x;\rho )} \right|}_{{x = {{x}^{{(\nu )}}}}}},$(27)
$\begin{gathered} D_{x}^{\alpha } = \frac{{{{\partial }^{{|\alpha |}}}}}{{\partial x_{1}^{{{{\alpha }_{1}}}}\partial x_{2}^{{{{\alpha }_{2}}}}\partial {{z}^{{{{\alpha }_{3}}}}}}},\,\,\,\,\rho = ({{\rho }_{1}},{{\rho }_{2}}), \\ \xi = ({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}),\,\,\,\,\hat {\xi } = ({{\xi }_{1}},{{\xi }_{2}}), \\ \end{gathered} $(28)
$\begin{gathered} P_{1}^{{(\nu )}}({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}) = \\ = \gamma {{( - 1)}^{{|\alpha |}}}D_{\xi }^{\alpha }{{\left. {\left( {\frac{{{{\xi }_{3}} - {{x}_{3}}}}{{{{R}^{3}}(\xi - x)}}} \right)} \right|}_{{x = {{x}^{{(\nu )}}}}}}, \\ P_{2}^{{(\nu )}}({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}) = \\ = \gamma {{( - 1)}^{{|\alpha |}}}D_{\xi }^{\alpha } \times \\ \times \,\,{{\left. {\left( {\frac{{{{{({{\xi }_{1}} - {{{\hat {x}}}_{1}})}}^{2}} + {{{({{\xi }_{2}} - {{{\hat {x}}}_{2}})}}^{2}} - 2{{{({{\xi }_{3}} - {{x}_{3}})}}^{2}}}}{{{{R}^{5}}(\xi - {{x}^{{(\nu )}}})}}} \right)} \right|}_{{x = {{x}^{{(\nu )}}}}}}. \\ \end{gathered} $В соотношении (23) ${{\rho }_{1}}({{\xi }_{1}},{{\xi }_{2}}),\,\,{{\rho }_{2}}({{\xi }_{1}},{{\xi }_{2}})$ находятся по заданным значениям ${{g}_{{k,\delta }}}$ аномалий силы тяжести из решения системы уравнений, к которой сводится вариационная задача (10), т.е. системы вида (7)–(9).
Аналогичные выражения можно получить для магнитного потенциала и его производных, если учесть соотношение:
Здесь: $\bar {I}$ – вектор постоянной намагниченности; U – магнитный потенциал; $\gamma ,\;\rho $ – гравитационная постоянная и средняя плотность породы соответственно; V – гравитационный потенциал. Поэтому в дальнейшем, без ограничения общности, производные геопотенциальных полей вычислялись по формуле (28).
Поскольку ${{\rho }_{1}},{{\rho }_{2}}$ представляется в виде (12), то из (28) следует, что
(29)
$\begin{gathered} P_{1}^{{(s)}}(\rho ) = \sum\limits_{k = 1}^N {{{\lambda }_{k}}b_{k}^{1}(P_{1}^{{(s)}})} = {{(\lambda ,{{b}^{1}}(P_{1}^{{(s)}}))}_{N}}, \\ P_{2}^{{(s)}}(\rho ) = \sum\limits_{k = 1}^N {{{\lambda }_{k}}b_{k}^{2}(P_{2}^{{(s)}})} = {{(\lambda ,{{b}^{2}}(P_{2}^{{(s)}}))}_{N}}, \\ \end{gathered} $(30)
$\begin{gathered} b_{l}^{k}(P_{k}^{{(s)}}) = \int\limits_D {P_{k}^{{(s)}}({{\xi }_{1}},{{\xi }_{2}})P_{k}^{{(l)}}({{\xi }_{1}},{{\xi }_{2}})d{{\xi }_{1}}d{{\xi }_{2}}{\kern 1pt} ,} \\ s = 1,2, \ldots ,S;\,\,\,\,l = 1,2,...,S;\,\,\,k = 1,2. \\ \end{gathered} $Вектора ${{b}^{k}}(P_{k}^{{(s)}})$ вычисляются из соотношений:
(31)
$\begin{gathered} b_{l}^{1}(P_{1}^{{(s)}}) = \int\limits_D {Q_{1}^{{(l)}}(\hat {\xi })P_{1}^{{(s)}}(\hat {\xi })d\hat {\xi }} = {{( - 1)}^{{|\alpha |}}}{{\gamma }^{2}}\int\limits_D {\left( {\frac{{{{\xi }_{3}} - {{x}_{{3,k}}}}}{{{{R}^{3}}(\xi - {{x}_{k}})}}} \right)D_{\xi }^{\alpha }{{{\left. {\left( {\frac{{{{\xi }_{3}} - {{x}_{3}}}}{{{{R}^{3}}(\xi - x)}}} \right)} \right|}}_{{x = {{x}^{{(s)}}}}}}} d{{\xi }_{1}}d{{\xi }_{2}} = \\ = {{\gamma }^{2}}D_{x}^{\alpha }{{\left. {\left( {\int\limits_D {\frac{{({{\xi }_{3}} - {{x}_{{3,k}}})({{\xi }_{3}} - {{x}_{3}})}}{{{{R}^{3}}(\xi - {{x}_{k}}){{R}^{3}}(\xi - x)}}d{{\xi }_{1}}d{{\xi }_{2}})} } \right)} \right|}_{{x = {{x}^{{(s)}}}}}}, \\ b_{l}^{2}(P_{2}^{{(s)}}) = \int\limits_D {Q_{2}^{{(l)}}(\hat {\xi })P_{2}^{{(s)}}(\hat {\xi })d\hat {\xi }} = {{( - 1)}^{{|\alpha |}}}{{\gamma }^{2}}\int\limits_D {\left( {\frac{{{{{({{\xi }_{1}} - {{{\hat {x}}}_{{k,1}}})}}^{2}} + {{{({{\xi }_{2}} - {{{\hat {x}}}_{{k,2}}})}}^{2}} - 2{{{({{\xi }_{3}} - {{x}_{{3,k}}})}}^{2}}}}{{{{R}^{5}}(\xi - {{x}_{k}})}}} \right.} \times \,\, \\ {{\left. { \times \,\,D_{\xi }^{\alpha }\left( {\frac{{{{{({{\xi }_{1}} - {{{\hat {x}}}_{1}})}}^{2}} + {{{({{\xi }_{2}} - {{{\hat {x}}}_{2}})}}^{2}} - 2{{{({{\xi }_{3}} - {{x}_{3}})}}^{2}}}}{{{{R}^{5}}(\xi - x)}}} \right)} \right|}_{{x = {{x}^{{(s)}}}}}}d{{\xi }_{1}}d{{\xi }_{2}} = \\ = {{\gamma }^{2}}D_{x}^{\alpha }{{\left. {\left( {\int\limits_D {\frac{{({{{({{\xi }_{1}} - {{{\hat {x}}}_{1}})}}^{2}} + {{{({{\xi }_{2}} - {{{\hat {x}}}_{2}})}}^{2}} - 2({{\xi }_{3}} - {{x}_{3}})_{{}}^{2}){{{({{\xi }_{1}} - {{{\hat {x}}}_{{1,k}}})}}^{2}} + {{{({{\xi }_{2}} - {{{\hat {x}}}_{{2,k}}})}}^{2}} - 2({{\xi }_{3}} - {{x}_{{3,k}}})_{{}}^{2})}}{{{{R}^{5}}(\xi - {{x}_{k}}){{R}^{5}}(\xi - x)}}d\xi d\eta )} } \right)} \right|}_{{x = {{x}^{{(s)}}}}}}. \\ \end{gathered} $Если D-горизонтальная плоскость ${{\varsigma }_{3}} = {\text{const}}$, то
(32)
$\begin{gathered} b_{l}^{1}(P_{1}^{{(s)}}) = 2\pi {{\gamma }^{2}}D_{x}^{\alpha }\,{{\left. {\left( {\frac{{2{{\xi }_{3}} - ({{x}_{3}} + {{x}_{{3,l}}})}}{{{{{[{{{(2{{\xi }_{3}} - ({{x}_{3}} + {{x}_{{3,l}}}))}}^{2}} + \rho _{l}^{2}(\hat {x})]}}^{{3/2}}}}}} \right)} \right|}_{{x = {{x}^{{(s)}}}}}}, \\ b_{l}^{2}(P_{2}^{{(s)}}) = 2\pi {{\gamma }^{2}}D_{x}^{\alpha }\,{{\left. {\left( {\frac{{{{{({{{\hat {x}}}_{{1,l}}} - {{{\hat {x}}}_{1}})}}^{2}} + {{{(\hat {x}_{{2,l}}^{{}} - {{{\hat {x}}}_{2}})}}^{2}} - 2{{{({{\xi }_{3}} - {{x}_{3}})}}^{2}}}}{{{{{[{{{(2{{\xi }_{3}} - ({{x}_{3}} + {{x}_{{3,l}}}))}}^{2}} + \rho _{l}^{2}(\hat {x})]}}^{{5/2}}}}}} \right)} \right|}_{{x = {{x}^{{(s)}}}}}}, \\ \end{gathered} $Например, если требуется вычислить первую производную силы тяжести по x1 в точке Мi, то элементы матрицы ${{a}_{{ij}}}$ нужно продифференцировать по х1.
Получим:
(33)
$\begin{gathered} {{a}_{{ij,{{x}_{1}}}}} = 2\pi ( - 3({{x}_{{3,i}}} + {{x}_{{3,j}}}){{({{x}_{{1,i}}} - {{x}_{{1,j}}})} \mathord{\left/ {\vphantom {{({{x}_{{1,i}}} - {{x}_{{1,j}}})} {{{R}^{5}}}}} \right. \kern-0em} {{{R}^{5}}}} + \\ + \,\,(60{{({{x}_{{3,i}}} + {{x}_{{3,j}}})}^{3}}({{x}_{{1,i}}} - {{x}_{{1,j}}}) - \\ - \,\,45({{x}_{{3,i}}} + {{x}_{{3,j}}}){{({{x}_{{1,i}}} - {{x}_{{1,j}}})*ru)} \mathord{\left/ {\vphantom {{({{x}_{{1,i}}} - {{x}_{{1,j}}})*ru)} {{{R}^{7}}}}} \right. \kern-0em} {{{R}^{7}}}}). \\ \end{gathered} $Здесь $ru = {{({{x}_{{1,i}}} - {{x}_{{1,j}}})}^{2}}$ + ${{({{x}_{{2,i}}} - {{x}_{{2,j}}})}^{2}},$ R = $ = {{[{{({{x}_{{3,i}}} + {{x}_{{3,j}}})}^{2}} + ru]}^{{1/2}}}.$
Затем необходимо матрицу ${{A}_{{{{x}_{1}}}}} = \{ {{a}_{{ij,{{x}_{1}}}}}\} $ умножить на вектор $\lambda $. Получим значения производной ${{g}_{{{{x}_{1}}}}}$ в совокупности точек i = 1, 2, …, S.
Аналогично вычисляются производные ${{g}_{{}}}$ по ${{x}_{2}},{{x}_{3}}$ и вторые производные.
Опишем модельный участок, на котором была апробирована новая методика. Общее количество расчетных гравиметрических пунктов составляет 6000, сеть нерегулярная. Рельеф земной поверхности горный, перепад высот составляет около 3 км. Для данной сети было также рассчитано модельное гравитационное поле, обусловленное 14 прямоугольными призмами, расположенными двумя группами по 7 призм в каждой. Одна группа призм залегала на глубине 7 км, другая –15 км. В целом, данный участок соответствует модельному примеру № 2, подробно описанному в работе [Страхов, Степанова, 2002б].
Для вычисления производных гравитационного поля ${{g}_{{{{x}_{1}}}}},{{g}_{{{{x}_{2}}}}},{{g}_{{{{x}_{3}}}}},$ создаваемого группой призматических тел, находились значения поля в близких по каждой координате точках, и затем разность этих значений делилась на приращение.
С целью проверки эффективности разработанной методики была вычислена сумма первых производных гравитационного поля ${{g}_{{{{x}_{1}}}}} + {{g}_{{{{x}_{2}}}}},$ а затем построена модифицированная S-аппроксимация этой суммы с помощью усовершенствованного метода блочного контрастирования. При этом элементы матрицы системы вычислялись следующим образом: в формуле (33) ${{x}_{1}}$ заменилось на ${{x}_{2}}$, затем находилась сумма значений элементов ${{a}_{{ij,{{x}_{1}}}}} + {{a}_{{ij,{{x}_{2}}}}}$ в каждой точке. Результаты разделения полей (т.е. значений каждой из производных в отдельности) представлены на рис. 4–рис. 8. При вычислении значений конкретной производной вектор решения системы линейных алгебраических уравнений умножался на соответствующую часть ${{a}_{{ij,{{x}_{k}}}}},k = 1,2.$
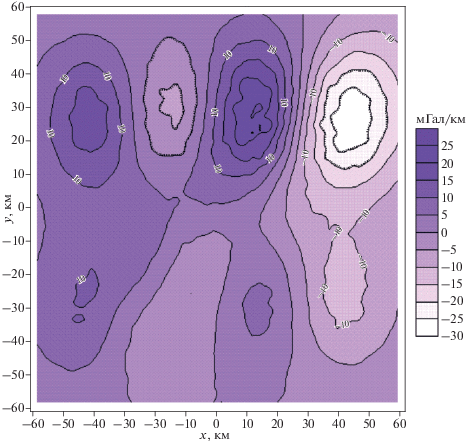
Рис. 4.
Карта изолиний разности производной гравитационного поля по х в модельном примере и производной, полученной с помощью модифицированной S-аппроксимации.
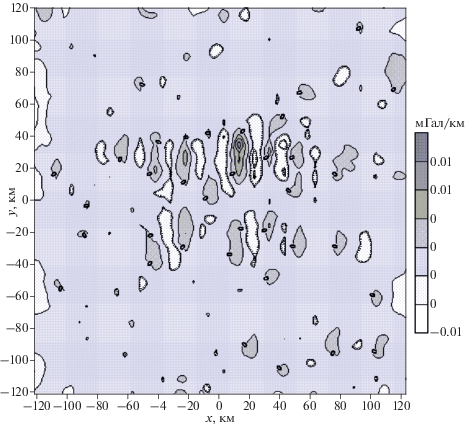
Относительная ошибка (показатель качества решения ${\Delta } = {{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}} \mathord{\left/ {\vphantom {{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}} {{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}} \right. \kern-0em} {{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$) не превысила 10% в данном модельном примере.
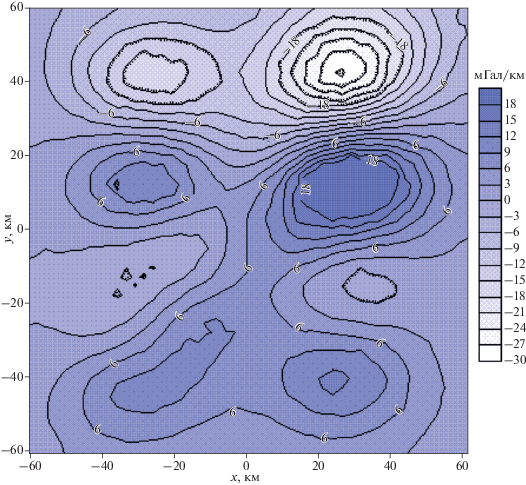
Рис. 6.
Карта изолиний разности производной гравитационного поля по y в модельном примере и производной, полученной с помощью модифицированной S-аппроксимации.
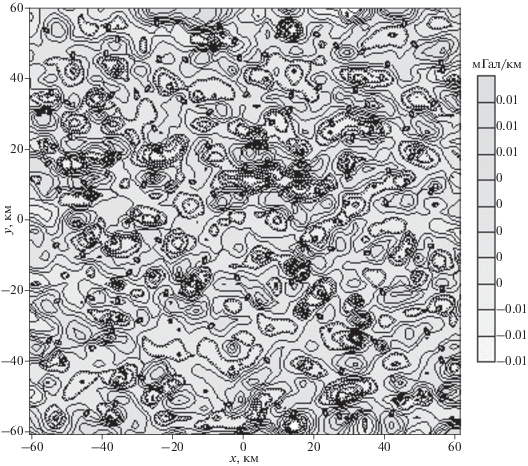
Для дальнейшего улучшения качества “разделенных” решений была построена аналитическая аппроксимация элемента потенциального поля (т.е. суммы производных ${{g}_{{{{x}_{1}}}}} + {{g}_{{{{x}_{2}}}}}$) полем источников, распределенных по граням двух двугранных углов (Ed.1 и Ed.2):
Выяснилось, что поле первой группы призм с точностью 10–12% восстанавливается с помощью первой конструкции, а поле второй (более глубоко залегающей и расположенной правее первой) – с помощью второго двугранного угла. Время решения системы линейных алгебраических уравнений на Pentium –IV (3 ГГц , ОЗУ -8 Гбайт) составило 17 мин при применении метода усовершенствованного блочного контрастирования.
ВЫВОДЫ
1. Построение линейных трансформаций магнитного поля по данным гидромагнитной съемки эффективно при использовании модифицированного метода S-аппроксимаций вместе с усовершенствованной методикой блочного контрастирования. Результаты математического эксперимента показали, что даже в случае горного рельефа возможно построение аппроксимационной конструкции со среднеквадратическим отклонением около 0.2 нТл. Однако при построении аппроксимаций сильно расчлененного рельефа следует выбирать модель с несколькими носителями для экономии вычислительного времени (см. табл. 1).
2. Усовершенствованный блочный метод контрастирования позволяет найти такое нулевое приближение для СЛАУ, что время решения всей системы существенно сокращается (см. табл. 1), если исследуемое поле не характеризуется малым количеством четко выраженных экстремумов. В противном случае заметного улучшения при использовании блочного метода контрастирования не наблюдается. Однако на практике исследуемое поле всегда характеризуется достаточным количеством геологических объектов, искажающих поле и усложняющих его картину, так что использование блочного метода оправдано при интерпретации данных детальной аэромагнитной съемки (см. табл. 1) и рис. 3–рис. 6.
3. При сложном рельефе земной поверхности и при наличии случайной помехи, а также если геологический объект представляет собой геометрическое тело невыпуклой формы, линейные трансформации поля, построенные при помощи модифицированного метода S-аппроксимаций, верно отражают морфологические особенности исследуемого поля.
4. На примерах съемки озера Кинерет показано, что при помощи модифицированного метода S-аппроксимаций восстанавливаются первые производные аномального магнитного поля.
Список литературы
Арнольд В.И. Теория катастроф. М.: Наука. 1990. 128 с.
Воеводин Вл.В., Жуматий С.А. Соболев С.И., Антонов А.С., Брызгалов П.А., Никитенко Д.А., Стефанов К.С., Воеводин В.В. Практика суперкомпьютера “Ломоносов” // Открытые системы. 2012. № 7. С. 36–39.
Долгаль А.С., Костицын В.И., Новикова П.Н., Рашидов В.А., Пугин А.В., Христенко Л.А. Практическое применение истокообразной аппроксимации геолого-геофизических данных // Геофизика. Вып. 5. 2017. С. 29–37.
Долгаль А.С., Новикова П.Н., Костицын В.И., Рашидов Л.А. Совместная оценка геометрических параметров и намагниченности геологических объектов монтажным методом // Геофизика. Вып. 5. 2013. С. 36–41.
Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Основные дифференциальные уравнения математической физики. М.: Физматгиз. 1962. 767 с.
Кризский В.Н. Структурная интерпретация локальных кусочно-анизотропных геологических включений / В.Н. Кризский, Р.Р. Яматов // Журнал Средневолжского математического общества. 2011. Т. 13. № 2. С. 8–16.
Мартышко П.С., Пруткин И.Л. технология разделения источников гравитационного поля по глубине // Геофизический журнал. 2003. Т. 25. № 3. С. 159.
Постон Т., Стюарт И. Теория катастроф и ее приложения. М.: Мир. 1980. 607 с.
Степанова И.Э., Раевский Д.Н., Конешов В.Н. Модифицированный метод S-аппроксимаций при решении обратных задач геофизики и геоморфологии // Геофизические исследования. 2017. Т. 18. № 1. С. 64–84.
Степанова И.Э., Керимов И.А., Раевский Д.Н., Щепетилов А.В. Комбинированный метод F-, S- и R-аппроксимаций при решении задач геофизики и геоморфологии // Физика Земли. 2018. № 1. С. 96–113.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (региональный вариант) // Физика Земли. 2002. № 7. С. 3–12.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (локальный вариант) // Физика Земли. 2002. № 2. С. 3–19.
Дополнительные материалы отсутствуют.