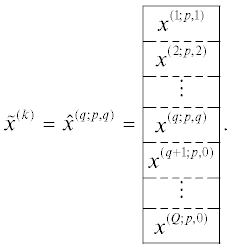Физика Земли, 2020, № 3, стр. 82-97
О совершенствовании методов обработки больших объемов данных в геофизике и геоморфологии на основе модифицированных S- и F-аппроксимаций
И. Э. Степанова 1, *, И. А. Керимов 1, Д. Н. Раевский 1, А. В. Щепетилов 2
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
2 МГУ им. М.В. Ломоносова
г. Москва, Россия
* E-mail: tet@ifz.ru
Поступила в редакцию 06.02.2019
После доработки 22.05.2019
Принята к публикации 22.06.2019
Аннотация
В работе рассматривается усовершенствованный вариант метода блочного контрастирования для обработки больших и сверхбольших объемов данных гравиразведки и геоморфологии. Элементы аномального гравитационного и магнитного полей находятся с помощью модифицированных S- и F-аппроксимаций. Приводятся результаты математического эксперимента.
1. ВВЕДЕНИЕ
Построению аналитических аппроксимаций элементов аномальных гравитационного и магнитного полей в локальном и региональном вариантах были посвящены ранее опубликованные работы авторов (см., например, [Cтрахов и др., 2000; 2002; Степанова, 2009а; б; 2008; Керимов и др., 2018; Stepanova, 2009].
В рамках метода линейных интегральных представлений известная компонента гравитационного или магнитного поля аппроксимируется некоторым интегралом: например, суммой простого и двойного слоев, распределенных на некоторой совокупности носителей (в локальном случае ими являются горизонтальные плоскости, в региональном – сферы или сфероиды). Однако носители масс могут представлять собой и более сложные фигуры. Важно подчеркнуть, что мы решаем только трехмерные задачи интерпретации, что в полной мере соответствует реальной геофизической практике. Двумерные задачи постепенно перестают привлекать внимание исследователей, даже в случае неоднородностей смешанного типа — когда имеются как конечные, так и бесконечные в каких-то измерениях носители. Хотелось бы отметить также важность перехода от реальных, т.е. трехмерных, источников, к гипотетическим, имеющим большую размерность. Такой подход может оказаться плодотворным, как показал опыт авторов при решении нелинейных задач гравиметрии для базовых цилиндров [Степанова и др., 2017].
2. ОПИСАНИЕ МЕТОДА
В методе S-аппроксимаций основная вычислительная проблема состоит в нахождении устойчивого приближенного решения $\hat {x}$ системы линейных алгебраических уравнений (СЛАУ):
в которой ${{f}_{\delta }}$ есть N – вектор заданных величин, измеренных на некоторой поверхности Земли; ${\mathbf{A}}$ – N×N-матрица со свойством ${\mathbf{A}} = {{{\mathbf{A}}}^{{\mathbf{T}}}} > 0,$ а $\delta f$ представляет собой N-вектор помехи. В настоящее время в задачах геофизики приходится работать с большим объемом данных ($N = {{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{5}}$), а если требуется построить аппроксимацию для целого континента или планеты в целом, система может иметь сверхбольшую размерность ($N = {{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{7}}$).В силу наличия в векторе правой части СЛАУ (1) вектора помехи $\delta f$, необходимо находить такое устойчивое приближенное решение $\hat {x}$, согласованное с имеющейся априорной информацией. В случае, когда решается обратная задача гравиметрии, имеется несколько видов априорной информации, которую нужно учитывать при ее решении [Страхов, 1999]. Напомним вкратце, что бывает известно о векторах помехи и полезного сигнала.
1. Нам заданы постоянные $\delta _{{\min }}^{2},$ $\delta _{{\max }}^{2}$, фигурирующие в неравенствах
(2)
$\delta _{{\min }}^{2} \leqslant \left\| {\delta f} \right\|_{E}^{2} \leqslant \delta _{{\max }}^{2},$2. Известно, что вектор полезного сигнала $f$ ортогонален вектору помехи $\delta f$:
(3)
${\text{ }}\left\| f \right\|_{E}^{2} + \left\| {\delta f} \right\|_{E}^{2} = \left\| {{{f}_{\delta }}} \right\|_{E}^{2}.{\text{ }}$3. Предполагается, что вектор помехи $\delta f$ случаен и однороден. Другими словами, все компоненты $\delta {{f}_{i}}$ являются некоррелированными и имеют нулевое математическое ожидание. Такое определение соответствует аппаратурно-методической помехе при полевых наблюдениях.
4. Нам известен некоторый функционал $\Omega (x)$, задающий отношение предпочтений на множестве приближенных решений $\hat {x}$ СЛАУ (1).
Определение [Степанова и др., 2015]: Пусть имеются два произвольных приближенных решения ${{\hat {x}}_{1}}$ и ${{\hat {x}}_{2}}$ СЛАУ (1), удовлетворяющих условию $\left\| {{\mathbf{A}}{{{\hat {x}}}_{1}} - {{f}_{\delta }}} \right\|_{E}^{2} = \left\| {{\mathbf{A}}{{{\hat {x}}}_{2}} - {{f}_{\delta }}} \right\|_{E}^{2}.$ Тогда функционал $\Omega (x)$ задает отношение предпочтения на множестве приближенных решений СЛАУ (1), если из неравенства $\Omega ({{\hat {x}}_{2}}) < \Omega ({{\hat {x}}_{1}})$ следует, что приближенное решение ${{\hat {x}}_{2}}$ предпочтительнее приближенного решения ${{\hat {x}}_{1}}$.
Ранее [Степанова и др., 2017; 2018], авторы изложили основы модифицированного метода S-аппроксимаций. Подчеркивалось, что для наиболее полного учета априорной информации о неизвестном носителе гравитационных или магнитных масс необходимо искать функции, описывающие распределение источников, в более узких, чем ${{L}_{2}}$, классах.
Возникает проблема выбора такой постановки обратной задачи, в которой сочетались бы простота и наиболее полный учет априорной информации об объекте изучения. Кроме того, необходимо учитывать также тот факт, что с ростом размерности системы линейных алгебраических уравнений ситуация с нахождением устойчивого приближенного решения стремительно ухудшается: растет (часто – неконтролируемым образом) число обусловленности системы, отрицательная роль ошибок округления драматически усиливается. В региональном варианте S-аппроксимаций выбор стабилизирующего функционала имеет еще большее значение по сравнению с локальной версией того же метода: обусловленность СЛАУ, к которой сводится решение обратной задачи, значительно увеличивается, как это уже было отмечено в предыдущей работе авторов [Степанова и др., 2017]. В большинстве случаев такое поведение системы объясняется уменьшением величины диагонального преобладания элементов матрицы. Ранг СЛАУ также становится меньше, и появляются постановки задачи, в которых требуется определить характеристики источника по недостаточно полной информации о поле. Поэтому возникает идея тонкой “настройки” метода в зависимости от априорной информации об аномальном поле: максимальном и минимальном значениях аномалии, симметрии поля, глубине залегания источников, плотностях пород, данных других методов исследования геологической среды.
Интерпретация любых данных об аномальных геофизических полях и функциях, задающих рельеф местности или грид глубин Мирового океана, невозможна без разработки специальных численных методов, с помощью которых и строятся искомые аппроксимации. При огромном числе входных данных (если речь идет о геофизических науках, то небольшим объемом информации об изучаемом объекте, как правило, обойтись нельзя) трудоемкость вычислительных процедур многократно увеличивается. Мы уже отмечали катастрофический рост числа обусловленности СЛАУ. Если ранг матрицы системы линейных уравнений значительно меньше, чем размерность этой системы, то лучше применять итерационные методы решения СЛАУ. Как хорошо известно, чебышевские полиномы менее всего отклоняются по норме от нуля на отрезке [–1,1].
Поэтому для минимизации невязки между точным и приближенным решением СЛАУ нужно выбирать итерационные методы на основе именно полиномов Чебышева. При построении итерационных методов следует также учитывать тот факт, что корни многочленов Чебышева должны выбираться в определенном порядке в двухслойной схеме; трехслойная схема более устойчива и не требует такого рода ограничений. Ранее [Страхов и др., 2009; Stepanova, 2009; Страхов, Страхов, 1999] был предложен и успешно апробирован при интерпретации данных гравиразведки и магниторазведки итерационный метод последовательного умножения полиномов.
Блочные методы решения систем линейных алгебраических систем уравнений особенно эффективны при интерпретации больших объемов геофизических данных [Страхов, Страхов, 1999; Степанова и др., 2017].
Здесь нужно учитывать два обстоятельства:
1) в настоящее время многие методы нахождения устойчивых приближенных решений СЛАУ требуют размещения элементов матрицы A и вектора ${{f}_{\delta }}$ в оперативной памяти компьютера – и в этой памяти возможно хранение необходимых вспомогательных величин;
2) в геофизических задачах (прежде всего – в задачах построения метрологических линейных аналитических аппроксимаций элементов аномальных гравитационных и магнитных полей) очень часто возникают ситуации, когда по причинам технического (указанного в (1)) порядка применения методов, основанных на последовательном умножении полиномов и на выполнении трансформаций Гаусса–Страхова, оказывается невозможным.
Напомним вкратце основные положения разработанного В.Н. Страховым метода МБКоорС – метода блочного координатного спуска.
Основные идеи МБКоорС позволяют строить устойчивые последовательности приближенных решений плохо обусловленных систем линейных алгебраических уравнений. При этом блоки в такого рода системах оказываются тесно связанными, что является весьма важным фактором при интерпретации гравиметрических и магнитометрических данных.
МБКоорС может применяться при решении: а) переопределенных систем (N > M); б) нормально определенных систем (N = M = n); в) недоопределенных систем (N < M).
Суть МБКоорС состоит в том, что матрица A, соответственно вектор $x$ в исходной системе (1), представляются в блочной форме:
(4)
${\text{A}} = \begin{array}{*{20}{c}} \vline & {{{{\text{A}}}_{1}}}&\vline & {{{{\text{A}}}_{2}}}&\vline & \ldots &\vline & {{{{\text{A}}}_{Q}}}\vline & \end{array}.$(5)
$x = \begin{array}{*{20}{c}} \vline & {{{x}^{{(1)}}}}\vline & \\ \hline \vline & {{{x}^{{(2)}}}}\vline & \\ \hline \vline & {\begin{array}{*{20}{c}} {} \\ {} \end{array}}\vline & \\ \hline \vline & {{{x}^{{(Q)}}}}\vline & \end{array},$Очевидно, в обоих случаях число c должно быть выбрано таким образом, чтобы блоки ${{{\text{A}}}_{q}}$ и векторы ${{f}_{\delta }}$ целиком размещались в оперативной памяти компьютера.
В соответствии с (4)–(5) систему (1) записываем в форме:
Опишем теперь схему нахождения приближенных решений ${{\tilde {x}}^{{(k)}}}$ системы (1). Принимается:
где и вводится развернутое определение: а также определениеСоответственно вводится последовательность векторов правых частей:
(16)
$f_{\delta }^{{(p;0)}},\,\,\,\,f_{\delta }^{{(p;q)}},\,\,\,\,p = 0{\text{, 1, 2, }}...{\text{, }}\,\,\,\,1 \leqslant q \leqslant Q,$(19)
$\begin{gathered} f_{\delta }^{{(p;q)}} = f_{\delta }^{{(p;q - 1)}} - {{{\text{A}}}_{q}}{{\Delta }_{p}}{{x}^{{(q)}}},\,\, \\ p = {\text{1,2, }}...{\text{,}}\,\,\,\,q = {\text{1,2,}}...{\text{,}}Q{\text{.}} \\ \end{gathered} $При этом вектор ${{\Delta }_{p}}{{x}^{{(q)}}}$ определяется как устойчивое приближенное решение задачи:
(20)
$\begin{gathered} \left\| {f_{\delta }^{{(p;q - 1)}} - {{{\text{A}}}_{q}}{{x}^{{(q;p,q)}}}} \right\|_{{\rm E}}^{2} = \mathop {{\text{min}}}\limits_{{{x}^{{(q;p,q)}}}} , \\ p = {\text{1,2,}}...{\text{,}}\,\,\,\,q = {\text{1,2, }}...{\text{, }}Q{\text{.}} \\ \end{gathered} $В соответствии с приведенными соотношениями имеем:
(21)
${{\tilde {x}}^{{(k)}}} = \left( {\sum\limits_{s = 0}^{p - 1} {\begin{array}{*{20}{c}} \vline & {{{\Delta }_{s}}{{x}^{{(1)}}}}\vline & \\ \hline \vline & {{{\Delta }_{s}}{{x}^{{(2)}}}}\vline & \\ \hline \vline & {}\vline & \\ \hline \vline & {{{\Delta }_{s}}{{x}^{{(q)}}}}\vline & \\ \hline \vline & {}\vline & \\ \hline \vline & {{{\Delta }_{s}}{{x}^{{(Q)}}}}\vline & \end{array}} } \right) + \begin{array}{*{20}{c}} \vline & {{{\Delta }_{p}}{{x}^{{(1)}}}}\vline & \\ \hline \vline & {{{\Delta }_{p}}{{x}^{{(2)}}}}\vline & \\ \hline \vline & {}\vline & \\ \hline \vline & {{{\Delta }_{p}}{{x}^{{(q)}}}}\vline & \\ \hline \vline & 0\vline & \\ \hline \vline & 0\vline & \end{array}.$Итак, основной в методе МБКоорС является проблема нахождения устойчивых приближенных решений задач наилучшего среднеквадратичного приближения (20).
В настоящей работе мы предлагаем усовершенствованный трехслойный блочный чебышевский итерационный метод, который не требует выбора определенной перестановки корней полиномов Чебышева для получения устойчивого приближенного решения СЛАУ. Благодаря учету априорной информации мы можем получить решение, адекватное реальной геофизической практике. Фактически, мы решаем задачу нахождения наилучшего среднеквадратичного приближения (20) с помощью трехслойного усовершенствованного чебышевского итерационного метода для каждого из блоков q = 1, 2, …, Q, на которые описанным ниже способом разбивается матрица системы. При этом, в отличие от работы [Степанова и др., 2017], вариационная постановка (20) формулируется для некоторого семейства блочных матриц, непрерывно зависящего от параметра t. Таким образом, строится своеобразный “конус” над пространством элементов матрицы исходной плохо обусловленной системы. Блоки могут иметь как прямоугольную форму, так и квадратную. Если каждая из постановок (20) рассматривается для квадратной матрицы, то зависимость размерности блока от параметра t можно описать следующим образом:
(22)
$\begin{gathered} M_{q}^{{(i + 1)}} = \sqrt {{{{\left( {M_{q}^{{(i)}}} \right)}}^{2}} - 4(M_{q}^{{(i)}} - 1)} , \\ q = 1,2,{\text{ }}...,Q,\,\,\,\,i = 1,...,{{N}_{i}}. \\ 1 \leqslant {{N}_{i}} \leqslant N. \\ \end{gathered} $В формуле (22) дискретный индекс i связан с непрерывным параметром t линейной зависимостью:
Здесь в правой части равенства стоит целая часть выражения в квадратных скобках. Число шагов ${{N}_{i}}$ зависит от размерности исходной системы уравнений, характера рельефа местности, степени контрастности отдельных выделенных блоков и т.п. Математический эксперимент показал, что слишком близко к вершине конуса над блоком “подбираться” не стоит: точность приближенного решения и время, за которое устойчивое приближенное решение можно получить, начинают достаточно сильно (на 20 и более процентов) отличаться от таковых в исходной задаче при ${{N}_{i}} \leqslant (0.5{\kern 1pt} - {\kern 1pt} 0.7)N.$ Здесь через N обозначена размерность первоначальной системы линейных алгебраических уравнений. Кроме того, особенностью новой методики является возможность “перемешивания” различных слоев конусов над блоками с целью достижения наилучшего результата по точности приближенного решения за фиксированное время (можно задавать некоторый временной интервал). Формула (22) получается, если на каждом шаге по i удалять из блока элементы граничных строк и столбцов – “кайму” матрицы, перемещаясь по спирали к центральной части матрицы. Следует отметить, что прямоугольная форма блоков, с которой приходится иметь дело в методе линейных интегральных представлений, не является препятствием для реализации такого алгоритма удаления матричных элементов. Полученные на каждом шаге решения системы уравнений имеют разные размерности, но можно построить векторы одинаковой длины (подобно (21)), добавляя нулевые элементы на свободные места. Затем необходимо, как и в ранее приведенных работах, усреднить приближенные решения по количеству шагов. Такой подход аналогичен методу нахождения пробных решений обратной задачи.
При интерпретации данных высокоточной гравиразведки, число гравиметрических пунктов может превышать 105. Такая ситуация может возникать, например, при изучении строения земной коры и верхней части мантии. Число элементов матрицы при этом часто превышает 1010, и данное обстоятельство сильно затрудняет решение плохо обусловленной системы (1). В этом случае ранг матрицы может быть значительно меньше, чем размерность самой матрицы ${\mathbf{A}}$, и применять прямые методы решения СЛАУ не имеет смысла: полученные решения будут неустойчивыми. Поэтому в случае больших объемов интерпретируемой информации целесообразно применение итерационных способов решения регуляризованных СЛАУ. Для нахождения устойчивого приближенного решения задачи (20) применялся предложенный в работе [Степанова и др., 2017] регуляризованный блочный итерационный метод Чебышева.
Вместо исходной системы (1) был, как и в предыдущих работах авторов, рассмотрен ее регуляризованный аналог [Тихонов и др., 1990; Ягола и др., 2014]:
где: $\alpha > 0$ – параметр регуляризации; ${\mathbf{S}} = {{{\mathbf{S}}}^{T}} > 0$ – N × N-матрица. В этом случае функционал $\Omega (x) = \left( {{\mathbf{S}}x,x} \right)$ задает отношение предпочтения на множестве решений приближенных решений. Далее, СЛАУ (24) решается с помощью блочного трехслойного итерационного метода Чебышева.Основной алгоритм этого метода имеет вид:
(25)
$\begin{gathered} {{x}^{{i + 1}}} = {{\beta }_{{i + 1}}}\left( {E - \tau \left( {{\mathbf{A}} + \alpha {\mathbf{S}}} \right)} \right){{x}^{i}} + \\ + \,\,\left( {1 - {{\beta }_{{i + 1}}}} \right){{x}^{{i - 1}}} + {{\beta }_{{i + 1}}}\tau {{f}_{\delta }}, \\ {{x}^{1}} = \left( {E - \tau \left( {{\mathbf{A}} + \alpha {\mathbf{S}}} \right)} \right){{x}^{0}} + \tau {{f}_{\delta }},\,\,\,\,i = 1,..., \\ \end{gathered} $(26)
$\begin{gathered} \tau = \frac{2}{{{{l}_{\alpha }} + {{L}_{\alpha }}}},\,\,\,\,{{\beta }_{{\text{1}}}} = 2, \\ {{\beta }_{{i + 1}}} = \frac{4}{{4 - {{\rho }^{2}}{{\beta }_{i}}}},\,\,\,\rho = \frac{{{{L}_{\alpha }} - {{l}_{\alpha }}}}{{{{L}_{\alpha }} + {{l}_{\alpha }}}}, \\ \end{gathered} $Как и в работе [Степанова и др., 2017], исследуемая область, в которой заданы элементы аномального потенциального поля или функция, описывающая рельеф местности, разбивается на блоки таким образом, чтобы начальное приближение было согласовано с физическими свойствами интерпретируемой величины. Затем для каждого из блоков решается своя СЛАУ, и в качестве нулевого приближения выбирается, как было описано выше в данной работе, усредненное по числу шагов деформации блоков приближенное решение. Нецелесообразно разбивать область на блоки, не опираясь на сами данные, например, на $R$-блоков одинакового размера. В этом случае каждое полученное решение будет физически адекватно только для своей области, но результирующее решение для всей исследуемой области может быть совсем другим. Поэтому блочное разбиение должно выполняться с учетом свойств исследуемой функции (поля или рельефа): рекомендуется поле или рельеф визуализировать тем или иным способом (нарисовать карту изолиний или построить трехмерное изображение поля с помощью существующих графических программ, например, Surfer или ArcView). Автоматическое разбиение области на блоки согласно заданным критериям также возможно. Однако выбор критериев все равно остается прерогативой человека, а не искусственного интеллекта. В дальнейшем предполагается создание продуманной стратегии такого выбора, что является одной из задач теории распознавания изображений.
Не ограничивая общности, рассмотрим локальный вариант. Реальное изучаемое поле имеет большое число неоднородностей, залегающих ниже дневной поверхности, тектоническими особенностями осадочного чехла земной коры и глубинным строением Земли и верхней мантии, поэтому оно всегда характеризуется большим количеством аномалий, которые накладываются друг на друга. На практике наблюденное поле имеет достаточное количество ($ \geqslant {\kern 1pt} 5$) ярко выраженных экстремумов, обусловленных геолого-физическими особенностями исследуемой территории. Так как имеется ограниченное количество данных и решается конечномерная задача, то экстремумы определяются по формуле [Степанова и др., 2017]:
(27)
$u\left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right) \leqslant u\left( {x,y,z} \right),\,\,\,\,{{\rho }_{r}}(x,y,z) \leqslant {{\rho }_{N}},$(28)
$u\left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right) \geqslant u\left( {x,y,z} \right),\,\,\,\,{{\rho }_{r}}(x,y,z) \leqslant {{\rho }_{N}},$(29)
$\begin{gathered} {{\rho }_{N}} = \\ = \frac{{\sqrt {{{{\left( {{{x}_{{\max }}} - {{x}_{{\min }}}} \right)}}^{2}}\, + \,{{{\left( {{{y}_{{\max }}} - {{y}_{{\min }}}} \right)}}^{2}}\, + \,{{{\left( {{{z}_{{\max }}} - {{z}_{{\min }}}} \right)}}^{2}}} }}{{\sqrt N }}, \\ \end{gathered} $(30)
$\begin{gathered} u\left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right) - \sqrt {\frac{{\delta _{{\min }}^{2} + \delta _{{\max }}^{2}}}{{2N}}} \leqslant u\left( {x,y,z} \right), \\ {{\rho }_{r}}(x,y,z) \leqslant {{\rho }_{N}}, \\ \end{gathered} $(31)
$\begin{gathered} u\left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right) + \sqrt {\frac{{\delta _{{\max }}^{2} + \delta _{{\min }}^{2}}}{{2N}}} \geqslant u\left( {x,y,z} \right), \\ {{\rho }_{r}}(x,y,z) \leqslant {{\rho }_{N}}.{\text{ }} \\ \end{gathered} $В этом случае “теоретических центров” аномалий $({{x}_{r}},{{y}_{r}},{{z}_{r}})$ может быть найдено достаточно большое количество. Тогда точки, расстояние между которыми меньше, чем характерный размер области, исключаются по следующему принципу: если найден локальный максимум, то среди всех “теоретических центров” выбирается тот, в котором достигается максимальное значение поля, и он принимается за центр аномалии, если же найден локальным минимум, то среди всех “теоретических центров” выбирается минимальное значение.
Допустим, таким образом всего найдено $R$ локальных аномалий, удовлетворяющих условию (30)–(31). Далее, для каждой аномалии оценивается ее интенсивность по оси OX и OY:
(32)
$u_{r}^{x} = {{\left| {u({{M}_{r}}) - u\left( {{{M}_{{r,x}}}} \right)} \right|} \mathord{\left/ {\vphantom {{\left| {u({{M}_{r}}) - u\left( {{{M}_{{r,x}}}} \right)} \right|} {\rho \left( {{{M}_{r}},{{M}_{{r,x}}}} \right)}}} \right. \kern-0em} {\rho \left( {{{M}_{r}},{{M}_{{r,x}}}} \right)}},$(33)
$\begin{gathered} u_{r}^{y} = {{\left| {u({{M}_{r}}) - u\left( {{{M}_{{r,y}}}} \right)} \right|} \mathord{\left/ {\vphantom {{\left| {u({{M}_{r}}) - u\left( {{{M}_{{r,y}}}} \right)} \right|} {\rho \left( {{{M}_{r}},{{M}_{{r,y}}}} \right)}}} \right. \kern-0em} {\rho \left( {{{M}_{r}},{{M}_{{r,y}}}} \right)}}, \\ r = 1,2,...,R. \\ \end{gathered} $Здесь: ${{M}_{r}} = \left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right)$ – координаты центра аномалии r; ${{M}_{{r,x}}}$ – ближайшая по оси OX точка к ${{M}_{r}}$ (координата по оси OY остается неизменной), а ${{M}_{{r,y}}}$ – ближайшая по оси OY точка к ${{M}_{r}}$ (координата по оси OX остается неизменной).
Теперь стоит определить критерий, по которому рассматриваемая точка наблюдения войдет в блок r: точка ${{M}_{s}} = \left( {{{x}_{s}},{{y}_{s}},{{z}_{s}}} \right)$ принадлежит блоку с аномалией с центром ${{M}_{r}} = \left( {{{x}_{r}},{{y}_{r}},{{z}_{r}}} \right)$, если выполнено следующее условие:
(34)
$\begin{gathered} \left| {u({{M}_{s}}) - u\left( {{{M}_{r}}} \right)} \right| \leqslant u_{r}^{x}\left| {{{x}_{r}} - {{x}_{s}}} \right| + u_{r}^{y}\left| {{{y}_{r}} - {{y}_{s}}} \right|, \\ {{\rho }_{r}}(x,y,z) \leqslant {{\rho }_{R}}, \\ \end{gathered} $(35)
$\begin{gathered} {{\rho }_{R}} = \\ = \frac{{\sqrt {{{{\left( {{{x}_{{\max }}} - {{x}_{{\min }}}} \right)}}^{2}}\, + \,{{{\left( {{{y}_{{\max }}} - {{y}_{{\min }}}} \right)}}^{2}}\, + \,{{{\left( {{{z}_{{\max }}} - {{z}_{{\min }}}} \right)}}^{2}}} }}{{\sqrt R }}. \\ \end{gathered} $Если размер рассматриваемого блока относительно мало по сравнению с общим количеством точек измерений
то этот блок следует объединить с тем блоком, расстояние между центрами которых наименьшее. Другими словами, следует ограничивать общее количество блоков. Поскольку каждый блок соответствует определенной локальной аномалии, то большое количество блоков может быть вызвано следующими причинами:1) большое количество локальных аномалий. В этом случае решение большого количества систем маленьких размерностей в итоге может давать плохое приближение для общей системы, так как исследуемое поле характеризуется большим количеством аномалий, которые накладываются друг на друга, и тогда рассматривать эффект отдельно от каждой аномалии нецелесообразно;
2) существенное искажение поля помехой и влияние рельефа с резкими перепадами высот. В этом случае рядом лежащие блоки соответствуют одному и тому же аномалиеобразующему объекту.
Мы решаем, далее, для каждого из блоков свою СЛАУ; априорная информация (2) при этом переписывается в следующем виде:
(36а)
$\frac{{\delta _{{\min }}^{2}{{N}_{r}}\left( {1 - \varepsilon } \right)}}{N} \leqslant \left\| {\delta {{f}_{r}}} \right\|_{E}^{2} \leqslant \frac{{\delta _{{\max }}^{2}{{N}_{r}}\left( {1 + \varepsilon } \right)}}{N}.$Здесь: ${{N}_{r}}$ – общее количество точек в блоке r; $\left\| {\delta {{f}_{r}}} \right\|_{E}^{2}$ – квадрат нормы ошибки в блоке r. Так как помеха является случайной величиной, то для каждого из блоков нельзя оценить квадрат нормы ошибки умножением $\delta _{{\min }}^{2}$ и $\delta _{{\max }}^{2}$ на ${{{{N}_{r}}} \mathord{\left/ {\vphantom {{{{N}_{r}}} N}} \right. \kern-0em} N}$ для r-го блока, поэтому в формуле (36а) занижена нижняя и завышена верхняя границы оценки квадрата нормы ошибки.
Таким образом, мы “персонифицируем” каждый блок и, в то же время, сохраняем связь блоков между собой с помощью верхней и нижней границ помехи в правой части. Опыт расчетов на модельных и практических примерах показал, что МБКоор В.Н. Страхова сходится медленно (часы и сутки на Pentium-IV 2 ГГц) для систем размерности, превышающей 10000.
По этой причине мы попытались разработать в ряде работ более эффективные алгоритмы решения больших и сверхбольших систем линейных алгебраических уравнений.
Разделение матрицы на блоки аналогичным образом выполняется и в региональном варианте. В географических координатах $(r,\lambda ,\varphi )$ ($r = R + h$, где $R$ – радиус Земли; h – высота над уровнем моря, $\lambda $ – долгота; $\varphi $ – широта) изменится только формула для расстояния между двумя точками $({{r}_{1}},{{\lambda }_{1}},{{\varphi }_{1}})$ и $({{r}_{2}},{{\lambda }_{2}},{{\varphi }_{2}}){\kern 1pt} :$
(37)
${{\rho }_{{{\text{geogr}}}}} = \sqrt {r_{1}^{2} + r_{2}^{2} - 2{{r}_{1}}{{r}_{2}}\left( {\cos \left( {{{\varphi }_{1}}} \right)\cos \left( {{{\varphi }_{2}}} \right)\cos \left( {{{\lambda }_{1}} - {{\lambda }_{2}}} \right) + \sin \left( {{{\varphi }_{1}}} \right)\sin \left( {{{\varphi }_{2}}} \right)} \right)} ,{\text{ }}$Важно подчеркнуть, что в предлагаемой в данной работе усовершенствованной методике решения больших и сверхбольших систем плохо обусловленных систем линейных алгебраических уравнений блоки при любом “механизме” удаления элементов из них должны быть связаны между собой. Как уже указывалось выше, МБКоорС разработан с учетом таких связей. В более ранних работах авторов [Страхов и др., 2002а; б] рассматривались примеры применения метода S-аппроксимаций при интерпретации гравиметрических данных на полигонах с лакунами, с выходом на нормальное поле и т.п. Анализ результатов интерпретации такого рода данных позволил сделать вывод о том, что расстояние между источниками наиболее интенсивных аномалий не должно превышать одного-полутора диаметров самого источника (при сравнимых размерах областей расположения гравитирующих масс). При деформации блоков в новой методике мы придерживались такого же принципа выбора диапазона изменения чисел ${{N}_{i}}.$
Для успешной работы описанной новой методики необходимо сформулировать четкий и понятный пользователю создаваемого на ее основе программного обеспечения алгоритм действий:
1) имеющуюся информацию о поле нужно визуализировать и выделить блоки согласно приведенным выше критериям (см. (30)–(36)). В случае относительно небольшой размерности системы можно считать матрицу системы единственным блоком;
2) для каждого из блоков с помощью программ на основе итерационных методов Чебышева решить систему линейных алгебраических уравнений, возникающую в рамках модифицированных S- и F-аппроксимаций или их комбинации;
3) построить деформации пространства матричных блоков по формулам (22)–(23) или их аналогам для прямоугольных блоков. Элементом такого пространства будет:
(38)
$\begin{gathered} B_{{ij}}^{{(q)}}(t) = (b_{{ij}}^{{(q)}},t),\,\,\,\,b_{{ij}}^{{(q)}} \in {{A}_{q}}, \\ q = 1,...,Q,\,\,\,t \in (0,1). \\ \end{gathered} $В (38) через ${{A}_{q}},q = 1,...,Q,$ обозначен блок “большой” матрицы. Параметр t идентифицирует слой конуса над данным блоком. Размерность такого блока, соответствующая параметру, определяется по формулам (22) и (23). Для дискретного набора параметров ${{t}_{i}} \in (0,1),$а $i = 1,...,I,$ так же, как в пункте 2), решаются системы с матрицами ${{A}_{q}}({{t}_{i}}),$ $q = 1,...,Q,$ ${{t}_{i}} \in (0,1).$ Решения этих систем являются нулевыми приближениями для алгоритма МБКоорС, описанного выше (см. выражения (4)–(21)). Размерности векторов решений полагаются при применении МБКоорС равными (недостающие элементы у блоков ${{x}^{{(q)}}}$ вектора $x$, q = 1, 2, …, Q, имеют нулевые значения);
4) полученные на предыдущем этапе решения “большой” системы с матрицей А при каждом значении анализируются: сравниваются абсолютные показатели качества решения: ${\Delta } = \frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}};$ определяется значение параметра t, при котором показатель качества решения отличается от показателя качества “большой” системы не более, чем на 10–15% (однако можно задавать и другие критерии корреляции указанных решений); вычисляется среднее значение по всем решениям (аналог пробного решения);
5) с целью повышения “контрастности” блоков выполняется следующая процедура. Составляется вспомогательный вектор, компонентами которого являются те значения параметра t, при которых показатели качества решения для отдельных блоков принимают почти одинаковые значения (в приведенных ниже примерах этот критерий соответствовал 7–8%): $T = \left( {t_{{i(1)}}^{1},...,t_{{i(Q)}}^{Q}} \right),$ i(q) – это значение индекса, соответствующее оптимальному качеству решения q-го блока. Далее, решения подсистем, описывающих найденные деформации блоков, выбираются в качестве начальных приближений для МБКоорС.
3. АПРОБАЦИЯ НОВОЙ МЕТОДИКИ ПРИ АППРОКСИМАЦИИ УЧАСТКА РЕЛЬЕФА В РАЙОНЕ ПЕРМИ
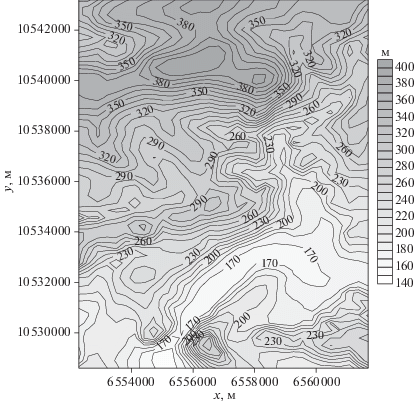
Исходными данными являются отметки рельефа земной поверхности в одном из районов Пермского края. Число точек наблюдений равно 3541. Рельеф относительно спокойный, без резких перепадов высот. Все данные сначала рассматривались как один блок, а затем выборка была разбита на четыре части. Каждый блок содержал кратное 4 число точек. Результаты расчетов по усовершенствованной методике приведены в табл.1 и на рис. 1, рис. 2.
Таблица 1.
Результаты аппроксимации рельефа с помощью усовершенствованного метода блочного контрастирования. Практический пример, Пермский Край
| N N1 N2 |
${{h}_{{\min }}}$, м | ${{h}_{{\max }}}$, м | ${{h}_{0}}$, м | ${{h}_{1}}$, ${{h}_{{{\text{контр1}}}}}$, м | ${{h}_{2}}$, ${{h}_{{{\text{контр2}}}}}$, м | Δ, t |
|---|---|---|---|---|---|---|
| 3541 | 2.1473 | 4.513 | 3.365 | 3.2613 | 3.167 | 1.056× 10–2, |
| 2956 | 4.912 | 4.114 | 15:18 | |||
| 3367 | ||||||
| 3520 | 1.8812 | 2.728 | 2.146 | 2.121 | 2.084 | 0.894 × 10–2, |
| 2924 | 2.976 | 2.810 | 13:45 | |||
| 3320 |
Примечания: ${{\sigma }_{0}} = \frac{{\left\| {Ax - {{f}_{\delta }}} \right\|_{E}^{{}}}}{{\sqrt N }}$ – среднеквадратическое отклонение, ${{\sigma }_{{\max }}} = \sqrt {\frac{{\delta _{{\max }}^{2}}}{N}} ,$ ${{\sigma }_{{\min }}} = \sqrt {\frac{{\delta _{{\min }}^{2}}}{N}} ,$ где: ${\Delta } = \frac{{{{{\left\| {Ax - {{f}_{\delta }}} \right\|}}_{E}}}}{{{{{\left\| {{{f}_{\delta }}} \right\|}}_{E}}}}$ – показатель качества решения; t – время решения СЛАУ (ч : мин : с): Н – координата ${{x}_{3}}$ плоскости, на которой распределены простой и двойной слои; N – число исходных точек; N1 – число точек бесконтрольных точек I типа; N2 – число точек бесконтрольных точек II типа. Количество пробных решений n = 10; ${{\sigma }_{0}}$ – среднеквадратичное отклонение, полученное с помощью аппроксимации по исходным точкам; ${{\sigma }_{1}}$ – среднеквадратичное отклонение, полученное с помощью аппроксимации по точкам рельефа бесконтрольных точек I типа; ${{\sigma }_{{{\text{конт}}1}}}$ – среднеквадратичное отклонение, полученное в контрольных точках I типа; ${{\sigma }_{2}}$ – среднеквадратичное отклонение, полученное с помощью аппроксимации по точкам рельефа без контрольных точек II типа. ${{\sigma }_{{{\text{конт}}2}}}$ – среднеквадратичное отклонение, полученное в контрольных точках II типа.
Рис. 1.
Карта изолиний разности между исходным рельефом и рельефом, полученным с помощью модифицированных S- и F-аппроксимаций.

В табл. 1 приводятся результаты расчетов как с помощью методики модифицированных S-аппроксимаций (“обычный” вариант, вторая строка таблицы), так и при применении усовершенствованной методики. Число шагов (деформаций единственного блока, которым является в данном случае вся матрица) $_{{}}{{N}_{i}}$ было равно 1800.
4. ТЕСТИРОВАНИЕ НОВОЙ МЕТОДИКИ ПРИ АППРОКСИМАЦИИ ПЕРВОЙ ПРОИЗВОДНОЙ РАДИАЛЬНОЙ СОСТАВЛЯЮЩЕЙ СИЛЫ ТЯЖЕСТИ В РЕДУКЦИИ ФАЯ В РАЙОНЕ ТИХОГО ОКЕАНА
Описанный в первом разделе статьи усовершенствованный метод блочного контрастирования был апробирован при решении задачи выявления тектонических разломов с помощью аппроксимации полного горизонтального градиента гравитационного поля. Ранее данная область исследовалась с помощью версии метода блочного контрастирования, описанного в работах Д.Н. Раевского и И.Э. Степановой (см., например, [Степанова и др., 2017]).
В настоящее время данные спутниковых измерений учитываются при построении глобальных моделей рельефа и геофизических полей [Pavlis et al., 2012; Sandwell et al., 2013; 2014]. Анализ данных, полученных с помощью различных космических аппаратов, позволяет существенно повысить точность приближенных решений различных задач интерпретационного характера.
Используемые данные получены путем объединения измерений с нескольких искуственных спутников: CryoSat-2, запущенного ESA (European Space Agency – Европейское Космическое Агентство) 08.04.2010 г., Envisat, запущенного ESA 01.03.2002 г., и Jason-1, запущенного NASA (National Aeronautics and Space Administration – Национальный Комитет по Воздухоплаванию и Исследованию Космического Пространства) и проработавшего с 07.12.2001 г. до 03.07.2013 г. Спутник CryoSat-2 был запущен для измерения толщины ледового покрова в рамках программы ESA “Living Planet” (“Живая планета”). Высокоточные измерительные приборы, установленные на перечисленных спутниках, в совокупности с большим объемом накопленных данных и использованием модели EGM2008 [Pavlis et al., 2012] позволили построить уточненную глобальную модель гравитационного поля акватории планеты [Sandwell 2013; 2014]. Аномальное гравитационное поле акватории вычисляется в редукции Фая. Полученные коллективом данные выкладываются в свободном доступе в сеть интернет11. В первую очередь, построенные карты аномального гравитационного поля планеты в работах [Sandwell, 2013; 2014] использовались для выявления неоднородностей и тектонических структур дна акваторий, в частности, зон разломов (ЗР). Гравиметрические данные целесообразно анализировать при тектоническом районировании глубоких океанических бассейнов из-за невозможности проведения достоверных измерений на кораблях и наличия толстого осадочного слоя [Sandwell, 2014].
5. ИСПОЛЬЗОВАНИЕ МЕТОДА ПОЛНОГО ГОРИЗОНТАЛЬНОГО ГРАДИЕНТА ПРИ ВЫЯВЛЕНИИ ТЕКТОНИЧЕСКИХ ОСОБЕННОСТЕЙ ИССЛЕДУЕМОЙ ТЕРРИТОРИИ
Аппроксимационный подход с успехом применяется при структурном тектоническом районировании территорий [Бабаянц и др., 2004]. В то же время, если возникает необходимость интерпретации геофизических данных областей большой площади (более 1 000 000 км2) при геологических и геоморфологических исследованиях, то исследователи сталкиваются с большими трудностями. Однако, как было показано в предыдущих работах авторов [Степанова и др., 2015; 2017; 2018], в рамках модифицированного метода S-аппроксимаций даже при интерпретации данных большого объема возможно построение эффективной аппроксимирующей конструкции и проведение на ее основе структурного анализа. Поэтому была поставлена задача по построению модифицированных F- и S-аппроксимаций больших территорий для исследования тектонических структур с анализом карт линейных трансформант поля. Указанная задача решалась как с помощью “обычного” метода блочного контрастирования, что подробно описано в работах [Степанова и др., 2017; 2018], так и с помощью предложенной в настоящей работе усовершенствованной методики деформации выделенных блоков с последующим “перемешиванием” слоев деформационного пространства и усреднением полученных на каждом этапе устойчивых приближенных решений вариационных задач.
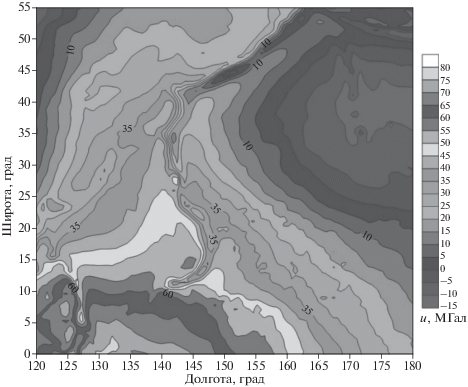
Исходные данные аномального гравитационного поля Земли распределены в области от 0 до 55° северной широты и от 120 до 180° восточной долготы характеризуются сложным строением поля, амплитуда поля изменяется от –15 до 80 мГал. Сетка регулярная, шаг сетки 0.5°, общее число пунктов измерений N = 13431. Рассматриваемая область соответствует северной части Тихого океана, охватывающая наиболее глубокие океанические желоба (Марианский, Алеутский, Курило-Камчатский, Японский, Филиппинский; Идзу-Бонинский, Рюкю, Яп) с соответствующими островными дугами (Марианские, Алеутские, Курильские, Японские, Филиппинские, Идзу-Бонинские, Рюкю, Яп ), а также Каролинские и Маршалловы острова и подводные горы (Магеллановы горы, Императорские горы). В рассматриваемом примере была проверена эффективность метода S-аппроксимаций по выявлению тектонических структур на обширной территории.
При построении модифицированных S-аппроксимаций использовался способ трехступенчатого контроля Страхова. В качестве априорной информации были выбраны следующие значения для оценки квадрата нормы ошибки $\delta _{{\min }}^{2} = 300,$ $\delta _{{\max }}^{2} = 2000.$ В рамках метода S-аппроксимации аномальное гравитационное поле аппроксимировалось суммой простого и двойного слоев, распределенных на сфере радиуса ${{R}_{0}} = 6365$ км. Полученная СЛАУ решалась регуляризованным итерационным трехслойным методом Чебышева (CH). Все вычисления в данном примере проводились на компьютере INTEL CORE i5-4570 3.2 ГГц. Затем для этого примера проводились расчеты по описанной выше усовершенствованной методике блочного контрастирования. Число точек наблюдения выбиралось из заданной выборки кратным 4. Матрица системы разбивалась на блоки в соответствии с рекомендациями, приведенными в работе [Степанова и др., 2017]. Далее, осуществлялась “работа” над каждым из блоков (их мы выделили 6) с помощью алгоритма, описанного в предыдущих разделах статьи. Следует отметить, что блок в данном примере может быть и один, ввиду небольшой размерности исходного массива данных.
В данной таблице вторая строка соответствует “обычной” методике, а третья строка – усовершенствованной.
При интерпретации гравиметрических данных широкое применение имеет полный горизонтальный градиент [Edwards et al., 1996; Кадиров, 2000; Утемов, 2009]:
Модуль полного горизонтального градиента $\left| \Gamma \right|$ с хорошей точностью определяет геологические структуры, выделяющиеся гравитационными ступенями. Это могут быть или приповерхностные тела, создающие наиболее интенсивное по амплитуде поле или же разломные структуры. Метод полного горизонтального градиента успешно применялся многими исследователями: в монографии [Кадиров, 2000] Ф.А. Кадировым проведен математический эксперимент и показано, что при моделировании призматических тел максимум модуля полного горизонтального градиента достигается на их гранях, то есть определяет формы аномалиеобразующих объектов. Также Ф.А. Кадиров при интерпретации гравиметрических данных на территории Азербайджана, анализируя карту изолиний $\left| \Gamma \right|$, определил основные известные разломы [Кадиров, 2000]. В работе [Edwards et al., 1996] продемонстрирована эффективность применения метода горизонтального градиента для анализа вертикальных и круто падающих границ Канадского осадочного бассейна.
Так как при использовании метода S-аппроксимаций, горизонтальные производные восстанавливаются с высокой степенью точности (в силу того, что плоскость распределения простого и двойного слоев расположена горизонтально), то наиболее целесообразным представляется использование именно метода полного горизонтального градиента для исследования особенностей территории. Для этого построим теневую карту исходного аномального гравитационного поля и теневую карту $\left| \Gamma \right|$.
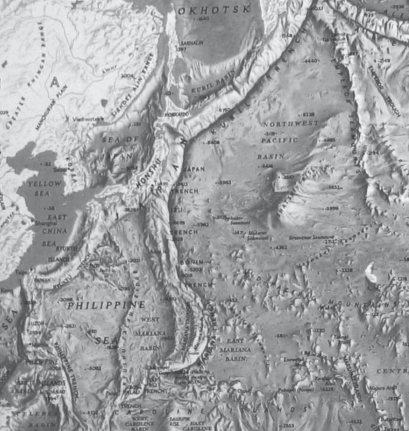
Как видно из рис. 4б, теневая карта модуля полного горизонтального градиента лучше отображает некоторые вытянутые геоморфологические структуры, которые трудно выделяются по исходному полю. Только основные зоны разломов, образовавшиеся в зонах субдукции литосферных плит, четко проявляются на обеих картах. Проведем сравнительный графический анализ теневой карты модуля полного горизонтального градиента (рис. 5) с детальной картой океанического дна (рис. 3).
Рис. 4.
(а) – Теневая карта гравитационного поля, полученного в рамках модифицированного метода S-аппроксимаций; (б) – теневая карта модуля полного горизонтального градиента |Г|.

Рис. 4.
Окончание
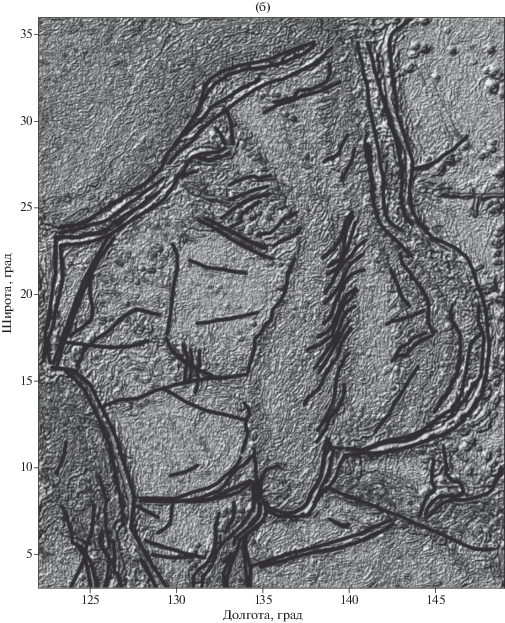
Рис. 5.
Теневая карта модуля полного горизонтального градиента с выделением основным структур исследуемого района.
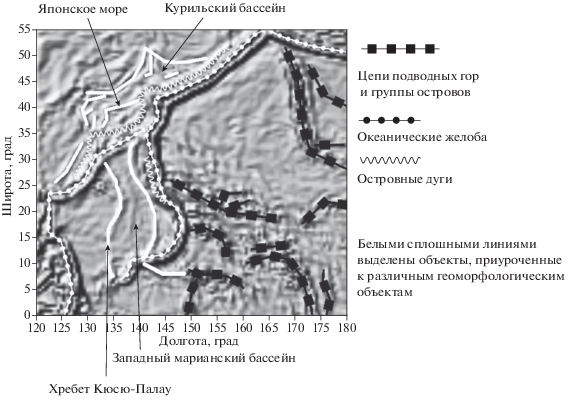
Все основные островные дуги, сводовые поднятия и другие геологические особенности морского дна отображены на рис. 5. Стоит отметить, что цепи подводных гор и острова, не лежащие над зонами субдукций, на карте изолиний $\left| \Gamma \right|$ проявляются в виде локальных максимумов, а вытянутым подводным объектам, таким как хребет Кюсю-Палау, соответствуют локальные аномалии приблизительно одного знака. Для цепей подводных гор характерно большое количество подводных вулканов, образующих вулканические и коралловые острова, поэтому они и проявляются в виде локальных максимумов (рис. 5). Также скопление малых по размеру экстремумов наблюдается также от 145 до 150° восточной долготы и 10° северной широты, соответствующие наиболее плотной части Каролинских островов, которые переходят в геоантиклинальную структуру, являющуюся Каролинским поднятием. На карте хорошо оконтуриваются Японское море и Курильский бассейн по краям материковой отмели, при этом в Японском море выделяется возвышенность Ямато (см. рис. 5). Четко прослеживается контур Западного Марианского бассейна (ЗМБ), который отличается более молодым возрастом коры по сравнению с прилежащими регионами и наличием осадочного покрова повышенной мощности [Müller et al., 2008]. По центру ЗМБ располагается некоторая линейно-вытянутая структура, отличающаяся по амплитуде, и, скорее всего, являющаяся амагматичным поднятием.
Океанические желоба и соответствующие им островные дуги (ОД) на рис. 4б, рис. 5 приурочены к двум рядом лежащим линейно-вытянутым аномалиям одного знака. Аномалия, соответствующая ОД, меньшей амплитуды по сравнению с аномалией, приуроченной непосредственно к океаническому желобу. Однако некоторые структуры подобного типа, например, Марианские острова с Марианским желобом, выражены только одной линейной аномалией повышенной амплитуды.
Несмотря на ограниченное количество данных для столь крупного региона (рис. 6), в рамках аппроксимационного подхода были успешно выявлены основные тектонические и геологические структуры исследуемой территории. Поэтому дальнейшее применение метода полного горизонтального градиента при использовании модифицированных S- и F-аппроксимаций поля является обоснованным.
6. ВЫВОДЫ
1. Блочный метод контрастирования и усовершенствованный метод деформации блоков с перемешиванием и усреднением позволяют найти такое нулевое приближение для СЛАУ, что время решения всей системы существенно сокращается (см. табл. 1, табл. 2), если исследуемое поле не характеризуется малым количеством четко выраженных экстремумов. Однако на практике исследуемое поле всегда характеризуется достаточным количеством геологических объектов, искажающих поле и усложняющих его картину, так что использование блочного метода оправдано при интерпретации данных гравиразведки. Усовершенствованный блочный метод контрастирования позволяет найти более устойчивое решение, чем ранее предложенные авторами: при относительной погрешности в правой части СЛАУ менее 10% относительная погрешность приближенных решений не превышает 10–15%.
Таблица 2.
Результаты модифицированной S-аппроксимации и усовершенствованного метода блочного контрастирования (модифицированные S- и F- аппроксимации). Практический пример
| N N1 N2 |
${{\sigma }_{{\min }}}$, мГал | ${{\sigma }_{{\max }}}$, мГал | ${{\sigma }_{0}}$, мГал, | ${{\sigma }_{1}}$, ${{\sigma }_{{{\text{контр 1}}}}}$, мГал, | ${{\sigma }_{2}}$, ${{\sigma }_{{{\text{контр }}2}}}$, мГал, |
Δ, t |
|---|---|---|---|---|---|---|
| 13 431 | 0.1495 | 0.3859 | 0.3556 | 0.3771 | 0.3673 | 1.0856 × 10–2, |
| 10 456 | 0.4189 | 0.3914 | 31:12 | |||
| 11 872 | ||||||
| 13 200 | 0.14 | 0.24 | 0.2134 | 0.2211 | 0.2208 | 0.9214 × 10–2, |
| 10 000 | 0.2867 | 0.2768 | 30:45 | |||
| 11 300 |
Примечания: см. примечания к табл. 1.
2. В региональном варианте модифицированный метод S-аппроксимаций позволяет определить региональные и глобальные разломные структуры (см. практический пример).
Список литературы
Бабаянц П.С. Возможности структурно-вещественного картирования по данным магниторазведки и гравиразведки в пакете программ СИГМА-3D / П.С. Бабаянц, Ю.И. Блох // Геофизический вестник. 2004. № 3. С. 11–15.
Кадиров Ф.А. Гравитационное поле и модели глубинного строения Азербайджана / Ф.А. Кадиров. Баку: “Nafta-Press”. 2000. 112 с.
Керимов И.А., Степанова И.Э., Раевский Д.Н. Комбинированные аппроксимационные методы решения задач гравиразведки и магниторазведки // Геология и геофизика Юга России. 2018. № 3. С. 37–50.
Лаврентьев М.А., Люстерник Л.А. Курс вариационного исчисления. М.–Л.: Гостоптехиздат. 1950.
Никитенко Д.А., Стефанов К.С., Воеводин Вад.В. Практика суперкомпьютера “Ломоносов” // Открытые системы. М.: Издательский дом “Открытые системы”. 2012. № 7. С. 36–39.
Степанова И.Э. Построение линейных трансформаций аномальных потенциальных полей с использованием S-аппроксимаций // Геофизический журнал. 2008. Т. 29. № 5. С. 191–201.
Степанова И.Э., Керимов И.А., Раевский Д.Н., Щепетилов А.В. Комбинированный метод F-, S- и R-аппроксимаций при решении задач геофизики и геоморфологии // Физика Земли. 2018. № 1. С. 96–113.
Степанова И.Э., Керимов И.А., Раевский Д.Н., Щепетилов А.В. Комбинированный метод F-, S- и R-аппроксимаций повышенной размерности при решении задач геофизики и геоморфологии // Физика Земли. 2018. № 6. С. 1–18.
Степанова И.Э., Керимов И.А., Раевский Д.Н., Щепетилов А.В. Интерпретация больших объемов данных при решении задач геофизики и геоморфологии с помощью модифицированного метода S-аппроксимаций // Физика Земли. 2017. № 1. С. 123–137.
Степанова И.Э. Метод R-аппроксимаций при интерпретации данных детальной гравиметрической и магнитометрической съемок // Физика Земли. 2009. № 4. С. 17–30.
Степанова И.Э. Метод R-аппроксимаций при интерпретации данных гравимагниторазведки // Геофизический журнал. 2009. Т. 31. № 3. С. 53–62.
Страхов В.Н. Геофизика и математика. М.: ОИФЗ РАН. 1999. 64 с.
Страхов В.Н., Керимов И.А., Степанова И.Э. Разработка теории и компьютерной технологии построения линейных аналитических аппроксимаций гравитационных и магнитных полей. М.: ИФЗ РАН. 2009. 254 с.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (локальный вариант) // Физика Земли. 2002. № 2. С. 3–19.
Страхов В.Н., Степанова И.Э. Метод S-аппроксимаций и его использование при решении задач гравиметрии (региональный вариант) // Физика Земли. 2002. № 7. С. 3–12.
Страхов В.Н., Степанова И.Э. Аппроксимационный подход к решению некоторых классических задач гравиметрии и магнитометрии. Основные проблемы теории интерпретации гравитационных и магнитных аномалий. М.: ОИФЗ РАН. 1999. С. 258–271.
Страхов В.Н., Степанова И.Э. Аналитическое продолжение и разделение трехмерных потенциальных полей // Докл. РАН. 2000. Т. 374. № 1. С. 103–107.
Страхов В.Н., Страхов А.В. О решении систем линейных алгебраических уравнений с приближенно заданной правой частью, возникающих при решении задач гравиметрии и магнитометрии. М.: ОИФЗ РАН. 1999. 68 с.
Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука. 1990. 230 с.
Ягола А.Г., Степанова И.Э., Ван Янфей, Титаренко В.Н. Обратные задачи и методы их решения. Приложения к геофизике. М.: Бином. Лаборатория знаний. 2014. 214 с.
Edwards D.J. Interpretation of gravity and magnetic data using the gorizontal-gradient vector method in the Western Canada Basin / D.J. Edwards, Lyatsky H.V., Brown R.J. // First Break. 1996. V. 14. № 6. P. 231–246.
Pavlis N.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008) / N.K. Pavlis, S.A. Holmes, S.C. Kenyon, J.K. Factor // J. Geophys. Res. 2012. V. 117. P. 1–38.
Sandwell D.T. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure / D.T. Sandwell, R.D. Müller, W.H.F. Smith, E. Garcia, R. Francis // Science. 2014. V. 346. № 6205. P. 65–67. https://doi.org/10.1126/science.1258213
Sandwell D.T. Towards 1 mGal Global Marine Gravity from CryoSat-2, Envisat, and Jason-1 / D.T. Sandwell, E. Garcia, K. Soofi, P. Wessel, W.H.F. Smith // The Leading Edge, 2013. V. 32. № 8. P. 892–899. https://doi.org/10.1190/tle32080892.1
Stepanova I.E. On the S-approximation of the Earth’s gravity field. Regional version, Inverse Problems in Science and Engineering. 2009. V. 17. Is. 8. P. 1095–1111.
Дополнительные материалы отсутствуют.