1. На главную
  2. Электронные версии
  3. Физика Земли
  4. № 3, 2021

Физика Земли, 2021, № 3, стр. 82-92

Количественный анализ образцов естественных коллекторов углеводородов методами интегральной геометрии и топологии

Д. А. Ивонин 1, *, П. А. Гришин 2, Е. А. Грачев 1

1 Московский государственный университет им. М.В. Ломоносова, физический факультет, кафедра Математического моделирования и информатики
г. Москва, Россия

2 Сколковский институт науки и технологий, территория Инновационного Центра “Сколково”
г. Москва, Россия

* E-mail: ivonin.dmitriy@physics.msu.ru

Поступила в редакцию 05.06.2020
После доработки 13.11.2020
Принята к публикации 03.12.2020

Полный текст (PDF)

Аннотация

В настоящей статье рассматривается количественный анализ трехмерных пористых сред (природных коллекторов углеводородов) на основе топологических инвариантов – функционалов Минковского (ФМ), а также продемонстрированы решения нескольких прикладных задач с помощью методов интегральной геометрии. Продемонстрирован анализ процесса бинаризации трехмерного изображения песчаника как динамического процесса и доказана устойчивость функционалов Минковского к выбору порога бинаризации. Предложен подход к решению задачи классификации образцов коллекторов углеводородов и поиска образцов-аналогов. Изучены модельные синтетические образцы пористых сред и образцы реальных геологических объектов.

Ключевые слова: интегральная геометрия, функционалы Минковского, цифровой керн, томография.

ВВЕДЕНИЕ

Для решения задач оценки запасов и подбора оптимальной технологии воздействия на коллектор углеводородов с целью их извлечения и оптимизации инженерных решений необходима информация о строении и свойствах порового пространства коллектора. Одной из ключевых характеристик природного коллектора углеводородов является его микроструктура, которая определяет такие ключевые параметры, как пористость (открытая и закрытая), удельная площадь поверхности пор пористого пространства и извилистость поровых каналов. Численное описание параметров, описывающих внутреннюю структуру образцов, позволяет как проводить прямые оптимизационные расчеты, так и подбирать представительные образцы для проведения натурных экспериментов. Существует ряд прямых экспериментальных методов изучения этой структуры, таких как компьютерная (рентгеновская) томография и электронная микроскопия в различных вариациях.

В настоящий момент наиболее информативным источником данных считается рентгеновская томография [Blunt и др., 2013], дополненная при необходимости повышения разрешения электронной микроскопией с ионным травлением [Lemmens, Butcher, Botha, 2010]. Однако для “классических” коллекторов, имеющих относительно крупные элементарные объемы, для проведения инженерных оценок достаточно данных только томографии. Вариации свойств поверхности (смачиваемости) в данной задаче не рассматриваются и для простоты рассматривается “классический” гидрофильный коллектор.

Для анализа томографических изображений трехмерных структур в настоящее время все большую популярность приобретают методы интегральной геометрии [Armstrong и др., 2018]. С их помощью исследуется структура почв [Vogel et al., 2010; San José Martínez et al., 2018; Ivonin и др., 2020], осадочных пород [Gong et al., 2020], пен [Gregorová и др., 2018], керамик [Pabst et al., 2018] и композитных материалов [Schröder-Turk и др., 2011; Tsukanov и др., 2020]. Их преимуществом является богатая фундаментальная теория, лежащая в областях статистической физики и топологии [Mecke, 2000]. Существуют исследования, посвященные применению методов интегральной геометрии для анализа искусственно сгенерированных сред [Arns et al., 2004; Mecke, Wagner, 1991], трехмерных томографических [Gong et al., 2020] и FIB-SEM изображений [Çeçen и др., 2012].

Авторы предлагают рассмотреть возможность применения функционалов Минковского для анализа томографических изображений образцов коллекторов углеводородов с целью решения ряда прикладных задач, возникающих у исследователей: классификации образцов коллекторов, подбора коллекторов-аналогов из различных регионов или пластов, поиска отличий во внешне схожих образцах.

ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ

С целью тестирования предложенных методик и проверки корреляции полученных результатов с традиционными представлениями был применен подход перехода от простых объектов к более сложным. В качестве объектов исследования на первом этапе был выбран синтетический образец, изготовленный путем высокотемпературного спекания стеклянных шариков (дроби). Шарики изготовлены таким образом, чтобы иметь близкую к сфере форму и узкое распределение по размерам. Полученная таким образом пористая среда является однородной и изотропной с очень узким распределением пустот по размерам и формам (небольшие вариации объекта одной формы и размера) в силу технологии производства. Такая среда является максимальным упрощением терригенного образца и позволяет получить простые аналитические и численные решения, что делает его весьма полезным для сравнения различных методов расчетов. Исходя из этого соображения он и был включен в перечень рассматриваемых объектов. В настоящей работе мы использовали синтетический образец, выполненный из сфер диаметром 400–600 мкм.

На втором этапе были использованы образцы “стандартных” коллекторов (рис. 1). Основные критерии выбора:

Рис. 1.

Томографические изображения (слои) песчаников Бентхаймер (слева), Каслгейт (по центру), а также синтетического образца (справа), полученного путем высокотемпературного спекания сфер диаметром 400–600 мкм. В нижнем ряду представлены сегментированные изображения соответствующих образцов (белым цветом показаны поры, черным – твердая матрица).

• наличие большого объема накопленных данных по данному коллектору;

• его относительная гомогенность и однородность для подтверждения представительности исследуемых образцов;

• его относительная простота для однозначности интерпретации полученных выводов.

Первый выбранный в настоящей работе объект изучения – верхнемеловой песчаник Бентхаймер, наиболее доступные отложения которого встречаются в Нидерландах (месторождение Шенебек) и в Германии (графстве Бад-Бентхайм). Этот песчаник часто используется в лабораториях в качестве природного эталона (из-за его однородности по составу и физическим свойствам) для тестирования и калибровки оборудования и проведения межлабораторных сравнительных исследований [Saenger и др., 2016]. Образец Бентхаймер представляет собой мелко- и среднезернистый богатый кварцем песчаник с пористостью ~0.2–0.27 и проницаемостью ~0.3–3 Дарси.

Другой исследуемый образец относится к формации Каслгейт и представляет собой высокопористый песчаник, который также часто применяется в лабораторных исследованиях в качестве аналога пласта-коллектора [DiGiovanni и др., 2007]. Образец Каслгейт представляет собой мелко- и среднезернистый песчаник с преобладающей фазой кварца. Другие второстепенные фазы включают полевой шпат, сидерит и твердые мелкозернистые фрагменты. Средние пористость и проницаемость находятся в том же диапазоне, что и для образцов Бентхаймер.

Для исследований был выбран стандартный типоразмер образцов цилиндрической формы диаметром 3 см и высотой 3 см. В дальнейшем образцы использовались для стандартных петрофизических и фильтрационных исследований. Томографические изображения всех образцов были получены в Центре добычи углеводородов Сколковского института науки и технологий с помощью индустриальной системы компьютерной томографии GENERAL ELECTRIC v|tome|x L240 с пространственным разрешением 20 мкм. Выбор разрешения съемки обусловлен оптимальным соотношением между временем работы томографа и возможностью производить съемку большого объема кернового материала.

ФУНКЦИОНАЛЫ МИНКОВСКОГО

В качестве объекта геометрического исследования может быть выбрано как пустотное пространство, так и различные твердые компоненты породы. Однако в настоящей работе мы предлагаем сосредоточиться на пустотном пространстве, поскольку с точки зрения массопереноса основной интерес представляет именно пустотное пространство, структура которого в первую очередь определяет фильтрационные свойства коллектора.

Пусть $X$ – тело, ограниченное гладкой поверхностью $\delta X$ в евклидовом d-мерном пространстве $E = {{R}^{d}}$ и соответствующее геометрическому месту пустотного пространства в образце. Для описания геометрических и топологических свойств такого тела интегральная геометрия позволяет определить $d~\, + \,\,1$ топологических инвариантов – функционалов Минковского [Arns et al., 2004; Hadwiger, 1975]. В случае трехмерного пространства эти функционалы с точностью до множителя соответствуют объему пустот, площади поверхности и интегральной средней кривизне поверхности раздела фаз пустоты–матрица, а также характеристике Эйлера–Пуанкаре пустотного пространства.

${{M}_{0}}\left( X \right) = V\left( X \right),$
${{M}_{1}}\left( X \right) = \int\limits_{{{\delta }}X} {dS} = S\left( X \right),$
${{M}_{2}}\left( X \right) = \int\limits_{{{\delta }}X} {\left( {\frac{1}{{{{r}_{1}}}} + \frac{1}{{{{r}_{2}}}}} \right)} dS = C\left( X \right),$
${{M}_{3}}\left( X \right) = \int\limits_{{{\delta }}X} {\frac{1}{{{{r}_{1}}{{r}_{2}}}}} dS = 2{{\pi \chi }}\left( {{{\delta }}X} \right) = 4{{\pi \chi }}\left( X \right),$
где: ${{r}_{1}}$ и ${{r}_{2}}$ – главные радиусы кривизны поверхности $dS$; а ${{\chi }}\left( {{{\delta }}X} \right)$ и ${{\chi }}\left( X \right)$ – характеристики Эйлера–Пуанкаре для поверхности ${{\delta }}X$ и выпуклого тела $X$ соответственно. Для того, чтобы избежать привязки значений функционалов к конкретному образцу, в дальнейшем мы будем использовать их удельные по объему вычислительной области значения [Vogel et al., 2010].

Характеристика Эйлера–Пуанкаре для выпуклого тела $X$ представляет собой интегральную оценку топологической сложности тела и может быть определена как знакопеременная сумма чисел Бетти:

${{\chi }}\left( X \right) = {{b}_{0}}\left( X \right) - {{b}_{1}}\left( X \right) + {{b}_{2}}\left( X \right),$
где может быть использована следующая интерпретация: ${{b}_{0}}$ – число несвязанных пор, ${{b}_{1}}$ – число проводящих каналов, а ${{b}_{2}}$ представляет собой число кластеров связности твердой фазы (матричных блоков), окруженных пустотным пространством.

К основным свойствам функционалов Минковского можно отнести их аддитивность, непрерывность и инвариантность относительно преобразований сдвига и поворота. Важное значение имеет теорема Хадвигера [Hadwiger, 1975], в соответствии с которой система функционалов Минковского является полной. Это позволяет сформулировать гипотезу о том, что система функционалов Минковского содержит всю необходимую информацию о геометрическом строении пустотного пространства для построения классификатора.

Алгоритм вычисления функционалов Минковского для бинарного изображения

Трехмерное изображение пустотного пространства может быть представлено в виде кубического клеточного комплекса – трехмерной карты, состоящей из вокселей (трехмерных пикселей). Геометрические и топологические свойства кубических комплексов изучает цифровая топология [Kong, 1995; Kong, Rosenfeld, 1989]. В работах [Legland et al., 2011; Michielsen, De Raedt, 2001; Schladitz et al., 2006; Toriwaki, Yonekura, 2002] предлагаются несколько алгоритмов, позволяющих вычислять значения функционалов Минковского. Остановимся на одном из них [Michielsen, De Raedt, 2001], основанном на подсчете числа вершин, ребер, граней и вокселей в кубическом комплексе:

$V\left( X \right) = {{n}_{c}},$
$S\left( X \right) = - 6{{n}_{c}} + 2{{n}_{f}},$
$2C\left( X \right) = 3{{n}_{c}} - 2{{n}_{f}} + {{n}_{e}},$
${{\chi }}\left( X \right) = - {{n}_{c}} + {{n}_{f}} - {{n}_{e}} + {{n}_{{{\nu }}}},$
где: ${{n}_{c}}$ – число вокселей; ${{n}_{f}}$ – число граней; ${{n}_{e}}$ – число ребер и ${{n}_{\nu }}$ – число вершин в кубическом клеточном комплексе, соответствующем пустотному пространству образца. Аддитивность функционалов Минковского позволяет реализовать комбинаторные алгоритмы их вычисления, которые не требуют значительных вычислительных ресурсов и допускают использование параллельных вычислений в случае, если исходное изображение имеет высокое разрешение.

РЕЗУЛЬТАТЫ

Процедура бинаризации

Для упрощения последующего анализа структуры пустотного пространства требуется сначала выделить на изображении соответствующие пустотам области, то есть разделить исследуемую среду на две фазы: пустоты и твердая матрица. Выбор порога бинаризации во многом субъективен, зависит от характера поставленной задачи и может быть осуществлен многими различными способами [Wang и др., 2011]. Для построения классификатора необходимо выделить пустотное пространство на всех изображениях с применением одного алгоритма, поскольку применение различных алгоритмов (в том числе и выбор порога бинаризации вручную) неизбежно внесет субъективность в результат.

Отметим, что выбор порога бинаризации для томографических изображений упаковок сфер хорошо изучен и не представляет значительной сложности ввиду мономинеральности образцов и наличия гладкой границы между твердой матрицей и поровым пространством [Eichheimer и др., 2020]. С другой стороны, выбор порога бинаризации для томографических изображений естественных пористых сред нетривиален ввиду неоднородности химического состава и сложной геометрии внутренней поверхности. Существуют как экспериментальные [Schlüter, Vogel, 2016], так и аналитические подходы, позволяющие определить структуру пустотного пространства. Для исследуемых изображений несколько широко применяемых аналитических методов бинаризации [Li, Tam, 1998; Otsu, 1979] продемонстрировали существенно завышенные значения порога бинаризации.

Методы интегральной геометрии и топологии могут лежать в основе алгоритма определения оптимального порога бинаризации [Pikaz, Averbuch, 1996]. В настоящей работе предлагается выбрать порог бинаризации, соответствующий экстремуму интегральной средней кривизны пустотного пространства (рис. 2). Интегральная средняя кривизна – важная морфометрическая характеристика трехмерных объектов, которая часто используется для описания формы поверхности раздела фаз [Akai и др., 2019; McClure и др., 2020]. Полученная подобным образом конфигурация пустотного пространства представляется нам соответствующей разумным представлениям о ее структуре. Сравнение расчетных и экспериментальных значений пористости позволяет сделать следующие выводы: для изображений песчаников, полученных с разрешением 20 мкм, полученные значения пористости (16.9% для песчаника Бентхаймер и 18.1% для песчаника Каслгейт) ниже, чем экспериментально определенные величины (23 и 26% соответственно). Подобная закономерность может быть объяснена как сравнительно низким разрешением съемки, при котором поверхность пор существенно огрубляется, так и наличием так называемой “неразрешенной пористости” – пор, которые при выбранном разрешении не видны на томографическом изображении. Применение данной методики позволяет одинаковым образом учитывать особенности микроструктуры и проводить бинаризацию томографических изображений в полуавтоматическом режиме. Отметим, что значения функционалов устойчивы к небольшим изменениям порога бинаризации, поэтому возможные незначительные отличия в выборе порога бинаризации не повлияют на решение задачи классификации.

Рис. 2.

Зависимости пористости $\phi $ и интегральной средней кривизны $\hat {C}$ пустотного пространства от порога бинаризации для томографических изображений песчаников Бентхаймер (слева) и Каслгейт (справа) с указанием значений порога бинаризации, соответствующего экстремуму интегральной средней кривизны поверхности. Величина $\hat {C}$ нормирована на отрезок [–1,1]. Для обоих образцов были определены значения пористости при выбранном пороге бинаризации 16.9% для песчаника Бентхаймер и 18.1% для песчаника Каслгейт.

Анализ образцов репрезентативного размера

После определения оптимального порога бинаризации и выделения пустотного пространства был выполнен анализ образцов репрезентативного объема. Отметим, что минимальный репрезентативный объем может быть определен с помощью методов интегральной геометрии путем построения зависимостей значений функционалов Минковского от размера вычислительной области. На рис. 3 приведены зависимости удельных значений функционалов Минковского от линейного размера вычислительной области. Анализ приведенных закономерностей показывает, что для исследуемых в работе структур репрезентативным объемом можно считать объем ${{200}^{3}}$ вокселей.

Рис. 3.

Зависимость удельных значений функционалов Минковского $\left( {\phi ,S,C,{{\chi }}} \right)$ от линейного размера вычислительной области $L$ для песчаника Бентхаймер. Для каждого значения $L$ случайным образом были отобраны 10 образцов, после чего были построены диаграммы размаха, отображающие первый и третий квартили выборки, ее дисперсию, а также выбросы при их наличии. Вертикальной чертой показано репрезентативное значение, используемое для последующего анализа.

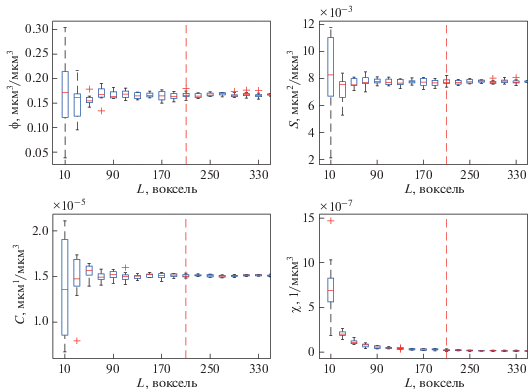
Бинаризованные изображения исследуемых образцов были разделены на серию подобразцов размером ${{200}^{3}}$, после чего для каждого подобразца были вычислены удельные значения функционалов Минковского. На рис. 4 представлены диаграммы рассеяния значений функционалов Минковского для песчаников Бентхаймер, Каслгейт и для синтетического образца.

Рис. 4.

Диаграммы рассеяния удельных значений $\left( {\phi ,S,C,{{\chi }}} \right)$ для песчаников Бентхаймер (синий цвет), Каслгейт (красный цвет) и синтетического образца (желтый цвет).

Точки, соответствующие синтетическому образцу, располагаются на всех диаграммах кучно, поскольку образец имеет сравнительно однородную структуру пустотного пространства. Несмотря на то, что пористость образца варьируется в пределах нескольких процентов (это вызвано незначительными деформациями сфер в процессе спекания), значения интегральной средней кривизны и характеристики Эйлера–Пуанкаре ${{\chi }}$ практически не меняются.

Для точек, соответствующих песчаникам, наблюдаются более сложные зависимости. Например, можно обнаружить выраженную положительную корреляцию между значениями пористости $\phi $ и удельной площади поверхности пор $S$, а также отрицательные корреляции между значениями пористости и характеристики Эйлера–Пуанкаре ${{\chi }}$. Также отрицательная корреляция наблюдается для значений удельной площади поверхности пор $S$ и характеристики Эйлера–Пуанкаре ${{\chi }}$.

Анализ распределений функционалов, представленных на рис. 4, показывает, что пустотное пространство песчаника Каслгейт имеет более сложную структуру по сравнению с песчаником Бентхаймер: стандартные отклонения для песчаника Каслгейт систематически превышают соответствующие значения для песчаника Бентхаймер (представлены в табл. 1). Особенно наглядно топологическую сложность пустотного пространства песчаника Каслгейт демонстрирует распределение характеристики Эйлера–Пуанкаре, стандартное отклонение которого в несколько раз превышает соответствующую величину для песчаника Бентхаймер. Чем сложнее и разнообразнее геометрическая форма пустотного пространства – тем больше размер соответствующего ему облака точек на диаграммах рассеяния.

Таблица 1.  

Характеристики распределений удельных значений функционалов Минковского для песчаников Бентхаймер и Каслгейт

Образец $\phi $ S, ×10–3, мкм–1 C, ×10–5, мкм–2 ${{\chi }}$, ×10–8, мкм–3
Бентхаймер 0.165 ± 0.008 7.7 ± 0.29 1.50 ± 0.02 2.48 ± 0.86
Каслгейт 0.196 ± 0.018 10.3 ± 0.63 2.19 ± 0.11 3.55 ± 3.94
Синтетический образец 0.251 ± 0.009 5.8 ± 0.08 0.026 ± 0.002 –3.17 ± 0.11

Снижение размерности данных и классификация

Отметим, что предлагаемая методология предполагает анализ четырехмерного пространства признаков: $\left( {\phi ,S,C,{{\chi }}} \right)$. В случае, если исследуемая структура имеет более сложную геометрию (например, содержит несколько разных масштабов), размерность пространства признаков может быть увеличена до 6. В таком случае вместо характеристики Эйлера–Пуанкаре возможно рассматривать три числа Бетти как отдельные характеристики. В связи с этим возникает необходимость в снижении размерности данных, которое может быть выполнено с помощью метода главных компонент. Данный метод часто применяется для снижения размерности данных и позволяет перейти к меньшему числу переменных с минимальной потерей информации. При этом новые переменные являются линейными комбинациями первоначальных. Результат применения метода главных компонент к результатам анализа песчаников Бентхаймер и Каслгейт приведен на рис. 5. Анализируя полученный результат, можно сделать следующие предположения:

Рис. 5.

Классификация песчаников Бентхаймер и Каслгейт с помощью метода главных компонент. Применение метода главных компонент позволило снизить размерность данных: изначальное пространство признаков состояло из 4 признаков: $\left( {\phi ,S,C,\chi } \right).$

• при формировании микроструктуры образца происходило лишь 2 истинно независимых процесса, а остальные процессы являются взаимосвязанными (зависимыми);

• процессы формирования микроструктуры образца песчаника Бентхаймер были гораздо более связанными (выше корреляция) в отличие от песчаника Каслгейт, для которого связь двух независимых процессов менее выражена. В пределе (если допустить причиной разброса данных по образцу экспериментальную погрешность) можно предположить, что за формирование микроструктуры образцов песчаника Бентхаймер отвечает один “суперпроцесс”;

• восстановив параметры процессов (“суперпроцесса” в отдельных случаях), возможно описать закон формирования микроструктуры, а значит эффективно решить задачу описания микроструктуры коллектора, его перемасштабирования, подбора или создания образцов-аналогов, определения представительности полученных данных.

При проведении исследований зачастую возникает задача определения принадлежности образца к одному из нескольких заранее известных классов (задача классификации), или наоборот – необходим инструмент для распределения серии образцов на несколько групп в соответствии с их свойствами (задача кластеризации). Обе задачи могут быть решены благодаря полноте системы функционалов Минковского. В соответствии с теоремой Хадвигера, геометрические свойства пустотного пространства выбранного образца задаются совокупностью функционалов Минковского однозначным образом. Следовательно, на их основе может быть продемонстрировано как различие между образцами кернового материала, представляющими различные литотипы или фации, так и сходство двух образцов.

Поиск образцов-аналогов

Немаловажной прикладной задачей является поиск образцов-аналогов на заданном томографическом изображении. Это необходимо как в случае более детального исследования (например, с большим пространственным разрешением), так и для проведения серии сопоставительных исследований, в ходе которых образец разрушается (например, геомеханические или пиролитические исследования). Полнота системы функционалов Минковского позволяет применить их для поиска образцов-аналогов в заданном образце. Под термином “аналоги” в контексте рассматриваемой задачи подразумевается сходство удельных интегральных характеристик образцов. Для этого исходное томографическое изображение разбивается на образцы репрезентативного размера, после чего для каждого из образцов вычисляются удельные значения функционалов Минковского. Построение матрицы расстояний в четырехмерном пространстве позволяет найти образцы, наиболее близкие по интегральным характеристикам пустотного пространства. Мы применили подобный подход для поиска образцов-аналогов в песчанике Бентхаймер. Удельные значения функционалов Минковского для наиболее схожих образцов приведены в табл. 2. Подобная методика может быть применена для подбора образцов-аналогов и последующего проведения серии сравнительных испытаний, но не гарантирует близость функциональных свойств подобранных образцов. Другим ограничением подобного подхода является недостаточность значений функционалов Минковского для реконструкции структуры пустотного пространства. Поэтому в случае необходимости последующей реконструкции пористой структуры могут быть использованы генеративные состязательные нейронные сети [Mosser et al., 2017] или корреляционные функции [Karsanina и др., 2020]. При этом система функционалов Минковского может быть использована для количественного описания качества реконструкции.

Таблица 2.  

Сравнение значений удельных функционалов Минковского для двух наиболее похожих подобразцов песчаника Бентхаймер

Функционал Минковского Подобразец 1 Подобразец 2
Удельный объем $V$ (пористость), мкм3/мкм3 0.2763025 0.2760833
Удельная площадь поверхности пор $S$, мкм2/мкм3 0.01071878 0.01071142
Удельная интегральная средняя кривизна C, мкм1/мкм3 0.12807×10–4 0.12827×10–4
Удельная характеристика Эйлера–Пуанкаре ${{\chi }}$, 1/мкм3 –0.10348×10–6 –0.10383×10–6

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрен подход к численному описанию микроструктуры пустотного пространства естественных коллекторов углеводородов с помощью методов интегральной геометрии – функционалов Минковского. Приведены математические определения используемых инвариантов и алгоритм их вычисления для трехмерных томографических изображений, после чего демонстрируется исследование с их помощью образцов песчаников Бентхаймер и Каслгейт, а также синтетического образца, изготовленного путем высокотемпературного спекания стеклянных шариков различного диаметра. Предложена методика автоматизированного подбора оптимального порога бинаризации томографического изображения песчаников обоих типов. Проведен анализ диаграмм рассеяния значений функционалов Минковского, наглядно продемонстрировавший существенные отличия в структуре пустотного пространства образцов песчаников. Продемонстрирована возможность снижения размерности данных с помощью метода главных компонент. Предложены методики классификации, кластеризации образцов и подбора образцов-аналогов, основанные на применении функционалов Минковского.

Совокупность предложенных методик и подходов позволяет применять подходы интегральной геометрии для решения ряда как инженерных, так и исследовательских задач:

• классификация, типизация и систематизация образцов коллекторов на основе их трехмерных томографических изображений;

• кластеризация серии образцов на несколько классов в соответствии со строением их пустотного пространства;

• поиск отличий во внешне схожих образцах в случае, когда традиционные методы описания структуры пустотного пространства не дают надежного или достаточно быстрого результата;

• поиск образцов-аналогов и оценка качества реконструкции пористых структур.

Отметим, что в данной работе были рассмотрены изображения пористых сред лишь на одном масштабе. Многие естественные пористые среды имеют различную структуру пустотного пространства на разных иерархических уровнях [Karsanina и др., 2018], поэтому схожая методология анализа может быть применена для изображений, полученных при разном разрешении и на разных масштабах. Дальнейшим развитием методов топологического анализа трехмерных структур, содержащих несколько различных масштабов, является применение теории персистентных гомологий [Armstrong и др., 2018; Bazaikin и др., 2017]. Также с помощью методов интегральной геометрии и топологии может быть количественным образом описана анизотропия пористых сред [Klatt et al., 2017; Ohser, Schladitz, 2009; Svitelman, Dinariev, 2013]. К другим перспективным направлениям исследования можно отнести:

• оценку функциональных характеристик пористых сред, зависящих от структуры пустотного пространства (например, проницаемости), с использованием подходов интегральной геометрии [Berg, 2014; Scholz и др., 2012] и их количественное сравнение с результатами, получаемыми прямым численным моделированием [Gerke и др., 2018; Yazynina и др., 2017] или в результате лабораторных испытаний;

• проведение исследований структуры пустотного пространства естественных сред на разных масштабах [Karsanina и др., 2018];

• классификацию и систематизацию данных по разным регионам и пластам, поиск и создание базы данных “отпечатков пальцев” (“генетических признаков”);

• определение параметров (функционалы Минковского, числа Бетти) для образцов различных песчаников [Lucas-Oliveira и др., 2020] ;

• изучение внутренней структуры более сложных коллекторов углеводородов, например, карбонатных коллекторов и пород Ачимовской и Баженовской свит;

• анализ физических причин выявленных тенденций в задаче бинаризации.

Список литературы

  1. Gerke K.M. et al. Finite-difference method Stokes solver (FDMSS) for 3D pore geometries: Software development, validation and case studies // Computers & Geosciences. 2018. Т. 114. С. 41–58.

  2. Berg C.F. Permeability Description by Characteristic Length, Tortuosity, Constriction and Porosity // Transport in Porous Media. 2014. V. 103. № 3. P. 381–400.

  3. Mosser L., Dubrule O., Blunt M.J. Reconstruction of three-dimensional porous media using generative adversarial neural networks // Physical Review E. 2017. V. 96. № 4.

  4. Akai T. et al. Quantification of Uncertainty and Best Practice in Computing Interfacial Curvature from Complex Pore Space Images // Materials. 2019. V. 12. № 13. P. 2138.

  5. Armstrong R.T. et al. Porous Media Characterization Using Minkowski Functionals: Theories, Applications and Future Directions // Transport in Porous Media. 2018.

  6. Arns C.H., Knackstedt M.A., Mecke K.R. Characterisation of irregular spatial structures by parallel sets and integral geometric measures // Colloids and Surfaces A: Physicochemical and Engineering Aspects. 2004. V. 241. № 1–3. P. 351–372.

  7. Bazaikin Y. et al. Effect of CT image size and resolution on the accuracy of rock property estimates: Effect of Ct Image Scale // J. Geophys. Res.: Solid Earth. 2017. V. 122. № 5. P. 3635–3647.

  8. Blunt M.J. et al. Pore-scale imaging and modelling // Advances in Water Resources. 2013. V. 51. P. 197–216.

  9. Çeçen A. et al. 3-D Microstructure Analysis of Fuel Cell Materials: Spatial Distributions of Tortuosity, Void Size and Diffusivity // J. Electrochemical Society. 2012. V. 159. № 3. P. B299–B307.

  10. DiGiovanni A.A. et al. Microscale damage evolution in compacting sandstone // Geological Society, London, Special Publications. 2007. V. 289. № 1. P. 89–103.

  11. Eichheimer P. et al. Combined numerical and experimental study of microstructure and permeability in porous granular media // Solid Earth. 2020. V. 11. № 3. P. 1079–1095.

  12. Gong L., Nie L., Xu Y. Geometrical and Topological Analysis of Pore Space in Sandstones Based on X-ray Computed Tomography // Energies. 2020. V. 13. № 15. P. 3774.

  13. Gregorová E. et al. Microstructure characterization of mullite foam by image analysis, mercury porosimetry and X-ray computed microtomography // Ceramics International. 2018. V. 44. № 11. P. 12315–12328.

  14. Hadwiger H. Inhalt, Oberfläche und Isoperimetrie // Vorlesungen Über Inhalt, Oberfläche und Isoperimetrie Die Grundlehren der Mathematischen Wissenschaften / Ed. H. Hadwiger. Berlin, Heidelberg: Springer. 1975. P. 179–198.

  15. Ivonin D. et al. Quantitative Analysis of Pore Space Structure in Dry and Wet Soil by Integral Geometry Methods // Geosciences. 2020. V. 10. № 9. P. 365.

  16. Karsanina M.V. et al. Enhancing image resolution of soils by stochastic multiscale image fusion // Geoderma. 2018. V. 314. P. 138–145.

  17. Karsanina M.V. et al. Compressing soil structural information into parameterized correlation functions // Eur. J. Soil Sci. 2020.

  18. Klatt M.A., Schröder-Turk G.E., Mecke K. Mean-intercept anisotropy analysis of porous media. II. Conceptual shortcomings of the MIL tensor definition and Minkowski tensors as an alternative // Medical Physics. 2017. V. 44. № 7. P. 3663–3675.

  19. Kong T.Y. On topology preservation in 2-D and 3-D thinning // International J. Pattern Recognition and Artificial Intelligence. 1995. V. 9. № 5. P. 813–844.

  20. Kong T.Y., Rosenfeld A. Digital topology: Introduction and survey // Computer Vision, Graphics, and Image Processing. 1989. V. 48. № 3. P. 357–393.

  21. Legland D., Kiêu K., Devaux M.-F. Computation of Minkowski measures on 2D and 3D binary images // Image Analysis & Stereology. 2011. V. 26. № 2. P. 83.

  22. Lemmens H., Butcher A., Botha P. W. FIB/SEM and Automated Mineralogy for Core and Cuttings Analysis. Society of Petroleum Engineers. 2010.

  23. Li C., Tam P. An iterative algorithm for minimum cross entropy thresholding // Pattern Recognit. Lett. 1998.

  24. Lucas-Oliveira E. et al. Sandstone surface relaxivity determined by NMR T2 distribution and digital rock simulation for permeability evaluation // J. Petroleum Science and Engineering. 2020. V. 193. P. 107400.

  25. McClure J.E. et al. Modeling Geometric State for Fluids in Porous Media: Evolution of the Euler Characteristic // Transp Porous Med. 2020. V. 133. № 2. P. 229–250.

  26. Mecke K.R. Additivity, Convexity, and Beyond: Applications of Minkowski Functionals in Statistical Physics. Statistical Physics and Spatial Statistics / Eds. K.R. Mecke, D. Stoyan. Berlin, Heidelberg: Springer Berlin Heidelberg. 2000. P. 111–184.

  27. Mecke K.R., Wagner H. Euler characteristic and related measures for random geometric sets // J. Stat. Phys. 1991. V. 64. № 3–4. P. 843–850.

  28. Michielsen K., De Raedt H. Integral-geometry morphological image analysis // Physics Reports. 2001. V. 347. № 6. P. 461–538.

  29. Ohser J., Schladitz K. 3D-Images of Materials Structures: Processing and Analysis. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA. 2009.

  30. Otsu N. A Threshold Selection Method from Gray-Level Histograms // IEEE Transactions on Systems, Man, and Cybernetics. 1979. Т. 9. № 1. С. 62–66.

  31. Pabst W., Uhlirova T., Gregorová E. Microstructure Characterization of Porous Ceramics Via Minkowski Functionals // Ceramic Transactions. 2018. P. 53–64.

  32. Pikaz A., Averbuch A. Digital image thresholding, based on topological stable-state // Pattern Recognition. 1996. V. 29. № 5. P. 829–843.

  33. Saenger E.H. et al. Analysis of high-resolution X-ray computed tomography images of Bentheim sandstone under elevated confining pressures // Geophys. Prospect. 2016. V. 64. № 4. P. 848–859.

  34. San José Martínez F., Martín L., García-Gutiérrez C. Minkowski Functionals of Connected Soil Porosity as Indicators of Soil Tillage and Depth // Frontiers in Environmental Science. 2018. V. 6. C. 55.

  35. Schladitz K., Ohser J., Nagel W. Measuring Intrinsic Volumes in Digital 3d Images. Discrete Geometry for Computer Imagery / Eds. A. Kuba, L.G. Nyúl, K. Palágyi. Berlin, Heidelberg: Springer Berlin Heidelberg. 2006. P. 247–258.

  36. Schlüter S., Vogel H.-J. Analysis of Soil Structure Turnover with Garnet Particles and X-Ray Microtomography // PLoS ONE. 2016. V. 11. № 7. P. e0159948.

  37. Scholz C. et al. Permeability of Porous Materials Determined from the Euler Characteristic // Phys. Rev. Lett. 2012. V. 109. № 26. P. 264504.

  38. Schröder-Turk G.E. et al. Minkowski tensor shape analysis of cellular, granular and porous structures // Adv. Mater. 2011. V. 23. № 22–23. P. 2535–2553.

  39. Svitelman V., Dinariev O. Geostatistical approach to the anisotropy analysis of 3D rock microtomographic models // Computers & Geosciences. 2013. V. 57. P. 116–123.

  40. Toriwaki J., Yonekura T. Euler number and connectivity indexes of a three dimensional digital picture // Forma. 2002. V. 17. P. 183–209.

  41. Tsukanov A.A. et al. Effect of Cold-Sintering Parameters on Structure, Density, and Topology of Fe–Cu Nanocomposites // Materials. 2020. V. 13. № 3. P. 541.

  42. Vogel H.-J., Weller U., Schlüter S. Quantification of soil structure based on Minkowski functions // Computers & Geosciences. 2010. V. 36. № 10. P. 1236–1245.

  43. Wang W. et al. Comparison of image segmentation methods in simulated 2D and 3D microtomographic images of soil aggregates // Geoderma. 2011. V. 162. № 3. P. 231–241.

  44. Yazynina I.V. et al. Testing a new approach to petrophysical trend determination from X-Ray tomography (Russian) // Oil Industry J. 2017. V. 2017. № 02. P. 36–40.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика Земли

Архивы выпусков Информация о журнале Отправить рукопись в журнал