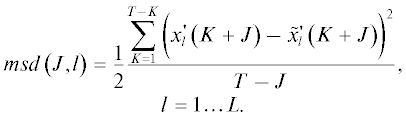Геомагнетизм и аэрономия, 2019, T. 59, № 1, стр. 98-109

1. ВВЕДЕНИЕ

Состояние ионосферы Земли оказывает определяющее воздействие на качество дальней радиосвязи и радиолокации, является важным фактором, влияющим на работоспособность спутниковых систем. В связи с этим задача прогнозирования ее состояния становится все более актуальной. Традиционный подход к созданию прогностических ионосферных систем, в отличие от задачи “атмосферного” прогноза погоды, основан на эмпирическом подходе. Прогностическими переменными обычно являются “медианные” величины ионосферных параметров – осредненные по значительному интервалу времени (порядка 30 сут) значения критической частоты foF2, или, например, поля полной электронной концентрации TEC. Модели используют стандартизованные базы данных ионосферных параметров [CCIR, 1967; Rush et al., 1984]. Наиболее распространенной моделью такого типа является семейство IRI [Bilitza et al., 2012, 2016]. Следует также отметить отечественные разработки SIMP [Лещинская и Михайлов, 2016] и SDMF2 [Шубин, 2017], основанные на схожих принципах. Для краткосрочных прогнозов ионосферы обычно разрабатываются системы, основанные на нейронных сетях и/или методике статистических регрессий [Oyeyemi et al., 2005; Hoque and Jakowski, 2012; Lin et al., 2014; и т.д.], обучаемые на некоторой выборке из данных наблюдений и настраиваемые на конкретный прогностический интервал.

С теоретической и практической точек зрения весьма важными в задаче прогноза являются вопросы о том, какие процессы обеспечивает предсказуемость в системе и какова длина временнóго интервала, в течение которого прогноз информативен. Начиная с работы Lorenz [1963] принято разделять предсказуемость по начальным условиям (предсказуемость 1-го рода) – информацию о начальной точке прогностической траектории и предсказуемость по правой части (предсказуемость 2-го рода) – информацию (влияние) от внешних воздействий на систему. В хаотических системах, традиционным примером которых является земная атмосфера, предсказуемость 1-го рода ограничена достаточно коротким временны́м интервалом (порядка 10 дней), поскольку изначально близкие траектории удаляются друг от друга с экспоненциальной скоростью. На больших временны́х интервалах доминирует предсказуемость 2-го рода, обеспечиваемая, например, периодической по времени солнечной активностью или долгоживущими аномалиями температуры поверхности океана. Похожая ситуация, по-видимому, имеет место и в задаче прогноза ионосферы. На больших (неделя и более) временны́х интервалах состояние ионосферы контролируется параметрами солнечной и геомагнитной активности, и именно эта информация используется в моделях типа IRI для определения ионосферных параметров. На временны́х масштабах порядка суток и менее преобладает предсказуемость первого рода – информация о состоянии ионосферы в начальный момент. Вопрос о длине интервала предсказуемости первого рода и ее зависимости от внешних факторов (времени суток, сезона, солнечной активности и т.п.) представляется нам весьма важным.

Трудность оценки интервала предсказуемости применительно к задаче прогнозирования ионосферы заключается в том, что прогностические модели ионосферы являются в настоящее время статистическими и не позволяют корректно оценивать расстояние между прогностической и реальной траекторией. Тем не менее, существуют способы оценки этой величины непосредственно по данным наблюдений. Метод основан на вычислении расстояния между ансамблем наблюдений и ансамблем аналогов – специальной выборке из ансамбля наблюдений, такой, что пары точек ансамблей отстоят друг от друга на минимальное расстояние, соответствуя при этом разнесенным по времени моментам измерений. Таким образом, для каждого наблюдения (поля TEC, например) подбирается другое, близкое ему в некоторой метрике, наблюдение. Траектория, соответствующая первому состоянию считается реальностью, а вторая – прогнозом. Изменение расстояния между ними в зависимости от времени характеризует потерю информации о начальном состоянии в системе. Время потенциальной предсказуемости определяется как время, за которое расстояние между точками ансамблей становится близким к среднеквадратичному расстоянию по архиву наблюдений. Реализации этого метода для архива данных поля полной электронной концентрации посвящен второй раздел настоящей работы.

Метод “аналогов” дает лишь оценку средней величины интервала предсказуемости, поэтому представляется интересным проверить полученные результаты с помощью какой-нибудь прогностической модели ионосферы. Для этой цели, в третьей части работы, мы рассматриваем простейшую линейную динамико-стохастическую эмпирическую модель: так называемую “обратную линейную модель” (от “linear inverse model”, или LIM [Penland and Sardeshmukh, 1995; Penland, 1996]). С помощью данной модели мы даем краткосрочный прогноз аномалии поля TEC (относительно средней за предыдущую неделю), оцениваем его успешность и заблаговременность и сравниваем с результатами, полученными с помощью метода “аналогов”. Кроме того, здесь рассматривается вопрос о влиянии геомагнитных и солнечных факторов на полученные результаты. В четвертой части статьи формулируются и обсуждаются основные результаты работы.

2. ОЦЕНКА ПРЕДСКАЗУЕМОСТИ ПО ДАННЫМ НАБЛЮДЕНИЙ. МЕТОД АНАЛОГОВ

Сформулируем сначала метод оценки времени предсказуемости системы, основанный на использовании данных наблюдений, далее – “метод аналогов”. Метод заключается в построении “прогностического” ансамбля состояний системы для точек архива наблюдений способом, изложенным в работах [Nicholls, 1980; Bergen and Harnack, 1982; Branstator et al., 2012]. Рассмотрим траекторию системы (архив данных наблюдений) за достаточно длительный период $\left\{ {X(K),K = 1...T} \right\}.$ Здесь и далее мы будем считать $X(K)$ двумерным полем, заданным на географической сетке с размерностью $L = {{L}_{x}}{{L}_{y}}.$ Для каждого $X(K)\quad$ подберем такое состояние $X(M),$ что расстояние между $X(K)$ и $X(M)$ минимально (в данной работе мы будем использовать обычную сферическую евклидову метрику). При этом близкие по времени состояния (т.е. состояния с близкими значениями K и M) не рассматриваются. Полученный таким образом набор состояний $\left\{ {\tilde {X}(K)} \right\}\mathop = \limits^{{\text{def}}} {\;}\left\{ {X(M)} \right\}$ содержит “аналоги” состояний ряда данных $\left\{ {X(K)} \right\}$ (в смысле минимальности расстояния) и является некоторой выборкой/перестановкой исходного ряда. По поведению его траекторий, близких в начальный момент к траекториям исходного ряда, можно оценивать прогностические характеристики системы. Заметим, что ансамбль должен быть достаточно большим, чтобы подбираемые пары точек были действительно близкими. Для оценки времени предсказуемости вычисляется среднеквадратичное (по ансамблям) расстояние между траекториями, выпущенными из соответствующих пар точек в зависимости от времени (т.е. расстояние между парами полей и $\tilde {X}\left( {K + J} \right)$ при $J = 1,2,...$ и т.д.). Расстояние при этом удобно нормировать на удвоенное число степеней свободы, а сами данные – на дисперсию в каждой точке.

По поведению $MSD\left( J \right)$ можно судить, насколько быстро изначально близкие друг к другу траектории расходятся и как быстро информация о начальном условии перестает быть значимой. Значение $MSD,$ равное 0.6, обычно считается пороговым при таких расчетах (см., например, [Branstator et al., 2012]), а соответствующее время J – временем потенциальной предсказуемости.

При практической реализации данного алгоритма зачастую оказывается, что размерность исходного поля высокая, а число данных невелико, поэтому задачу поиска аналогов приходится рассматривать в некотором редуцированном пространстве. В данной работе мы будем использовать пространство ведущих мод изменчивости исходного поля (в метеорологической терминологии имеющих название “естественные ортогональные функции”, или ЕОФ [Storch and Zwiers, 1999; Dvinskikh, 1988]).

Выбор такого базиса обусловлен тем фактом, что ведущие ЕОФ – это направления максимальной амплитуды временнóй изменчивости, ортогональные друг другу. Обозначим за $\bar {X}$ среднее состояние системы

По определению, ковариационная матрица ${{{\Xi }}_{0}}$ ряда $X(K)$ – это матрица размерности L × L:

Перемножение элементов двумерных векторов в нашем случае осуществляется с учетом сферической метрики, таким образом, каждый элемент матрицы ${{{\Xi }}_{0}}$ вычисляется по формуле

где $X{\text{'}}(t) = X(t)--\bar {X},$ а $X{\text{'}}\left( {{{l}_{1}},t} \right)$ и $X{\text{'}}\left( {{{l}_{2}},t} \right)$ – это значения двумерного поля $X{\text{'}}(t)$ в точках ${{l}_{1}} = \left( {{{\varphi }_{1}},{{\phi }_{1}}} \right)$ и ${{l}_{2}} = \left( {{{\varphi }_{2}},{{\phi }_{2}}} \right)$ с соответствующими широтами и долготами.

Решая задачу на собственные значения для симметричной, положительно определенной ковариационной матрицы ${{{\Xi }}_{0}}$

мы находим набор нормированных на единицу (с учетом сферической метрики) собственных векторов $\left\{ {{{{\Psi }}_{i}},i = 1...L} \right\},$ который удобно упорядочить по убыванию собственного числа ${{\lambda }_{i}}.$ Векторы ${{{\Psi }}_{i}}$ и есть, по определению, искомые ЕОФ ряда $\left\{ {X(K)} \right\}.$ Собственные числа ${{\lambda }_{i}}$ матрицы (2) при этом равны дисперсиям поля вдоль направлений ${{{\Psi }}_{i}}.$ Выбирая n первых ЕОФ и проецируя на них исходный ряд $\left\{ {X{\text{'}}(K)} \right\}$ получим

Таким образом, ${\mathbf{x}}{\text{'}}(K)$ это n – компонентный вектор коэффициентов Фурье проекций аномалии исходного поля на базис ведущих ЕОФ, каждая компонента которого нормирована на единицу дисперсии. Именно в этом пространстве мы и будем решать задачу о поиске ансамбля “аналогов” для набора $\left\{ {{\mathbf{x}}{\text{'}}(K)} \right\},$ который мы обозначим $\left\{ {{\mathbf{\tilde {x}}}{\text{'}}(K)} \right\}.$ Для результатов, обсуждаемых ниже, значение n было принято равным 20.

Расстояние между $\left\{ {{\mathbf{x}}{\text{'}}(K)} \right\}$ и $\left\{ {{\mathbf{\tilde {x}}}{\text{'}}(K)} \right\}$ мы будем определять аналогичным образом

где $\left\| \ldots \right\|$ – это обычная евклидова метрика.

После того, как аналоги в пространстве ЕОФ найдены, данные можно трансформировать обратно в физическое пространство и вычислить разницу между соответствующими парами членов ансамбля для каждой точки исходной географической сетки. В результате мы можем измерить среднее расстояние между точками ансамблей для каждой точки географической сетки и получить пространственное распределение роста ошибки прогноза. А именно,

Здесь $x_{l}^{'}(K)$ – это просто значение рассматриваемой величины в данной точке географической сетки. Определив величину интервала предсказуемости в данной точке как время, за которое $msd\left( {J,l} \right)\quad$ принимает значение, превышающее 0.6, мы получим географическое распределение времен потери предсказуемости.

В работе описанная выше технология была использована для данных полей TEC с сайта архива данных NASA ftp.cddis.nasa.gov. Данные представляют собой двумерные массивы на географической широтно-долготной сетке с разрешением 5 и 2.5 град по долготе и широте с временны́м шагом 2 ч. Данные доступны с середины 1998 г. по настоящее время. В работе используется весь имеющийся архив. Поскольку мы интересуемся оценкой времени предсказуемости по начальным условиям (определяемого внутренней динамикой ионосферы/верхней атмосферы на достаточно коротких временны́х интервалах) нам необходимо выделить компоненту динамики, наименее зависящую от геомагнитных и солнечных факторов (кроме суточного хода солнечной радиации, который будет учтен напрямую). Для этого мы рассматриваем предсказуемость компоненты поля TEC – ее аномалии относительно средней за предыдущую неделю (${\Delta } = 24\,{\text{hr}}$):

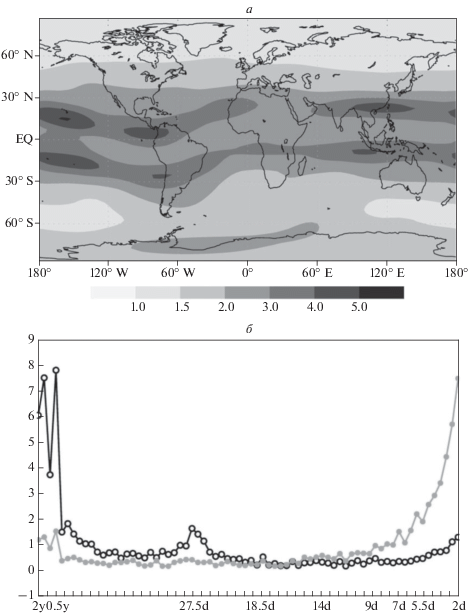
На рисунке 1 показаны спектры Фурье исходного поля TEC(K) (рис. 1б, черная линия) и поля аномалии относительной ее недельной средней $X{\text{'}}(K)$ (рис. 1б, серая линия). При вычислении спектров данные были разбиты на 8 двухлетних интервалов, для каждого был вычислен соответствующий спектр, а результаты вычислений усреднены. Масштаб спектров подобран так, чтобы их значения на правом конце (т.е. для периода 2 дня) совпадали. Для исходного поля (рис. 1б, черная линия) хорошо видны известные суточный, годовой и полугодовой максимумы, выделяется также 27-дневный период и период, равный трети года. Остальные максимумы (18.5, 14 и 9 дней) статистически малозначимы. В спектре аномалии $X{\text{'}}(K)$ (рис. 1б, серая линия) выделяется лишь суточный цикл. Максимумы в районе 7 и 5.5 сут, по-видимому, являются артефактами осреднения. Средняя по всем данным амплитуда аномалии $X{\text{'}}(K)$ в единицах TECU показана на рис. 1а. Она естественным образом вызывается суточным ходом солнечной радиации.

Перейдем теперь к анализу результатов, полученных с помощью вычисления характеристик $msd\left( {J,l} \right)$ (т.е. среднего расстояния между ансамблем наблюдений и аналогов вычисленного по формуле (5)). На рисунке 2а показано отношение среднего расстояния между ансамблем наблюдений и ансамблем аналогов через 6 ч и в начальный момент $msd{{\left( {6{\text{Hr}},l} \right)} \mathord{\left/ {\vphantom {{\left( {6{\text{Hr}},l} \right)} {msd\left( {0{\text{Hr}},l} \right)}}} \right. \kern-0em} {msd\left( {0{\text{Hr}},l} \right)}},$ характеризующее величину роста ошибок шестичасового прогноза. Хорошо видна та же самая структура, что и на рис. 2а, что свидетельствует о том, что в первые часы основным фактором роста аномалий является непосредственное солнечное воздействие в светлое время суток в низких широтах. В следующие 12 ч рост аномалий происходит в высоких широтах (рис. 2б, $msd{{\left( {18{\text{Hr}},l} \right)} \mathord{\left/ {\vphantom {{\left( {18{\text{Hr}},l} \right)} {msd\left( {6{\text{Hr}},l} \right)}}} \right. \kern-0em} {msd\left( {6{\text{Hr}},l} \right)}}$), что может быть связано как с распространением аномалий из экваториальной зоны, так и влиянием аномальной солнечной или геомагнитной активности. На рисунке 2в показано распределение времени J (в часах), при котором значение $msd\left( {J,l} \right)$ становится большим, чем пороговое (0.6). Видно, что в среднем (по всем годам, сезонам, датам и т.п.) наибольшей предсказуемостью обладают средние широты, где в некоторых районах прогноз аномалии TEC относительно недельной средней может сохранять информативность чуть более суток. Наименее предсказуемы экваториальная зона и высокие широты с характерным временем предсказуемости в 6–12 ч.

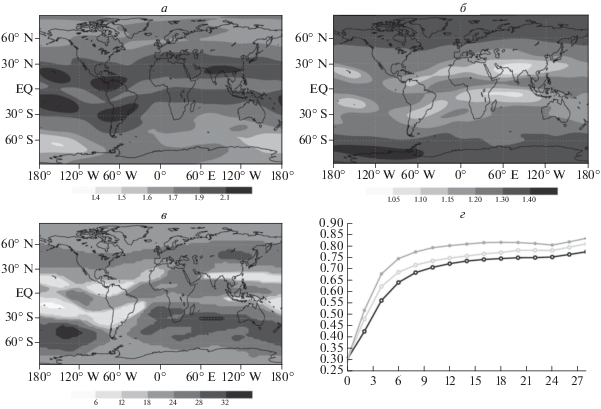
Представляет интерес оценить предсказуемость TEC для сезонов высокой и низкой солнечной активности. Для этого необходимо повторить расчеты, используя данные для соответствующих периодов времени. На рисунке 2г показана эволюция интегрального расстояния между ансамблем данных и ансамблем “аналогов” ${\mathbf{msd}}(J)$ (формула (4)) в зависимости от времени J, полученная для 2001–2003 гг. (обозначена черным цветом), 2013–2015 гг. (светло-серый) и 2007–2009 гг. (темно-серый). Из рисунка 2г следует, что структура двумерного поля аномалии TEC предсказуема в течение 4–8 ч, причем предсказуемость выше в годы с сильной солнечной активностью. В данном случае ситуация является обратной по отношению к практике прогнозирования медианных значений TEC (см., например, [Лещинская и Михайлов, 2016]), когда более предсказуемыми являются годы со слабой солнечной активностью.

Рассмотрим теперь географическую структуру отношения расстояний между ансамблями для различных сезонов и пятилетий. На рисунках 3 и 4 показано отношение $msd{{\left( {4{\text{Hr}},l} \right)} \mathord{\left/ {\vphantom {{\left( {4{\text{Hr}},l} \right)} {msd\left( {0{\text{Hr}},l} \right)}}} \right. \kern-0em} {msd\left( {0{\text{Hr}},l} \right)}}$ для ноября–марта (рис. 3) и мая–сентября (рис. 4) для каждого из пятилетий 1999–2003 гг., 2000–2004 гг., …, 2012–2016 гг. Снова можно заключить, что наименьшая предсказуемость характерна для периодов низкой солнечной активности, причем для летних полушарий.

3. ЭМПИРИЧЕСКИЙ ПРОГНОЗ С ПОМОЩЬЮ ПОСТРОЕНИЯ ОБРАТНОЙ ЛИНЕЙНОЙ МОДЕЛИ (LIM)

Недостатком предыдущей методологии является необходимость использования длинных рядов данных, поскольку требуется обеспечить близость пар “аналогов”. Кроме того, метод не позволяет оценивать предсказуемость, обусловленную сигналом от среднего состояния возмущенного ансамбля (ансамбль “аналогов” строится по данным равновесной траектории и имеет близкую к нулю аномалию среднего). Наконец, в результате вычислений определяется время предсказуемости, среднее по всем возможным состояниям; при этом предсказуемость системы для разных начальных условий может существенно отличаться. Обычно, для уточнения полученных результатов прибегают к прямому численному моделированию исходной системы с помощью численной модели, с хорошей точностью аппроксимирующей поведение реальной системы. В случае моделирования ионосферы это не представляется в настоящий момент возможным: качество динамических моделей пока недостаточно высоко [Fuller-Rowell et al., 2011; Pedatella et al., 2016] поэтому приходится использовать эмпирические модели – модели, аппроксимирующие реальность в статистическом смысле. В настоящей работе для построения прогностической системы предлагается использовать эмпирический подход, предложенный в работах [Penland and Sareshmukh, 1995; Penland, 1996] для задач описания динамики атмосферы и носящий название “линейная обратная модель” от “linear inverse model”, или сокращенно LIM. Методика основана на предположении, что эволюцию исходной нелинейной системы можно приблизить с помощью линейной динамико-стохастической модели вида

где матрица $B(t)$ является периодической по времени ($B\left( {t + {\Delta }} \right) = B(t))\quad$ с периодом Δ = 1 сут. Здесь и далее будет предполагаться, что матрица $B(t)$ устойчива по Ляпунову (все действительные части ее собственных значений строго отрицательны) для всех значений времени. Зависящий от времени форсинг в правой части представляет собой белый шум по времени с не зависящей от времени ковариационной матрицей. Среднее состояние исходной системы предполагается нулевым (в случае ненулевого среднего задача рассматривается в отклонениях).

Решение этого уравнения для начального значения ${\mathbf{x}}\left( {{{t}_{0}}} \right) = {{{\mathbf{x}}}_{0}},$ усредненное по ансамблю реализаций, выглядит как

Матричная экспонента в этом выражении подразумевается упорядоченной по времени: матрицы $B(\tau )$ не коммутируют друг с другом. Аналогичное выражение справедливо и для ковариационной матрицы системы с запаздыванием:

где $С \left( {t,{{t}_{0}}} \right) = \left\langle {{\mathbf{x}}\left( {t,{{t}_{0}}} \right){{{[{\mathbf{x}}\left( {{{t}_{0}}} \right)]}}^{T}}} \right\rangle .$ Из выражений (7, 8) следует, что матрица линейной системы и ее разрешающий оператор (матричная экспонента) могут быть вычислены по данным наблюдений (моделирования) исходной системы. Для этого необходимо подставить в уравнение (8) ковариационные матрицы ${\Xi }\left( {t,{{t}_{0}}} \right)$ и ${\Xi }\left( {{{t}_{0}},{{t}_{0}}} \right),$ вычисленные для данных наблюдений согласно выражению (2), и определить соответствующую матричную экспоненту. Везде далее будет предполагаться, что рассматриваемая нами система является циклически стационарной, а именно, что ковариационные матрицы ${\Xi }\left( {t,{{t}_{0}}} \right)$ и ${\Xi }\left( {{{t}_{0}},{{t}_{0}}} \right)$ зависят лишь от времени суток, т.е. ${\Xi }\left( {{{t}_{0}},{{t}_{0}}} \right)$ = ${\Xi }\left( {{{t}_{0}} + \Delta ,{{t}_{0}} + \Delta } \right),$ $\quad\forall {{t}_{0}} \in \left[ {0,\Delta } \right]$ и ${{t}_{0}}$ можно считать принимающим значения внутри суточного интервала. Тогда

Формула (9) будет использована далее для построения прогнозов. Вектор состояния ${\mathbf{x}}\left( {t,{{t}_{0}}} \right)$ в нашем случае это, как и в разделе 2, – поле аномалии TEC, к которой вновь применяется процедура понижения размерности с помощью проецирования в базис ведущих ЕОФ (3). Это необходимо для того, чтобы корректно вычислять обратные ковариационные матрицы в выражении (9). Согласно (3)

Здесь, как и в разделе 2, ${\mathbf{z}}\left( {{{t}_{0}}} \right) = {\Psi }{{({{t}_{0}})}^{T}}{\mathbf{x}}\left( {{{t}_{0}}} \right)$ и ${{{\mathbf{z}}}_{0}} = {\Psi }{{({{t}_{0}})}^{T}}{{{\mathbf{x}}}_{0}}\quad$ это вектор аномалии и начальное состояние, спроектированные в базис ведущих ЕОФ. В результате, с учетом процедуры понижения размерности, прогноз аномалии TEC для заданного начального условия ${{{\mathbf{x}}}_{0}}$ и заданного времени дается выражением

Поскольку набор данных имеет разрешение 2 ч, то ${{t}_{0}} = 0,\quad2,\quad4, \ldots ,\quad22\quad{\text{GMT,}}$ $t = {{t}_{0}} + J\delta t,$ $\quad\delta t = 2$ ч. Для каждого значения ${{t}_{0}}$ мы вычисляем разложение (3), проектируем набор данных и начальную аномалию в пространство ведущих ЕОФ и определяем прогноз по формуле (11). В отличие от раздела 2 здесь мы используем 40 компонент проекции, что необходимо для более точной аппроксимации начального условия. В результате вычислений для каждой даты в диапазоне от 00:00 GMT 01.01.1999 г. до 22:00 GMT 31.12.2016 г. мы получаем прогнозы аномалии TEC на 2, 4, 6, 8, … 24 ч, которые сравниваем с наблюденными значениями. Рассмотрим результаты анализа сделанных прогнозов.

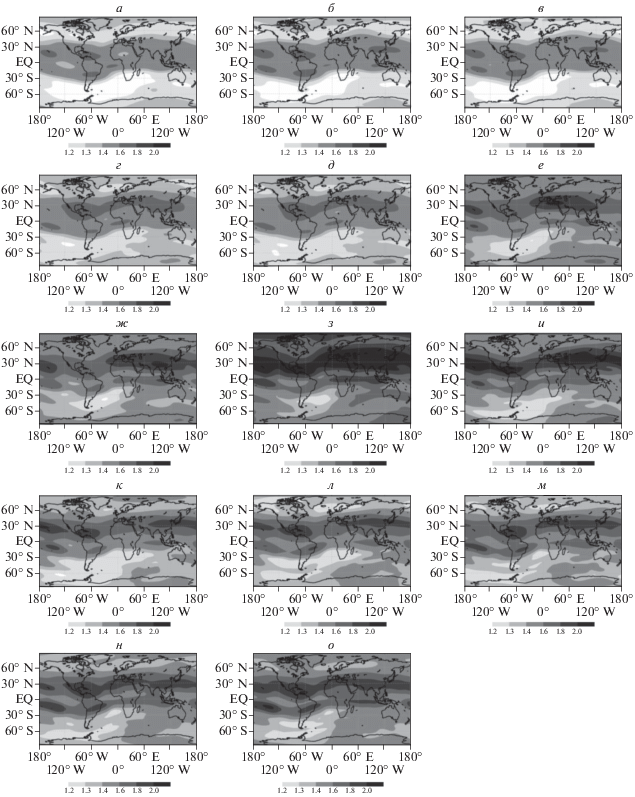
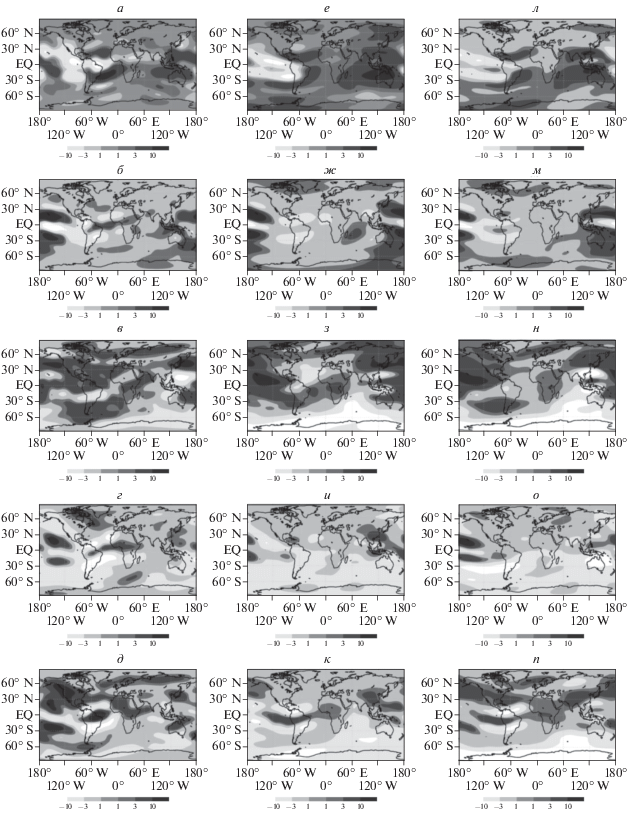
На рисунке 5 представлен пример прогноза аномалии TEC на 4 ч, сделанный в 00:00 GMT 20, 21, 22, 23 и 24.12.2014 г. В левом столбце показана аномалия в 00:00 GMT, в среднем – ее реальная величина через 4 ч, в правом – прогноз по формуле (11). Прогноз по формуле (11) систематически занижает амплитуду решения, поэтому все прогностические поля (правая колонка рис. 5) умножена на 1.4. В отличие от нормы решения, пространственная структура воспроизводится достаточно хорошо. Пространственные корреляции для сделанных прогнозов равны 0.86, 0.80, 0.83, 0.72 и 0.75 соответственно. Следует заметить, что геомагнитные условия, соответствующие рассмотренным начальным условиям, различны. Так, 20 и 21 декабря значение индекса ap равнялось 12, 22 декабря достигло значения 48, 23 декабря упало до 3, а 24 декабря вернулось к значению 27. При этом индекс F10.7 превышал значение 200 в течение 3 дней: 19–21.12. Обращает на себя внимание тот факт, что ярко выраженной корреляции между качеством краткосрочного прогноза и характеристиками геомагнитной и солнечной активности не наблюдается, однако корреляции выше для сильных откликов (см. первая и третья строчки рис. 5, соответствующие 20.12 и 22.12).

Рассмотрим далее статистику прогнозов за весь архив наблюдений. На рисунке 6а показаны средние корреляции между прогнозами и реальными значениями для каждого сезона (зима, весна, лето, осень) каждого года (с 1999 по 2016 г.). Кривая, соответствующая летним месяцам, показана светло-серым цветом, зимним – черным, весенним – серым, а осенним – темно-серым. Таким образом, прогнозы для осени, зимы и весны примерно одного качества, успешность прогнозов для летних месяцев ниже. В годы высокой солнечной активности прогнозы более успешны.

Зависимость успешности прогнозов от времени суток показана на рис. 6б. Разными оттенками серого цвета выделены прогнозы для разных сезонов (так же, как и на рис. 6а). Можно сделать вывод, что зависимость качества прогноза от времени суток слабая, аномалия TEC в летние месяцы предсказывается хуже.

На рисунке 6в представлены зависимости корреляций между прогнозами и наблюдениями от заблаговременности прогноза. Черная сплошная кривая соответствует зиме 2015 г., черная пунктирная – зиме 2009 г., сплошная серая – лету 2015 г., серая пунктирная – лету 2009 г. Снова видно, что в летние месяцы в годы низкой солнечной активности предсказуемость аномалий минимальна. В целом, 10 часов является пределом предсказуемости для данной модели.

На рисунке 6г рассматривается предсказуемость для случаев, когда амплитуда аномалии сильная (превышает на 10% среднюю величину, темно-серая кривая), слабая (меньше 90% от средней, светло-серая кривая). Расчет проведен для зимы 2014 г. Среднее значение корреляций для всех случаев показано черным. Основной вывод из данного сравнения заключается в том, что для сильных аномалий предсказуемость выше.

4. ЗАКЛЮЧЕНИЕ

В работе рассмотрена возможность оценить потенциальную предсказуемость (предельное время предсказуемости и наиболее предсказуемые пространственные структуры) поля аномалии TEC относительно недельной средней на часовых интервалах времени по данным наблюдений. Для этого используется метод аналогов – поиск пар близких наблюдений и оценка изменения расстояния между последующими измерениями. Полученные результаты уточняются и верифицируются с помощью простейшей эмпирической прогностической модели, так называемой модели LIM – Linear Inverse Model, основанной на регрессионном подходе.

Проведенные расчеты показывают следующее.

– На временны́х интервалах от 2 до 12 ч поле аномалии TEC наиболее предсказуемо в зимнем полушарии для периодов сильной солнечной активности.

– Основной процесс, отвечающий за потерю предсказуемости, – прямое солнечное воздействие.

– Геомагнитная активность и создаваемые ей аномалии увеличивают предсказуемость в системе, эволюция наиболее сильных аномалий лучше всего предсказывается. Типичная ситуация здесь – это аномальная солнечная активность с высоким значением индекса F10.7, высокий индекс геомагнитной активности и сильная аномалия TEC в полярной области с некоторым временны́м лагом, высокая предсказуемость в последующие несколько часов–дней.

– Худшая предсказуемость в летние месяцы связана с тем фактом, что летние аномалии TEC статистически самые слабые.

– Время потери предсказуемости составляет от 6 ч (в летние месяцы периодов слабой активности) до 12 ч (осенью, зимой, весной в годы высокой солнечной активности).

– Описанные выше результаты являются обратными по отношению к задаче прогнозирования медианных значений TEC на масштабах порядка месяца [Лещинская и Михайлов, 2016], когда наилучший прогноз дается для летних месяцев со слабой солнечной активностью. Причина, по-видимому, заключается в том, что на более длинных масштабах плохо предсказуемые геомагнитные аномалии являются фактором потери предсказуемости. На часовых же масштабах они не успевают значительно менять поле электронной концентрации и портить его прогноз (во всяком случае, в статистическом смысле). Это подтверждается тем фактом, что качество прогноза слабо зависит от короткопериодных (несколько часов) вариаций индекса ap.

Работа выполнена в ИВМ РАН при поддержке РНФ, грант № 17-17-01305.