Геомагнетизм и аэрономия, 2019, T. 59, № 2, стр. 236-248

1. ВВЕДЕНИЕ

Движение проводящей морской среды в волне цунами в геомагнитном поле приводит к появлению электрического тока и, соответственно, к геомагнитным возмущениям. В работе [Toh et al., 2011] приведены результаты регистрации геомагнитных вариаций, связанных с прохождением волны цунами от двух землетрясений в районе Курильских о-вов 15.11.2006 г. и 13.01.2007 г. Эти данные дали возможность определить направление распространения волны цунами. Амплитуда горизонтальной компоненты геомагнитного возмущения изменяла знак на противоположенный для стадий роста и спада волны. Электромагнитные поля, генерируемые движением морской среды, могут регистрироваться на поверхности земли и на океанском дне. В работе [Manoj and Maus, 2011] приведены данные регистрации геомагнитных возмущений, сопровождающих цунами, которое возникло в результате сильного землетрясения в Чили 27.02.2010 г. Измерения, проведенные на расстоянии 3500 км на запад от эпицентра, обнаружили периодический сигнал амплитудой 1 нТл, совпадающий по времени c приходом волны цунами. В работе [Zhang et al., 2014] представлено численное моделирование возмущений магнитного поля, возникающих в результате приливных течений и волн цунами. Проведено сопоставление модели с результатами наблюдений. Wang and Liu [2013] исследовали магнитные аномалии, индуцированные волнами цунами в океане. Проведенный анализ показал, что волна цунами высотой в 1 м сопровождается возмущением магнитного поля амплитудой 10 нТл на поверхности океана. Его амплитуда зависит как от параметров волны, так и от ориентации магнитного поля Земли.

Впервые в работе [Peltier and Hines, 1976] обсуждается возможность регистрации цунами с использованием методов мониторинга ионосферных возмущений. Воздействие на ионосферу осуществляется акустико-гравитационной волной (АГВ), которая распространяется вверх в атмосфере от поверхности океана до высот ионосферы. Artru et al. [2005] получили изображение возмущения ионосферы с помощью метода ионосферного зондирования, основанного на использовании сети GPS-приемников. Было показано, что возмущение ионосферы связано с волной цунами, которая достигла побережья Японии через 22 ч после землетрясения в Перу 23 июня 2001 г. Характеристики распространения внутренних гравитационных волн, генерируемых цунами, в нейтральной атмосфере и их взаимодействие с ионосферной плазмой рассмотрены в работе [Occhipinti et al., 2008]. Проанализирована роль геомагнитного поля во взаимодействии нейтральной и ионизованной компонент ионосферы в экваториальной и среднеширотной ее областях. Hickey et al. [2009] провели численное моделирование спектральных характеристик АГВ и их взаимодействие с F-областью ионосферы. Полученные результаты использованы для интерпретации связанных с цунами возмущений плотности электронов в F-области ионосферы и полного электронного содержания. Характерная скорость распространения возмущений и их горизонтальный пространственный масштаб составляют 200 м/с и 400 км соответственно. Результаты наблюдения возмущений ионосферы после землетрясений 2006 г. на Курильских о-вах, 2009 г. на о-ве Самоа и 2010 г. в Чили обсуждались в работе [Rolland et al., 2010]. Анализировались данные вариаций полного электронного содержания, полученные с помощью сети GPS-приемников, расположенных на Гавайских о-вах. Обнаружены возмущения ионосферы, сопровождающие предположительно смещение уровня морской среды волной цунами. Возмущения обусловлены распространением гравитационной волны в ионосфере со скоростью, направлением и временем ее прихода, коррелируемым с цунами. Galvan et al. [2012] провели наблюдения возмущений ионосферы, возникающих во время землетрясения и цунами в Тохоку 11 марта 2011 г. Зарегистрированы возмущения полного электронного содержания с использованием сети GPS-приемников в Японии. Обнаружены движущиеся ионосферные возмущения в направлении от эпицентра со скоростями 3400 м/с, 1000 м/с и 200–300 м/с. В работах [Ma et al., 2015; Wei et al., 2015] изучаются внутренние акустико-гравитационные волны в атмосфере, генерируемые волнами цунами, с использованием модельных и численных методов. Рассмотрено влияние электрического динамо-поля в ионосфере на плотность электронов и полное электронное содержание в присутствии АГВ. Coïsson et al. [2015] получили данные наблюдения возмущения ионосферы над Тихим океаном, возможно связанного с цунами у побережья Tohoku. Цунами возникло после землетрясения 11 марта 2011 г. Данные получены с помощью спутниковой системы мониторинга. Анализ данных регистрации возмущения полного электронного содержания ионосферы показал, что характерная вертикальная длина волны составляла 50 км, а область возмущения охватывала интервал высот порядка 200 км.

Авторы приведенных выше работ полагают, что распространение волны цунами сопровождается генерацией АГВ и значительным возмущением ионосферы. Сорокин и Федорович [1982] показали, что возмущение состояния ионосферы в результате движения ионосферной плазмы в геомагнитном поле или изменения ее ионизации в зоне протекания ионосферных токов, сопровождается вариациями геомагнитного поля. Следовательно, волна цунами генерирует возмущение геомагнитного поля, которое формируется не только электрическим током в морской среде, но и током в ионосфере. Электрический ток в морской среде возникает под действием ее движения в волне цунами в геомагнитном поле. Электрический ток в ионосфере возникает в результате ее движения в АГВ в геомагнитном поле. Эта волна генерируется вертикальным смещением поверхности морской среды в результате распространения волны цунами. Далее, АГВ распространяется в атмосфере вверх в ионосферу. Амплитуда электрического тока как в морской среде, так и в ионосфере пропорциональна произведению проводимости и скорости движения каждой из этих сред. Несмотря на то, что проводимость морской среды на три-четыре порядка превышает проводимость ионосферы, скорость движения проводящей ионосферы на три-четыре порядка превышает скорость движения морской среды в волне цунами. Это обусловлено экспоненциальным ростом скорости газа в АГВ в процессе ее распространения вверх. Как будет показано ниже, величина плотности тока в ионосфере сравнима или больше величины плотности тока в морской среде. Кроме того, возможно взаимодействие токов в результате взаимной индукции проводящей ионосферы и морской среды. В работе анализируются отмеченные выше механизмы формирования возмущения геомагнитного поля. Для проведения оценок вклада каждого механизма в амплитуду возмущения использована модель среды с вертикальным магнитным полем. В рамках такой модели возможно получить менее громоздкие выражения, которые позволяют наглядно проанализировать каждый механизм генерации и сравнить его эффективность, а также понять влияние параметров среды на формирование сигнала.

2. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Рассмотрим модель генерации геомагнитных возмущений волной цунами, схема формирования токов в которой приведена на рис. 1. В левой части рисунка показаны токи в морской среде и в ионосфере, которые с помощью продольного тока связаны с током в сопряженной ионосфере в правой части рисунка. Введем правостороннюю декартову систему координат с осью z, направленной вертикально вверх. Ось $x$ совпадает с направлением распространения волны цунами. Начало координат расположим на поверхности морской среды. Геомагнитное поле ${{{\mathbf{B}}}_{0}}$ направлено вертикально вверх. В слое $ - h < z < 0$ расположена морская среда, проводимость которой ${{\sigma }_{w}}$ не зависит от глубины. На высоте $z = {{z}_{1}}$ расположен максимум тонкого проводящего слоя ионосферы, проводимость которой характеризуется тензором проводимости $\hat {\sigma }.$ Выше ионосферы расположена магнитосфера, в которой проводимости поперек магнитного поля равны нулю. Между морской средой и ионосферой расположена непроводящая атмосфера. В полупространстве ниже дна морской среды $z < - h$ расположены донные породы, проводимостью которых пренебрегаем по сравнению с проводимостью морской среды. Движение проводящей среды в геомагнитном поле приводит к генерации электрического тока с плотностью ${\mathbf{j}}$ и возмущению магнитного поля ${\mathbf{b}} = {\mathbf{B}} - {{{\mathbf{B}}}_{0}}.$ Электрическое поле ${\mathbf{E}}$ и возмущение магнитного поля ${\mathbf{b}}$ определяются из системы уравнений Максвелла, в которых пренебрегается током смещения по сравнению с током проводимости ${\mathbf{j}}{\text{:}}$

где ${{\mu }_{0}}$ − магнитная постоянная, а плотность тока проводимости ${\mathbf{j}}$ определяется из закона Ома для движущихся сред. Так как возмущение магнитного поля мало $b \ll B,$ то в морской среде ток определяется законом Ома: где ${\mathbf{V}}\left( {{\mathbf{r}},t} \right)$ − поле скоростей жидкости в волне цунами. Рассмотрим возмущение электромагнитного поля, генерируемое волной цунами, распространяющейся в плоскости $\left( {x,z} \right).$ Полагая ${\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}} = 0,$ получим уравнения для компоненты ${{E}_{y}}$ возмущения электрического поля в морской среде:

Величина скин-слоя в морской среде равна $\sqrt {{\tau \mathord{\left/ {\vphantom {\tau {2\pi {{\mu }_{0}}{{\sigma }_{w}}}}} \right. \kern-0em} {2\pi {{\mu }_{0}}{{\sigma }_{w}}}}} \approx 10$ км, что значительно превышает ее глубину. Для оценки использовано значение периода изменения электрического поля $\tau \approx 10$ мин, совпадающее с периодом волны цунами, и выбрано значение проводимости ${{\sigma }_{w}} = 3\,\,{{{\text{С м }}} \mathord{\left/ {\vphantom {{{\text{С м }}} {\text{м }}}} \right. \kern-0em} {\text{м }}}$ морской среды. Следовательно, электрическое поле в морской среде мало меняется в зависимости от ее глубины. Кроме того, горизонтальная компонента скорости в волне цунами практически постоянна по глубине морской среды. Это позволяет проинтегрировать уравнение (3) по высоте при условии ${{\sigma }_{w}}h = {\text{const}};h \to 0$ и получить граничное условие для компоненты ${{E}_{y}}$ при переходе через тонкий проводящий слой морской среды. В результате получим:

где ${{\Sigma }_{w}} = {{\sigma }_{w}}h$ − интегральная проводимость морской среды, а фигурными скобками $\left\{ {...} \right\}$ обозначена разность значения величины на верхней и нижней границах проводящего слоя.

Рассмотрим поле в ионосфере, генерируемое АГВ в результате ее распространения вверх от возмущенной волной цунами поверхности морской среды. Закон Ома в ионосфере имеет вид:

где ${{\sigma }_{P}}_{{,H}},{{\sigma }_{{11}}}$ − проводимости Педерсена, Холла и продольная проводимость ионосферной плазмы; ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ − скорость газа в АГВ, распространяющейся из атмосферы. Т.к. в ионосфере ${{\sigma }_{{11}}} \gg {{\sigma }_{{P,H}}},$ то устремляя в (5) ${{\sigma }_{{11}}} \to \infty ,$ получим ${{E}_{z}} = 0.$ Подставляя закон Ома (5) в уравнения Максвелла (1) получим уравнение горизонтальной компоненты электрического поля в ионосфере:

Будем полагать, что проводимости σ_P и σ_H отличны от нуля в слое нижней ионосферы толщиной ~30 км, достигая максимума на высоте ~120 км. Полагая значения проводимости ионосферы равными ${{\sigma }_{{P,H}}} \approx 3 \times {{10}^{{ - 4}}}$ См/м, получим величину скин-слоя $\sqrt {{\tau \mathord{\left/ {\vphantom {\tau {2\pi {{\mu }_{0}}{{\sigma }_{{P,H}}}}}} \right. \kern-0em} {2\pi {{\mu }_{0}}{{\sigma }_{{P,H}}}}}} \approx {{10}^{3}}$ км, которая значительно превышает толщину проводящего слоя. Следовательно, горизонтальная компонента поля не меняется в вертикальном направлении внутри проводящего слоя. Это позволяет заменить уравнение (6) граничными условиями при переходе через проводящий слой ионосферы путем его интегрирования по вертикальной координате. Формально высотную зависимость проводимости можно заменить δ-функцией в точке ее максимума. Введем интегральные проводимости Педерсена и Холла по формулам:

Подставляя это равенство в уравнение (6) и интегрируя по z, получим граничное условие на тонком проводящем слое ионосферы:

В равенстве (7) исключим компоненту ${{E}_{x}},$ воспользовавшись уравнением непрерывности тока в ионосфере $\nabla \cdot {\mathbf{j}} = 0.$ Проинтегрируем это равенство по толщине проводящего слоя ионосферы:

где ${{j}_{{11}}} = {{j}_{z}}({{z}_{1}} + 0)$ − продольный ток, протекающий из ионосферы вверх в магнитосферу, а ток на нижней границе ионосферы равен нулю ${{j}_{z}}({{z}_{1}} - 0) = 0.$ Вследствие высокой проводимости магнитосферы вдоль силовых линий геомагнитного поля, продольный ток в магнитосфере протекает вдоль магнитных силовых линий и замыкается на проводящем слое сопряженной ионосферы, как показано на рис. 1. В квазистатическом приближении электрическое поле в верхней ионосфере и магнитосфере определяется из второго уравнения системы (1) $\nabla \times \left( {\nabla \times {\mathbf{E}}} \right) = 0,$ компоненты которого имеют вид:

Из этих уравнений следует, что компонента ${{E}_{x}}$ переносится вдоль силовых линий геомагнитного поля без изменения в сопряженную ионосферу, а компонента ${{E}_{y}}$ убывает вверх на расстояниях от ионосферы порядка горизонтального масштаба цунами. Так как этот масштаб составляет сотни километров, то компонента ${{E}_{y}}$ не достигает сопряженной ионосферы. Свойства компоненты ${{E}_{x}}$ в магнитосфере определяются квазистационарным пределом направляемой альвеновской волны, а свойства компоненты ${{E}_{y}}$ определяются квазистационарным пределом магнитозвуковой волны. Запишем уравнение (8) в сопряженной ионосфере, в которую продольный ток переносится без изменения:

Складывая и вычитая уравнения (8) и (9), получим:

Подставляя первую из формул (10) в граничное условие на ионосфере (7), и полагая зависимость компонент поля от x и t в виде $\exp \left( {ikx - i\omega t} \right),$ преобразуем граничные условия (4) и (7) для компоненты поля ${{E}_{y}}$ в морской среде и в ионосфере:

Электрическое поле в атмосфере и ниже морской среды в земле определяется уравнениями (1), в которых ${\mathbf{j}} = 0.$ В верхней ионосфере в магнитосфере электрическое поле определяется уравнениями (1) и (5), в которых ${\mathbf{v}} = 0$ и компоненты тензора проводимости ${{\sigma }_{P}} = {{\sigma }_{H}} = 0.$ Для компоненты ${{E}_{y}}$ в трех средах имеем уравнение:

Решение этого уравнения имеет вид:

где ${{c}_{{1...4}}}$ − произвольные константы, которые определяются подстановкой решений в граничные условия (11). Компоненты возмущения магнитного поля определяется из второго уравнения системы (1):

Определяя константы, получим выражения для компонент возмущения магнитного поля в слое $0 < z < {{z}_{1}}$ атмосферы в виде:

где ${{\text{v}}_{x}}(k,\omega ,{{z}_{1}})$ − горизонтальная скорость газа в АГВ на высоте ионосферы; ${{V}_{x}}(k,\omega )$ − горизонтальная компонента скорости морской среды в волне цунами. В равенствах (12) введены обозначения: где знак (−) соответствует x-компоненте, а знак (+) соответствует z-компоненте. Положив в равенствах (12) ${{\Sigma }_{с }} = 0;{{c}_{i}} \to \infty $ найдем выражение компоненты возмущения магнитного поля, генерируемого волной цунами без влияния ионосферы:

Это выражение совпадает с равенством, полученным в работе [Wang and Liu, 2013], в которой рассматривался механизм генерации возмущений магнитного поля волной цунами.

Рассмотрим возмущение геомагнитного поля в верхней ионосфере и магнитосфере, возникающее в результате распространения волны цунами в морской среде. Возникновение этого возмущения связано с генерацией поперечных токов и продольного тока в ионосфере движением нейтральной компоненты. Механизм формирования продольного тока в процессе движения нейтральной компоненты ионосферы рассматривался в работе [Pokhotelov et al., 1999]. В представленной выше модели гидродинамического возмущения генерируется акустическая ветвь АГВ. Эта ветвь генерирует продольный ток, который пропорционален интегральной проводимости Холла ${{\Sigma }_{H}}$ ионосферы. В области высот $z > {{z}_{1}}$ из первого уравнения системы (1) имеем:

Как будет показано ниже, в ионосфере справедливо неравенство ${{E}_{y}} \ll {{E}_{x}}.$ Следовательно, в формулах (10) можно пренебречь величиной компоненты ${{E}_{y}}{\text{:}}$

Следует заметить, что формула (14) получена для частной модели, рассматриваемой в статье. В более общем случае дополнительный вклад в продольный ток дает гравитационная ветвь АГВ, связанная с проводимостью Педерсена (см. [Pokhotelov et al., 1999]). Из равенств (13) и (14) получим пространственно-временнóе распределение амплитуды возмущения геомагнитного и электрического поля в верхней ионосфере и магнитосфере:

Из равенств (15) следует, что возмущение геомагнитного поля и электрическое поле в области высот $z > {{z}_{1}}$ генерируются преимущественно движением газа в проводящем слое нижней ионосферы.

3. ГЕНЕРАЦИЯ АКУСТИКО-ГРАВИТАЦИОННОЙ ВОЛНЫ

Рассмотрим генерацию и распространение АГВ в атмосфере, генерируемой поднятием поверхности воды в крупномасштабной волне цунами, распространяющейся в океане. Уравнение, определяющее скорость газа ${\mathbf{v}}\left( {{\mathbf{r}},t} \right)$ в АГВ, распространяющейся в слоисто-неоднородной изотермической атмосфере, в линейном приближении и в отсутствие ветра, имеет вид [Nappo, 2002; Гершман, 1974]:

где $\gamma = 1.4$ − показатель адиабаты; c = $\sqrt {{{{\gamma }p} \mathord{\left/ {\vphantom {{{\gamma }p} \rho }} \right. \kern-0em} \rho }} $ = = const − скорость звука; $p,\rho $ − давление и плотность атмосферы; ${\mathbf{g}} = - g\,{{{\mathbf{e}}}_{z}}$ − ускорение свободного падения. Из (16) следуют уравнения, определяющие вертикальную и горизонтальную компоненты скорости для пространственно-временнóй зависимости вида $\exp \left( { - i\omega t + ikx} \right){\text{:}}$где $H = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{\gamma }g}}} \right. \kern-0em} {{\gamma }g}}$ − высота однородной атмосферы; ${{\omega }_{g}} = {{\sqrt {\left( {\gamma - 1} \right)} g} \mathord{\left/ {\vphantom {{\sqrt {\left( {\gamma - 1} \right)} g} с }} \right. \kern-0em} с }$ − частота Брента−Вяйсяля. Общее решение уравнения (17) имеет вид:

На поверхности морской среды $z = 0$ имеем $A + B = {{\text{v}}_{z}}\left( {k,0,\omega } \right),$ где ${{\text{v}}_{z}}\left( {k,0,\omega } \right)$ − вертикальная компонента скорости АГВ на поверхности морской среды. Константы $A,B$ в уравнении (18) определяются из условия положительности величины усредненного вертикального потока энергии АГВ. Это условие рассмотрено в Приложении. Согласно результатам, полученным в Приложении, решение (18) уравнений (17) для вертикальной и горизонтальной компонент скорости АГВ определяется формулой (A8) Приложения:

Вертикальная компонента скорости в АГВ на поверхности морской среды совпадает с вертикальной компонентой скорости жидкости на этой поверхности в волне цунами:

Выразим вертикальную и горизонтальную компоненты скорости в волне цунами на поверхности морской среды ${{V}_{x}}(k,0,\omega ),\;{{V}_{z}}(k,0,\omega )$ через ее смещение $\xi \left( {k,\omega } \right).$ Т.к. ${{V}_{z}}(x,z = 0,t) = {{\partial \xi (x,t)} \mathord{\left/ {\vphantom {{\partial \xi (x,t)} {\partial t}}} \right. \kern-0em} {\partial t}},$ то получим равенство: ${{V}_{z}}(k,0,\omega ) = - i\omega \xi (k,\omega ).$ Для определения горизонтальной компоненты скорости морской среды в волне цунами воспользуемся условием не сжимаемости $\nabla \cdot {\mathbf{V}} = 0,$ которое для компонент имеет вид: $ik{{V}_{x}}(k,z,\omega )$ = = $ - {{d{{V}_{z}}(k,z,\omega )} \mathord{\left/ {\vphantom {{d{{V}_{z}}(k,z,\omega )} {dz}}} \right. \kern-0em} {dz}}.$ В работе [Pelinovsky, 2006] показано, что в приближении мелкой воды $kh \ll 1$ и малых смещений поверхности ${\xi \mathord{\left/ {\vphantom {\xi {h \ll 1}}} \right. \kern-0em} {h \ll 1}}$ горизонтальная компонента скорости в волне цунами не меняется с глубиной. Следовательно, вертикальная компонента скорости зависит от глубины линейно ${{V}_{z}}\left( {k,z,\omega } \right) = {{V}_{z}}\left( {k,0,\omega } \right)\left( {{{1 + z} \mathord{\left/ {\vphantom {{1 + z} h}} \right. \kern-0em} h}} \right).$ В результате получим искомую связь компонент скорости в волне цунами со смещением поверхности морской среды:

Подставляя полученные соотношения (20) и (21) в равенства (19), получим выражение для горизонтальной компоненты скорости газа в АГВ в ионосфере на высоте $z = {{z}_{1}}{\text{:}}$

4. ГЕОМАГНИТНЫЕ ВОЗМУЩЕНИЯ, ГЕНЕРИРУЕМЫЕ ВОЛНОЙ ЦУНАМИ

Волны цунами представляют собой длинные поверхностные гравитационные волны $kh \ll 1,$ которые распространяются без дисперсии со скоростью $a = \sqrt {gh} .$ Пусть волна цунами распространяется в положительном направлении оси $x$. Выберем пространственно-временнýю зависимость вертикального смещения поверхности морской среды в волне $\xi = \xi \left( {x - at} \right)$ в виде:

Применяя Фурье-преобразование к этой формуле, получим:

где ${{\xi }_{0}}$ − максимальное вертикальное смещение поверхности морской среды в волне.

Для того чтобы получить пространственно-временнóе распределение скорости газа в АГВ, генерируемой волной цунами, подставим выражение (23) в формулы (19), (20), (21) и применим обратное Фурье-преобразование. Интегрируя по $\omega ,\,k$ с учетом выбора знака $q,$ получим:

Выражения (24) позволяют анализировать закономерности распространения АГВ в атмосфере. На рисунке 2 приведено распределение вертикальной компоненты скорости газа в вертикальной плоскости $(x,z)$ в момент времени $t = {x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a}.$ Расчет функции $W(x,z) = {{\text{v}}_{x}}(x,z)\exp \left( { - {z \mathord{\left/ {\vphantom {z {2H}}} \right. \kern-0em} {2H}}} \right)$ проведен с помощью формулы (24). Из графиков следует, что АГВ распространяется вверх в атмосфере над областью волны цунами. Ее амплитуда в ионосфере достигает значения порядка 10 м/с.

Рассмотрим возмущение магнитного поля в атмосфере. Подставим выражения (21), (22) и (23) в формулы (12) и применим обратное Фурье-преобразование. Далее, интегрируя по $\omega ,k$ с учетом выбора знака $q,$ получим пространственно-временнóе распределение компонент возмущения магнитного поля в слое атмосферы от поверхности морской среды до ионосферы:

Следует отметить, что в условиях земной атмосферы и морской среды всегда ${{1 - h} \mathord{\left/ {\vphantom {{1 - h} {\gamma H > 0}}} \right. \kern-0em} {\gamma H > 0}}.$ Это условие означает, что скорость волны цунами меньше скорости звука в атмосфере. Входящие в (25) функции ${{F}_{{i,w}}}\left( {k,ka,z} \right)$ и вертикальное волновое число $q\left( {k,ka} \right)$ имеют вид:

Приведем оценки величин в равенствах (26). Полагая ${{\Sigma }_{с }} = 10\;{\text{С м ,}}$ $h = {{10}^{3}}\;{\text{м ,}}$ получим ${{c}_{i}} \approx 2 \times {{10}^{5}}\;{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}}$ и $a \approx {{10}^{2}}\;{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}}{\text{.}}$ Следовательно, формулы (26) можно упростить, воспользовавшись неравенством ${{c}_{i}} \gg a{\text{:}}$

Подставляя равенства (27) в (25), получим формулы для расчета компонент возмущения геомагнитного поля в виде:

Из равенств (28) следует, что возмущение геомагнитного поля, генерируемого волной цунами в атмосфере, складывается из двух источников. Первый источник, определяемый функцией ${{\Phi }_{i}}(k,z)$ — это ток в ионосфере, который возникает при распространении в ней АГВ, а второй источник, определяемый функцией ${{\Phi }_{w}}(k,z)$ − это ток, который возникает при движении морской среды в волне цунами. Сравним их величины. Для оценки отношения величин токов в ионосфере и в морской среде выберем функцию ${{\Phi }_{i}}(k,z)$ в точке $z = {{z}_{1}},$ а функцию ${{\Phi }_{w}}(k,z)$ в точке $z = 0.$ Полагая ${{k \ll 1} \mathord{\left/ {\vphantom {{k \ll 1} {\sqrt {hH,} }}} \right. \kern-0em} {\sqrt {hH,} }}$ из (28) получим:

Положив ${{\Sigma }_{P}} = {{\Sigma }_{H}} = 10$ См, ${{\sigma }_{w}} = 4$ См/м, $h = 1$ км, ${{\Sigma }_{w}} = 4 \times {{10}^{3}}$ См, ${{z}_{1}} = 120$ км, $H = 8$ км, ${{\Sigma }_{c}} = 15$ См, получим:

Следовательно, амплитуды возмущений геомагнитного поля, генерируемые движением морской среды в волне цунами и движением ионосферы в АГВ, сравнимы по величине. Надо отметить, что для оценки выбрано значение интегральной проводимости в дневных условиях. В ночной ионосфере интегральная проводимость на порядок меньше и, следовательно, уменьшается вклад в наблюдаемое возмущение магнитного поля тока, протекающего в ионосфере. Положив ${{\Sigma }_{c}} = 0$ в (28), получим пространственно-временнóе распределение возмущения магнитного поля на поверхности морской среды без влияния ионосферы:

Расчеты амплитуд возмущений геомагнитного поля, генерируемого токами в ионосфере и в морской среде проведены по формулам (25). Для сравнения проведены расчеты по формуле (29) амплитуды возмущения геомагнитного поля, генерируемого током в морской среде без влияния ионосферы. Выбраны следующие значения параметров: ${{B}_{0}} = 5 \times {{10}^{{ - 5}}}$ Тл, ${{\sigma }_{w}} = 4$ См/м, максимальная амплитуда волны цунами ${{\xi }_{0}} = 0.5\;{\text{м ,}}$ скорость звука в атмосфере $с = 330\;{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}}{\text{,}}$ интегральные проводимости ионосферы ${{\Sigma }_{P}} = {{\Sigma }_{H}} = 10$ См, высота максимума проводящего слоя ионосферы ${{z}_{1}} = 120\,{\text{к м ,}}$ высота однородной атмосферы $H = 8\,\,{\text{к м }}{\text{.}}$ На рисунке 3 приведено пространственное распределение компонент возмущения геомагнитного поля на поверхности морской среды для различных ее глубин и различных горизонтальных масштабов волны цунами. Из графиков следует, что появление тока в ионосфере сохраняет характер зависимости амплитуд компонент возмущения геомагнитного поля от времени на поверхности морской среды. Однако с ростом горизонтального масштаба волны цунами и глубины морской среды ток в ионосфере увеличивает амплитуду возмущения в пять раз. На рисунке 4 приведено пространственное распределение компонент возмущения геомагнитного поля в ионосфере на высоте максимума проводимости 120 км для различных глубин морской среды и различных горизонтальных масштабов волны цунами. Из графиков следует, что учет тока в ионосфере приводит к увеличению амплитуды сигнала в четыре–пять раз. С увеличением горизонтального масштаба и глубины морской среды характер зависимости от времени амплитуды возмущения сохраняется. Однако с уменьшением этих параметров происходит качественное изменение временны́х характеристик сигналов. Именно, учет тока в ионосфере приводит к перемене знака горизонтальной компоненты возмущения геомагнитного поля по сравнению с однополярной временнóй зависимостью, в то время как вертикальная компонента возмущения становится однополярной. На рисунке 5 приведено пространственное распределение в вертикальной плоскости атмосферы компоненты возмущения геомагнитного поля, генерируемого волной цунами. Из рисунка следует, что учет тока в ионосфере приводит к принципиальному изменению высотной зависимости амплитуды возмущения в слое Земля – ионосфера. Ее величина достигает значения (1−10) нТл и не убывает с высотой.

В верхней ионосфере и магнитосфере отлична от нуля компонента возмущения геомагнитного поля ${{b}_{y}},$ которая генерируется АГВ согласно формуле (15). Подставляя (24) в (15), получим:

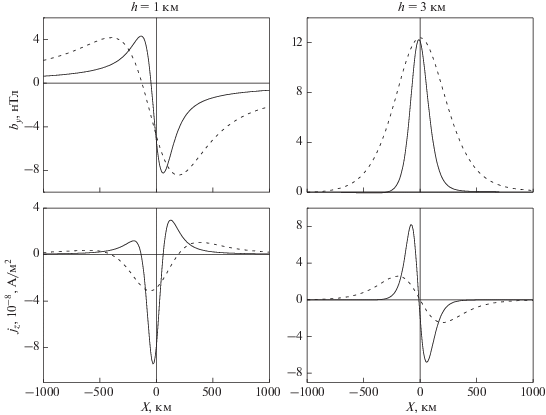
Формулы (30) позволяют рассчитать пространственно-временнóе распределение возмущения геомагнитного поля, электрического поля и продольного тока в верхней ионосфере и магнитосфере. На рисунке 6 приведены результаты расчета возмущения геомагнитного поля и продольного тока. Из графиков следует, что увеличение глубины морской среды приводит к росту горизонтального масштаба продольного тока и его магнитного поля. Амплитуда магнитного поля может достигать значений порядка 10 нТл, а амплитуда продольного тока достигает ${{j}_{{11}}} \approx 8 \times {{10}^{{ - 8}}}\;{{\text{А }} \mathord{\left/ {\vphantom {{\text{А }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}}.$

Приведем оценку величины компонент электрического поля в области $z > {{z}_{1}}.$ Из уравнения $\nabla \times {\mathbf{E}} = {{ - \partial {\mathbf{b}}} \mathord{\left/ {\vphantom {{ - \partial {\mathbf{b}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ и условия ${\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} = {{ - a\partial } \mathord{\left/ {\vphantom {{ - a\partial } {\partial x}}} \right. \kern-0em} {\partial x}}$ получим ${{E}_{y}} = a{{b}_{z}}.$ Из графиков следует, что на высотах ионосферы ${{b}_{z}}\sim (1{\kern 1pt} - {\kern 1pt} 10)\;{\text{н Т л }}{\text{.}}$ Полагая $a = 100$ м/с, получим ${{E}_{y}} \approx (0.1{\kern 1pt} - {\kern 1pt} 1.0)$ мкВ/м. Из графиков рис. 6 следует, что ${{b}_{y}} \approx 10$ нТл. Полагая ${{\Sigma }_{P}} \approx (1{\kern 1pt} - {\kern 1pt} 10)$ См, из (30) получим ${{E}_{x}} \approx (1{\kern 1pt} - {\kern 1pt} 10)$ мВ/м. Следовательно, в формулах (10) можно пренебречь величиной ${{E}_{y}} \ll {{E}_{x}}.$ Из (14) следует, что ${{E}_{y}} \approx 1\;{{{\text{м к В }}} \mathord{\left/ {\vphantom {{{\text{м к В }}} {\text{м }}}} \right. \kern-0em} {\text{м }}}{\text{,}}\,\,\,\,{{E}_{x}} \approx 10\;{{{\text{м В }}} \mathord{\left/ {\vphantom {{{\text{м В }}} {\text{м }}}} \right. \kern-0em} {\text{м }}}{\text{,}}$ ${{j}_{{11}}} \approx {{10}^{{ - 8}}}\;{{\text{А }} \mathord{\left/ {\vphantom {{\text{А }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}}.$ Следует отметить, что значение компоненты ${{E}_{x}}$ получается из электростатического приближения, а ${{E}_{y}}$ − генерируется индукционными эффектами и в электростатическом приближении обращается в нуль (${{E}_{y}} = {{ - \partial \varphi } \mathord{\left/ {\vphantom {{ - \partial \varphi } {\partial y}}} \right. \kern-0em} {\partial y}} \equiv 0$). Приведенные оценки показывают, что компонента ${{b}_{y}}$ магнитного поля продольного тока и компонента ${{E}_{x}}$ электрического поля в верхней ионосфере и магнитосфере, генерируемые движением волны цунами, вполне измеримы спутниковыми методами.

5. ЗАКЛЮЧЕНИЕ

При анализе данных регистрации возмущений геомагнитного поля, генерируемого волной цунами, как правило, полагают, что источником этого возмущения служит электрический ток, протекающий в морской среде в результате ее движения в волне цунами. В работе показано, что наряду с этим током источником возмущения геомагнитного поля является электрический ток в ионосфере. Ток в ионосфере возникает в результате падения на нее акустико-гравитационной волны, распространяющейся из атмосферы. Источником волны является вертикальное смещение поверхности морской среды во время распространения в ней волны цунами. Несмотря на то, что проводимость ионосферы значительно меньше проводимости морской среды, величина тока в ней может превышать величину тока в морской среде в результате экспоненциального роста амплитуды акустико-гравитационной волны в процессе ее распространения вверх. Максимальная амплитуда возмущения геомагнитного поля достигает значений (1–10) нТл. Эта оценка получена для дневной ионосферы. В ночной ионосфере интегральная проводимость уменьшается на порядок, что приводит к уменьшению вклада в наблюдаемый сигнал магнитного поля тока, генерируемого в ионосфере в результате падения на нее АГВ.

Наличие электрического тока в ионосфере значительно меняет характеристики возмущения геомагнитного поля, генерируемого волной цунами. Появление тока в ионосфере сохраняет характер зависимости амплитуд компонент возмущения геомагнитного поля от времени на поверхности морской среды. С ростом горизонтального масштаба волны цунами и глубины морской среды ток в ионосфере увеличивает амплитуду возмущения в пять раз. Учет тока в ионосфере приводит к увеличению амплитуды сигнала в четыре-пять раз на высотах ионосферы. С увеличением горизонтального масштаба и глубины морской среды характер зависимости от времени амплитуды возмущения сохраняется. Однако с уменьшением этих параметров происходит качественное изменение временны́х характеристик сигналов. Именно учет тока в ионосфере приводит к перемене знака горизонтальной компоненты возмущения геомагнитного поля по сравнению с однополярной временнóй зависимостью, в то время как вертикальная компонента возмущения становится однополярной. Кроме того, меняется высотная зависимость амплитуды возмущения в слое Земля–ионосфера. Ее величина достигает значения (1−10) нТл и не убывает с высотой.

В работе показано, что электрический ток в ионосфере, генерируемый волной цунами, замыкается на сопряженную ионосферу с помощью продольных токов. При этом в верхней ионосфере и магнитосфере возникают поперечные компоненты магнитного и электрического полей. Амплитуда магнитного поля и продольного тока могут достигать значений порядка 10 нТл и ${{10}^{{ - 8}}}\;{{\text{А }} \mathord{\left/ {\vphantom {{\text{А }} {{{{\text{м }}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{2}}}}}},$ а амплитуда электрического поля достигает величины 10 мВ/м. Увеличение глубины морской среды приводит к росту горизонтального масштаба продольного тока и его магнитного поля. Полученные значения амплитуд возмущения магнитного и электрического полей в верхней ионосфере и магнитосфере, генерируемые движением волны цунами, вполне измеримы спутниковыми методами. Это позволяет сделать вывод о возможности мониторинга волны цунами космическими методами.

ПРИЛОЖЕНИЕ A

Рассмотрим АГВ в атмосфере, генерируемую поднятием поверхности морской среды. Пусть горизонтальная и вертикальная компоненты скорости ${\mathbf{v}} = \left( {{{\text{v}}_{x}},0,{{\text{v}}_{z}}} \right)$ в АГВ, а также возмущение давления $p$ зависят от $x,t$ по гармоническому закону:

Величины, имеющие физический смысл, определяются действительными частями комплексных выражений (A1). Поток энергии волны определяется по формуле ${\mathbf{S}} = \operatorname{Re} \left( p \right)\operatorname{Re} \left( {\mathbf{v}} \right)$ [Yeh and Liu, 1974]. Т. к. энергия волны распространяется от ее источника, то усредненная по $x,t$ вертикальная компонента ${\mathbf{S}}$ должна быть положительной:

Возмущение давления в волне определяется из уравнения движения:

Из этого уравнения получим равенство:

где $\bar {\rho }$ − плотность воздуха на уровне моря. Подставляя равенство (A3) в (A2), получим зависимость вертикальной компоненты плотности потока энергии волны от компонент скорости:

Согласно формулам (17) и (18), зависимость компонент скорости в волне от высоты имеет вид:

Подставляя равенства (A5) в (A4), получим:

Источником АГВ является смещение поверхности морской среды волной цунами, которое двигается с фазовой скоростью ${\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k} = a$ вдоль оси $x.$ Подставляя $\omega = ka$ в знаменатель выражения (A6), получим ${{1 - {{\omega }^{2}}} \mathord{\left/ {\vphantom {{1 - {{\omega }^{2}}} {\left( {{{c}^{2}}{{k}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{c}^{2}}{{k}^{2}}} \right)}} = {{1 - {{a}^{2}}} \mathord{\left/ {\vphantom {{1 - {{a}^{2}}} {{{c}^{2}} > 0}}} \right. \kern-0em} {{{c}^{2}} > 0}}.$ Следовательно, выражение (A6) можно упростить:

Равенство (A7) позволяет получить условие, при котором вертикальная компонента плотности потока энергии положительна ${{S}_{z}} > 0{\text{:}}$

Отсюда следует, что условие излучения определяется только знаком $\omega $ и решение (18) уравнения (17) принимает вид: