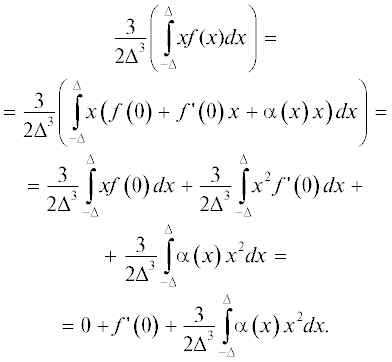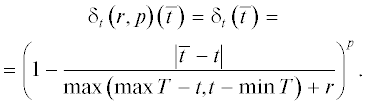1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 59, № 3, 2019

Геомагнетизм и аэрономия, 2019, T. 59, № 3, стр. 383-392

Регрессионные производные и их применение в изучении геомагнитных джерков

С. М. Агаян 1, А. А. Соловьев 1, 2, Ш. Р. Богоутдинов 1, 2, Ю. И. Николова 1, *

1 Геофизический центр РАН (ГЦ РАН)
г. Москва, Россия

2 Институт физики Земли им. О.Ю. Шмидта РАН (ИФЗ РАН)
г. Москва, Россия

* E-mail: j.zharkikh@gcras.ru

Поступила в редакцию 12.03.2018
После доработки 16.04.2018
Принята к публикации 27.09.2018

Полный текст (PDF)

Аннотация

Построены новые математические конструкции регрессионного сглаживания дискретных временны́х рядов, заданных на нерегулярной сетке. Разработанный метод использован для изучения трендов векового хода за период 1991–2015 гг. по данным наблюдений трех компонент магнитного поля на пяти выбранных геомагнитных обсерваториях сети ИНТЕРМАГНЕТ. Обнаруженные смены трендов совпали по времени с измерениями джерков классическими методами, что свидетельствует о применимости метода регрессионных производных в геофизических задачах.

1. ВВЕДЕНИЕ

Анализ геофизического процесса понятие сложное и многозначное. Объясняется это как объективной сложностью самого процесса, так и субъективной природой анализирующего его эксперта. Поэтому адекватная формализация этого требует совершенно нового аппарата, с одной стороны способного преодолеть объективную сложность геофизических данных (нерегулярность и неточность), а с другой – нечеткий характер суждений эксперта. Развитие Дискретного математического анализа (ДМА) (например, [Гвишиани и др., 2010; Agayan et al., 2018]) является важным шагом в этом направлении. ДМА значительно ориентирован на эксперта и занимает промежуточное положение в анализе данных между жесткими математическими методами (статистический анализ, СВАН и др.) и мягкими комбинаторными (имитационное моделирование, нейронные сети и др.). Концепция ДМА состоит, во-первых, в том, что преимущество эксперта при анализе данных перед формальными методами объясняется в нем гибким, адаптивным восприятием экспертом фундаментальных свойств предельности, близости, непрерывности, связности, тренда и других. Именно из этих свойств, как из конструктора, складываются все алгоритмы анализа данных. Таким образом, необходимо найти дискретные аналоги упомянутых выше свойств, далее (вторая часть концепции) соединить их в сценарии классической непрерывной математики и извлечь из этого пользу для анализа данных. При реализации концепции сразу было принято во внимание то обстоятельство, что эксперт мыслит и оперирует не числами, а нечеткими понятиями. Поэтому в техническую основу нашего моделирования наряду с классической математикой вошла также нечеткая математика и опосредованно через нее искусственный интеллект.

ДМА нашел широкое применение в задачах морфологического анализа временны́х рядов, включая построение геометрических мер [Агаян и др., 2005], динамических коридоров [Каган и др., 2009] и выделение трендов. В рамках последнего направления в настоящей работе предлагаются новые математические конструкции регрессионных производных для дискретных временны́х рядов, заданных в общем случае на нерегулярной сетке. В их основе также лежит моделирование логики эксперта: взгляд эксперта на геофизический ряд y в узле t моделируется нечеткой структурой δt, показывающей в какой степени к узлу t близки остальные узлы, а касательной к y в t считается взвешенная с помощью δt линейная регрессия $R_{{y,{\delta }}}^{'}$ (t) для y, угловой коэффициент которой R'y(t) = R'y(t, δ) и будет регрессионной производной для y в t (относительно δ). Ожидаемая связь между трендами y и областями знакопостоянства R'y по аналогии с классическими трендами и производными из классического математического анализа в действительности превзошла все ожидания и стала приятным сюрпризом для авторов.

В области изучения главного магнитного поля Земли (ГМПЗ) все больший интерес вызывают так называемые быстрые вариации поля (например, [Finlay et al., 2010; Mandea et al., 2010]), для которых характерен временнóй масштаб порядка десятка лет и меньше. Во многом этот интерес обусловлен тем, что с 2000 г. в распоряжении научного сообщества появились высокоточные геомагнитные данные низкоорбитальных спутниковых измерений, обладающие высокой плотностью географического покрытия (например, [Chulliat et al., 2017]). Характерными сигналами ГМПЗ, отражающими его быстрые вариации, являются геомагнитные джерки на поверхности Земли (наиболее полный обзор приведен в работе [Brown et al., 2013]) и всплески векового ускорения (ВУ) на границе ядро-мантия [Chulliat et al., 2010; Chulliat and Maus, 2014; Chulliat et al., 2015; Finlay et al., 2016; Soloviev et al., 2017]. Джерки представляют собой смену квазилинейного тренда первой производной магнитного поля по времени (вековой ход) [Mandea et al., 2010], всплески – высокоамплитудный сигнал во второй производной магнитного поля по времени (вековое ускорение). В работах [Chulliat and Maus, 2014; Soloviev et al., 2017] отмечалось, что джерки на поверхности Земли, как правило, имеют место между парами всплесков ВУ на границе ядро–мантия. В частности, за период с 1991 по 2015 гг. были выявлены следующие джерки в промежутках между всплесками ВУ 1997, 1999, 2002, 2006, 2009, 2012 и 2015 гг.: 1998 г. (преимущественно в европейском регионе) [Mandea et al., 2000; De Michelis and Tozzi, 2005; Brown et al., 2013], 2001 г. [Soloviev et al., 2017], 2003 г. (преимущественно в европейском регионе) [Olsen and Mandea, 2007], 2007 г. [Chulliat et al., 2010], 2011 г. [Chulliat and Maus, 2014] и 2014 г. (преимущественно в атлантическом, европейском и австралийском регионах) [Torta et al., 2015]. Как видно, многие джерки носят достаточно локальный характер, часть из них обнаружена только в определенных регионах. Датировка джерков осуществляется с погрешностью около 1 года из-за их медленной миграции от региона к региону и фильтрующего эффекта слабопроводящей мантии.

Важно отметить, что традиционно анализ джерков осуществляется по обсерваторским данным, которые в большой степени зашумлены в основном из-за влияния внешних полей. Зачастую шумовая магнитуда сравнима с магнитудой искомого сигнала внутреннего происхождения, но различна по частотным характеристикам. Это приводит к необходимости использования различных математических методов, позволяющих детектировать джерки в автоматическом или полуавтоматическом режиме (например, [De Michelis and Tozzi, 2005; Mandea et al., 2010]). К таким методам можно отнести и регрессионные производные, поскольку они обеспечивают поиск трендов и локальных экстремумов в зашумленных временны́х рядах.

В настоящей работе исследуются указанные свойства регрессионных производных для обнаружения геомагнитных джерков по зашумленным данным множества магнитных обсерваторий стандарта ИНТЕРМАГНЕТ [Kerridge, 2001]. Для оценки эффективности детектирования джерков рассматривался временнóй интервал 1991–2015 гг., за который имела место заведомо известная серия джерков, перечисленных выше.

2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РЕГРЕССИОННЫХ ПРОИЗВОДНЫХ

2.1. Теоретические предпосылки

Пусть функция f определена вокруг нуля на отрезке [a, b], (ab < 0), и интегрируема на нем. Для $0 \leqslant \Delta \leqslant \min \left( {\left| a \right|,\left| b \right|} \right)$ через fΔ обозначим ограничение f на отрезок $\left[ { - \Delta ,\Delta } \right]{\text{:}}\,\,{{f}_{\Delta }} = f\left| {_{{\left[ { - \Delta ,\Delta } \right]}}} \right.$ и вычислим проекцию prfΔ функции fΔ в пространстве L2[–Δ, Δ] на двумерное пространство линейных функций Lin2[–Δ, Δ].

Обозначим через e1 = e1(Δ), e2 = e2(Δ) ортонормированный базис в Lin2[–Δ, Δ], получающийся из естественного базиса (1, x) путем ортогонализации Грама–Шмидта [Колмогоров и Фомин, 1976], тогда:

$pr{{f}_{\Delta }} = {{({{f}_{\Delta }},{{e}_{1}})}_{\Delta }}{{e}_{1}} + {{({{f}_{\Delta }},{{e}_{2}})}_{\Delta }}{{e}_{2}}.$
Положим e1 = c, e2 = ax + b. На a, b, c возникают три условия:

${{\left\| {{{e}_{1}}} \right\|}_{\Delta }} = 1 \Leftrightarrow \mathop \smallint \limits_{ - \Delta }^\Delta {{c}^{2}}dx = 1 \Leftrightarrow {{c}^{2}} = \frac{1}{{2\Delta }}{\text{,}}$
${{\left( {{{e}_{1}},{{e}_{2}}} \right)}_{\Delta }} = 0 \Leftrightarrow \mathop \smallint \limits_{ - \Delta }^\Delta c\left( {ax + b} \right)dx = 0 \Leftrightarrow b = 0,$
${{\left\| {{{e}_{2}}} \right\|}_{\Delta }} = 1 \Leftrightarrow \mathop \smallint \limits_{ - \Delta }^\Delta {{a}^{2}}{{x}^{2}}dx = 1 \Leftrightarrow {{a}^{2}} = \frac{3}{{2{{\Delta }^{3}}}}\quad.$

Таким образом,

$\left( {pr{{f}_{\Delta }}} \right)(x) = \frac{1}{{2\Delta }}\mathop \smallint \limits_{ - \Delta }^\Delta f(x)dx + \frac{3}{{2{{\Delta }^{3}}}}\left( {\mathop \smallint \limits_{ - \Delta }^\Delta xf(x)dx} \right)x.$

Дополнительно потребуется дифференцируемость функции f в нуле:

$f(x) = f(0) + f{\kern 1pt} {\text{'}}(0)x + \alpha (x)x,$
где $\alpha (x) \to 0$ при $x \to 0.$

Тогда стремление:

$\frac{1}{{2\Delta }}\mathop \smallint \limits_{ - \Delta }^\Delta f(x)dx \to f(0)$
в свободном члене проекции prfΔ объясняется теоремой о среднем [Фихтенгольц, 1969].

Разберем коэффициент разложения prfΔ при x:

Последний интеграл стремится к нулю при $\Delta \to 0{\kern 1pt} {\text{:}}$

${{\left. {_{{_{{_{{}}}}}}\forall \varepsilon > 0\,\,\quad\exists \quad\Delta \left( \varepsilon \right):\quad\forall \quad\Delta < \Delta \left( \varepsilon \right)\quad\left| \alpha \right|} \right|}_{{[ - \Delta ,\,\Delta ]}}} < \varepsilon \Rightarrow $
$ \Rightarrow \left| {\frac{3}{{2{{\Delta }^{3}}}}\mathop \smallint \limits_{ - \Delta }^\Delta \alpha \left( x \right){{x}^{2}}dx} \right| \leqslant \frac{3}{{2{{\Delta }^{3}}}}\mathop \smallint \limits_{ - \Delta }^\Delta \varepsilon {{x}^{2}}dx \equiv \varepsilon .$

Таким образом, доказано следующее:

Утверждение. Если функция f дифференцируема в нуле, то при $\Delta \to 0$ линейная проекция prfΔ стремится к ее касательной в нуле.

Замена касательной к f на проекцию prfΔ при малых Δ дает возможность определить касательную для дискретных функций, поскольку проекция prfΔ есть не что иное, как линейная регрессия для f на [–Δ, Δ] и допускает обобщение на дискретный случай.

2.2. Дискретная регрессионная касательная

Пусть T – период наблюдения, представляющий собой конечное, в общем случае, нерегулярное множество узлов t: $T = \left\{ t \right\},\left| T \right| < \infty .$ Функция y – временнóй ряд, заданный на T: $y{\text{:}}\,T \to \mathbb{R},$ $y = \left\{ {{{y}_{t}} = y(t),t \in T} \right\}.$

Предельный переход $\Delta \to 0$ в дискретном случае заменяется мерой близости ${{\delta }_{t}}(\bar {t})$ – нечетким бинарным отношением на T, показывающим в какой степени узел $\bar {t}$ близок к узлу t в T.

Касательной ${{R}_{{y,t}}}(\bar {t}) = {{a}_{t}}\bar {t} + {{b}_{t}}$ к функции y в узле $t \in T$ считается линейная регрессия, построенная по взвешенному графику ${{\Gamma }_{y}}({{\delta }_{t}})$ = $ = \left\{ {\left( {\left( {\bar {t},{{y}_{{\bar {t}}}}} \right),{{\delta }_{t}}(\bar {t})} \right),\bar {t} \in T} \right\}.$ Опуская стандартные вещи, связанные с линейными регрессиями, приведем формулы для at и bt:

${{a}_{t}} = \frac{{\left| {\begin{array}{*{20}{c}} {\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right){{y}_{{\bar {t}}}}} }&{\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} } \\ {\sum\limits_{\bar {t} \in T} {{{\delta }_{t}}\left( {\bar {t}} \right){{y}_{{\bar {t}}}}} }&{\sum\limits_{\bar {t} \in T} {{{\delta }_{t}}\left( {\bar {t}} \right)} } \end{array}} \right|}}{{\left| {\begin{array}{*{20}{c}} {\sum\limits_{\bar {t} \in T} {{{{\bar {t}}}^{2}}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} } \\ {\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {{{\delta }_{t}}\left( {\bar {t}} \right)} } \end{array}} \right|}},$
${{b}_{t}} = \frac{{\left| {\begin{array}{*{20}{c}} {\sum\limits_{\bar {t} \in T} {{{{\bar {t}}}^{2}}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right){{y}_{{\bar {t}}}}} } \\ {\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {{{\delta }_{t}}\left( {\bar {t}} \right){{y}_{{\bar {t}}}}} } \end{array}} \right|}}{{\left| {\begin{array}{*{20}{c}} {\sum\limits_{\bar {t} \in T} {{{{\bar {t}}}^{2}}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} } \\ {\sum\limits_{\bar {t} \in T} {\bar {t}{{\delta }_{t}}\left( {\bar {t}} \right)} }&{\sum\limits_{\bar {t} \in T} {{{\delta }_{t}}\left( {\bar {t}} \right)} } \end{array}} \right|}}.$

Определение 1. Угловой коэффициент at регрессионной касательной ${{R}_{{y,t}}}$ называется регрессионной производной функции y в узле t и обозначается через (R 'y)(t).

Определение 2. Значение Ry, t(t) касательной Ry, t в узле t называется регрессионным значением y в узле t и обозначается через (Ry)(t).

Итак,

$\left( {R{\kern 1pt} {\text{'}}y} \right)\left( t \right) = {{a}_{t}},$
$\left( {Ry} \right)\left( t \right) = {{a}_{t}}t + {{b}_{t}}.$

2.3. Примеры и свойства регрессионных производных и значений

При построении регрессионных производных и значений будем использовать два варианта (глобальный и локальный) одной конструкции близости, зависящей от двух неотрицательных параметров r и p:

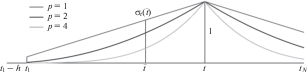
Глобальная мера близости (рис. 1):

Рис. 1.

Глобальная мера близости: зависимость от p при фиксированном r.

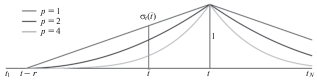
Локальная мера близости (рис. 2):

$\begin{gathered} {{\delta }_{t}}\left( {r,p} \right)\left( {\bar {t}} \right) = {{\delta }_{t}}\left( {\bar {t}} \right) = \\ = \left\{ \begin{gathered} {{\left( {1 - \frac{{\left| {\bar {t} - t} \right|}}{r}} \right)}^{p}}{\text{,}}\,\,\,\,{\text{е с л и }}\,\,\quad\left| {\bar {t} - t} \right| \leqslant r \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{е с л и }}\,\,\left| {\bar {t} - t} \right| > r. \hfill \\ \end{gathered} \right. \\ \end{gathered} $
Рис. 2.

Локальная мера близости: зависимость от p при фиксированном r.

Следует отметить, что мера близости является одним из базовых понятий ДМА и построенных на его основе алгоритмов обработки временны́х рядов [Agayan et al., 2016; Bogoutdinov et al., 2010; Gvishiani et al., 2008a,b; Soloviev et al., 2012a; Zelinskiy et al., 2014]. Последние нашли широкое применение в целом ряде геофизических задач [Gvishiani et al., 2014, 2016a,b; Kulchinsky et al., 2010; Sidorov et al., 2012; Soloviev et al., 2016, 2013, 2012b; Zlotnicki et al., 2005].

Сформулируем основные свойства регрессионных производных и значений:

1. В обозначениях и с учетом определений 1 и 2 регрессионная производная $R{\text{',}}\,y \to R{\text{'}}y,$ и регрессионное значение R, $y \to Ry,$ – линейные операторы в пространстве Ф(T) функций на T.

2. Операции R ' и R основаны на регрессии и потому устойчивы к возмущениям исходных функций (рис. 3, 4).

Рис. 3.

Устойчивость операции R к возмущениям (исходный ряд показан на графике серым цветом, регрессионное сглаживание – черным): (а) – применение к гладкой функции, (б) – к зашумленной функции.

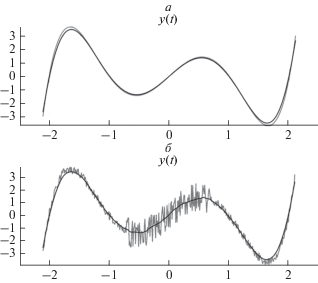
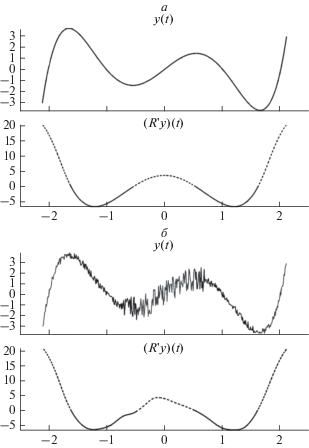
Рис. 4.

Устойчивость операции R ' к возмущениям: (а) – применение к гладкой функции, (б) – к зашумленной функции. Пунктиром на графике обозначены зоны возрастания функции y(t), сплошной линией – зоны ее убывания.

3. В отличие от классического непрерывного случая дискретная касательная Ry, t не обязана принимать в точке t значение y(t), так что операцию R можно считать новым сглаживанием, по своей универсальности не только не уступающим обычному усреднению, но и превосходящим его по результату (рис. 5).

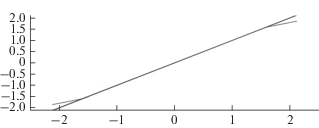
Рис. 5.

Регрессионное сглаживание (черное) и классическое усреднение (серое) прямой y = x относительно одинаковой меры близости δ.

4. Операция R ' тесно связана со стохастическими трендами: области положительного (отрицательного) знакопостоянства R'y соответствуют возрастающим (убывающим) трендам y, а границы между ними – экстремумам для y (рис. 4).

5. Зависимость операций R ' и R от меры близости δ на T дает возможность решать вопросы сглаживания (рис. 6), поиска трендов и экстремумов для функции y в разных масштабах. Именно это обстоятельство лежит в основе применения регрессионных производных к детектированию геомагнитных джерков, изложенного в следующем разделе статьи, поскольку джерки представляют собой экстремумы в определенном масштабе на вековом ходе магнитного поля.

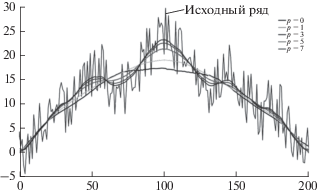
Рис. 6.

Регрессионное сглаживание на основе локальной меры близости: зависимость от p при фиксированном r.

На рисунках 7, 8 показаны возможности регрессионной производной для поиска экстремумов и интервалов монотонности различного уровня. На рисунке 7 сверху изображена анализируемая кривая, на нижней части рисунка для каждого значения показателя p темно-серым выделены зоны ее возрастания, черным – зоны убывания, а светло-серым – зоны экстремумов четырех уровней.

Рис. 7.

Регрессионная производная гладкой функции: зависимость от p при фиксированном r. На верхнем графике представлена исходная кривая, на нижнем – знак регрессионной производной при разном значении p. Возрастание анализируемой кривой отмечено темно-серым цветом, убывание – черным, зоны экстремумов – светло-серым.

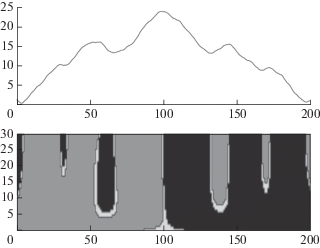
Рис. 8.

Регрессионная производная зашумленного ряда: зависимость от p при фиксированном r. Обозначения аналогичны рис. 7.

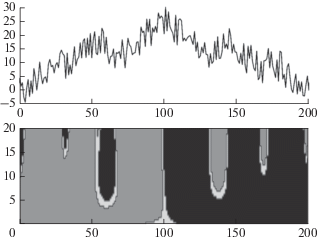
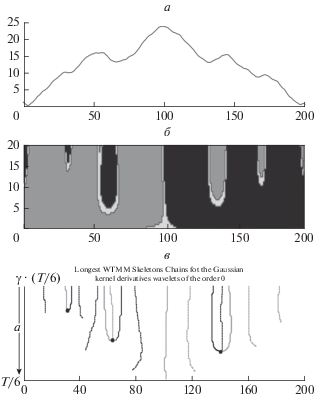
6. В настоящее время существует ряд способов определения трендов и экстремумов на стохастических временны́х рядах [Гумбель, 1965; Лидбеттер и др., 1989; Любушин, 2007; Малла, 2005]. На примере функции f, приведенной на рис. 7, сравним работу регрессионных производных с работой алгоритма WTMM (Wavelet Transform Modulus Maxima) поиска трендов и экстремумов с помощью точек максимума модуля вейвлет-преобразования [Любушин, 2007; Малла, 2005]. Алгоритм WTMM взят из программы Spectra_ Analyzer (http://www.ifz.ru/applied/analiz-dannykh-monitoringa/programmnoe-obespechenie/). Для удобства рис. 9а, 9б дублируют рис. 7, а работа алгоритма WTMM показана на рис. 9в, где темно-серые цепи дают разномасштабную картину максимумов функции f, а черные – ее минимумов. Серые (светло-серые) цепи характеризуют наиболее сильные точки на разномасштабных возрастающих (убывающих) трендах f. Сравнение необходимо производить по верхней границе: как видно из рисунков 9б, 9в регрессионные производные дали на два крайних экстремума больше, чем алгоритм WTMM, а по трендам на внутренних участках они практически совпали.

Рис. 9.

Сравнение работы регрессионных производных и алгоритма WTMM: (а) – исходная функция, (б) – результат применения регрессионных производных, (в) – результат применения алгоритма WTMM. Обозначения рис. 9а, 9б аналогичны рис. 7. На рис. 9в представлена структура длинных цепей скелетов модулей вейвлет-преобразования с нулевой производной от гауссиана. В обозначениях программы Spectra_Analyzer: a – масштаб обзора (a ∈ [γ × (T/6), T/6]), γ = 0.12 – параметр метода, T = 201 – количество элементов выборки. Черными сплошными линиями показаны минимумы усредненных кривых, серыми сплошными линиями – максимумы усредненных кривых, черными пунктирными линиями – максимумы отрицательных трендов, серыми пунктирными линиями – максимумы положительных трендов.

3. ДЕТЕКТИРОВАНИЕ ГЕОМАГНИТНЫХ ДЖЕРКОВ

В настоящем разделе исследуются возможности регрессионных производных для обнаружения геомагнитных джерков по зашумленным данным множества магнитных обсерваторий стандарта ИНТЕРМАГНЕТ [Kerridge, 2001]. Для оценки эффективности детектирования джерков рассматривался временнóй интервал 1991–2015 гг. За этот период имела место серия джерков, хорошо изученных в научной литературе. В рамках настоящего исследования исходными данными послужили вариации векового хода трех компонент магнитного поля (dX/dt, dY/dt, dZ/dt), полученные по измерениям следующих обсерваторий (перечислены IAGA-коды): GUA (о. Гуам), MMB (Мемамбецу, Япония), NGK (Нимегк, Германия), SJG (Сан-Хуан, Пуэрто-Рико) и TAM (Таманрассет, Алжир). Вековой ход рассчитывался по обсерваторским измерениям статуса “окончательные” (definitive) [Love and Chulliat, 2013], что гарантирует их высокое качество за весь рассматриваемый период. Метод для расчета векового хода подробно изложен в [Soloviev et al., 2017]. Выбор обсерваторий обусловлен их широким географическим охватом.

В качестве параметров алгоритма выступают значения r и p, которые используются для определения локальной меры близости δ(r, p) (рис. 2). Для параметра p был выбран единый диапазон значений от 0 до 50, а r полагался равным от 50 до 100. В указанном диапазоне график регрессионной производной достаточно точно характеризует исходный график вариаций. Поскольку метод чувствителен к малейшим изменениям знака производной, нами не рассматривались значения p и r, превышающие указанный диапазон. В противном случае результирующий график будет отражать множество резких изменений знака производной (скачков), которые по большей части носят шумовой характер (особенно при небольших значениях r). При значении r > 100 результирующий график не будет содержать подобных мелких скачков, однако при таких значениях r возникают пропуски целей (видимый на исходном графике переход от зоны возрастания функции к зоне убывания или от зоны убывания к зоне возрастания не фиксируется на графике регрессионных производных). Для каждой обсерватории/компоненты были построены два графика: график исходного векового хода и результат применения регрессионных производных (рис. 10–12).

Рис. 10.

Применение метода для поиска трендов векового хода X- компоненты по данным обсерватории GUA за период 1991–2015 гг.: исходный график dX/dt (нТл/год, сверху) и график регрессионных производных при значениях параметра p от 0 до 50 (снизу). На нижнем графике темно-серым помечены положительные тренды, черным – отрицательные. Диапазон 25 < p' < 35 помечен горизонтальными линиями. Ранее изученные всплески ВУ 1997, 1999, 2002, 2006, 2009, 2012 и 2015 гг. помечены вертикальными линиями.

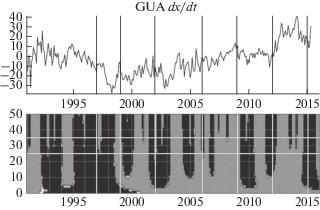
Рис. 11.

Применение метода для поиска трендов векового хода Y-компоненты по данным обсерватории NGK за период 1991–2015 гг. Обозначения аналогичны рис. 10.

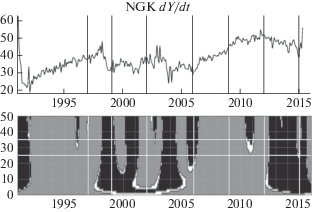
Рис. 12.

Применение метода для поиска трендов векового хода Z-компоненты по данным обсерватории TAM за период 1991–2015 гг. Обозначения аналогичны рис. 10.

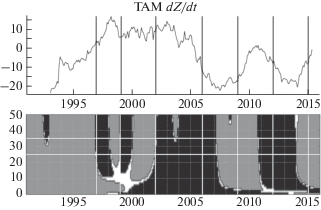
На графиках регрессионной производной присутствуют три цвета: темно-серый, черный и светло-серый. Темно-серый цвет показывает, что функция в указанных диапазонах значений преимущественно возрастает, черный – убывает, а светло-серый означает, что исходная функция квазипостоянна. С увеличением p внешний вид результирующей функции меняется, так как происходит уточнение ее значений путем более локального рассмотрения графика исходной функции (происходит поиск более локальных экстремумов). Серыми и белыми вертикальными линиями на графиках обозначены эпохи зафиксированных всплесков ВУ. Они соответствуют временны́м границам интервалов, внутри которых имели место джерки.

Нами изучались результаты работы алгоритма, полученные при разных конструкциях δ. Для каждого зафиксированного значения ri мы искали такой диапазон $p_{i}^{'}$ (внутри 0 < p < 50), при котором его нижняя граница обеспечивает попадание большинства известных джерков, а верхняя обеспечивает минимальное количество ложных срабатываний (шума). Поиск велся эмпирическим путем с помощью многочисленных экспериментов. Таким образом, для каждого ri был получен единый для всех обсерваторий диапазон p'. На рис. 10–12 его границы обозначены горизонтальными белыми линиями на втором графике. Результаты анализа построений для нескольких конструкций δ(ri, $p_{i}^{'}$), где r1 = 50, r2 = 80, r3 = 100, приведены в таблицах 1–3.

Таблица 1.  

Результат при r1 = 50, 25 < $p_{1}^{'}$ < 35

Компонента 1997–1999 1999–2002 2002–2006 2006–2009 2009–2012 2012–2015
% обсерваторий, для которых нет пропуска цели
X 100 100 100 100 100 100
Y 80 100 100 80 80 100
Z 100 100 100 100 100 100
% обсерваторий, для которых ≥1 ложных срабатываний
X 80 100 100 100 100 100
Y 60 80 100 60 60 80
Z 60 80 100 100 60 80
Таблица 2.  

Результат при r2 = 80, 25 < $p_{2}^{'}$ < 40

Компонента 1997–1999 1999–2002 2002–2006 2006–2009 2009–2012 2012–2015
% обсерваторий, для которых нет пропуска цели
X 100 100 100 100 100 100
Y 80 100 100 40 80 100
Z 100 60 100 80 80 100
      % обсерваторий, для которых ≥1 ложных срабатываний
X 60 100 100 100 100 100
Y 20 80 100 20 60 60
Z 40 40 100 80 60 60
Таблица 3.  

Результат при r3 = 100, 30 < $p_{3}^{'}$ < 45

Компонента 1997–1999 1999–2002 2002–2006 2006–2009 2009–2012 2012–2015
% обсерваторий, для которых нет пропуска цели
X 100 80 100 100 100 100
Y 80 100 100 40 60 100
Z 100 60 100 80 80 100
% обсерваторий, для которых ≥1 ложных срабатываний
X 40 60 100 100 100 80
Y 20 60 80 0 40 60
Z 40 40 100 60 60 60

Из результатов, представленных в таблицах, видно, что при увеличении значения параметра r закономерно увеличивается число обсерваторий, для которых наблюдается пропуск цели, однако и число ложных срабатываний уменьшается. При небольших значениях параметра фиксируются все события, даже незначительные, а при увеличении значения мелкие события игнорируются. Поскольку в нашей постановке задачи доминирующую роль играет факт наличия джерка между парой соседний всплесков ВУ, для нас бóльшим приоритетом является максимизация процента обсерваторий без пропуска цели. Иными словами, значения параметров r1 = 50, 25 < $p_{1}^{'}$ < 35 являются наиболее предпочтительными (табл. 1). При этих параметрах пропуск цели был обнаружен только на одной компоненте Y и лишь для одной обсерватории по каждому из трех рассматриваемых интервалов: за 1997–1999 гг. на обсерватории MMB, за 2006–2009 гг. на обсерватории TAM и 2009–2012 гг. на обсерватории SJG. Данный результат можно считать вполне удовлетворительным с учетом (1) столь малого количества рассматриваемых обсерваторий, (2) пространственной локализации геомагнитных джерков и (3) проявления джерков только на отдельных компонентах.

4. ЗАКЛЮЧЕНИЕ

Целями настоящей работы явились математическое изложение новых операций регрессионного сглаживания и производных на дискретных временны́х рядах, а также демонстрация их эффективности при поиске и анализе геомагнитных джерков. В ходе работы впервые с помощью аппарата регрессионных производных были определены тренды векового хода за период 1991–2015 гг. по трем компонентам для пяти выбранных геомагнитных обсерваторий. Анализ полученных результатов показал, что в большинстве случаев смена трендов от возрастающего к убывающему или от убывающего к возрастающему происходят в те же периоды времени, когда были определены указанные джерки классическими методами. Этот факт свидетельствует о применимости метода регрессионных производных в задачах геофизики. Благодаря своему универсальному характеру регрессионные сглаживания и производные помогут значительно упростить и ускорить вычисления при работе с зашумленными временны́ми рядами.

В будущем предлагается дальнейшее применение регрессионных сглаживаний и производных для более детального изучения процессов, происходящих на границе жидкого ядра и мантии. Во-первых, планируется создание полномасштабного алгоритма поиска джерков, включающего в себя сначала поиск всплесков векового ускорения на основе второй регрессионной производной, а затем поиск самих джерков между всплесками на основе первой. Во-вторых, планируется применение такого алгоритма для изучения пространственно-временнóй миграции джерков по данным всей глобальной сети обсерваторий ИНТЕРМАГНЕТ.

5. БЛАГОДАРНОСТИ

В работе использовались данные ЦКП “Аналитический центр геомагнитных данных” Геофизического центра РАН.

6. ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнена в рамках государственного задания ГЦ РАН, утвержденного Министерством науки и высшего образования РФ.

Список литературы

  1. − Агаян С.М., Богоутдинов Ш.Р., Гвишиани А.Д., Граева Е.М., Злотники Ж., Родкин М.В. Исследование морфологии сигнала на основе алгоритмов нечеткой логики // Геофизические исследования. М.: ИФЗ РАН. Вып. 1. С. 143–155. 2005.

  2. − Гвишиани А.Д., Агаян С.М., Богоутдинов Ш.Р., Соловьев А.А. Дискретный математический анализ и геолого-геофизические приложения // Вестн. КРАУНЦ. Науки о Земле. № 2. Вып. № 16. С. 109–125. 2010.

  3. − Гумбель Э. Статистика экстремальных значений. М.: Мир, 451 с. 1965.

  4. − Каган А.И., Агаян С.М., Богоутдинов Ш.Р. Определение стохастической непрерывности методами нечеткой логики и геофизические приложения // Международная конференция “Итоги Электронного Геофизического Года”. 3–6 июня 2009 г., Переславль-Залесский, Россия. Тез. док. С. 99. 2009.

  5. − Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука. 544 с. 1976.

  6. − Лидбеттер М., Линдгрен Г., Ротсен X. Экстремумы случайных последовательностей и процессов. М.: Мир. 392 с. 1989.

  7. − Любушин А.А. Анализ данных систем геофизического и экологического мониторинга. М.: Наука, 228 с. 2007.

  8. − Малла С. Вэйвлеты в обработке сигналов. М.: Мир, 671 с. 2005.

  9. − Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. II. М.: Наука, 800 с. 1969.

  10. − Agayan S., Bogoutdinov S., Soloviev A., Sidorov R. The study of time series using the DMA methods and geophysical applications // Data Sci. J. V. 15. P. 1–21. 2016. doi http://dx.doi.org/.https://doi.org/10.5334/dsj-2016-016

  11. − Agayan S.M., Bogoutdinov Sh.R., Krasnoperov R.I. Short introduction into DMA // Russ. J. Earth. Sci. V. 18. ES2001. 2018. https://doi.org/10.2205/2018ES000618

  12. − Bogoutdinov S.R., Gvishiani A.D., Agayan S.M., Solovyev A.A., Kihn E. Recognition of Disturbances with Specified Morphology in Time Series. Part 1: Spikes on Magnetograms of the Worldwide INTERMAGNET Network // Izv.– Phys. Solid Eart. V. 46. P. 1004–1016. 2010.

  13. − Brown W.J., Mound J.E., Livermore P.W. Jerks abound: An analysis of geomagnetic observatory data from 1957 to 2008 // Phys. Earth Planet. In. V. 223. P. 62–76. ISSN 0031-9201. 2013.

  14. − Chulliat A., Thebault E., Hulot G. Core field acceleration pulse as a common cause of the 2003 and 2007 geomagnetic jerks // Geophys. Res. Lett. V. 37. L07301. 2010. https://doi.org/10.1029/2009GL042019

  15. − Chulliat A., Maus S. Geomagnetic secular acceleration, jerks, and a localized standing wave at the core surface from 2000 to 2010 // J. Geophys. Res. Solid Earth. V. 119. P. 1531–1543. 2014. https://doi.org/10.1002/2013JB010604

  16. − Chulliat A., Alken P., Maus S. Fast equatorial waves propagating at the top of the Earth’s core // Geophys. Res. Lett. V. 42. P. 3321–3329. 2015. https://doi.org/10.1002/2015GL064067

  17. − Chulliat A., Matzka J., Masson A., Milan S.E. Key Ground-Based and Space-Based Assets to Disentangle Magnetic Field Sources in the Earth’s Environment // Space Sci. Rev. V. 206. P. 123–156. 2017. https://doi.org/10.1007/ s11214-016-0291-y

  18. − Finlay C.C., Dumberry M., Chulliat A., Pais A. Short timescale core dynamics: theory and observations // Space Sci. Rev. V. 155. P. 177–218. 2010.

  19. − Finlay C.C., Olsen N., Kotsiaros S., Gillet N., Toeffner-Clausen L. Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model // Earth Planets Space. V. 68. № 112. 2016. https://doi.org/10.1186/s40623-016-0486-1

  20. − Gvishiani A.D., Agayan S.M., Bogoutdinov Sh.R. Fuzzy recognition of anomalies in time series // Dokl. Earth Sci. V. 421. № 1. P. 838–842. 2008a.

  21. − Gvishiani A.D., Agayan S.M., Bogoutdinov Sh.R., Zlotnicki J., Bonnin J. Mathematical Methods of Geoinformatics: III. Fuzzy Comparisons and Recognition of Anomalies in Time Series // Cybernet Sys Analys. V. 44. № 3. P. 309–323. 2008b.

  22. − Gvishiani A., Lukianova R., Soloviev A., Khokhlov A. Survey of Geomagnetic Observations Made in the Northern Sector of Russia and New Methods for Analysing Them // Surv. Geophys. V. 35. № 5. P. 1123–1154. 2014. https://doi.org/10.1007/s10712-014-9297-8

  23. − Gvishiani A.D., Sidorov R.V., Lukianova R.Yu., Soloviev A.A. Geomagnetic activity during St. Patrick’s Day storm inferred from global and local indicators // Russ. J. Earth Sci. V. 16. ES6007. 2016a. https://doi.org/10.2205/2016ES000593

  24. − Gvishiani A., Soloviev A., Krasnoperov R., Lukianova R. Automated hardware and software system for monitoring the Earth’s magnetic environment // Data Sci. J. V. 15. P. 18. 2016b. doi http://dx.doi.org/https://doi.org/10.5334/dsj-2016-018

  25. − Kerridge D. INTERMAGNET: Worldwide near-real-time geomagnetic observatory data // Proc. the Workshop on Space Weather. ESTEC. 2001.

  26. − Kulchinsky R.G., Kharin E.P., Shestopalov I.P., Gvishiani A.D., Agayan S.M., Bogoutdinov Sh. R. Fuzzy logic methods for geomagnetic events detections and analysis // Russ. J. Earth Sci.V. 11. RE4003. 2010. https://doi.org/10.2205/2009ES000371

  27. − Love J.J., Chulliat A. An international network of magnetic observatories // EOS Trans. Am. Geophys. Union. V. 94. № 42. P. 373–374. 2013. https://doi.org/10.1002/2013EO420001

  28. − Mandea M., Bellanger E., Le Mouël J.L. A geomagnetic jerk for the end of the 20th century? // Earth Planet. Sci. Lett. V. 183. № 3–4. P. 369–373. 2000. https://doi.org/10.1016/S0012-821X(00)00284-3

  29. − Mandea M., Holme R., Pais A., Pinheiro K., Jackson A., Verbanac G. Geomagnetic jerks: Rapid core field variations and core dynamics // Space Sci. Rev. V. 155. P. 147–175. 2010.

  30. − De Michelis P., Tozzi R. A Local Intermittency Measure (LIM) approach to the detection of geomagnetic jerks // Earth Planet. Sci. Lett. V. 235. № 1–2. P. 261–272. 2005.

  31. − Olsen N., Mandea M. Investigation of a secular variation impulse using satellite data: The 2003 geomagnetic jerk // Earth Planet. Sci. Lett. V. 255. P. 94–105. 2007.

  32. − Sidorov R.V., Soloviev A.A., Bogoutdinov Sh.R. Application of the SP Algorithm to the INTERMAGNET Magnetograms of the Disturbed Geomagnetic Field // Izv.– Phys. Solid Eart. V. 48. № 5. P. 410–414. 2012.

  33. − Soloviev A., Agayan S., Bogoutdinov S. Estimation of geomagnetic activity using measure of anomalousness // Ann. Geophys. V. 59. № 6. G0653. 2016. https://doi.org/10.4401/ag-7116

  34. − Soloviev A.A., Agayan S.M., Gvishiani A.D., Bogoutdinov Sh.R., Chulliat A. Recognition of Disturbances with Specified Morphology in Time Series: Part 2. Spikes on 1-s Magnetograms // Izv.– Phys. Solid Eart. V. 48. № 5. P. 395–409. 2012a.

  35. − Soloviev A., Bogoutdinov S., Gvishiani A., Kulchinskiy R., Zlotnicki J. Mathematical Tools for Geomagnetic Data Monitoring and the INTERMAGNET Russian Segment // Data Sci. J. V. 12. P. 114–119. 2013. https://doi.org/10.2481/dsj.WDS-019

  36. − Soloviev A., Chulliat A., Bogoutdinov S., Gvishiani A., Agayan S., Peltier A., Heumez B. Automated recognition of spikes in 1 Hz data recorded at the Easter Island magnetic observatory // Earth Planets Space. V. 64. № 9. P. 743–752. 2012b. https://doi.org/10.5047/eps.2012.03.004

  37. − Soloviev A., Chulliat A., Bogoutdinov S. Detection of secular acceleration pulses from observatory data // Phys. Earth Planet. In. V. 270. P. 128–142. 2017. https://doi.org/10.1016/j.pepi.2017.07.005

  38. − Torta J.M., Pavón-Carrasco F.J., Marsal S., Finlay C.C. Evidence for a new geomagnetic jerk in 2014 // Geophys. Res. Lett. V. 42. P. 7933–7940. 2015. https://doi.org/10.1002/ 2015GL065501

  39. − Zelinskiy N.R., Kleimenova N.G., Kozyreva O.V., Agayan S.M., Bogoutdinov Sh.R., Soloviev A.A. Algorithm for recognizing Pc3 geomagnetic pulsations in 1-s data from INTERMAGNET equatorial observatories // Izv.-Phys. Solid Eart. V. 50. № 2. P. 240–248. 2014.

  40. − Zlotnicki J., LeMouel J.-L., Gvishiani A., Agayan S., Mikhailov V., Bogoutdinov Sh. Automatic fuzzy-logic recognition of anomalous activity on long geophysical records. Application to electric signals associated with the volcanic activity of la Fournaise volcano (Réunion Island) // Earth Planet. Sci. Lett. V. 234. P. 261–278. 2005.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал