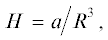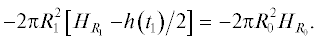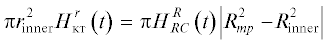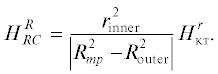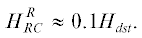Геомагнетизм и аэрономия, 2019, T. 59, № 4, стр. 449-460

Представление третьего адиабатического инварианта в потоковой форме и некоторые следствия его сохранения на примерах конкретных аксиальных магнитных систем

В. В. Богданов^*

Институт космофизических исследований и распространения радиоволн Дальневосточного отделения РАН (ИКИР ДВО РАН)
Елизовский район, Камчатский край, с. Паратунка, Россия

^* E-mail: vbogd@ikir.ru

Поступила в редакцию 05.05.2017
После доработки 26.12.2018
Принята к публикации 24.01.2019

DOI: 10.1134/S0016794019040072

Полный текст (PDF)

Аннотация

На примерах магнитных систем аксиальной симметрии рассматривается динамика инвариантных магнитных поверхностей. В системе, образованной двумя витками с током, выделена внутренняя ловушка (пробкотрон) и внешняя ловушка (диполь). Для вектора возмущения, удовлетворяющего условию сохранения третьего инварианта, в дрейфовом приближении рассмотрена динамика невзаимодействующих частиц, двигающихся в плоскости магнитного экватора. Полученные результаты распространены на экватор геомагнитной ловушки, в которой внешнее возмущающее поле задается кольцевым током. Показано, что в ограниченной магнитосфере Земли в приближении постоянства третьего инварианта реальное влияние кольцевого тока на динамику плазмы отличается от общепринятых модельных расчетов, выполненных на основе дипольных представлений геомагнитного поля. При этом практический смысл имеет не магнитный поток, а только его изменение, равное разнице конечного и начального значений потоков, рассчитанных по параметрам реального поля. Для главной фазы конкретной магнитной бури выполнена оценка минимальных значений энергий заряженных частиц в радиационных поясах, которой они должны обладать, чтобы удовлетворять условию сохранения третьего адиабатического инварианта.

1. ВВЕДЕНИЕ

Возможность захвата заряженных частиц неоднородными магнитными полями объясняется существованием трех адиабатических инвариантов движения. Первый инвариант $\mu $ связан с вращательным движением заряженных частиц вокруг силовой линии. Второй инвариант J обусловлен колебательным движением вдоль силовых линий между магнитными пробками. Третий адиабатический инвариант Ф связан с азимутальным дрейфом частиц по замкнутой магнитной поверхности в полях с аксиальной симметрией и обычно отождествляется с сохранением магнитного потока, охватываемого этой поверхностью. В постоянных аксиальных полях третий инвариант сохраняется при сохранении первых двух инвариантов. Первый инвариант $\mu $ определяет “зеркальные точки”, второй инвариант J – силовую линию, поворот которой на угол 2π определяет инвариантную поверхность. Физический смысл третьего инварианта проявляется в переменных полях, изменение которых ограничено условием адиабатической инвариантности Ф. Если это условие выполнено, то заряженные частицы (точнее ведущие центры) дрейфуют по инвариантной поверхности с сохранением потока Ф.

Дрейфовое приближение, которое описывает движение заряженной частицы в магнитном поле, основано на возможности линеаризации поля в интервале траектории, которое соответствует ларморовскому периоду вращения Т_L [Сивухин, 1963]. Подобная линеаризация возможна при соблюдении классического условия адиабатической инвариантности, имеющего в данном конкретном случае вид ${{T}_{L}}\left| {\frac{{dH}}{{dt}}} \right| \ll \left| H \right|.$ В связи с замкнутостью магнитных полей $\left( {\nabla \cdot H = 0} \right)$ линеаризация эквивалентна симметризации (“спрямлению” оси силовой трубки) поля в пределах Т_L. Именно поэтому с точностью приближения выполняется µ = const = c₀Ф_k, где µ – магнитный момент частицы, Ф_k – магнитный поток, охватываемый магнитной трубкой, с₀ – постоянная. Действительно, дрейфовое приближение основано на возможности абсолютной инвариантности µ в поле магнитного монополя [Богуславский, 1961] и однородном магнитном поле, для которых траектория движения заряженной частицы является симметричной. Именно в этом случае магнитный поток трубки и магнитный момент эквивалентны с точки зрения инвариантности.

Приближение среднего дрейфа требует дополнительных условий адиабатической инвариантности ${{T}_{{osc}}}\left| {\frac{{dH}}{{dt}}} \right| \ll \left| H \right|,$ где$\quad{{T}_{{osc}}}\quad$ – период колебаний между зеркальными точками. В этом случае Н и ${{T}_{{osc}}}$ – усредненные по Т_L величины. Если этим условиям соответствует адиабатическая инвариантность µ и J, имеющих каноническую форму $I = \frac{1}{{2\pi }}\oint {{{P}_{i}}d{{q}_{i}}} ,$ то условию ${{T}_{d}}\left| {\frac{{dH}}{{dt}}} \right| \ll \left| H \right|$ (${{T}_{d}}$ – период дрейфа) обычно сопоставляется адиабатическая инвариантность так называемого суммарного магнитного потока $\Phi = \int {\int {Hd{\mathbf{S}},} } $ где Ф является потоком магнитного поля через сечение замкнутой дрейфовой оболочки частицы. Вопросы корректности замены канонической формы третьего инварианта на потоковую были рассмотрены в работах [Богданов и Плетнев, 1972а; Богданов и Плетнев, 1972б]. В данной работе вычисление и следствия из сохранения третьего адиабатического инварианта, представленного в потоковой форме, будут рассмотрены на примере двух магнитных аксиальных систем. Плазма рассматривается как система независимых частиц, удовлетворяющих дрейфовому приближению и имеющих свои независимые траектории. В этом случае, пренебрегая внутренними полями, происходящими от взаимодействия частиц, и учитывая электрическое поле поляризации, вследствие разделения зарядов, можно построить квазимагнитогиродинамическую модель, описывающую динамику плазмы поперек магнитного поля в терминах сплошной среды. В этом приближении давление передается за счет дрейфовых токов и током намагничивания, явный вид которых позволяет получить одночастичное приближение [Франк–Каменецкий, 1964].

2. АДИАБАТИЧЕСКАЯ ДЕФОРМАЦИЯ АКСИАЛЬНОГО МАГНИТНОГО ПОЛЯ ДВУХ ВИТКОВ С ТОКОМ

2.1. Магнитная система двух параллельных витков с однонаправленными токами (качественное рассмотрение)

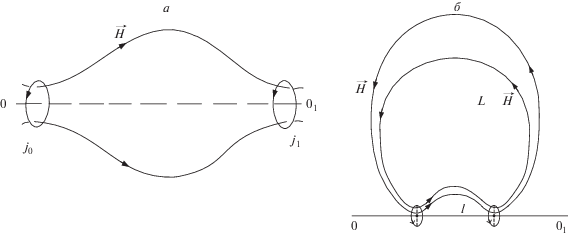
Рассмотрим магнитную аксиальную систему, создаваемую двумя параллельными витками с током, направленными в одну сторону. Будем называть внутренней областью l (внутренней ловушкой, пробкотроном) системы область, расположенную в окрестности оси 0–0₁, для которой радиальные расстояния r ~ b, где b – характерный радиус токовых систем ${{j}_{0}},$ ${{j}_{1}},$ создающих магнитное поле (рис. 1а). Внешняя область магнитной системы L (внешняя ловушка) занимает пространство R $ \gg $ b и, как следует из рис. 1б, представляет собой часть замкнутой трубки 0–0₁, выходящей за пределы токовой системы ${{j}_{0}},$ ${{j}_{1}}.$ (Здесь и далее радиальные расстояния для внутренней ловушки будем обозначать через r, а для внешней ловушки R). Если R $ \gg $ 00₁, то получаем систему подобную дипольному полю (рис. 1б). Во внутренней ловушке в области захвата магнитное поле с ростом радиуса увеличивается, а во внешней уменьшается.

Рис. 1.

Внутренняя (а) и внешняя (б) магнитные ловушки, образованные токовой системой j₀, j₁.

Наложим на поле магнитной системы, показанной на рис. 2, некоторое внешнее возмущающее однородное магнитное поле h определенного направления (знака). Для определенности положим, что h является возрастающей функцией времени и, кроме того, будем полагать выполнение условия адиабатической инвариантности изменения поля, т.е.

(1)

$\frac{{dH}}{{dt}} = \frac{d}{{dt}}\left| {{{H}_{0}} + h} \right| \ll \frac{H}{{{{T}_{d}}}}.$

Рис. 2.

Влияние возмущающего магнитного поля h на внешнюю и внутреннюю области магнитной системы. Величины полей H и h представлены не в масштабе.

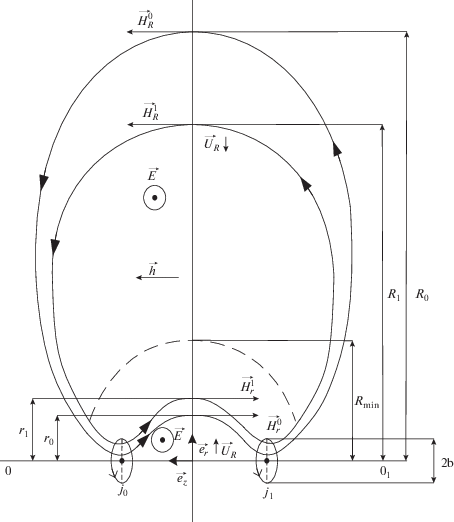
На рисунке 2 в качестве примера показаны замкнутые силовые линии, которые выходят из внутренней ловушки l, проходят через внешнюю L и возвращаются в l (рис. 1б). Магнитная поверхность получается поворотом указанной силовой линии на 2π вокруг оси 0–0₁. Из рисунка видно, что если возмущающее поле уменьшает напряженность основного поля во внутренней области $\left( {\left( {{{\partial {{H}_{{{\text{inner}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{inner}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) < 0} \right),$ то во внешней области напряженность поля возрастает $\left( {\left( {{{\partial {{H}_{{{\text{outer}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{outer}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) > 0} \right).$ В рассматриваемом случае индукционное электрическое поле, вследствие уравнения Максвелла ${\text{rot}}E = - \frac{1}{c}\left( {\frac{{\partial H}}{{\partial t}}} \right),$ в обеих областях направлено к нам, поскольку ${\text{rot}}E \cong - \frac{1}{c}\frac{h}{{\Delta t}}$ (на рис. 2 обозначено значком ⨀).

Выберем для качественного рассмотрения адиабатической деформации магнитного поля, удовлетворяющей условию (1), плоскость магнитного экватора Z = 0 (плоскость минимума поля). На рисунке 2 сплошная линия по направлению единичного вектора ${{{\mathbf{e}}}_{r}}$ обозначает линию пересечения плоскости экватора с плоскостью рисунка. Рассмотрим заряженные частицы, для которых в этой плоскости ${{\text{v}}_{{{\text{II}}}}} = 0.$ Частицы дрейфуют в скрещенных полях $E,H$ (направление дрейфа совпадает с вектором $\left[ {E,H} \right]$) в сторону от оси симметрии системы 0–0₁ во внутренней области и к оси – во внешней области. Из условия сохранения первого адиабатического инварианта $\mu = \left( {{{m\text{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{m\text{v}_{ \bot }^{2}} H}} \right. \kern-0em} H}} \right)$ = const следует, что частицы, дрейфующие во внутренней области ловушки, теряют энергию, а во внешней области, наоборот, приобретают энергию (ускоряются). Поскольку справедливо (1), то частицы дрейфуют с постоянством третьего адиабатического инварианта, т.е. остаются на инвариантных поверхностях постоянного потока. При этом относительно общей оси токовой системы 0–0₁ дрейф во внутренней области направлен от оси (объем ловушки увеличивается), а во внешней – к этой оси (объем ловушки уменьшается).

Из рисунка 2 видно, что магнитный поток исходной токовой системы, который проходит через экваториальную плоскость внутренней ловушки, задаваемый фиксированной силовой линией с экваториальным радиусом r (S_inner= πr²), выходит из объема токовой системы j₀, j₁ и распространяется во внешнее пространство. Далее он пересекает экваториальную плоскость внешней ловушки S_outer, но уже в обратном направлении. Площадь S_outer ограничена внутренней окружностью радиуса R, соответствующей вершине рассматриваемой силовой линии, и уходит на бесконечность при R → ∞. При этом магнитное поле Н стремится к 0, как 1/R³ (поле диполя). Иначе говоря, магнитный поток внутренней ловушки, выходя из токовой системы j₀, j₁, как бы выворачивается “наизнанку” во внешней области, заполняя все пространство. Это пространство ограничено объемом, который получается поворотом исходной силовой линии, представленной на рис. 2, вокруг оси 0–0₁ на 2π. Из геометрии силовых линий (рис. 2) ясно, что магнитные потоки Ф_inner и Ф_outer направлены противоположно и для одной и той же силовой линии равны по модулю. При этом, с ростом радиуса от оси 0–0₁ во внутренней и во внешней ловушках поле уменьшается.

Рассмотрим в самом общем виде сохранение третьего адиабатического инварианта при возмущении основного магнитного поля за счет включения внешних источников магнитного поля h. Положим, что начальный поток, охватываемый дрейфовой оболочкой до включения возмущения, равен Ф₀ и определяется характеристиками дипольного магнитного поля и геометрией дрейфовой поверхности. Через время ΔТ после включения возмущения дрейфовая поверхность будет определять новое значение потока Ф₁, вычисляемого по новым характеристикам магнитного поля. Изменение потока равно Ф₁ – Ф₀, при выполнении условия (1), и компенсируется потоком возмущающего поля ΔФ, охватываемого новой инвариантной поверхностью. В нашем случае $h||{{e}_{z}},$ поэтому ΔФ > 0 (рис. 2). При этом, в зависимости от соотношения между потоками Ф₀ и Ф₁, возможны два варианта: или эта разница больше нуля, или меньше. Если разница меньше нуля, то справедливо

$({{{\text{Ф }}}_{1}} + \Delta {\text{Ф }})--{{{\text{Ф }}}_{0}} = {{{\text{Ф }}}_{1}}--{\text{ }}({{{\text{Ф }}}_{0}}--\Delta {\text{Ф }}) = 0$

или

(2)

${{{\text{Ф }}}_{1}} = {{{\text{Ф }}}_{0}}--\Delta {\text{Ф }}.$

В случае, когда разница больше нуля, то

$({{{\text{Ф }}}_{1}}--\Delta {\text{Ф }})--{{{\text{Ф }}}_{0}} = {{{\text{Ф }}}_{1}}--({{{\text{Ф }}}_{0}} + \Delta {\text{Ф }}) = 0$

или

(3)

${{{\text{Ф }}}_{1}} = {{{\text{Ф }}}_{0}} + \Delta {\text{Ф }}.$

Последние выражения означают, что если разница Ф₁– Ф₀ меньше нуля, то из большего вычитается поток ΔФ (2), а если разница Ф₁– Ф₀ больше нуля, то к меньшему прибавляется ΔФ (3).

Для того, чтобы воспользоваться соотношениями (2), (3) необходимо знать явные значения потоков Ф₁, Ф₀ и ΔФ. Рассмотрим этот вопрос подробнее отдельно для внутренней и внешней ловушки.

2.2. Внутренняя ловушка

В нашем случае единичный вектор оси Z цилиндрической системы координат совпадает по направлению с возмущающим полем h (Z = 0 в центре пробкотрона на оси ОО₁/2). Обозначая радиальное расстояние внутренней ловушки прописной буквой r (см. рис. 2), имеем для магнитного потока в плоскости экватора $\left( {dS = {{e}_{z}}dS} \right)$

(4)

$\begin{gathered} {{\Phi }_{r}} = \iint\limits_S {({{H}_{r}}dS)} = \\ = \iint\limits_S {( - {{H}_{r}}{{{\mathbf{e}}}_{z}}\quad)}\left( {{{{\mathbf{e}}}_{z}}dS} \right) = - 2\pi \int\limits_0^r {{{H}_{r}}rdr} , \\ \end{gathered} $

где магнитное поле H_r(r) в области захвата с ростом r уменьшается, и градиент магнитного поля противоположен единичному вектору $\quad{{e}_{z}}.$ (Область захвата и пределы интегрирования в плоскости экватора для внутренней ловушки ограничены радиусом r_кр, на которой магнитное поле обращается в нуль. (Эту пограничную область со сложной топологией, разделяющую внешнюю и внутреннюю ловушки, мы не рассматриваем). Для потока возмущающего поля h можем записать

(5)

$\Delta \Phi = 2\pi \int\limits_0^r h \left( t \right)rdr = \pi h\left( {{{t}_{1}}} \right){{r}^{2}} > 0.$

По теореме о среднем для внутренней ловушки интеграл (4) можно представить $ - 2\pi \int_0^r {{{H}_{r}}} rdr$ = = $ - \pi {{r}^{2}}H_{r}^{{{\text{av}}}},$ где $H_{r}^{{{\text{av}}}}$(r_av) – среднее значение магнитного поля в некоторой точке r_av на интервале от 0 до r. Учитывая отрицательный знак потока (4), замечаем, что с ростом r поток во внутренней ловушке уменьшается. Для начального момента времени t₀= 0 и текущего t₁ изменение потоков исходного поля пробкотрона определяется разницей потоков (Ф_r1–Ф_r0) (4), которая меньше нуля

$ - \pi r_{1}^{2}H_{{{{r}_{1}}}}^{{{\text{av}}}} + \pi r_{0}^{2}H_{{{{r}_{0}}}}^{{{\text{av}}}} < 0.$

Это изменение компенсируется потоком возмущающего поля, т.е. из большего необходимо вычесть $\Delta \Phi \quad$ (вектор h совпадает по направлению с вектором ${{e}_{z}}$), следовательно, согласно (2) имеем

$ - \pi r_{1}^{2}H_{{{{r}_{1}}}}^{{{\text{av}}}} = - \pi r_{0}^{2}H_{{{{r}_{0}}}}^{{{\text{av}}}} - \quad\pi r_{1}^{2}h\left( {{{t}_{1}}} \right)$

или

(6)

$ - \pi r_{1}^{2}\left[ {H_{{{{r}_{1}}}}^{{{\text{av}}}} - h\left( {{{t}_{1}}} \right)} \right] = - \pi r_{0}^{2}H_{{{{r}_{0}}}}^{{{\text{av}}}}.$

Введя обозначение в (6)

$\left( {H_{{{{r}_{1}}}}^{{{\text{av}}}} - h} \right) = H_{{{\text{av}}\,\,{{r}_{1}}}}^{{{\text{dist}}}},$

получаем окончательно для равных потоков

(7)

$ - r_{1}^{2}H_{{{\text{av}}\,\,{{r}_{1}}}}^{{{\text{dist}}}} = - r_{0}^{2}{{H}_{{{\text{av}}\,\,{{r}_{0}}}}}.$

Из соотношения (7), которое получено на основе сохранения потоков, следует, что изменение магнитного поля на инвариантной поверхности совпадает с изменением магнитного поля в объеме внутренней ловушки при заданном внешнем возмущении. При этом с ростом r значение потока по модулю растет, а значение магнитного поля $\left| H \right|$ уменьшается.

2.3. Внешняя ловушка

2.3.1. Согласно вышесказанному магнитный поток внутренней ловушки, выходя за пределы токовой системы j₀, j₁, распространяется во внешнее пространство. Далее он пересекает экваториальную плоскость внешней ловушки S_outer, но уже в обратном направлении. Определим теперь этот магнитый поток через параметры внешней ловушки. Обозначая радиус-вектор через R, можем записать

(8)

$\iint\limits_{{{S}_{{{\text{outer}}}}}} {({{H}_{r}}dS)} = \iint\limits_{{{S}_{{{\text{outer}}}}}} {({{H}_{R}}{{e}_{z}})}\quad\left( {dS{{e}_{z}}} \right) = 2\pi \int\limits_R^\infty {{{H}_{R}}} RdR.$

Поскольку магнитное поле внешней ловушки представляет собой диполь, для которого в плоскости экватора (см. рис. 2) справедливо выражение

(9)

где а – магнитный момент токовой системы j₀, j₁, то подставив значение поля (9) в выражение (8) и проинтегрировав непосредственно от вершины силовой линии до бесконечности, получим

(10)

$\begin{gathered} \quad{{\Phi }_{{{\text{outer}}}}} = 2\pi \int\limits_R^\infty {{{H}_{R}}} RdR = \\ = 2\pi \int\limits_R^\infty {\frac{a}{{{{R}^{2}}}}} dR = 2\pi \frac{a}{R} = 2\pi {{R}^{2}}{{H}_{R}}, \\ \end{gathered} $

где H_R значение дипольного поля на экваторе с радиусом R. Из (10) следует, что с ростом R магнитный поток уменьшается, как 1/R.

В момент t₀ = 0, согласно (10), для начального магнитного потока дипольной составляющей внешней ловушки имеем $\Phi _{{{\text{outer}}}}^{0} = 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}},$ а к моменту t₁, за счет электрического дрейфа инвариантной поверхности к оси системы 0–0₁ (R₀ > R₁), можем записать, сохраняя дипольную зависимость H ~ 1/R³, $\Phi _{{{\text{outer}}}}^{1} = 2\pi R_{{1\quad}}^{2}{{H}_{{{{R}_{1}}}}}.$

Следовательно, за счет смещения инвариантной поверхности изменение магнитного потока, с учетом (9), определяется выражением

(11)

$\begin{gathered} \Phi _{{{\text{outer}}}}^{1} - \Phi _{{{\text{outer}}}}^{0} = 2\pi R_{{1\quad}}^{2}{{H}_{{{{R}_{1}}}}} - 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}} = \\ = 2\pi \frac{a}{{{{R}_{{0\quad}}}{{R}_{1}}}}\left( {{{R}_{0}} - {{R}_{1}}} \right) > 0. \\ \end{gathered} $

Пусть возмущающее поле h(t), включаясь в начальный момент t₀= 0, возрастает в течение времени t₁ по некоторому закону, который удовлетворяет условию (1). Тогда магнитный поток $\Delta \Phi $ возмущающего поля h, который к моменту t₁ охватывается инвариантной поверхностью с радиусом R₁, также определяется формулой (5) ($h$ по направлению совпадает с единичным вектором $\quad{{e}_{z}}$)

$\Delta \Phi = 2\pi \int\limits_0^{{{R}_{1}}} h \left( t \right)RdR = \pi h\left( {{{t}_{1}}} \right)R_{1}^{2} > 0.$

С учетом этого выражения и (11) из условия сохранения третьего адиабатического инварианта на основании (3) можем записать

$2\pi R_{{1\quad}}^{2}{{H}_{{{{R}_{1}}}}} = \pi h\left( {{{t}_{1}}} \right)R_{{1\quad}}^{2} + 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}}$

или

(12)

$2\pi R_{{1\quad}}^{2}\left[ {{{H}_{{{{R}_{1}}}}} - h{{\left( {{{t}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{t}_{1}}} \right)} 2}} \right. \kern-0em} 2}} \right] = 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}}.$

Из последнего выражения видно, что из условия сохранения потока, магнитное поле на инвариантной поверхности определяется разностью

$H_{{{{R}_{1}}}}^{{{\text{dist}}}} = \left[ {{{H}_{{{{R}_{1}}}}} - {{h}_{{{\text{av}}}}}\left( {{{t}_{1}}} \right)} \right],$

где ${{h}_{{{\text{av}}}}}\left( {{{t}_{1}}} \right) = {\;}h{{\left( {{{t}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{t}_{1}}} \right)} 2}} \right. \kern-0em} 2}$ – среднее значение возмущающего поля за временнóй интервал от t₀ до t₁. Окончательно это выражение можно представить

(13)

$R_{{1\quad}}^{2}H_{{{{R}_{1}}}}^{{{\text{av}}}} = R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}}.$

Следовательно, при таком вычислении потока (от R до ∞, см. (10)) на основании (13) и условия его сохранения, магнитное поле на инвариантной поверхности 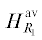уменьшается. Такой результат был ожидаем, т.к. из (10) следует, что с уменьшением радиуса R магнитный поток увеличивается, и разница (R₀– R₁) в выражении (11) имеет положительное значение. Поэтому для выполнения условия сохранения адиабатического инварианта в потоковой форме необходимо из большего конечного значения $\Phi _{{{\text{outer}}}}^{1}$ (см. формулу (11)) вычесть компенсацию, которая $\Delta \Phi > 0.$ Однако в нашем случае (см. рис. 2) магнитное поле во всем пространстве внешней ловушки возрастает.

2.3.2. Магнитный поток в геомагнитной ловушке, подобной внешней ловушке токовой системы ${{j}_{{\text{0}}}},{{j}_{1}},$ принято рассчитывать, вычисляя интеграл (8) с обратным знаком (это, в принципе, равносильно изменению пределов интегрирования от ∞ до R). В этом случае для потока (10) имеем

(14)

$\begin{gathered} {{\Phi }_{{{\text{outer}}}}} = 2\pi \int\limits_\infty ^R {HR} dR = --2\pi \int\limits_R^\infty {HR} dR = \\ = --2\pi \int\limits_R^\infty {\frac{a}{{{{R}^{2}}}}} dR = --2\pi \frac{a}{R} = \quad--2\pi {{R}^{2}}{{H}_{R}}. \\ \end{gathered} $

Из (14) следует, что с ростом R отрицательный поток также растет, стремясь к нулю из отрицательной области. При этом значения для потока внутренней ловушки (4) и внешней (14), соответствующие одной силовой линии, равны уже и по знаку. Теперь разность потоков $\Phi _{{{\text{outer}}}}^{1}$ и $\Phi _{{{\text{outer}}}}^{0}$ примет вид

(15)

$\begin{gathered} \Phi _{{{\text{outer}}}}^{1} - \Phi _{{{\text{outer}}}}^{0} = --2\pi R_{{{\kern 1pt} 1\quad}}^{2}{{H}_{{{{R}_{1}}}}} + 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}} = \\ = 2\pi \frac{a}{{{{R}_{{0\quad}}}{{R}_{{{\kern 1pt} 1}}}}}\left( {{{R}_{{{\kern 1pt} 1}}} - {{R}_{0}}} \right) < 0. \\ \end{gathered} $

Для отрицательной разницы потоков при $\Delta \Phi > 0$ справедливо выражение (2), согласно которому можем записать

$ - 2\pi R_{{{\kern 1pt} 1\quad}}^{2}{{H}_{{{{R}_{1}}}}} = - 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}} - \pi h\left( {{{t}_{1}}} \right)R_{1}^{2}$

или

(16)

Следует отметить, что выражение (16) совпадает с выражением, следующего из закона сохранения потока и полученного в работе [Редерера, 1972].

Введя обозначение

$H_{{{{R}_{1}}}}^{{{\text{dist}}}} = \left[ {{{H}_{{{{R}_{1}}}}} - \quad{{h\left( {{{t}_{1}}} \right)} \mathord{\left/ {\vphantom {{h\left( {{{t}_{1}}} \right)} 2}} \right. \kern-0em} 2}} \right],$

окончательно получаем

(17)

$\quad - R_{{1\quad}}^{2}H_{{{{R}_{1}}}}^{{{\text{dist}}}} = - R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}}.$

Сравнив между собой выражения (13) и (17), представляющие собой условия сохранения третьего адиабатического инварианта для внешней ловушки при одинаковом внешнем воздействии, вычисленные разными путями, замечаем, что они отличаются знаками. При этом, изменение магнитного поля на инвариантной поверхности не совпадает с его реальным изменением в пространстве ловушки. Из (12) и (16) следует, что согласно условию сохранения третьего инварианта в потоковой форме, магнитное поле на инвариантной поверхности уменьшается.

2.3.3. Расчет конкретного значения потока, проведенный в разделе 2.3.1 и 2.3.2 двумя способами, привел к двум соотношениям (13) и (17), отличающимся только знаками. Однако к расчету сохранения третьего инварианта в потоковой форме можно подойти несколько иначе. Действительно, поскольку нам, в конечном счете, необходимо знать разницу между потоками магнитного поля $\Phi _{{{\text{outer}}}}^{1}\quad$ и $\Phi _{{{\text{outer}}}}^{0},$ то можем вычислить интересующие нас потоки, проинтегрировав, например (10), от R_min до некоторого текущего значения R (см. рис. 2). Получим

(18)

$\begin{gathered} \quad{{\Phi }_{{{\text{outer}}}}} = 2\pi \mathop \smallint \limits_{{{R}_{{{\text{min}}}}}{\;}}^R \frac{a}{{{{R}^{2}}}}dR = - 2\pi \quad\frac{a}{R} + 2\pi \frac{a}{{{{R}_{{{\text{min}}}}}}} = \\ = - 2\pi {{R}^{2}}H + 2\pi R_{{{\text{min}}}}^{2}{{H}_{{{\text{min}}}}}, \\ \end{gathered} $

где R_min, например, нижняя граница внешней ловушки (R_min < R). Очевидно, что $\quad{{\Phi }_{{{\text{outer}}}}}$ в (18) больше нуля. На основе выражения (18) вычислим значения потоков $\Phi _{{{\text{outer}}}}^{1}\quad$ и $\Phi _{{{\text{outer}}}}^{0}$ для конкретных значений R₀ и R₁, соответствующих внешнему возмущающему полю h$\left( t \right),$ представленному на рис. 2, и определим их разницу

$\Phi _{{{\text{outer}}}}^{1} - \Phi _{{{\text{outer}}}}^{0} = - 2\pi R_{{{\kern 1pt} 1\quad}}^{2}{{H}_{{{{R}_{1}}}}} + 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}}.$

Последнее выражение больше нуля и, поскольку само$\quad\Delta \Phi > 0$ (см. (5)), окончательно получаем

$ - 2\pi R_{{{\kern 1pt} 1\quad}}^{2}{{H}_{{{{R}_{1}}}}} = - 2\pi R_{{0\quad}}^{2}{{H}_{{{{R}_{0}}}}} - \pi h\left( {{{t}_{1}}} \right)R_{{{\kern 1pt} 1}}^{2},$

что совпадает с условием сохранения (16).

Естественно, что аналогичный результат для разницы потоков получится, если магнитный поток вычислять как неопределенный интеграл и константу интегрирования определить, задав значение потока при R = R_min.

Из геометрии рис. 2 мы видим, что потоки, вычисляемые по формулам (10) и (18), разные и общим для них является силовая линия с фиксированным экваториальным радиусом, например, R₀, параметры которой и определяют значения потока. Эта силовая линия разделяет весь магнитный поток внешней ловушки на две части: от R_min до R₀ и от R₀ до ∞. Однако, воспользовавшись вычислением изменения потоков через определенный интеграл (18), мы избегаем физической некорректности, возникающей при интегрировании от конечного значения R до бесконечности, которая возникает, например, при вычислении потокового инварианта в реальной магнитосфере.

Положим теперь, что внешнее возмущающее поле $h\left( t \right),$ удовлетворяющее условию (2), имеет в начальный момент противоположный знак по сравнению с возмущающим полем, представленным на рис. 2. В этом случае электрический дрейф частиц и динамика инвариантных поверхностей представит обратную картину: во внутренней ловушке поле вместе с энергией частиц будут увеличиваться, и частицы дрейфуют к оси (ловушка сжимается, и радиус инвариантных поверхностей уменьшается); а во внешней ловушке, наоборот, поле вместе с энергией частиц будут уменьшаться, и частицы дрейфуют от оси (ловушка разбухает, и радиус растет).

В работе [Лонгмайер, 1966] доказывается теорема, в которой утверждается, что “Движение силовых линий магнитного поля можно всегда представить так, что точки пересечения этих линий с некоторой поверхностью, направленной нормально к ним в данный момент, будут двигаться со ско-ростью V_E”, т.е. со скоростью электрического дрейфа, т.е. плазма в скрещенных полях Н и Е должна увлекать в свое движение силовые линии магнитного поля. Известно, что в теории поля введение понятий силовых линий, а тем более их движение, не является необходимым. Однако понятие силовых линий и магнитных поверхностей равных потоков, ими образованных и обусловленных симметрией магнитных систем, является полезным и наглядным. Именно это и позволяет говорить о разбухании или сжатии магнитной ловушки.

3. АДИАБАТИЧЕСКАЯ ДЕФОРМАЦИЯ МАГНИТОСФЕРЫ ЗЕМЛИ ВО ВРЕМЯ МАГНИТОСФЕРНОЙ БУРИ

Взаимодействие магнитосферы Земли с потоком возмущенного солнечного ветра, сформировавшегося в результате активных процессов на Солнце, приводит к развитию различной совокупности физических процессов в околоземном космическом пространстве, получивших название магнитосферной бури. Из всей совокупности явлений, сопровождающих развитие бури на главной и восстановительной фазах, нас будет интересовать только деформация магнитного поля и соответствующая этому динамика захваченной радиации, обусловленные кольцевым током (RC). Будем полагать, что действие RC удовлетворяет адиабатическому условию (1). Сам механизм формирования RC нами не рассматривается.

3.1. Главная фаза магнитной бури

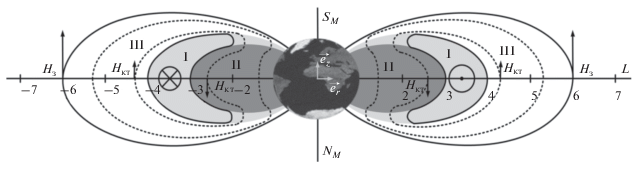
На рисунке 3 представлен симметричный разрез магнитосферы, на котором обозначены RC (I) и (по отношению к нему) внутренняя (II) и внешняя области (III) магнитосферы. Положим, что область формирования RC ограничена силовыми линиями диполя в интервале параметра Мак-Илвейна L = 3–4.

Рис. 3.

Схематическое представление магнитосферы Земли в области захвата.

Знание реальной области расположения RC при нашем анализе не принципиально, для нас важным является то, что этот ток разделяет дипольное магнитное поле на внутреннюю и внешнюю область). Магнитный северный полюс дипольного поля N_м расположен в районе южного географического полюса Земли. Силовые линии RC на рис. 3 обозначены мелким пунктиром, а сам ток направлен на запад. В левой полуплоскости на рис. 3 это обозначено символом ⨂ (“от нас”), в правой полуплоскости – ⨀ (“к нам”). Магнитное поле кольцевого тока во внутренней области (II) $H_{{RC}}^{r} = {{H}_{{dst}}}$ направлено противоположно магнитному полю Земли Н_E $\left( {{\mathbf{H}}_{{RC}}^{r} = - Н _{{RC}}^{r}{{e}_{z}}} \right),$ а во внешней области (III) $Н _{{Rc}}^{R}$ совпадает с магнитным полем Земли $(H_{{RC}}^{R} = Н _{{RC}}^{R}{{{\mathbf{e}}}_{z}}).$ (Объяснение введения верхних индексов при Н “r” и “R” будет дано ниже). Исходное магнитное поле в областях II и III является дипольным. На главной фазе развития магнитной бури за счет Dst – вариации во внутренней области происходит уменьшение магнитного поля $\left( {\left( {{{\partial {{H}_{{{\text{inner}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{inner}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) < 0} \right),$ электрическое поле направлено от нас, а во внешней – увеличение поля $\left( {\left( {{{\partial {{H}_{{{\text{outer}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{outer}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) > 0} \right)$ и электрическое поле направлено к нам). Вихревое электрическое поле в этих областях имеет противоположное направление: по часовой стрелке, если смотреть по направлению вектора ${{e}_{z}},$ в области II, и против часовой стрелки в области III. Следовательно, возникшие индукционные электрические поля приводят к дрейфу заряженных частиц от Земли по направлению к RC во внутренней области II, а во внешней области III – к дрейфу и к Земле, и к RC. Если выполняется условие адиабатической деформации магнитного поля (1), то этот дрейф осуществляется с сохранением третьего адиабатического инварианта. Выбрав только плоскость экватора (${{\text{v}}_{{{\text{II}}}}}$ = 0), из условия сохранения первого инварианта $\mu = \left( {{{m\text{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{m\text{v}_{ \bot }^{2}} H}} \right. \kern-0em} H}} \right) = {\text{const}}$ следует, что частицы, дрейфующие во внутренней области ловушки, теряют энергию (остывают), а во внешней области, наоборот, приобретают энергию (ускоряются). Данная картина полностью совпадает с ситуацией, описанной в предыдущем разделе на примере внутренней и внешней ловушках, образованных двумя витками с током при параллельном их включении. Отличие заключается в существовании реального источника возмущающего поля h, создаваемого кольцевым током, а также в дипольном приближении исходного поля обеих ловушек.

Рассмотрим динамику магнитных поверхностей, соответствующих адиабатической деформации магнитного поля и соответствующую динамику магнитосферной плазмы во внутренней II и внешней III областях с точки зрения сохранения третьего инварианта Ф. Чтобы отличать внутреннюю область ловушки от внешней, поступим аналогично разделу 1, обозначив радиус-вектор частицы во внутренней ловушке через прописную букву r, а во внешней ловушке – заглавной буквой R. Кроме того, верхними индексами “r” и “R” будем обозначать магнитные поля дипольного поля и RC во внутренней и внешней ловушках. Полагаем, что выполняется условие (1) и влияние кольцевого тока на исходное дипольное поле как во внешней, так и во внутренней ловушке зависит только от времени, а асимметрия поля и его радиальная зависимости отсутствуют. Дипольная составляющая магнитного поля определяется по формуле (9) и обозначается индексом “r” для области II и индексом “R” для области III. Индекс “0” при буквенном обозначении соответствует начальным значениям этого параметра, индекс “1” – конечным значениям. Для вычисления потоков воспользуемся формулой (18), в которой можно положить, что R_min = R_Е, где R_Е – радиус Земли.

Во внутренней области II разница потоков $\Phi _{{{\text{inner}}}}^{1} - \Phi _{{{\text{inner}}}}^{0} > 0.$ Тогда учитывая, что r₀ < r₁, $\Delta \Phi = - \pi r_{1}^{2}H_{{RC}}^{r} < 0$ и с учетом знаков 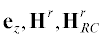из условия сохранения потока, имеем (см. (4))

$ - \quad2\pi r_{1}^{2}H_{1}^{r} + \left( { - \pi r_{1}^{2}H_{{RC}}^{r}} \right) = - 2\pi r_{0}^{2}H_{0}^{r}$

или

(19)

$ - r_{1}^{2}\left[ {H_{1}^{r} + \frac{{H_{{RC}}^{r}}}{2}} \right] = - r_{0}^{2}H_{0}^{r}.$

Для внешней области III R₀ > R₁, ΔΦ = = $\pi R_{1}^{2}H_{{RC}}^{R} > 0$ и с учетом знаков 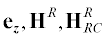из условия сохранения потока имеем (см. (14))

$ - 2\pi R_{{1\quad}}^{2}{{H}_{{{{R}_{1}}}}} + \pi H_{{RC}}^{R}R_{1}^{2} = - 2\pi R_{{0\quad}}^{2}H_{0}^{R}$

или

(20)

$ - R_{{{\kern 1pt} 1}}^{2}\left[ {H_{1}^{R} - \frac{{H_{{RC}}^{R}}}{2}} \right] = - R_{{0\quad}}^{2}H_{0}^{R}.$

Следовательно, в результате действия RC складываются условия, при которых энергичные частицы начинают со скоростью электрического дрейфа стягиваться к нему как с внешней, так и внутренней (по отношению к току) областей. Если при этом во внутренней области частицы замедляются, то во внешней, наоборот, ускоряются. В тоже время на главной фазе магнитной бури в всем пространстве внутренней ловушки за счет Dst-вариации поле уменьшается, а в пространстве внешней растет.

Из рисунка 3 следует, что магнитный поток, создаваемый RC, выходит из области II и распространяется во внешней области III. Асимметрия магнитного поля также отсутствует. Кроме того, будем предполагать, что внутренний поток магнитного поля RC, выходя наружу во внешнюю ловушку, пересекает экваториальную плоскость, ограниченную с подсолнечной и с полуночной стороны радиусом R, равным расстоянию до магнитопаузы R_mp и соответствующим максимальному сжатию магнитосферы на главной фазе магнитной бури. С ночной стороны радиус R_mp превышает расстояния, на котором силовые линии замкнуты, но, тем самым, мы, в какой-то мере, учтем часть потока RC, уносимого незамкнутыми силовыми линиями в хвост магнитосферы.

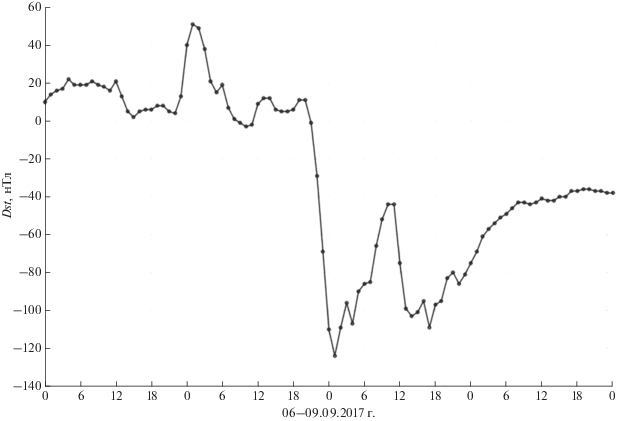
Рис. 4.

Графическое представление Dst-вариации горизонтальной Н-компоненты магнитного поля магнитной бури в сентябре 2017 года согласно (http://wdc.kugi.kyoto-u.ac.jp/dst_realtime/201709/index.html).

Из условия сохранения магнитного потока по модулю для внутренней и внешней областей КТ можем записать

отсюда

(21)

В (21) приняты следующие обозначения $H_{{RC}}^{r} = {{H}_{{dst}}},$ $H_{{RC}}^{R}$ – соответствующие значения внутреннего и внешнего магнитного поля RC; ${{r}_{{{\text{inner}}}}}$ и ${{R}_{{{\text{outer}}}}}$ – радиусы внутренней и внешней границ поверхности КТ в плоскости экватора. При наших предположениях согласно рис. 3 имеем ${{r}_{{{\text{inner}}}}} = 3{{R}_{E}},$ ${{R}_{{{\text{outer}}}}} = 4{{R}_{E}},$ ${{R}_{{mp}}} = 10{{R}_{E}}$ и из (18) имеем

Выполненная оценка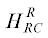

показывает, что увеличение поля во внешней области магнитосферы за счет магнитного поля RC составляет порядка 10% от ${{H}_{{dst}}}$ – вариации во внутренней области. Данная оценка находится в согласии с результатами прямых измерений [Hoffman and Bracken, 1965; Sugiura and Poros, 1973].

3.2. Восстановительная фаза магнитной бури

На заключительной фазе магнитной бури происходит ослабление солнечного ветра, прекращается действие механизма накачки RC энергичными частицами, магнитосфера начинает расширяться и восстанавливаться до своих первоначальных границ. Динамика инвариантных поверхностей, меняется на обратную. Во внутренней ловушке магнитное поле возрастает $\left( {\left( {{{\partial {{H}_{{{\text{inner}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{inner}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) > 0} \right)$ и электрическое поле (см. рис. 3) направлено к нам), и плазма со скоростью электрического дрейфа движется от RC по направлению к Земле. При этом, энергия заряженных частиц растет. В свою очередь, во внешней ловушке магнитное поле убывает $\left( {{{\partial {{H}_{{{\text{outer}}}}}} \mathord{\left/ {\vphantom {{\partial {{H}_{{{\text{outer}}}}}} {\partial t}}} \right. \kern-0em} {\partial t}}} \right) < 0,$ электрическое поле направлено от нас, и частицы, удаляясь от RC и Земли, замедляются.

В результате действия электрического дрейфа частицы начинают двигаться от RC как во внешней, так и внутренней области.

4. ОЦЕНКА ЭНЕРГИИ ЗАРЯЖЕННЫХ ЧАСТИЦ, УДОВЛЕТВОРЯЮЩИХ УСЛОВИЮ СОХРАНЕНИЯ ТРЕТЬЕГО ИНВАРИАНТА ДЛЯ МАГНИТНОЙ БУРИ 07.09.2017 г.

Оценим энергию, которой должны обладать заряженные частицы, чтобы удовлетворять условию сохранения третьего адиабатического инварианта ${{Т }_{d}}\left| {\frac{{dH}}{{dt}}} \right| \ll \left| H \right|$ для конкретной магнитной бури на главной фазе. Рассмотрим магнитную бурю с внезапным началом в 22 UT от 06.09.2017 г. (http://wdc.kugi.kyoto-u.ac.jp/dst_realtime/201709/ index.html). Главная фаза бури развивалась с 20 UT 07.09 и продолжалась Δt = 5 ч, завершившись в 01 UT 08.09.2017. Восстановительная фаза бури закончилась 11.09.2017 г. (см. рис. 4).

Из этого рисунка, построенного на основе табличных данных, приведенных в (http://wdc.kugi.kyoto-u.ac.jp/dst_realtime/201709/index.html), следует, что на главной фазе бури за 5 ч амплитуда Dst-вариации составила $\Delta {{H}_{{dst}}}$ = $\Delta H_{{К С }}^{r}$ = 135 нТл. Изменение происходило практически по линейному закону, поэтому можем записать

(22)

${{T}_{d}}\left| {\frac{{dH}}{{dt}}} \right| \approx {{T}_{d}}\left| {\frac{{\Delta {{H}_{{dst}}}}}{{\Delta t}}} \right| \ll \left| H \right|,$

где в нашем случае ($\left( {{{\Delta {{H}_{{dst}}}} \mathord{\left/ {\vphantom {{\Delta {{H}_{{dst}}}} {\Delta t}}} \right. \kern-0em} {\Delta t}}} \right) = 0.45\quad({\text{н Т л /м и н }})$ для внутренней области RC (в нашем случае L < 3) и, согласно (22), равно 0.045 (нТл/мин) для внешней области тока (L > 4). Главная фаза бури имела длительность 300 мин, следовательно, периоды дрейфа должны быть, как минимум, на порядок меньше этой величины, т.е ${{Т }_{d}} \leqslant 30\quad$ мин. В свою очередь, каноническое условие сохранения третьего инварианта (23), говорит о том, что изменение магнитного поля за период дрейфа частицы должно быть много меньше исходного поля, т.е. заметные изменения происходят за много периодов дрейфа. Действительно, для L = 1.5 магнитное поле на экваторе, определяемое согласно ${{H}_{E}}\left( L \right) = {{(3 \times {{{10}}^{4}})} \mathord{\left/ {\vphantom {{(3 \times {{{10}}^{4}})} {{{L}^{3}}}}} \right. \kern-0em} {{{L}^{3}}}}$ (нТл), равно ${{H}_{E}}\left( {L = 1.5} \right)$ = $ = 8.9 \times {{10}^{3}}\left[ {{\text{н Т л }}} \right]$ и за 30 мин изменится только на ΔН = $\quad0.45 \times 30 = 3.5\left[ {{\text{н Т л }}} \right],$ что много меньше исходного поля ${{H}_{E}}\left( {L = 1.5} \right) \gg \Delta H.$ Для внешней области RC, например, для L = 6, где ${{H}_{E}}\left( {L = 6} \right) = 140{\;}\left[ {{\text{н Т л }}} \right]\quad$ изменение составит ΔН = = $\quad0.045 \times 30 = 1.35\left[ {{\text{н Т л }}} \right],$ что также много меньше исходного поля.

Следовательно, максимальное значение периода дрейфа для выбранной бури должно равняться 30 мин независимо от параметра L. Чем меньше этот период дрейфа, тем лучше, согласно (23), условия для сохранения третьего инварианта.

В свою очередь, период дрейфа связан с энергией частицы и параметром Мак-Илвейна соотношением [Кузнецов и Тверская, 2007]

(23)

${{T}_{d}} = \frac{{88}}{{LE}}\frac{{(1 + {E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}})}}{{(2 + {E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}})}}{{f}_{{\varphi \quad}}}\left( {{{\lambda }_{{{\text{mirr}}}}}} \right).$

Для плоскости экватора ${{\lambda }_{{{\text{mirr}}}}} = 0$ и функция ${{f}_{{\varphi \quad}}}\left( {{{\lambda }_{{{\text{mirr}}}}}} \right),$ определяющая зависимость ${{T}_{d}}$ от широты зеркальной точки ${{\lambda }_{{{\text{mirr}}}}},$ равна 1. С учетом этого последнее выражение можно представит для трех продельных случаев

(23а)

${{T}_{d}} = \frac{{44}}{{LE}}\quad\,\,({\text{м и н }})\,\,\,\,\left( {E \ll {{E}_{0}}} \right),$

(23б)

${{T}_{d}} = \frac{{88}}{{LE}}\quad\,\,({\text{м и н }})\,\,\,\,\left( {E \gg {{E}_{0}}} \right),$

(23в)

${{T}_{d}} = \frac{{59}}{{LE}}\quad\,\,({\text{м и н }})\,\,\,\,\left( {E\sim {{E}_{0}}} \right).$

Энергия покоя электрона – 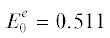МэВ, а энергия покоя протона – $E_{0}^{p} = 938\quad$ МэВ. Для протонов энергия покоя будет заведомо много больше энергии захваченных протонов, поэтому оценку минимальной энергии при заданных периоде ${{T}_{d}}$ и параметрах L можно делать по формуле (23а) (см. табл. 1). В свою очередь, из таблицы видно, что полученные энергии ${{E}^{p}}\quad$ порядка энергии покоя электрона $({{E}^{е }}\sim E_{0}^{е }),$ поэтому для оценки нижнего порога энергии электрона можно воспользоваться соотношением (23в) (см. табл. 1).

Таблица 1.

Минимальные значения энергий протонов Е_р и электронов Е_е, обеспечивающих сохранение третьего адиабатического инварианта в потоковой форме на главной фазе для магнитной бури 06.09.2017 г.

L	1.5	2	3	4	5	6
Е_р кэВ	980	735	490	370	290	245
Е_е кэВ	1310	985	660	490	390	330

Согласно результатам, представленными в таблице, можно отметить, что чем выше энергия частиц по отношению к рассчитанным минимальным энергиям для данных параметров L, тем лучше сохраняется третий адиабатический инвариант на главной фазе рассматриваемой бури. Тем более это будет справедливо для восстановительной фазы, продолжавшейся три дня с 08.09. по 11.09.2017 г. Следовательно, можно сказать, что приведенная в качестве примера магнитная буря для частиц, энергия которых, как функция параметра L, равна или больше энергий, представленных в таблице, сопровождается обратимыми процессами и сохранением экваториальных заряженных частиц на конкретных инвариантных поверхностях. Чем выше энергия частицы, тем устойчивей они к изменениям поля на главной фазе бури.

5. ОБСУЖДЕНИЕ

Пусть в начальный момент формирования главной фазы магнитной бури (t₀ = 0) частица находится в точке с экваториальным радиусом r₀ и значением поля Н₀ (для определенности выберем внутреннюю область геомагнитной ловушки II (см. рис. 3)). Включение поля $H_{{RC}}^{r}$ приводит к тому, что частица через время Δt приходит в точку r₁ = r₀ + Δr (Δr > 0), в которой дипольное магнитное поле стало $H_{1}^{r}\left( {{{r}_{1}}} \right){\;}\sim {1 \mathord{\left/ {\vphantom {1 {{{{({{r}_{1}})}}^{3}}}}} \right. \kern-0em} {{{{({{r}_{1}})}}^{3}}}}.$ Поскольку $H_{{RC}}^{r}\quad$ < 0, то реальное возмущенное поле в точке с r₁ в момент t₁ = Δt будет иметь значение $H_{1}^{{{\text{dist}}}}\left( {{{r}_{{1\quad}}},\Delta t} \right)\quad$ = = $H_{1}^{r}\left( {{{r}_{1}}} \right)$ – $H_{{RC}}^{r}\left( {\Delta t} \right)$ т.е. меньше $H_{1}^{r}$ на величину возмущения. Однако инвариантная поверхность, которая рассчитывается из условия сохранения третьего инварианта, определяет поле, согласно выражению (19), как сумму $H_{1}^{{{\text{dist}}}}\left( {{{r}_{{1\quad}}},\Delta t} \right) = H_{1}^{r} + \frac{{H_{{RC}}^{r}}}{2},$ где $\frac{{H_{{RC}}^{r}}}{2}$ – среднее значение возмущения на интервале Δr. Т.е. в этом случае возмущенное поле больше дипольной составляющей $H_{1}^{r}.$ Следовательно, третий адиабатический инвариант в потоковой форме для переменного поля имеет чисто математическое понятие, говорящее о балансе потоков. В этом случае на первый план должно выходить каноническое понятие третьего инварианта как инварианта движения заряженной частицы по циклической координате φ [Богданов, Плетнев, 1972а; Богданов, Плетнев, 1972б].

6. ЗАКЛЮЧЕНИЕ

Подводя итог, следует отметить следующее.

1. Магнитное поле определенного знака $h\left( t \right),$ наложенное на магнитную систему двух витков с параллельными токами (см. рис. 2), приводит к возникновению электрического поля одинакового знака как во внутренней, так и внешней магнитных ловушках, но к разному поведению инвариантных оболочек. При этом:

– с ростом радиуса-вектора во внутренней ловушке по модулю поле уменьшается, а поток растет. В тоже время во внешней ловушке с ростом радиуса поле уменьшается (Н ~ 1/r ³), поток также уменьшается (r²Н ~ 1/r).

– если при заданном знаке возмущающего поля h (рис. 2) во внутренней ловушке магнитное поле уменьшается как в пространстве, так и на поверхности постоянного третьего инварианта в потоковой форме, то во внешней ловушке магнитное поле в пространстве растет, а на инвариантной поверхности уменьшается;

– общим для внутренней и внешней ловушек является то, что при уменьшении поля (ловушка разбухает) плазма дрейфует от оси системы, при увеличении поля (ловушка сжимается) плазма дрейфует к оси.

2. Аналогичная ситуация, с точки зрения динамики плазмы и инвариантных поверхностей, возникает и при рассмотрении возмущенного геомагнитного поля (см. рис. 3). Разница заключается в том, что для двух витков с током внешнее дипольное поле не ограничено, в то время, как в геомагнитном поле область устойчивого захвата плазмы ограничена с дневной стороны магнитопаузой, а с ночной – замкнутыми силовыми линиями.

3. RC (область I, см. рис. 3) разделяет магнитосферу на две области. На главной фазе магнитной бури во внутренней области поле за счет Dst-вариации поле уменьшается (область II), а во внешней области поле увеличивается (область III). При этом на инвариантной поверхности в области II поле увеличивается (см. (19)), а в области III оно уменьшается (см. (20)).

4. Показано, что при вычислении третьего инварианта практическое значение имеет не численное значение самого магнитного потока Ф, а только его изменение, равное разнице конечного и начального значений потоков, рассчитанных по параметрам дипольного невозмущенного поля. В этом случае при вычислении потоков отпадает необходимость в использовании несобственных интегралов, что для реальных ограниченных магнитных полей является принципиальным.

5. Для описания поведения инвариантных поверхностей в возмущенном геомагнитном поле приближенному к реальному, необходимо учитывать модель деформации силовых линий. Для такого описания, подходит модель уравнения силовой линии, имеющей вид r = r₁cos^kλ, где k ≤ 2–4. Если k = 2, то уравнение соответствует диполю, а если k = 4 – сильной магнитной бури [Плетнев и Шалимов, 1970]. Кроме того, необходимо учитывать ограниченность геомагнитной ловушки и наличие RC, разделяющего магнитосферу на две части.

6. В центральной части RC существует область, в которой магнитное поле не изменяется. В этой области происходит обращение знака производной ${{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial t}}} \right. \kern-0em} {\partial t}}.$ Поэтому и магнитное поле h, возбуждаемое RC, и индукционное поле E здесь обращаются в нуль. Можно предположить, что эта область соответствует параметру L_m, характеризующему положения максимума давления КТ и являющимся функцией Dst-вариации [Ковтюх, 2001].

7. По результатам расчетов минимальных значений энергий (см. табл. 1) можно отметить, что чем выше энергия частиц по отношению к рассчитанным минимальным значениям энергии для конкретных параметров L, тем лучше сохраняется третий адиабатический инвариант на главной фазе рассмотренной в качестве примера бури. В этом случае для частиц, энергия которых, как функция параметра L, равна или больше энергий, представленных в таблице, динамика сопровождается обратимыми процессами, т.е. с сохранением экваториальных заряженных частиц на конкретных инвариантных поверхностях. Следовательно, чем выше энергия частицы, тем устойчивей они к изменениям поля на главной фазе бури.

7. БЛАГОДАРНОСТИ

В заключении автор приносит благодарность исполняющему обязанности заведующего обсерватории Паратунка (ИКИР ДВО РАН), ведущему научному сотруднику, к.ф.-м.н. Хомутову С.Ю. за предоставленные данные по магнитной бури 07.09.2017 г.

Список литературы

− Богданов В.В., Плетнев В.Д. К вопросу о точности сохранения третьего адиабатического инварианта движения заряженной частицы в аксиально-симметричных полях. I // Космич. исслед. Т. 10. № 3. С. 358–367. 1972а.
− Богданов В.В., Плетнев В.Д. К вопросу о точности сохранения третьего адиабатического инварианта движения заряженной частицы в аксиально-симметричных полях. II // Космич. исслед. Т. 10. № 4. С. 528–531. 1972б.
− Богуславский С.А. Пути электронов в электромагнитных полях // Избранные труды по физике. М.: ГИФМЛ. С. 237–403. 1961.
− Ковтюх А.С. Радиальный профиль давления буревого кольцевого тока как функция Dst // Космич. исслед. Т. 48. № 3. С. 218–238. 2010.
− Лонгмайр К. Физика плазмы. М.: Атомиздат, 341 с. 1966.
− Плетнев В.Д., Шалимов В.П. Адиабатическое втягивание квазизахваченных заряженных частиц полем геомагнитной ловушки во время восстановительной фазы магнитной бури. // Космич. исслед. Т.8. № 2. С. 251–260. 1970.
− Редерер Х. Динамика радиации, захваченной геомагнитным полем. М.: Мир, 192 с. 1972.
− Сивухин Д.В. Дрейфовая теория движения заряженной частицы в электромагнитных полях // Вопросы теории плазмы. М.: Госатомиздат. № 1. С. 7–97. 1963.
− Кузнецов С.Н., Тверская Л.В. Радиационные пояса. Модель космоса. М.: ООО “КДУ”. Т. 1. С. 518–546. 2007
− Hoffman R.A., Bracken P.A. Magnetic effects of the quiet-time proton belt // J. Geophys. Res. V. 70. P. 3541–3556. 1965.
− Sugiura M., Poros D.J. A magnetospheric field model incorporating the OGO 3 and 5 magnetic field observation // Planet. Space Sci. V. 21. P. 1763–1773. 1973.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал