Геомагнетизм и аэрономия, 2020, T. 60, № 2, стр. 195-207
Влияние геомагнитного поля на движение пассивных проводящих спутников
1 Научно производственная корпорация
“Системы прецизионного приборостроения”
г. Москва, Россия
2 Институт земного магнетизма, ионосферы и распространения радиоволн
им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Москва, г. Троицк, Россия
3 Институт физики Земли им. О.Ю. Шмидта РАН (ИФЗ РАН)
г. Москва, Россия
* E-mail: surkovvadim@yandex.ru
Поступила в редакцию 07.05.2019
После доработки 04.07.2019
Принята к публикации 26.09.2019
Аннотация
В работе теоретически исследуется воздействие геомагнитного поля на вращение пассивных проводящих спутников сферической формы, таких как российско-австралийский спутник WESTPAC и российский спутник Ларец. Основной механизм рассматриваемого эффекта заключается в генерации вихревых токов и магнитного момента спутника, которые взаимодействуют с магнитным полем Земли. Получены аналитические выражения для орбитального и собственного магнитных моментов спутника, возникающих за счет поступательного движения спутника по орбите и его вращения вокруг осей, проходящих через центр масс, при произвольном соотношении между толщиной скин-слоя и радиусом спутника. Рассчитываются механический момент сил, действующих на спутник в геомагнитном поле, и изменение его угловой скорости вращения. Рассматривается движение спутника по круговой орбите с произвольным наклонением с учетом вращения вектора геомагнитного дипольного момента. Оценивается характерное время экспоненциального уменьшения со временем угловой скорости вращения спутника вокруг собственной оси. Исследуются особенности остаточных нерегулярных колебаний вращательной скорости спутника.
1. ВВЕДЕНИЕ
В последнее время наблюдается рост популярности микро ‒ и наноспутников, а также спутников класса Cube Sat, запускаемых на низкие орбиты. Возрастание научного потенциала этих спутников приводит к увеличению их производства во многих странах. Важной и еще не до конца решенной проблемой является воздействие космической плазмы и электромагнитных полей на движение низкоорбитальных спутников, которое может приводить к изменению параметров орбиты и положения спутников на орбите [Müncheberg et al., 1996; Petrukovich and Nikiforov, 2016]. К числу крайних примеров такого воздействия относится происшествие с пассивным лазерным наноспутником BLITS, запущенным 17.09.2009 г. на орбиту высотой 832 км, а затем разрушенным предположительно в результате столкновения с космическим мусором [Kucharski et al., 2013; Руйбис, 2016; Васильев, 2018]. Другой возможной причиной разрушения наноспутника BLITS мог стать пробой диэлектрика в его корпусе в результате накопления электрического заряда при взаимодействии спутника с электронами радиационных поясов Земли [Сурков и Мозгов, 2019].
Еще один пример связан с российским лазерным микроспутником Ларец, запущенным 27.09.2003 г. на орбиту высотой 690 км. Этот пассивный микроспутник сферической формы был предназначен для лазерной дальнометрии и был снабжен ретрорефлекторами, расположенными на его поверхности [Руйбис, 2016; Vasiliev et al., 2007]. Наблюдения показали, что вращение спутника вокруг собственной оси постепенно замедлялось и практически прекратилось по истечении двух с половиной лет, что сделало невозможным его дальнейшую эксплуатацию. Возможной причиной данного эффекта является генерация вихревых электрических токов в проводящем корпусе спутника при его вращении в геомагнитном поле. Магнитный момент этих токов взаимодействует с геомагнитным полем, что приводит к появлению механического момента, тормозящего вращение спутника [Rosenstock, 1957; Зонов, 1959; Белецкий, 1965].
Системы магнитной стабилизации положения спутника основаны на том же эффекте, т.е. на взаимодействии магнитного момента спутника с геомагнитным полем [Ovchinnikov et al., 2016, 2018; Pichuzhkina and Roldugin, 2016; Ivanov et al., 2017; Samotokin et al., 2018]. Основными структурными элементами пассивной системы контроля положения спутника могут быть постоянные магниты, гистерезисные стержни, выполненные из магнитомягких материалов [Santoni and Zelli, 2009], сферический магнитный демпфер, представляющий из себя поплавок с собственным магнитным моментом, который может вращаться в вязкой жидкости, что приводит к рассеиванию механической энергии [Садов, 1969]. Во многих случаях предпочтительнее применять активные магнитные системы контроля положения спутника, в которых используются магнитные катушки с или без намагниченного сердечника [Candini et al., 2012; Guo and Bouwmeester, 2016].
Проблема взаимодействия спутников с космической плазмой и геомагнитным полем вновь становится актуальной после появления пассивных низкоорбитальных микро- и наноспутников, предназначенных для систем космической связи, лазерной дальнометрии и других целей. Несмотря на малость магнитных эффектов они могут повлиять на точность прецизионных лазерных измерений расстояний от спутника до земли. При теоретическом анализе этих эффектов обычно предполагают, что период вращения спутника вокруг собственной оси намного больше характерного времени диффузии магнитных возмущений в проводящую оболочку спутника. В этом случае из соображений размерности и подобия следует, что механический момент силы Ампера, действующей на спутник, пропорционален его угловой скорости и квадрату индукции геомагнитного поля с коэффициентом пропорциональности, зависящим от угла между этими векторами, формы спутника и других параметров (см, например, [Белецкий, 1965]). Если угловая скорость собственного вращения спутника мала, то необходимо дополнительно учитывать орбитальный эффект, связанный с изменением потока геомагнитного поля через корпус спутника при его поступательном движении по орбите.
В настоящем исследовании эта проблема рассматривается для пассивных сферических спутников, таких как GFZ-1, WESTPAC, Ларец и других, что позволяет получить более точное решение задачи при произвольном соотношении между глубиной скин-слоя и радиусом спутника. Основное внимание уделяется выводу аналитических выражений, описывающих не только магнитный момент, связанный с собственным вращением спутника, но и орбитальный магнитный момент спутника, а также их взаимодействию с геомагнитным полем.
2. ОРБИТАЛЬНЫЙ МАГНИТНЫЙ МОМЕНТ СПУТНИКА
В различных точках орбиты спутника геомагнитное поле принимает различные значения как по модулю, так и по направлению. Поэтому во время движения спутника постоянно меняется поток вектора геомагнитной индукции через корпус спутника. Если в конструкции спутника имеются проводящие детали, то в них возникают индукционные токи. Сила Ампера, действующая на эти токи, может оказать воздействие на параметры движения пассивных спутников, не имеющих системы стабилизации положения. Полагаем, что магнитная проницаемость вещества спутника равна единице, т.е. эффект намагничивания вещества здесь не рассматривается.
В дальнейшем будем различать два вида движения спутника. Это поступательное движение по орбите в том смысле, что оси системы координат, жестко связанные с центром масс спутника, остаются параллельными самим себе, и вращательное движение спутника вокруг собственной оси симметрии. Оба типа движений спутника в геомагнитном поле сопровождаются генерацией индукционных токов и образованием магнитных моментов, которые мы будем называть орбитальным и спиновым (или собственным) моментами по аналогии с атомной физикой, в которой рассматривается орбитальный и собственный, т.е. связанный со спином, магнитные моменты электрона в атоме.
Вначале исследуем поступательное движение спутника по орбите и связанный с этим движением магнитный момент. Рассмотрим систему координат $\left( {{{x}_{e}},{{y}_{e}},{{z}_{e}}} \right)$, начало которой расположим в центре Земли, а ось ${{z}_{e}}$ направим вдоль вектора угловой скорости Земли ${{{\mathbf{\omega }}}_{e}}$. Затем перейдем в систему отсчета, которая движется поступательно со скоростью спутника ${\mathbf{V}}$. Начало отсчета этой системы координат расположено в центре масс спутника. Из закона преобразования электромагнитного поля в нерелятивистском пределе ($\left| {\mathbf{V}} \right| \ll c$) следует, что магнитное поле Земли в движущейся системе отсчета остается практически прежним [Ландау и Лифшиц, 1960]. Поскольку размеры спутника малы, то магнитное поле Земли ${{{\mathbf{B}}}_{e}}$ в пределах корпуса спутника практически однородное, хотя его величина и направление зависят от времени, т.е. ${{{\mathbf{B}}}_{e}} = {{{\mathbf{B}}}_{e}}\left( t \right)$.
Для упрощения задачи рассмотрим спутник в виде однородного проводящего шара радиуса $a$. Если пренебречь токами смещения в шаре, то квазистационарное уравнение Максвелла для магнитного поля ${\mathbf{B}}$ в шаре имеет вид:
где символ ${{\partial }_{t}}$ обозначает частную производную по времени; $D = {{\left( {{{\mu }_{0}}\sigma } \right)}^{{ - 1}}}$ – коэффициент диффузии магнитных возмущений; $\sigma $ – электропроводность шара; ${{\mu }_{0}}$ – магнитная постоянная. Проводимостью космической плазмы пренебрегаем, полагая, что вне шара выполняется уравнение: ${{\nabla }^{2}}{\mathbf{B}} = 0$. Система уравнений дополняется следующими граничными условиями. Магнитное поле на поверхности шара должно быть непрерывным, в центре шара конечным, а в бесконечности оно должно стремиться к величине невозмущенного геомагнитного поля. Решение задачи ищем в виде ${\mathbf{B}}\left( {{\mathbf{r}},t} \right) = {{{\mathbf{B}}}_{e}}\left( t \right) + {\mathbf{b}}\left( {{\mathbf{r}},t} \right),$ где невозмущенное геомагнитное поле ${{{\mathbf{B}}}_{e}}$ удовлетворяет уравнению ${{\nabla }^{2}}{{{\mathbf{B}}}_{e}} = 0$, а ${\mathbf{b}}\left( {{\mathbf{r}},t} \right)$ обозначает малые возмущения геомагнитного поля, обусловленные вихревыми индукционными токами в шаре. Подставляя указанное выше представление функции ${\mathbf{B}}\left( {{\mathbf{r}},t} \right)$ в уравнение (1), получаем для области $r < a$(2)
${{\partial }_{t}}{\mathbf{b}} = D{{\nabla }^{2}}{\mathbf{b}} - {{\partial }_{t}}{{{\mathbf{B}}}_{e}}.$Используем сферическую систему координат с полярной осью ${{z}_{s}}$, направленной вдоль вектора ${{\partial }_{t}}{{{\mathbf{B}}}_{e}}$. Решение уравнения ${{\nabla }^{2}}{\mathbf{b}} = 0,$ определяющего магнитные возмущения вне шара, можно искать в виде поля магнитного диполя $\left( {r > a} \right)$:
(3)
${{{\mathbf{b}}}_{1}}\left( {{\mathbf{r}},t} \right) = \frac{{{{\mu }_{0}}{{M}_{{{\text{orb}}}}}\left( t \right)}}{{4\pi {{r}^{3}}}}\left\{ {\frac{{3\left( {{\mathbf{r}} \cdot {{{{\mathbf{\hat {z}}}}}_{s}}} \right){\mathbf{r}}}}{{{{r}^{2}}}} - {{{{\mathbf{\hat {z}}}}}_{s}}} \right\}.$(4)
$\begin{gathered} {{{\mathbf{M}}}_{{{\text{orb}}}}}\left( t \right) = - \frac{{12{{a}^{3}}}}{{\pi {{\mu }_{0}}}} \times \\ \times \,\,\sum\limits_{n = 1}^\infty {\frac{1}{{{{n}^{2}}}}\int\limits_0^t {\exp \left\{ {\frac{{{{\pi }^{2}}{{n}^{2}}}}{{{{\mu }_{0}}\sigma {{a}^{2}}}}\left( {t{\kern 1pt} '\,\, - t} \right)} \right\}{{\partial }_{{t'}}}{{{\mathbf{B}}}_{e}}\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} } . \\ \end{gathered} $(5)
${{{\mathbf{M}}}_{{{\text{orb}}}}}\left( t \right) \approx - \frac{{12\sigma {{a}^{5}}}}{{{{\pi }^{3}}}}{{\partial }_{t}}{{{\mathbf{B}}}_{e}}\left( t \right).$(6)
${{{\mathbf{M}}}_{{{\text{orb}}}}}\left( t \right) = - \frac{{2\sigma {{a}^{5}}}}{{15}}{{\partial }_{t}}{{{\mathbf{B}}}_{e}}\left( t \right).$3. МОДЕЛЬ ГЕОМАГНИТНОГО ПОЛЯ
Во внутренней магнитосфере до расстояний, не превышающих приблизительно три радиуса Земли, структура геомагнитного поля близка к полю геомагнитного диполя, которое описывается формулой, аналогичной формуле (3). Поэтому для низкоорбитальных спутников магнитное поле Земли можно рассматривать в магнитодипольном приближении, структура которого схематически изображена на рис. 1 линиями 1. Здесь стрелка на оси диполя изображает вектор, противоположный вектору ${{{\mathbf{M}}}_{e}}$ магнитного момента геомагнитного диполя.
Рис. 1.
Схематическое изображение магнитного поля Земли в магнитодипльном приближении и систем координат, используемых в работе. 1 – линии индукции магнитного поля Земли; 2 – плоскость орбиты спутника; 3 – плоскость магнитного экватора, показанная пунктирным овалом; 4 – земной шар; 5 – спутник на орбите.
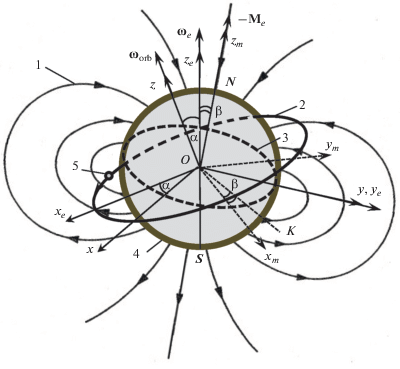
Пусть $\alpha $ обозначает угол наклонения плоскости орбиты спутника, а ${{{\mathbf{\omega }}}_{{{\text{orb}}}}}$ – угловая скорость вращения радиус-вектора спутника. Будем считать, что угол $\alpha $ не зависит от времени. Тогда угол между вектором ${{{\mathbf{\omega }}}_{{{\text{orb}}}}}$ и вектором ${{{\mathbf{\omega }}}_{e}}$ угловой скорости вращения Земли также будет равен $\alpha $. Ось геомагнитного диполя образует с осью вращения Земли постоянный угол $\beta \approx 11.5^\circ $. Расположение орбиты спутника и плоскости магнитного экватора схематически изображены на рис. 1 линиями 2 и 3, соответственно. У неподвижной системы координат с началом отсчета в центре Земли ось ${{z}_{e}}$ параллельна вектору ${{{\mathbf{\omega }}}_{e}}$, а оси ${{x}_{e}}$ и ${{y}_{e}}$ находятся в плоскости географического экватора. Рассмотрим еще одну неподвижную систему координат $x$, $y$, $z$, связанную с орбитой спутника с началом отсчета в центре Земли. Предположим, что ось $z$ перпендикулярна плоскости орбиты и параллельна вектору ${{{\mathbf{\omega }}}_{{{\text{orb}}}}}$, а оси $x$ и $y$ расположены в плоскости орбиты, причем ось $y$ совпадает с осью ${{y}_{e}}$. Тогда углы между осями $x$ и ${{x}_{e}}$, а также между осями $z$ и ${{z}_{e}}$ будут равны $\alpha $ (рис. 1).
Используем также третью систему координат, связанную с магнитным полем Земли. Оси ${{x}_{m}}$ и ${{y}_{m}}$ этой системы координат расположены в плоскости магнитного экватора, а ось ${{z}_{m}}$, противоположная по направлению к вектору геомагнитного дипольного момента ${{{\mathbf{M}}}_{e}}$, образует с осью ${{z}_{e}}$ угол $\beta \approx 11.5^\circ $ (рис. 1). Эта система координат жестко связана с Землей и вращается вместе с ней с угловой скоростью ${{{\mathbf{\omega }}}_{e}}$ так, чтобы угол $\beta $ между осями ${{z}_{m}}$ и ${{z}_{e}}$ оставался неизменным. Выберем ось ${{y}_{m}}$ таким образом, чтобы она располагалась в плоскости ${{x}_{e}}$, ${{y}_{e}}$. Из-за вращения Земли плоскость магнитного экватора и ось ${{y}_{m}}$ будут вращаться относительно неподвижной системы координат ${{x}_{e}}$, ${{y}_{e}}$, ${{z}_{e}}$. Пусть ${{\varphi }_{m}} = {{\omega }_{e}}t + {{\varphi }_{0}}$ обозначает угол поворота оси ${{y}_{m}}$ относительно оси ${{y}_{e}}$, измеряемый в плоскости ${{x}_{e}}$, ${{y}_{e}}$, а ${{\varphi }_{0}}$ – некоторая константа. На такой же угол ${{\varphi }_{m}}$ повернется вертикальная плоскость ${{x}_{m}}$, ${{z}_{m}}$, которая пересекает горизонтальную плоскость ${{x}_{e}}$, ${{y}_{e}}$ по линии OK (рис. 1). Найдем зависимость координат этих двух систем отсчета, а затем выразим эту зависимость через координаты $x$, $y$, $z$ неподвижной системы отсчета. В результате получим: ${{{\mathbf{r}}}_{m}} = {{\widehat {\mathbf{A}}}_{1}}{{\widehat {\mathbf{A}}}_{2}}{\mathbf{r}}$, где ${{{\mathbf{r}}}_{m}} = \left( {{{x}_{m}},{{y}_{m}},{{z}_{m}}} \right)$, ${\mathbf{r}} = \left( {x,y,z} \right)$, а также использованы следующие матрицы
(7)
$\begin{gathered} {{{{\mathbf{\hat {A}}}}}_{1}} = \left( {\begin{array}{*{20}{c}} {\cos \beta \cos {{\varphi }_{m}}\left( t \right)}&{\cos \beta \sin {{\varphi }_{m}}\left( t \right)}&{ - \sin \beta } \\ { - \sin {{\varphi }_{m}}\left( t \right)}&{\cos {{\varphi }_{m}}\left( t \right)}&0 \\ {\sin \beta \cos {{\varphi }_{m}}\left( t \right)}&{\sin \beta \sin {{\varphi }_{m}}\left( t \right)}&{\cos \beta } \end{array}} \right), \\ {{{{\mathbf{\hat {A}}}}}_{2}} = \left( {\begin{array}{*{20}{c}} {\cos \alpha }&0&{\sin \alpha } \\ 0&1&0 \\ { - \sin \alpha }&0&{\cos \alpha } \end{array}} \right). \\ \end{gathered} $(8)
${{{\mathbf{B}}}_{e}} = - \frac{{{{\mu }_{0}}{{M}_{e}}}}{{4\pi {{R}^{3}}}}\left\{ {\frac{{3{{z}_{m}}\left( {{{x}_{m}}{{{{\mathbf{\hat {x}}}}}_{m}} + {{y}_{m}}{{{{\mathbf{\hat {y}}}}}_{m}}} \right)}}{{{{R}^{2}}}} + \left( {\frac{{3z_{m}^{2}}}{{{{R}^{2}}}} - 1} \right){{{{\mathbf{\hat {z}}}}}_{m}}} \right\},$(9)
${{{\mathbf{\hat {A}}}}_{3}} = \left( {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta \cos {{\varphi }_{m}} + \sin \alpha \sin \beta \,\,}&{ - \cos \alpha \sin {{\varphi }_{m}}\,\,\,\,}&{\cos \alpha \sin \beta \cos {{\varphi }_{m}} - \sin \alpha \cos \beta } \\ {\cos \beta \sin {{\varphi }_{m}}}&{\cos {{\varphi }_{m}}}&{\sin \beta \sin {{\varphi }_{m}}} \\ {\sin \alpha \cos \beta \cos {{\varphi }_{m}} - \cos \alpha \sin \beta \,\,\,\,}&{ - \sin \alpha \sin {{\varphi }_{m}}\,\,\,\,}&{\sin \alpha \sin \beta \cos {{\varphi }_{m}} + \cos \alpha \cos \beta } \end{array}} \right).$Полученные формулы позволяют рассчитать магнитный момент спутника, если заданы параметры его траектории, т.е. функции $x = x\left( t \right)$ и $y = y\left( t \right)$ в плоскости орбиты $z = 0$. Использовав эти функции, а также соотношения (7)–(9) можно найти зависимость от времени компонентов вектора геомагнитного поля в месте нахождения спутника. Затем, подставив эти компоненты, а также их производные по времени в формулы (4) или (5), можно найти искомый орбитальный магнитный момент, приобретаемый спутником.
4. ВОЗДЕЙСТВИЕ ГЕОМАГНИТНОГО ПОЛЯ НА ОРБИТАЛЬНЫЙ МАГНИТНЫЙ МОМЕНТ СПУТНИКА
В магнитном поле Земли на систему токов, возникающих в спутнике, действует механический момент силы Ампера ${{{\mathbf{L}}}_{{{\text{orb}}}}} = \left[ {{{{\mathbf{M}}}_{{{\text{orb}}}}} \times {{{\mathbf{B}}}_{e}}} \right]$, где ${{{\mathbf{B}}}_{e}}$ – индукция невозмущенного геомагнитного поля. В частности, подставляя сюда приближенную формулу (5), получим
(10)
${{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right) \approx \frac{{12\sigma {{a}^{5}}}}{{{{\pi }^{3}}}}\left[ {{{{\mathbf{B}}}_{e}}\left( t \right) \times {{\partial }_{t}}{{{\mathbf{B}}}_{e}}\left( t \right)} \right].$В качестве примера рассмотрим пассивный спутник, равномерно вращающийся вокруг Земли по круговой орбите с радиусом $R$ и циклической частотой вращения ${{\omega }_{{{\text{orb}}}}} = {{\left( {{{G{{m}_{E}}} \mathord{\left/ {\vphantom {{G{{m}_{E}}} {{{R}^{3}}}}} \right. \kern-0em} {{{R}^{3}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ где ${{m}_{E}}$ – масса Земли, $G$ – гравитационная постоянная. Координаты спутника в плоскости орбиты меняются по закону: $x\left( t \right) = R\cos {{\psi }_{{{\text{orb}}}}}\left( t \right),$ $y\left( t \right) = R\sin {{\psi }_{{{\text{orb}}}}}\left( t \right),$ где ${{\psi }_{{{\text{orb}}}}} = {{\omega }_{{{\text{orb}}}}}t + {{\psi }_{0}}.$ Константа ${{\psi }_{0}}$ связана с координатами ${{x}_{0}}$, ${{y}_{0}}$ “начала движения” спутника по орбите: ${\text{tg}}{{\psi }_{0}} = {{{{y}_{0}}} \mathord{\left/ {\vphantom {{{{y}_{0}}} {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}}$. Подставляя эти соотношения, а также $z = 0$ в формулу (7), получим:
(11)
$\begin{gathered} {{{{x}_{m}}\left( t \right)} \mathord{\left/ {\vphantom {{{{x}_{m}}\left( t \right)} R}} \right. \kern-0em} R} = 0.5f\left( t \right)\cos \beta + \sin \alpha \sin \beta \cos {{\psi }_{{{\text{orb}}}}}\left( t \right), \\ {{{{y}_{m}}\left( t \right)} \mathord{\left/ {\vphantom {{{{y}_{m}}\left( t \right)} R}} \right. \kern-0em} R} = 0.5\left[ {\left( {1 + \cos \alpha } \right)\sin \left\{ {{{\psi }_{{{\text{orb}}}}}\left( t \right) - {{\varphi }_{m}}\left( t \right)} \right\}} \right. + \\ \left. { + \,\,\left( {1 - \cos \alpha } \right)\sin \left\{ {{{\psi }_{{{\text{orb}}}}}\left( t \right) + {{\varphi }_{m}}\left( t \right)} \right\}} \right], \\ {{{{z}_{m}}\left( t \right)} \mathord{\left/ {\vphantom {{{{z}_{m}}\left( t \right)} R}} \right. \kern-0em} R} = 0.5f\left( t \right)\sin \beta - \sin \alpha \cos \beta \cos {{\psi }_{{{\text{orb}}}}}\left( t \right), \\ f\left( t \right) = \left( {1 + \cos \alpha } \right)\cos \left\{ {{{\psi }_{{{\text{orb}}}}}\left( t \right) - {{\varphi }_{m}}\left( t \right)} \right\} - \\ - \,\,\left( {1 - \cos \alpha } \right)\cos \left\{ {{{\psi }_{{{\text{orb}}}}}\left( t \right) + {{\varphi }_{m}}\left( t \right)} \right\}. \\ \end{gathered} $Для лучшего понимания смысла полученных выше соотношений рассмотрим вначале упрощенный случай, который позволит избежать громоздких выражений для механического момента, действующего на спутник. Поскольку ${{\omega }_{e}} \ll {{\omega }_{{{\text{orb}}}}},$ то за один виток спутника по орбите можно пренебречь изменением фазы ${{\varphi }_{m}}$, считая ее константой. Рассмотрим, например, случай ${{\varphi }_{m}} = 0$, когда вектор ${{{\mathbf{M}}}_{e}}$ лежит в плоскости векторов ${{{\mathbf{\omega }}}_{e}}$ и ${{{\mathbf{\omega }}}_{{{\text{orb}}}}}$. Тогда формулы (11) упрощаются к виду:
(12)
$\begin{gathered} {{x}_{m}}\left( t \right) = R\cos \left( {\beta - \alpha } \right)\cos {{\psi }_{{{\text{orb}}}}}\left( t \right), \\ {{y}_{m}}\left( t \right) = R\sin {{\psi }_{{{\text{orb}}}}}\left( t \right), \\ {{z}_{m}}\left( t \right) = R\sin \left( {\beta - \alpha } \right)\cos {{\psi }_{{{\text{orb}}}}}\left( t \right). \\ \end{gathered} $(13)
$\begin{gathered} {{B}_{{ex}}} = {{B}_{*}}\sin \left( {\beta - \alpha } \right)\left\{ {3{{{\cos }}^{2}}{{\psi }_{{{\text{orb}}}}}\left( t \right) - 1} \right\}, \\ {{B}_{{ey}}} = 3{{B}_{*}}\sin \left( {\beta - \alpha } \right)\sin {{\psi }_{{{\text{orb}}}}}\left( t \right)\cos {{\psi }_{{{\text{orb}}}}}\left( t \right), \\ {{B}_{{ez}}} = - {{B}_{*}}\cos \left( {\beta - \alpha } \right),\,\,\,\,B{\text{*}} = - {{{{\mu }_{0}}{{M}_{e}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}{{M}_{e}}} {(4\pi {{R}^{3}})}}} \right. \kern-0em} {(4\pi {{R}^{3}})}}. \\ \end{gathered} $Подставляя соотношения (13) и их производные по времени в формулу (10), находим механический момент, действующий на спутник, в неподвижной системе координат, связанной с орбитой спутника:
(14)
$\begin{gathered} {{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right) \approx \frac{{18\sigma {{\omega }_{{{\text{orb}}}}}{{a}^{5}}}}{{{{\pi }^{3}}}}{{\left( {\frac{{{{\mu }_{0}}{{M}_{e}}}}{{4\pi {{R}^{3}}}}} \right)}^{2}}\sin \left( {\beta - \alpha } \right) \times \\ \times \,\,\left\{ {2\cos \left( {\beta - \alpha } \right)} \right.\left[ {{\mathbf{\hat {x}}}\cos \left( {2{{\psi }_{{{\text{orb}}}}}} \right) + {\mathbf{\hat {y}}}\sin \left( {2{{\psi }_{{{\text{orb}}}}}} \right)} \right] + \\ \left. { + \,\,{\mathbf{\hat {z}}}\sin \left( {\beta - \alpha } \right)\left[ {3 + \cos \left( {2{{\psi }_{{{\text{orb}}}}}} \right)} \right]} \right\}. \\ \end{gathered} $Рассмотрим несколько частных случаев. Если плоскость орбиты спутника приблизительно совпадает с плоскостью магнитного экватора $\left( {\alpha \approx \beta } \right)$, то из формулы (14) следует, что ${{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right) \approx 0.$ Этот результат можно объяснить тем, что в данном случае магнитное поле Земли (8) на орбите спутника имеет приблизительно постоянное значение, т.е. ${{\partial }_{t}}{{{\mathbf{B}}}_{e}} = 0$. Поэтому механический момент (10) должен давать нулевое значение.
Если орбита полярная, т.е. плоскость орбиты близка к плоскости магнитного меридиана $\left( {\beta - \alpha \approx {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)$, то формула (14) упрощается к виду:
(15)
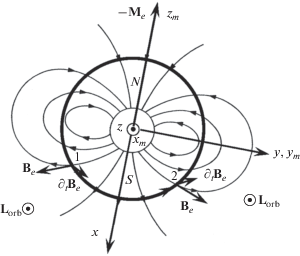
$\begin{gathered} {{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right) \approx \left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle \left[ {1 + \frac{{\cos \left( {2{{\omega }_{{{\text{orb}}}}}t} \right)}}{3}} \right], \\ \left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle = {\mathbf{\hat {z}}}\frac{{54\sigma {{\omega }_{{{\text{orb}}}}}{{a}^{5}}}}{{{{\pi }^{3}}}}{{\left( {\frac{{{{\mu }_{0}}{{M}_{e}}}}{{4\pi {{R}^{3}}}}} \right)}^{2}}. \\ \end{gathered} $Поясним качественно наличие ненулевого среднего значения момента силы Ампера (15). На рисунке 2 схематично изображены линии магнитного поля Земли, круговая орбита спутника, лежащая в плоскости магнитного меридиана ${{y}_{m}},{{z}_{m}}$, и оси $x,y,z$ системы координат, связанной с орбитой спутника. Ось $z$, изображенная кружком с точкой в центре, направлена “на нас” перпендикулярно плоскости рисунка. Рассмотрим, например, положения спутника на орбите в точках 1 и 2, расположенных симметрично относительно оси $x$. Векторы ${{{\mathbf{B}}}_{e}}$ и ${{\partial }_{t}}{{{\mathbf{B}}}_{e}}$ в этих точках, имеют такие направления, что их векторное произведение и, соответственно, вектор ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ направлены вдоль оси $z$. Поскольку точки 1 и 2 выбраны произвольно, то вектор ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ везде направлен вдоль оси $z$. Следовательно, вектор его среднего значения будет также направлен вдоль оси $z$.
Рис. 2.
Схема, поясняющая расположение координатных осей и направление орбитального механического момента силы Ампера ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ для случая кругового движения проводящего спутника в плоскости, близкой к плоскости магнитного меридиана.
Применим полученные результаты к лазерному микро-спутнику Ларец, запущенному в 2003 г. на орбиту высотой 690 км. Для численных оценок используем значение ${{M}_{e}} = 8.3 \times {{10}^{{22}}}$ А м2, а также следующие параметры спутника: $R = 7.06 \times {{10}^{3}}$ км; ${{\omega }_{{{\text{orb}}}}} \approx 1.07 \times {{10}^{{ - 3}}}$ рад/с; радиус спутника a = $ = 107.5$ мм; масса спутника ${{m}_{s}} = 23.4$ кг; $\sigma = \left( {1{\kern 1pt} - {\kern 1pt} 4} \right) \times {{10}^{7}}$ См/м (сталь или алюминий) [Руйбис, 2016]. Угол наклонения орбиты спутника составлял $\alpha = 98.202^\circ $, т.е. плоскость орбиты была близка к плоскости магнитного меридиана. Поэтому можно приближенно использовать формулу (15). В результате получим, что $\left| {\left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right)} \right\rangle } \right|$ ≈ $ \approx 1.5 \times {{10}^{{ - 10}}}$ Н м. Полагая, что спутник является однородным шаром с моментом инерции $I = {{2{{m}_{s}}{{a}^{2}}} \mathord{\left/ {\vphantom {{2{{m}_{s}}{{a}^{2}}} 5}} \right. \kern-0em} 5}$, находим, что средний угол поворота спутника вокруг своей оси за время $t$ составит $\left\langle \phi \right\rangle = {{\left| {\left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle } \right|{{t}^{2}}} \mathord{\left/ {\vphantom {{\left| {\left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle } \right|{{t}^{2}}} {\left( {2I} \right)}}} \right. \kern-0em} {\left( {2I} \right)}}.$ Подставляя сюда указанные выше числовые значения параметров, а также время одного оборота спутника вокруг Земли, т.е. $t = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\omega }_{{{\text{orb}}}}}}}} \right. \kern-0em} {{{\omega }_{{{\text{orb}}}}}}} = 5.8 \times {{10}^{3}}$ с, получим, что $\left\langle \phi \right\rangle \approx 0.82^\circ .$
Для иллюстрации полученных закономерностей проведем расчеты по более точным формулам, учитывающим суточное вращение вектора геомагнитного диполя. Ввиду того, что расчетные формулы для магнитного поля Земли на орбите спутника и его производных по времени имеют громоздкий вид, они приведены в Приложении 2. Подставляя эти формулы в соотношение (10), можно затем вычислить компоненты угловой скорости и углов вращения в системе центра масс спутника при любых параметрах круговой орбиты спутника. Например, для проекции на ось $z$ имеем:
(16)
${{\omega }_{z}} = {{\omega }_{{0z}}} + \frac{5}{{2{{m}_{s}}{{a}^{2}}}}\int\limits_0^t {{{L}_{{{\text{orb,}}\;z}}}\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} ,$В качестве примера на рис. 3 и 4 приведены результаты расчетов, в которых использовались указанные выше параметры спутника Ларец, а также $\beta = 11.5^\circ $ и ${{\omega }_{{0x,y,z}}} = 0.$ Расчеты показали, что “начальные параметры” орбиты мало влияют на ход графиков спустя несколько часов, поэтому были выбраны значения ${{\psi }_{0}} = {{\varphi }_{0}} = 0$. Проекции на оси $x$, $y$, $z$ орбитального момента силы Ампера изображены на рис. 3 на промежутке времени от 0 до 24 ч. Проекции угловой скорости на данные оси показаны на рис. 4, соответственно, для того же промежутка времени. Для удобства компоненты ${{\omega }_{x}}$ и ${{\omega }_{y}}$ увеличены в 100 раз.
Рис. 3.
Проекции орбитального механического момента ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ силы Ампера, действующей на спутник, в зависимости от времени. Кривые 1, 2, 3 отвечают проекциям ${{L}_{x}}$, ${{L}_{y}}$, ${{L}_{z}}$, соответственно.
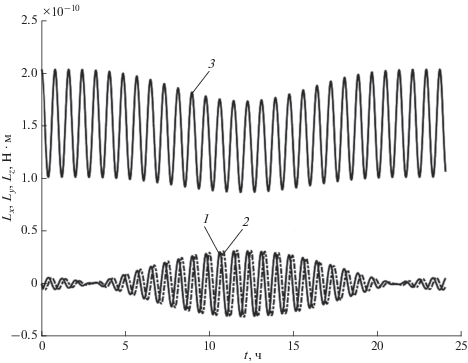
Рис. 4.
Проекции угловой скорости вращения спутника на оси, проходящие через его центр масс, в зависимости от времени, рассчитанные с учетом взаимодействия орбитального магнитного момента спутника с геомагнитным полем. Кривые 1, 2, 3 отвечают проекциям ${{\omega }_{x}}$, ${{\omega }_{y}}$, ${{\omega }_{z}}$, соответственно.
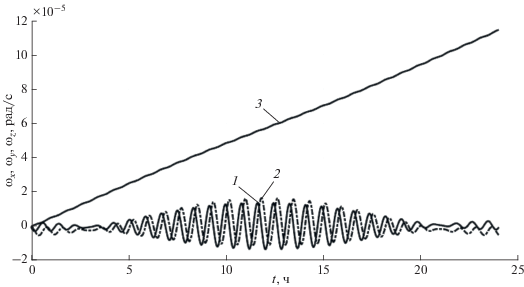
Как видно из рис. 3, при данных параметрах преобладает механический момент относительно оси $z$, перпендикулярной плоскости орбиты спутника. Проекция угловой скорости ${{\omega }_{z}}$ на данную ось максимальна, т.е. вращением вокруг других осей в первом приближении можно пренебречь. Быстрые колебания на графиках проекций орбитального момента происходят с частотой приблизительно равной $2{{\omega }_{{{\text{orb}}}}}$. Эти колебания модулируются по амплитуде с частотой порядка ${{\omega }_{e}}$. Приблизительно линейный рост со временем проекции угловой скорости на ось $z$ (рис. 4) объясняется тем, что среднее по времени значение ${{L}_{{{\text{orb}},\;z}}}$ отлично от нуля.
Угол поворота вокруг оси $z$ увеличивается со временем приблизительно по квадратичному закону и, несмотря на малую величину ${{\omega }_{z}}$, может достигнуть за сутки величины $ \sim {\kern 1pt} 2\pi $. Следует, однако, учесть, что вращение спутника вызовет дополнительную генерацию индукционных токов в корпусе спутника и соответствующий магнитный момент, который будет рассмотрен в следующем разделе. Далее мы покажем, что взаимодействие орбитального и собственного магнитных моментов с геомагнитным полем приведет к торможению вращения спутника.
5. ВОЗДЕЙСТВИЕ ГЕОМАГНИТНОГО ПОЛЯ НА СПИНОВЫЙ МАГНИТНЫЙ МОМЕНТ СПУТНИКА
В этом разделе рассмотрим влияние магнитного поля Земли на проводящий сферический спутник движущейся по орбите и вращающийся вокруг оси, проходящей через его центр масс. В системе отсчета центра масс спутника возникает переменное магнитное поле, которое приводит к возникновению в корпусе спутника вихревых токов. Найдем спиновый (или собственный) магнитный момент этих токов. В течение небольшого промежутка времени геомагнитное поле в малой окрестности спутника можно считать приблизительно однородным и постоянным. За этот промежуток времени собственная угловая скорость спутника меняется мало, и поэтому также может рассматриваться как константа. Таким образом, в первом приближении мы приходим к известной задаче о вращении однородного проводящего шара в постоянном магнитном поле [Ландау и Лифшиц, 1982].
Рассмотрим систему центра масс спутника $(x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ')$, в которой ось $z{\kern 1pt} '$ направлена вдоль вектора угловой скорости вращения ${{{\mathbf{\omega }}}_{{{\text{spin}}}}}$. Предположим, что вектор невозмущенного магнитного поля Земли расположен в плоскости $x{\kern 1pt} '$, $z{\kern 1pt} '$ и имеет компоненты ${{B}_{{ex{\kern 1pt} '}}} = {{B}_{ \bot }}$ и ${{B}_{{ez{\kern 1pt} '}}}$. Тогда собственный магнитный момент ${{{\mathbf{M}}}_{{{\text{spin}}}}}$ системы токов, индуцированных в шаре, имеет следующие проекции:
(17)
$\begin{gathered} {{M}_{{{\text{spin}},\;x{\kern 1pt} '}}} = {{{{p}_{1}}V{{B}_{ \bot }}} \mathord{\left/ {\vphantom {{{{p}_{1}}V{{B}_{ \bot }}} {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}},\,\,\,\,{{M}_{{{\text{spin}},\;y{\kern 1pt} '}}} = {{{{p}_{2}}V{{B}_{ \bot }}} \mathord{\left/ {\vphantom {{{{p}_{2}}V{{B}_{ \bot }}} {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}}, \\ {{M}_{{{\text{spin}},\;z{\kern 1pt} '}}} = 0. \\ \end{gathered} $(18)
$\begin{gathered} {{p}_{1}} = - \frac{3}{{8\pi }}\left\{ {1 - \frac{{3\delta }}{{2a}}\left[ {\frac{{\operatorname{sh} \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right) - \sin \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right)}}{{\operatorname{ch} \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right) - \cos \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right)}}} \right]} \right\}, \\ {{p}_{2}} = - \frac{{9{{\delta }^{2}}}}{{16\pi {{a}^{2}}}}\left\{ {1 - \frac{a}{\delta }\left[ {\frac{{\operatorname{sh} \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right) + \sin \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right)}}{{\operatorname{ch} \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right) - \cos \left( {{{2a} \mathord{\left/ {\vphantom {{2a} \delta }} \right. \kern-0em} \delta }} \right)}}} \right]} \right\}, \\ \end{gathered} $В системе центра масс спутника геомагнитное поле является медленно меняющейся функцией времени. Поэтому спиновый магнитный момент также постепенно меняется со временем. Предположим, что вектор начальной угловой скорости спутника ${{{\mathbf{\omega }}}_{0}}$, а также ось $z{\kern 1pt} '$ перпендикулярны плоскости орбиты спутника и параллельны оси $z$ неподвижной системы координат (рис. 1). При движении спутника по орбите плоскость $x{\kern 1pt} ',$ $z{\kern 1pt} '$, в которой располагается вектор ${{{\mathbf{B}}}_{e}}$, будет изменять свое положение. Поэтому вначале выразим проекции спинового магнитного момента (17) через его проекции на оси $x$, $y$, $z$ неподвижной системы координат, а затем найдем проекции спинового механического момента на те же оси:
(19)
${{{\mathbf{L}}}_{{{\text{spin}}}}}\left( t \right) = \frac{V}{{{{\mu }_{0}}}}\left\{ {{{B}_{{ez}}}\left( {{{p}_{2}}{{B}_{{ex}}} + {{p}_{1}}{{B}_{{ey}}}} \right),{\kern 1pt} {{B}_{{ez}}}\left( {{{p}_{2}}{{B}_{{ey}}} - {{p}_{1}}{{B}_{{ex}}}} \right), - {\kern 1pt} {{p}_{2}}\left( {B_{{ex}}^{2} + B_{{ey}}^{2}} \right)} \right\}.$В первом приближении механические моменты (5) и (19), связанные с орбитальным и собственным вращениями спутника, полагаем независимыми друг от друга. Тогда в системе центра масс спутника динамика его вращательного движения, обусловленного магнитными силами, описывается известным выражением
(20)
${{I{\mathbf{d\omega }}} \mathord{\left/ {\vphantom {{I{\mathbf{d\omega }}} {dt}}} \right. \kern-0em} {dt}} = {{{\mathbf{L}}}_{{{\text{orb}}}}}\left( t \right) + {{{\mathbf{L}}}_{{{\text{spin}}}}}\left( t \right),$Если глубина скин-слоя $\delta \gg a,$ то магнитная поляризуемость шара (18) упрощается к виду:
(21)
${{p}_{1}} = - \frac{1}{{105\pi }}{{\left( {\frac{a}{\delta }} \right)}^{4}},\,\,\,\,{{p}_{2}} = \frac{1}{{20\pi }}{{\left( {\frac{a}{\delta }} \right)}^{2}}.$(22)
$\frac{{d{{\omega }_{x}}}}{{dt}} = {{s}_{1}}\left( {{{B}_{{ey}}}{{{\dot {B}}}_{{ez}}} - {{B}_{z}}{{{\dot {B}}}_{y}}} \right) + {{\omega }_{z}}{{s}_{2}}{{B}_{{ez}}}{{B}_{{ex}}},$(23)
$\frac{{d{{\omega }_{y}}}}{{dt}} = {{s}_{1}}\left( {{{B}_{{ez}}}{{{\dot {B}}}_{{ex}}} - {{B}_{{ex}}}{{{\dot {B}}}_{{ez}}}} \right) + {{\omega }_{z}}{{s}_{2}}{{B}_{{ez}}}{{B}_{{ey}}},$(24)
$\frac{{d{{\omega }_{z}}}}{{dt}} = {{s}_{1}}\left( {{{B}_{{ex}}}{{{\dot {B}}}_{{ey}}} - {{B}_{{ey}}}{{{\dot {B}}}_{{ex}}}} \right) - {{\omega }_{z}}{{s}_{2}}B_{ \bot }^{2},$Решение уравнения (24) имеет вид:
Подставляя это решение в уравнения (22), (23), находим остальные проекции угловой скорости(26)
$\begin{gathered} {{\omega }_{x}} = {{s}_{1}}\int\limits_0^t {\left\{ {{{B}_{{ey}}}\left( {t{\kern 1pt} '} \right){{{\dot {B}}}_{{ez}}}\left( {t{\kern 1pt} '} \right) - {{B}_{{ez}}}\left( {t{\kern 1pt} '} \right){{{\dot {B}}}_{{ey}}}\left( {t{\kern 1pt} '} \right)} \right\} \times } \\ \times \,\,\exp \left[ {{{g}_{x}}\left( {t{\kern 1pt} ',t} \right)} \right]dt{\kern 1pt} ', \\ {{\omega }_{y}} = {{s}_{1}}\int\limits_0^t {\left\{ {{{B}_{{ez}}}\left( {t{\kern 1pt} '} \right){{{\dot {B}}}_{{ex}}}\left( {t{\kern 1pt} '} \right) - {{B}_{{ex}}}\left( {t{\kern 1pt} '} \right){{{\dot {B}}}_{{ez}}}\left( {t{\kern 1pt} '} \right)} \right\}} \times \\ \times \,\,\exp \left[ {{{g}_{y}}\left( {t{\kern 1pt} ',t} \right)} \right]dt{\kern 1pt} ', \\ \end{gathered} $(28)
${{\omega }_{z}} = {{\omega }_{{0z}}}\exp \left( { - \frac{t}{{{{t}_{r}}}}} \right),\,\,\,\,{{t}_{r}} = \frac{{12{{m}_{s}}}}{{\sigma \left\langle {B_{ \bot }^{2}} \right\rangle {{a}^{3}}}}.$На рисунке 5 приведена зависимость проекции ${{\omega }_{z}}$ угловой скорости вращения спутника в зависимости от времени, которая была получена с помощью численного интегрирования соотношения (24). При расчетах использовались параметры спутника Ларец и начальная угловая скорость вращения ${{\omega }_{{0z}}} = 4\pi $ рад/с. Заметим, что результаты вычислений ${{\omega }_{z}}$ по приближенной формуле (28) практически совпадают с результатами, представленными на рис. 5, при $\left\langle {B_{ \bot }^{2}} \right\rangle $ = $ = 1.35 \times {{10}^{{ - 9}}}$ Тл2 за исключением малых колебаний, не видимых на рис. 5. Поэтому можно полагать, что ${{\omega }_{z}}$ убывает со временем приблизительно по экспоненциальному закону с характерным временем релаксации ${{t}_{r}}$.
Рис. 5.
Проекция угловой скорости вращения спутника на ось $z$, проходящую через его центр масс, в зависимости от времени, рассчитанная с учетом взаимодействия собственного и орбитального магнитных моментов спутника с геомагнитным полем. Для расчета использовались параметры, близкие к параметрам спутника Ларец.
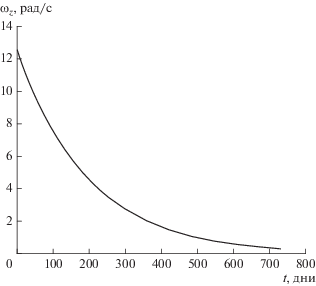
Анализ уравнений (22)–(24) показывает, что по истечении большого промежутка времени $\left( {t \gg {{t}_{r}}} \right)$ или в пределе $t \to \infty $ угловая скорость вращения спутника не будет стремиться к нулевому значению. Это связано с тем, что орбитальный момент ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ в уравнении (20) не убывает со временем, и его среднее значение не равно нулю. Асимптотическое поведение ${{\omega }_{z}}$ при $t \to \infty $ определяется приблизительным балансом слагаемых в правой части уравнения (24). В этом случае сумма собственного момента ${{{\mathbf{L}}}_{{{\text{spin}}}}}$ и среднего значения орбитального момента ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ приблизительно равна нулю, что отвечает значению $k \sim 1$. Отсюда получаем, что асимптотическое значение ${{\omega }_{z}}$ колеблется около среднего значения $\left\langle {{{\omega }_{z}}} \right\rangle $ ~ $ \sim {{360{{\omega }_{{{\text{orb}}}}}} \mathord{\left/ {\vphantom {{360{{\omega }_{{{\text{orb}}}}}} {{{\pi }^{3}}}}} \right. \kern-0em} {{{\pi }^{3}}}} \approx 0.012$ рад/с, которому соответствует период вращения около девяти минут. Эти остаточные вращения происходят в форме колебаний и могут быть малозаметны из-за их нерегулярного характера. Например, такой режим с амплитудой около 0.0035 рад/с проявлялся после пятидесятого витка третьего советского искусственного спутника [Белецкий, 1965].
В заключение отметим, что при быстром вращении спутника может возникнуть ситуация, когда глубина скин слоя меньше радиуса спутника. В этом случае следует воспользоваться точным соотношениями (18), (19) для магнитной поляризуемости шара и спинового механического момента или соответствующими предельными выражениями, когда $\delta \ll a.$
6. ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
Проведенный анализ показал, что воздействие магнитного поля Земли на проводящие пассивные спутники зависит как от параметров спутника, включая его массу, моменты инерции, размеры и начальную угловую скорость вращения в системе центра масс, так и от параметров орбиты спутника. Изменение потока геомагнитного поля через поперечное сечение спутника, вызывающее вихревые индукционные токи в его корпусе, обусловлено как орбитальным движением спутника, так и его вращением относительно осей, проходящих через центр масс спутника. Системы токов, связанные с этими видами движения спутника, можно охарактеризовать с помощью орбитального ${{{\mathbf{M}}}_{{{\text{orb}}}}}$ и собственного или спинового ${{{\mathbf{M}}}_{{{\text{spin}}}}}$ магнитных моментов спутника. Для модели спутника в виде однородного проводящего шара момент ${{{\mathbf{M}}}_{{{\text{orb}}}}}$ направлен противоположно вектору ${{\partial }_{t}}{{{\mathbf{B}}}_{e}}$, который определяет изменение магнитного потока через спутник при его поступательном движении по орбите. Вектор ${{{\mathbf{M}}}_{{{\text{spin}}}}}$ зависит только от составляющей геомагнитного поля, перпендикулярной вектору собственной угловой скорости ${{{\mathbf{\omega }}}_{{{\text{spin}}}}}$ вращения спутника вокруг оси, проходящей через его центр масс. Оба эти утверждения для магнитных моментов ${{{\mathbf{M}}}_{{{\text{orb}}}}}$ и ${{{\mathbf{M}}}_{{{\text{spin}}}}}$ следуют из общего закона электромагнитной индукции Фарадея и, по-видимому, справедливы для спутников любой формы.
Взаимодействие магнитных моментов с магнитным полем Земли приводит к появлению орбитального ${{{\mathbf{L}}}_{{{\text{orb}}}}}$ и спинового ${{{\mathbf{L}}}_{{{\text{spin}}}}}$ механических моментов, влияющих на вращение спутника. Анализ этого взаимодействия, проведенный в предположении о дипольном характере магнитного поля Земли показал, что орбитальный механический момент существенно зависит от угла наклонения орбиты спутника. Его величина колеблется из-за орбитального движения спутника и суточного вращения вектора ${{{\mathbf{M}}}_{e}}$ геомагнитного диполя. В частности, при движении спутника по круговой орбите, лежащей близко к плоскости магнитного экватора, геомагнитное поле практически не меняется и, поэтому среднее значение $\left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle \approx 0$. В тоже время для круговой орбиты, близкой к плоскости магнитного меридиана, вектор $\left\langle {{{{\mathbf{L}}}_{{{\text{orb}}}}}} \right\rangle $ отличен от нуля и направлен перпендикулярно плоскости орбиты.
Величина ${{{\mathbf{L}}}_{{{\text{spin}}}}}$ для модели спутника в форме проводящего шара зависит от его магнитной поляризуемости. При малых значениях ${{\omega }_{{{\text{spin}}}}}$ (несколько оборотов в секунду), что характерно для пассивных микроспутников типа Ларец, глубина скин слоя $\delta $ превосходит радиус шара $a$. В этом случае отношение орбитального и спинового механических моментов порядка $k = {{360{{\omega }_{{{\text{orb}}}}}} \mathord{\left/ {\vphantom {{360{{\omega }_{{{\text{orb}}}}}} {({{\pi }^{3}}{{\omega }_{{{\text{spin}}}}})}}} \right. \kern-0em} {({{\pi }^{3}}{{\omega }_{{{\text{spin}}}}})}}$. Анализ уравнений показывает, что такое взаимодействие индукционных токов с геомагнитным полем приводит торможению собственного вращения спутника приблизительно по экспоненциальному закону. Основная физическая причина этого явления – это диссипация механической энергии вращения спутника и постепенное превращение ее в тепловую энергию. Для сферического спутника характерное время, за которое угловая скорость ${{{\mathbf{\omega }}}_{{{\text{spin}}}}}$ уменьшается в $e$ раз, составляет порядка ${{t}_{r}} \sim {{12{{m}_{s}}} \mathord{\left/ {\vphantom {{12{{m}_{s}}} {\left( {\sigma \left\langle {B_{ \bot }^{2}} \right\rangle {{a}^{3}}} \right)}}} \right. \kern-0em} {\left( {\sigma \left\langle {B_{ \bot }^{2}} \right\rangle {{a}^{3}}} \right)}}$, где ${{m}_{s}}$ масса спутника, $\sigma $ его электропроводность, а $\left\langle {B_{ \bot }^{2}} \right\rangle $ – средний по времени квадрат проекции геомагнитного поля на плоскость орбиты. Причем это среднее берется вдоль траектории движения спутника. Для микроспутника Ларец это время составляет, согласно полученной оценке, около одного года, что согласуется с экспериментальной величиной.
Анализ асимптотического поведения решения при $t \gg {{t}_{r}}$ показывает, что небольшие по амплитуде иррегулярные вращения спутника не убывают со временем. Это можно объяснить генерацией вихревых токов в спутнике и орбитального механического момента при его орбитальном движении, что, в свою очередь, приводит к возникновению компенсирующего спинового момента. В более точной модели можно дополнительно принять во внимание другие слабые эффекты, такие как различие в структуре геомагнитного поля на дневной и ночной сторонах ионосферы или вариации геомагнитного поля, связанные с распространением альвеновских волн.
Список литературы
− Аблязов М.К., Сурков В.В., Чернов А.С. Искажение внешнего магнитного поля расширяющимся плазменным шаром, находящимся в слабопроводящем полупространстве // Журн. прикладной механики и технической физики. № 6. С. 22−29. 1988.
− Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, Главная редакция физ.-мат. лит. 416 с. 1965.
− Васильев В.П. Путь к точности // Российский космос. Т. 2. № 145. С. 10−14. 2018.
− Зонов Ю.В. К вопросу о взаимодействии спутника с магнитным полем Земли // “Искусственные спутники Земли”, Изд-во АН СССР. Вып. 3. С. 118–124. 1959.
− Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Теория поля. Т. 2. М.: Физ.-мат. лит. 400 с. 1960.
− Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Электродинамика сплошных сред. Т. 7, 2-ое изд., перераб. и доп. Е.М. Лифшицем и Л.П. Питаевским. М.: Физ.-мат. лит. 623 с. 1982.
− Руйбис А. Ларец и Блиц – наноспутники ГЛОНАСС // Воздушно космическая сфера. № 3/4. С. 88–89. 2016.
− Садов Ю.А. Периодические движения спутника с магнитным демпфером в плоскости круговой орбиты // Космич. исслед. Т. 7. № 1. С. 51−60. 1969.
− Сурков В.В., Мозгов К.С. Эффекты воздействия потоков частиц и геомагнитных вариаций на низкоорбитальные спутники сферической формы // Космич. исслед. Т. 57. № 4. С. 269−277. 2019.https://doi.org/10.1134/S0023420619040071
− Candini G.P., Piergentili F., Santoni F. Miniaturized attitude control system for nanosatellites // Acta Astronaut. V. 81. № 1. P. 325–334. 2012.
− Guo J., Bouwmeester J., Gill E. In-orbit results of Delfi-n3Xt: Lessons learned and move forward // Acta Astronaut. V. 121. P. 39–50. 2016.
− Ivanov D., Ovchinnikov M., Penkov V., Roldugin D., Doronin D., Ovchinnikov A. Advanced numerical study of the three-axis magnetic attitude control and determination with uncertainties // Acta Astronaut. V. 132. P. 103–110. 2017.
− Kucharski D., Kirchner G., Lim H.-C., Koidl F. New results on spin determination of nanosatellite BLITS from High Repetition Rate SLR data // Adv. Space Res. V. 51. № 5. P. 912–916. 2013.https://doi.org/10.1016/j.asr.2012.10.008
− Müncheberg S., Krischke M., Lemke N. M. K. Nanosatellites and micro systems technology – capabilities, limitations and applications // Acta Astronaut. V. 39. № 9–12. P. 799–808. 1996.https://doi.org/10.1016/S0094-5765(97)00063-5
− Ovchinnikov M.Yu., Roldugin D.S., Tkachev S.S. Study of the accuracy of active magnetic damping algorithm / Keldysh Institute Preprints. № 133. 16 p. 2016.https://doi.org/10.20948/prepr-2016-133-e
− Ovchinnikov M.Yu., Penkov V.I., Roldugin D.S., Pichuzhkina A.V. Geomagnetic field models for satellite angular motion studies // Acta Astronaut. V. 144. P. 171–180. 2018.
− Petrukovich A.A., Nikiforov O. Small satellites for scientific research // Rocket-Space Device Engineering and Information Systems. V. 3. № 4. P. 22–31. 2016.https://doi.org/10.17238/issn2409-0239.2016.4.22
− Pichuzhkina A.V., Roldugin D.S. Geomagnetic field models for satellite angular motion / Keldysh Institute Preprints. № 87. 25 p. 2016.https://doi.org/10.20948/prepr-2016-87-e
− Rosenstock H.B. The effect of the Earth’s magnetic field on the spin of the satellite // Astronaut. Acta. V. 3. № 3. P. 215–226. 1957.
− Samotokin B., Shostachuk D., Korobiichuka I., Kachniarzb M., Nowicki M. The satellites orientation method using a torque magnetic drive // Acta Phys. Pol. A. V. 133. № 3. 722–724. 2018.https://doi.org/10.12693/APhysPolA.133.722
− Santoni F., Zelli M. Passive magnetic attitude stabilization of the UNISAT-4 microsatellite // Acta Astronaut. V. 65. № 5–6. P. 792–803. 2009.
− Vasiliev V.P., Shargorodsky V.D., Novikov S.B., Chubykin A.A., Parkhomenko N.N., Sadovnikov M.A. Progress in laser systems for precision ranging, angle measurements, photometry, and data transfer / In: International Laser Ranging Service (ILRS) Fall 2007 Workshop. Grasse, France, 25–28 September, 2007.
Дополнительные материалы отсутствуют.
Инструменты
Геомагнетизм и аэрономия




