Геомагнетизм и аэрономия, 2021, T. 61, № 2, стр. 240-258

Восстановление высотных профилей электронной концентрации по данным внешнего спутникового зондирования с использованием модели IRI во внутренней ионосфере

П. Ф. Денисенко^1, *, В. В. Соцкий^1, **

¹ Научно-исследовательский институт физики Южного федерального университета
г. Ростов-на-Дону, Россия

^* E-mail: denis@sfedu.ru
^** E-mail: vvsotsky@sfedu.ru

Поступила в редакцию 23.05.2020
После доработки 03.07.2020
Принята к публикации 24.09.2020

DOI: 10.31857/S0016794021020061

Аннотация

Предложен способ определения полных высотных профилей электронной концентрации в ионосфере по ионограммам внешнего спутникового зондирования, содержащим следы отражений зондирующих сигналов от земной поверхности. Монотонный профиль от спутника до некоторой высоты hm, находящейся выше высоты hmF2 максимума слоя F2, рассчитывается классическим методом по отражениям от внешней ионосферы. Ниже высоты hm вплоть до основания ионосферы профиль представляется системой взаимосвязанных аналитических функций с ограниченным числом параметров. Их значения находятся методами оптимизации при совместном использовании следов отражений сигналов как от внешней части ионосферы, так и от Земли. Для повышения устойчивости задачи нижняя часть искомого профиля в области E задается неизменяемым профилем из модели IRI-2016. Способ обеспечивает надежное определение параметров максимума hmF2, NmF2 и профиля в его окрестности. Введение в модель IRI ключевых параметров – hmF2, NmF2 и дополнительно рассчитанных значений B0 и B1, определяющих форму профиля в области F, позволяет получить IRI-профиль, скорректированный для реальных условий эксперимента. Рассчитанный и скорректированный профили близки друг к другу во внутренней ионосфере и могут заметно отличаться во внешней ионосфере. Таким образом, использование предлагаемого в работе способа для реконструкции полного высотного профиля электронной концентрации расширяет информационную ценность внешнего спутникового зондирования ионосферы.

1. ВВЕДЕНИЕ

На многих ионограммах внешнего спутникового зондирования ионосферы (ВнЗ) помимо следов отражений зондирующих сигналов от внешней ионосферы содержатся также следы отражений сигналов от земной поверхности. Фактически последние – это сигналы вертикального трансионосферного зондирования (ТИЗ), реализованного естественным образом без применения специальной аппаратуры. В настоящей работе предлагается способ использования групповых путей этих сигналов для определения вертикальных (высотных) распределений электронной концентрации (n_e(h)-профилей) во всей толще ионосферы ниже высоты спутника h_s.

Поставленная задача не является новой. Впервые идею использования данных ТИЗ для получения сведений об электронном строении ионосферы высказал H.П. Данилкин [1974]. При этом трансионограммы – частотные зависимости групповых путей P '(f) сигналов, прошедших ионосферу насквозь от спутника до наземного пункта приема, рассматривались в качестве дополнения к данным ВнЗ. Предполагалось, что наличие трансионограмм позволит дополнить вертикальные профили электронной концентрации, рассчитанные для внешней ионосферы (h ≥ hmF2) по данным ВнЗ, профилями во внутренней ионосфере (h ≤ hmF2), рассчитанными с использованием трансионограмм. В итоге получается полный n_e(h)-профиль от высоты спутника h_s до начальной высоты ионосферы h₀. Схема расчетов включает три этапа. На первом из ионограммы ВнЗ определяется n_{e top}(h)-профиль во внешней ионосфере от высоты h_s до высоты hmF2 (сверху вниз). Затем по нему определяется вклад внешней ионосферы $\Delta P_{{{\text{top}}}}^{'}\left( f \right)$ в групповые пути трансионосферных сигналов, и вычисляются групповые пути этих сигналов во внутренней ионосфере $~\Delta P_{{{\text{bot}}}}^{'}\left( f \right) = P{\kern 1pt} '\left( f \right) - \Delta P_{{{\text{top}}}}^{'}\left( f \right)$. На заключительном этапе методом математической оптимизации находится n_{e bot}(h)-профиль во внутренней ионосфере, минимизирующий функционал

${\text{Ф}} = \sum\limits_i {{{{\left[ {P_{{{\text{calc}},i}}^{'} - \Delta P_{{{\text{bot,}}i}}^{'}} \right]}}^{2}}} ,$

где суммирование ведется по отсчетам на выбранных частотах трансионосферных сигналов; $P_{{{\text{calc}},i}}^{'}$ – вычисляемые групповые пути, зависящие от распределения n_e(h) во внутренней ионосфере.

В дальнейшем было показано [Денисенко и Соцкий, 1987; Danilkin et al., 1988], что задача определения n_{e bot}(h)-профиля во внутренней ионосфере по групповым путям $\Delta P_{{{\text{bot}}}}^{{\text{'}}}\left( f \right)$ сигналов, пронизывающим ее насквозь, аналогична задаче решения интегрального уравнения Фредгольма первого рода. Подобные задачи принадлежат к классу некорректных задач математической физики [Тихонов и Арсенин, 1979], отличающихся отсутствием устойчивости решения относительно различного рода случайных погрешностей в экспериментальных данных. Другими словами, возможно получение бесконечного множества n_{e bot}(h)-профилей, каждый из которых в пределах экспериментальной погрешности удовлетворяет имеющимся групповым путям $\Delta P_{{{\text{bot}}}}^{{\text{'}}}\left( f \right)$. Исследования, проведенные в модельном эксперименте [Данилкин и др., 1987] с применением метода регуляризации [Тихонов и Арсенин, 1979], показали, что восстановление исходного n_{e bot}(h)-профиля во внутренней ионосфере, описываемого тремя параметрами, требует точности групповых путей сигналов ТИЗ не менее 1 км. Поскольку имеющиеся на сегодня экспериментальные данные такой точностью не обладают, то для повышения устойчивости задачи необходимо привлечение дополнительной информации о решении (n_{e bot}(h)-профиле). Чем меньшим числом параметров описывается n_{e bot}(h)-профиль, тем выше его устойчивость к погрешностям в экспериментальных данных ВнЗ и ТИЗ. Поэтому максимальную устойчивость задачи обеспечивает модельный n_{e bot}(h)-профиль, описываемый одним параметром при известных значениях hmF2 и NmF2. Это может быть, например, параболическое или квазигауссовское распределение n_e(h), которое наиболее адекватно описывает высотный ход электронной концентрации в окрестности максимума области F. Однако даже в этом случае на решение существенно влияют погрешности определения n_{e top}(h)-профиля во внешней ионосфере и особенно высоты hmF2 [Данилкин и др., 1987], поскольку от них зависит вклад внешней ионосферы $\Delta P_{{{\text{bot}}}}^{{\text{'}}}\left( f \right)$ в групповые пути трансионосферных сигналов. Ситуация ухудшается еще и тем, что для интерпретации экспериментов по ТИЗ используются модели ионосферы, предполагающие отсутствие в ионосфере пространственных горизонтальных градиентов электронной концентрации между зонами ВнЗ и ТИЗ, которые при наклонном ТИЗ не совпадают. Именно по этим причинам в литературе описаны только немногочисленные (самые удачные) результаты определения полных n_e(h)-профилей по данным ВнЗ и ТИЗ, несмотря на то, что только в экспериментах с ИСЗ “Интеркосмос-19” было получено более 2000 трансионограмм [Данилкин, 1987]. Таким образом, предложенная в работе [Данилкин, 1974] схема расчетов может быть рекомендована при некоторых ограничениях только при слабонаклонном или при вертикальном ТИЗ. В последнем случае могут быть также использованы следы отражений сигналов на ионограммах ВнЗ от земной поверхности. История метода ТИЗ, полученные к настоящему времени достижения и перспективы дальнейшего использования подробно описаны в обзорах [Данилкин, 2017; Ivanov et al., 2018]. В дополнение отметим, что в работе [Иванов и Соцкий, 2016] впервые предложен способ использования модели IRI для восстановления полных n_e(s)-профилей вдоль линии, соединяющей ИСЗ и наземную станцию приема, по данным прямого ТИЗ.

В настоящей работе предлагается способ определения полного n_e(h)-профиля по данным ВнЗ и вертикального ТИЗ (отражения от поверхности Земли). Применяется та же трехэтапная схема расчетов. При этом n_{e top}(h)-профиль во внешней ионосфере рассчитывается сверху вниз от высоты спутника h_s до некоторой высоты hm> hmF2. Ниже этой высоты n_e(h)-профиль представляется системой взаимосвязанных функций, параметры которых оптимизируются по минимальному отклонению расчетных групповых путей от экспериментальных при совместном использовании следов отражений сигналов как от внешней части ионосферы, так и от Земли. Для повышения устойчивости задачи нижняя часть искомого n_e(h)-профиля в области E задается неизменяемым профилем из модели IRI-2016 [Bilitza et al., 2017] (в дальнейшем модель IRI) для соответствующих условий эксперимента.

2. РАСЧЕТ f_N(h)-ПРОФИЛЕЙ ВО ВНЕШНЕЙ ИОНОСФЕРЕ

Рассмотрим задачу определения профиля электронной плазменной частоты f_N(h) во внешней ионосфере по данным об отражениях сигналов ВнЗ. Расчет f_N(h)-профилей основан на обращении нелинейного интегрального уравнения

(1)

$P{\kern 1pt} '\left( f \right) = ~\int\limits_0^{{{z}_{r}}\left( f \right)} {\mu {\kern 1pt} {\text{'}}{\kern 1pt} [f,{{f}_{N}}\left( z \right),{{f}_{H}}\left( z \right),\theta ]dz,} ~$

где Р '(f) – зависимость групповых путей (действующих глубин отражения) сигналов от частоты зондирования f; z_r(f) = h_s – h_r(f) – истинная глубина отражения сигнала, отсчитываемая от спутника; h_s – высота спутника; h_r(f) – высота отражения сигнала, отсчитываемая от поверхности Земли; μ' – групповой показатель преломления волны – функция частоты f, плазменной частоты f_N, гирочастоты f_H, угла θ между направлением вектора напряженности магнитного поля и вектором волновой нормали (вертикалью); относительно функции f_N(z), однозначно связанной с электронной концентрацией n_e(z) соотношением f_N(z) = $ = k\sqrt {{{n}_{e}}\left( z \right)} $, где k – константа, зависящая от выбора единиц измерений. Далее в тексте запись зависимости μ' от параметров f_H и θ будем опускать.

Отражение сигнала происходит на глубине z_r(f), где частоты f_N и f связаны соотношениями: f_N = f – для о-волны и ${{f}_{N}} = ~\sqrt {f\left( {f - {{f}_{H}}} \right)} $ – для х-волны. Таким образом, в области определения функции z_r(f) ее значения (для о-волн) совпадают со значениями функции z(f_N), обратной к f_N(z)-профилю. Отметим, что при монотонном возрастании частоты монотонно возрастает и функция f_N = f_N(f).

Для решения задачи в работе используется метод Джексона [Jackson, 1969] с отсчетами действующих глубин отражения по x-компоненте ионограммы. Вся толща ионосферы h₀ ≤ h ≤ h_s разбивается на ряд плоских слоев, внутри которых предполагается какое-либо аналитическое изменение электронной концентрации (т.н. ламинарный метод). Для внешней ионосферы во всех высотных интервалах вплоть до некоторой высоты hm, находящейся в верхней окрестности максимума слоя F2 (hm > hmF2), в работе применяется кусочно-непрерывная функция n_e(z):

(2)

${{n}_{e}}\left( z \right) = {{n}_{{e~j - 1}}}{\text{exp}}\left[ {{{\left( {z--{{z}_{{j - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {z--{{z}_{{j - 1}}}} \right)} {{{H}_{j}}}}} \right. \kern-0em} {{{H}_{j}}}}} \right],\,\,\,\,~{{z}_{{j - 1}}} \leqslant ~~z \leqslant ~~{{z}_{j}},~$

где j – номер слоя, отсчитываемый от спутника, 1 ≤ j ≤ m, m – максимальный номер, соответствующий глубине z_m (высоте hm), z₀ = 0; H_j – шкала высоты слоя; n_e0 = n_e(0) – электронная концентрация на высоте спутника (известная величина).

При численном задании функции P '(f) уравнение (1) линеаризуется и переходит в систему линейных алгебраических уравнений с треугольной матрицей

(3)

${\mathbf{P}}{\kern 1pt} ' = {\mathbf{MH}},$

где P' = [P '(f₁); P '(f₂); …; P '(f_m)]^T, f₁ < f₂ < … < f_m – вектор-столбец отсчетов действующих глубин отражения сигналов x-компоненты, здесь и ниже индекс “T” означает транспонирование; матрица M состоит из матричных элементов для экспоненциального профиля (см. подраздел 7.2) и имеет вид

${\mathbf{M}} = \left[ {\begin{array}{*{20}{c}} {{{M}_{{11}}}}&0& \cdots &0 \\ {{{M}_{{21}}}}&{{{M}_{{22}}}}& \cdots &0 \\ \cdots & \cdots & \cdots & \cdots \\ {{{M}_{{m1}}}}&{{{M}_{{m2}}}}& \cdots &{{{M}_{{mm}}}} \end{array}} \right]{\text{,}}$

H = [H₁; H₂; …; H_m]^T – вектор-столбец шкал высот слоев.

В рамках выбранной модели (2) решение системы (3)

(4)

${\mathbf{H}} = {{{\mathbf{M}}}^{{ - 1}}}{\mathbf{P}}{\kern 1pt} '$

единственно.

На заключительном этапе расчетов по известному решению (4) определяем функцию z(n_e), обратную к n_e(z)-профилю. Из модели (2) получаем таблицу истинных глубин отражения сигналов

$\begin{gathered} {{z}_{j}} = {{z}_{{j--1}}} + {{H}_{j}}{\text{ln}}\left( {{{{{n}_{{e~j}}}} \mathord{\left/ {\vphantom {{{{n}_{{e~j}}}} {{{n}_{{e~j--1}}}}}} \right. \kern-0em} {{{n}_{{e~j--1}}}}}} \right) = \\ = {{z}_{{j--1}}} + 2{{H}_{j}}{\text{ln}}\left( {{{{{f}_{{N\,j}}}} \mathord{\left/ {\vphantom {{{{f}_{{N\,j}}}} {{{f}_{{N\,j--1}}}}}} \right. \kern-0em} {{{f}_{{N\,j--1}}}}}} \right),~ \\ \end{gathered} $

где j = 1, 2, …, m; z₀ = z_s = 0. Пересчет в n_e(h)-профиль проводим по формуле h_j = h_s – z_j, которая определяет высоты от поверхности Земли с концентрацией n_ej (или плазменной частотой f_Nj). Последняя рассчитанная точка f_N(h)-профиля во внешней ионосфере находится на высоте hm > > hmF2 с плазменной частотой f_Nm, связанной с частотой зондирования x-сигнала f_m соотношением ${{f}_{{Nm}}} = \sqrt {{{f}_{m}}\left( {{{f}_{m}} - {{f}_{H}}} \right)} $.

Отметим, что при расчете матричных элементов M_ij в системе уравнений (3) необходимо учитывать изменение гирочастоты электронов f_H(h) с высотой. В работе для этого используется зависимость для дипольной модели магнитного поля:

${{f}_{H}}\left( h \right) = {{f}_{{Hs}}}{{\left( {\frac{{{{R}_{s}}}}{{R + h}}} \right)}^{3}},~$

где f_Hs – гирочастота электронов на высоте спутника; R = 6378 км – радиус Земли; R_s = R + h_s – расстояние от спутника до центра Земли.

3. ВОССТАНОВЛЕНИЕ f_N(h)-ПРОФИЛЕЙ ВО ВНУТРЕННЕЙ ИОНОСФЕРЕ ПО ДАННЫМ ВНЕШНЕГО И ТРАНСИОНОСФЕРНОГО ЗОНДИРОВАНИЯ

После определения f_{N top}(h)-профиля, hm ≤ h ≤ h_s, во внешней ионосфере по нему прямым расчетом по формуле (1) находятся групповые пути $\Delta P_{{{\text{top}}}}^{'}\left( f \right)$ для x-сигналов, отраженных, во-первых, во внешней ионосфере в области высот hmF2 < < h < hm, на частотах, меньших критической частоты х-следа, f_m < f < fxF2 (первая группа), и, во-вторых, отраженных земной поверхностью, на частотах, больших критической частоты х-следа, f > fxF2 (вторая группа). Далее вычисляются групповые пути этих сигналов ниже высоты hm: $\Delta P{\kern 1pt} '\left( f \right) = P{\kern 1pt} '\left( f \right) - \Delta P_{{{\text{top}}}}^{'}\left( f \right)$ для сигналов первой группы, и $~{{P}_{g}}\left( f \right) = P{\kern 1pt} '\left( f \right) - \Delta P_{{{\text{top}}}}^{'}\left( f \right)$ для сигналов второй группы. Таким образом, для восстановления f_N(h)-профиля ниже высоты hm имеется система интегральных уравнений:

(5)

$\left\{ \begin{gathered} \Delta P{\kern 1pt} '\left( f \right) = \int\limits_{{{h}_{r}}\left( f \right)}^{hm} {\mu _{x}^{'}\left[ {f,{{f}_{N}}\left( h \right)} \right]} {\kern 1pt} dh,~\,\,\,\,~{{f}_{m}} < f < fxF2 \hfill \\ {{P}_{g}}\left( f \right) = \int\limits_0^{hm} {\mu _{x}^{'}\left[ {f,{{f}_{N}}\left( h \right)} \right]} {\kern 1pt} dh,\,\,\,\,~f > fxF2. \hfill \\ \end{gathered} \right.$

Первое уравнение сводится к интегральному уравнению Вольтерра первого рода, второе – к интегральному уравнению Фредгольма первого рода. Как было отмечено выше, наличие второго уравнения делает всю задачу некорректной. Одним из способов решения подобных задач является использование физически обоснованных моделей с минимально возможным числом параметров.

3.1. Система функций для представления f_N(h)-профиля. Решение системы уравнений с выбором оптимального значения критической частоты слоя F2

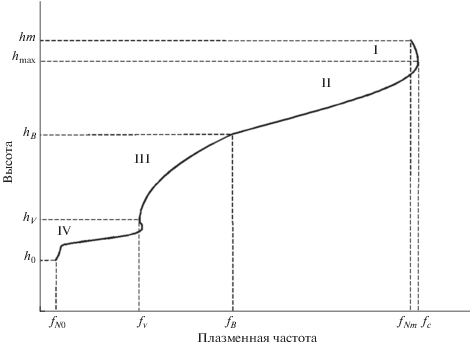
Наш подход заключается в следующем. Интервал высот [0, hm] разбивается на четыре области (рис. 1), в каждой из которых принимается своя модель:

(6)

$\begin{gathered} {\text{I}}){\text{\;}}\,\,{{f}_{N}}\left( h \right) = {{f}_{c}}{\text{exp}}\left[ { - \frac{1}{2}{{{\left( {\frac{{h - {{h}_{{{\text{max}}}}}}}{{{{H}_{{{\text{top}}}}}}}} \right)}}^{2}}} \right], \\ {{h}_{{{\text{max}}}}} < h \leqslant hm, \\ \end{gathered} $

(7)

$\begin{gathered} {\text{II}})\,\,{\text{\;}}{{f}_{N}}\left( h \right) = {{f}_{c}}{\text{exp}}\left[ { - \frac{1}{2}{{{\left( {\frac{{{{h}_{{{\text{max}}}}} - h}}{{{{H}_{{{\text{bot}}}}}}}} \right)}}^{2}}} \right], \\ {{h}_{B}} < h \leqslant {{h}_{{{\text{max}}}}},~ \\ \end{gathered} $

(8)

$\begin{gathered} {\text{III}}){\text{\;}}\,\,{{f}_{N}}\left( h \right) = {{f}_{{v}}} + \left( {{{f}_{B}} - {{f}_{v}}} \right){{\left( {\frac{{h - {{h}_{v}}}}{{{{h}_{B}} - {{h}_{v}}}}} \right)}^{2}}~, \\ ~{{h}_{v}} < h \leqslant {{h}_{B}}, \\ \end{gathered} $

(9)

${\text{IV}}){\text{\;}}\,\,{{f}_{N}}\left( h \right) \Rightarrow {\text{модель\;IRI}},~\,\,\,\,~{{h}_{0}} \leqslant h \leqslant {{h}_{v}}.$

Здесь приняты следующие обозначения: f_c = foF2 – критическая частота области F2, f_c = f_N(hmF2); h_max = hmF2; f_B – плазменная частота, рекомендуемая моделью IRI, для сшивки слоя F2 с нижележащей областью на высоте h_B: f_B = foF1 при наличии слоя F1 и f_B = 0.4883foF2, если слоя F1 нет; f_v = = f_N(h_v)– минимальная плазменная частота в долине на высоте h_v; h₀ – высота начала ионосферы. Распределение f_N(h), h₀ ≤ h ≤ h_v в IV области и параметр foF1 задаются моделью IRI, рассчитанной для конкретных географических координат, времени и значений f_c и h_max.

Рис. 1.

Представление f_N(h)-профиля ниже высоты hm модельными зависимостями (6)–(9).

Для принятой модели распределения f_N(h) ниже hm из уравнений (5) после их линеаризации получаем систему уравнений:

(10)

$\Delta P{\kern 1pt} '\left( f \right) = {{H}_{{{\text{top}}}}}{{A}_{{{\text{top}}}}}\left( {f,{{f}_{c}}} \right),~\,\,\,\,{{f}_{m}} < f < fxF2,$

(11)

$\begin{gathered} {{P}_{g}}\left( f \right) = {{h}_{0}} + \Delta {{P}_{{{\text{IRI}}}}}\left( f \right) + \left( {{{h}_{B}} - {{h}_{v}}} \right){{A}_{{vB}}}\left( f \right) + \\ + \,\,{{H}_{{{\text{bot}}}}}{{A}_{2}}\left( {f,{{f}_{c}}} \right) + {{H}_{{{\text{top}}}}}{{A}_{1}}\left( {f,{{f}_{c}}} \right),~\,\,\,\,~f > fxF2, \\ \end{gathered} $

где H_top и H_bot – шкалы высот квазигауссовских распределений (6) и (7), подлежащие определению; A_top и A₁, A₂, A_vB – матричные элементы соответственно для распределений (6), (7) и (8) (см. раздел 8); $\Delta {{P}_{{{\text{IRI}}}}}\left( f \right) = \int_{{{h}_{0}}}^{{{h}_{v}}} {\mu _{x}^{'}\left[ {f,{{f}_{N}}\left( h \right)} \right]} {\kern 1pt} dh$ – постоянный вклад областей D и E в групповые пути, рассчитываемый по модели IRI. Отметим, что в уравнении (11) каждое слагаемое (справа налево) выражает вклад областей I–IV в групповые пути сигналов второй группы.

Преобразуем уравнение (11) к более удобному виду. Используя зависимость (6), определим высоту h_max

(12)

${{h}_{{{\text{max}}}}} = hm - {{H}_{{{\text{top}}}}}\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{{Nm}}}}}} \right. \kern-0em} {{{f}_{{Nm}}}}}} \right)} ~,$

где f_Nm – плазменная частота на высоте hm. Используя зависимость (7), определим высоту h_B

(13)

${{h}_{B}} = {{h}_{{{\text{max}}}}} - {{H}_{{{\text{bot}}}}}\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{B}}}}} \right. \kern-0em} {{{f}_{B}}}}} \right)} ~,~$

или с учетом (12)

${{h}_{B}} = hm - {{H}_{{{\text{top}}}}}\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{{Nm}}}}}} \right. \kern-0em} {{{f}_{{Nm}}}}}} \right)} - {{H}_{{{\text{bot}}}}}\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{B}}}}} \right. \kern-0em} {{{f}_{B}}}}} \right)} {\kern 1pt} .$

После подстановки h_B в уравнение (11) запишем систему уравнений (10)–(11) в виде

(14)

$\begin{gathered} {{A}_{{{\text{top}}}}}\left( {{{f}_{i}},{{f}_{c}}} \right){{H}_{{{\text{top}}}}} = \Delta P{\kern 1pt} '\left( {{{f}_{i}}} \right), \\ {{f}_{m}} < {{f}_{i}} < fxF2,\,\,\,\,~i = 1,~2, \ldots ,{{n}_{{{\text{top}}}}}, \\ \end{gathered} $

(15)

$\begin{gathered} {{A}_{{d1}}}\left( {{{f}_{i}},{{f}_{c}}} \right){{H}_{{{\text{top}}}}} + {{A}_{{d2}}}\left( {{{f}_{i}},{{f}_{c}}} \right){{H}_{{{\text{bot}}}}} = \Delta {{P}_{g}}\left( {{{f}_{i}}} \right), \\ {{f}_{i}} > fxF2,\,\,\,\,~i = 1,~2, \ldots ,n, \\ \end{gathered} $

где введены обозначения

${{A}_{{d1}}}\left( {f,{{f}_{c}}} \right) = {{A}_{1}}\left( {f,{{f}_{c}}} \right) - {{A}_{{{v}B}}}\left( f \right)\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{{Nm}}}}}} \right. \kern-0em} {{{f}_{{Nm}}}}}} \right)} ,~$

${{A}_{{d2}}}\left( {f,{{f}_{c}}} \right) = {{A}_{2}}\left( {f,{{f}_{c}}} \right) - {{A}_{{{v}B}}}\left( f \right)\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{B}}}}} \right. \kern-0em} {{{f}_{B}}}}} \right)} ,$

$\Delta {{P}_{g}}\left( f \right) = {{P}_{g}}\left( f \right) - {{h}_{0}} - \Delta {{P}_{{{\text{IRI}}}}}\left( f \right) - \left( {hm - {{h}_{v}}} \right){{A}_{{vB}}}\left( f \right),$

n_top – количество сигналов первой группы, отражающихся во внешней ионосфере; n – количество сигналов второй группы, проходящих ионосферу насквозь, n_top + n > 2; ΔP_g(f) – групповые пути в интервале высот h_B ≤ h ≤ hm. Таким образом, при заданном значении критической частоты f_c мы имеем переопределенную систему уравнений с двумя неизвестными H_top и H_bot – шкалами высот квазигауссовских зависимостей f_N(h) в I и II областях (рис. 1).

Запишем систему (14)–(15) в матричных обозначениях:

(16)

${\mathbf{Au}} = {\mathbf{y}},$

где ${\mathbf{A}}{\kern 1pt} \left( {{{f}_{c}}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{{{\text{top}}}}}{\kern 1pt} \left( {{{f}_{c}}} \right)}&0 \\ {{{{\mathbf{A}}}_{{d1}}}{\kern 1pt} \left( {{{f}_{c}}} \right)}&{{{{\mathbf{A}}}_{{d2}}}{\kern 1pt} \left( {{{f}_{c}}} \right)} \end{array}} \right){\kern 1pt} ,{\mathbf{u}}{\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{c}} {{{H}_{{{\text{top}}}}}} \\ {{{H}_{{{\text{bot}}}}}} \end{array}} \right){\kern 1pt} ,{\mathbf{y}}{\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{c}} {\Delta {\mathbf{P}}{\kern 1pt} '} \\ {{\mathbf{\Delta }}{{{\mathbf{P}}}_{{\mathbf{g}}}}} \end{array}} \right){\kern 1pt} .$

Для заданного значения критической частоты f_ct решение системы находится методом наименьших квадратов (МНК) [Худсон, 1970]:

${{{\mathbf{u}}}_{t}} = {{{\mathbf{B}}}^{{ - 1}}}{{{\mathbf{A}}}^{T}}{\mathbf{y}},~\,\,\,\,~~{\mathbf{B}} = {{{\mathbf{A}}}^{T}}{\mathbf{A}}.$

Данное решение характеризуется значением функционала суммы квадратов невязок между вычисленными и экспериментальными значениями групповых путей:

(17)

$S\left( {{{f}_{{{\text{ct}}}}},{{{\mathbf{u}}}_{t}}} \right) = {{\left( {{\mathbf{y}} - {\mathbf{A}}{{{\mathbf{u}}}_{t}}} \right)}^{T}}\left( {{\mathbf{y}} - {\mathbf{A}}{{{\mathbf{u}}}_{t}}} \right).$

Варьируя допустимые значения критической частоты f_ct и решая каждый раз систему (16), определяем оптимальное решение ${\mathbf{x}}_{0}^{T} = \left( {{\mathbf{u}}_{{t0}}^{T},~{{f}_{{c0}}}} \right)$ = $~ = \left( {{{H}_{{{\text{top0}}}}},{{H}_{{{\text{bot0}}}}},~{{f}_{{c0}}}} \right)$, при котором функционал (17) достигает минимума.

3.2. Уточнение решения и оценка погрешностей параметров

Полученное решение, однако, не всегда является точным (оптимальным), поскольку варьирование величины f_c возможно только с каким-либо шагом. Для уточнения решения в окрестности $~{\mathbf{x}}_{0}^{T}$ и оценки дисперсий определяемых параметров воспользуемся схемой МНК с линеаризацией зависимости групповых путей по нелинейному параметру f_c [Худсон, 1970]. Новая система линеаризованных уравнений имеет вид

(18)

${{{\mathbf{A}}}_{e}}{\mathbf{x}} = {\mathbf{y}},$

где матрица A_e состоит из трех столбцов: A_e= = (A₁, A₂, A₃); A₁ и A₂ – первый и второй столбцы матрицы A в (16); ${{{\mathbf{A}}}_{3}} = {{H}_{{{\text{top0}}}}}\frac{{\partial {{{\mathbf{A}}}_{1}}}}{{\partial {{f}_{c}}}} + {{H}_{{{\text{bot0}}}}}\frac{{\partial {{{\mathbf{A}}}_{2}}}}{{\partial {{f}_{c}}}}$ – третий столбец, в котором производные вычисляются при f_c0; ${{{\mathbf{x}}}^{T}} = \left( {{{H}_{{{\text{top}}}}},{{H}_{{{\text{bot}}}}},\delta {{f}_{c}}} \right)$ – вектор неизвестных параметров; δf_c = f_c – f_c0 – отклонение критической частоты от значения f_c0. Решая уравнение (18) методом наименьших квадратов, получаем:

${\mathbf{x}} = {\mathbf{B}}_{e}^{{ - 1}}{\mathbf{A}}_{e}^{T}{\mathbf{y}},~\,\,\,\,~{{{\mathbf{B}}}_{e}} = {\mathbf{A}}_{e}^{T}{{{\mathbf{A}}}_{e}}.$

Таким образом, окончательный (уточненный) результат есть ${{{\mathbf{x}}}^{T}} = \left( {{{H}_{{{\text{top}}}}},{{H}_{{{\text{bot}}}}},\delta {{f}_{c}}} \right)$, f_c = f_c0 + δf_c. Остаточная сумма квадратов невязок есть

${{S}_{{{\text{min}}}}} = {{\left( {{\mathbf{y}} - {{{\mathbf{A}}}_{e}}{\mathbf{x}}} \right)}^{T}}\left( {{\mathbf{y}} - {{{\mathbf{A}}}_{e}}{\mathbf{x}}} \right).~$

Искомое высотное распределение f_N(h), h < hm рассчитывается по формулам (6)–(9), (12)–(13).

Матрица ошибок искомых параметров находится как [Худсон, 1970]

${\mathbf{D}}\left( {\mathbf{x}} \right) = \frac{{{{S}_{{{\text{min}}}}}}}{{\left( {{{n}_{{{\text{top}}}}} + n - 3} \right)}}{\mathbf{B}}_{e}^{{ - 1}}.~~$

С ее помощью определяются среднеквадратичные отклонения (СКО):

$\begin{gathered} \sigma \left( {{{H}_{{{\text{top}}}}}} \right) = \sqrt {{{D}_{{11}}}} ,\,\,\,\,~\sigma \left( {{{H}_{{{\text{bot}}}}}} \right) = \sqrt {{{D}_{{22}}}} ~, \\ ~\sigma \left( {{{f}_{c}}} \right) = \sigma \left( {\delta {{f}_{c}}} \right) = \sqrt {{{D}_{{33~}}}} .~ \\ \end{gathered} $

Соответственно по формуле (12) находится СКО высоты максимума области F

$\begin{gathered} \sigma ({{h}_{{{\text{max}}}}}) = {{\left[ {\left( {\frac{{\partial {{h}_{{{\text{max}}}}}}}{{\partial {{H}_{{{\text{top}}}}}}}} \right)_{{\mathbf{x}}}^{2}{{D}_{{11}}} + \left( {\frac{{\partial {{h}_{{{\text{max}}}}}}}{{\partial {{f}_{c}}}}} \right)_{{\mathbf{x}}}^{2}{{D}_{{33~}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \\ = {{\left[ {L{{D}_{{11}}} + {{{\left( {\frac{{{{H}_{{{\text{top}}}}}}}{{{{f}_{c}}}}} \right)}}^{2}}\frac{{{{D}_{{33~}}}}}{L}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},~ \\ \end{gathered} $

где L = 2 ln(f_c/f_Nm).

Качество решения оценивается по среднеквадратичным невязкам исходных и рассчитанных групповых путей в высотных интервалах, находящихся выше и ниже h_max. Для h_max ≤ h ≤ hm (первая группа сигналов)

${{s}_{{{\text{top}}}}} = {{\left[ {\mathop \sum \limits_{i = 1}^{{{n}_{{{\text{top}}}}}} {{{{{\left( {\Delta P{\kern 1pt} '\left( {{{f}_{i}}} \right) - {{H}_{{{\text{top}}}}}{{A}_{{{\text{top}}}}}\left( {{{f}_{i}},{{f}_{c}}} \right)} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\Delta P{\kern 1pt} '\left( {{{f}_{i}}} \right) - {{H}_{{{\text{top}}}}}{{A}_{{{\text{top}}}}}\left( {{{f}_{i}},{{f}_{c}}} \right)} \right)}}^{2}}} {{{n}_{{{\text{top}}}}}}}} \right. \kern-0em} {{{n}_{{{\text{top}}}}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.~$

Для второй группы сигналов выделяются их групповые пути в области F на высотах h_v ≤ h ≤ h_max

(19)

$\Delta {{P}_{F}}\left( f \right) = {{P}_{g}}\left( f \right) - {{h}_{0}} - \Delta {{P}_{{{\text{IRI}}}}}\left( f \right) - {{H}_{{{\text{top}}}}}{{A}_{1}}\left( {f,{{f}_{c}}} \right),$

а затем определяются соответствующие невязки

(20)

$\begin{gathered} {{s}_{F}} = \left[ {\sum\limits_{i = 1}^n {\left( {\Delta {{P}_{F}}\left( {{{f}_{i}}} \right) - \left( {{{h}_{B}} - {{h}_{v}}} \right){{A}_{{vB}}}\left( {{{f}_{i}}} \right)} \right.} } \right. - \\ {{\left. {{{^{{^{{^{{^{{}}}}}}}}{{{\left. { - \,\,{{H}_{{{\text{bot}}}}}{{A}_{2}}\left( {{{f}_{i}},{{f}_{c}}} \right)} \right)}}^{2}}} \mathord{\left/ {\vphantom {{^{{^{{^{{^{{}}}}}}}}{{{\left. { - \,\,{{H}_{{{\text{bot}}}}}{{A}_{2}}\left( {{{f}_{i}},{{f}_{c}}} \right)} \right)}}^{2}}} n}} \right. \kern-0em} n}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

где второе слагаемое выражает групповые пути сигналов в промежуточной области III, а третье – в области II под высотой максимума hmF2. Чем меньше значения s_top и s_F, тем более адекватно найденное решение истинному распределению f_N(h). На этом решение задачи восстановления f_N(h)-профиля во внутренней ионосфере в рамках сформулированной кусочно-непрерывной модели (6)–(9) можно считать законченным.

3.3. Коррекция решения для получения гладкого f_N(h)-профиля

Отметим, что восстановленный f_N(h)-профиль имеет разрыв производной df_N/dh в точке (h_B, f_B). При наличии слоя F1 это естественное обстоятельство. В отсутствии слоя F1 получение f_N(h)-профиля с непрерывной первой производной возможно путем коррекции найденного решения. Представим, что вместо распределения (8) на интервале III задано распределение плазменной частоты в более общем виде

(21)

${{f}_{{Np}}}\left( h \right) = {{f}_{v}} + \left( {{{f}_{B}} - {{f}_{v}}} \right){{\left( {\frac{{h - {{h}_{v}}}}{{{{h}_{B}} - {{h}_{v}}}}} \right)}^{p}},~$

где показатель степени p > 1. Из требования равенства производных слева и справа в точке (h_B, f_B) получаем

(22)

$p = \frac{{{{f}_{B}}}}{{{{f}_{B}} - {{f}_{v}}}}~\,\frac{{\left( {{{h}_{B}} - {{h}_{v}}} \right)\left( {{{h}_{{{\text{max}}}}} - {{h}_{B}}} \right)}}{{H_{{{\text{bot}}}}^{2}}}.$

Подстановка этого значения в (21), с одной стороны, обеспечивает непрерывность f_N(h)-профиля в точке (h_B, f_B), с другой, при p ≠ 2 приводит к искажению первоначального профиля (8) и, как следствие, к изменению вклада промежуточной области III в групповые пути, который теперь равен

${\Delta }{{P}_{{vB}}}\left( {f,{{f}_{B}},p} \right) = \int\limits_{{{h}_{{v}}}}^{{{h}_{B}}} {\mu _{x}^{'}\left[ {f,{{f}_{{Np}}}\left( h \right)} \right]dh} .$

Соответственно изменяется сумма квадратов невязок групповых путей в интервале высот h_v ≤ h ≤ ≤ h_max в выражении (20):

(23)

$\begin{gathered} {{s}_{F}}\left( {{{f}_{B}},p} \right) = \sum\limits_{i = 1}^n {\left[ {\Delta {{P}_{F}}\left( {{{f}_{i}}} \right) - \Delta {{P}_{{{v}B}}}\left( {{{f}_{i}},{{f}_{B}},p} \right) - } \right.} \\ {{\left. { - \,\,{{H}_{{{\text{bot}}}}}{{A}_{2}}\left( {{{f}_{i}},{{f}_{c}},{{f}_{B}}} \right)} \right]}^{2}}. \\ \end{gathered} $

Для получения наилучшего согласия расчетных и исходных групповых путей минимизируем функционал (23) по параметру f_B. При изменении f_B в соответствии с формулой (13) изменяется положение точки сшивки (h_B, f_B) модельных зависимостей (7) и (21), что по формуле (22) приводит к новому значению параметра p и в конечном итоге к новому значению функционала (23). Значение f_B, при котором функционал (23) достигает минимума, определяет оптимальное значение параметра p, и, следовательно, окончательное решение задачи восстановления f_N(h)-профиля во внутренней ионосфере в рамках модели (6)–(7), (21), (9) с непрерывной производной df_N/dh в точке (h_B, f_B).

При наличии слоя F1 точка (h_B, f_B) фиксирована, и функционал (23) минимизируется только по показателю степени p. После нахождения минимального значения s_F,_min находится соответствующая среднеквадратичная невязка ${{s}_{{Fp}}} = \sqrt {{{{{s}_{{F,~{\text{min}}}}}} \mathord{\left/ {\vphantom {{{{s}_{{F,~{\text{min}}}}}} n}} \right. \kern-0em} n}} $.

3.4. Отображение рассчитанного f_N(h)-профиля в профиль модели IRI

В ряде прикладных программ для расчета распространения радиоволн используется модель IRI. Рассчитанный f_N(h)-профиль можно использовать для получения соответствующего ему IRI-профиля путем введения в модель IRI значений ключевых параметров: hmF2, foF2, B0 и B1. Параметры B0 и B1 определяют в модели IRI форму f_N(h)-профиля в области F на высотах h_B ≤ h ≤ h_max (область II на рис. 1):

(24)

$\begin{gathered} {{f}_{{NF2}}}\left( h \right) = {{f}_{c}}\frac{{{\text{exp}}\left[ { - 0.5X{{{\left( h \right)}}^{{B1}}}} \right]}}{{\sqrt {{\text{ch}}\left[ {X\left( h \right)} \right]} }},~ \\ X\left( h \right) = \frac{{{{h}_{{{\text{max}}}}} - h}}{{B0}},~\,\,\,~\,B0 = {{h}_{{{\text{max}}}}} - {{h}_{B}},~ \\ \end{gathered} $

где h_B – высота c плазменной частотой f_B.

Для определения значений параметров B0 и B1 можно рекомендовать следующую процедуру расчетов. Зададим в интервале h_B ≤ h ≤ h_max массив высот h_F2, i, i = 1, 2, …, m_F, для которого по формулам (24) при B1 = 2 рассчитаем значения плазменных частот f_N, i = f_NF2(h_F2, i), i = 1, 2, …, m_F. Далее по формуле (7) определим соответствующие им высоты квазигауссовского распределения f_N(h) в области II

${{h}_{{g,i}}} = {{h}_{{{\text{max}}}}} - {{H}_{{{\text{bot}}}}}\sqrt {2{\text{ln}}\left( {{{{{f}_{c}}} \mathord{\left/ {\vphantom {{{{f}_{c}}} {{{f}_{{N,i}}}}}} \right. \kern-0em} {{{f}_{{N,i}}}}}} \right)} ,~\,\,\,\,i = 1,2, \ldots ,{{m}_{F}}.$

Различие между высотами будем характеризовать суммой квадратов

(25)

$S\left( {B0} \right) = \mathop \sum \limits_i {{\left( {{{h}_{{g,i}}} - {{h}_{{F2,i}}}} \right)}^{2}}.$

При B1 = 2 по минимуму функционала (25) найдем оптимальное значение B0_opt. Затем уточним параметр B1 путем минимизации функционала

(26)

${{S}_{{F,{\text{IRI}}}}}\left( {B1} \right) = \sum\limits_{i = 1}^n {{{{\left[ {\Delta {{P}_{F}}\left( {{{f}_{i}}} \right) - \Delta {{P}_{{F,{\text{IRI}}}}}\left( {{{f}_{i}},B1} \right)} \right]}}^{2}}} $

от суммы квадратов отклонений групповых путей (19) на высотах h_v ≤ h ≤ h_max от групповых путей, рассчитанных на основе модели IRI

$\begin{gathered} \Delta {{P}_{{F,{\text{IRI}}}}}\left( {f,B1} \right) = \\ = \int\limits_{{{h}_{v}}}^{{{h}_{{{\text{max}}}}}} {\mu _{x}^{'}} \left[ {f,{{f}_{{N,{\text{IRI}}}}}\left( {h,B1,B{{0}_{{{\text{opt}}}}},{{h}_{{{\text{max}}}}},{{f}_{c}}} \right)} \right]dh, \\ \end{gathered} $

где f_N, IRI – профиль, рассчитанный по модели IRI. После нахождения минимального значения S_F, IRImin в (26) c B1 = B1_opt находится соответствующая среднеквадратичная невязка ${{s}_{{F,{\text{IRI}}}}} = \sqrt {{{{{S}_{{F,{\text{IRImin}}}}}} \mathord{\left/ {\vphantom {{{{S}_{{F,{\text{IRImin}}}}}} n}} \right. \kern-0em} n}} $, характеризующая соответствие полученного оптимального f_N, IRI(h)-профиля истинному распределению f_N(h). Полученный f_N, IRI(h)-профиль может быть рассчитан для любого высотного интервала.

4. ИСПЫТАНИЕ МЕТОДА НА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ. ВЫБОР ВОЗМОЖНЫХ РЕШЕНИЙ

В качестве экспериментальных используем данные внешнего зондирования, полученные в 70–80 гг. прошлого века на спутнике ISIS-2 (International Satellite for Ionospheric Studies). Данные в электронном виде доступны на сайте NASA’s Space Physics Data Facility (SPDF) по адресу (https://spdf.sci.gsfc.nasa.gov). Ионограммы ВнЗ в виде cdf-файлов (common data format) доступны из этой же базы по адресу (https://spdf.sci.gsfc.nasa. gov/ pub/data/isis/topside_sounder/ionogram_cdf/isis2/). Разработанная в НИИ физики ЮФУ специальная программа на языке MATLAB “topionFrame” позволяет получить из скачанных cdf-файлов изображения ионограмм и провести их ручную оцифровку с записью в mat-файлы для дальнейшей обработки.

Рассмотрим последовательность восстановления f_N(h)-профиля на конкретном примере. На рисунке 2 показан скриншот ионограммы ВнЗ, полученной на спутнике ISIS-2 22 октября 1979 г. в 22:34:03 UT, с точками оцифровки следов отражений o-, x- и z-сигналов ВнЗ, включая отражения от земной поверхности. Результаты расчетов приведены в таблице 1.

Рис. 2.

Скриншот ионограммы ВнЗ, полученной на спутнике ISIS-2 22 октября 1979 г. в 22:34:03 UT, с точками оцифровки следов отражений o-, x- и z-сигналов. Хорошо видны отражения от земной поверхности.

Таблица 1.

Параметры f_N(h)-профилей, рассчитанные по трем ионограммам спутника ISIS-2

Параметры	Ионограммы			Примечания
Дата	22.10.1979	22.03.1973	22.03.1980
Время, UT	22:34:03	17:09:30	20:29:48
Широта	25.48° N	35.71° N	–29.29° N	Географические координаты
Долгота	146.6° E	–80.43° E	–176.1° E
h_s, км	1392.8	1363.1	1391.1	Высота ИСЗ
f_Nm, МГц	13.21	7.14	10.98	Нижняя точка f_Ntop(h)-профиля во внешней ионосфере
hm, км	351.1	334.7	347.6	Нижняя точка f_Ntop(h)-профиля во внешней ионосфере
f_c, est, МГц	13.56	8.24	12.96	Оценочные значения для использования модели IRI
h_max, est, км	317.2	258.0	262.3	Оценочные значения для использования модели IRI
foE, МГц	3.30	3.39	3.45	Максимум и долина в области E
hmE, км	110	110	110
fv, МГц	3.21	3.31	3.34
hv, км	117.5	120	120
foF2, МГц	13.51	7.97	12.40	Максимум области F после уточнения, оценка погрешностей foF2 и hmF2 по невязкам групповых путей
σ(f_c), МГц	0.023	0.019	0.087
hmF2, км	320.5	282.9	289.6
σ(h_max), км	2.51	1.96	3.98
f_B, МГц	6.62	4.59 (foF1)	6.33	Точка сшивки зависимостей (7) и (8) для p = 2
h_B, км	228.0	206 (hmF1)	199.4	Точка сшивки зависимостей (7) и (8) для p = 2
B0_opt, км	92.74	76.88	93.20	Ключевые параметры (вместе с hmF2 и foF2) для получения f_N, IRI(h)-профиля
B1_opt	2.16	2.87	2.53
p	2.60	2.44	2.02	Показатель степени для функции f_Np(h) в (21) и точка сшивки зависимостей (7) и (21) для гладкого профиля
f_B, МГц	8.41	4.59 (foF1)	7.92
h_B, км	245.1	206 (hmF1)	215.9
s_top	6.70	3.25	6.80	СКО групповых путей первой группы сигналов во внешней ионосфере
s_F	5.82	2.47	5.86	СКО групповых путей второй группы сигналов для кусочно-непрерывного профиля
s_Fp	5.87	2.45	5.86	СКО групповых путей второй группы сигналов для гладкого профиля
s_F, IRI	6.20	2.13	6.33	СКО групповых путей второй группы сигналов для IRI-профиля

Вначале по x-компоненте ионограммы рассчитывается f_N top(h)-профиль во внешней ионосфере в интервале высот hm ≤ h ≤ h_s (см. раздел 2) и определяется его вклад $\Delta P_{{{\text{top}}}}^{'}\left( f \right)$ в групповые пути зондирующих сигналов первой и второй групп. Далее вычисляются групповые пути ΔP '(f) и P_g(f) этих сигналов ниже высоты hm = 351.1 км, необходимые для решения системы уравнений (10)–(11).

При заданном оценочном значении f_c,_est = = 13.56 МГц, определенном из ионограммы, решаем уравнение (10) относительно H_top и по формуле (12) получаем h_{max, est} = 317.2 км – оценку высоты максимума слоя F2. Для заданных географических координат и времени проведения эксперимента вводим значения f_{c, est} и h_{max, est} в модель IRI. Для высот h < hm результат изображен на рис. 3 точечной линией. Слои D, E и долина зависят только от географических координат и времени. Они имеют следующие параметры: foE = = 3.3 МГц, hmE = 110 км, f_v = 3.21 МГц, h_v = 117.5 км. Плазменная частота стыковки моделей (7) и (8) f_B = 0.4883f_{c, est} = 6.62 МГц.

Рис. 3.

f_N(h)-профили, h ≤ hm, полученные из ионограммы на рис. 2. Точечная линия – IRI-профиль с оценочными значениями параметров f_c и h_max; штрихпунктирная линия – кусочно-непрерывный f_N(h)-профиль с параболической моделью (8); сплошная линия – гладкий f_N(h)-профиль с полиномиальной моделью (21); штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1. В правой части рисунка линия со звездочками – групповые пути ΔP '(f) сигналов, отраженных во внешней ионосфере; линия с крестиками – уменьшенные в два раза групповые пути P_g(f) трансионосферных сигналов, отраженных земной поверхностью.

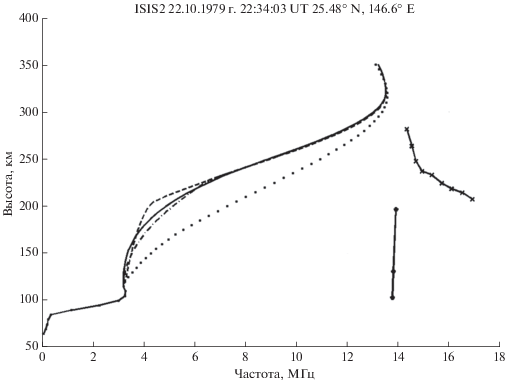
Полученные значения используем для расчета зависимости ΔP_g(f) в уравнении (15). Далее решаем систему уравнений (16) с минимизацией функционала (17). Получаем решение ${\mathbf{x}}_{0}^{T} = \left( {{{H}_{{{\text{top0}}}}},{{H}_{{{\text{bot0}}}}},~{{f}_{{c0}}}} \right)$, в котором f_c0 = 13.51 МГц, и высоту максимума из формулы (12) h_max0 = 320.7 км. Уточняем полученные значения параметров, решая расширенную систему уравнений (18). Уточненное значение h_max = 320.5 км, поправка к критической частоте составляет δf_c = 0.001 МГц. Среднеквадратичные отклонения (погрешности) параметров: σ(h_max) = = 2.25 км, σ(f_c) = 0.023 МГц. СКО групповых путей для первой группы сигналов во внешней ионосфере s_top = 6.70 км. СКО групповых путей для второй группы сигналов во внутренней ионосфере s_F= 5.82 км. f_N(h)-профиль с разрывом первой производной в точке h_B = 228.0 км, f_B = = 6.62 МГц изображен штрихпунктирной линией на рис. 3.

В принципе на этом этапе поставленную задачу восстановления f_N(h)-профиля во внутренней ионосфере по данным ВнЗ и вертикального ТИЗ в рамках сформулированной кусочно-непрерывной модели (6)–(9) можно считать решенной. Объединяя восстановленный f_N(h)-профиль в точке (hm, f_Nm) с f_Ntop(h)-профилем, получаем полный профиль ионосферы до высоты спутника h_s.

Для отображения рассчитанного кусочно-непрерывного f_N(h)-профиля в профиль модели IRI воспользуемся методикой из подраздела (3.4). При известных значениях критической частоты f_c = 13.51 МГц и высоты максимума h_max = 320.5 км определяем оптимальные значения параметров B0_opt = 92.74 км и B1_opt = 2.16. Вводя значения h_max, f_c, B0_opt и B1_opt в модель IRI, получаем f_N, IRI(h)-профиль, изображенный на рис. 3 штриховой линией. Характеристикой IRI-профиля является величина s_F, IRI = 6.20 км.

При необходимости получения гладкого f_N(h)-профиля (без разрыва производной df_N/dh в точке (h_B, f_B)) можно воспользоваться методикой из подраздела (3.3). В этом случае определяются параметры модели (21), обеспечивающей непрерывность производной на границе второй и третьей областей (см. рис. 1). Оптимальное решение достигается при показателе степени p = 2.60, сшивка моделей производится в точке h_B = 245.1 км, f_B = 8.41 МГц. СКО групповых путей s_Fp = 5.87 км. f_N(h)-профиль с непрерывной первой производной изображен сплошной кривой на рис. 3.

Заметим, что величины s_F = 5.82 км и s_Fp = 5.87 км практически равны. Это означает практически одинаковый вклад кусочно-непрерывного и гладкого f_N(h)-профилей (штрихпунктирная и сплошная линии на рис. 3) в групповые пути трансионосферных сигналов. Поэтому оба профиля равноценны, и ни одному из них нельзя отдать предпочтение. Более того, если считать, что погрешность измерения групповых путей составляет не менее 7 км (на самом деле, гораздо больше), то и IRI-профиль (штриховая линия) с s_F, IRI = 6.20 км можно считать решением поставленной задачи. Мы будем считать решением гладкий f_N(h)-профиль с непрерывной производной df_N/dh в точке (h_B, f_B).

Для ионограммы на рис. 2 полный f_N(h)-профиль представлен на рис. 4 сплошной линией. Штриховой линией изображен IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1. Видно хорошее совпадение профилей во внешней ионосфере вплоть до высоты спутника.

Рис. 4.

Полный f_N(h)-профиль ионосферы (сплошная линия), рассчитанный до высоты спутника по ионограмме на рис. 2. Штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1.

Рассмотрим восстановление профиля для случая, когда модель IRI указывает на наличие слоя F1. Соответствующая ионограмма ВнЗ приведена на рис. 5. Значения всех рассчитанных параметров кусочно-непрерывного, гладкого и IRI профилей приведены в таблице 1, а сами профили изображены на рис. 6. При использовании зависимости (21) вместо (8) уточняется только параметр p, так как в точке стыковки (h_B, f_B) профилей (7) и (21) непрерывности производной df_N/dh не требуется. Отметим, что все три профиля характеризуются среднеквадратичными невязками групповых путей, меньшими 2.5 км, что не превышает погрешностей измерений групповых путей. Поэтому любой из них является решением задачи.

Рис. 5.

Скриншот ионограммы ВнЗ, полученной на спутнике ISIS-2 22 марта 1973 г. в 17:09:30 UT, с точками оцифровки следов отражений o-, x- и z-сигналов. Хорошо видны отражения от земной поверхности.

Рис. 6.

f_N(h)-профили со слоем F1, h ≤ hm, полученные из ионограммы на рис. 5. Сплошная линия – f_N(h)-профиль с полиномиальной моделью (21) с разрывом производной df_N/dh в точке максимума слоя F1. Остальные обозначения те же, что на рис. 3.

Для ионограммы на рис. 5 полный (с зависимостью (21)) f_N(h)-профиль представлен на рис. 7 сплошной линией. Штриховой линией изображен IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1. Отметим, что в этом случае наблюдается систематическое превышение значений плазменных частот IRI-профиля во внешней ионосфере над значениями рассчитанного по ионограмме f_Ntop(h)-профиля.

Рис. 7.

Полный f_N(h)-профиль ионосферы (сплошная линия), рассчитанный до высоты спутника по ионограмме на рис. 5. Штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1.

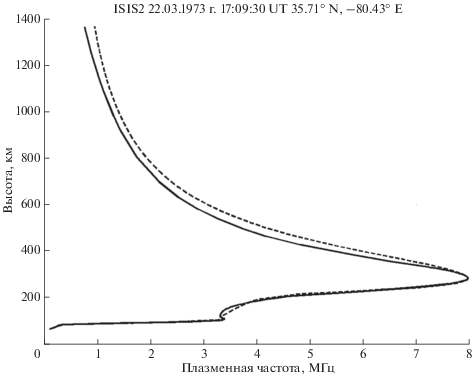
Предыдущие два примера относились к северному полушарию. На рисунках 8–10 представлены ионограмма и результаты расчетов f_N(h)-профилей для южного полушария. На рисунках 9–10 изображены только два профиля – с непрерывной производной (сплошная кривая) и скорректированный IRI-профиль (штриховая линия). Параметры кусочно-непрерывного, гладкого и IRI-профилей представлены в таблице. Анализ величин s_F, s_Fp и s_F, IRI показывает, что они не превышают принятый выше уровень погрешности 7 км, и поэтому любой из профилей можно считать решением задачи. Так же, как в предыдущем случае, на рис. 10 наблюдаем превышение у IRI-профиля значений f_N(h) во внешней ионосфере над значениями рассчитанного по ионограмме f_Ntop(h)-профиля.

Рис. 8.

Скриншот ионограммы ВнЗ, полученной на спутнике ISIS-2 22 марта 1980 г. в 20:29:48 UT, с точками оцифровки следов отражений o-, x- и z-сигналов. Хорошо видны отражения от земной поверхности.

Рис. 9.

f_N(h)-профили, h ≤ hm, полученные из ионограммы на рис. 8. Сплошная линия – гладкий f_N(h)-профиль с полиномиальной моделью (21); штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1. Остальные обозначения те же, что на рис. 3.

Рис. 10.

Полный f_N(h)-профиль ионосферы (сплошная линия), рассчитанный до высоты спутника по ионограмме на рис. 8. Штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1.

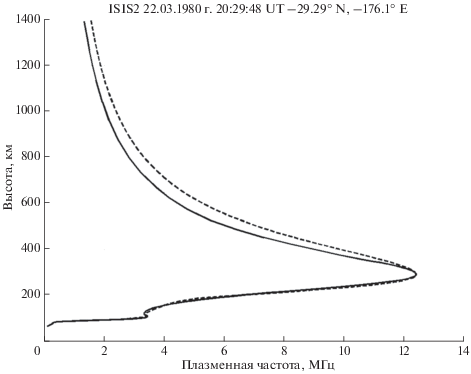
Таким образом, проведенные расчеты показывают, что предлагаемый метод восстановления f_N(h)-профилей во внутренней ионосфере по данным ВнЗ и вертикального ТИЗ может быть рекомендован для получения устойчивых решений задачи при использовании моделей (6)–(9), (21). К сожалению, авторы не могут проверить метод в экспериментах с прямыми измерениями электронной концентрации. Поэтому был поставлен модельный эксперимент, результаты которого описаны в следующем разделе.

5. ВЕРИФИКАЦИЯ МЕТОДИКИ ВОССТАНОВЛЕНИЯ f_N(h)-ПРОФИЛЕЙ ВНУТРЕННЕЙ ИОНОСФЕРЫ ПО ДАННЫМ ВЕРТИКАЛЬНОГО НАЗЕМНОГО ЗОНДИРОВАНИЯ

Для оценки адекватности получаемых по предлагаемой методике f_N(h)-профилей реальным распределениям был проведен модельный эксперимент. В качестве экспериментальных были использованы два f_N(h)-профиля из работы [Денисенко и Соцкий, 2019], восстановленные из дневной и ночной ионограмм ВЗ в п. Ростов (47.24° N, 39.63° E). Оба профиля были известным образом продолжены от высоты h_max до высоты hm во внешней ионосфере. По каждому из профилей были рассчитаны “экспериментальные” групповые пути сигналов первой ΔP '(f) и второй групп P_g(f) (см. раздел 3). После этого предлагаемым в работе методом решалась обратная задача.

Рассмотрим более подробно методику тестирования на примере дневного f_N(h)-профиля. Результаты тестирования представлены на рис. 11. Исходный дневной f_N(h)-профиль с параметрами: f_c = 6.50 МГц, h_max = 222.7 км представлен штрихпунктирной линией. Он продлен выше высоты максимума слоя F2 на 30 км: hm = h_max + 30 км. Было принято значение f_Nm = 0.95f_c. На трех частотах были рассчитаны групповые пути ΔP '(f) сигналов, отражающихся во внешней ионосфере (линия со звездочками), и на десяти частотах групповые пути P_g(f) трансионосферных сигналов, отражающихся от поверхности Земли (линия с крестиками). Оценочные значения f_{c, est} и h_{max, est} были выбраны путем увеличения точных значений соответственно на 0.1 МГц и 10 км. Соответствующий значениям f_{c, est} и h_{max, est} IRI-профиль представлен на рис. 11 точечной линией. С его помощью находятся необходимые для зависимостей (6)–(9) параметры f_v, h_v, f_B. В результате дальнейших расчетов получаем восстановленный гладкий f_N(h)-профиль с зависимостью (21) и p = 3.11 (сплошная линия), в котором критическая частота полностью совпала с ее точным значением, а высота максимума отличается от точной на 0.5 км. Профиль характеризуется среднеквадратичными невязками s_top = 0.58 км, s_Fp = = 0.30 км. Вводя рассчитанные ключевые параметры (f_c, h_max, B0, B1) в модель IRI, получаем скорректированный IRI-профиль, изображенный штриховой линией на рис. 11. Для него СКО групповых путей s_F, IRI = 0.39 км. Из графиков видно, что в области F оба решения хорошо согласуются с результатами наземного вертикального зондирования (исходным профилем), причем в основании области F предпочтительнее распределение с непрерывной производной. В слое E имеет место существенное расхождение, особенно для высоты максимума hmE.

Рис. 11.

Результаты тестирования метода с использованием дневного f_N(h)-профиля. Штрихпунктирная линия – исходный (“экспериментальный”) f_N(h)-профиль, по которому рассчитаны групповые пути $\Delta P{\kern 1pt} '\left( f \right)$ x-сигналов (линия со звездочками), отражающихся во внешней ионосфере, и групповые пути P_g(f) x-сигналов (на линии с крестиками уменьшены в два раза), отражающихся от земной поверхности. Точечная линия – модель IRI с оценочными значениями параметров f_c и h_max. Результаты обратных расчетов: сплошная линия – гладкий f_N(h)-профиль с полиномиальной моделью (21), штриховая линия – IRI-профиль, скорректированный по параметрам hmF2, foF2, B0, B1.

Аналогичное моделирование было проведено для f_N(h)-профиля, рассчитанного из ночной ионограммы ВЗ. Результаты представлены на рис. 12 в тех же обозначениях, что и на рис. 11. В данном случае оценочное значение f_{c, est} было увеличено на 0.1 МГц от точного, а значение h_{max, est} было занижено на 10 км. Рассчитанное значение foF2 совпало с точным, а высота hmF2 оказалась меньше на 0.7 км. Среднеквадратичные невязки групповых путей s_top = 0.60 км, s_Fp = 0.30 км, s_F, IRI = = 0.38 км. Из графиков видно, что в области F оба решения – рассчитанный и IRI профили хорошо согласуются с исходным f_N(h)-профилем. Существенные расхождения наблюдаются в Е-области и долине.

Рис. 12.

Результаты тестирования метода с использованием ночного f_N(h)-профиля. Обозначения те же, что на рис. 11.

Таким образом, проведенное тестирование показывает, что предлагаемый в работе метод восстановления f_N(h)-профиля во внутренней ионосфере по данным ВнЗ и вертикального ТИЗ обеспечивает надежное определение параметров foF2 и hmF2 с распределением f_N(h) в области высот, примыкающих к максимуму слоя F2. На высотах межслоевой области (долины) и ниже точность восстановленного решения определяется точностью представления f_N(h)-профиля моделью IRI.

6. ЗАКЛЮЧЕНИЕ

В работе предложен новый способ определения полных f_N(h)-профилей ионосферы по ионограммам спутникового ВнЗ, содержащим следы отражений зондирующих сигналов от земной поверхности.

Основное внимание уделено восстановлению f_N(h)-профиля во внутренней ионосфере по частотной зависимости групповых путей сигналов, отраженных поверхностью Земли (трансионосферных сигналов). Сформулированная задача является обратной некорректной задачей, требующей для своего решения максимального привлечения дополнительной информации об искомом f_N(h)-профиле. В работе решение задачи находится на физически обоснованной системе взаимосвязанных аналитических функций f_N(h) с малым числом параметров. Для повышения устойчивости задачи дополнительно привлекается информация из модели IRI: 1) о слоевой структуре искомого решения; 2) об f_N(h)-профиле в областях D и E, который считается известной частью решения.

Особенностью предлагаемого способа является совместное использование групповых путей сигналов, отраженных во внешней ионосфере и от земной поверхности, для получения надежных значений параметров hmF2, NmF2 максимума области F и профиля в его окрестности. О надежности свидетельствуют результаты верификации по данным наземного вертикального зондирования.

Введение в модель IRI ключевых параметров – hmF2, NmF2 и дополнительно рассчитанных значений B0 и B1, определяющих форму профиля в области F, позволяет получить IRI-профиль, скорректированный для реальных условий эксперимента. Расчеты показывают, что рассчитанный по данным ВнЗ и скорректированный IRI профили близки друг к другу во внутренней ионосфере и могут заметно отличаться во внешней ионосфере.

Таким образом, предлагаемый в работе способ дает два решения задачи: 1) f_N(h)-профиль, непосредственно рассчитанный по данным ВнЗ и ТИЗ; 2) f_N(h)-профиль, полученный отображением первого профиля с помощью его ключевых параметров в модель IRI. Оба профиля могут использоваться для решения задач, связанных с распространением радиоволн.

Представленный способ расширяет информационную ценность внешнего спутникового зондирования ионосферы. Однако в настоящее время он может быть рекомендован только для проведения каких-либо отдельных исследований. Широкое применение метод может получить в будущем при создании системы глобального мониторинга ионосферы и программ-роботов для автоматической оцифровки данных ВнЗ с отражениями сигналов от земной поверхности.

Список литературы

– Данилкин H.П. О получении и возможном использовании трансионограмм // Геомагнетизм и аэрономия. Т. 14. № 2. С. 369–371. 1974.
– Данилкин Н.П. Трансионосферное радиозондирование как средство контроля состояния ионосферы / Ионосферно-магнитная служба. Ред. С.И. Авдюшин, А.Д. Данилов. Л.: Гидрометиздат. С. 79–110. 1987.
– Данилкин Н.П., Денисенко П.Ф., Ковалев В.A., Соцкий В.В. О возможности использования метода регуляризации в задаче трансионосферного зондирования // Геомагнетизм и аэрономия. Т. 27. № 4. С. 550–552. 1987.
– Данилкин Н.П. Трансионосферное радиозондирование (обзор) // Геомагнетизм и аэрономия. Т. 57. № 5. С. 543–554. 2017.https://doi.org/10.1134/S0016793217050048
– Денисенко П.Ф., Соцкий В.В. Особенности обратных задач вертикального зондирования ионосферы (обзор) // Изв. Сев.-Кавк. науч. центра высш. шк. Естеств. науки. № 2. С. 59–71. 1987.
– Денисенко П.Ф., Соцкий В.В. Восстановление высотных профилей электронной концентрации по данным вертикального зондирования с использованием модели IRI // Геомагнетизм и аэрономия. Т. 59. № 6. С. 774–785. 2019.https://doi.org/10.1134/S0016794019050031
– Иванов И.И., Соцкий В.В. Определение распределений электронной концентрации по данным трансионосферного зондирования c использованием модели IRI // Известия высших учебных заведений. Физика. Т. 59. № 12-2. С. 126–129. 2016.
– Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 288 с. 1979.
– Худсон Д. Статистика для физиков. М.: Мир, 296 с. 1970.
– Bilitza D., Altadill D., Truhlik D., et al.International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions // Space Weather. V. 15. P. 418–429. https://doi.org/10.1002/2016SW001593
– Danilkin N.P., Denisenko P.F., Sotsky V.V. Peculiarities of the inverse problems of vertical radio sounding of the ionosphere // Adv. Space Res. V. 8. № 4. P. (4)91–(4)94. 1988.
– Ivanov I., Maltseva O., Sotskii V., Tertyshnikov A., Zhbankov G. Reverse satellite transionospheric sounding: advantages and prospects / Satellite information classification and interpretation. Ed. R.B. Rustamov. Intech Open. Chapter 4. 2018.https://doi.org/10.5772/intechopen.80240
– Jackson J.E. The reduction of topside ionograms to electron-density profiles // Proc. IEEE. V. 57. № 6. P. 960–976. 1969.
– Paul A.K. Use of virtual-height slopes for determination of electron density profiles // Radio Sci. V. 2. № 10. P. 1195–1204. 1967.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал