1. На главную
  2. Электронные версии
  3. Геомагнетизм и аэрономия
  4. T. 62, № 2, 2022

Геомагнетизм и аэрономия, 2022, T. 62, № 2, стр. 139-143

Простейшее динамо Солнца и новый механизм стабилизации

С. В. Старченко *

Институт земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова РАН (ИЗМИРАН)
г. Троицк, г. Москва, Россия

* E-mail: sstarchenko@mail.ru

Поступила в редакцию 28.02.2021
После доработки 04.09.2021
Принята к публикации 24.09.2021

Полный текст (PDF)

Аннотация

Показано, что для гидромагнитного динамо Солнца и подобных ему динамо, возможно, значимой является стабилизирующая нелинейность, обратно пропорциональная величине электрического тока. Соответствующая простейшая локальная гидромагнитная модель для магнитной энергии состоит из одного неоднородного линейного обыкновенного дифференциального уравнения, которое детализируется для солнечных пятен. Простейшее же глобальное солнечное динамо может достоверно определяться двумя однородными линейными обыкновенными дифференциальными уравнениями, имитирующими известные альфа-эффект и омега-эффект.

1. ВВЕДЕНИЕ

Моделирование динамо-процессов генерации солнечных и многих других астрофизических магнитных полей конвективными течениями остается преимущественно теоретическим почти уже век [Charbonneau, 2020; Moffatt and Dormy, 2019; Larmor, 1919]. И это несмотря на впечатляющие численные и физические эксперименты, способные воспроизвести некоторые существенные особенности таких динамо [Warnecke and Kapyla, 2020; Cameron et al., 2017; Lathrop and Forest, 2011; Christensen et al., 2009]. Однако основные коэффициенты подобия таких экспериментов все еще на много порядков величины отстоят от реальных коэффициентов подобия Солнца, звезд, планет и прочих астрофизических объектов.

Поэтому, а еще больше для понимания физической сути, необходимы упрощенные модели. Исторически таковыми были и остаются различным образом усредненные, маломодовые и феноменологические модели. Смотрите, например, работы [Charbonneau, 2020; Moffatt and Dormy, 2019, Brandenburg, 2018; Kleeorin and Rogachevskii, 1999; Рузмайкин и Старченко, 1987]. Стабилизирующую нелинейность для генерирующих эффектов большинство авторов таких работ задают в виде, подобном $({{1 - {{{\mathbf{B}}}^{2}}} \mathord{\left/ {\vphantom {{1 - {{{\mathbf{B}}}^{2}}} {B_{*}^{2}}}} \right. \kern-0em} {B_{*}^{2}}})$ и ${1 \mathord{\left/ {\vphantom {1 {({{1 + {{{\mathbf{B}}}^{2}}} \mathord{\left/ {\vphantom {{1 + {{{\mathbf{B}}}^{2}}} {B_{*}^{2}}}} \right. \kern-0em} {B_{*}^{2}}})}}} \right. \kern-0em} {({{1 + {{{\mathbf{B}}}^{2}}} \mathord{\left/ {\vphantom {{1 + {{{\mathbf{B}}}^{2}}} {B_{*}^{2}}}} \right. \kern-0em} {B_{*}^{2}}})}}$ [Charbonneau, 2020], ${{B}_{*}}$ – установившееся поле. Реже нелинейность задается в сходной, но чрезвычайно сложной и неоднозначной, форме тензоров [Warnecke and Kapyla, 2020; Kleeorin and Rogachevskii, 1999], которые определяются силой Лоренца, пропорциональной квадрату вектора магнитного поля B. В обоих случаях, после приведения к общему знаменателю (например, при умножении записанного в конечных разностях или через полоидальное-тороидальное поле уравнения индукции на вышеприведенный знаменатель $({{1 + {{{\mathbf{B}}}^{2}}} \mathord{\left/ {\vphantom {{1 + {{{\mathbf{B}}}^{2}}} {B_{*}^{2}}}} \right. \kern-0em} {B_{*}^{2}}})$) получается, что старшая нелинейность по магнитному полю – это кубическая, соответствующая B 3. Подобная нелинейность практически не имеет под собой физических обоснований, а вводится искусственно из простейших математических соображений о стабилизации во всех известных автору упрощенных моделях гидромагнитного динамо. Во многих известных динамо-моделях присутствуют и квадратичные нелинейности ~B 2, которые тоже не обосновываются физически. При этом, кроме квадратичной и кубической нелинейностей, другие нелинейности, насколько автору известно, в модельных уравнениях для магнитного поля, приведенных для непосредственных вычислений к самому простому виду, не рассматривались.

Основная цель этой работы – из физических соображений (т.е. на основе уравнений Максвелла и Навье–Стокса) оценить нелинейность, стабилизирующую гидромагнитное динамо. Для этого оцениваются различные компоненты векторного произведения скорости на магнитное поле. Компонента, параллельная электрическому току или ротору B, представляется основным кандидатом для формирования искомой нелинейности, которая приводит к линейному эволюционному обыкновенному дифференциальному уравнению (ОДУ) для магнитной энергии ~B 2. При этом оказалось, что остальные компоненты могут формировать линейные или, точнее, квазилинейные (по магнитному полю) зависимости в эволюционных уравнениях. Поэтому второй целью этой работы является моделирование такого простейшего глобального динамо, подобного солнечному, которое может вполне достоверно определяться лишь двумя линейными ОДУ, имитирующими известные альфа-эффект и омега-эффект.

2. НЕЛИНЕЙНОСТЬ ТИПА ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ И ЛИНЕЙНОЕ УРАВНЕНИЕ ДЛЯ ЭНЕРГИИ СОЛНЕЧНЫХ ПЯТЕН

Векторное произведение скорости течений V на магнитное поле B является единственным отвечающим за генерацию и адвекцию магнитного поля членом в общеизвестном уравнении магнитной индукции (η – магнитная диффузия):

(1)
$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = \nabla \times ({\mathbf{V}} \times {\mathbf{B}} - \eta \nabla \times {\mathbf{B}}).$

Естественно оценить это произведение непосредственно из силового уравнения Навье–Стокса в упрощенной форме [Moffatt and Dormy, 2020; Charbonneau, 2020; Кичатинов, 2019; Starchenko, 2019], пренебрегая эффектами сжимаемости из-за огромных вариаций плотности в конвективной зоне (КЗ) Солнца, в приближении, подобном приближению Буссинеска:

(2)
$\begin{gathered} \frac{{\partial {\mathbf{V}}}}{{\partial t}} + (2\Omega {{{\mathbf{1}}}_{z}} + \nabla \times {\mathbf{V}}) \times {\mathbf{V}} - \nu \nabla \times (\nabla \times {\mathbf{V}}) = \\ = {\mathbf{A}} - \nabla p - \frac{{{\mathbf{B}} \times \nabla \times {\mathbf{B}}}}{{{{\mu }_{0}}\rho }}. \\ \end{gathered} $

Такая форма уравнения вполне допустима с учетом большой неопределенности основных параметров и соответствующих усреднений. Здесь ν – коэффициент вязкости; p – модифицированное давление; ρ – усредненная плотность; µ0 – магнитная проницаемость вакуума (фундаментальная постоянная), а A – преимущественно радиальное Архимедово ускорение плавучести, порождающее динамо-течение. Постоянная $\Omega $ – модуль угловой скорости вращения, которая параллельна единичному вектору 1z.

Оценим направленную вдоль электрического тока ${\mathbf{j}} = \nabla \times {{\mathbf{B}} \mathord{\left/ {\vphantom {{\mathbf{B}} {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}}$ (и поэтому, возможно, основную) составляющую ${\mathbf{V}} \times {\mathbf{B}},$ скалярно умножая (2) на V и тождественно преобразуя это произведение до

(3)
$({\mathbf{V}} \times {\mathbf{B}}) \cdot {\mathbf{j}} = \rho {\mathbf{V}} \cdot \left[ {{\mathbf{A}} - \nabla p - {{\partial {\mathbf{V}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{V}}} {\partial t}}} \right. \kern-0em} {\partial t}} + \nu \nabla \times (\nabla \times {\mathbf{V}})} \right].$
Удельное напряжение Рейнольдса ${\mathbf{V}} \times \nabla \times {\mathbf{V}}$ и сравнительно большое (при значимом вращении) ускорение Кориолиса отсутствуют в выражении (3), поскольку они перпендикулярны V. Для оценки в соотношении (3) пренебрегаем вязкостью и градиентом давления по сравнению с ускорением A. Оно доминирует, поскольку по порядку величины сравнимо в (2) с напряжением Рейнольдса (с большой турбулентной вязкостью) и с ускорением Кориолиса за вычетом градиента давления, как показали Warnecke and Kapyla [2020], Moffatt and Dormy [2020]. Пренебрежем и временной производной скорости, которая мала при усреднении из-за сильной турбулентности. Для соответственно грубо усредненной (обозначено везде далее как $\left\langle {...} \right\rangle $) по несколько неопределенному пространству – времени оценки из (3) получим:
(4)
${{E}_{j}} \equiv \left\langle {({\mathbf{V}} \times {\mathbf{B}}) \cdot {{{\mathbf{1}}}_{j}}} \right\rangle \approx {{{{\mu }_{0}}\rho VAh} \mathord{\left/ {\vphantom {{{{\mu }_{0}}\rho VAh} {B.}}} \right. \kern-0em} {B.}}$
Здесь B – средняя величина магнитного поля, рассчитанного по электрическому току j, а h – его характерный пространственный масштаб; A – характерное (усредненное/типичное) ускорение Архимеда; V – характерная скорость и Ej – характерная напряженность электрического поля, генерирующая и поддерживающая рассматриваемое гидромагнитное динамо вдоль электрического тока j, направленного по единичному вектору 1j.

Достаточно обоснованно [Charbonneau, 2020; Moffatt and Dormy, 2020; Brandenburg, 2018] предположим, что все параметры, находящиеся в числителе последней формулы (4), слабо зависят от магнитного поля. Из этого следует, что составляющая Ej из (4) обратно пропорциональна усредненному магнитному полю B или, точнее, – электрическому току.

Поэтому локальная эволюция B в солнечном пятне или в группе пятен, как в минимальной четко выраженной структурной единице, может быть грубо описана следующим простейшим неоднородным линейным ОДУ для магнитной энергии ~B 2, которое получается из (4) и соответственно упрощенной версии (1).

(5)
${{d{{B}^{2}}} \mathord{\left/ {\vphantom {{d{{B}^{2}}} {dt}}} \right. \kern-0em} {dt}} = 2{\kern 1pt} [({{{{\mu }_{0}}\rho VAh} \mathord{\left/ {\vphantom {{{{\mu }_{0}}\rho VAh} l}} \right. \kern-0em} l}) - ({\eta \mathord{\left/ {\vphantom {\eta {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}){{B}^{2}}].$
Здесь l – типичный пространственный масштаб скорости V динамо-течения. В первом приближении считаем все параметры (4) и (5) постоянными. Тогда время t в (5) можно нормировать на время магнитной диффузии [Charbonneau, 2020; Moffatt and Dormy, 2020]
(6)
${{\tau }_{*}} = {{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} \eta }} \right. \kern-0em} \eta },$
а поле B – на модуль соответствующего установившегося поля
(7)
${{B}_{*}} = \sqrt {{{{{\mu }_{0}}\rho W{{\tau }_{*}}h} \mathord{\left/ {\vphantom {{{{\mu }_{0}}\rho W{{\tau }_{*}}h} l}} \right. \kern-0em} l}} \approx 0.1{\text{ }}{{({{{{\tau }_{*}}} \mathord{\left/ {\vphantom {{{{\tau }_{*}}} {86{\kern 1pt} 400\,{\text{с}}}}} \right. \kern-0em} {86{\kern 1pt} 400\,{\text{с}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\,\,{\text{Тл}}.$
Здесь произведение скорости на ускорение AV из (5) заменено на удельную мощность конвекции в зоне динамо W, которая для Солнца в среднем ~4 мВт/кг, если следовать численным и качественным оценкам Кичатинова [2019] и Starchenko and Jones [2002]. Грубое равенство в (7) получено при условии, что h = l, ${{\tau }_{*}}$ примерно или по порядку величины соответствует времени жизни солнечного пятна или группы пятен, а 86 400 с – это длительность суток в секундах. При временах жизни ${{\tau }_{*}}$ от одного дня до двух месяцев получаем наблюдаемую напряженность ${{B}_{*}}$ от одного до нескольких кГс.

После нормировки (5) на (6) и (7) получим общее решение

(8)
$B = \pm \sqrt {1 + C\exp ( - 2t)} .$
Соответственно, как это показано на рисунке 1, различные стадии эволюции B могут быть представлены различными знаками и константами C из нормированной на (6) и (7) версии (5). При изначально (t = 0) малом по модулю магнитном поле происходит его рост или генерация до величины (7), а если модуль начального поля превосходит величину из (7) – то наоборот – происходит уменьшение модуля до этой стабилизационной величины.

Рис. 1.

Эволюция магнитного поля B из уравнения (8) при различных константах C и знаках перед корнем. По вертикальной оси отложены величины B, выраженные в (7), а по горизонтальной – диффузионное время t в (6).

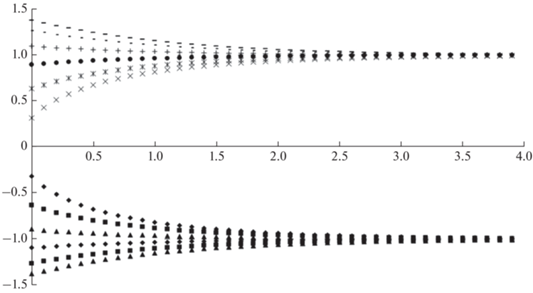
По существу величина стабилизирующегося среднего поля B определяется доступной плотностью мощности W = AV. Когда эта плотность сильно уменьшается и становится практически равной нулю – тогда уравнение (5) превращается в чисто диффузионное уравнение и за два диффузионных времени (6) модуль B убывает в e2 = = 7.4 раза. Соответствующее этому процессу пятно или группа пятен тогда практически полностью распадется.

3. ПРОСТЕЙШЕЕ ЛИНЕЙНОЕ ДИНАМО СОЛНЦА

Общеизвестным примером подобной (4), но линейной зависимости является генерация так называемого “тороидального” поля T из “полоидального” поля P за счет градиента угловой скорости вращения ϖ [Moffatt and Dormy, 2020; Кичатинов и Непомнящих, 2017; Рузмайкин и Старченко, 1987]. При наших упрощениях эта генерация может быть выведена из (1) и принимает вид уравнения (L – “крупный” внешний масштаб, и мы далее везде пренебрегли магнитной диффузией):

(9)
${{dT} \mathord{\left/ {\vphantom {{dT} {dt}}} \right. \kern-0em} {dt}} = - L\varpi P.$
Здесь левая часть уравнения непосредственно следует из левой части (1), а из правой части (1) взята только составляющая $\left| {\nabla \times ({\mathbf{V}} \times {\mathbf{B}})} \right|\sim L\varpi P,$ отвечающая за генерацию дифференциальным вращением $ - L\varpi .$ Оно в КЗ Солнца в среднем отрицательно [Charbonneau, 2020; Moffatt and Dormy, 2020], а все параметры в этой работе – положительны.

Умножая теперь уравнение Навье–Стокса (2) скалярно на B, получим направленную вдоль $2\Omega {{{\mathbf{1}}}_{z}} + \nabla \times {\mathbf{V}}$ составляющую ${\mathbf{V}} \times {\mathbf{B}}{\kern 1pt} {\text{:}}$

(10)
$\begin{gathered} (2\Omega {{{\mathbf{1}}}_{z}} + \nabla \times {\mathbf{V}}) \cdot ({\mathbf{V}} \times {\mathbf{B}}) = \\ = {\mathbf{B}} \cdot \left[ {{\mathbf{A}} - \nabla p - {{\partial {\mathbf{V}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{V}}} {\partial t}}} \right. \kern-0em} {\partial t}} + \nu \nabla \times (\nabla \times {\mathbf{V}})} \right]. \\ \end{gathered} $
При достаточно значимом, но как на Солнце, небыстром вращении относительно большое ускорение Кориолиса сбалансируется, прежде всего, градиентом давления $2\Omega {{{\mathbf{1}}}_{z}} \times {\mathbf{V}} \cong - \nabla p,$ что приведет к оценке
(11)
$\begin{gathered} (\nabla \times {\mathbf{V}}) \cdot ({\mathbf{V}} \times {\mathbf{B}}) \cong {\mathbf{B}} \cdot {\mathbf{A}} \Rightarrow {{E}_{\alpha }} \equiv \\ \equiv \left\langle {{\mathbf{V}} \times {\mathbf{B}} \cdot {{{\mathbf{1}}}_{\alpha }}} \right\rangle = ({{Al} \mathord{\left/ {\vphantom {{Al} V}} \right. \kern-0em} V})T. \\ \end{gathered} $
Здесь индексом α – обозначена составляющая вдоль $\nabla \times {\mathbf{V}}.$ Также мы опять пренебрегли типично малой молекулярной вязкостью и производной от скорости течения ${{\partial {\mathbf{V}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{V}}} {\partial t,}}} \right. \kern-0em} {\partial t,}}$ которая в среднем практически равна нулю на ее сравнительно коротких временах. Опять же, как и в предыдущем разделе, будем считать, что заключенные в последние скобки параметры (11) практически не зависят от величины усредненного магнитного поля P и T. Тогда получаем линейную зависимость Eα от T. Следует отметить, что соотношения, подобные (11), широко применяются в теории среднего поля при оценках альфа-эффекта [Charbonneau, 2020; Moffatt and Dormy, 2019, Brandenburg, 2018; Kleeorin and Rogachevskii, 1999; Рузмайкин и Старченко, 1987]. Поэтому соотношение (11) может быть получено и независимым образом путем упрощения хотя и упрощенных (извините за каламбур), но все-таки несравненно более сложных, чем (11), уравнений этой теории.

Соответственно динамо-модель состоит из уравнения (9) и следующего из уравнений (1) и (11) упрощенного аналога известного альфа-эффекта:

(12)
${{dP} \mathord{\left/ {\vphantom {{dP} {dt}}} \right. \kern-0em} {dt}} = ({A \mathord{\left/ {\vphantom {A V}} \right. \kern-0em} V})T.$
Глобальный альфа-эффект тут естественно оценить как
(13)
$\alpha = {{LA} \mathord{\left/ {\vphantom {{LA} {V.}}} \right. \kern-0em} {V.}}$
При постоянных параметрах системы из уравнений (9) и (12) ее решением является
(14)
$\begin{gathered} P = {{({{ - 1} \mathord{\left/ {\vphantom {{ - 1} {L\varpi }}} \right. \kern-0em} {L\varpi }}){\kern 1pt} dT} \mathord{\left/ {\vphantom {{({{ - 1} \mathord{\left/ {\vphantom {{ - 1} {L\varpi }}} \right. \kern-0em} {L\varpi }}){\kern 1pt} dT} {dt,}}} \right. \kern-0em} {dt,}} \\ T = {{C}_{c}}\cos (\omega t) + {{C}_{s}}\sin (\omega t), \\ \omega = \sqrt {{{L\varpi A} \mathord{\left/ {\vphantom {{L\varpi A} V}} \right. \kern-0em} V}} = \sqrt {\alpha \varpi } . \\ \end{gathered} $
Это простейшее решение согласуется с наблюдаемой и общеизвестной магнитной активностью Солнца и других звезд. Подобная циклическая активность, в первом приближении, также описывается синусом и косинусом с полным 22-летним периодом для Солнца. Аналогичной зависимости следует ожидать и в других подобных (по магнитной активности) Солнцу звездах.

Для дальнейшего прояснения физической сути солнечного цикла воспользуемся оценками, приведенными в публикациях [Kitchatinov et al., 2018; Кичатинов и Непомнящих, 2017; Рузмайкин и Старченко, 1987], входящего в последнюю формулу системы (14) глобально усредненного альфа-эффекта α ~ 0.1 м/с.

Следует особо отметить уже давно и до сих пор общепризнанную большую неопределенность в величине и природе альфа-эффекта. Поэтому развиваемую здесь теорию можно использовать и для решения обратной задачи: оценки величины и источника α по непосредственно наблюдаемым и сравнительно хорошо оцениваемым значениям ω и ϖ.

В качестве среднего и в нашем случае преимущественно радиального градиента угловой скорости вращения естественно взять значение ϖ = = 10–15 м–1 с–1. Оно непосредственно измеряется гелиосейсмологами и моделируется теоретиками в центральной части конвективной зоны Солнца [Cameron et al., 2017; Кичатинов и Непомнящих, 2017]. Тогда из (14) получим величину, согласующуюся с наблюдаемым полным периодом магнитной активности Солнца [Sokoloff et al., 2020]:

(15)
${{T}_{S}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \omega }} \right. \kern-0em} \omega } = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\sqrt {\alpha \varpi } }}} \right. \kern-0em} {\sqrt {\alpha \varpi } }} = 20\,\,{\text{лет}}.$

Так же из (14), (15) определим для всех подобных динамо-объектов и оценим для Солнца среднее отношение тороидального поля к полоидальному (средние модули полей в следующей формуле обозначены звездочкой, а в качестве L = 200 Мм использована стандартная толщина конвективной зоны Солнца):

(16)
${{{{T}_{*}}} \mathord{\left/ {\vphantom {{{{T}_{*}}} {{{P}_{*}}}}} \right. \kern-0em} {{{P}_{*}}}} = L\sqrt {{\varpi \mathord{\left/ {\vphantom {\varpi \alpha }} \right. \kern-0em} \alpha }} = 20.$
Эта оценка хорошо согласуется как с давними, например, [Рузмайкин и Старченко, 1987], так и с недавними, например, [Кичатинов и Непомнящих, 2017] несравненно более детальными моделями. Из прямых наблюдений проверить (16) непросто, поскольку здесь подразумеваются усредненные практически по всей конвективной зоне поля, которые малодоступны на большой глубине.

4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

1. Показано, что для вращающихся МГД динамо-систем значима стабилизирующая нелинейность типа обратной пропорциональности величине электрического тока.

2. Исследованы всевозможные модели нелинейных и линейных динамо-эффектов, которые задаются различными компонентами векторного произведения скорости течения на магнитное поле, определяемыми непосредственно из исходных уравнений.

3. Получена ранее не исследованная, простейшая модель солнечного пятна или группы пятен, которая состоит всего из одного неоднородного линейного ОДУ для магнитной энергии, пропорциональной квадрату магнитного поля B 2.

4. Представлено глобальное динамо, подобное солнечному, которое состоит из системы двух однородных линейных ОДУ, которые несколько по-новому описывают альфа-эффект, а эффект дифференциального вращения – традиционно.

5. Полученные модели успешно как воспроизводят, так и проясняют физическую природу основных проявлений солнечных пятен или их выделенных групп и глобального динамо Солнца.

Список литературы

  1. − Кичатинов Л.Л. Распад крупномасштабного магнитного поля на трубки у основания конвективной зоны Солнца // Письма в Астрон. журн. Т. 45. № 1. С. 45–54. 2019.

  2. − Кичатинов Л.Л., Непомнящих А.А. Согласованная модель солнечного динамо и дифференциального вращения // Письма в Астрон. журн. Т. 43. № 5. С. 370–382. 2017.

  3. − Рузмайкин А. А., Старченко С.В. Магнитные проявления солнечного вращения // Астрон. журн. Т. 64. С. 1057–1065. 1987.

  4. − Brandenburg A. Advances in mean-field dynamo theory and applications to astrophysical turbulence // J. Plasma Phys. 84. 735840404. 2018. https://doi.org/10.1017/S0022377818000806

  5. − Cameron R.H., Dikpati M., Brandenburg A. The global Solar dynamo // Spa. Sci. Rev. V. 210. P. 367–395. 2017.

  6. − Charbonneau P. Dynamo models of the solar cycle // Living Rev. Solar Phys. 17:4. 104 p. 2020. https://doi.org/10.1007/s41116-020-00025-6

  7. − Christensen U.R., Holzwarth V., Reiners A. Energy flux determines magnetic field strength of planets and stars // Nature. V. 457. P. 167–169. 2009.

  8. − Kitchatinov L.L., Mordviniv A.A., Nepomnyashchikh A. Modeling variability of solar activity cycles // Astron. Astrophys. V. 615. № A38. 2018.

  9. − Kleeorin N., Rogachevskii I. Magnetic helicity tensor for an anisotropic turbulence // Phys. Rev. E 59. P. 6724–6729. 1999.

  10. − Larmor J. How could a rotating body such as the sun become a magnet // Rep. Brit. Assoc. Adv. Sci. V. 159. P. 412. 1919.

  11. − Lathrop D.P., Forest C.B. Magnetic dynamos in the lab // Phys. Today. V. 64. P. 40–45. 2011.

  12. − Moffatt K., Dormy E. Self-exiting fluid dynamos. Cambridge: Cambridge University Press. 234 p. 2019.

  13. − Sokoloff D.D., Shibalova A.S., Obridko V.N., Pipin V.V. Shape of solar cycles and mid-term solar activity oscillations // Mon. Not. R. Astron. Soc. V. 497(4). P. 4376–4383. 2020.

  14. − Starchenko S.V., Jones C.A. Typical velocity and magnetic field strengths in planetary interiors // Icarus. V. 157. P. 426–435. 2002.

  15. − Starchenko S.V. Analytic scaling laws in planetary dynamo models // Geophys. Astrophys. Fluid Dyn. V. 113. P. 71–79. 2019.

  16. − Warnecke J., Kapyla M.J. Rotational dependence of turbulent transport coefficients in global convective dynamo simulations of solar-like stars // Astron. Astrophys. V. 642. № A66. 2020. https://doi.org/10.1051/0004-6361/201936922

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал