Известия РАН. Энергетика, 2019, № 5, стр. 148-158

Процессы теплопереноса в системе с активной теплозащитой, обладающей обратной связью и анизотропным покрытием

А. В. Аттетков^1, *, И. К. Волков¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)”
Москва, Россия

^* E-mail: fn2@bmstu.ru

Поступила в редакцию 17.09.2019
После доработки 21.10.2019
Принята к публикации 23.10.2019

DOI: 10.1134/S0002331019050030

Полный текст (PDF)

Аннотация

Предложена математическая модель процесса теплопереноса в системе, имитируемой изотропным полупространством с ортотропной термоактивной прокладкой, функционирующей по принципу обратной связи, и анизотропным покрытием, подверженного локальному тепловому воздействию в условиях теплообмена с внешней средой. Показано, что температурное поле системы представляет собой композицию двух независимых аддитивных составляющих. С применением интегрального преобразования Лапласа найдено решение для первой из аддитивных составляющих температурного поля, формирование которого обусловлено лишь отличием начальной температуры системы от температуры внешней среды. Идентифицирована вторая независимая аддитивная составляющая температурного поля, формируемого за счет воздействия нестационарного теплового потока на внешнюю поверхность анизотропного покрытия системы. С применением композиции двумерного экспоненциального интегрального преобразования Фурье и интегрального преобразования Лапласа в аналитически замкнутом виде найдено решение соответствующей задачи нестационарной теплопроводности. Полученные результаты подтверждают обнаруженный раннее эффект “сноса” температурного поля в анизотропном материале с анизотропией свойств общего вида.

Ключевые слова: изотропное полупространство, термоактивная прокладка, анизотропное покрытие, локальное тепловое воздействие, температурное поле, интегральные преобразования

ВВЕДЕНИЕ

В математической теории теплопроводности [1–6] специфическое положение занимают исследования процессов теплопереноса в изотропном полупространстве, подверженным воздействию сосредоточенных и пространственно-распределенных тепловых потоков [1, 7, 8], или его локальному нагреву внешней средой [9]. Отмеченная специфика обусловлена относительной простой реализуемой математической модели и трудностями, возникающими при нахождении аналитического решения соответствующей задачи нестационарной теплопроводности. Указанные трудности усугубляются при наличии покрытия на неподвижной или движущейся границе объекта исследований [10–12].

Особое место в исследованиях занимают задачи нестационарного теплопереноса в изотропном полупространстве с активной теплозащитой, использующей термоэлектрические явления при регулировании температурного состояния системы, или принцип обратной связи в процессе ее функционирования [13–17]. При этом актуальным и требующим дальнейшего развития остается вопрос о влиянии анизотропии свойств покрытия активной теплозащиты на формируемое температурное поле анализируемой системы [18]. Рассмотрению этого вопроса и посвящены проводимые в данной работе исследования.

ИСХОДНЫЕ ДОПУЩЕНИЯ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Для достижения поставленной цели, при построении математической модели процесса формирования искомого температурного поля $T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}},t} \right)$ объекта исследований в фиксированной декартовой системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ пространства ${{\mathbb{R}}^{3}}$ предполагалось, что:

1) объект исследований представляет собой систему, образованную изотропным полупространством $\left( {0 < {{x}_{2}} < + \infty } \right),$ ограничивающая поверхность которого $\left( {{{x}_{2}} = 0} \right)$ обладает анизотропным покрытием $\left( { - \left( {{{h}_{{\text{п}}}} + {{h}_{{{\text{тп}}}}}} \right) < {{x}_{2}} < - {{h}_{{{\text{тп}}}}}} \right)$ с термоактивной прокладкой [13–18] $\left( { - {{h}_{{{\text{тп}}}}} < {{x}_{2}} < 0} \right),$ где значения геометрических характеристик ${{h}_{{\text{п}}}}$, ${{h}_{{{\text{тп}}}}}$ элементов объекта исследований являются величинами постоянными;

2) термоактивная прокладка является ортотропной и функционирует по принципу обратной связи [17, 19, 20], т.е. в системах “анизотропное покрытие–термоактивная прокладка” и “термоактивная прокладка–изотропное полупространство” для искомого температурного поля реализуются следующие условия сопряжения:

$T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} - 0,{{x}_{3}},~t} \right) = T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} + 0,{{x}_{3}},t} \right),$

${{\left. {\left[ {\lambda _{{12}}^{{\text{п}}}\frac{{\partial T}}{{\partial {{x}_{1}}}} + \lambda _{{22}}^{{\text{п}}}\frac{{\partial T}}{{\partial {{x}_{2}}}} + \lambda _{{23}}^{{\text{п}}}\frac{{\partial T}}{{\partial {{x}_{3}}}}} \right]} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} - 0}}} - {{\left. {\lambda _{2}^{{{\text{тп}}}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} + 0}}} = - q_{{{\text{тп}}}}^{{\text{п}}}{{\left. {\left[ {T - {{T}_{0}}} \right]} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} + 0}}};$

$T\left( {{{x}_{1}},~0 - 0,{{x}_{3}},t} \right) = T\left( {{{x}_{1}},0 + 0,{{x}_{3}},t} \right),$

${{\left. {\lambda _{2}^{{{\text{тп}}}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = 0 - 0}}} - {{\left. {{{\lambda }^{{{\text{пп}}}}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = 0 + 0}}} = - q_{{{\text{тп}}}}^{{{\text{пп}}}}{{\left. {\left[ {T - {{T}_{0}}} \right]} \right|}_{{{{x}_{2}} = 0 + 0}}},$

где $\left\{ {\lambda _{{ij}}^{{\text{п}}}} \right\},$ $\left\{ {\lambda _{k}^{{{\text{тп}}}}} \right\}$ и ${{\lambda }^{{{\text{пп}}}}}$ – компоненты тензоров теплопроводности анизотропного материала покрытия, ортотропного материала термоактивной прокладки при $\lambda _{1}^{{{\text{тп}}}} = \lambda _{3}^{{{\text{тп}}}}$ и изотропного материала полупространства соответственно; $q_{{{\text{тп}}}}^{{\text{п}}}~$ и $q_{{{\text{тп}}}}^{{{\text{пп}}}}$ – определяющие параметры обратной связи термоактивной прокладки со стороны анизотропного покрытия и изотропного полупространства соответственно; ${{T}_{0}}$ – начальная температура объекта исследований и ${{T}_{0}} - {\text{const;}}$

3) обратная связь термоактивной прокладки настроена по начальной температуре объекта исследований, которая отлична от температуры внешней среды ${{T}_{{\text{с}}}} - {\text{const;}}$

4) термоактивная прокладка является “термически тонкой”, т.е. допускает реализацию идеи “сосредоточенная емкость” [4], суть которой определена следующими равенствами:

$T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} - 0,{{x}_{3}},~t} \right) = \left\langle {T\left( {{{x}_{1}},{{x}_{3}},t} \right)} \right\rangle = T\left( {{{x}_{1}},0 - 0,{{x}_{3}},t} \right);$

$\left\langle {T\left( {{{x}_{1}},{{x}_{3}},t} \right)} \right\rangle \triangleq \frac{1}{{{{h}_{{{\text{тп}}}}}}}\mathop \smallint \limits_{ - {{h}_{{{\text{тп}}}}}}^0 T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}},t} \right)d{{x}_{2}};$

5) теплообмен в системе “внешняя поверхность анизотропного покрытия–внешняя среда” реализуется по закону Ньютона с коэффициентом теплоотдачи ${{\alpha }_{{\text{п}}}}$ [2, 3];

6) внешняя поверхность анизотропного покрытия находится под воздействием не только внешней среды, температура которой отлична от начальной температуры объекта исследований, но и внешнего теплового потока, который воздействует на поверхность ${{x}_{2}} = - \left( {{{h}_{{\text{п}}}} + {{h}_{{{\text{тп}}}}}} \right)$ анизотропного покрытия в направлении его внутренней нормали и обладает плотностью мощности $q\left( {{{x}_{1}},{{x}_{3}},~t} \right);$

7) при любых фиксированных значениях пространственных переменных, представленных вектором ${{\left[ {{{x}_{1}},{{x}_{3}}} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{2}},$ функционал $q\left( {{{x}_{1}},{{x}_{3}},~t} \right)$ интегрируем с квадратом по временному переменному $t \in \left[ {0,} \right.\left. { + \infty } \right)$ и при любых фиксированных значениях временного переменного $t \in \left[ {0,} \right.\left. { + \infty } \right)$ интегрируем с квадратом по совокупности пространственных переменных, представленных вектором ${{\left[ {{{x}_{1}},{{x}_{3}}} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}$, т.е.

${{\left. {q\left( {{{x}_{1}},{{x}_{3}},~t} \right)} \right|}_{{{{{\left[ {{{x}_{1}},{{x}_{3}}} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}}}} \in {{L}^{2}}\left[ {0,} \right.\left. { + \infty } \right);$

${{\left. {q\left( {{{x}_{1}},{{x}_{3}},~t} \right)} \right|}_{{t \in \left[ {0,} \right.\left. { + \infty } \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right).$

Для удобства дальнейших рассуждений целесообразно воспользоваться следующими обозначениями:

$\theta = \frac{{T - {{T}_{0}}}}{{{{T}_{{\text{с}}}} - {{T}_{0}}}};\,\,\,\,x = \frac{{{{x}_{1}}}}{{{{l}_{*}}}},\,\,\,\,y = \frac{{{{x}_{2}}}}{{{{l}_{*}}}},\,\,\,\,~z = \frac{{{{x}_{3}}}}{{{{l}_{*}}}};\,\,\,\,{\text{Fo}} = \frac{{\lambda _{{22}}^{{\text{п}}}~t}}{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}l_{*}^{2}}};\,\,\,\,{{H}_{1}} = \frac{{{{h}_{{\text{п}}}}}}{{{{l}_{*}}}};$

${{H}_{2}} = \frac{{{{h}_{{{\text{тп}}}}}}}{{{{l}_{*}}}};\,\,\,\,{{\mu }_{{ij}}} = \frac{{\lambda _{{ij}}^{{\text{п}}}}}{{\lambda _{{22}}^{{\text{п}}}}};\,\,\,\,\mu = \frac{{\lambda _{1}^{{{\text{тп}}}}}}{{\lambda _{{22}}^{{\text{п}}}}};\,\,\,\,{{\mu }_{*}} = \frac{{{{\lambda }^{{{\text{пп}}}}}}}{{\lambda _{{22}}^{{\text{п}}}}};\,\,\,\,{{Q}_{*}} = \frac{{\left( {q_{{{\text{тп}}}}^{{\text{т}}} - q_{{{\text{тп}}}}^{{{\text{пп}}}}} \right){{l}_{*}}}}{{\lambda _{{22}}^{{\text{п}}}}};$

$a = \frac{{{{c}_{{{\text{тп}}}}}{{\rho }_{{{\text{тп}}}}}}}{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}}};\,\,\,\,b = \frac{{{{c}_{{{\text{пп}}}}}{{\rho }_{{{\text{пп}}}}}}}{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}}};\,\,\,\,{\text{Bi}} = \frac{{\alpha {{l}_{*}}}}{{\lambda _{{22}}^{{\text{п}}}}};\,\,\,\,\left\langle \theta \right\rangle = \frac{{\left\langle T \right\rangle - {{T}_{0}}}}{{{{T}_{{\text{с}}}} - {{T}_{0}}}};\,\,\,\,{{Q}_{0}} = \frac{{q{{l}_{*}}}}{{\left( {{{T}_{{\text{с}}}} - {{T}_{0}}} \right)\lambda _{{22}}^{{\text{п}}}}},$

где ${{l}_{*}}$ – используемая единица масштаба пространственных переменных. В этом случае, согласно исходным допущениям, представленным выше, функционалы $\theta \left( {x,y,z,{\text{Fo}}} \right)$ и $\left\langle {\theta \left( {x,z,{\text{Fo}}} \right)} \right\rangle $ должны удовлетворять системе трех линейных дифференциальных уравнений в частных производных второго порядка параболического типа [1–6, 21]:

(1)

$\begin{gathered} \frac{{\partial \theta }}{{\partial {\text{Fo}}}} = {{\mu }_{{11}}}\frac{{{{\partial }^{2}}\theta }}{{\partial {{x}^{2}}}} + 2{{\mu }_{{12}}}\frac{{{{\partial }^{2}}\theta }}{{\partial x\partial y}} + 2{{\mu }_{{13}}}\frac{{{{\partial }^{2}}\theta }}{{\partial x\partial z}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}} + 2{{\mu }_{{23}}}\frac{{{{\partial }^{2}}\theta }}{{\partial y\partial z}} + {{\mu }_{{33}}}\frac{{{{\partial }^{2}}\theta }}{{\partial {{z}^{2}}}}, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\, - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}};\,\,\,\,{\text{Fo}}\,\,{\text{ > }}\,\,0; \\ a\frac{{\partial \left\langle \theta \right\rangle }}{{\partial {\text{Fo}}}} = \mu \left[ {\frac{{{{\partial }^{2}}\left\langle \theta \right\rangle }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\left\langle \theta \right\rangle }}{{\partial {{z}^{2}}}}} \right] + \frac{1}{{{{H}_{2}}}}\left\{ {{{Q}_{*}}\left\langle \theta \right\rangle + {{{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \theta }}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial \theta }}{{\partial z}}} \right]} \right|}}_{{y = - {{H}_{2}} - 0}}} - \,\,{{\mu }_{*}}{{{\left. {\frac{{\partial \theta }}{{\partial y}}} \right|}}_{{y = 0 + 0}}}} \right\}, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\, - {\kern 1pt} {{H}_{2}} < y < 0;\,\,\,\,{\text{Fo}}\,\,{\text{ > }}\,\,0; \\ b\frac{{\partial \theta }}{{\partial {\text{Fo}}}} = {{\mu }_{*}}\left[ {\frac{{{{\partial }^{2}}\theta }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\theta }}{{\partial {{z}^{2}}}}} \right],\,\,\,\,~\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},y > 0;\,\,\,\,{\text{Fo}}\,\,{\text{ > }}\,\,0, \\ \end{gathered} $

однородным начальным условиям:

(2)

$\theta \left( {x,y,z,0} \right) = 0 = \left\langle {\theta \left( {x,z,0} \right)} \right\rangle ,$

условиям сопряжения:

(3)

$\theta \left( {x, - {{H}_{2}} - 0,z,{\text{Fo}}} \right) = \left\langle {\theta \left( {x,z,{\text{Fo}}} \right)} \right\rangle = \theta \left( {x,0 + 0,z,{\text{Fo}}} \right)$

и краевому условию [2, 6]:

(4)

${{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \theta }}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial \theta }}{{\partial z}} - {\text{Bi}}\left( {1 - \theta } \right)} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = {{Q}_{0}}\left( {x,z,{\text{Fo}}} \right),$

где функционал

(5)

$\begin{gathered} {{\left. {{{Q}_{0}}\left( {x,z,{\text{Fo}}} \right)} \right|}_{{{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}}}} \in {{L}^{2}}\left[ {0,} \right.\left. { + \infty } \right); \\ {{\left. {{{Q}_{0}}\left( {x,z,{\text{Fo}}} \right)} \right|}_{{{\text{Fo}} \in \left[ {0,} \right.\left. { + \infty } \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right). \\ \end{gathered} $

Кроме того, в соответствии с исходными допущениями, естественно считать, что функционалы $\theta \left( {x,y,z,{\text{Fo}}} \right),$ $\theta \left( {x,z,{\text{Fo}}} \right)$ удовлетворяют следующим требованиям [21]:

(6)

$\begin{gathered} {{\left. {\theta \left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {\left( {{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {y \in \left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right]} \right)\bigvee {\kern 1pt} *\left( {y \in \left[ {0,} \right.\left. { + \infty } \right)} \right)} \right)}}} \in {{L}^{2}}\left[ {0,} \right.\left. { + \infty } \right), \\ {{\left. {\left\langle {\theta \left( {x,z,{\text{Fo}}} \right)} \right\rangle } \right|}_{{{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}}}} \in {{L}^{2}}\left[ {0,} \right.\left. { + \infty } \right); \\ {{\left. {\theta \left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {\left( {y \in \left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right]} \right)\bigvee {\kern 1pt} *\left( {y \in \left[ {0,} \right.\left. { + \infty } \right)} \right) \wedge {\text{Fo}} \in \left[ {0,} \right.\left. { + \infty } \right)} \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right),~ \\ {{\left. {\left\langle {\theta \left( {x,z,{\text{Fo}}} \right)} \right\rangle } \right|}_{{{\text{Fo}} \in \left[ {0,} \right.\left. { + \infty } \right)}}} \in {{L}^{2}}\left( {{{\mathbb{R}}^{2}}} \right); \\ {{\left. {\theta \left( {x,y,z,{\text{Fo}}} \right)} \right|}_{{\left( {\left( {{{{\left[ {x,z} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge {\text{Fo}} \in \left[ {0,} \right.\left. { + \infty } \right)} \right)}}} \in {{L}^{2}}\left( {\left[ { - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right] \cup \left[ {0,} \right.\left. { + \infty } \right)} \right). \\ \end{gathered} $

Таким образом, исходная математическая модель (1)–(6) процесса формирования искомого температурного поля объекта исследований представляет собой смешанную задачу для системы уравнений в частных производных параболического типа со специфическими условиями сопряжения.

ТЕМПЕРАТУРНОЕ ПОЛЕ

Далее, с учетом известных результатов [22–24], будем предполагать, что процесс формирования искомого температурного поля имеет аддитивную структуру с двумя независимыми составляющими:

(7)

$\theta \left( {x,y,z,{\text{Fo}}} \right) = {{\theta }_{1}}\left( {y,{\text{Fo}}} \right) + {{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$

где функционал ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ – решение смешанной задачи (1)–(6) при ${{Q}_{0}}\left( {x,z,{\text{Fo}}} \right) \equiv 0,$ а функционал ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)$ – решение смешанной задачи (1)–(6), где в краевом условии (4) комплекс ${\text{Bi}}\left( {1 - \theta } \right)$ заменен комплексом $\left( { - {\text{Bi}}\theta } \right)$.

Таким образом, в пространстве изображений интегрального преобразования Лапласа, определенного парой линейных интегральных операторов [9]:

(8)

$L\left[ \cdot \right] \equiv \mathop \smallint \limits_0^\infty \cdot {\text{exp}}\left( { - s{\text{Fo}}} \right)d{\text{Fo}};\,\,\,\,~{{L}^{{ - 1}}}\left[ \cdot \right] \equiv \frac{1}{{2\pi i}}\mathop \smallint \limits_{\sigma - i\infty }^{\sigma + i\infty } \cdot {\text{exp}}\left( {s{\text{Fo}}} \right)ds,$

изображения

(9)

${{U}_{1}}\left( {y,s} \right) \triangleq L\left[ {{{\theta }_{1}}\left( {y,{\text{Fo}}} \right)} \right],~\,\,\,\,\left\langle {{{U}_{1}}\left( s \right)} \right\rangle \triangleq L\left[ {\left\langle {{{\theta }_{1}}\left( {{\text{Fo}}} \right)} \right\rangle } \right]$

должны удовлетворять следующей краевой задаче:

$\frac{{{{d}^{2}}{{U}_{1}}}}{{d{{y}^{2}}}} = s{{U}_{1}},~\,\,\,\,~ - \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}};$

$\left( {{{H}_{2}}as - {{Q}_{*}}} \right)\left\langle {{{U}_{1}}} \right\rangle = {{\left. {\frac{{d{{U}_{1}}}}{{dy}}} \right|}_{{y = - {{H}_{2}} - 0}}} - {{\mu }_{*}}{{\left. {\frac{{d{{U}_{1}}}}{{dy}}} \right|}_{{y = 0 + 0}}},\,\,\,\,~ - {{H}_{2}} < y < 0;$

$\frac{{{{d}^{2}}{{U}_{1}}}}{{d{{y}^{2}}}} = \frac{b}{{{{\mu }_{*}}}}s{{U}_{1}},\,\,\,\,y > 0;~$

${{\left. {\frac{{d{{U}_{1}}}}{{dy}}} \right|}_{{y = - ({{H}_{1}} + {{H}_{2}})}}} = {{\left. {{\text{Bi}}\left[ {\frac{1}{s} - {{U}_{1}}} \right]} \right|}_{{y = - ({{H}_{1}} + {{H}_{2}})}}};$

${{U}_{1}}\left( { - {{H}_{2}} - 0,s} \right) = \left\langle {{{U}_{1}}\left( s \right)} \right\rangle = {{U}_{1}}\left( {0 + 0,s} \right);$

${{\left. {{{U}_{1}}\left( {y,s} \right)} \right|}_{{\left( {s \in \mathbb{C}} \right)}}} \in {{L}^{2}}\left( {\left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right] \cup \left[ {0,} \right.\left. { + \infty } \right)} \right),$

решение которой может быть найдено с использованием стандартных методов [25] и представлено в следующем виде:

(10)

$\begin{gathered} {{\left. {{{U}_{1}}\left( {y,s} \right)} \right|}_{{ - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}}}} = {{c}_{1}}\left( s \right){\text{exp}}\left[ { - \left( {y + {{H}_{2}}} \right)\sqrt s } \right] + {{c}_{2}}\left( s \right){\text{exp}}\left[ {\left( {y + {{H}_{2}}} \right)\sqrt s } \right]; \\ {{\left. {{{U}_{1}}\left( {y,s} \right)} \right|}_{{y \geqslant 0}}} = \left\langle {{{U}_{1}}\left( s \right)} \right\rangle {\text{exp}}\left[ { - y\sqrt {b\mu _{*}^{{ - 1}}s} } \right]; \\ {{\left. {{{c}_{k}}\left( s \right)} \right|}_{{k \in \left\{ {1,2} \right\}}}} = \frac{{{{{\left( { - 1} \right)}}^{k}}}}{{2\sqrt s }}\left\{ {{{H}_{2}}as - \left[ {\sqrt {b{{\mu }_{*}}} - {{{\left( { - 1} \right)}}^{k}}} \right]\sqrt s - {{Q}_{*}}} \right\}\left\langle {{{U}_{1}}\left( s \right)} \right\rangle ; \\ \left\langle {{{U}_{1}}\left( s \right)} \right\rangle = \frac{{2{\text{Bi}}}}{{\sqrt s }}\left\{ {\left( {\sqrt s - {\text{Bi}}} \right)\left[ {{{H}_{2}}as - \left[ {\sqrt {b{{\mu }_{*}}} + 1} \right]\sqrt s - {{Q}_{*}}} \right]{\text{exp}}\left( {{{H}_{1}}\sqrt s } \right) + } \right. \\ {{\left. { + \,\,\left( {\sqrt s + {\text{Bi}}} \right)\left[ {{{H}_{2}}as - \left[ {\sqrt {b{{\mu }_{*}}} - 1} \right]\sqrt s - {{Q}_{*}}} \right]{\text{exp}}\left( { - {{H}_{1}}\sqrt s } \right)} \right\}}^{{ - 1}}}. \\ \end{gathered} $

А так как естественно предполагать, что ${{Q}_{*}} > 0,$ т.е. предполагать доминирующее значение определяющего параметра обратной связи термоактивной прокладки со стороны анизотропного покрытия, то согласно (10) имеем:

(11)

$\begin{gathered} \left\langle {{{U}_{1}}\left( s \right)} \right\rangle = \frac{{2{\text{Bi}}}}{{{{H}_{2}}a}}\mathop \sum \limits_{k = 0}^\infty {{\left( { - 1} \right)}^{k}}\frac{1}{{\sqrt s }}{{G}_{k}}\left( {\sqrt s } \right); \\ {{G}_{k}}\left( s \right) = \frac{{{{{\left( {s - {{s}_{{20}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{21}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{22}}}} \right)}}^{k}}}}{{{{{\left( {s - {{s}_{{10}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{11}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{12}}}} \right)}}^{{k + 1}}}}}{\text{exp}}\left[ { - {{H}_{2}}\left( {2k + 1} \right)s} \right]; \\ {{s}_{{n0}}} = {{\left( { - 1} \right)}^{{n + 1}}}{\text{Bi}},~\,\,\,\,n \in \left\{ {1,2} \right\}; \\ {{s}_{{nj = }}}\frac{{\sqrt {b{{\mu }_{*}}} - {{{\left( { - 1} \right)}}^{n}}}}{{2{{H}_{2}}a}} + {{\left( { - 1} \right)}^{{j + 1}}}\sqrt {{{{\left( {\frac{{\sqrt {b{{\mu }_{*}}} - {{{\left( { - 1} \right)}}^{n}}}}{{2{{H}_{2}}a}}} \right)}}^{2}} + {{Q}_{*}}} ,~\,\,\,\,~j \in \left\{ {1,2} \right\},~n \in \left\{ {1,2} \right\}. \\ \end{gathered} $

Анализ структуры изображения $\left\langle {{{U}_{1}}\left( s \right)} \right\rangle ,$ представленного равенствами (11), убеждает в том, что при переходе в пространство оригиналов целесообразно использовать линейность оператора ${{L}^{{ - 1}}}\left[ \cdot \right]$ обращения интегрального преобразования Лапласа (8), теорему Эфроса, теорему запаздывания и обобщенную теорему разложения [2, 26]. В этом случае, согласно (9), (11) имеем:

(12)

$\begin{gathered} \left\langle {{{\theta }_{1}}\left( {{\text{Fo}}} \right)} \right\rangle = \frac{{2{\text{Bi}}}}{{{{H}_{2}}a}}\mathop \sum \limits_{k = 0}^\infty \frac{{{{{\left( { - 1} \right)}}^{k}}}}{{\sqrt {\pi {\text{Fo}}} }}\mathop \smallint \limits_0^\infty {{g}_{k}}\left( \tau \right){\text{exp}}\left( { - \frac{{{{\tau }^{2}}}}{{4{\text{Fo}}}}} \right)d\tau ; \\ {{g}_{k}}\left( \tau \right) \triangleq {{L}^{{ - 1}}}\left[ {{{G}_{k}}\left( s \right)} \right] = \mathop \sum \limits_{j = 0}^2 \frac{1}{{k!}}\mathop {\lim }\limits_{s \to {{s}_{{1j}}}} \frac{{{{d}^{k}}}}{{d{{s}^{k}}}}\left\{ {{{{\left( {s - {{s}_{{1j}}}} \right)}}^{{k + 1}}}\frac{{{{{\left( {s - {{s}_{{20}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{21}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{22}}}} \right)}}^{k}}}}{{{{{\left( {s - {{s}_{{10}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{11}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{12}}}} \right)}}^{{k + 1}}}}} \times } \right. \\ \left. { \times \,\,{\text{exp}}\left[ {s\left( {\tau - \left( {2k + 1} \right){{H}_{2}}} \right)} \right]} \right\}J\left( {\tau - \left( {2k + 1} \right){{H}_{2}}} \right), \\ \end{gathered} $

где $J\left( \tau \right)$ – единичная функция-оригинал [2]. Далее, согласно (10)–(11),

(13)

$\begin{gathered} {{\left. {{{\theta }_{1}}\left( {y,{\text{Fo}}} \right)} \right|}_{{y \geqslant 0}}} = \frac{{2{\text{Bi}}}}{{{{H}_{2}}a}}\mathop \sum \limits_{k = 0}^\infty \frac{{{{{\left( { - 1} \right)}}^{k}}}}{{\sqrt {\pi {\text{Fo}}} }}\mathop \smallint \limits_0^\infty g_{k}^{ + }\left( {y,\tau } \right){\text{exp}}\left( { - \frac{{{{\tau }^{2}}}}{{4{\text{Fo}}}}} \right)d\tau ; \\ g_{k}^{ + }\left( {y,\tau } \right) = \mathop \sum \limits_{j = 0}^2 \frac{1}{{k!}}\mathop {\lim }\limits_{s \to {{s}_{{1j}}}} \frac{{{{d}^{k}}}}{{d{{s}^{k}}}}\left\{ {{{{\left( {s - {{s}_{{1j}}}} \right)}}^{{k + 1}}}\frac{{{{{\left( {s - {{s}_{{20}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{21}}}} \right)}}^{k}}{{{\left( {s - {{s}_{{22}}}} \right)}}^{k}}}}{{{{{\left( {s - {{s}_{{10}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{11}}}} \right)}}^{{k + 1}}}{{{\left( {s - {{s}_{{12}}}} \right)}}^{{k + 1}}}}} \times } \right. \\ \left. { \times \,\,{\text{exp}}\left[ {s\left( {\tau - \left( {2k + 1} \right){{H}_{2}} - y\sqrt {b\mu _{*}^{{ - 1}}} } \right)} \right]} \right\}J\left( {\tau - \left( {2k + 1} \right){{H}_{2}} - y\sqrt {b\mu _{*}^{{ - 1}}} } \right). \\ \end{gathered} $

При этом функционал ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right)$ при $y \in \left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right]$ определяется совершенно аналогично с учетом соответствующих равенств, представленных в (10).

Для идентификации функционала ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$ определяющего вторую независимую аддитивную составляющую процесса формирования искомого температурного поля, к смешанной задаче (1)–(6), где в краевом условии (4) комплекс ${\text{Bi}}\left( {1 - \theta } \right)$ заменен комплексом $\left( { - {\text{Bi}}\theta } \right)$, последовательно применяем сначала двумерное экспоненциальное интегральное преобразование Фурье по совокупности пространственных переменных $x~$ и $z,$ задаваемое парой линейных интегральных операторов [19]:

(14)

$\begin{gathered} {\Phi }\left[ \cdot \right] \equiv \mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_{ - \infty }^\infty \cdot {\text{exp}}\left( { - ipx - irz} \right)dxdz; \\ {{{\Phi }}^{{ - 1}}}\left[ \cdot \right] \equiv \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}}\mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_{ - \infty }^\infty \cdot {\text{exp}}\left( {ipx + irz} \right)dpdr, \\ \end{gathered} $

а затем интегральное преобразование Лапласа (8) по временному переменному ${\text{Fo}}$. В этом случае в пространстве композиции интегральных преобразований (14) и (8) с использованием следующих обозначений:

(15)

$\begin{gathered} A\left( {p,y,r,{\text{Fo}}} \right) \triangleq {\Phi }\left[ {{{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)} \right]; \\ \left\langle {A\left( {p,r,{\text{Fo}}} \right)} \right\rangle \triangleq {\Phi }\left[ {\left\langle {{{\theta }_{2}}\left( {x,z,{\text{Fo}}} \right)} \right\rangle } \right]; \\ f\left( {p,r,{\text{Fo}}} \right) \triangleq {\Phi }\left[ {{{Q}_{0}}\left( {x,z,{\text{Fo}}} \right)} \right]; \\ B\left( {p,y,r,{\text{s}}} \right) \triangleq L\left[ {A\left( {p,y,r,{\text{Fo}}} \right)} \right]; \\ \left\langle {B\left( {p,r,{\text{s}}} \right)} \right\rangle \triangleq L\left[ {\left\langle {A\left( {p,r,{\text{Fo}}} \right)} \right\rangle } \right]; \\ F\left( {p,r,s} \right) \triangleq L\left[ {f\left( {p,r,{\text{Fo}}} \right)} \right],~ \\ \end{gathered} $

и стандартных свойств линейных интегральных операторов ${\Phi }\left[ \cdot \right]$ и $L\left[ \cdot \right]$ [27, 2, 3, 26 ] модифицированная смешанная задача (1)–(6) может быть представлена в виде краевой задачи для системы обыкновенных линейных дифференциальных уравнений второго порядка со специфическими условиями сопряжения:

(16)

$\begin{gathered} \frac{{{{d}^{2}}B}}{{d{{y}^{2}}}} + 2i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\frac{{dB}}{{dy}} - \left[ {\left( {{{\mu }_{{11}}}{{p}^{2}} + 2{{\mu }_{{13}}}pr + {{\mu }_{{33}}}{{r}^{2}}} \right) + s} \right]B = 0,\,\,\,\,~ - \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}; \\ \frac{{{{d}^{2}}B}}{{d{{y}^{2}}}} - \left[ {\left( {{{p}^{2}} + {{r}^{2}}} \right) + b\mu _{*}^{{ - 1}}s} \right]B = 0,~\,\,\,\,y > 0; \\ {{\left. {\left[ {\frac{{dB}}{{dy}} + i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)B + {\text{Bi}}B} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = F\left( {p,r,s} \right); \\ B\left( {p, - {{H}_{2}} - 0,r,s} \right) = \left\langle {B\left( {p,r,s} \right)} \right\rangle = B\left( {p,0 + 0,r,s} \right); \\ \left\{ {\left[ {as + \mu \left( {{{p}^{2}} + {{r}^{2}}} \right)} \right] - {{Q}_{*}}} \right\}\left\langle B \right\rangle = {{\left. {\left[ {\frac{{dB}}{{dy}} + i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)B} \right]} \right|}_{{y = - {{H}_{2}} - 0}}} - {{\left. {{{\mu }_{*}}\frac{{dB}}{{dy}}} \right|}_{{y = 0 + 0}}}; \\ {{\left. {B\left( {p,y,r,{\text{s}}} \right)} \right|}_{{\left( {{{{\left[ {p,r} \right]}}^{{\text{T}}}} \in {{\mathbb{R}}^{2}}} \right) \wedge \left( {s \in \mathbb{C}} \right)}}} \in {{L}^{2}}\left( {\left[ { - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right] \cup \left[ {0,} \right.\left. { + \infty } \right)} \right). \\ \end{gathered} $

Решение краевой задачи (16) может быть найдено с использованием стандартных методов [25] и представлено в следующем виде:

$\begin{gathered} {{\left. {B\left( {p,y,r} \right)} \right|}_{{y \in \left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right), - {{H}_{2}}} \right]}}} = {{C}_{1}}\left( {p,r,s} \right){\text{exp}}\left\{ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right) + \sqrt {s + {{\gamma }_{1}}\left( {p,r} \right)} \left( {y + {{H}_{2}}} \right)} \right\} + \\ + \,\,{{C}_{2}}\left( {p,r,s} \right){\text{exp}}\left\{ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right) - \sqrt {s + {{\gamma }_{2}}\left( {p,r} \right)} \left( {y + {{H}_{2}}} \right)} \right\}; \\ {{\left. {B\left( {p,y,r,s} \right)} \right|}_{{y \in \left[ {0,} \right.\left. { + \infty } \right)}}} = \left\langle {B\left( {p,r} \right)} \right\rangle {\text{exp}}\left\{ { - y{{b}^{{1/2}}}\mu _{*}^{{ - 1/2}}\sqrt {s + {{\gamma }_{2}}\left( {p,r} \right)} } \right\}; \\ {{\left. {{{C}_{k}}\left( {p,r} \right)} \right|}_{{k \in \left\{ {1,2} \right\}}}} = 0.5\left[ {1 - {{{\left( { - 1} \right)}}^{k}}D\left( {p,r,s} \right)} \right]\left\langle {B\left( {p,r,s} \right)} \right\rangle ; \\ \end{gathered} $

(17)

$\begin{gathered} {{\left. {\left\langle {B\left( {p,r,s} \right)} \right\rangle } \right|}_{{y \in \left[ { - {{H}_{2}},0} \right]}}} = 2F\left( {p,r,s} \right){{\kappa }^{{ - 1}}}\left( {p,r,s} \right){\text{exp}}\left\{ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right){{H}_{1}}} \right\}; \\ \kappa \left( {p,r,s} \right) = \left[ {{\text{Bi}} - \sqrt {s + {{\gamma }_{1}}\left( {p,r} \right)} } \right]\left[ {1 + D\left( {p,r,s} \right)} \right]{\text{exp}}\left\{ {{{H}_{1}}\sqrt {s + {{\gamma }_{1}}\left( {p,r} \right)} } \right\} + \\ \end{gathered} $

$\begin{gathered} + \,\,\left[ {{\text{Bi}} + \sqrt {s + {{\gamma }_{1}}\left( {p,r} \right)} } \right]\left[ {1 - D\left( {p,r,s} \right)} \right]{\text{exp}}\left\{ { - {{H}_{1}}\sqrt {s + {{\gamma }_{1}}\left( {p,r} \right)} } \right\}; \\ D\left( {p,r,s} \right) = \left\{ {\mu _{*}^{{1/2}}{{b}^{{1/2}}}\sqrt {s + {{\gamma }_{2}}\left( {p,r} \right)} + {{Q}_{*}} - \left[ {0.5 + \mu {{H}_{2}}\left( {{{p}^{2}} + {{r}^{2}}} \right)} \right]} \right\}{{\left\{ {s + {{\gamma }_{1}}\left( {p,r} \right)} \right\}}^{{ - 1/2}}}; \\ {{\gamma }_{1}}\left( {p,r} \right) = \left( {{{\mu }_{{11}}} - \mu _{{12}}^{2}} \right){{p}^{2}} + 2\left( {{{\mu }_{{13}}} - {{\mu }_{{12}}}{{\mu }_{{23}}}} \right)pr + \left( {{{\mu }_{{33}}} - \mu _{{32}}^{2}} \right){{r}^{2}}; \\ {{\gamma }_{2}}\left( {p,r} \right) = {{b}^{{ - 1}}}{{\mu }_{*}}\left( {{{p}^{2}} + {{r}^{2}}} \right), \\ \end{gathered} $

где квадратичные формы ${{\gamma }_{1}}\left( {p,r} \right)$ и ${{\gamma }_{2}}\left( {p,r} \right)$ положительно определены [3, 6].

При дальнейших рассуждениях ограничимся анализом процедуры перехода от изображения $\left\langle {B\left( {p,r,s} \right)} \right\rangle $ к оригиналу $\left\langle {{{\theta }_{2}}\left( {x,z,{\text{Fo}}} \right)} \right\rangle $, так как согласно (17) и (15) эта процедура имеет основополагающее значение для идентификации второй независимой аддитивной составляющей процесса формирования искомого температурного поля объекта исследований. А так как изображение $\left\langle {B\left( {p,r,s} \right)} \right\rangle $ в качестве множителя содержит изображение $F\left( {p,r,s} \right)$ плотности мощности воздействующего на объект исследований внешнего теплового потока, задаваемой функционалом ${{Q}_{0}}\left( {x,z,{\text{Fo}}} \right),$ про который известно лишь, что он интегрируем с квадратом как по совокупности пространственных переменных в ${{\mathbb{R}}^{2}},$ так и по временному переменному на полуинтервале $\left[ {0,} \right.\left. { + \infty } \right)$, то с учетом (15) сначала воспользуемся теоремой о свертках для реализованных интегральных преобразований (14) и (8) в сочетании с теоремой запаздывания для интегральных преобразований (14) [2, 3, 26, 27]. Таким образом, имеем:

(18)

$\begin{gathered} \left\langle {{{\theta }_{2}}\left( {x,z,{\text{Fo}}} \right)} \right\rangle = {{{\Phi }}^{{ - 1}}}\left[ {{{L}^{{ - 1}}}\left[ {\left\langle {B\left( {p,r,s} \right)} \right\rangle } \right]} \right] = \\ = 2\mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_0^{{\text{Fo}}} {{Q}_{0}}\left( {x - {{\mu }_{{12}}}{{H}_{1}} - u,z - {{\mu }_{{23}}}{{H}_{1}} - v,{\text{Fo}} - {\tau }} \right)E\left( {u,v,\tau } \right)dudvd\tau ,~\,\,\,\,\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,{\text{Fo}} \geqslant 0; \\ E\left( {x,z,{\text{Fo}}} \right) = {{{\Phi }}^{{ - 1}}}\left[ {{{L}^{{ - 1}}}[{{\kappa }^{{ - 1}}}\left( {p,r,s} \right)]} \right]. \\ \end{gathered} $

Согласно (18), процедура идентификации функционала $\left\langle {{{\theta }_{2}}\left( {x,z,{\text{Fo}}} \right)} \right\rangle $ завершается определением оригинала $E\left( {x,z,{\text{Fo}}} \right),$ для чего сначала необходимо реализовать операцию обращения интегрального преобразования Лапласа (8) для изображения ${{\kappa }^{{ - 1}}}\left( {p,r,s} \right),$ которое согласно (17) имеет две точки ветвления, определенные следующими равенствами:

(19)

${{s}_{1}} = - {{\gamma }_{1}}\left( {p,r} \right);\,\,\,\,{{s}_{2}} = - {{\gamma }_{2}}\left( {p,r} \right),$

где квадратичные формы ${{\gamma }_{1}}\left( {p,r} \right)$ и ${{\gamma }_{2}}\left( {p,r} \right)$ положительно определены. А так как даже поверхностный анализ структуры изображения ${{\kappa }^{{ - 1}}}\left( {p,r,s} \right)$ убеждает в бесперспективности попыток непосредственного обращения в рассматриваемой ситуации интегрального преобразования Лапласа (8) с использованием его свойств [2, 3, 26] и соответствующих таблиц “изображение–оригинал” [2, 28, 29], то для вычисления интеграла Римана–Меллина при определении ${{L}^{{ - 1}}}\left[ {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right)} \right]$ воспользуемся стандартным подходом [2, 24, 26] и информацией, представленной на рис. 1. При этом будем предполагать реализуемость естественного неравенства

(20)

${{\gamma }_{1}}\left( {p,r} \right) < {{\gamma }_{2}}\left( {p,r} \right),~\,\,\,\,\forall {{\left[ {p,r} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{2}},$

корректность которого следует непосредственно из исходных допущений и равенств (17), определяющих положительно определённые квадратичные формы ${{\gamma }_{1}}\left( {p,r} \right)~$ и ${{\gamma }_{2}}\left( {p,r} \right).$ Таким образом, с учетом сказанного выше, приходим к следующему результату:

(21)

$\begin{gathered} {{L}^{{ - 1}}}\left[ {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right)} \right] = \frac{1}{{2\pi i}}\left\{ { - \mathop \smallint \limits_{\gamma \left( {p,r} \right)}^0 {{{\left. {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right){\text{exp}}\left( {s\tau } \right)ds} \right|}}_{{s = {{s}_{1}} + \omega {\text{exp}}\left( {i\pi } \right)}}} + } \right. \\ + \,\,\mathop \smallint \limits_0^{\gamma \left( {p,r} \right)} {{\left. {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right){\text{exp}}\left( {s\tau } \right)ds} \right|}_{{s = {{s}_{1}} + \omega {\text{exp}}\left( { - i\pi } \right)}}} = \frac{2}{\pi }{\text{exp}}\left[ { - ~~{{\gamma }_{1}}\left( {p,r} \right)\tau } \right] \times \\ \times \,\,\mathop \smallint \limits_0^{\gamma \left( {p,r} \right)} \left\{ {\left[ {{\text{Bi}} - \frac{{d\left( {p,r,\omega } \right)}}{{\sqrt \omega }}} \right]{\text{cos}}\left( {{{H}_{1}}\sqrt \omega } \right) + } \right.{{\left. {\left[ {\sqrt \omega + \frac{{{\text{Bi}}}}{{\sqrt \omega }}d\left( {p,r,\omega } \right)} \right]{\text{sin}}\left( {{{H}_{1}}\sqrt \omega } \right)} \right\}}^{{ - 1}}}{\text{exp}}\left( { - \tau \omega } \right)d\omega ; \\ \gamma \left( {p,r} \right) \triangleq {{\gamma }_{2}}\left( {p,r} \right) - {{\gamma }_{1}}\left( {p,r} \right); \\ d\left( {p,r,\omega } \right) \triangleq \sqrt {{{\mu }_{*}}b\left[ {\gamma \left( {p,r} \right) - \omega } \right]} + {{Q}_{*}} + a\left[ {{{\gamma }_{1}}\left( {p,r} \right) + \omega } \right] - \mu \mu _{*}^{{ - 1}}{{H}_{2}}{{\gamma }_{2}}\left( {p,r} \right). \\ \end{gathered} $

Рис. 1.

Контур для вычисления интеграла Римана–Меллина для изображения ${{\kappa }^{{ - 1}}}\left( {p,r,s} \right),$ имеющего точки ветвления ${{s}_{1}}$ и ${{s}_{2}},$ определенные равенствами (19), при условии реализуемости требования (20).

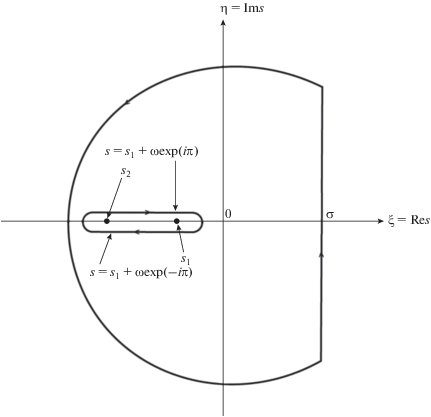
Для завершения процедуры идентификации функционала $\left\langle {{{\theta }_{2}}\left( {x,z,{\text{Fo}}} \right)} \right\rangle $ согласно равенствам (18), (17) и (21) достаточно воспользоваться изображением ${{L}^{{ - 1}}}\left[ {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right)} \right]$, представленным в (21), и оператором ${{{\Phi }}^{{ - 1}}}\left[ \cdot \right]$ обращения двумерного экспоненциального интегрального преобразования Фурье (14). При этом следует обратить внимание на то, что изображение ${{L}^{{ - 1}}}\left[ {{{\kappa }^{{ - 1}}}\left( {p,r,s} \right)} \right]$ зависит не от параметров $p$ и $r$ двумерного экспоненциального интегрального преобразования Фурье (14) как таковых, а от двух положительно определенных квадратичных форм ${{\gamma }_{1}}\left( {p,r} \right)$ и ${{\gamma }_{2}}\left( {p,r} \right),$ представленных в (17). Данное обстоятельство обеспечивает возможность применения известного подхода [30], позволяющего трансформировать результат настоящих исследований к виду, удобному для проведения вычислительных экспериментов.

Суть этого подхода заключается в следующем: (1) в соответствии с известной теоремой теории матриц [31] определяем матрицу ${\Gamma } \in {{M}_{{2 \times 2}}}\left( \mathbb{R} \right)$ невырожденного преобразования, приводящего одновременно к каноническому виду положительно определенные квадратичные формы ${{\gamma }_{1}}\left( {p,r} \right)$ и ${{\gamma }_{2}}\left( {p,r} \right)$; (2) в двойном несобственном интеграле, реализующем оператор ${{{\Phi }}^{{ - 1}}}\left[ \cdot \right],$ производим замену переменных с невырожденной матрицей ${\Gamma }$, после чего используем существующую связь между двумерным экспоненциальным интегральным преобразованием Фурье и двумерным интегральным косинус-преобразованием Фурье [27].

ЗАКЛЮЧЕНИЕ

1. Процесс формирования искомого температурного поля полностью определен двумя независимыми аддитивными составляющими, первая из которых представлена функционалом ${{\theta }_{1}}\left( {y,{\text{Fo}}} \right),$ описывающим процесс формирования температурного поля системы вследствие отличия ее начальной температуры от температуры внешней среды, а вторая – функционалом ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right),$ описывающим процесс формирования температурного поля за счет воздействия нестационарного теплового потока на внешнюю поверхность анизотропного покрытия системы.

2. Специфика структуры функционала ${{\theta }_{2}}\left( {x,y,z,{\text{Fo}}} \right)$ в пространстве изображений композиции используемых интегральных преобразований (17) явно указывает на проявление известного эффекта “сноса” температурного поля в анизотропном покрытии системы, обладающим анизотропией свойств общего вида [32].

3. Механизм функционирования “термически тонкой” термоактивной прокладки, не учитывающий возможность протекания в ней теплодиффузионных процессов, качественно не искажает формируемое температурное поле объекта исследований, но требует количественных оценок [4].

Список литературы

Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Карташов Э.М. Аналитические методы в теории теплопроводности твёрдых тел. М.: Высшая школа, 2001. 552 с.
Пудовкин М.А., Волков И.К. Краевые задачи математической теории теплопроводности в приложении к расчетам температурных полей в нефтяных пластах при заводнении. Казань: Изд-во Казанского ун-та, 1978. 188 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: USSR, 2012. 653 с.
Формалев В.Ф. Теплопроводность анизотропных тел. Аналитические методы решения задач. М.: Физматлит, 2014. 312 с.
Козлов В.П. Двумерные осесимметричные нестационарные задачи теплопроводности. Минск: Наука и техника, 1986. 391 с.
Козлов В.П., Мандрик П.А. Нестационарные температурные поля в изотропном полупространстве при смешанных граничных условиях, характерных для лазерной терапии в медицине // Инженерно–физический журнал. 2000. Т. 73. № 3. С. 637–644.
Аттетков А.В., Волков И.К., Тверская Е.С. Осесимметричное температурное поле изотропного полупространства при локальном нестационарном нагреве внешней средой // Теплофизика высоких температур. 2010. Т. 48. № 4. С. 612–616.
Аттетков А.В., Волков И.К. Аналитический метод решения задач теплопроводности для полупространства с покрытием в нестационарных условиях теплообмена с внешней средой // Вестник МГТУ им. Н.Э. Баумана. Машиностроение. 2000. № 1. С. 18–28.
Аттетков А.В., Волков И.К. Термоконвективная осесимметричная двухслойная задача // Изв. РАН. Энергетика. 2016. № 5. С. 140–151.
Аттетков А.В., Волков И.К. Термоконвективная осесимметричная двухслойная задача изотропной теплопроводности // Тепловые процессы в технике. 2016. Т. 8. № 11. С. 500–505.
Аттетков А.В., Волков И.К., Тверская Е.С. Термоактивная прокладка как средства управляемого воздействия на температурное поле конструкции // Изв. РАН. Энергетика. 2002. № 4. С. 131–141.
Аттетков А.В., Волков И.К., Тверская Е.С. Математическое моделирование процесса теплопереноса в экранированном полупространстве с термоактивной прокладкой при осесимметричном тепловом воздействии // Инженерно–физический журнал. 2008. Т. 81. № 3. С. 559–568.
Аттетков А.В., Волков И.К., Тверская Е.С. Базовая модель процесса теплопереноса в экранированном полупространстве с термоактивной прокладкой // Изв. РАН. Энергетика. 2009. № 2. С. 147–155.
Аттетков А.В., Волков И.К., Тверская Е.С. Температурное поле многослойного полупространства при неидеальном тепловом контакте между слоями // Изв. РАН. Энергетика. 2010. № 3. С. 83–91.
Волков И.К., Тверская Е.С. Оптимальная толщина экранированной стенки с термоактивной прокладкой, функционирующей по принципу обратной связи // Наука и образование. МГТУ им. Н.Э. Баумана. Электронный журнал. 2012. № 5. С. 172–187.
Аттетков А.В., Волков И.К. Установившееся температурное поле системы с активной теплозащитой // Тепловые процессы в технике. 2014. Т. 6. № 2. С. 81–86.
Негойце К. Применение теории систем к проблемам управления. М.: Мир, 1981. 184 с.
Дезоер Ч. Системы с обратной связью: Вход–выходные соотношения. М.: Наука, 1983. 278 с.
Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970. 712 с.
Аттетков А.В., Власова Л.Н., Волков И.К. Особенности формирования температурного поля в системе под воздействием осциллирующего теплового потока // Тепловые процессы в технике. 2012. Т. 4. № 12. С. 553–558.
Аттетков А.В., Волков И.К. Осциллирующая составляющая квазистационарного температурного поля системы, находящейся под воздействием импульсно-периодического теплового потока // Изв. РАН. Энергетика. 2015. № 5. С. 124–134.
Аттетков А.В., Волков И.К. Осциллирующая составляющая температурного поля анизотропного полупространства, на изотропное покрытие подвижной границы которого воздействует импульсно-периодический тепловой поток // Тепловые процессы в технике. 2017. Т. 9. № 1. С. 19–26.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. 424 с.
Диткин В.А., Прудников А.П. Операционное исчисление. М.: Высшая школа, 1966. 408 с.
Снеддон И. Преобразования Фурье. М.: Изд-во иностр. лит., 1955. 668 с.
Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. 344 с.
Диткин В.А., Прудников А.П. Справочник по операционному исчислению. М.: Высшая школа, 1965. 466 с.
Аттетков А.В., Волков И.К. Третья краевая задача математической теории теплопроводности для двухслойного анизотропного полупространства // Изв. РАН. Энергетика. 2017. № 4. С. 136–142.
Беллман Р. Введение в теорию матриц. М.: Наука, 1969. 368 с.
Аттетков А.В., Волков И.К. Температурное поле охлаждаемой изотропной пластины с анизотропным покрытием, находящейся под воздействием внешнего потока // Тепловые процессы в технике. 2013. Т. 5. № 2. С. 50–58.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал