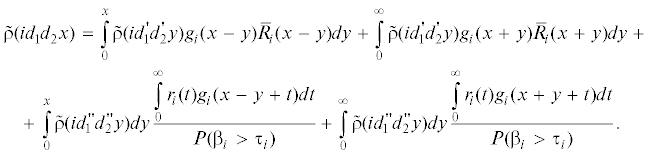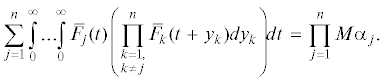1. На главную
  2. Электронные версии
  3. Известия РАН. Энергетика
  4. № 6, 2019

Известия РАН. Энергетика, 2019, № 6, стр. 66-77

Анализ надежности и фазовое укрупнение систем с поэлементными накопителями

Ю. Е. Обжерин 1, *, С. М. Сидоров 1, М. М. Никитин 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Севастопольский государственный университет”
Севастополь, Россия

* E-mail: objsev@mail.ru

Поступила в редакцию 10.12.2018
После доработки 10.12.2018
Принята к публикации 28.11.2019

Полный текст (PDF)

Аннотация

Временное резервирование является методом повышения надежности и эффективности функционирования систем энергетики различного назначения. Системе с резервом времени предоставляется дополнительное время (резерв времени) на восстановление характеристик. В системах энергетики одним из важнейших источников резерва времени являются накопители энергии. В данной работе на основе теории полумарковских процессов с общим фазовым пространством состояний построена полумарковская модель двухкомпонентной системы с поэлементным мгновенно пополняемым резервом времени. Определены стационарные характеристики надежности рассматриваемой системы, проведен анализ влияния величины резерва времени на полученные характеристики. Для построения упрощенной модели функционирования рассматриваемой системы использован алгоритм стационарного фазового укрупнения.

Ключевые слова: резерв времени, накопители энергии, полумарковская модель, характеристики надежности, стационарное фазовое укрупнение

ВВЕДЕНИЕ

Временное резервирование [1–7] – это метод повышения надежности и эффективности функционирования систем, при котором системе в процессе работы предоставляется возможность израсходовать некоторое дополнительное время (резерв времени) на восстановление характеристик. Для систем с временным резервированием нарушение работоспособности системы не обязательно сопровождается отказом системы, так как имеется возможность восстановить ее работоспособность за резервное время.

Временное резервирование широко применяется в системах энергетики различного назначения: газотранспортных системах, в которых для повышения надежности используются подземные хранилища газа [8, 9]; в системах теплоэнергетики источниками резерва времени являются резервные источники тепловой энергии, накопители тепловой энергии и инерционность технологических процессов [2, 10–12]; в системах электроэнергетики одним из источников резерва времени являются накопители электроэнергии, которые в настоящее время получили достаточно широкое применение [13–15]. Важное значение имеет временное резервирование в системах ядерной энергетики, наличие резерва времени в которых позволяет исправить ошибки, допущенные оператором.

При использовании в системах резерва времени возникают задачи построения моделей систем с учетом наличия резерва времени, анализа влияния величины резерва времени на надежность и эффективность систем, в частности, определения емкостей накопителей и мест их расположения.

В настоящее время для моделирования систем различного назначения, в частности, систем энергетики, и анализа их функционирования используются полумарковские процессы [16–22].

В данной работе на основе теории полумарковских процессов с общим фазовым пространством состояний [16–19] построена полумарковская модель двухкомпонентной системы с поэлементным мгновенно пополняемым резервом времени. Найдены стационарные характеристики надежности системы, проведен анализ влияния величины резерва времени на полученные характеристики. Для построения упрощенной модели функционирования рассматриваемой системы использован алгоритм стационарного фазового укрупнения [16, 17, 23].

1. ОПИСАНИЕ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ

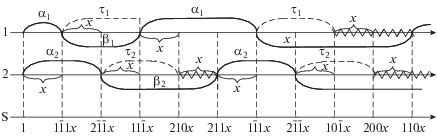
Рассматривается система $S,$ состоящая из 2-х элементов, времена безотказной работы которых случайные величины (СВ) ${{\alpha }_{i}}$ с функциями распределения (ФР) ${{F}_{i}}(t),$ а времена восстановления – СВ ${{\beta }_{i}}$ с ФР ${{G}_{i}}(t)$, $i = \overline {1,2} .$ Каждый элемент системы имеет случайный мгновенно пополняемый резерв времени ${{\tau }_{i}}$ с ФР ${{R}_{i}}(t).$ СВ ${{\alpha }_{i}},$ ${{\beta }_{i}},$ ${{\tau }_{i}}$ предполагаются независимыми в совокупности, имеющими конечные математические ожидания; ФР ${{F}_{i}}(t),$ ${{G}_{i}}(t),$ ${{R}_{i}}(t)$ – имеющими плотности ${{f}_{i}}(t),$ ${{g}_{i}}(t),$ ${{r}_{i}}(t).$

Резерв времени начинает использоваться в момент начала восстановления элемента. Отказ системы $S$ наступает тогда, когда оба элемента восстанавливаются и полностью израсходован резерв времени для каждого элемента. Он продолжается до восстановления одного из отказавших элементов, при этом резерв времени у восстановленного элемента мгновенно пополняется до уровня ${{\tau }_{i}}.$

2. ПОСТРОЕНИЕ ПОЛУМАРКОВСКОЙ МОДЕЛИ СИСТЕМЫ

Для описания функционирования системы $S$ используем полумарковский процесс $\xi (t)$ [16–19] с дискретно-непрерывным фазовым пространством состояний.

Введем фазовое пространство состояний вида:

(1)
$Е = \{ 1, i\bar {d}x:\bar {d} = ({{d}_{1}},{{d}_{2}}), x > 0\} ,$
где 1 – начальное состояние системы, $i = \overline {1,2} $ – номер элемента, в котором произошло изменение состояния. Компонента ${{d}_{k}}$ вектора $\bar {d}$ описывает физическое состояние элемента с номером $k{\kern 1pt} :$

${{d}_{k}} = \left\{ \begin{gathered} 1, если к{\kern 1pt} - {\kern 1pt} ый \,элемент\, работоспособен, \hfill \\ \bar {1}, если к{\kern 1pt} - {\kern 1pt} ый \,элемент\, восстанавливается \,{\text{и}} \hfill \\ функционирует\, за\, счет\, резерва \,времени, \hfill \\ 0, если\, к{\kern 1pt} - {\kern 1pt} ый \,элемент\, находится\, в \,отказе. \hfill \\ \end{gathered} \right.$

Непрерывная компонента $x$ указывает время, прошедшее с момента последнего изменения состояния системы. Временная диаграмма функционирования системы представлена на рис. 1 .

Рис. 1.

Временная диаграмма функционирования системы.

Построим процесс марковского восстановления $\{ {{\xi }_{n}}, {{\theta }_{n}};n \geqslant 0\} $ [16, 17], описывающий функционирование системы $S.$

Определим вероятности переходов вложенной цепи Маркова (ВЦМ) $\{ {{\xi }_{n}};n \geqslant 0\} $. Введем обозначения:

$\bar {F}(t) = 1 - F(t),\,\,\,\,\bar {i} = \left\{ \begin{gathered} 2, i = 1, \hfill \\ 1, i = 2. \hfill \\ \end{gathered} \right.$

1. Рассмотрим случай состояний $i{{d}_{1}}{{d}_{2}}x,$ ${{d}_{i}} = \bar {1},$ ${{d}_{{\bar {i}}}} = 1.$

В этом случае возможны следующие переходы:

а) $i{{d}_{1}}{{d}_{2}}x \to id_{1}^{'}d_{2}^{'}y$ в условиях: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{i}^{'} = 1,$ $y > x.$ Плотность вероятности перехода в этом случае вычисляется по формуле:

(2)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{id_{1}^{'}d_{2}^{'}y} = \frac{{{{g}_{i}}(y - x){{{\bar {R}}}_{i}}(y - x){{{\bar {F}}}_{{\bar {i}}}}(y)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}},$

б) $i{{d}_{1}}{{d}_{2}}x \to id_{1}^{'}d_{2}^{'}y,$ где $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{i}^{'} = 0,$ $y > x.$ Тогда:

(3)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{i{{{d'}}_{1}}{{{d'}}_{2}}y} = \frac{{{{r}_{i}}(y - x){{{\bar {G}}}_{i}}(y - x){{{\bar {F}}}_{{\bar {i}}}}(y)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}},$

в) $i{{d}_{1}}{{d}_{2}}x \to \bar {i}d_{1}^{'}d_{2}^{'}y$ в условиях: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{{\bar {i}}}^{'} = \bar {1},$ $y > 0$. В этом случае:

(4)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{\bar {i}d_{1}^{'}d_{2}^{'}y} = \frac{{{{f}_{{\bar {i}}}}(y + x){{{\bar {G}}}_{i}}(y){{{\bar {R}}}_{i}}(y)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}}.$

2. Рассмотрим состояния $i{{d}_{1}}{{d}_{2}}x,$ ${{d}_{1}} = {{d}_{2}} = 0.$

Возможны переходы:

а) $i{{d}_{1}}{{d}_{2}}x \to id_{1}^{'}d_{2}^{'}y$ в условиях: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i$, $d_{i}^{'} = 1,$ $y > x.$ Плотность вероятности перехода вычисляется по формуле:

(5)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{i{{{d'}}_{1}}{{{d'}}_{2}}y} = \frac{{\int\limits_0^\infty {{{r}_{i}}(t){{g}_{i}}(y - x + t)dt} \int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(y + t)dt} }}{{P({{\beta }_{i}} > {{\tau }_{i}})\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t)dt} }},$

б) $i{{d}_{1}}{{d}_{2}}x \to \bar {i}d_{1}^{'}d_{2}^{'}y,$ где $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{{\bar {i}}}^{'} = 1,$ $y > 0.$ Тогда:

(6)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{\bar {i}d_{1}^{'}d_{2}^{'}y} = \frac{{\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{g}_{{\bar {i}}}}(y - x + t)dt} \int\limits_0^\infty {{{r}_{i}}(t){{{\bar {G}}}_{i}}(y + t)dt} }}{{P({{\beta }_{i}} > {{\tau }_{i}})\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t)dt} }}.$

3. Рассмотрим случай состояний $i{{d}_{1}}{{d}_{2}}x,$ ${{d}_{1}} = {{d}_{2}} = \bar {1}.$

а) $i{{d}_{1}}{{d}_{2}}x \to id_{1}^{'}d_{2}^{'}y,$ где: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{i}^{'} = 1,$ $y > x.$ Плотность вероятности перехода в этом случае определяется формулой:

(7)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{id_{1}^{'}d_{2}^{'}y} = \frac{{{{g}_{i}}(y - x){{{\bar {R}}}_{i}}(y - x){{{\bar {G}}}_{{\bar {i}}}}(y){{{\bar {R}}}_{{\bar {i}}}}(y)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}},$

б) $i{{d}_{1}}{{d}_{2}}x \to id_{1}^{'}d_{2}^{'}y,$ в условиях: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{i}^{'} = 0,$ $y > x.$ В этом случае:

(8)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{id_{1}^{'}d_{2}^{'}y} = \frac{{{{r}_{i}}(y - x){{{\bar {G}}}_{i}}(y - x){{{\bar {G}}}_{{\bar {i}}}}(y){{{\bar {R}}}_{{\bar {i}}}}(y)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}},$

в) $i{{d}_{1}}{{d}_{2}}x \to \bar {i}d_{1}^{'}d_{2}^{'}y,$ где $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d{{_{{\bar {i}}}^{'}}_{{}}} = 1,$ $y > 0.$ Тогда:

(9)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{\bar {i}d_{1}^{'}d_{2}^{'}y} = \frac{{{{g}_{{\bar {i}}}}(y + x){{{\bar {R}}}_{{\bar {i}}}}(y + x){{{\bar {G}}}_{i}}(y){{{\bar {R}}}_{i}}(y)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}}.$

г) $i{{d}_{1}}{{d}_{2}}x \to \bar {i}d_{1}^{'}d_{2}^{'}y,$ в условиях: $d_{k}^{'} = {{d}_{k}}$ при $k \ne i,$ $d_{{\bar {i}}}^{'} = 0,$ $y > 0$. Имеем:

(10)
$\mathop p\nolimits_{i{{d}_{1}}{{d}_{2}}x}^{\bar {i}d_{1}^{'}d_{2}^{'}y} = \frac{{{{r}_{{\bar {i}}}}(y + x){{{\bar {G}}}_{{\bar {i}}}}(y + x){{{\bar {G}}}_{i}}(y){{{\bar {R}}}_{i}}(y)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}}.$

Для остальных состояний системы вероятности переходов определяются аналогичным образом.

3. НАХОЖДЕНИЕ СТАЦИОНАРНЫХ ХАРАКТЕРИСТИК СИСТЕМЫ

Для определения стационарных характеристик надежности системы найдем стационарное распределение ВЦМ $\{ {{\xi }_{n}};n \geqslant 0\} .$

Предположим, что у стационарного распределения ВЦМ $\{ {{\xi }_{n}};n \geqslant 0\} $ существуют плотности $\rho (i{{d}_{1}}{{d}_{2}}x)$.

Введем следующие замены:

$\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \frac{{\rho (i{{d}_{1}}{{d}_{2}}x)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}}, {{d}_{{\bar {i}}}} = 1,\,\,\,\,\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \frac{{\rho (i{{d}_{1}}{{d}_{2}}x)}}{{{{{\bar {R}}}_{{\bar {i}}}}(x){{{\bar {G}}}_{{\bar {i}}}}(x)}}, {{d}_{{\bar {i}}}} = \bar {1},$
$\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \frac{{\rho (i{{d}_{1}}{{d}_{2}}x)}}{{\frac{{\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t)dt} }}{{P({{\beta }_{{\bar {i}}}} > {{\tau }_{{\bar {i}}}})}}}}, {{d}_{{\bar {i}}}} = 0.$

Система интегральных уравнений для стационарного распределения ВЦМ $\{ {{\xi }_{n}};n \geqslant 0\} $ имеет следующий вид:

1. В случае $d_{i}^{'} = \bar {1}, d_{{\bar {i}}}^{'} = {{d}_{{\bar {i}}}}{\kern 1pt} :$

(11)
$\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \int\limits_0^x {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{f}_{i}}(x - y)dy} + \int\limits_0^\infty {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{f}_{i}}(x + y)dy.} $

2. Если $d_{i}^{'} = \bar {1}, d_{{\bar {i}}}^{'} = {{d}_{{\bar {i}}}},$ то

(12)
$\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \int\limits_0^x {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{r}_{i}}(x - y){{{\bar {G}}}_{i}}(x - y)dy} + \int\limits_0^\infty {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{r}_{i}}(x + y){{{\bar {G}}}_{i}}(x + y)dy} .$

3. При $d_{i}^{'} = \bar {1}, d_{{\bar {i}}}^{'} = {{d}_{{\bar {i}}}} = 0,$ имеем

(13)
$\tilde {\rho }(i{{d}_{1}}{{d}_{2}}x) = \int\limits_0^x {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{g}_{i}}(x - y){{{\bar {R}}}_{i}}(x - y)dy} + \int\limits_0^\infty {\tilde {\rho }(id_{1}^{'}d_{2}^{'}y){{g}_{i}}(x + y){{{\bar {R}}}_{i}}(x + y)dy} .$

4. Если 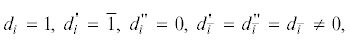получаем

(14)
(15)
$5.\,\int\limits_E {\rho (i\bar {d}x)dx} = 1\,\left( {{\text{условие}}\,{\text{нормировки}}} \right).$

Подстановкой можно убедиться, что стационарное распределение ВЦМ имеет вид:

(16)
$\rho (i{{d}_{1}}{{d}_{2}}x) = с{{\rho }_{i}}{{\rho }_{{\bar {i}}}}{{\bar {F}}_{{\bar {i}}}}(x), {{d}_{{\bar {i}}}} = 1,$
(17)
$\rho (i{{d}_{1}}{{d}_{2}}x) = с{{\rho }_{i}}{{\rho }_{{\bar {i}}}}{{p}_{i}}{{\bar {R}}_{{\bar {i}}}}(x){{\bar {G}}_{{\bar {i}}}}(x), {{d}_{{\bar {i}}}} = \bar {1},$
(18)
$\rho (i{{d}_{1}}{{d}_{2}}x) = \frac{{с{{\rho }_{i}}{{\rho }_{{\bar {i}}}}{{p}_{{\bar {i}}}}\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t)dt} }}{{P({{\beta }_{{\bar {i}}}} > {{\tau }_{{\bar {i}}}})}}, {{d}_{{\bar {i}}}} = 0,$
(19)
$\rho (i{{d}_{1}}{{d}_{2}}x) = \frac{{с{{\rho }_{i}}{{\rho }_{{\bar {i}}}}{{p}_{i}}{{p}_{{\bar {i}}}}\int\limits_0^\infty {{{r}_{{\bar {i}}}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t)dt} }}{{P({{\beta }_{{\bar {i}}}} > {{\tau }_{{\bar {i}}}})}}, {{d}_{i}} = {{d}_{{\bar {i}}}} = 0,$
где ${{p}_{i}} = P({{\beta }_{i}} > {{\tau }_{i}}) = \int_0^\infty {{{{\bar {G}}}_{i}}(t){{r}_{i}}(t)dt} ,$ ${{\rho }_{i}} = {\text{const,}}$ которая равна ${{\rho }_{i}} = \frac{1}{{2 + {{p}_{i}}}},$ константа $с$ находится из условия нормировки.

Вычислим средние времена пребывания в состояниях ВЦМ.

1. В случае ${{d}_{i}} = {{d}_{{\bar {i}}}} = 1$

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\alpha }_{i}} \wedge {{[{{\alpha }_{{\bar {i}}}} - x]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {F}}}_{i}}(t){{{\bar {F}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}}dt} .$

2. Если ${{d}_{i}} = \bar {1},{{d}_{{\bar {i}}}} = 1,$ то

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\beta }_{i}} \wedge {{\tau }_{i}} \wedge {{[{{\alpha }_{{\bar {i}}}} - x]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {G}}}_{i}}(t){{{\bar {R}}}_{i}}(t){{{\bar {F}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)}}dt} .$

3. Пусть ${{d}_{i}} = {{d}_{{\bar {i}}}} = \bar {1},$ тогда

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\beta }_{i}} \wedge {{\tau }_{i}} \wedge {{[{{\beta }_{{\bar {i}}}} - x]}^{ + }} \wedge {{[{{\tau }_{{\bar {i}}}} - x]}^{ + }},\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {G}}}_{i}}(t){{{\bar {R}}}_{i}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t){{{\bar {R}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}}dt.} $

4. В случае ${{d}_{i}} = 0, {{d}_{{\bar {i}}}} = 1$

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{[{{\beta }_{i}} - {{\tau }_{i}}]}^{ + }} \wedge {{[{{\alpha }_{{\bar {i}}}} - x]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {F}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {F}}}_{{\bar {i}}}}(x)P({{\beta }_{i}} > {{\tau }_{i}})}}dt} \int\limits_0^\infty {{{r}_{i}}(z){{{\bar {G}}}_{i}}(t + z)dz} .$

5. Если ${{d}_{i}} = 1,{{d}_{{\bar {i}}}} = \bar {1},$ то

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\alpha }_{i}} \wedge {{[{{\beta }_{{\bar {i}}}} - x]}^{ + }} \wedge {{[{{\tau }_{{\bar {i}}}} - x]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {F}}}_{i}}(t){{{\bar {G}}}_{{\bar {i}}}}(x + t){{{\bar {R}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)}}dt} .$

6. В случае ${{d}_{i}} = 0, {{d}_{{\bar {i}}}} = \bar {1},$

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{[{{\beta }_{i}} - {{\tau }_{i}}]}^{ + }} \wedge {{[{{\beta }_{{\bar {i}}}} - x]}^{ + }} \wedge {{[{{\tau }_{{\bar {i}}}} - x]}^{ + }},$ $М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \int\limits_0^\infty {\frac{{{{{\bar {G}}}_{{\bar {i}}}}(x + t){{{\bar {R}}}_{{\bar {i}}}}(x + t)}}{{{{{\bar {G}}}_{{\bar {i}}}}(x){{{\bar {R}}}_{{\bar {i}}}}(x)P({{\beta }_{i}} > {{\tau }_{i}})}}dt} \int\limits_0^\infty {{{r}_{i}}(z){{{\bar {G}}}_{i}}(t + z)dz} .$

7. Пусть ${{d}_{i}} = \bar {1}, {{d}_{{\bar {i}}}} = 0,$ тогда

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\tau }_{i}} \wedge {{\beta }_{i}} \wedge {{\left[ {{{{[{{\beta }_{{\bar {i}}}} - {{\tau }_{{\bar {i}}}}]}}^{ + }} - x} \right]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \frac{{\int\limits_0^\infty {{{{\bar {G}}}_{i}}(t){{{\bar {R}}}_{i}}(t)dt} \int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + t + z)dz} }}{{\int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + z)dz} }}.$

8. В случае ${{d}_{i}} = 1, {{d}_{{\bar {i}}}} = 0$

${{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{\alpha }_{i}} \wedge {{\left[ {{{{[{{\beta }_{{\bar {i}}}} - {{\tau }_{{\bar {i}}}}]}}^{ + }} - x} \right]}^{ + }},\,\,\,\,М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \frac{{\int\limits_0^\infty {{{{\bar {F}}}_{i}}(t)dt} \int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + t + z)dz} }}{{\int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + z)dz} }}.$

9. Если ${{d}_{i}} = {{d}_{{\bar {i}}}} = 0,$ то

$\begin{gathered} {{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = {{[{{\beta }_{i}} - {{\tau }_{i}}]}^{ + }} \wedge {{\left[ {{{{[{{\beta }_{{\bar {i}}}} - {{\tau }_{{\bar {i}}}}]}}^{ + }} - x} \right]}^{ + }}, \\ М{{\theta }_{{i{{d}_{1}}{{d}_{2}}x}}} = \frac{{\int\limits_0^\infty {dt} \int\limits_0^\infty {{{r}_{i}}(y){{{\bar {G}}}_{{\bar {i}}}}(t + y)dy} \int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + t + z)dz} }}{{P({{\beta }_{i}} > {{\tau }_{i}})\int\limits_0^\infty {{{r}_{{\bar {i}}}}(z){{{\bar {G}}}_{{\bar {i}}}}(x + z)dz} }}, \\ \end{gathered} $
где СВ ${{[\alpha - x]}^{ + }},$ ${{[\beta - \tau ]}^{ + }},$ ${{\left[ {{{{[{{\beta }_{{\bar {i}}}} - {{\tau }_{{\bar {i}}}}]}}^{ + }} - x} \right]}^{ + }}$ имеют следующие законы распределения:

$P\{ {{[\alpha - x]}^{ + }} > t\} = \frac{{\bar {F}(x + t)}}{{\bar {F}(x)}},\,\,\,\,P\{ {{[\alpha - x]}^{ + }} \in dt\} = \frac{{f(x + t)}}{{\bar {F}(x)}},$
$P\{ {{[\beta - \tau ]}^{ + }} > t\} = \frac{{\int\limits_0^\infty {r(z)\bar {G}(t + z)dz} }}{{P(\beta > \tau )}},\,\,\,\,P\{ {{[\beta - \tau ]}^{ + }} \in dt\} = \frac{{\int\limits_0^\infty {r(z)g(t + z)dz} }}{{P(\beta > \tau )}},$
$\begin{gathered} P\left\{ {{{{\left[ {{{{[\beta - \tau ]}}^{ + }} - x} \right]}}^{ + }} > t} \right\} = \frac{{\int\limits_0^\infty {r(z)\bar {G}(t + x + z)dz} }}{{\int\limits_0^\infty {r(z)\bar {G}(x + z)dz} }}, \\ P\left\{ {{{{\left[ {{{{[\beta - \tau ]}}^{ + }} - x} \right]}}^{ + }} \in dt} \right\} = \frac{{\int\limits_0^\infty {r(z)g(t + x + z)dz} }}{{\int\limits_0^\infty {r(z)\bar {G}(x + z)dz} }}. \\ \end{gathered} $

Перейдем к нахождению стационарных характеристик надежности системы $S{\kern 1pt} :$ средней стационарной наработки системы на отказ ${{Т}_{ + }},$ среднего стационарного времени восстановления системы ${{Т}_{ - }},$ стационарного коэффициента готовности ${{K}_{{\text{Г}}}}.$

Для нахождения характеристик используем следующие формулы [16]:

(20)
${{Т}_{ + }} = \frac{{\int\limits_{{{Е}_{ + }}} {m(e)\rho (de)} }}{{\int\limits_{{{Е}_{ + }}} {P(e,{{E}_{ - }})\rho (de)} }},\,\,\,\,{{Т}_{ - }} = \frac{{\int\limits_{{{Е}_{ - }}} {m(e)\rho (de)} }}{{\int\limits_{{{Е}_{ + }}} {P(e,{{E}_{ - }})\rho (de)} }},\,\,\,\,{{K}_{{\text{Г}}}} = \frac{{{{Т}_{ + }}}}{{{{Т}_{ + }} + {{Т}_{ - }}}},$
где ${{E}_{ + }}$ – множество работоспособных состояний, ${{E}_{ - }}$ – множество отказовых состояний, $\rho (de)$ – стационарное распределение ВЦМ $\left\{ {{{\xi }_{n}};\;n \geqslant 0} \right\}$, $P(e,{{E}_{ - }})$ – вероятности переходов ВЦМ $\{ \xi _{n}^{{}};n \geqslant 0\} $ в подмножество отказовых состояний ${{E}_{ - }},$ $m(e)$ – среднее время пребывания полумарковского процесса в состоянии $e \in E.$

Рассматривается параллельное соединение элементов системы. В этом случае

${{Е}_{ + }} = \{ i\bar {d}x:\bar {d} = ({{d}_{1}},{{d}_{2}}),\,\,\,\,\bar {d} \ne (0,0), x > 0\} ,\,\,\,\,{{Е}_{ - }} = \{ 100x, 200x\} .$

Используя выражения для $m(e)$ и $\rho (de),$ найденные выше, и формулы (20), получаем

$\begin{gathered} \int\limits_{{{Е}_{ - }}} {m(e)\rho (de)} = с{{\rho }_{1}}{{\rho }_{2}}{{p}_{1}}{{p}_{2}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right), \\ \int\limits_{{{Е}_{ + }}} {P(e,{{E}_{ - }})\rho (de)} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right], \\ \end{gathered} $
$\begin{gathered} \int\limits_{{{Е}_{ + }}} {m(e)\rho (de)} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + } \right. \\ \left. { + \,\,{{p}_{2}}M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right) + \left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right)} \right]. \\ \end{gathered} $
(21)
$\begin{gathered} {{Т}_{ + }} = \frac{{{{p}_{1}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + {{p}_{2}}M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)}}{{{{p}_{1}}{{p}_{2}}\left( {M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right) + M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)} \right)}} + \\ + \frac{{\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right)}}{{{{p}_{1}}{{p}_{2}}\left( {M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right) + M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)} \right)}}, \\ \end{gathered} $
(22)
$\begin{gathered} {{Т}_{ - }} = \frac{{с{{\rho }_{1}}{{\rho }_{2}}{{p}_{1}}{{p}_{2}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)}}{{с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right]}} = \\ = \frac{{M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)}}{{M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right) + M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)}}. \\ \end{gathered} $

В преобразованиях использовалась следующая формула, доказанная в [24]:

Используя формулы (20)–(22), можно найти стационарный коэффициент готовности ${{K}_{{\text{Г}}}}.$

Пример 1. В качестве примера использования формул (21)–(22) рассмотрим систему, у которой время безотказной работы элементов ${{K}_{1}}$ и ${{K}_{2}}$ равны Мα1 = 8 ч, Мα2 = 6 ч; времена восстановления элементов ${{K}_{1}}$ и ${{K}_{2}}$ равны Мβ1 = 0.71 ч, Мβ2 = 0.83 ч, СВ α1, α2, β1, β2 имеют распределение Эрланга 5-го порядка. Каждый элемент имеет неслучайный резерв времени (${{R}_{i}}(t) = 1(t - {{h}_{i}})$), который изменяется от 0 до 0.7 часа с шагом 0.1 ч. В табл. 1 представлены значения средней стационарной наработки на отказ ${{Т}_{ + }}({{h}_{1}},{{h}_{2}}),$ среднего стационарного времени восстановления ${{Т}_{ - }}({{h}_{1}},{{h}_{2}})$ и стационарного коэффициента готовности ${{K}_{{\text{Г}}}}({{h}_{1}},{{h}_{2}})$ рассматриваемой системы, при условии, что ${{h}_{1}} + {{h}_{2}} = 0.7.$

Таблица 1.  

Влияние резерва времени на характеристики надежности

${{h}_{1}},$ ч ${{h}_{2}},$ ч ${{Т}_{ - }}({{h}_{1}},{{h}_{2}}),$ ч ${{Т}_{ + }}({{h}_{1}},{{h}_{2}}),$ ч ${{K}_{{\text{Г}}}}({{h}_{1}},{{h}_{2}})$
0 0 0.385 49.551 0.99230
0 0.7 0.241 102.274 0.99765
0.1 0.6 0.241 91.035 0.99736
0.2 0.5 0.238 84.365 0.99719
0.3 0.4 0.233 82.291 0.99717
0.4 0.3 0.228 85.172 0.99733
0.5 0.2 0.224 93.617 0.99762
0.6 0.1 0.219 108.690 0.99799
0.7 0 0.214 132.300 0.99839

Данные табл. 1 показывают, что величина резерва времени оказывает существенное влияние на характеристики надежности системы.

4. ПОСТРОЕНИЕ УКРУПНЕННОЙ ПОЛУМАРКОВСКОЙ МОДЕЛИ

Для построения упрощенной модели функционирования рассматриваемой системы используем алгоритм стационарного фазового укрупнения, разработанный в работах [16, 17]. При использовании этого алгоритма целый класс состояний укрупняется в одно, что позволяет уменьшить размерность фазового пространства.

Укрупненные классы состояний введем следующим образом:

$\begin{gathered} {{Е}_{0}} = \{ 100x;200x\} ,\,\,\,\,{{Е}_{1}} = \{ 210x;101x;10\bar {1}x;2\bar {1}0x;20\bar {1}x;1\bar {1}0x;201x;110x\} , \\ {{Е}_{2}} = \{ 1\bar {1}1x;111x;211x;21\bar {1}x;2\bar {1}\bar {1}x;1\bar {1}\bar {1}x;11\bar {1}x;2\bar {1}1x\} . \\ \end{gathered} $

Состояние ${{Е}_{0}}$ означает, что оба элемента находятся в отказе, ${{Е}_{1}}$ – работоспособен только один из элементов системы, ${{Е}_{2}}$ – оба элемента работоспособны. Отметим, что укрупненные классы состояний можно вводить различными способами.

Определим вероятности перехода ВЦМ $\left\{ {\widehat {{{\xi }_{n}}};\;n \geqslant 0} \right\}$ и средние времена пребывания в состояниях ${{\hat {m}}_{k}}$ укрупненной системы по следующим формулам [16, 17]:

(23)
${{p}_{{kr}}} = {{\int\limits_{{{Е}_{k}}} {\rho (de)P(e,{{E}_{r}})} } \mathord{\left/ {\vphantom {{\int\limits_{{{Е}_{k}}} {\rho (de)P(e,{{E}_{r}})} } {\rho ({{Е}_{k}})}}} \right. \kern-0em} {\rho ({{Е}_{k}})}},\,\,k,r = \overline {1,N} ;\,\,\,{{m}_{k}} = М{{\theta }_{k}} = {{\int\limits_{{{Е}_{к}}} {\rho (dе)m(е)} } \mathord{\left/ {\vphantom {{\int\limits_{{{Е}_{к}}} {\rho (dе)m(е)} } {\rho ({{Е}_{k}})}}} \right. \kern-0em} {\rho ({{Е}_{k}})}},\,\,\,\,k = \overline {1,N} .$

Найдем выражения знаменателей и числителей формул (23), используя (2)–(10) и (16)–(19):

$\rho ({{E}_{0}}) = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right],$ $\rho ({{E}_{2}}) = 2с{{\rho }_{1}}{{\rho }_{2}}\left[ {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}}) + M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right],$
$\begin{gathered} \rho ({{E}_{1}}) = с{{\rho }_{1}}{{\rho }_{2}}{{p}_{1}}\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + с{{\rho }_{1}}{{\rho }_{2}}{{p}_{2}}\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right) + \hfill \\ + 2с{{\rho }_{1}}{{\rho }_{2}}\left[ {\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + \int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right], \hfill \\ \end{gathered} $
$\int\limits_{{{Е}_{1}}} {\rho (dе)P(е,{{E}_{0}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right],$ $\int\limits_{{{Е}_{0}}} {\rho (dе)P(е,{{E}_{1}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right],$
$\int\limits_{{{Е}_{1}}} {\rho (dе)P(е,{{E}_{2}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + {{p}_{2}}\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)} \right],$
$\begin{gathered} \int\limits_{{{Е}_{2}}} {\rho (dе)P(е,{{E}_{2}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {(1 - {{p}_{1}})\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + (1 - {{p}_{2}})\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right) + } \right. \hfill \\ \left. { + \,\,M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}}) + M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right], \hfill \\ \end{gathered} $
$\int\limits_{{{Е}_{1}}} {\rho (dе)P(е,{{E}_{1}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {(2 - {{p}_{1}})\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + (2 - {{p}_{2}})\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right],$
$\begin{gathered} \int\limits_{{{Е}_{2}}} {\rho (dе)P(е,{{E}_{1}})} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + {{p}_{2}}\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)} \right], \\ {{p}_{{20}}} = {{p}_{{02}}} = 0. \\ \end{gathered} $

Составим систему уравнений для стационарного распределения ВЦМ $\left\{ {{{\xi }_{n}};\;n \geqslant 0} \right\}$ укрупненной системы:

(24)
$\left\{ \begin{gathered} {{\rho }_{1}} = {{p}_{{01}}}{{\rho }_{0}} + {{p}_{{11}}}{{\rho }_{1}} + {{p}_{{21}}}{{\rho }_{2}}, \hfill \\ {{\rho }_{0}} = {{p}_{{10}}}{{\rho }_{1}}, \hfill \\ {{\rho }_{2}} = {{p}_{{12}}}{{\rho }_{1}} + {{p}_{{22}}}{{\rho }_{2}}, \hfill \\ {{\rho }_{0}} + {{\rho }_{1}} + {{\rho }_{2}} = 1. \hfill \\ \end{gathered} \right.$

Решение системы (24) имеет вид:

(25)
${{\rho }_{0}} = \frac{{{{p}_{{10}}}{{p}_{{21}}}}}{{{{p}_{{21}}} + {{p}_{{12}}} + {{p}_{{10}}}{{p}_{{21}}}}},\,\,\,\,{{\rho }_{1}} = \frac{{{{p}_{{21}}}}}{{{{p}_{{21}}} + {{p}_{{12}}} + {{p}_{{10}}}{{p}_{{21}}}}},\,\,\,\,{{\rho }_{2}} = \frac{{{{p}_{{12}}}}}{{{{p}_{{21}}} + {{p}_{{12}}} + {{p}_{{10}}}{{p}_{{21}}}}}.$

Найдем средние времена пребывания в состояниях укрупненной системы, используя формулы (23).

Выражения для числителей этих формул имеют вид:

$\int\limits_{{{Е}_{0}}} {\rho (dе)m(е)} = с{{\rho }_{1}}{{\rho }_{2}}{{p}_{1}}{{p}_{2}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right),$
$\begin{gathered} \int\limits_{{{Е}_{1}}} {\rho (dе)m(е)} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {{{p}_{1}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + } \right. \\ \left. { + \,\,{{p}_{2}}M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)} \right], \\ \end{gathered} $
$\begin{gathered} \int\limits_{{{Е}_{2}}} {\rho (dе)m(е)} = с{{\rho }_{1}}{{\rho }_{2}}\left[ {M{{\alpha }_{1}}M{{\alpha }_{2}} + M{{\alpha }_{1}}M({{\beta }_{2}} \wedge {{\tau }_{2}}) + } \right. \\ + \,\,\left. {M{{\alpha }_{2}}M({{\beta }_{1}} \wedge {{\tau }_{1}}) + M({{\beta }_{1}} \wedge {{\tau }_{1}})M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right]. \\ \end{gathered} $

Используя формулы (23), получаем

${{m}_{0}} = \frac{{{{p}_{1}}{{p}_{2}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)}}{{{{p}_{1}}\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} + {{p}_{2}}\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} }},$
${{m}_{1}} = \frac{{\left[ {{{p}_{1}}M\left( {{{{[{{\beta }_{1}} - {{\tau }_{1}}]}}^{ + }}} \right)\left( {M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right) + } \right.\left. {{{p}_{2}}M\left( {{{{[{{\beta }_{2}} - {{\tau }_{2}}]}}^{ + }}} \right)\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)} \right]}}{{{{p}_{1}}\left( {M{{\alpha }_{2}}\, + \,M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right)\, + \,{{p}_{2}}\left( {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}})} \right)\, + \,2\left[ {\int\limits_0^\infty {{{{\bar {G}}}_{2}}(x){{R}_{2}}(x)dx} \, + \,\int\limits_0^\infty {{{{\bar {G}}}_{1}}(x){{R}_{1}}(x)dx} } \right]}},$
${{m}_{2}} = \frac{{M{{\alpha }_{1}}M{{\alpha }_{2}} + M{{\alpha }_{1}}M({{\beta }_{2}} \wedge {{\tau }_{2}}) + M{{\alpha }_{2}}M({{\beta }_{1}} \wedge {{\tau }_{1}}) + M({{\beta }_{1}} \wedge {{\tau }_{1}})M({{\beta }_{2}} \wedge {{\tau }_{2}})}}{{2\left[ {M{{\alpha }_{1}} + M({{\beta }_{1}} \wedge {{\tau }_{1}}) + M{{\alpha }_{2}} + M({{\beta }_{2}} \wedge {{\tau }_{2}})} \right]}}.$

Следовательно, стационарные характеристики надежности укрупненной системы $S{\kern 1pt} :$ средняя стационарная наработка системы на отказ ${{T}_{ + }},$ среднее стационарное время восстановления системы ${{T}_{ - }},$ стационарный коэффициент готовности ${{K}_{{\text{Г}}}}$ имеют вид:

(26)
${{T}_{ + }} = \frac{{{{m}_{1}}{{\rho }_{1}} + {{m}_{2}}{{\rho }_{2}}}}{{{{\rho }_{0}}}},\,\,\,\,{{T}_{ - }} = {{m}_{0}},\,\,\,\,{{K}_{{\text{Г}}}} = \frac{{{{T}_{ + }}}}{{{{T}_{ + }} + {{T}_{ - }}}} = \frac{{{{m}_{1}}{{\rho }_{1}} + {{m}_{2}}{{\rho }_{2}}}}{{{{m}_{1}}{{\rho }_{1}} + {{m}_{2}}{{\rho }_{2}} + {{m}_{0}}{{\rho }_{0}}}}.$

Пример 2. В качестве примера использования формул (26) рассмотрим систему, описанную в примере 1. Результаты расчетов представлены в таблице 2.

Таблица 2.  

Характеристики надежности укрупненной системы

${{h}_{1}},$ ч ${{h}_{2}},$ ч ${{T}_{ - }}({{h}_{1}},{{h}_{2}}),$ ч ${{T}_{ + }}({{h}_{1}},{{h}_{2}}),$ ч ${{K}_{{\text{Г}}}}({{h}_{1}},{{h}_{2}})$
0 0 0.385 49.551 0.9923
0 0.7 0.241 102.274 0.99765
0.1 0.6 0.241 91.035 0.99736
0.2 0.5 0.238 84.365 0.99719
0.3 0.4 0.233 82.291 0.99717
0.4 0.3 0.228 85.172 0.99733
0.5 0.2 0.224 93.617 0.99762
0.6 0.1 0.219 108.690 0.99799
0.7 0 0.214 132.300 0.99839

Отметим, что результаты, полученные по укрупненной модели, совпадают с результатами для исходной модели.

ЗАКЛЮЧЕНИЕ

В данной работе построена полумарковская модель двухкомпонентной системы с поэлементным случайным мгновенно пополняемым резервом времени, которая может быть использована при моделировании систем энергетики различного назначения. Показано, что наличие резерва времени существенно влияет на характеристики надежности системы.

Используя алгоритм стационарного фазового укрупнения, разработанный в работах В.С. Королюка, А.Ф. Турбина, построена укрупненная полумарковская модель двухкомпонентной системы с поэлементным мгновенно пополняемым резервом времени. Найдены стационарные характеристики надежности укрупненной системы, проведено их сравнение с характеристиками исходной системы.

Результаты данной работы могут быть использованы при проектировании и эксплуатации систем энергетики при наличии резерва времени и решении оптимизационных задач, связанных с резервом времени.

В дальнейшем планируется построение полумарковских моделей многокомпонентных систем с поэлементным резервом времени и их применение для анализа надежности и эффективности систем энергетики.

Работа выполнена в рамках государственного задания Министерства образования и науки Российской Федерации (№ 1.10513.2018/11.12), при финансовой поддержке Российского фонда фундаментальных исследований (№ 18-01-00392а).

Список литературы

  1. Черкесов Г.Н. Надежность технических систем с временной избыточностью. М.: Сов. радио, 1974. 296 с.

  2. Креденцер Б.П. Прогнозирование надежности систем с временной избыточностью. Киев: Наук. думка, 1978. 240 с.

  3. Ushakov I.A. Probabilistic Reliability Models. San Diego: Wiley, 2012. 248 p.

  4. Копп В.Я., Обжерин Ю.Е., Песчанский А.И. Стохастические модели автоматизированных производственных систем с временным резервированием. Севастополь: Изд-во СевГТУ, 2000. 284 с.

  5. Obzherin Yu.E., Sidorov S.M., Fedorenko S.N. Analysis of the time reserve influence on the technological cell productivity // MATEC Web of Conferences, 2017. 129. 03009. 4 p.

  6. Yao D.D., Buzacott J.A. Flexible Manufacturing Systems: A Review of Analytical Models // Management Science. 1986. 32. P. 890–905.

  7. Yao D.D., Buzacott J.A. Models of Flexible Manufacturing Systems with Limited Local Buffers // International Journal of Production Research, 1986. 24. P. 107–118.

  8. Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. 2-е изд., перераб. и доп. Новосибирск: Наука. Сиб. отд-ние, 1989. 328 с.

  9. Надежность систем энергетики и их оборудования: в 4 т. / [Г.Н. Антонов и др.], под общ. ред. Ю.Н. Руденко. М.: Энергоатомиздат, 1994.

  10. Dekka A., Ghaffari R., Venkatesh B., Wu Bin A survey on energy storage technologies in power systems // IEEE Electrical Power and Energy Conference (EPEC), London, 2015, pp. 105–111.

  11. Cabeza L.F., Martorell I., Miró L., Fernández A.I., Barreneche C. Introduction to thermal energy storage (TES) systems // Editor(s): Luisa F. Cabeza. Advances in Thermal Energy Storage Systems, Woodhead Publishing, 2015. P. 1–28.

  12. Joseph A., Shahidehpour M. Battery storage systems in electric power systems // IEEE Power Engineering Society General Meeting, Montreal, Que. 2006 8 pp.

  13. Xu X., Bishop M., Oikarinen D. G., Hao C. Application and modeling of battery energy storage in power systems // CSEE Journal of Power and Energy Systems, V. 2. № 3. 2016. P. 82–90.

  14. Obzherin Yu.E., Sidorov S.M., Fedorenko S.N. Semi-Markov model of a technical system with the component-wise instantly replenished time reserve // MATEC Web of Conferences, 2018. 224. 04008. 7 p.

  15. Liu M., Li W., Wang C., Polis M. P., Wang L. Y., Li J. Reliability Evaluation of Large Scale Battery Energy Storage Systems // IEEE Transactions on Smart Grid, V. 8. № 6. 2017. P. 2733–2743.

  16. Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах надежности систем. Киев: Наук. думка, 1982. 236 с.

  17. Королюк В.С. Стохастические модели систем. Киев: Наук. думка, 1989. 208 с.

  18. Корлат А.Н., Кузнецов В.Н., Новиков М.М., Турбин А.Ф. Полумарковские модели восстанавливаемых систем и систем массового обслуживания. Кишинев: Штиинца, 1991. 276 с.

  19. Obzherin Y.E., Boyko E.G. Semi-Markov Models: Control of Restorable Systems with Latent Failures. London: Elsevier Academic Press, 2015. 212 p.

  20. Jansen J., Limnios N. (Eds.) Semi-Markov Models and Applications. The Netherlands: Kluwer Academic Publishers, 1999. 404 p.

  21. Grabski F. Semi-Markov Processes: Applications in System Reliability and Maintenance. Elsevier Science, 2014. 270 p.

  22. Limnios N., Oprisan G. Semi-Markov Processes and Reliability. New York: Springer Science+Business Media, 2001. 222 p.

  23. Korolyuk V.S., Limnios N. Stochastic Systems in Merging Phase Space. World Scientific, Imperial Coledge Press, 2005. 348 p.

  24. Кузнецов В.Н., Турбин А.Ф., Цатурян Г.Ж. Полумарковская модель восстанавливаемых систем. Киев: Ин-т математики АН УССР, 1981. 44 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал