Известия РАН. Энергетика, 2020, № 2, стр. 103-111

Индуктивность круговых контуров с произвольной ориентацией осей

Г. Н. Цицикян^1, *, А. И. Сенченко^1, **

¹ Филиал “ЦНИИ СЭТ” “ФГУП Крыловский государственный научный центр”
Санкт-Петербург, Россия

^* E-mail: george.20021940@mail.ru
^** E-mail: spb-1205@inbox.ru

Поступила в редакцию 26.12.2019
После доработки 13.01.2020
Принята к публикации 14.01.2020

DOI: 10.31857/S0002331020010112

Аннотация

Даны выражения для коэффициентов взаимной индукции и их градиентов посредством адаптации исходных выражений, содержащих сферические функции Лежандра и производные от них для трех конфигураций круговых контуров с пересекающимися осями, с параллельными осями и с осями, пересекающимися в произвольной точке, что дает возможность получения непосредственных оценок и численных результатов.

Ключевые слова: взаимная индуктивность, круговые контуры, электродинамические силы

В известных руководствах по расчету коэффициентов взаимной индукции круговых контуров с различным расположением от концентрических круговых контуров с пересекающимися осями до контуров с параллельными осями, записаны выражения для коэффициентов взаимной индукции [1, 2] в виде рядов, содержащих полиномы Лежандра и их производные. Оперирование такими рядами без подробных таблиц значений полиномов Лежандра и их производных представляется неудобным и возникает потребность в их адаптации с подстановкой развернутых выражений для полиномов Лежандра и их производных, известных по справочным руководствам и пособиям, например, в [3, 4]. В этом будет состоять одна из задач, решаемая в данной статье. В качестве другой задачи рассматривается возможность такой же адаптации и для производных от коэффициентов взаимоиндукции круговых контуров с целью оценки электродинамических взаимодействий, которые могут быть использованы в интересах прикладной электродинамики.

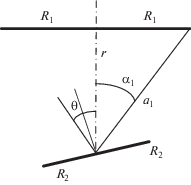
Начнем изложение вопроса с решения о взаимной индуктивности круговых контуров с пересекающимися осями [2] (рис. 1).

Рис. 1.

Два контура, оси которых пересекаются в центре меньшего из них.

В случае, когда $\delta = \frac{{{{R}_{2}}}}{{{{R}_{1}}}} < 0.5$ можно использовать выражение (5.49) в [2] в виде:

(1)

$\begin{gathered} M = \frac{\pi }{2}{{\mu }_{0}}{{\left( {\frac{{{{R}_{1}}}}{{{{a}_{1}}}}} \right)}^{2}}{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}^{2}}{{a}_{1}}\cos \theta \left[ {1 - \frac{1}{4}\frac{{R_{2}^{2}}}{{a_{1}^{2}}}P_{3}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right)\frac{{{{P}_{3}}\left( {\cos \theta } \right)}}{{\cos \theta }} + \frac{1}{8}\frac{{R_{2}^{4}}}{{a_{1}^{4}}}P_{5}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right)\frac{{{{P}_{5}}\left( {\cos \theta } \right)}}{{\cos \theta }} - } \right. \\ \left. { - \,\,\frac{5}{{64}}\frac{{R_{2}^{6}}}{{a_{1}^{6}}}P_{7}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right)\frac{{{{P}_{7}}\left( {\cos \theta } \right)}}{{\cos \theta }} + \ldots + } \right]. \\ \end{gathered} $

Применяя формулы 840 и 845 [5] для полиномов Лежандра и их первых производных, где

${{P}_{3}}\left( {\cos \theta } \right) = \frac{1}{2}\cos \theta \left( {5\cos \theta - 3} \right),\,\,\,\,{{P}_{5}}\left( {\cos \theta } \right) = \frac{1}{8}\cos \theta \left( {63{{{\cos }}^{4}}\theta - 70{{{\cos }}^{2}}\theta + 15} \right),$

${{P}_{7}}\left( {\cos \theta } \right) = \frac{1}{{16}}\cos \theta \left( {429{{{\cos }}^{6}}\theta - 693{{{\cos }}^{4}}\theta + 315{{{\cos }}^{2}}\theta - 35} \right),$

$P_{3}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right) = \frac{3}{2}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 1} \right],\,\,\,\,P_{5}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right) = \frac{{15}}{8}\left[ {21{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} - 14{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} + 1} \right],$

$P_{7}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right) = \frac{7}{{16}}\left[ {429{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{6}} - 495{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} + 135{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 5} \right],$

перепишем (1) в виде:

(2)

$\begin{gathered} M = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{1}^{2}R_{2}^{2}}}{{a_{1}^{3}}}\left\{ {\cos \theta - \frac{3}{8}\frac{{R_{2}^{2}}}{{a_{1}^{2}}}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}}\, - \,1} \right]{{P}_{3}}{\kern 1pt} \left( {\cos \theta } \right)\, + \,\frac{{15}}{{64}}\frac{{R_{2}^{4}}}{{a_{1}^{4}}}\left[ {21{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}}\, - \,14{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}}\, + \,1} \right]{\kern 1pt} {{P}_{5}}\left( {\cos \theta } \right) - } \right. \\ \left. { - \,\,\frac{{35}}{{1024}}\frac{{R_{2}^{6}}}{{a_{1}^{6}}}\left[ {429{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{6}} - 495{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} + 135{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 5} \right]{{P}_{7}}\left( {\cos \theta } \right) \ldots } \right\} = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{1}^{2}R_{2}^{2}}}{{a_{1}^{3}}} \times \\ \times \,\,\cos \theta \left\{ {1 - \frac{3}{{16}}\frac{{R_{2}^{2}}}{{a_{1}^{2}}}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 1} \right]\left( {5{{{\cos }}^{2}}\theta - 3} \right) + \frac{{15}}{{512}}\frac{{R_{2}^{4}}}{{a_{1}^{4}}}\left[ {21{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} - 14{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} + 1} \right] \times } \right. \\ \times \,\,\left( {63{{{\cos }}^{4}}\theta - 70{{{\cos }}^{2}}\theta + 15} \right) - \frac{{35}}{{16{\kern 1pt} {\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{a_{1}^{6}}}\left[ {429{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{6}} - 495{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} + 135{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 5} \right] \times \\ \left. {_{{_{{_{{_{{_{{}}}}}}}}}}^{{^{{^{{^{{}}}}}}}} \times \,\,\left( {429{{{\cos }}^{6}}\theta - 693{{{\cos }}^{4}}\theta + 315{{{\cos }}^{2}}\theta - 35} \right) \ldots } \right\}. \\ \end{gathered} $

При $\theta = \frac{\pi }{2}$ имеем 0, а при $\theta = 0$ в соответствии с (2) (рис. 1)

(3)

$\begin{gathered} {{\left. M \right|}_{{\theta = 0}}} = \frac{\pi }{2}{{\mu }_{0}}\frac{{{{R}_{1}}^{2}{{R}_{2}}^{2}}}{{{{a}_{1}}^{3}}}\left\{ {1 - \frac{3}{8}\frac{{{{R}_{2}}^{2}}}{{{{a}_{1}}^{2}}}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 1} \right] + \frac{{15}}{{64}}\frac{{{{R}_{2}}^{4}}}{{{{a}_{1}}^{4}}}\left[ {21{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} - 14{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} + 1} \right] - } \right. \\ \left. { - \,\,\frac{{35}}{{1024}}\frac{{{{R}_{2}}^{6}}}{{{{a}_{1}}^{6}}}\left[ {429{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{6}} - 495{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}} + 135{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 5} \right] \ldots } \right\}. \\ \end{gathered} $

При $r = 0$ и ${{a}_{1}} = {{R}_{1}}$ (рис. 1) получаем из (2)

(4)

$\begin{gathered} M\left( {r = 0,\,\,{{a}_{1}} = {{R}_{1}}} \right) = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{2}^{2}}}{{{{R}_{1}}}}\cos \theta \left\{ {1 + \frac{3}{{16}}\frac{{R_{2}^{2}}}{{R_{1}^{2}}}\left( {5{{{\cos }}^{2}}\theta - 3} \right) + } \right. \\ + \,\,\frac{{15}}{{512}}\frac{{R_{2}^{4}}}{{R_{1}^{4}}}\left( {63{{{\cos }}^{4}}{\kern 1pt} \theta - 70{{{\cos }}^{2}}{\kern 1pt} \theta + 15} \right)\, + \,\left. {\frac{{175}}{{16{\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{R_{1}^{6}}}\left( {429{{{\cos }}^{6}}{\kern 1pt} \theta - 693{{{\cos }}^{4}}{\kern 1pt} \theta + 315{{{\cos }}^{2}}{\kern 1pt} \theta - 35} \right)...} \right\}. \\ \end{gathered} $

Можно показать, что ряд (4) при $r = 0$ и ${{a}_{1}} = {{R}_{1}}$ не будет отличаться от ряда (5–37) в [2], если в него подставить выражения для ${{P}_{1}}\left( {\cos \theta } \right) = \cos \theta ,\,\,{{P}_{3}}\left( {\cos \theta } \right),\,\,{{P}_{5}}\left( {\cos \theta } \right),\,\,{{P}_{7}}\left( {\cos \theta } \right)$ и т.д. так, как это осуществлялось при выводе выражения (2).

Внося $\cos \theta $ в фигурные скобки в (4), для случая $r = 0$ и ${{a}_{1}} = {{R}_{1}},$ получим

$\begin{gathered} \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{2}^{2}}}{{{{R}_{1}}}}\left\{ {\cos \theta + \frac{3}{{16}}\frac{{R_{2}^{2}}}{{R_{1}^{2}}}\left( {5{{{\cos }}^{3}}\theta - 3\cos \theta } \right) + \frac{{15}}{{512}}\frac{{R_{2}^{4}}}{{R_{1}^{4}}}\left( {63{{{\cos }}^{5}}\theta - 70{{{\cos }}^{3}}\theta + 15\cos \theta } \right) + } \right. \\ + \,\,\left. {\frac{{175}}{{16{\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{R_{1}^{6}}}\left( {429{{{\cos }}^{7}}\theta - 693{{{\cos }}^{5}}\theta + 315{{{\cos }}^{3}}\theta - 35\cos \theta } \right) \ldots } \right\} \\ \end{gathered} $

и, осуществляя дифференцирование по θ, найдем:

(5)

$\begin{gathered} \frac{{dM}}{{d\theta }}\, = \,\frac{\pi }{2}{{\mu }_{0}}\frac{{R_{2}^{2}}}{{R_{1}^{{}}}}\left( { - \sin \theta } \right)\left\{ {1\, + \,\frac{3}{{16}}\frac{{R_{2}^{2}}}{{R_{1}^{2}}}\left( {5\, \times \,3{\kern 1pt} {{{\cos }}^{2}}{\kern 1pt} \theta \, - \,3} \right) + \frac{{15}}{{512}}\frac{{R_{2}^{4}}}{{R_{1}^{4}}}\left( {63\, \times \,5{\kern 1pt} {{{\cos }}^{4}}{\kern 1pt} \theta \, - \,70\, \times \,3{{{\cos }}^{2}}{\kern 1pt} \theta + 15} \right) + } \right. \\ + \,\,\left. {\frac{{175}}{{16{\kern 1pt} {\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{R_{1}^{6}}}\left( {429 \times 7{{{\cos }}^{6}}\theta - 693 \times 5{{{\cos }}^{4}}\theta + 315 \times 3{{{\cos }}^{2}}\theta - 35} \right) \ldots } \right\} = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{2}^{2}}}{{R_{1}^{{}}}}\left( { - \sin \theta } \right) \times \\ \times \,\,\left\{ {1 + \frac{9}{{16}}\frac{{R_{2}^{2}}}{{R_{1}^{2}}}\left( {5{{{\cos }}^{2}}\theta - 1} \right) + \frac{{225}}{{512}}\frac{{R_{2}^{4}}}{{R_{1}^{4}}}\left( {21{{{\cos }}^{4}}\theta - 14{{{\cos }}^{2}}\theta + 1} \right) + \frac{{1225}}{{16{\kern 1pt} {\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{R_{1}^{6}}}} \right. \times \\ \times \left. {_{{_{{_{{}}}}}}^{{^{{^{{}}}}}}\left( {429{{{\cos }}^{5}}\theta - 495{{{\cos }}^{3}}\theta + 135{{{\cos }}^{2}}\theta - 5} \right) \ldots } \right\}. \\ \end{gathered} $

Из (5) при $\theta = \frac{\pi }{2}$ получим:

(6)

$\frac{{dM}}{{d\theta }}\left| {_{{\theta = \frac{\pi }{2}}}} \right. = - \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{2}^{2}}}{{R_{1}^{{}}}}\left\{ {1 - \frac{9}{{16}}\frac{{R_{2}^{2}}}{{R_{1}^{2}}} + \frac{{225}}{{512}}\frac{{R_{2}^{4}}}{{R_{1}^{4}}} - \frac{{6125}}{{16{\kern 1pt} {\kern 1pt} 384}}\frac{{R_{2}^{6}}}{{R_{1}^{6}}} \ldots } \right\}.$

Следует отметить, что взаимодействие концентрических круговых контуров с током лежит в основе принципа действия электродинамического ваттметра.

При умножении (5) и (6) на токи, протекающие в контурах, получим выражения для вращающих моментов. Наконец, ограничиваясь первыми тремя членами, запишем производную $\frac{{dM}}{{d\theta }}$ для (рис. 1) на основании (2):

(7)

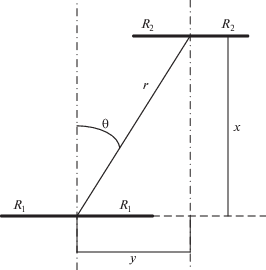
$\begin{gathered} \frac{{dM}}{{d\theta }}\, = \,\frac{\pi }{2}{{\mu }_{0}}\frac{{R_{1}^{2}R_{2}^{2}}}{{a_{1}^{3}}}\left( { - \sin \theta } \right){\kern 1pt} \left\{ {1\, - \,\frac{9}{{16}}\frac{{R_{2}^{2}}}{{a_{1}^{2}}}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}}\, - \,1} \right]\left( {5{{{\cos }}^{2}}{\kern 1pt} \theta - 1} \right) + \frac{{225}}{{512}}\frac{{R_{2}^{4}}}{{a_{1}^{4}}}\left[ {21{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{4}}\, - \,14{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}}\, + \,1} \right]} \right. \times \\ \left. { \times _{{_{{_{{}}}}}}^{{^{{^{{^{{}}}}}}}}\left( {21{{{\cos }}^{4}}\theta - 14{{{\cos }}^{2}}\theta + 1} \right)...} \right\}. \\ \end{gathered} $

В следующем примере изберем конфигурацию контуров с параллельными осями с радиусами ${{R}_{1}}$ и ${{R}_{2}}$ (рис. 2).

Рис. 2.

Контуры с параллельными осями.

Для этого случая известно выражение для М в виде, предполагающим однократное интегрирование, предложенное еще Гровером [6], а затем приводимое в более поздних публикациях, например, в [7, 8]. Это выражение в [8] записано с учетом обозначений рис. 2 в виде:

(8)

$M = \frac{{{{\mu }_{0}}}}{\pi }\sqrt {{{R}_{1}}{{R}_{2}}} \int\limits_0^\pi {\frac{{\left( {1 - \frac{y}{{{{R}_{2}}}}\cos \vartheta } \right)\phi (k)}}{{{{\nu }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} d\vartheta ,$

где

(9)

$\phi (k) = \left( {\frac{2}{k} - k} \right)K\left( k \right) - \frac{2}{k}E\left( k \right) = \frac{2}{k}\left[ {\left( {1 - \frac{{{{k}^{2}}}}{2}} \right)K\left( k \right) - E\left( k \right)} \right].$

(10)

${{k}^{2}} = \frac{{4\frac{{{{R}_{2}}}}{{{{R}_{1}}}}\nu }}{{{{{\left( {1 + \frac{{{{R}_{2}}}}{{{{R}_{1}}}}\nu } \right)}}^{2}} + {{{\left( {\frac{x}{{{{R}_{1}}}}} \right)}}^{2}}}} = \frac{{4{{R}_{1}}{{R}_{2}}\nu }}{{{{{\left( {{{R}_{1}} + {{R}_{2}}\nu } \right)}}^{2}} + {{x}^{2}}}},$

где

(11)

$\nu = {{\left( {1 + \frac{{{{y}^{2}}}}{{R_{2}^{2}}} - 2\frac{y}{{{{R}_{2}}}}\cos \vartheta } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

При $x = 0$ и $y = 0,$ и, следовательно, $\nu = 1,0$

(12)

${{k}^{2}}\left| {_{{x = 0,y = 0}}} \right. = \frac{{4{{R}_{1}}{{R}_{2}}}}{{{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}}}}.$

Тогда выражение (8) оказывается равным:

(13)

$M = {{\mu }_{0}} \times 2{{k}^{{ - 1}}}{{\left( {{{R}_{1}}{{R}_{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left[ {\left( {1 - \frac{{{{k}^{2}}}}{2}} \right)K\left( k \right) - E\left( k \right)} \right],$

как это и записано в [9].

Приступая к записи производной М по координате x, заметим, что в отличии от ${{k}^{2}}$ безразмерная величина ν не зависит от x. Учитывая (8) и (10), имеем:

(14)

$\frac{{dM}}{{dx}} = \frac{{{{\mu }_{0}}}}{\pi }{{\left( {{{R}_{1}}{{R}_{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\int\limits_0^\pi {\frac{{1 - \frac{y}{{{{R}_{2}}}}\cos \theta }}{{{{\nu }^{{3/2}}}}}\frac{{d\phi (k)}}{{dk}}\frac{{dk}}{{dx}}d\vartheta } ,$

где

(15)

$k = \frac{{2{{{\left( {{{R}_{1}}{{R}_{2}}\nu } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}\nu } \right)}}^{2}} + {{x}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$

Используя выражение для производной $\phi (k)$ по k, записываемой в виде

(16)

$\frac{{d\phi (k)}}{{dk}} = {{k}^{{ - 2}}}\left( {\frac{{2 - {{k}^{2}}}}{{1 - {{k}^{2}}}}E - 2K} \right),$

а также производную по k от x в соответствии с (15):

$\begin{gathered} \frac{{dk}}{{dx}} = 2{{\left( {{{R}_{1}}{{R}_{2}}\nu } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( { - \frac{1}{2}} \right){{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}\nu } \right)}}^{2}} + {{x}^{2}}} \right]}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}2x = \\ = - 2{{\left( {{{R}_{1}}{{R}_{2}}\nu } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}x{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}\nu } \right)}}^{2}} + {{x}^{2}}} \right]}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = - \frac{{x{{k}^{3}}}}{{4\left( {{{R}_{1}}{{R}_{2}}\nu } \right)}}, \\ \end{gathered} $

получим для $\frac{{dM}}{{dx}}$ следующее выражение

(17)

$\begin{gathered} \frac{{dM}}{{dx}} = - \frac{{{{\mu }_{0}}x}}{{4\pi {{{\left( {{{R}_{1}}{{R}_{2}}} \right)}}^{{1/2}}}}}\int\limits_0^\pi {\frac{{1 - \frac{y}{{{{R}_{2}}}}\cos \theta }}{{{{\nu }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}k\left( {\frac{{2 - {{k}^{2}}}}{{1 - {{k}^{2}}}}E - 2K} \right)d\vartheta } = \\ = - \frac{{{{\mu }_{0}}x}}{{2\pi }}\int\limits_0^\pi {\frac{{1 - \frac{y}{{{{R}_{2}}}}\cos \theta }}{{{{\nu }^{2}}}}{{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}\nu } \right)}}^{2}} + {{x}^{2}}} \right]}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \left( {\frac{{2 - {{k}^{2}}}}{{1 - {{k}^{2}}}}E - 2K} \right)d\vartheta . \\ \end{gathered} $

При $y = 0$ и $\nu = 1,$ найдем:

(18)

$\frac{{dM}}{{dx}} = - \frac{{{{\mu }_{0}}}}{2}\frac{x}{{{{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}} + {{x}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left( {\frac{{2 - {{k}^{2}}}}{{1 - {{k}^{2}}}}E - 2K} \right)$

(19)

$k\left| {_{{y = 0}}} \right. = \frac{{2{{{\left( {{{R}_{1}}{{R}_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}} + {{x}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$

В этой связи следует отметить, что в работе [10] в формуле (П. 2–3) допущены опечатки: для исправления квадратную скобку в знаменателе следует дополнить показателем степени 1/2, а в формуле (П. 2–4) для ${{k}^{2}}$ в знаменателе минус должен быть заменен на плюс.

Выражение (18) можно видоизменить и записать с заменой x на h в виде

(20)

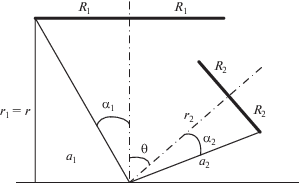
$\frac{{dM}}{{dh}} = \frac{{{{\mu }_{0}}h}}{{{{{\left[ {{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}} + {{h}^{2}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left( {K - \frac{{2 - {{k}^{2}}}}{{2\left( {1 - {{k}^{2}}} \right)}}E} \right) = - \frac{{{{\mu }_{0}}kh}}{{4{{{\left( {{{R}_{1}}{{R}_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left( {\frac{{2 - {{k}^{2}}}}{{1 - {{k}^{2}}}}E - 2K} \right)$

в полном согласии с [11].

Рассмотрим теперь случай, когда имеются два контура, оси которых пересекаются в произвольной точке в соответствии с (рис. 3).

Рис. 3.

Два контура, оси которых пересекаются в произвольной точке.

Этой конфигурации соответствуют формулы для коэффициента взаимной индукции М, записанные в [1], а также в [9] и в [2].

При ${{\alpha }_{2}} = \frac{\pi }{2}$ и ${{a}_{2}} = {{R}_{2}}$ будем иметь случай, отвечающий (рис. 1).

В соответствии с [2] (формула 5–50) коэффициент взаимной индукции можно представить в виде (рис. 3):

(21)

$M = {{\mu }_{0}}\pi \frac{{{{R}_{1}}^{2}{{R}_{2}}^{2}}}{{{{a}_{1}}^{3}}}{{\sum\limits_{n = 1}^\infty {\left( {\frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)} }^{{n - 1}}}\frac{{P_{n}^{'}\left( {\cos {{\alpha }_{1}}} \right)P_{n}^{'}\left( {\cos {{\alpha }_{2}}} \right){{P}_{n}}\left( {\cos \theta } \right)}}{{n\left( {n + 1} \right)}}.$

Используем те же приемы, что и при выводе выражения (2), позволяющие развернуть полиномы Лежандра ${{P}_{n}}$ и $P_{n}^{'}.$

Раскрывая ряд (21) с учетом формул (840) и (845) [5], запишем (рис. 3):

(22)

$\begin{gathered} M = {{\mu }_{0}}\pi \frac{{R_{1}^{2}R_{2}^{2}}}{{2a_{1}^{3}}}\left[ {\cos \theta + \frac{3}{2}\frac{{{{a}_{2}}}}{{{{a}_{1}}}}\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}\left( {3{{{\cos }}^{2}}\theta - 1} \right) + \frac{3}{{16}}{{{\left( {\frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)}}^{2}}\left( {5{{{\cos }}^{2}}{{\alpha }_{1}} - 1} \right)} \right. \times \\ \times \,\,\left( {5{{{\cos }}^{2}}{{\alpha }_{2}} - 1} \right)\cos \theta \left( {5{{{\cos }}^{2}}\theta - 3} \right) + \frac{5}{{64}}{{\left( {\frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)}^{3}}\cos {{\alpha }_{1}}\left( {7{{{\cos }}^{2}}{{\alpha }_{1}} - 3} \right)\cos {{\alpha }_{2}} \times \\ \times \,\,\left( {7{{{\cos }}^{2}}{{\alpha }_{2}} - 3} \right)\left( {35{{{\cos }}^{4}}\theta - 30{{{\cos }}^{2}}\theta + 3} \right) + \frac{{15}}{{512}}{{\left( {\frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)}^{4}}\left( {21{{{\cos }}^{4}}{{\alpha }_{1}} - 14{{{\cos }}^{2}}{{\alpha }_{1}} + 1} \right) \times \\ \left. { \times _{{^{{^{{^{{^{{}}}}}}}}}}^{{^{{^{{^{{}}}}}}}}\left( {21{{{\cos }}^{4}}{{\alpha }_{2}} - 14{{{\cos }}^{2}}{{\alpha }_{2}} + 1} \right)\cos \theta \left( {63{{{\cos }}^{4}}\theta - 70{{{\cos }}^{2}}\theta + 15} \right) \ldots } \right]. \\ \end{gathered} $

При ${{\alpha }_{2}} = \frac{\pi }{2}$ , ${{a}_{2}} = {{R}_{2}}$ и $\cos {{\alpha }_{2}} = 0$ из (22) вытекает выражение, совпадение с (2):

$\begin{gathered} M\left| {_{{\cos {{\alpha }_{2}} = 0}}} \right. = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{1}^{2}R_{2}^{2}}}{{a_{1}^{3}}}\cos \theta \left[ {1 - \frac{3}{{16}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{2}}\left( {5{{{\cos }}^{2}}{{\alpha }_{1}} - 1} \right)\left( {5{{{\cos }}^{2}}\theta - 3} \right) + } \right. \\ \left. { + \,\,\frac{{15}}{{512}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{4}}\left( {21{{{\cos }}^{4}}{{\alpha }_{1}} - 14{{{\cos }}^{2}}{{\alpha }_{1}} + 1} \right)\left( {63{{{\cos }}^{4}}\theta - 70{{{\cos }}^{2}}\theta + 15} \right) - \ldots } \right], \\ \end{gathered} $

где $\cos {{\alpha }_{1}} = \frac{r}{{{{a}_{1}}}},$ что также служит подтверждением правильности формулы (22).

Теперь можно проверить выражение (2.4’) работы [1] на предмет соответствия формуле (2). Формула (2.4’) в наших обозначениях может быть записана в виде (рис. 1):

$M = \frac{{{{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{2}{{\mu }_{0}}{{R}_{2}}{{\left( {\frac{{{{R}_{1}}}}{{{{a}_{1}}}}} \right)}^{2}}\sum\limits_{n = 1}^\infty {{{{\left( { - 1} \right)}}^{n}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{{2n + 1}}}\frac{{Г\left( {n + \frac{1}{2}} \right)}}{{\left( {n + 1} \right)!}}P_{{2n + 1}}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right){{P}_{{2n + 1}}}\left( {\cos \theta } \right)} ,$

где $Г\left( {n + \frac{1}{2}} \right)$ – гамма-функция.

Здесь, в отличие от (2.4’), индекс суммирования по n взят от нуля.

По первым двум членам имеем, таким образом, выражение:

$M = \frac{\pi }{2}{{\mu }_{0}}\frac{{R_{1}^{2}R_{2}^{2}}}{{a_{1}^{3}}}\cos \theta \left\{ {1 - \frac{3}{{16}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{2}}\left[ {5{{{\left( {\frac{r}{{{{a}_{1}}}}} \right)}}^{2}} - 1} \right]\left[ {5{{{\cos }}^{2}}\theta - 3} \right] \ldots } \right\},$

совпадающее с (2), откуда и вытекает необходимость изменения индекса суммирования от нуля и исправления явной опечатки в (2.4’), где вместо $\mu _{2}^{2}$ должно стоять $\mu _{1}^{2},$ что также подтверждается записью последующей формулы (2.5) в [1].

Осуществляя дифференцирование выражения (22) по $\theta $ с учетом только первых трех членов будем иметь:

(23)

$\begin{gathered} \frac{{dM}}{{d\theta }} = {{\mu }_{0}}\pi \frac{{R_{1}^{2}R_{2}^{2}}}{{2a_{1}^{3}}}\left( { - \sin \theta } \right)\left[ {1 + 9\frac{{{{a}_{2}}}}{{{{a}_{1}}}}\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}\cos \theta + \frac{9}{{16}}{{{\left( {\frac{{{{a}_{2}}}}{{{{a}_{1}}}}} \right)}}^{2}} \times } \right. \\ \left. { \times _{{^{{^{{^{{^{{}}}}}}}}}}^{{^{{^{{^{{}}}}}}}}\left( {5{{{\cos }}^{2}}{{\alpha }_{1}} - 1} \right)\left( {5{{{\cos }}^{2}}{{\alpha }_{2}} - 1} \right)\left( {{{{\cos }}^{2}}\theta - 1} \right)} \right]. \\ \end{gathered} $

При ${{\alpha }_{2}} = \frac{\pi }{2}$ и ${{a}_{2}} = {{R}_{2}}$

(24)

$\frac{{dM}}{{d\theta }}\left| {_{{{{\alpha }_{2}} = \frac{\pi }{2},{{a}_{2}} = {{R}_{2}}}}} \right. = {{\mu }_{0}}\pi \frac{{R_{1}^{2}R_{2}^{2}}}{{2a_{1}^{3}}}\left( { - \sin \theta } \right)\left[ {1 - \frac{9}{{16}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{2}}\left( {5{{{\cos }}^{2}}{{\alpha }_{1}} - 1} \right)\left( {5{{{\cos }}^{2}}\theta - 1} \right) \ldots } \right].$

Формулу для $\frac{{dM}}{{d\theta }}$ на основании (2.5) литературы [1], но без учета знака, можно записать, сохраняя суммирование от $n = 0$, следующим образом:

(25)

$\frac{{dM}}{{d\theta }} = {{\mu }_{0}}{{\frac{\pi }{2}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{R}_{2}}\sin \theta {{\left( {\frac{{{{R}_{1}}}}{{{{a}_{1}}}}} \right)}^{2}}\sum\limits_{n = 0}^\infty {{{{\left( { - 1} \right)}}^{n}}{{{\left( {\frac{{{{R}_{2}}}}{{{{a}_{1}}}}} \right)}}^{{2n + 1}}}\frac{{Г\left( {n + \frac{1}{2}} \right)}}{{\left( {n + 1} \right)!}}} P_{{2n + 1}}^{'}\left( {\frac{r}{{{{a}_{1}}}}} \right)P_{{2n + 1}}^{'}\left( {\cos \theta } \right),$

которая должна совпадать с выражением (24).

Проверка показывает, что при суммировании от $n = 0$ предыдущее утверждение действительно имеет место.

Под конец приведем численный пример определения взаимной индуктивности для случаев, когда ${{\alpha }_{1}} = \frac{\pi }{3}$ и $\cos {{\alpha }_{1}} = \frac{1}{2} = \frac{r}{{{{a}_{1}}}},$ (рис. 1), но в одном из них $\theta = \frac{\pi }{3},$ а в другом $\theta = 0$ и $\frac{{{{R}_{2}}}}{{{{a}_{1}}}} = 0.5.$ Тогда по выражению (2) для индуктивности будем иметь величину $\frac{\pi }{2}{{\mu }_{0}}{{R}_{1}} \times 0.107,$ а по формуле (3) получим величину $\frac{\pi }{2}{{\mu }_{0}}{{R}_{1}} \times 0.2071,$ т.е. практически в два раза большую, что и должно иметь место по физическим соображениям.

ЗАКЛЮЧЕНИЕ

Получены развернутые выражения для коэффициентов взаимной индукции и их производных для круговых контуров с различным расположением осей (пересекающиеся в центре меньшего из них, параллельные, пересекающиеся в произвольной точке), свободных от полиномов Лежандра и их производных, что открывает возможность непосредственного получения соответствующих оценок и численных результатов. Последние могут быть весьма полезны при решении ряда прикладных вопросов.

Список литературы

Snow Chester. Formulas for Computing Capacitance and Inductance. Washington National Bureau of Standards, Circular 544, Dec. 1954.
Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. Справочная книга. Энергоатомиздат. Ленинградское отделение, 1986, 488 с.
Белоусов С.Л. Таблицы нормированных присоединенных полиномов Лежандра. Изд. АН СССР, М., 1956.
Справочник по специальным функциям с формулами, графиками и математическими таблицами. Под ред. Абрамовица М. и Стиган И. Москва, “Наука”, ГРФМЛ, 1979.
Двайт Г.Б. Таблицы интегралов и другие математические формулы. Изд. “Наука” ГРФМЛ, Москва, 1977, 228 с.
Grover F.W. Inductance calculations. Working formulas and tables. D. VAN Nostrand company, Inc.: New York. 1947.
Akyel C., Babic S.I., and Mahmoudi M.-M. Mutual Inductance calculation for Non-coaxial circular air coils with paralles axes. Progress in Electromagnetics Research, PIER91, 2009, 287–301.
Ren Young. Magnetic force calculation between Misaligned Coils for a superconducting Magnet. IEEE Transition on applied superconductivity, vol. 20, № 6, 2010. pp. 2350–2353.
Смайт В. Электростатика и электродинамика. Издательство иностранной литературы. Москва, 1954, 606 с.
Цицикян Г.Н. О коэффициентах взаимной индукции и силах взаимодействия круговых коаксиальных контуров. Электричество, 2019, № 6, С. 59–65.
Цицикян Г.Н. О взаимной индуктивности и электродинамических силах взаимодействия коаксиальных контуров. Изв. РАН. Энергетика. 2018, № 4. С. 40–45.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал