Известия РАН. Энергетика, 2020, № 4, стр. 3-10
Энергоэффективные поверхности с многорядными наклонными овально-траншейными лунками для воздушных конденсаторов
С. А. Исаев 1, *, А. И. Леонтьев 2, О. О. Мильман 3, 6, Д. В. Никущенко 4, И. А. Попов 5
1 Санкт-Петербургский государственный университет гражданской авиации
Санкт-Петербург, Россия
2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
3 ЗАО “Турбокон”
Калуга, Россия
4 Санкт-Петербургский государственный морской технический университет
Санкт-Петербург, Россия
5 Казанский национальный исследовательский технический университет
им. А.Н. Туполева – Казанский авиационный институт
Казань, Россия
6 Калужский Государственный университет им. К.Э. Циолковского
Калуга, Россия
* E-mail: isaev3612@yandex.ru
Поступила в редакцию 01.06.2020
После доработки 05.06.2020
Принята к публикации 11.06.2020
Аннотация
Численно исследуется интенсификация ламинарного теплообмена в межреберном пространстве воздушного конденсатора с помощью пакета многорядных овально-траншейных лунок с углом наклона к набегающему потоку 45° при Re = 1000. Для участка узкого канала высотой 1, длиной 80 и шириной 4 в качестве предпочтительного вариант выбран однорядный пакет из 31 лунки глубиной 0.25. Для него достигнуто почти 2-кратное увеличение теплоотдачи при 46% росте гидравлических потерь в сравнении с плоскопараллельным каналом.
ВВЕДЕНИЕ
Интенсификация теплообмена в ламинарном потоке в межреберном пространстве воздушных конденсаторов [1] является важной практической и научной проблемой. Для ее решения используются поверхностные вихревые генераторы [2] в форме наклонных овально-траншейных лунок (ОТЛ), размещенных на стенках узких каналов [3–9]. Их использование позволяет значительно улучшить теплогидравлические характеристики облуненных каналов, причем возрастание тепловой эффективности опережает по темпу роста увеличение гидравлических потерь. Компоновка ОТЛ состоит из двух сферических сегментов – половинок исходной сферической лунки, соединенных длинной цилиндрической траншеей. Удлинение ОТЛ имеет существенное значение. Установлено, что целесообразно выбирать длину ОТЛ порядка 4 (по отношению к ширине). Угол наклона лунки к набегающему потоку задается равным 45°. Глубина является одним из важных факторов достижения высоких теплогидравлических характеристик облуненных узких каналов. Наилучшие теплотехнические характеристики получаются при глубинах ОТЛ 0.3–0.4 высоты канала. Число Рейнольдса, основанное на среднемассовой скорости потока и высоте канала, задается равным 1000. При проектировании луночного рельефа важную роль играет расположение и плотность упаковки ОТЛ. В последних исследованиях [6–9] были рассмотрены однорядные рельефы с коридорным расположением и разреженной упаковкой лунок на участке стабилизации конвективного теплообмена в облуненном канале. Рассчитаны предельные асимптотические характеристики конвективного теплообмена в периодической секции канала с наклонной ОТЛ, расположенной в центре участка нагретой стенки. На проточных границах секции ставятся периодические граничные условия. Поставленная задача решается с использованием процедур коррекции давления и среднемассовой температуры. Обнаружены эффекты 1.5-кратного ускорения ламинарного течения и почти 2-кратного увеличения теплопередачи.
ПОСТАНОВКА ЗАДАЧИ. МЕТОД РЕШЕНИЯ. РАСЧЕТНЫЕ СЕТКИ
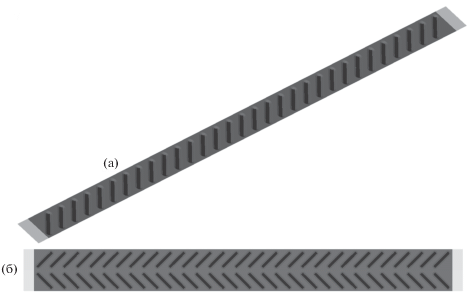
Численно рассматривается ускорение ламинарного потока воздуха (Pr = 0.7) и интенсификация отрывного течения и теплообмена при заданном числе Рейнольдса (Re = 1000) на длинном участке облуненного канала, который имитирует межреберное пространство воздушного конденсатора. Узкий канал имеет длину 84, ширину 4 и высоту 1. В контрольной секции длиной 80 на нагретой стенке располагаются однорядные пакеты, набранные из 20 и 31 ОТЛ с углом наклона 45° к продольной оси канала. Ширина лунки равна 1, длина – 4.5, глубина Δ в базовом варианте – 0.25, радиус скругления кромки – 0.2 (рис. 1а). Длины входного и выходного плоскопараллельного участка канала перед и за облуненной секцией канала выбраны равными 2. Шаги между центрами лунок равны 4 и 2.53 как и в [10]. Плотность лунок на контрольном участке изменяется от малых величин (0.26) до умеренных (0.51) в сравнении с рекомендуемой плотностью нанесения сферических лунок [2]. На боковых границах канала задаются условия симметрии, на входе в канал ламинарный воздушный поток равномерный, в выходном сечении канала выполняются мягкие граничные условия, а на стенках канала – условие прилипания. Вводится система декартовых координат x, y, z с центром на нижней стенке в начале облуненной секции канала. Ось x ориентирована вдоль, ось y направлена вверх, а ось z – поперек канала. Все линейные размеры относятся к высоте канала. Декартовые составляющие скорости u, v, w и число Re определяются по среднемассовой скорости потока. В качестве характерной выбрана комнатная температура Т = 293 К. Стенки канала изотермические и перепад температуры незначительный: на нижней стенке с лунками Т = 1.034 и на верхней стенке Т = 1.
Рис. 1.
Узкий канал с 31 ОТЛ (а) и зигзагообразные коридорные пакеты ОТЛ на ребре воздушного конденсатора (б). Верхняя стенка канала не показана.
Система стационарных уравнений Навье–Стокса для несжимаемой среды и уравнение энергии решаются с использованием факторизованного метода конечного объема второго порядка аппроксимации на многоблочных расчетных перекрывающихся сетках различного масштаба [2–11]. Многоблочная вычислительная технология (MBT) заключается в использовании разномасштабных структурированных сеток с перекрытием, согласованных с геометрией канала. В двух рядах граничных ячеек каждой из перекрывающихся сеток параметры определяются с использованием линейной интерполяции [2, 11]. В [12] показано, что такой подход эквивалентен применению адаптивных неструктурированных сеток, но требует существенно меньших вычислительных ресурсов. Он также обеспечивает надлежащую точность без уточнения сеток, поскольку автоматически разрешает все значимые гидродинамические и теплофизические особенности. Пересчеты из сетки в сетку с помощью линейной интерполяции являются источником погрешностей. Однако, как показали тестовые расчеты установившегося циркуляционного течения в каверне с подвижной крышкой [12], величины неопределенностей оказываются вполне приемлемыми. Характерной особенностью использованного алгоритма является основанная на концепции расщепления по физическим процессам [13] процедура коррекции давления SIMPLEC [14] с монотонизацией по Рхи–Чоу для заданного центрированного расчетного шаблона [15, 16]. Представление конвективных членов в неявной части уравнения переноса по схеме против потока с односторонними разностями позволяет повысить устойчивость вычислительной процедуры. Для снижения влияния искусственной диффузии при расчете отрывных течений аппроксимация конвективных членов в явной части линеаризованных исходных уравнений проводится с использованием одномерной квадратичной противопоточной схемы Леонарда [17]. Алгебраические уравнения решаются методом сопряженных градиентов BiCGSTAB [18] с предуславливателем. Алгебраический многосеточный ускоритель AMG из библиотеки Демидова (amgcl) [19] применяется в блоке коррекции давления, и ILU0 метод используется для других переменных. Код VP2/3 (скорость–давление, 2D/3D), реализующий MBT, выбран в качестве базового кода в этом численном исследовании и применяется для решения задач на многоядерных вычислительных системах (аналогично, например, коду OpenFOAM).
Многоблочная разномасштабная сетка конструируется с помощью наложения заданных алгебраических и дифференциальных сеток разной топологии. Декартовая сетка канала сгущается к верхней плоской стенке и нижней криволинейной стенке. Продольные и поперечные шаги этой сетки задаются порядка 0.07, а пристенный шаг выбирается равным 0.0005. В эту сетку встраивается криволинейная неортогональная сетка высотой 0.175, которая согласуется с лунками на нижней поверхности канала. Эта сетка более подробная, чем базовая сетка. Продольные и поперечные шаги сетки имеют величину 0.05, а пристенный шаг 0.0005. Общее количество вычислительных ячеек составляет порядка 11 миллионов.
На рисунке 2 демонстрируются сетки для различных по плотности пакетов наклонных OTЛ на ребре воздушного конденсатора. Показано сечение канала z = 1, проходящее через середины стыковочных сечений соединений входных сферических сегментов лунок и цилиндрических траншей. Выделение указанного сечения имеет целью показать эволюцию параметров отрывного течения в лунках по мере развития потока в облуненном канале.
АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
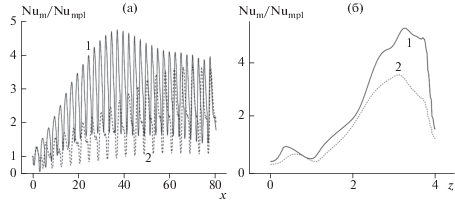
Рисунки 3, 4 и таблица 1 иллюстрируют некоторые из полученных результатов. Сравниваются пакеты разреженных (20) и плотно упакованных однорядных лунок (31). Пакет разреженных лунок аналогичен периодическим участкам узкого канала с одной наклонной ОТЛ в центре нагретой стенки [6–9]. В таблице 1 оценивается влияние глубины Δ OТЛ на теплогидравлические характеристики канала (осредненные по контрольной секции размером 80 на 4): абсолютные значения Numm, ζ и относительные значения Numm/Nummpl, ζ/ζpl в диапазоне изменения Δ от 0 до 0.35. При Δ = 0.25 сравниваются локальные относительные значения проекции трения по продольной координате fx/fxpl(x) и числа Нуссельта Nu/Nupl(x) в сечении нагретой стенки канала при z = 1 (рис. 3). Также для Δ = 0.25 сравниваются осредненные по поперечным полосам относительные распределения чисел Нуссельта Num/Numpl, построенные вдоль продольной координаты x и поперечной оси z (рис. 4).
Таблица 1.
Влияние Δ на тепловые и гидравлические характеристики в канале с 31 наклонной ОТЛ
| Δ | Numm | ζ | Numm/Nummpl | ζ/ζpl | umax |
|---|---|---|---|---|---|
| 0 | 3.151 | 0.023728 | 1 | 1 | 1.51 |
| 0.1 | 3.462 | 0.023821 | 1.087 | 1.013 | 1.62 |
| 0.2 | 4.865 | 0.029088 | 1.54 | 1.24 | 1.80 |
| 0.25 | 6.040 | 0.034245 | 1.92 | 1.46 | 1.94 |
| 0.3 | 7.36 | 0.043022 | 2.34 | 1.83 | 2.11 |
| 0.35 | 8.041 | 0.049683 | 2.55 | 2.11 | 2.23 |
Рис. 3.
Относительные величины локального трения (а) и числа Нуссельта (б) для пакетов наклонных разреженных (1) и плотно упакованных (2) однорядных ОТЛ при Δ = 0.25.
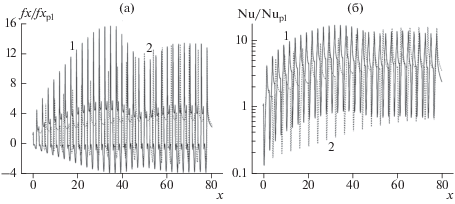
Рис. 4.
Осредненные по поперечным полосам продольные (а) и трансверсальные (б) распределения Num/Numpl в облуненном канале для пакетов наклонных разреженных (1) и плотно упакованных (2) однорядных ОТЛ при Δ = 0.25.
Анализ распределений fx/fxpl(x) в сечении канала (рис. 3а), проходящем через формирующиеся в ОТЛ отрывные зоны, свидетельствует об их циклическом характере и возрастании локальных максимумов и минимумов по мере продвижения по длине канала от лунки к лунке. Влияние обтекания вышерасположенных по потоку лунок на лунки, находящиеся в следе за ними, в однорядных пакетах приводит к значительной интенсификации отрывного течения в лунках и росту трения на участках между лунками. Минимумы относительного трения в отрывных зонах приближаются к –2.5 для разреженного пакета наклонных ОТЛ и примерно с середины канала не выходят из диапазона –3–(–4) для уплотненного пакета их 31 ОТЛ. Это свидетельствует о том, что и для ламинарного течения наблюдается открытая в турбулентном режиме аномальная интенсификация отрывного течения в наклонной ОТЛ [20]. Максимумы относительного трения доходят до величин порядка 13 для разреженного пакета лунок. В плотном пакете из 31 ОТЛ в первой половине облуненного канала максимумы приближаются к 16, а затем снижаются и выходят на уровень, соответствующий разреженному пакету. Однако при уплотнении ОТЛ уровень относительного трения в промежутках между лунками заметно подрастает, причем локальные минимумы в этих местах выходят на уровень порядка 4.
Распределения относительного числа Нуссельта (рис. 3б) также имеет циклический характер с резкими падениями в отрывных зонах и подъемами на кромках и промежуточных участках между лунками. По мере продвижения по однорядному пакету ОТЛ максимумы и минимумы монотонно возрастают для разреженного пакета и имеют волнообразную природу для плотного пакета ОТЛ. В последнем случае наблюдается нарастание теплоотдачи в первой половине канала (максимум доходит до 17) и некоторое снижение ее во второй половине (локальные максимум порядка 13.5). Для разреженного пакета ОТЛ максимум достигается в окрестности выхода из канала и составляет величину близкую к 16. Минимумы относительной теплоотдачи в отрывных зонах ОТЛ оказываются ниже 1. Для разреженного пакета ОТЛ они монотонно нарастают примерно до 0.7, а в плотном пакете ОТЛ уже в первой половине они выходят на уровень 0.8, хотя в дальнейшем несколько снижаются до 0.7.
Размещение наклонных ОТЛ на нагретой стенке узкого канала существенно повышает интегральные теплообменные характеристики устройства при использовании для воздушного охлаждения ОТЛ в отличие от сферических лунок [4, 5]. Как показано на рис. 4, увеличение плотности лунок одинаковой глубины 0.25 приводит к существенному усилению теплообмена. Для плотного пакета OTЛ осредненная по поперечной координате относительная теплопередача растет с высокой скоростью в первой половине канала, достигая локального максимального значения 4.7. В дальнейшем с увеличением x относительное число Нуссельта медленно снижается, оставаясь выше 4 (рис. 4a). Анализ распределений осредненных по продольной координате относительных чисел Нуссельта (рис. 4б) показывает, что левая сторона канала имеет пониженную относительную тепловую нагрузку (меньше 1). На правой стороне канала наблюдается интенсификация теплообмена, доходящая до 5-кратного увеличения относительной интегральной тепловой нагрузки для плотного пакета ОТЛ. Для разреженного пакета ОТЛ максимум Num/Numpl снижается до 3.5.
Следует отметить, что пакет из разреженных лунок характеризуется монотонным увеличением теплопередачи, которое стремится к его значению на участке стабилизации конвективного теплообмена.
Увеличение глубины ОТЛ (табл. 1) вызывает усиление теплообмена в канале. Высокий темп роста теплопередачи наблюдается в диапазоне изменения глубин от умеренных (порядка 0.2) до больших (выше 0.3) значений. Максимальные теплогидравлические характеристики характерны для каналов с ОТЛ глубиной 0.25. Максимальная скорость потока umax в облуненном канале увеличивается с глубиной ОТЛ. Для глубин более 0.25 она превышает 2 и коррелирует с предельными характеристиками для стабилизированного участка облуненного канала [6–9].
В настоящей работе анализируется ускорение ламинарного потока воздуха и усиление теплообмена в узких каналах с однорядными наклонными ОТЛ. Размещение поверхностных лунок на ребре вызывает появление выступов на другой его стороне. Как известно, большие выступы обуславливают формирование нестационарного течения в канале и увеличивают гидравлические потери. При проектировании энергоэффективного канала с поверхностными вихревыми генераторами [21] относительная высота выступа выбирается в пределах 0.1 высоты канала. Таким образом, для конструирования рационального по теплогидравлическим характеристикам воздушного конденсатора предлагается структурировать пакет облуненных ребер набором плоских промежуточных пластин с переменными зазорами между ребрами и пластинами.
ВЫВОДЫ
Проводится численное моделирование интенсификации ламинарного теплообмена в пространстве между облуненными ребрами воздушного конденсатора, рассматривая узкий канал с пакетом наклонных однорядных овально-траншейных лунок (ОТЛ) при Re = 1000. Сравниваются каналы с разреженными (20) и плотно упакованными (31) ОТЛ на стенке длиной 80 для ширины канала 4. Оценивается влияние глубины углубления на теплогидравлические характеристики. Вариант с 31 ОТЛ глубиной 0.25 является предпочтительным. Рост гидравлических потерь не превышает 46% при почти 2‑кратном увеличении теплопередачи по сравнению с плоскопараллельным каналом. Технологическое решение предлагается для перспективных воздушных конденсаторов, состоящих из облуненных ребер и промежуточных пластин с переменными зазорами между ребрами и пластинами.
Работа выполнена при финансовой поддержке Российского научного фонда (грант № 19-19-00259 (расчет) и грант № 16-19-10292 (валидация)).
Список литературы
Федоров В.А., Мильман О.О. Конденсаторы паротурбинных установок. М., Изд-во МГТУ им. Н.Э. Баумана, 2013. 560 с.
Вихревые технологии для энергетики / Под общ. ред. акад. Леонтьева А.И. М.: Изд. дом МЭИ, 2017. 350 с.
Leontiev A., Isaev S., Kornev N., Chudnovsky Ja., Hassel E. Numerical modeling and physical simulation of vortex heat transfer enhancement mechanisms over dimpled relief // Proc. 14 Int. Heat Transfer Conf. IHTC 14, IHTC14-22334. 2010. 10 p.
Isaev S. A., Leonardi E., Timchenko V., Usachov A. E. Vortical investigation of heat transfer in microchannels with oval dimples // Heat Transfer Research. 2010. V. 41. № 4. P. 413–424.
Исаев С.А., Леонтьев А.И., Корнев Н.В., Хассель Э., Чудновский Я.П. Интенсификация теплообмена при ламинарном и турбулентном течении в узком канале с однорядными овальными лунками // Теплофизика высоких температур. 2015. Т. 53. № 3. С. 390–402.
Isaev S., Leontiev A., Chudnovsky Ya., Popov I. Vortex heat transfer enhancement by oval-trench dimples in narrow channels // Proc. 16th Int. Heat Transfer Conf., IHTC-16, 2018, Beijing, China, IHTC16-22874. 8 p.
Исаев С.А., Баранов П.А., Леонтьев А.И., Попов И.А. Интенсификация ламинарного течения в узком микроканале с однорядными наклоненными овально-траншейными лунками // Письма в ЖТФ. 2018. Т. 44. Вып. 9. С. 73–80.
Исаев С.А., Леонтьев А.И., Мильман О.О., Судаков А.Г., Усачов А.Е., Гульцова М.Е. Интенсификация теплообмена при ламинарном вихревом течении воздуха в узком канале с однорядными наклоненными овальными лунками // Инженерно-физический журн. 2018. Т. 91. № 4. С. 1022–1034.
Isaev S.A., Leontiev A.I., Milman O.O., Popov I.A., Sudakov A.G. Influence of the depth of single-row oval-trench dimples inclined to laminar air flow on heat transfer enhancement in a narrow micro-channel // International J. Heat and Mass Transfer. 2019. V. 134. P. 338–358.
Isaev S.A., Gritckevich M.S., Leontiev A.I., Milman O.O., Nikushchenko D.V. Vortex enhancement of heat transfer and flow in the narrow channel with a dense packing of inclined one-row oval-trench dimples // International J. Heat and Mass Transfer. 2019. V. 145 (118737). P. 1–13.
Исаев С.А., Баранов П.А., Усачов А.Е. Многоблочные вычислительные технологии в пакете VP2/3 по аэротермодинамике. Саарбрюкен: LAP LAMBERT Academic Publishing. 2013. 316 с.
Исаев С.А., Судаков А.Г., Баранов П.А., Жукова Ю.В., Усачов А.Е. Анализ погрешностей многоблочных вычислительных технологий при расчете циркуляционного течения в квадратной каверне с подвижной крышкой для Re = 1000 // Инженерно-физический журн. 2013. Т. 86. № 5. С. 1064–1079.
Jasak H. Error analysis and estimation for the finite volume method with applications to fluid flows. Thesis submitted for the Degree of Doctor of Philosophy of the University of London and Diploma of Imperial College of Science, Technology and Medicine, 1996. 394 p.
Van Doormaal J.P., Raithby G.D. Enhancement of the SIMPLE method for predicting incompressible fluid flow // Numerical Heat Transfer. 1984. V. 7. № 2. P. 147–163.
Rhie C.M., Chow W.L. A numerical study of the turbulent flow past an isolated airfoil with trailing edge separation // AIAA J. 1983. V. 21. P. 1525–1532.
Pascau A., Garcia N. Consistency of SIMPLEC scheme in collocated grids // Proc. V European Conf. on Computational Fluid Dynamics ECCOMAS CFD 2010. Lisbon, Portugal, 2010. 12 p.
Leonard B.P. A stable and accurate convective modeling procedure based on quadratic upstream interpolation // Comp. Meth. Appl. Mech. Eng. 1979. V. 19. № 1. P. 59–98.
Saad Y. Iterative methods for sparse linear systems. 2nd ed., Society for Industrial and Applied Mathematics, Philadelphia, 2003. 567 p.
Demidov D. AMGCL: C++ library for solving large sparse linear systems with algebraic multigrid method. http://amgcl.readthedocs.org/.
Isaev S., Gritckevich M., Leontiev A., Popov I. Abnormal enhancement of separated turbulent air flow and heat transfer in inclined single-row oval-trench dimples at the narrow channel wall // Acta Astronautica. 2019. V. 163 (Part.A). P. 202–207.
Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчет конвективного теплообмена в трубе с периодически размещенными на поверхности вихревыми генераторами // Теплофизика высоких температур. 2005. Т. 43. № 2. С. 223–230.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика



