Известия РАН. Энергетика, 2020, № 4, стр. 11-23
Методика управления спросом на электро- и теплоэнергию в интегрированной энергосистеме c активными потребителями
Н. И. Воропай 1, В. А. Стенников 1, Е. А. Барахтенко 1, *, О. Н. Войтов 1
1 Федеральное государственное бюджетное учреждение науки Институт систем энергетики
им. Л.А. Мелентьева Сибирского отделения Российской академии наук
Иркутск, Россия
* E-mail: barakhtenko@isem.irk.ru
Поступила в редакцию 17.04.2020
После доработки 05.06.2020
Принята к публикации 11.06.2020
Аннотация
Предложены методические принципы формирования оптимальных суточных графиков потребления электро- и теплоэнергии в интегрированной энергосистеме. Приводится описание методики управления спросом на электро- и теплоэнергию в интегрированной энергосистеме с учетом наличия накопителей энергии, смещаемых во времени нагрузок отдельных потребителей, дополнительных источников энергии, а также суточных тарифов на энергию из систем централизованного энергоснабжения. Для получения решения используются процедуры смешанного целочисленного линейного программирования. Полученные графики учитываются при расчете допустимого потокораспределения в электрической и тепловой сети при краткосрочной оптимизации затрат на покупку энергии регулируемыми потребителями. При отсутствии допустимости производится коррекция оптимальных суточных графиков. Приведены результаты численных расчетов, иллюстрирующие основные этапы работы предложенной методики. Полученные оптимальные суточные графики потребления электро- и теплоэнергии существенно отличаются от исходного вида и обеспечивают ощутимое снижение издержек на покупку энергии потребителями.
ВВЕДЕНИЕ
Современные города и промышленные центры имеют развитую энергетическую инфраструктуру, включающую различные типы систем энергоснабжения (топливоснабжения, электроснабжения, теплоснабжения, хладоснабжения). Обладая определенной функциональной независимостью, эти системы могут взаимодействовать друг с другом в нормальных и аварийных режимах функционирования, а также на уровне взаимозаменяемости первичных энергоресурсов и использования энергоносителей. Совместно они представляют новую конструкцию в виде интегрированных энергетических систем (ИЭС) [1–4].
В настоящее время в практику эксплуатации ИЭС входит управление спросом потребителей электрической и тепловой энергии [5]. ИЭС включает подсистемы централизованного электро- и теплоснабжения потребителей. Системы централизованного энергоснабжения содержат электрические и тепловые сети, связывающие потребителей с источниками электроэнергии (ЭЭ) и теплоэнергии (ТЭ). Каждый потребитель ЭЭ и ТЭ обладает ресурсами как для минимизации издержек на покупку энергии от систем централизованного энергоснабжения, так максимизации прибыли от ее продажи при наличии собственных источников энергии [6, 7]. В рамках ИЭС появляются потребители, называемые активными, которые в полной мере участвуют в управлении своим спросом с возможностью покрытия его от собственных энергоисточников, а, с другой стороны, они могут существенно влиять на режимы функционирования ИЭС [8, 9]. Такие потребители имеют в своем составе средства аккумулирования и собственной генерации энергии, что дает им возможность изменения графика суточного потребления для минимизации затрат на покупку ЭЭ и ТЭ. Реализация такой возможности требует формирования инфраструктуры управления ИЭС, существенного расширения объема оперативной информации о характеристиках потребления между диспетчерскими службами энергосистем и отдельными потребителями, что позволит повысить надежность и экономичность планирования режима на предстоящие сутки как для ИЭС в целом, так и для отдельных потребителей. Технология управления спросом привлекает внимание исследователей и технологов, и результаты их работы в настоящее время внедряются в практику планирования и эксплуатации ИЭС [10]. В статье приводится описание методики управления спросом на электро- и теплоэнергию регулируемых потребителей в зависимости от уровня тарифов. Предполагается, что потребители, подключенные к системам централизованного снабжения электрической и тепловой энергии, в общем случае, могут располагать собственной генерацией, средствами аккумулирования энергии [11], возможностью смещения во времени своих нагрузок. Излагаются численные результаты, иллюстрирующие работоспособность разработанной методики и вычислительного инструментария. Оптимальные суточные графики активной мощности получены как для усредненного коммунального потребителя, так и для других с регулируемой нагрузкой.
Формирование суточного графика потребления. Краткосрочное управление ИЭС выполняется с учетом иерархического принципа ее построения. В модели ИЭС города выделены два уровня иерархии:
1) уровень централизованных систем энергоснабжения;
2) уровень децентрализованно управляемых объектов (потребителей электро- и теплоэнергии).
Основные положения по формированию оптимальных суточных графиков потребления электро- и теплоэнергии ИЭС базируются на следующих принципах:
– независимый расчет потокораспределения в сети систем централизованного энергоснабжения при условии взаимного обмена информацией о состоянии каждой системы (уровень потребления, тарифы на энергию);
– представление каждой системы в виде совокупности относительно самостоятельных (децентрализовано управляемых) объектов, получающих энергию от систем централизованного энергоснабжения;
– агрегированное представление некоторой совокупности таких объектов на уровне систем централизованного энергоснабжения;
– использование динамических моделей потокораспределения как в сети объектов, так и в сети систем централизованного энергоснабжения, позволяющих учесть зависимость ряда параметров от времени, наличие накопителей энергии и распределенной генерации;
– учет дискретности изменения управляющих переменных;
– учет различных типов распределенной генерации и накопителей энергии, а также современных средств управления потокораспределением.
При оптимизации суточных графиков потребления ЭЭ и ТЭ используются суточные графики цен на ЭЭ и ТЭ. Возможность модификации исходных суточных графиков нагрузки основана на учете при расчете потокораспределения в сети – накопителей ЭЭ (электрические аккумуляторы) и ТЭ (накопительный электроводонагреватель), смещаемых во времени нагрузок отдельных потребителей (сушилки, стиральные машины и т.д.), а также генерации мощности дополнительными источниками ЭЭ и ТЭ (фотоэлектрические преобразователи, ветроэлектрические установки, тепловые насосы).
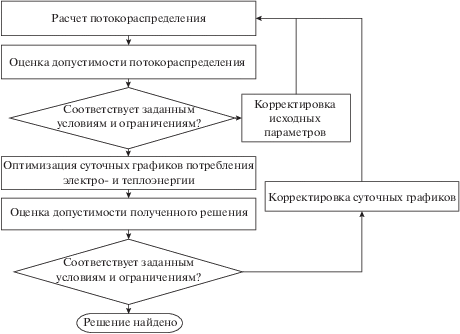
Процесс формирования суточных графиков потребления реализован на основе методики, алгоритм которой приведен на рис. 1. Согласно этому алгоритму вначале производится расчет исходного допустимого потокораспределения в электрической сети систем централизованного электроснабжения (СЦЭ) и тепловой сети систем централизованного теплоснабжения (СЦТ) для заданных суточных графиков нагрузки потребителей ЭЭ и ТЭ с учетом технологических ограничений. Для перехода к оптимизации суточных графиков потребителей требуется существование допустимого решения. При его отсутствии выполняется корректировка исходных данных, обеспечивающая получение допустимого потокораспределения.
Рис. 1.
Алгоритм методики управления спросом на электро- и теплоэнергию в интегрированной энергосистеме c активными потребителями.
Оптимизация суточных графиков потребления ЭЭ и ТЭ для каждого потребителя производится с учетом заданного графика часовых тарифов на ЭЭ и ТЭ, состава смещаемой электрической нагрузки; средств аккумулирования ЭЭ и ТЭ, наличия собственных источников электроэнергии, а также ограничений на перетоки активной и отпускаемой тепловой мощности от СЦЭ и СЦТ.
Для описания электрической сети используется либо одноузловая, либо многоузловая модель баланса активной мощности, а тепловой сети потребителя – одноузловая модель баланса тепловой мощности. В основе процедуры получения оптимальных графиков лежит процедура смешанного целочисленного линейного программирования. Поскольку каждый потребитель связан линией с сетями СЦЭ и СЦТ, то полученные из расчета задачи оптимизации часовые значения перетоков активной и отпускаемой тепловой мощности образуют искомые суточные графики потребления ЭЭ и ТЭ.
После обновления суточных графиков электрической и тепловой нагрузки потребителей в результате их оптимизации вновь проверяется существование допустимости потокораспределения в сетях СЦЭ и СЦТ. При ее отсутствии производится коррекция часовых значений мощностей оптимальных суточных графиков.
Конкретизируем общее описание алгоритма и приведем основные математические формулировки, используемые при реализации предложенной методики.
Определение исходного потокораспределения в централизованных системах энергоснабжения. Расчет и проверка допустимости потокораспределения для краткосрочного (суточного) цикла управления производится раздельно для сетей СЦЭ и СЦТ.
Для сети СЦЭ для каждого интервала $t \in \left( {1,{{N}_{T}}} \right)$ краткосрочного цикла управления, содержащего ${{N}_{T}}$ интервалов, осуществляется поиск допустимого потокораспределения, переменные которого удовлетворяют следующим ограничениям
где $W_{e}^{t}(Z_{e}^{t},D_{e}^{t})$ – система уравнений баланса узловых активных и реактивных мощностей в интервале времени $t$; $Z_{e}^{t}$ – вектор переменных режима функционирования электрической сети (ЭС) в интервале $t$, который включает комплексные значения узловых напряжений, коэффициенты трансформации, активные и реактивные мощности генерации; $D_{e}^{t}$ – вектор значений графиков узловых нагрузок активных и реактивных мощностей в интервале $t$; $f_{e}^{t}(Z_{e}^{t})$ – вектор функциональных переменных, который включает контролируемые токи и перетоки в линиях в интервале $t$.Алгоритм решения подзадачи (1)–(3) рассмотрен в [12] и реализован в программном комплексе СДО [13].
Для сети СЦТ для каждого интервала $t \in \left( {1,{{N}_{T}}} \right)$ определяется допустимое потокораспределение, переменные которого удовлетворяют следующим ограничениям
где $W_{h}^{t}(Z_{h}^{t},D_{h}^{t})$ – система уравнений материального баланса для тепловой сети (ТС) в интервале $t$; $Z_{h}^{t}$ – вектор переменных режима в ТС в интервале $t$, который включает расходы теплоносителя; $D_{h}^{t}$ – вектор значений графиков узловых тепловых нагрузок в ТС в интервале $t$; $\Delta S_{h}^{t}$ – вектор, описывающий изменение напора на участках сети в интервале $t$.Алгоритм решения подзадачи (4)–(6) рассмотрен в [14] и реализован в программном комплексе IRNET-Flow [15].
Если допустимое решение для каждого интервала времени $t$ для сетей СЦЭ и СЦТ получено, то производится оптимизация суточных графиков потребления ЭЭ и ТЭ потребителей. Иначе выполняется корректировка используемой информации для каждой сети, обеспечивающая возможность получения допустимых решений.
Оптимизация суточных графиков потребления энергии потребителем. При построении суточных графиков потребления учитываются прогнозные значения собственной генерации активной мощности потребителя (фотоэлектрические преобразователи, ветроэлектрические установки), возможность аккумулирования электрической и тепловой энергии и последующего ее использования.
Построение и оптимизация графика нагрузки отдельного потребителя основано на результатах решения задачи смешанного целочисленного линейного программирования.
При описании задачи используются следующие допущения и обозначения для основных элементов потребителя.
Суточные графики потребления электрической и тепловой энергии рассматриваются для часовых интервалов и имеют одинаковую размерность, поскольку численные часовые значения мощности и энергии совпадают. Для перехода от размерности тепловой энергии к размерности электрической используется соотношение (1 Гкал = = 1163 кВт · ч).
Для расчета параметров режима электрической и тепловой сети используются линейные модели – уравнения узловых напряжений для ЭС и математическое описание потокораспределения для ТС в виде системы линейных и нелинейных уравнений.
Электрическая сеть потребителя является фрагментом электрической сети энергосистемы и связана с ней линией, по которой передается переток активной мощности $P_{e}^{t}$, обеспечивающий электроснабжение потребителя. Суточный график предельных значений перетока $P_{{e\_{\text{min}}}}^{t}$ и $P_{{e\_{\text{max}}}}^{t}$ задается при расчете электрической сети централизованного электроснабжения и уточняются при необходимости коррекции после оптимизации графиков потребителей. Модель электрической сети потребителя может представляться либо упрощенно в виде одноузловой модели, либо подробно в виде многоузловой сети, которая в этом случае описывается следующими выражениями:
Параметры генерации фотоэлектрического преобразователя: $P_{{fv\_G}}^{t},$ $t \in \left( {1,{{N}_{T}}} \right)$ – заданный суточный график генерации активной мощности фотоэлектрическим преобразователем.
Параметры заданной электрической нагрузки: $P_{{e\_L}}^{t},$ $t \in \left( {1,{{N}_{T}}} \right)$ – суточный график потребления активной мощности, который задает суммарное потребление электроэнергии за сутки, получаемой потребителем из электрической сети централизованного электроснабжения.
Параметры смещаемой электрической нагрузки: $P_{{sh\_k}}^{t},$ $k \in \left( {1,{{N}_{{sh}}}} \right)$ – заданное значение активной мощности отдельной нагрузки (посудомойка, сушилка и т.д.), которая может быть подключена в диапазоне интервалов, границами которого являются начальный ${{t}_{{b\_i}}}$ и конечный ${{t}_{{e\_i}}}$ интервал; ${{N}_{{sh}}}$ – число смещаемых нагрузок потребителя. Время подключения нагрузки может определяться, например, экономической целесообразностью. К смещаемой нагрузке относится и накопитель тепловой энергии (накопительный электроводонагреватель), работающий в режиме заряда (нагрева). При учете теплового накопителя ему присваивается номер $\left( {{{N}_{{sh}}} + 1} \right)$.
Параметры накопителя электроэнергии: ${{E}_{{ae\_{\text{max}}}}}$ – максимальный запас электроэнергии, кВт ч; $E_{{ae}}^{t}$ – запас электроэнергии в интервале $t$, кВт ч; ${{P}_{{ae\_L\_{\text{max}}}}}$ – максимальное часовое потребление активной мощности в режиме заряда, кВт; ${{P}_{{ae\_G\_{\text{max}}}}}$ – максимальная часовая генерация активной мощности в режиме разряда, кВт; $\mu _{{ae\_G}}^{t}$ – признак режима разряда в интервале $t$, 0/1 – нет/есть разряд; $\mu _{{ae\_L}}^{t}$ – признак режима заряда в интервале $t$, 0/1 – нет/есть разряд; $\mu _{{ae\_K}}^{t}$ – признак режима хранения в интервале $t$, 0/1 – нет/есть хранение. Накопитель в каждом интервале может находится в одном из трех режимов – заряд, разряд и хранение.
Параметры заданной тепловой нагрузки: $P_{{h\_L}}^{t},$ $t \in \left( {1,{{N}_{T}}} \right)$ – суточный график потребления тепловой мощности, который задает суммарное потребление тепловой энергии за сутки, получаемой потребителем из тепловой сети централизованного теплоснабжения.
Параметры накопителя тепловой энергии. Список параметров накопителя включает следующие величины: ${{P}_{{ah\_L\_{\text{max}}}}}$ – максимальный запас тепловой энергии, определяемый нагревом заданного объема холодной воды до требуемой температуры горячей воды, кВт ч; ${{P}_{{ah\_G}}}$ – максимальная выдача тепловой мощности в режиме разряда в интервале $t$, кВт; $\mu _{{ah\_G}}^{t}$ – признак режима разряда, 0/1 – нет/есть разряд; $\mu _{{ah\_L}}^{t}$ – признак режима заряда, 0/1 – нет/есть заряд (нагрев); $\mu _{{ah\_K}}^{t}$ – признак режима хранения, 0/1 – нет/есть хранение. В отличие от электрического тепловой накопитель может находиться в режиме заряда только в одном интервале ${{t}_{{ah\_L}}}$, а в остальных интервалах – в режимах разряда и хранения. Значение интервала ${{t}_{{ah\_L}}}$ принимается равным единице.
Параметры тепловой сети включают: $P_{h}^{t}$ – объем тепловой энергии, поставляемой потребителю в интервале $t$, кВт. Суточный график предельных значений тепловой энергии $P_{{h\_{\text{min}}}}^{t}$ и $P_{{h\_{\text{max}}}}^{t}$ задается при расчете тепловой сети централизованного теплоснабжения и уточняется при необходимости коррекции после оптимизации графиков потребителей.
Экономические параметры: $c_{{e\_k}}^{t},~$ $c_{{h\_k}}^{t}$ – тарифы в интервале $t$ на покупку электроэнергии от электрической сети и тепловой энергии от системы централизованного теплоснабжения.
Описание задачи минимизации суточных издержек на покупку электрической и тепловой энергии. Требуется найти минимум целевой функции
(7)
$\mathop {\min }\limits_\mu \mathop \sum \limits_{t = 1}^{{{N}_{T}}} \left( {c_{e}^{t}P_{e}^{t} + c_{h}^{t}P_{h}^{t}} \right)$– накопитель электроэнергии не может одновременно находится в режиме заряда $\left( {\mu _{{ae\_L}}^{t} = 1} \right),~$ разряда $\left( {\mu _{{ae\_G}}^{t} = 1} \right)$ и хранения $\left( {\mu _{{ae\_K}}^{t} = 1} \right)$
– мощности заряда $P_{{ae\_L}}^{t}$ и разряда $P_{{ae\_G}}^{t}$ накопителя электроэнергии ограничены
где $E_{{ae}}^{1},~~E_{{ae}}^{t}$ – значение исходной или начальной и накопленной электроэнергии в интервале $t$. Величина $E_{{ae}}^{t}$ определяется как(13)
$E_{{ae}}^{t} = E_{{ae}}^{1} + \mathop \sum \limits_{k = 1}^{t - 1} \left( {\mu _{{ae\_L}}^{k}P_{{ae\_L}}^{k} - \mu _{{ae\_G}}^{k}P_{{ae\_G}}^{k}} \right),$– значение электроэнергии в накопителе $E_{{ae}}^{t}$ в интервале $t$ ограничено
– смещаемая нагрузка $P_{{sh\_i}}^{t},$ $~i \in \left( {1,~{{N}_{{sh}}}} \right)$ может быть подключена только в одном интервале
(15)
$\mathop \sum \limits_{t = 1}^{{{N}_{T}}} \mu _{{sh\_i}}^{t} = 1,\,\,\,\,~i \in \left( {1,~{{N}_{{sh}}}} \right),$– смещаемая нагрузка $P_{{sh\_i}}^{t},$ $~i \in \left( {1,~{{N}_{{sh}}}} \right)$ может быть подключена в заданном диапазоне интервалов, границами которого являются начальный ${{t}_{{b\_i}}}$ и конечный ${{t}_{{e\_i}}}$ интервалы
(16)
$\mathop \sum \limits_{t = 1}^{{{t}_{{b\_i}}}} \mu _{{sh\_i}}^{t} = 0,\,\,\,\,{\text{если}}\,\,\,\,{{t}_{{b\_i}}} > 1,$(18)
$\mathop \sum \limits_{t = {{t}_{{e\_i}}} + 1}^{{{N}_{T}}} \mu _{{sh\_i}}^{t} = 1,\,\,\,\,{\text{если}}\,\,\,\,{{t}_{{e\_i}}} < {{N}_{T}},$– накопитель тепловой энергии, который по определению является смещаемой нагрузкой с номером $\left( {{{N}_{{sh}}} + 1} \right),$ находится в режиме заряда (нагрева) только в одном интервале ${{t}_{{ah\_L}}}$
(20)
$\mu _{{({{N}_{{sh}}} + 1)\_L}}^{t} = 0\,\,\,\,{\text{и}}\,\,\,\,\mu _{{({{N}_{{sh}}} + 1)\_G}}^{t} \geqslant 0\,\,\,\,{\text{для}}\,\,\,\,t > {{t}_{{ah\_L}}},$– накопитель тепловой энергии полностью расходует накопленную энергию
(21)
$\mathop \sum \limits_{t = {{t}_{{a{{h}_{L}} + 1}}}}^{{{N}_{T}}} \mu _{{ah\_G}}^{t}P_{{ah\_G}}^{t} - P_{{ah\_L\_{\text{max}}}}^{t} = 0,$– величина перетока активной мощности $P_{e}^{t}$ ограничена
– величина подаваемой тепловой мощности $P_{h}^{t}$ ограничена
– в каждом интервале $~t \in \left( {1,{{N}_{T}}} \right),$ если не учитывается подробно электрическая сеть потребителя, должен выполняться суммарный баланс активной мощности
(24)
$w_{e}^{t} = P_{e}^{t} - P_{{fv\_G}}^{t} + \sum\limits_{i = 1}^{{{N}_{{sh}}} + 1} {\mu _{{sh\_i}}^{t}} P_{{sh\_i}}^{t} + \mu _{{ae\_L}}^{t}P_{{ae\_L}}^{t} - \mu _{{ae\_G}}^{t}P_{{ae\_G}}^{t} + P_{{e\_L}}^{t} = 0,$– в каждом интервале $~t \in \left( {1,{{N}_{T}}} \right),$ должен выполняться суммарный баланс тепловой мощности
Для решения задачи (7)–(25) используется среда MATLAB, в которой разработана и реализована программа формирования суточных графиков потребления как активной мощности $P_{e}^{t},$ $~t \in \left( {1,{{N}_{T}}} \right),$ так и тепловой энергии $P_{h}^{t},~$ $~t \in \left( {1,{{N}_{T}}} \right).$
Проверка допустимости потокораспределения в централизованной системе электроснабжения после оптимизации суточных графиков. Для каждого интервала $~t \in \left( {1,{{N}_{T}}} \right)$ для полученных оптимальных суточных графиков активной мощности потребителей выполняется проверка выполнения условий (1)–(3). Если в интервале ${{t}_{k}}$условия не выполняются, то формируется и решается задача, в которой ищется минимальное отклонение часовых значений мощности в интервале ${{t}_{k}}$ для каждого оптимального суточного графика от часовых значений мощности соответствующего исходного графика, для которых, как было установлено выше, существует допустимое решение. Это однопараметрическая задача, имеющая следующее математическое описание
Результатом решения этой задачи является вектор $D_{e}^{*}$, который содержит часовые значения активной мощности суточных графиков в интервале ${{t}_{k}}$, при которых обеспечивается допустимое потокораспределение в сети СЦЭ. Поскольку их значения не совпадают с часовыми значениями мощности оптимальных графиков в интервале ${{t}_{k}}$, то требуется перерасчет оптимальных графиков с учетом дополнительных ограничений, накладываемых на значения перетоков активной мощности, которые получают потребители от СЦЭ. Дополнительные ограничения для потребителя $m$ формируются следующим образом:
С учетом скорректированных ограничений неравенства (22) выполняется новая оптимизация суточных графиков электрических нагрузок потребителей.
Проверка допустимости потокораспределения в централизованной системе теплоснабжения после оптимизации суточных графиков. Для каждого интервала $~t \in \left( {1,{{N}_{T}}} \right)$ полученных оптимальных суточных графиков тепловой нагрузки потребителей выполняется проверка выполнения условий (4)–(6). Если в интервале ${{t}_{k}}$ условия не выполняются, то формируется и решается задача, в которой ищется минимальное отклонение часовых значений мощности в интервале ${{t}_{k}}$ для каждого оптимального суточного графика от часовых значений мощности соответствующего исходного графика, для которых, как было установлено выше, существует допустимое решение. Это однопараметрическая задача, имеющая следующее математическое описание
Результатом решения этой задачи является вектор $D_{h}^{*}$, который содержит часовые значения n тепловой мощности суточных графиков в интервале ${{t}_{k}}$, при которых обеспечивается допустимое потокораспределение в сети СЦТ. Поскольку их значения не совпадают с часовыми значениями мощности оптимальных графиков в интервале ${{t}_{k}}$, то требуется перерасчет оптимальных графиков с учетом дополнительных ограничений, накладываемых на значения подаваемой тепловой мощности, которую получают потребители от СЦТ. Дополнительные ограничения для потребителя $m$ формируются следующим образом:
С учетом скорректированных ограничений неравенства (23) выполняется новая оптимизация суточных графиков тепловых нагрузок потребителей.
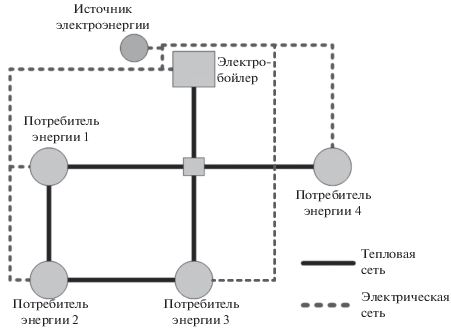
Результаты исследования ИЭС. Ниже приводятся результаты исследования ИЭС, схема которой приведена на рис. 2. ЭС напряжением 10 кВ содержит шесть узлов, один из которых является источником питания, а к остальным узлам подключены потребители электроэнергии. ТС содержит также шесть узлов, один из которых электробойлер, четыре узла – потребители тепловой энергии, один узел – узел соединения. Потребители имеют источники возобновляемой ЭЭ (фотоэлектрический преобразователь) и накопители, как ЭЭ (электрический аккумулятор), так и ТЭ (накопительный электроводонагреватель). Все потребители подключены к централизованной системе электроснабжения и теплоснабжения по отдельной ветви, остальные узлы нагрузочные. Для каждого потребителя известен характерный или исходный график потребления активной мощности и тепловой энергии, а также принятый суточный график цен на ЭЭ и ТЭ. Они содержат электрические нагрузки (смещаемые нагрузки), время включения которых определяется исходя из экономических соображений.
Для приведенной на рис. 2 схемы ИЭС были получены оптимальные суточные графики потребления ЭЭ и ТЭ на основе предложенной методики. На рисунках 3 и 4 приведены результаты расчета оптимальных суточных графиков потребления ЭЭ и ТЭ для одного узла. На рисунке 3а приведены суточные графики исходного и оптимального потребления активной мощности, а также тарифов на ЭЭ. На рисунке 3б приведены суточные графики генерации фотоэлектрического преобразователя, смещаемой нагрузки, аккумулятора ЭЭ и накопительного электроводонагревателя. В результате расчетов были получены суточные графики использования накопителей ЭЭ и ТЭ и графики средних часовых значений узловых напряжений ЭС.
Рис. 3.
Суточные графики потребления активной мощности: (а): ${{P}_{{dini}}}\left( t \right),$ $~{{P}_{{dopt}}}\left( t \right)$ – исходный и оптимальный суточные графики активной нагрузки потребителя; ${{C}_{{ep}}}\left( t \right)$ – суточный график тарифа на покупку электрической энергии; (б): ${{P}_{{phv}}}\left( t \right)$ – суточный график генерации активной мощности солнечной панелью; ${{P}_{{dsh}}}\left( t \right)$ – суточные графики активной смещаемой нагрузки; ${{P}_{{aep}}}\left( t \right)$ – суточный график аккумулирования электрической энергии; ${{P}_{{adtp}}}\left( t \right)$ – суточный график потребления электрической энергии аккумулятором тепловой энергии.
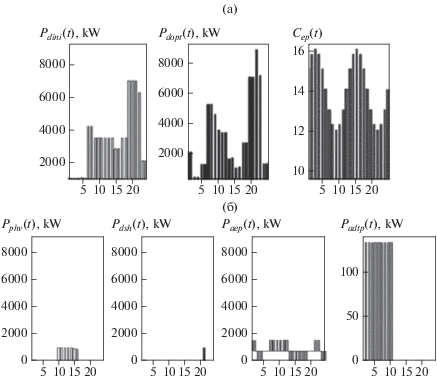
Рис. 4.
Суточные графики потребления тепловой энергии потребителем: ${{P}_{{hini}}}\left( t \right),$ ${{P}_{{hopt}}}\left( t \right)$ – исходный и оптимальный суточные графики тепловой нагрузки потребителя; ${{P}_{{ahp}}}\left( t \right)$ – суточный график аккумулирования тепловой энергии; ${{C}_{{hp}}}\left( t \right)$ – суточный график тарифа на покупку тепловой энергии.
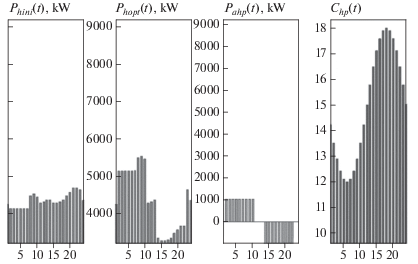
Графики показывают, что аккумуляторы накапливают ЭЭ и ТЭ в часы “дешевой” энергии и отдают ее в “дорогие” часы. Оптимальные суточные графики потребления ЭЭ и ТЭ получают в результате суммирования исходных графиков потребления и графиков фотоэлектрических преобразователей, аккумуляторов, смещаемой нагрузки.
ВЫВОДЫ
Предложены принципы реализации методики управления спросом на электро- и теплоэнергию в ИЭС c активными потребителями. Планирование управлением каждой подсистемой в составе ИЭС, построенной по иерархическому принципу, выполняется как централизовано, так и автономно в зависимости от тарифов на электро- и теплоэнергию с упреждением на сутки и возможностью изменения плановых режимов при оперативном управлении ИЭС.
Разработана методика управления спросом на электро- и теплоэнергию ИЭС с учетом наличия накопителей ЭЭ и ТЭ, смещаемых во времени электрических нагрузок отдельных потребителей, дополнительных источников ЭЭ и ТЭ, а также суточных тарифов на ЭЭ и ТЭ.
Сформирована укрупненная схема ИЭС, на которой проведены численные исследования. Их результаты показали работоспособность разработанной методики. Полученные оптимальные суточные графики потребления ЭЭ и ТЭ существенно отличаются от исходных, обеспечивая снижение издержек на покупку энергии потребителями.
Список литературы
Geidl M. Optimal power flow of multiple energy carrier // IEEE Transactions on Power Systems. 2007. V. 22. № 1. P. 145–155.
Li Z., Huo Z., Yin H. Optimization and Analysis of Operation Strategies for Combined Cooling, Heating and Power System // Asia-Pacific Power and Energy Engineering Conference, 2011, P. 1–4.
Voropai N., Stennikov V., Senderov S., Barakhtenko E., Voitov O., Ustinov A. Modeling of Integrated Energy Supply Systems: Main Principles, Model, and Applications // Journal of Energy Engineering. V. 143. № 5. 2017.
Voropai N.I., Stennikov V.A., Barakhtenko E.A. Methodological principles of constructing the integrated energy supply systems and their technological architecture // Journal of Physics: Conference Series. 2018. V. 1111. № 1.
Гительман Л.Д., Ратников Б.Е., Кожевников М.В. Управление спросом – универсальный метод решения современных проблем электроснабжения // Энергорынок. 2012. № 5. С. 44–49.
Болоев Е.В., Войтов О.Н., Голуб И.И., Семенова Л.В. Алгоритм оптимизации реконфигурации и суточных графиков нагрузки распределительной электрической сети // Изв. РАН. Энергетика. 2018. № 1. С. 1–10.
Воропай Н.И., Стычински З.А., Козлова Е.В., Степанов В.С., Суслов К.В. Оптимизация суточных графиков нагрузки активных потребителей // Изв. РАН. Энергетика. 2014. № 1. С. 84–90.
Аюев Б.И. Управление электропотреблением: административные и экономические методы // Энергорынок. 2007. № 4. С. 14–18.
Стенников В.А., Барахтенко Е.А., Соколов Д.В., Шелехова В.Б. Активное участие потребителя в управлении своим энергоснабжением // Известия высших учебных заведений. Проблемы энергетики. 2017. Т. 19. № 11–12. С. 88–100.
Olivala A.G., Madureira M., Matosa P.C. Advanced voltage control for smart microgrids using distributed energy resources // Electric Power Systems Research. 2017. V. 146. P. 132–140.
Алексеев Б.А. Применение накопителей энергии в электроэнергетике // Электро. 2005. № 2. С. 48–52.
Системные исследования в энергетике: Ретроспектива научных направлений СЭИ-ИСЭМ / отв. ред. Воропай Н.И. Новосибирск: Наука. 2010. 686 с.
Сертификат соответствия № РОСС RU.СП20.H00008 “Программное средство ПС СДО-7 для анализа, оптимизации установившихся режимов и оценки потерь электроэнергии в ЭС” – Система сертификации ГОСТ Р Госстандарт России. Срок действия: с 31.01.2009 по 31.01.2012.
Меренков А.П., Сеннова Е.В., Сумароков С.В. и др. Математическое моделирование и оптимизация систем тепло-, водо-, нефте- и газоснабжения. Новосибирск: Наука. 1992.
Свидетельство № 2020612333 Российская Федерация. Программно-вычислительный комплекс “IRNET-Flow”: Свидетельство об официальной регистрации программы для ЭВМ. Зарегистр. 20.02.2020.
Мельников Н.А. Матричный метод анализа электрических сетей. М.: Энергия. 1972.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика