Известия РАН. Энергетика, 2022, № 1, стр. 66-80
Комбинированный алгоритм определения углового коэффициента излучения между многоугольниками контурным интегрированием
А. А. Басов 1, *, Д. К. Винокуров 2, **, М. А. Клочкова 1
1 ПАО “Ракетно-космическая корпорация “Энергия” им. С.П. Королева” (ПАО “РКК "Энергия”)
Королев, Россия
2 Акционерное общество “Центральный научно-исследовательский институт машиностроения” (АО “ЦНИИмаш”)
Королев, Россия
* E-mail: andrey.basov@rsce.ru
** E-mail: vinokurovdk@tsniimash.ru
Поступила в редакцию 01.06.2021
После доработки 07.10.2021
Принята к публикации 15.10.2021
- EDN: ASXQII
- DOI: 10.31857/S0002331022010034
Аннотация
Предложен алгоритм расчета диффузных угловых коэффициентов излучения для произвольно расположенных многоугольников, реализующий комбинированный метод контурного интегрирования. Метод сочетает интегрирование по квадратурным формулам Гаусса невысокого порядка с точным аналитическим решением. Показаны особенности, связанные с погрешностью расчета угловых коэффициентов численными методами контурного интегрирования. Предложены способы, позволяющие обеспечить заданную точность расчета.
ВВЕДЕНИЕ
Среди факторов, определяющих успешное функционирование любого технического устройства, немаловажное значение имеют условия теплообмена с окружающей средой и внутренний теплообмен. Для технических устройств, эксплуатируемых в разряженной газовой среде (вакууме) и при высоких температурах внешней поверхности, главенствующее значение приобретает радиационный теплообмен.
Задачи расчета радиационного теплообмена встречаются при проектировании СОТР для моделирования тепловых потоков как в условиях полета для сложных многомодульных объектов типа международной космической станции [1] и небольших конструкций [2], так и для условий наземной экспериментальной отработки [3].
Для численного моделирования радиационного теплообмена широко применяется зональный метод, в котором поверхности, участвующие в радиационном теплообмене, разбиваются на зоны [4 стр. 130] , в пределах которых теплофизические свойства принимаются однородными. При этом зачастую используется диффузная модель излучения и отражения, в которой излучение и поглощение каждой поверхности не зависит от направления. В таком случае расчет радиационного теплообмена сводится к определению диффузных угловых коэффициентов излучения [5].
Для космических аппаратов расчет внешних воздействующих тепловых потоков сводится по сути к расчету угловых коэффициентов радиационного теплообмена внешних элементов конструкции между собой и внешних элементов конструкции и естественными источниками тепловой энергии в космосе (излучением Солнца и Земли), а для расчета внутреннего радиационного теплообмена в полостях – к расчету угловых коэффициентов элементов конструкции между собой.
Определение и основные формулы расчета диффузных угловых коэффициентов можно найти в [5–7]. Классификация методов расчета угловых коэффициентов приведена в [8].
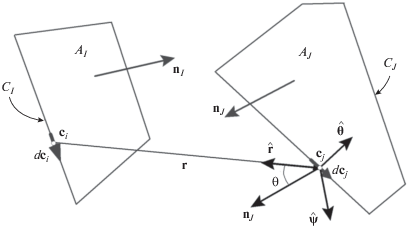
Сегодня особые требования предъявляются к скорости и точности расчетов. При отсутствии препятствий между поверхностями ${{A}_{I}}$ и ${{A}_{J}}$ (рис. 1) одним из используемых приближенных численных методов определения угловых коэффициентов является контурное интегрирование.
Имеется множество форм контурного интеграла, который выводится из двойного интеграла по площадям с использованием теоремы Стокса [9–12].
В общем виде интегралы можно записать
(1)
${{F}_{{I - J}}} = \frac{1}{{2\pi {{A}_{I}}}}\oint\limits_{{{C}_{I}}} {\oint\limits_{{{C}_{J}}} {d{{{\mathbf{c}}}_{i}} \cdot {\mathbf{M}}({{{\mathbf{c}}}_{i}},{{{\mathbf{c}}}_{j}}) \cdot d{{{\mathbf{c}}}_{j}}} } ,$Таблица 1.
Вид матрицы в подынтегральном выражении
| Вид матрицы ${\mathbf{M}}({{{\mathbf{c}}}_{i}},{{{\mathbf{c}}}_{j}})$ | Обозначение |
|---|---|
| ${\text{ln\;}}\left| {\mathbf{r}} \right|{\mathbf{E}}$ | IS |
| $ - {\mathbf{\hat {r}}} \otimes {\mathbf{\hat {r}}}$ | IDL1 |
| $\left( {1 - \theta {\text{/tg}}\theta } \right){\mathbf{\hat {\psi }}} \otimes {\mathbf{\hat {\psi }}}$ | IDL2 |
| ${\mathbf{\hat {\theta }}} \otimes {\mathbf{\hat {\theta }}} + {\mathbf{\hat {\psi }}} \otimes {\mathbf{\hat {\psi }}}$ | IDL3 |
Примечание: подынтегральное выражение ${\text{ln\;}}\left| {\mathbf{r}} \right|{\mathbf{E}}$ соответствует диаде ${\mathbf{\hat {r}}} \otimes {\mathbf{\hat {r}}} + {\mathbf{\hat {\theta }}} \otimes {\mathbf{\hat {\theta }}} + {\mathbf{\hat {\psi }}} \otimes {\mathbf{\hat {\psi }}}$, которая является единичным афинором.
Для многоугольников вычисления производятся для каждой стороны независимо
(2)
${{F}_{{I - J}}} = \frac{1}{{2\pi {{A}_{I}}}}\sum\limits_{k = 1}^{{{K}_{I}}} {\sum\limits_{m = 1}^{{{K}_{J}}} {\int\limits_0^{{{L}_{m}}} {\int\limits_0^{{{L}_{k}}} {d{{{\mathbf{c}}}_{i}} \cdot {\mathbf{M}}({{{\mathbf{c}}}_{i}},{{{\mathbf{c}}}_{j}}) \cdot d{{{\mathbf{c}}}_{j}}} } } } = \frac{1}{{2\pi {{A}_{I}}}}\sum\limits_{k = 1}^{{{K}_{I}}} {\sum\limits_{m = 1}^{{{K}_{J}}} {{{S}_{{km}}}\left( {{{f}_{{\mathbf{M}}}}} \right)} } .$При численном определении угловых коэффициентов используются квадратурные формулы [13] – на каждой стороне выбирается набор узловых точек c с весами g и единичными векторами ${\mathbf{\hat {c}}}.$ Имеем
(3)
${{L}_{k}} = \sum\limits_{i = 1}^{{{n}_{k}}} {{{g}_{i}}} ,\,\,\,\,{{L}_{m}} = \sum\limits_{j = 1}^{{{n}_{m}}} {{{g}_{j}}} ,$(4)
${{S}_{{km}}}\left( {{{f}_{{\mathbf{M}}}}} \right) = \sum\limits_{i = 1}^{{{n}_{k}}} {\sum\limits_{j = 1}^{{{n}_{m}}} {{{g}_{i}}{{g}_{j}}{{{{\mathbf{\hat {c}}}}}_{i}} \cdot {\mathbf{M}}({{{\mathbf{c}}}_{i}},{{{\mathbf{c}}}_{j}}) \cdot {{{{\mathbf{\hat {c}}}}}_{j}}} } .$Выбор узловых точек с весами фактически означает построение на сторонах сетки.
Самым простым численным методом определения значения интеграла является сеточный метод с квадратурной формулой средних (прямоугольников), в котором сторона делится на интервалы, как правило, равной длины, а в качестве узловых точек выступают середины интервалов, при этом веса узловых точек равны длинам интервалов. Широкое распространение получило использование квадратурных формул Гаусса, в которых в качестве узловых точек выступают корни полиномов Лежандра. Формулы Гаусса позволяют получить точное значение интеграла, если подынтегральная функция является полиномом. Однако подынтегральные функции в формуле (1) не являются полиномами, поэтому сходимость интегралов с применением формул Гаусса в ряде случаев оказывается хуже, чем с применением формулы средних.
Применение любого численного метода означает, что рассчитываемая величина определяется с некоторой погрешностью. Проведенное исследование показывает, что на некоторых конфигурациях многоугольников применение квадратурных методов не позволяет получить значения угловых коэффициентов с требуемой точностью. Использование же точных аналитических формул [14, 15] достаточно ресурсоемко (выражения не приводим из-за их громоздкости).
В данной работе показаны особенности, связанные с погрешностью расчета угловых коэффициентов численными методами контурного интегрирования, и предложен алгоритм, позволяющий обеспечить заданную погрешность расчета.
Предложенный алгоритм сочетает интегрирование по квадратурным формулам Гаусса невысокого порядка с точным аналитическим решением.
Алгоритмы расчета угловых коэффициентов контурным интегрированием с использованием квадратурных формул средних и Гаусса для четырех интегралов из табл. 1, а также с использованием точного аналитического решения [14, 16] по программе CONTVF [17].
1. ОБЩИЙ АЛГОРИТМ
Для практических вычислений необходимо иметь алгоритм, позволяющий проводить расчеты для выбранного типа интеграла, квадратурной формулы и ее степени. Общий алгоритм определения угловых коэффициентов между многоугольниками ${{A}_{I}}$ и ${{A}_{J}}$ при разбиении каждой стороны на n интервалов состоит из следующих шагов
Алгоритм 1. Расчет угловых коэффициентов между многоугольниками квадратурными формулами двойным контурным интегрированием
| А.1 | $S \leftarrow 0$ |
| А.2 | for$k \leftarrow 1,{{K}_{I}}$do !Цикл по сторонам многоугольника ${{A}_{I}}$ |
| А.3 | for$m \leftarrow 1,{{K}_{J}}$do !Цикл по сторонам многоугольника ${{A}_{J}}$ |
| А.4 | ${{S}_{{km}}} \leftarrow 0$ |
| А.5 | Построение сетки на стороне ${{L}_{k}}$ |
| А.6 | Построение сетки на стороне ${{L}_{m}}$ |
| А.7 | for$i \leftarrow 1,{{n}_{k}}$do !Цикл по узловым точкам на стороне ${{L}_{k}}$ |
| А.8 | for$j \leftarrow 1,{{n}_{m}}$do !Цикл по узловым точкам на стороне ${{L}_{m}}$ |
| А.9 | ${{S}_{{km}}} \leftarrow {{S}_{{km}}} + {{g}_{i}}{{g}_{j}}{{{\mathbf{\hat {c}}}}_{i}} \cdot {\mathbf{M}}({{{\mathbf{c}}}_{i}},{{{\mathbf{c}}}_{j}}) \cdot {{{\mathbf{\hat {c}}}}_{j}}$ |
| А.10 | end for |
| А.11 | end for |
| А.12 | $S \leftarrow S + {{S}_{{km}}}$ |
| А.13 | end for |
| А.14 | end for |
| А.15 | ${{F}_{{I - J}}} \leftarrow {S \mathord{\left/ {\vphantom {S {2\pi {{A}_{I}}}}} \right. \kern-0em} {2\pi {{A}_{I}}}}$ |
Общий алгоритм реализует все подынтегральные выражения из табл. 1. При расчете по формуле (4) возникают особенности при совпадении узловых точек [18]. В интеграле IS возникает сингулярность из-за того, что ${\text{\;}}\left| {\mathbf{r}} \right|$ становится равным нулю при конечных значениях ${{g}_{i}}$ и ${{g}_{j}},$ а во всех интегралах IDL происходит вырождение единичного вектора ${\mathbf{\hat {r}}}$ в нулевой. Эти особенности можно обойти, например, изменением степени разбиения одного из пары отрезков.
При расчетах на ЭВМ из-за особенностей применяемых алгоритмов вычисления координат узловых точек может возникнуть ситуация, когда точки должны были совпасть, но не совпали. В таком случае для интеграла IS получаем большое по абсолютной величине значение логарифма, а для интегралов IDL получаем неверное направление вектора ${\mathbf{\hat {r}}}$ и, соответственно, большую общую погрешность. Во всех случаях это приводит к большим суммарным погрешностям.
Подобная ситуация может возникнуть при определении узловых точек на двух совпадающих отрезках. В такой ситуации направления обхода отрезков в контурных интегралах будут противоположными. Пусть имеем ${\mathbf{v}}_{1}^{1} = {\mathbf{v}}_{2}^{2} = {{{\mathbf{V}}}_{1}}$ и ${\mathbf{v}}_{2}^{1} = {\mathbf{v}}_{1}^{2} = {{{\mathbf{V}}}_{2}}.$ При разбиении стороны на n интервалов имеем
(5)
${\mathbf{c}}_{i}^{1} = {\mathbf{v}}_{1}^{1} + {{(2i - 1)\left( {{\mathbf{v}}_{2}^{1} - {\mathbf{v}}_{1}^{1}} \right)} \mathord{\left/ {\vphantom {{(2i - 1)\left( {{\mathbf{v}}_{2}^{1} - {\mathbf{v}}_{1}^{1}} \right)} {2n}}} \right. \kern-0em} {2n}} = {{{\mathbf{V}}}_{1}} + {{(2i - 1)({{{\mathbf{V}}}_{2}} - {{{\mathbf{V}}}_{1}})} \mathord{\left/ {\vphantom {{(2i - 1)({{{\mathbf{V}}}_{2}} - {{{\mathbf{V}}}_{1}})} {2n}}} \right. \kern-0em} {2n}},$(6)
${\mathbf{c}}_{k}^{2} = {\mathbf{v}}_{1}^{2} + {{(2k - 1)\left( {{\mathbf{v}}_{2}^{2} - {\mathbf{v}}_{1}^{2}} \right)} \mathord{\left/ {\vphantom {{(2k - 1)\left( {{\mathbf{v}}_{2}^{2} - {\mathbf{v}}_{1}^{2}} \right)} {2n}}} \right. \kern-0em} {2n}} = {{{\mathbf{V}}}_{2}} + {{(2k - 1)({{{\mathbf{V}}}_{1}} - {{{\mathbf{V}}}_{2}})} \mathord{\left/ {\vphantom {{(2k - 1)({{{\mathbf{V}}}_{1}} - {{{\mathbf{V}}}_{2}})} {2n}}} \right. \kern-0em} {2n}}.$Несмотря на то, что с точки зрения математики значения ${\mathbf{c}}_{i}^{1}$ и ${\mathbf{c}}_{{n - i + 1}}^{2}$ тождественно равны, при расчетах на ЭВМ их значения зачастую различаются из-за различной последовательности вычислений и присутствия ошибок округления.
Для того чтобы обеспечить точное совпадение точек (а, следовательно, иметь возможность устранить возникшую особенность) предлагается использовать следующие выражения, получаемые из (5) и (6):
(7)
${\mathbf{c}}_{i}^{1} = {{\left[ {\left( {2n - 2i + 1} \right){{{\mathbf{V}}}_{1}} + \left( {2i - 1} \right){{{\mathbf{V}}}_{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {2n - 2i + 1} \right){{{\mathbf{V}}}_{1}} + \left( {2i - 1} \right){{{\mathbf{V}}}_{2}}} \right]} {2n}}} \right. \kern-0em} {2n}},$(8)
${\mathbf{c}}_{k}^{2} = {{\left[ {\left( {2k - 1} \right){{{\mathbf{V}}}_{1}} + \left( {2n - 2k - 1} \right){{{\mathbf{V}}}_{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {2k - 1} \right){{{\mathbf{V}}}_{1}} + \left( {2n - 2k - 1} \right){{{\mathbf{V}}}_{2}}} \right]} {2n}}} \right. \kern-0em} {2n}}.$При $k = n - i + 1$ формулы (7) и (8) совпадают.
Еще одна выявленная ситуация – при задании геометрии модели вершины “общей стороны” двух многоугольников могут не совпадать, если на это не обратить внимание. Для того чтобы подобная ситуация не возникала, необходимо проводить предварительное отождествление концов отрезков, например, на этапе построения геометрии.
Несмотря на имеющиеся способы устранения указанных особенностей, все же остается проблема, связанная с большими вычислительными погрешностями применительно к некоторым конфигурациям многоугольников, которая обусловлена свойствами подынтегральной функции.
Следует отметить, что, несмотря на наличие формул, позволяющих оценить ошибку вычислений [19], в некоторых конфигурациях полную ошибку предсказать не представляется возможным. Так для интеграла
общая ошибка для формулы среднего n-ой степени может быть записана как где ${{M}_{p}} = \mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {{{u}^{{(p)}}}(x)} \right|.$ В случае интегрирования IS по двум сторонам с общей вершиной значение ${{M}_{2}}$ равно бесконечности. Подобная ситуация возникает при использовании квадратур Гаусса, так как мы имеем следующую оценку ошибки(11)
$\left| {{{R}_{N}}} \right| \leqslant \frac{{{{{\left[ {\left( {N + 1} \right)!} \right]}}^{4}}}}{{\left( {2N + 3} \right){{{\left[ {\left( {2N + 2} \right)!} \right]}}^{3}}}}{{\left( {b - a} \right)}^{{2N + 3}}}{{M}_{{2N + 2}}}.$Таким образом интеграл IS для конфигураций, в которых стороны расположены близко друг к другу, формула (11) дает оценку ошибки, непригодную для практического применения. Плохая сходимость квадратурных формул в данном случае следует из значения остаточного члена ${{R}_{n}}\left( x \right)$ в ряде Тейлора
(12)
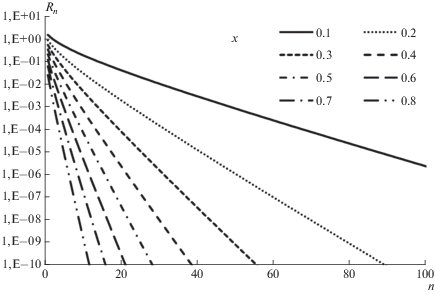
$\ln x = \sum\limits_{k = 1}^n {\frac{{{{{\left( { - 1} \right)}}^{{k + 1}}}{{{\left( {x - 1} \right)}}^{k}}}}{k}} \,\,{\text{ + }}\,\,{{R}_{n}}\left( x \right){\text{,}}\,\,\,\,x \in (0,2].$При $x < 1$ ряд становится знакопостоянным. Зависимость ${{R}_{n}}\left( x \right)$ от количества членов n для разных x представлена на рис. 2.
Видно, что для получения 6 точных цифр после запятой необходимо использовать более 100 членов ряда. Подобная степень квадратурных формул для практических расчетов является неприемлемой.
2. ПОГРЕШНОСТЬ НА ПАРЕ СТОРОН
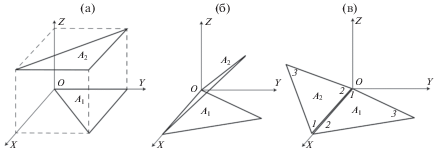
Покажем на примерах насколько широкий диапазон погрешностей может возникать при расчетах угловых коэффициентов контурным интегрированием с использованием квадратурных формул. Рассмотрим несколько конфигураций треугольников (рис. 3) и выполним расчеты угловых коэффициентов по программе CONTVF с использованием различных подынтегральных функций из табл. 1 и квадратурных формул (Гаусса или средних).
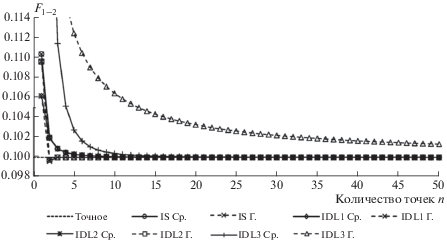
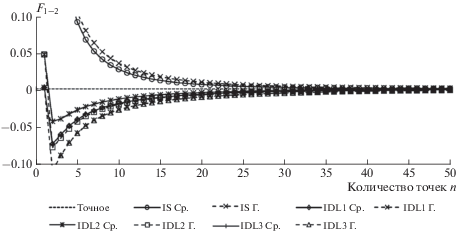
Пример 1. Возьмем два треугольника (рис. 3а) из работы [20] с координатами вершин (0, 0, 0), (1, 1, 0), (0, 1, 0) и (1, 0, 1), (0, 1, 1), (1, 1, 1), для которых точное значение углового коэффициента равно 0.099912. Результаты расчета угловых коэффициентов разными интегралами по квадратурам средних и Гаусса приведены на рис. 4.
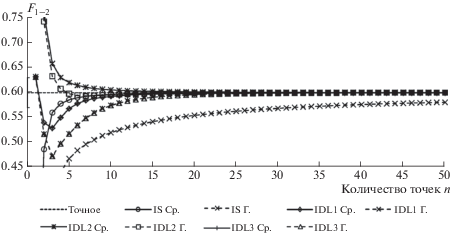
Пример 2. Возьмем два треугольника (рис. 3б) с координатами вершин (0, 0, 0), (1, 0, 0), (0.8, 1, 0) и (1, 0, 0), (0, 0, 0), (0.8, 1, 0). Повернем второй треугольник вокруг первой стороны на угол 45°. Точное значение равно 0.5988134. Результаты расчета угловых коэффициентов разными интегралами по квадратурам средних и Гаусса приведены на рис. 5.
В этих двух примерах получена хорошая сходимость по всем методам за исключением IDL3 с квадратурами Гаусса в примере 1 и IS с квадратурами Гаусса в примере 2, что подтверждает тезис о том, что сходимость интегралов с применением формул Гаусса в ряде случаев оказывается хуже, чем с применением формулы средних.
Пример 3. Возьмем два треугольника (рис. 3в) с координатами вершин (0, 0, 0), (1, 0, 0), (0.8, 1, 0) и (1, 0, 0), (0, 0, 0), (0.8, 1, 0). Повернем второй треугольник вокруг первой стороны на угол $170^\circ $ и переместим по оси OY на расстояние –0.1. Точное значение углового коэффициента равно 0.00248. Результаты расчета угловых коэффициентов разными интегралами по квадратурам средних и Гаусса приведены на рис. 6.
Значения, полученные для IS и IDL1, приведены в табл. 2 . В таблице приняты следующие обозначения: n – степень разбиения сторон; $\Delta F$ – абсолютная погрешность рассчитанного углового коэффициента; δF – относительная погрешность рассчитанного углового коэффициента.
Таблица 2.
Результаты расчета угловых коэффициентов для примера 3
| Квадратурная формула |
Среднего | Гаусса | Среднего | Гаусса | Среднего | Гаусса | Среднего | Гаусса |
|---|---|---|---|---|---|---|---|---|
| n | 4 | 4 | 10 | 10 | 25 | 25 | 50 | 50 |
| Решение с применением интеграла IS | ||||||||
| ${{F}_{{1 - 2}}}$ | 0.13262 | 0.14352 | 0.02883 | 0.03713 | 0.00583 | 0.00797 | 0.00286 | 0.00327 |
| ΔF | 0.13014 | 0.14104 | 0.02635 | 0.03465 | 0.00335 | 0.00549 | 0.00038 | 0.00079 |
| δF | 5247% | 5686% | 1062% | 1397% | 135% | 221% | 15% | 32% |
| Решение с применением интеграла IDL1 | ||||||||
| ${{F}_{{1 - 2}}}$ | –0.04773 | –0.07053 | –0.01719 | –0.02591 | –0.00231 | –0.00528 | 0.00247 | 0.00061 |
| ΔF | –0.05022 | –0.07301 | –0.01968 | –0.02839 | –0.00479 | –0.00776 | –0.00001 | –0.00187 |
| δF | –2024% | –2944% | –793% | –1144% | –193% | –313% | –0.58% | –75.5% |
Можно заметить неудовлетворительные результаты по всем вариантам расчетов с использованием квадратурных формул. Данный пример показывает, что вывод, приведенный в работе [20], о достаточности применения 10-точечных квадратур Гаусса не подтверждается. Проблема заключается в том, что на паре сторон 1–1 из-за их близости возникает большая погрешность расчетов, которая и является определяющей.
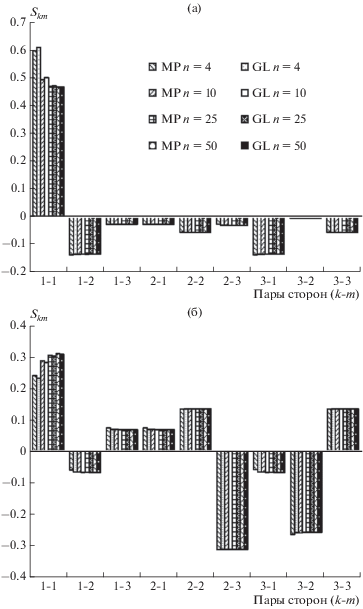
Характерной чертой контурного интегрирования является то, что ряд, получаемый в процессе вычисления значения контурного интеграла по квадратурным формулам, в отличие от двойного интегрирования по площадям, не является монотонно неубывающей функцией. Результаты вычисления интегралов на парах сторон (рис. 7) показывают, что значения отдельных слагаемых могут быть как положительными, так и отрицательными с абсолютными значениями, на порядки превышающими конечный результат.
Абсолютные ошибки расчета угловых коэффициентов не превышают суммы абсолютных ошибок на парах сторон
(13)
$\Delta F \leqslant \frac{1}{{2\pi {{A}_{I}}}}\sum\limits_{k = 1}^{{{K}_{I}}} {\sum\limits_{m = 1}^{{{K}_{J}}} {\left| {{{\Delta }_{{km}}}} \right|} } .$Значения ошибок по парам сторон представлены в табл. 3. В качестве точного значения для IS принимались расчеты по формулам [14], для IDL1 в качестве оценки точного решения взято значение интеграла при n = 4000.
Таблица 3.
Абсолютные ошибки на парах сторон
| Пара сторон |
Квадратурные формулы | |||||||
|---|---|---|---|---|---|---|---|---|
| среднего n = 4 |
Гаусса n = 4 |
среднего n = 10 |
Гаусса n = 10 |
среднего n = 25 |
Гаусса n = 25 |
среднего n = 50 |
Гаусса n = 50 |
|
| Решение с применением интеграла IS | ||||||||
| 1 1 | 0.13077588 | 0.14248197 | 0.02647416 | 0.03466102 | 0.00336609 | 0.00549116 | 0.00038257 | 0.00079022 |
| 1 2 | –0.00309524 | –0.00070398 | –0.00057654 | –0.00000508 | –0.00009918 | 0.00000000 | –0.00002521 | –0.00000001 |
| 1 3 | –0.00015264 | –0.00008585 | –0.00003429 | –0.00000115 | –0.00000674 | 0.00000000 | –0.00000180 | 0.00000000 |
| 2 1 | –0.00015246 | –0.00008553 | –0.00003417 | –0.00000112 | –0.00000669 | 0.00000000 | –0.00000177 | 0.00000000 |
| 2 2 | 0.00087537 | –0.00000074 | 0.00013996 | 0.00000002 | 0.00002240 | 0.00000002 | 0.00000561 | 0.00000002 |
| 2 3 | 0.00364358 | 0.00017923 | 0.00073233 | 0.00000151 | 0.00013352 | 0.00000000 | 0.00003505 | 0.00000000 |
| 3 1 | –0.00309127 | –0.00070055 | –0.00057511 | –0.00000490 | –0.00009878 | 0.00000001 | –0.00002509 | 0.00000000 |
| 3 2 | 0.00046091 | –0.00004703 | 0.00008278 | –0.00000119 | 0.00001381 | –0.00000000 | 0.00000345 | 0.00000000 |
| 3 3 | 0.00087553 | –0.00000078 | 0.00013995 | –0.00000003 | 0.00002237 | –0.00000003 | 0.00000557 | –0.00000003 |
| Решение с применением интеграла IDL1 | ||||||||
| 1 1 | –0.07016388 | –0.07748990 | –0.02298190 | –0.02840219 | –0.00530472 | –0.00775526 | –0.00004344 | –0.00187373 |
| 1 2 | 0.00825070 | 0.00177381 | 0.00138225 | 0.00000319 | 0.00021805 | –0.00000016 | 0.00001317 | –0.00000001 |
| 1 3 | 0.00597063 | 0.00096532 | 0.00111721 | 0.00000943 | 0.00019189 | –0.00000000 | 0.00001186 | –0.00000001 |
| 2 1 | 0.00596527 | 0.00096216 | 0.00111541 | 0.00000919 | 0.00019141 | –0.00000000 | 0.00001183 | –0.00000001 |
| 2 2 | –0.00052577 | –0.00000486 | –0.00008491 | 0.00000000 | –0.00001361 | 0.00000000 | –0.00000085 | 0.00000000 |
| 2 3 | –0.00054668 | –0.00007355 | –0.00012180 | –0.00000112 | –0.00002369 | –0.00000000 | –0.00000167 | 0.00000000 |
| 3 1 | 0.00824159 | 0.00176574 | 0.00137980 | 0.00000264 | 0.00021760 | –0.00000016 | 0.00001315 | –0.00000001 |
| 3 2 | –0.00688273 | –0.00090465 | –0.00139650 | –0.00001504 | –0.00025774 | 0.00000001 | –0.00001747 | 0.00000001 |
| 3 3 | –0.00052569 | –0.00000487 | –0.00008490 | 0.00000000 | –0.00001360 | 0.00000000 | –0.00000085 | 0.00000000 |
Видно, что в примере 3 основной вклад в суммарную погрешность вносит пара 1–1, поэтому точность расчетов может быть существенно повышена, если на паре сторон 1–1 использовать точное аналитическое значение. В табл. 4 приводятся значения ${{F}_{{1 - 2}}},$ ΔF и δF, посчитанные при известном точном значении интеграла на паре сторон 1–1.
Таблица 4.
Результаты расчета угловых коэффициентов для примера 3 с использованием точного значения на паре сторон 1–1
| Квадратурная формула |
Среднего | Гаусса | Среднего | Гаусса | Среднего | Гаусса | Среднего | Гаусса |
|---|---|---|---|---|---|---|---|---|
| n | 4 | 4 | 10 | 10 | 25 | 25 | 50 | 50 |
| Решение с применением интеграла IS | ||||||||
| ${{F}_{{1 - 2}}}$ | 0.00184 | 0.00104 | 0.00236 | 0.00247 | 0.00246 | 0.00248 | 0.00247 | 0.00248 |
| ΔF | –0.00067 | –0.00145 | –0.00012 | –0.00001 | –0.00002 | 0.00000 | –0.00001 | –0.00000 |
| δF | –25.65% | –58.27% | –5.04% | –0.48% | –0.78% | 0.00% | –0.17% | 0.00% |
| Решение с применением интеграла IDL1 | ||||||||
| ${{F}_{{1 - 2}}}$ | 0.02243 | 0.00696 | 0.00579 | 0.00249 | 0.00299 | 0.00248 | 0.00251 | 0.00248 |
| ΔF | 0.01995 | 0.00448 | 0.00331 | 0.00001 | 0.00051 | 0.00000 | 0.00003 | 0.00000 |
| δF | 804.2% | 180.6% | 133.3% | 0.3% | 20.6% | 0.0% | 1.2% | 0.0% |
Видно, что использование точного решения только на одной паре сторон (из девяти) привело к значительному уменьшению погрешности.
Следует отметить, что погрешности на разных парах сторон имеют разные знаки и могут компенсироваться. Так, при использовании квадратурной формулы средних с n = 4 сумма абсолютных погрешностей равна 0.01235, т.е. практически составляет 500%! Тем не менее расчетное значение имеет погрешность менее 26%. Для IDL1 при использовании квадратурной формулы средних с n = 25 сумма абсолютных погрешностей равна 0.00113, т.е. 45%, расчетное значение имеет погрешность 20.6%. Уменьшение ошибки только на некоторых парах сторон может привести к росту полной ошибки, поэтому необходимо на каждой паре сторон двух многоугольников проводить вычисления одним и тем же видом интеграла, но с применением различных квадратурных формул и степеней разбиений сторон вплоть до применения точного аналитического решения.
3. КОМБИНИРОВАННЫЙ АЛГОРИТМ
Исходя из особенностей численного интегрирования и невозможности заранее предсказать величины погрешностей без выполнения громоздких вычислений, для получения результата с заданной точностью предлагается алгоритм, реализующий комбинированный метод, сочетающий интегрирование по квадратурным формулам Гаусса невысокого порядка с точным аналитическим решением. Комбинированный алгоритм заключается в следующем
Алгоритм 2. Расчет УК между многоугольниками комбинированным методом
| А.1 | $S \leftarrow 0$ |
| А.2 | for$k \leftarrow 1,{{K}_{I}}$do !Начало цикла по сторонам многоугольника I |
| А.3 | for$m \leftarrow 1,{{K}_{J}}$do !Начало цикла по сторонам многоугольника J |
| А.4 | ${{S}_{{km}}} \leftarrow 0$ |
| А.5 | $n1 \leftarrow {{n}_{k}}$ |
| А.6 | $n2 \leftarrow {{n}_{m}}$ |
| А.7 | if$СтороныНаОднойПрямой$then |
| А.8 | ${{S}_{{km}}} \leftarrow АналитическоеРешение(k,m)$ |
| А.9 | else |
| А.10 | Построение сетки на стороне ${{L}_{k}}$ |
| А.11 | Построение сетки на стороне ${{L}_{m}}$ |
| А.12 | for$i \leftarrow 1,n1$do !Цикл по узловым точкам на стороне ${{L}_{k}}$ |
| А.13 | for$j \leftarrow 1,n2$do !Цикл по узловым точкам на стороне ${{L}_{m}}$ |
| А.14 | if${{{\mathbf{c}}}_{i}} = = {{{\mathbf{c}}}_{j}}$then |
| А.15 | ${{S}_{{km}}} \leftarrow АналитическоеРешение(k,m)$ |
| А.16 | go to А.30 |
| А.17 | else |
| А.18 | ${{S}_{{km}}} \leftarrow {{S}_{{km}}} + {{g}_{i}}{{g}_{j}}\ln \left| {{{{\mathbf{r}}}_{{i - j}}}} \right|{{{\mathbf{\hat {c}}}}_{i}} \cdot {{{\mathbf{\hat {c}}}}_{j}}$ |
| А.19 | end if |
| А.20 | end for |
| А.21 | end for |
| А.22 | if${{n}_{m}} = = n1$then !Первый проход? |
| А.23 | $n1 \leftarrow n1 + 1$ |
| А.24 | $n2 \leftarrow n2 + 1$ |
| А.25 | $St \leftarrow {{S}_{{km}}}$ |
| А.26 | go to А.10 |
| А.27 | else if$\left| {St - {{S}_{{km}}}} \right| > {{2\pi {{A}_{I}}{{\alpha }_{{{\text{err}}}}}} \mathord{\left/ {\vphantom {{2\pi {{A}_{I}}{{\alpha }_{{{\text{err}}}}}} {{{K}_{I}}{{K}_{J}}}}} \right. \kern-0em} {{{K}_{I}}{{K}_{J}}}}$then |
| А.28 | ${{S}_{{km}}} \leftarrow АналитическоеРешение(k,m)$ |
| А.29 | end if |
| А.30 | $S \leftarrow S + {{S}_{{km}}}$ |
| А.31 | end if |
| А.32 | end for |
| А.33 | end for |
| А.34 | ${{F}_{{I - J}}} = {S \mathord{\left/ {\vphantom {S {2\pi {{A}_{I}}}}} \right. \kern-0em} {2\pi {{A}_{I}}}}$ |
Для комбинированного алгоритма выбран интеграл IS, так как для него имеется точное аналитическое решение для многоугольников. Тогда для пары сторон имеем интегральную сумму
(14)
$S_{{km}}^{{({{n}_{k}},{{n}_{m}})}} = \sum\limits_{i = 1}^{{{n}_{k}}} {\sum\limits_{j = 1}^{{{n}_{m}}} {{{g}_{i}}{{g}_{j}}\ln \left| {{{{\mathbf{r}}}_{{i - j}}}} \right|{{{{\mathbf{\hat {c}}}}}_{i}} \cdot {{{{\mathbf{\hat {c}}}}}_{j}}} } ,$Суть комбинированного алгоритма заключается в том, что интеграл на паре сторон рассчитывается по аналитическим формулам только при выполнении одного из условий:
– стороны лежат на одной прямой (может определяться предварительно на этапе построения геометрии);
– в ходе вычислений $S_{{km}}^{{({{n}_{k}},{{n}_{m}})}}$ или $S_{{km}}^{{({{n}_{k}} + 1,{{n}_{m}} + 1)}}$ обнаружено совпадение узловых точек;
– разница между вычислениями по квадратурным формулам для последовательных степеней разбиения сторон превышает заданную погрешность
(15)
$\left| {S_{{km}}^{{({{n}_{k}} + 1,{{n}_{m}} + 1)}} - S_{{km}}^{{({{n}_{k}},{{n}_{m}})}}} \right| > {{2\pi {{A}_{I}}{{\alpha }_{{{\text{err}}}}}} \mathord{\left/ {\vphantom {{2\pi {{A}_{I}}{{\alpha }_{{{\text{err}}}}}} {{{K}_{I}}{{K}_{J}}}}} \right. \kern-0em} {{{K}_{I}}{{K}_{J}}}}.$В остальных случаях в качестве значения интеграла на паре сторон берется $S_{{km}}^{{({{n}_{k}} + 1,{{n}_{m}} + 1)}}.$
После проведения многочисленных численных экспериментов мы рекомендуем использовать ${{n}_{k}} = {{n}_{m}} = 4.$
4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ
Для сравнения расчетных методов контурного интегрирования УК в части точности и быстродействия проведем несколько численных экспериментов. Для этого рассмотрим модель, представляющую внутреннюю поверхность сферы единичного радиуса, разбитую на 96 плоских многоугольников: 24 треугольника и 72 четырехугольника. Данная модель позволяет изучить поведение вычислительных алгоритмов в широком диапазоне взаимного расположения площадок и пар отрезков, возникающих при интегрировании.
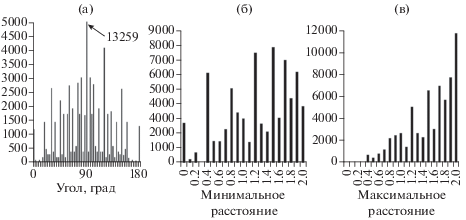
На рис. 8 представлено частотное распределение пар отрезков по углу между ними (а), а также минимальному (б) и максимальному (в) расстояниям между концами отрезков.
Рис. 8.
Распределение пар отрезков: (а) по углу; (б) по минимальному расстоянию; (в) по максимальному расстоянию.
Кроме того, в данной модели присутствует неточность – при построении сферы использовался алгоритм, приведший к тому, что координаты “совпадающих” вершин 1-й и 12-й площадок не совпадают. Одна из координат оказалась равной 0.33141357403559185 и 0.33141357403559174 (различающиеся цифры выделены курсивом).
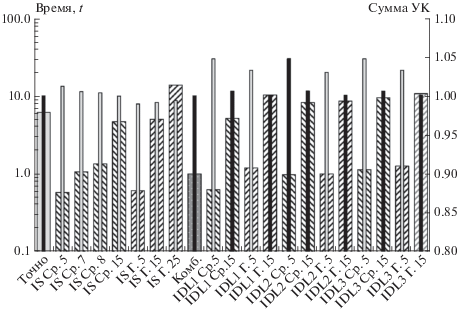
Проведены расчеты угловых коэффициентов по вариантам, различающимся используемыми алгоритмами, квадратурными формулами и степенью разбиения (количеством точек на стороне). Полученные результаты приведены на рис. 9. Тонким столбцам соответствует сумма значений угловых коэффициентов первой площадки с остальными площадками сферы. При этом отрицательные значения, которые получались в некоторых расчетных случаях, при суммировании не учитывались, как не имеющие физического смысла. Случаи, в которых были получены отрицательные угловые коэффициенты, отмечены розовым цветом, случаи, где все угловые коэффициенты положительные – красным.
Теоретическое значение суммы угловых коэффициентов для каждой площадки равно единице. Отклонение суммы угловых коэффициентов, полученных в конкретном расчетном случае для первой площадки, от единицы может служить оценкой точности данного алгоритма при заданном количестве точек на стороне.
Широкими столбцами показано относительное время счета t всех угловых коэффициентов модели в разных расчетных случаях по отношению ко времени счета по комбинированному алгоритму. Данное исследование проводилось на компьютерном коде без каких-либо оптимизаций для того, чтобы результаты не зависели от того, как компилятор осуществляет оптимизацию. Проведенное сравнение, тем не менее, позволяет сделать качественные выводы о предпочтительности применения алгоритмов.
Видно, что быстрее комбинированного алгоритма угловые коэффициенты рассчитываются только по квадратурным методам с пятью точками на стороне, при этом погрешности расчета составляют более 1%. Приемлемая точность порядка 0.1% достигается при n = 15 для IS по формуле средних (присутствуют отрицательные угловые коэффициенты) и для всех IDL по формуле Гаусса. При этом время счета по указанным алгоритмам примерно в 10 раз больше, чем время счета комбинированного алгоритма и сопоставимо со временем счета точного аналитического решения.
Количество отрицательных угловых коэффициентов между площадкой 1 и другими площадками модели по расчетным вариантам приведено в табл. 5.
Таблица 5.
Количество отрицательных угловых коэффициентов
| Расчетный вариант |
Точно | IS Ср. 5 | IS Ср. 7 | IS Ср. 8 | IS Ср. 15 | IS Г. 5 | IS Г. 15 | IS Г. 25 | Комб. | IDL1 Ср. 5 | IDL1 Ср. 15 | IDL1 Г. 5 | IDL1 Г. 15 | IDL2 D 5 | IDL2 D 15 | IDL2 Г. 5 | IDL2 Г. 15 | IDL3 D 5 | IDL3 D 15 | IDL3 Г. 5 | IDL3 Г. 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Количество отрицательных значений |
– | 3 | 2 | 2 | 2 | 3 | 2 | 2 | – | 3 | – | 2 | – | – | – | 2 | – | 3 | – | 2 | – |
Результаты для случаев, в которых получены отрицательные значения угловых коэффициентов, не могут считаться удовлетворительными.
Предложенный автором комбинированный метод показал высокую точность при достаточно малом времени счета.
5. ВЫВОДЫ
Проведенное исследование показывает, что на некоторых конфигурациях многоугольников применение квадратурных методов не позволяет получить значения угловых коэффициентов с требуемой точностью. При этом сходимость интегралов с применением формулы Гаусса в ряде случаев оказывается хуже, чем с применением формулы средних. Использование же имеющихся точных аналитических формул для произвольных многоугольников достаточно ресурсоемко.
Для получения значения углового коэффициента с заданной точностью предложен алгоритм, реализующий комбинированный метод, сочетающий интегрирование по квадратурным формулам Гаусса невысокого порядка с точным аналитическим решением. По результатам численного эксперимента предложенный метод показал высокую точность при достаточно малом времени счета по сравнению с другими методами контурного интегрирования.
Предложенный алгоритм позволяет производить расчеты угловых коэффициентов с заданной точностью для любых конфигураций многоугольников.
Список литературы
Басов А.А., Елчин А.П. Отработка на борту международной космической станции перспективных технических решений по обеспечению теплового режима космических аппаратов // Космонавтика и ракетостроение. 2018. № 4(103) С. 61–71.
Клочкова М.А. Проектирование системы обеспечения теплового режима узлового модуля Международной космической станции // Космонавтика и ракетостроение. 2013. № 1(70). С. 46–50.
Залетаев С.В., Румынский Н.А., Басов А.А., Клочкова М.А., Федорук Г.Д. Применение обобщенной характеристики лучистого взаимодействия двух тел для оценки температурного влияния термобарокамеры на космический аппарат при проведении тепловакуумных испытаний // Тепловые процессы в технике. 2020. № 6. Т. 12. С. 282–288.
Финченко В.С., Котляров Е.Ю., Иванков А.А. Системы обеспечения тепловых режимов межпланетных станций. Химки: АО “НПО С.А. Лавочкина”, 2018. 400 с.
Блох А.Г. Теплообмен излучением: Справочник / Блох А.Г., Журавлев Ю.А., Рыжков Л.Н. М.: Энергоатомиздат, 1991. 432 с.: ил. – ISBN 5-283-00118-0.
Howell J.R. Thermal radiation heat transfer / John R.Howell, M. Pinar Mengüç, Kyle Daun, Robert Siegel.– 7th ed. – Boca Raton: CRC press, 2021. – 1006, [34] p. – ISBN 978-0-367-34707-9.
Modest M. Radiative Heat Transfer / Michael F. Modest. – 3rd ed. – N.Y.; San Francisco; London: Elsevier Science, 2013. 882, [22] p. – ISBN: 978-0-12-386944-9.
Винокуров Д.К. Классификация методов расчета диффузных угловых коэффициентов излучения // Математическое моделирование. 2019. Т. 31. № 12. С. 57–70. https://doi.org/10.1134/S0234087919120050
Фок В.А. Избранные труды. СПб.: Изд-во С.-Петербургского университета, 2003. 488 с.
DiLaura D.L., Santoro S. Nondiffuse Radiative Transfer 4: General Procedure for Planar Area Sources and Area Receivers // J. Illuminating Engineering Society. 1997. V. 26:1. P. 188–200. https://doi.org/10.1080/00994480.1997.10748179
Sparrow E.M. A New and Simpler Formulation for Radiative Angle Factors // ASME J. Heat Transfer. 1963. V. 85. Iss. 2. P. 81–88. https://doi.org/10.1115/1.3686058
Herman R.A. A Treatise on Geometrical Optics. London: C.J.Clay and Sons, Cambridge University Press Warehouse, 1900. P. 344+[10].
Калиткин Н.Н., Альшина Е.А. Численные методы: в 2 кн. Кн. 1. Численный анализ. М.: Издательский центр “Академия”, 2013. 304 с.
Schröder P., Hanrahan P. On the form factor between two polygons // Proceedings of the 20th annual conference on Computer graphics and interactive techniques (SIGGRAPH '93). – ACM, N.Y., NY, USA, 1993. P. 163–164. https://doi.org/10.1145/166117.166138
Narayanaswamy A. An analytic expression for radiation view factor between two arbitrarily oriented planar polygons // International J. Heat and Mass Transfer. 2015. V. 91. P. 841–847. https://doi.org/10.1016/j.ijheatmasstransfer.2015.07.131
Glass M.W. CHAPARRAL: A Library for Solving Large Enclosure Radiaton Heat Transfer Problems. – Sandia National Laboratories.Technical Report SAND95-2049, Albuquerque, New Mexico. 1995. https://doi.org/10.2172/120875
Винокуров Д.К. Методы контурного интегрирования угловых коэффициентов излучения – CONTVF.. – Св-во о гос. регистр. программы для ЭВМ № 2018663500 29.10.2018.
Винокуров Д.К. Особенности определения углового коэффициента излучения между многоугольниками контурным интегрированием // Космонавтика и ракетостроение. 2019. № 4(109). С. 36–47.
Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высш. шк., 1994. 554 с.
Mazumder S., Ravishankar M. General Procedure for Calculation of Diffuse View Factors Between Arbitrary Planar Polygons // International J. Heat and Mass Transfer. 2012. V. 55(23–24). P. 7330–7335. https://doi.org/10.1016/j.ijheatmasstransfer.2012.07.066
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика